Pretomanid dose selection for pulmonary tuberculosis: An application of multi‐objective optimization to dosage regimen design

Abstract

Clinical development of combination chemotherapies for tuberculosis (TB) is complicated by partial or restricted phase II dose‐finding. Barriers include a propensity for drug resistance with monotherapy, practical limits on numbers of treatment arms for component dose combinations, and limited application of current dose selection methods to multidrug regimens. A multi‐objective optimization approach to dose selection was developed as a conceptual and computational framework for currently evolving approaches to clinical testing of novel TB regimens. Pharmacokinetic‐pharmacodynamic (PK‐PD) modeling was combined with an evolutionary algorithm to identify dosage regimens that yield optimal trade‐offs between multiple conflicting therapeutic objectives. The phase IIa studies for pretomanid, a newly approved nitroimidazole for specific cases of highly drug‐resistant pulmonary TB, were used to demonstrate the approach with Pareto optimized dosing that best minimized sputum bacillary load and the probability of drug‐related adverse events. Results include a population‐typical characterization of the recommended 200 mg once daily dosage, the optimality of time‐dependent dosing, examples of individualized therapy, and the determination of optimal loading doses. The approach generalizes conventional PK‐PD target attainment to a design problem that scales to drug combinations, and provides a benefit‐risk context for clinical testing of complex drug regimens.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Dose selection for tuberculosis (TB) drugs is based on pharmacokinetic‐pharmacodynamic target attainment, with limited application to codevelopment of regimens that contain three or more drugs.

• WHAT QUESTION DID THIS STUDY ADDRESS?

How can multi‐objective optimization be applied to clinical trial data as an alternate method of dose selection for TB drug regimen development?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

A demonstration of a general method of model‐based analysis for dosage regimen design applied to an example of early phase clinical trial data for the recently approved nitroimidazole pretomanid. The results support the recommended dosage, but expand the context, and extend the clinical trial data to identification of more complex dosage regimens.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

The approach provides a computational benefit‐risk tool for dosage regimen design problems that are not currently addressed in the context of clinical trial transitions for codevelopment, and which may improve the chances of pivotal phase III trial success for novel TB regimens.

INTRODUCTION

The current treatment of pulmonary tuberculosis (TB) requires combination chemotherapy with 3 or more drugs and duration of at least 6 months. ¹ Although TB (caused by Mycobacterium tuberculosis) is curable, there are concerted efforts to shorten and simplify the four‐drug standard regimen and to better treat drug‐resistant disease. ² Conventional regimen development is a process of sequential addition or replacement of single new drugs in an existing combination, with each drug included at previously determined doses. ³ , ⁴ , ⁵ Codevelopment is intended to accelerate this process with regulatory pathways for novel drug combinations that are analogous to those for single drugs. ⁶ However, phase II dose‐finding for TB drugs in a regimen is constrained by a 14‐day maximum on phase IIa monotherapy studies to minimize drug resistance, and by practical limits on numbers of treatment arms to identify component drug doses that may optimize the regimen as a whole. ⁷ Although a combination regimen is the therapeutic unit for TB, the current approaches to regimen development are based on potentially suboptimal single‐drug doses, which may lessen the chances of successful outcomes for pivotal phase III trials. An approach to dose selection aimed at the component drugs in a regimen would more closely implement the “drug combination as unit of development” concept. ⁸

Dose optimization for TB drugs is based on antimicrobial pharmacokinetic‐pharmacodynamic (PK‐PD) target attainment. ⁹ , ¹⁰ Target drug exposures are specified from the minimum inhibitory concentration (MIC) and exposure‐efficacy profiles determined from measurements of bacterial load and MIC‐normalized PK parameters in nonclinical systems. ¹¹ Refinement of the efficacy target may be obtained as a therapeutic window around the maximum of a clinical utility function, which is a composite of weighted exposure‐efficacy and exposure‐toxicity profiles. ¹² Monte–Carlo (MC) simulations of a population PK model are then used to calculate the probability of target attainment (PTA) as the fraction of simulated patients that meet the target exposure for specified doses, with optimal values identified in a trial and error manner with reference to a desired performance. Although PTA‐based dose selection provides a rational approach for transition of single drugs from phase I to phase IIa testing, ¹³ its extension to a TB regimen entering phase IIb or phase III is limited by uncertainties in identification of the efficacy targets, ¹⁴ in the assignment of weighting factors to treatment outcomes, ¹⁵ and in the generation and interpretation of multidimensional dose‐response output of PK‐PD model simulations. ¹⁶ , ¹⁷

An alternate approach to dose selection based on multi‐objective optimization ¹⁸ , ¹⁹ , ²⁰ is considered here for application across clinical trial transitions for TB regimen development. Dose selection involves conflicting therapeutic objectives for safety and efficacy, and value judgments on their relative importance. ²¹ Clinical utility combines these elements through value judgments on the weighting factors, which become part of the optimal solution. Multi‐objective optimization treats the objectives separately with trade‐off comparisons between outcomes, with the best trade‐offs (or Pareto optimal solutions) defined as those for which further improvement in one objective becomes a detriment to another. Instead of a single optimum value, the results are a set of equally permissible trade‐off optimal solutions with a final selection made by application of the value judgments after, rather than before, the optimization process. Additionally, in contrast to the forward approach of PTA methods where specified input doses are evaluated against the computed outcomes, multi‐objective optimization operates as an inverse method where the desired treatment outcome is the specified input, and the corresponding dosage parameters are determined as the optimization output. This casts dose selection as a design problem, and provides for identification of complex dosage regimens using a standard engineering process of modeling, optimization, and decision making. ²²

In the present study, Pareto optimal dosage regimens were determined for pretomanid monotherapy as part of a model‐based analysis of the phase IIa early bactericidal activity (EBA) studies PA‐824‐CL‐007 (CL‐007) ²³ and PA‐824‐CL‐010 (CL‐010). ²⁴ Pretomanid is a recently approved nitroimidazole for limited and specific use in combination with bedaquiline and linezolid to treat highly drug‐resistant pulmonary TB, ²⁵ but for which further clinical testing remains. ³ A pretomanid dose‐response model was evaluated using an evolutionary algorithm (EA) to determine safety‐ and efficacy‐optimized dosage regimens under several different design criteria. Examples included optimized regimens for fixed and variable dosing intervals, the identification of loading doses, and benefit‐risk stratified regimens from which final choices can be made based on external clinical judgment and the context of subsequent clinical trial aims.

METHODS

Pretomanid EBA study data

The PA‐824‐CL‐007 (CL‐007, ClinicalTrials.gov identifier NCT00567840) and PA‐824‐CL‐010 (CL‐010, ClinicalTrials.gov identifier NCT00944021) study data were obtained from the TB‐Platform Aggregation of Clinical TB Studies (TB‐PACTS; https://c‐path.org/programs/tb‐pacts). There were 122 adult participants (63 men and 59 women) with newly diagnosed pulmonary TB who received 14 days of once‐daily oral pretomanid in separate dose groups of 50, 100, 150, or 200 mg in CL‐010, and 200, 600, 1000, or 1200 mg in CL‐007. Data used for dose‐response modeling included plasma drug concentrations, sputum solid culture colony forming unit (CFU) counts, and treatment emergent adverse event counts. Detailed descriptions of the study design, patient characteristics, and clinical outcomes from both studies are available in their respective publications. ²³ , ²⁴

Multi‐objective optimization

A standard formulation of multi‐objective optimization ²² was used for dosage regimen design, with one or more design (or decision) variables, two or more objective functions, and a problem statement of the form:

Minimize: $f\left(x\right)=\left(f_1,\left(x\right),,,f_2,\left(x\right),,,.,.,.,,,f_k,\left(x\right)\right),$

Subject to: $x=\left(x_1,,,.,.,.,,,x_n\right)\in S$

Here, $x$ is a design variable vector, or solution, with values in a feasible region, $S\subset R^n$, that includes bounds and constraint functions on the design variables. The $f_i\left(x\right):S\to R$ are the objective functions. For each solution, x, these functions define a point $z=f\left(x\right)=\left(f_1,\left(x\right),,,.,.,.,,,f_k,\left(x\right)\right)$ in an objective space $Z\subset R^k$. A decision vector $x^{\ast }\in S$ is Pareto optimal if it is no worse than another in all objectives, and strictly better in at least one (i.e., there does not exist another $x\in S$ such that $f_i\left(x\right)\le f_i\left(x^{\ast }\right)$ for all $i=1,...,k$ and $f_j\left(x\right)<f_j\left(x^{\ast }\right)$ for at least one index value j). The Pareto optimal points in objective space are termed the Pareto front, and the corresponding decision vectors are termed the Pareto optimal solutions or the Pareto set.

The dosage regimen design vector was defined as $x=\left(D_{1,},{\nu }_{1,},D_{2,},{\nu }_{2,},t_{\varphi }\right)$, where $D_{1,}{D}_2$ are different doses (loading and maintenance doses, respectively), constrained by $D_1>D_2$, with ${\nu }_1,{\nu }_2$ the corresponding frequencies of administration, and $t_{\varphi }$ the transition time from the first to second dose. The dose‐response model equations were used to define the objective vector, $f\left(x\right)$ = (−EBA[CFU], Pr[AE]), where EBA(CFU) is the early bactericidal activity assessed by the decrease of log₁₀ CFU per milliliter sputum per day, and Pr(AE) is the probability of a drug‐related adverse event (AE).

Software

The operating system was Linux (version 3.16.0‐4‐amd64; Debian distribution [https:// www.debian.org]). NSGA‐II ²⁶ (version 1.1.6; [https://www.iitk.ac.in/kangal/codes.shtml]) was used for Pareto optimization. The GNU MCSim Modeling and Simulation Suite ²⁷ (version 5.6.5; [http://www.gnu.org/software/mcsim]) was used for numerical evaluation of the dose‐response model equations. The R statistical software (version 3.3.3; R Development Team, [https://www.R‐project.org]) was used for statistical analysis, including apcluster (version 1.4.8; [http://www.bioinf.jku.at/software/apcluster/]) for cluster analysis.

RESULTS

Modeling, optimization, and dose selection

The pretomanid dose‐response model was based on the plasma drug concentrations, sputum CFU counts, and drug‐related AE counts observed in the CL‐007 and CL‐010 studies. ²³ , ²⁴ The dose‐efficacy relationship was described previously as a population PK‐PD model that included sputum CFU kinetics as a function of plasma concentration, with the latter being a function of time and the dosage. ²⁸ , ²⁹ The model included PK‐PD parameter sets for the study population, the male and female subpopulations, and for the individual participants. The dose‐safety relationship was modeled as a pretomanid concentration‐dependent probability of a drug‐related AE; $\text{Pr( AE )}=exp\left(\alpha ,+,\mathrm{\beta },·,\overline{C}\right)/\left[1,+,e,x,p,\left(\alpha ,+,\mathrm{\beta },·,\overline{C}\right)\right]$. The location (α = −3.49) and scale (β = 0.263 ml/μg) parameters were determined by a least‐squares fit to the observed relative frequencies of drug‐related AE counts for each dose group, and corresponding 14‐day average plasma concentrations, $\overline{C}$, obtained from PK model simulations for population‐typical parameter values. The full system of dose‐response equations, representative PK‐PD parameter sets, and AE analysis details are provided in the Supplementary Materials.

Dose optimization was formulated as a multi‐objective optimization problem with design variables and objective functions defined by the dose‐response model. The design variables were the discrete oral doses, their corresponding frequencies of administration, and the duration of administration for a loading dose. The values for each variable were the complete set of integers within specified lower and upper bounds. The doses were bounded by 50–1200 mg as the experimentally measured range; the frequencies of administration by 6–72 h, with the lower bound providing for attainment of peak concentration, and upper bound for a washout period of ~ 4 times the elimination half‐life ²⁸ , ³⁰ ; and the time of transition from a loading dose to maintenance dose by 1–13 days as the earliest and latest values for a 14‐day study. The objective function for safety was the Pr(AE), and for efficacy the EBA(CFU). The optimization problem was to maximize the EBA(CFU) and minimize Pr(AE) from the beginning to the end of treatment (24 h after the 14th dose) subject to the bounds and design conditions on the dosage regimen parameters.

Pareto optimal solutions were found using an EA, ²² with the basic operations of random sampling from a population of values for the design variables, comparison and selection of the corresponding objective function outputs that best satisfy the optimization criteria, and regeneration of the design space population through a random process of mutation and crossover operations. Each of these generations is repeated until adequate convergence of the Pareto front is attained. The optimization was implemented using NSGA‐II ²⁶ with parameter values: population sample size equal to 400, number of generations equal to 50, crossover probability equal to 0.9 with distribution index equal to 15, and probability of mutation equal to 0.3 with distribution index equal to 30. The NSGA‐II problem definition and MCSim model files are provided in the Supplementary Materials.

Final dose selection from the Pareto optimal solutions requires external evaluation criteria, such as threshold values for EBA(CFU) and Pr(AE). A partial unsupervised reduction of Pareto optimal dosages was made using a clustering algorithm, ³¹ and by benefit‐risk (BR) ratios of normalized EBA to Pr(AE), where the maximum EBA value was the normalization constant. The number of clusters was set manually to four or five as typical numbers of treatment arms for early phase TB studies, ²³ , ³² and dosage regimens for maximum BR values were identified. The maximum BR values were also reported as a mean (SD) from an additional 15 Pareto fronts that were generated for each of the total, male, and female PK‐PD parameter sets, with the latter as normally distributed samples defined by the mean and SE of each parameter (Table S2), and bounded by the mean ± 2·SE. The optimized dosage variables were reported to the nearest 10 mg for dose and to the hour for frequency of administration. Summaries were also described in practical units, with doses rounded to the nearest 50 mg as the smallest tested tablet unit, ³⁰ , ³³ and frequencies to the nearest 12 h as a product target for a maximum twice‐daily dosing. ³⁴

Once‐daily dosing

Optimized once‐daily pretomanid doses, as a variable‐dose and fixed‐frequency problem, were determined for population‐typical, male‐typical, and female‐typical dose‐response profiles; and for the first 3 participants randomized to the CL‐007 200 mg dose group as examples of individualized dosing. Figure 1 shows the Pareto fronts, BR profiles, dose‐response model MC simulations using previously described model parameter distributions, ²⁸ , ²⁹ and the individual dose‐exposure‐response outcomes. The differences between male and female dosing can be accounted for as a PK effect. For the same dosage, there are typically higher pretomanid plasma concentrations observed in women than men, ²⁴ , ³⁵ which results in correspondingly larger modeled Pr(AE) values. However, the differences are small and the cluster exemplars and ranges shown in Table 1 are similar across the population‐typical PK‐PD parameter sets. Optimal once‐daily mean (SD) doses corresponding to the maximum BR values were, 220 mg (10 mg), 230 mg (10 mg), and 200 mg (10 mg), respectively, for the population total, male, and female PK‐PD parameter sets (Table S2). The MC simulations show the day 14 efficacy and safety outcome distributions (sample size equal to 10,000), which may provide a basis for decisions on subsequent testing. For example; a desired limit on Pr(AE) values equal to 5%, suggests 200 mg as a cutoff based on an acceptable level for safety. To the nearest 50 mg, the once‐daily 100, 200, 400, and 800 mg cluster exemplars represent a selection of (low‐risk and low‐efficacy) to (high‐risk and high‐efficacy) stratified regimens for population‐typical dose‐response profiles.

Figure 1.

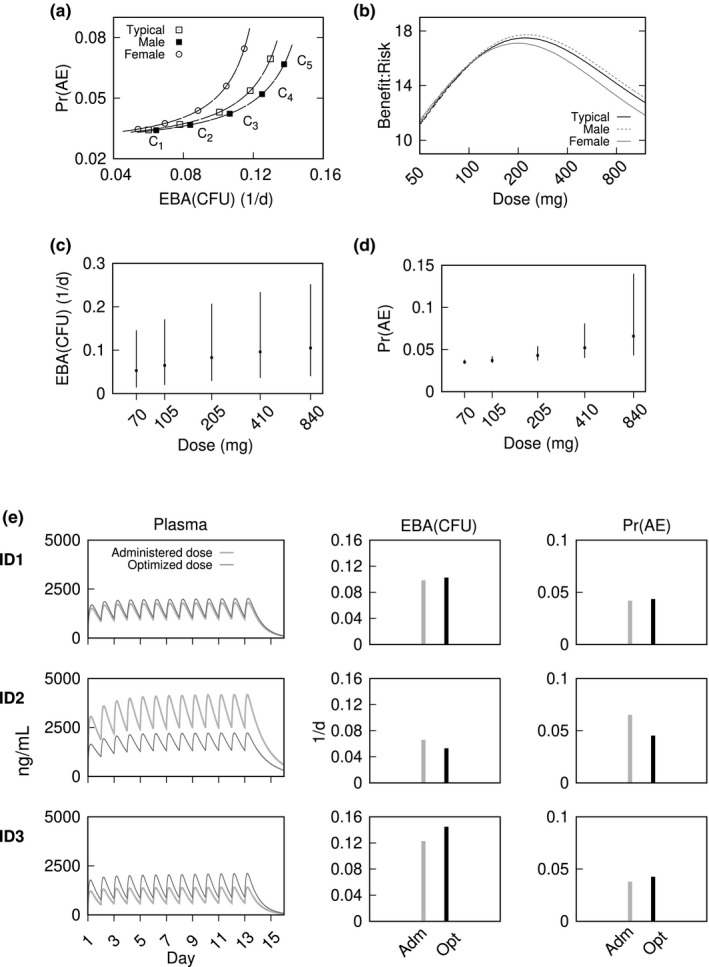
Once‐daily dosing to maximize early bactericidal activity (EBA) colony forming unit (CFU) and minimize probability of a drug‐related adverse event (Pr(AE)). Pareto fronts and cluster exemplars (a), and benefit‐risk profiles (b), for population‐typical, male‐typical, and female‐typical dose‐response. Monte‐Carlo simulations of end‐of‐treatment outcomes for EBA(CFU) (c) and Pr(AE) (d) for population‐typical Pareto front cluster exemplars. Plots show median (points) and 90th percentile range (error bars) with simulation sample size equal to 10,000. Plasma concentration‐time profiles and day‐14 outcomes for EBA(CFU) and Pr(AE) with once‐daily dosing for the first 3 participants in the CL‐007 200 mg dose group (e). Each row shows model simulations for the administered (Adm) 200 mg doses and optimized (Opt) doses of 230, 100, and 380 mg for participants ID1, ID2, and ID3; respectively

Table 1.

Optimized once‐daily dosing to maximize EBA(CFU) and minimize Pr(AE) for the total population‐typical, male‐typical, and female‐typical CL‐007 and CL‐010 study participants. Pareto front ^a cluster exemplars and ranges

Regimen (mg/day)	Total	Male	Female
C1	70 (50, 90)	70 (50, 90)	70 (50, 80)
C2	110 (90, 150)	110 (90, 150)	110 (80, 140)
C3	210 (150, 290)	210 (150, 280)	200 (140, 270)
C4	410 (290, 580)	400 (280, 560)	400 (280, 580)
C5	840 (590, 1200)	800 (570, 1200)	840 (590, 1200)

C_i , i = 1, ..., 5: cluster exemplar label.

Abbreviations: EBA(CFU) early bactericidal activity (colony forming unit); Pr(AE), probability of a drug‐related adverse event.

^aEvolutionary algorithm population size equal to 400.

Model simulations of individual plasma concentration‐time profiles and 14‐day EBA and Pr(AE) outcomes are shown in Figure 1E. The benefit‐risk optimal doses were 220 mg, 100 mg, and 380 mg, for ID1, ID2, and ID3, respectively. The simulations show the difference in outcomes between the optimized and originally administered 200 mg doses. Participant ID1 was nearly optimally dosed at the original 200 mg, whereas 100 mg for ID2 improves safety with a relatively small reduction in efficacy, and 380 mg for ID3 would improve efficacy while maintaining Pr(AE) below 5%.

Dosing interval

Optimal frequencies of administration, as a fixed‐dose and variable‐frequency problem, were determined for population‐typical PK‐PD parameters as the maximum values of BR profiles for fixed 100, 200, 300, and 400 mg doses. Expressing the results as (dose, frequency mean [SD]; EBA[CFU], Pr[AE]), the optimized regimens and outcomes were: (100 mg, 13 h [1 h]; 0.102 /d, 0.043), (200 mg, 22 h [1 h]; 0.103 /d, 0.044), (300 mg, 28 h [1 h]; 0.105 /d, 0.045), and (400 mg, 33 h [1 h]; 0.105 /d, 0.046). The optimized frequencies can be summarized as twice‐daily for 100 mg, once‐daily for 200 mg, once‐daily for 300 mg, and once every 36 h for 400 mg. The less‐than‐proportional increase in frequency with dose implies a potential for suboptimal treatment with concentration‐dependent or intermittent dosing.

Pattern of bactericidal effect

Optimal (dose and frequency) pairs, as a variable‐dose and variable‐frequency problem, were determined for a population‐typical PK‐PD profile. Constraints for a minimum EBA of 0.09 log₁₀ CFU/ml/day and maximum Pr(AE) less than 0.05 were included as an example of a target profile guided design. Figure 2 shows the optimal solutions, Pareto front, and benefit‐risk profile, together with the cluster exemplars. The optimal dose range was 70–250 mg and frequency range equal to 11–21 h. These results distinguish time‐dependent and concentration‐dependent patterns of drug kill, with pretomanid being consistent with the former by the presence of small doses more frequently administered and the absence of large doses with longer dose intervals. The (dose, frequency; EBA[CFU), Pr[AE]) values for the cluster exemplars were C₁ = (110 mg, 17 h; 0.094/d, 0.041), C₂ = (150 mg, 15 h; 0.108/d, 0.046), C₃ = (160 mg, 19 h; 0.0102/d, 0.044), and C₄ = (200 mg, 18 h; 0.113/d, 0.049). The maximum benefit‐risk regimen was (120 mg, 15 h; 0.103/d, 0.044), or ~ 100 mg twice daily.

Figure 2.

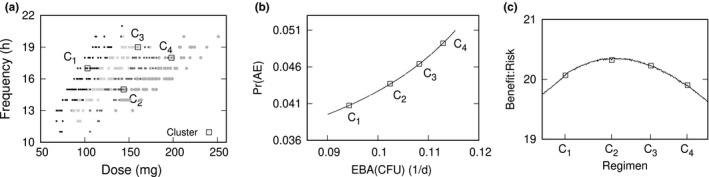
Bactericidal effect. Cluster exemplars and dosage parameter sampling space (a), Pareto front (b), and benefit‐risk curve (c), for variable dose and frequency of administration to maximize early bactericidal activity (EBA) colony forming unit (CFU) and minimize probability of a drug‐related adverse event (Pr(AE))

Loading dose

Optimized loading dose regimens, with variable loading and maintenance doses, and variable duration of loading dose administration, were determined for population‐typical PK‐PD parameters. Constraints were specified for a minimum EBA of 0.09 log₁₀ CFU/ml/day, maximum Pr(AE) less than 0.05, and loading dose larger than the maintenance dose. Figure 3 shows plots of the optimal dosage regimen parameter values, the Pareto front, and the benefit‐risk profile. The dosages and corresponding outcomes for the cluster exemplars, expressed as (loading dose, maintenance dose, duration of loading dose; EBA[CFU], Pr[AE]), were C₁ = (250 mg, 150 mg, day 1; 0.0936/d, 0.041), C₂ = (300 mg, 200 mg, day 2; 0.0999/d, 0.043), C₃ = (400 mg, 250 mg, day 1; 0.106/d, 0.046), and C₄ = (500 mg, 300 mg, day 1; 0.112/d, 0.049), and for the maximum benefit‐risk (350 mg, 200 mg, day 2; 0.1030/d, 0.044). The loading dose for 1 day is ~ 1.6 times the maintenance dose, which matches the standard PK loading dose calculation ¹² for a pretomanid elimination half‐life of 17 h. ³⁶

Figure 3.

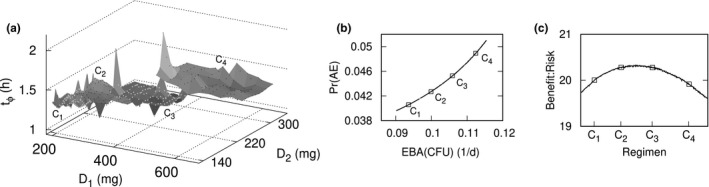
Loading dose. Cluster exemplars and dosage parameter sampling space (a), Pareto front (b), and benefit‐risk curve (c) for two variable doses and day of dose change to maximize early bactericidal activity (EBA) colony forming unit (CFU) and minimize probability of a drug‐related adverse event (Pr(AE))

DISCUSSION

Although phase II dose‐finding is a critical prerequisite for phase III trials, the current and proposed implementations of codevelopment for TB drug regimens do not include a dose‐finding phase beyond the single‐drug level. ⁷ The objective of this study was to demonstrate a multi‐objective optimization approach to dose selection aimed at the component drugs and clinical trial transitions of novel TB regimens. The approach is a model‐based analysis of drug exposure, safety, and efficacy data that results in a set of trade‐off optimal dosage regimens with final selections made in the context and aims of subsequent testing. The analysis can be applied with each advancing stage of development, where the dose‐response model from a previous stage is updated based on current study results, and the optimization process repeated to inform dosage regimens for the next. This application to pretomanid served as an example for a phase IIa starting point, with the CL‐007 and CL‐010 studies being the first with safety and efficacy outcomes for pretomanid‐containing regimens, and which provided for comparison between the analysis and empirically established results as a measure of validation.

The recommended dosage for pretomanid is 200 mg once‐daily (for 26 weeks in combination with bedaquiline and linezolid), and was established from testing in 19 clinical studies with more than 1000 participants who were administered pretomanid alone or in combination with other TB drugs. ³⁶ In this analysis, the same dosage was identified (within 20 mg) as a maximum benefit‐risk dose for a fixed once‐daily administration, and as maximum benefit‐risk frequency (within 2 h) for a fixed 200 mg dose. The recommended dosage was also placed in a population‐typical context, and optimization examples for individual participants demonstrated the extent of potential suboptimal response for differing PK‐PD profiles. The Pareto optimal solutions from the variable frequency and variable dose optimization problem showed a difference between time‐dependent and concentration‐dependent dosing, with the former being optimal and in agreement with the time‐dependent activity characterized by preclinical dose‐fractionation results. ³⁷ The application of the analysis method to more complex regimens was demonstrated for three parameters in the loading dose example. This approach to loading dose identification differs from the conventional PK method aimed at rapid attainment of a specified target concentration, ¹² where here it arises from the regimen design goal and includes the drug exposure and response dynamics. Although the results of this computational analysis were also established empirically, the comparison provided a first test of Pareto optimization and a basis for future applications to later phase clinical testing.

The basic sources of uncertainty are the dose‐response model, the EA optimization process, and the selection of doses from the Pareto front for subsequent testing. Beyond model specification error, ³⁸ there is uncertainty in the objective functions calculated with dosage parameter values that were not experimentally tested. This may be minimized by the bounds and constraints on the sampled dosage parameters. Although the pretomanid doses were restricted to the tested ranges in CL‐007 and CL‐010, the frequencies of administration were sampled from a larger range than the tested once‐daily values. The validity of model results for this wider range of dosing intervals have not been accessed, and the AE model is uncertain due to the sparseness of the data on which it was developed. However, the identification of once‐daily optimal dosing for 200 mg was consistent with both the fixed‐dose and variable‐frequency, and fixed‐frequency and variable‐dose problems. The EA involves the sorting and ranking of model simulation outputs, and acts as a source of error propagation. The accuracy and precision of the dose‐response model is the primary determinant for minimizing this error. For the case of pretomanid, the large tested dose range was exceptional, and provided for accurate model specification including the identification of nonlinear effects. The ability to identify complex dosage regimens using such highly determined models may motivate wider dose‐ranging EBA study designs. The dose selection process includes subjective decisions based on external criteria that include clinical judgment and the aims and purpose of subsequent clinical trial designs. Final choices from the set of equally permissible Pareto optimized regimens are context‐dependent and are not included as part of the computational framework. The dosage regimens that result from the partial reduction of possible choices based on the BR profile and cluster analysis may vary depending on the EA population size used to generate the Pareto front. This source of uncertainty may be minimized with EA population sizes that are large enough to fill in the Pareto fronts without significant gaps from unsampled dosage regimen parameters.

Multi‐objective optimization and evolutionary algorithms are widely used throughout engineering and the sciences, ²² including examples from drug discovery and development, ³⁹ , ⁴⁰ and with several theoretical descriptions of Pareto optimal dosing appearing over the past 20 years. ¹⁸ , ¹⁹ , ²⁰ , ⁴¹ , ⁴² However, for conventional drug development there is no apparent advantage to such methods over the simplicity and transparency of target exposure attainment. It is only with the recent regulatory changes for codevelopment ⁶ that the problem of regimen‐based dose optimization in a clinical trial setting has become an option. There are a wide range of clinical trial designs for TB regimens, including adaptive studies with multiple stages and seamless progression ⁴³ for which quantitative analysis tools have not been fully developed. The barriers of combinatorial complexity for testing regimens with three or more drugs ¹⁷ provides a motivation for Pareto optimization. The safety and efficacy outcomes are bacterial load and a limited set of measures for toxicity, which remain relatively fixed and independent of the number and type of drugs. The EA optimization acts on these outcomes rather than the input doses, which provides for the efficient sampling and identification of highly complex dosage regimens. The ability to identify optimized individual dosing based on initial PK‐PD profiles provides a tool for seamless trial designs, where an interim analysis could be performed with dose adjustments at the individual participant level. The effect of such an approach is the replacement of variation in response from a predefined small set of input doses, with possibly large variation in dosing that instead leads to a narrow and desired response by design.

Although applied here to pretomanid monotherapy, the method of analysis was developed for the large number of new drugs and possible regimens that are advancing through the TB drug pipeline. ⁴⁴ Several ways to extend these preliminary results with phase III data include the use of an updated population PK model developed with pretomanid in combination regimens, particularly with bedaquiline and linezolid, ⁴⁵ and the use of a model for QT prolongation ⁴⁶ as an objective function for toxicity. The three parameters used for the loading dose example could equivalently be the doses for three separate drugs administered once‐daily, with extension to several larger parameter sets being well within the operating specifications for EA algorithms. Although Pareto optimization and target‐attainment for dose selection differ in the method of PK‐PD model input sampling and evaluation of the model output, both approaches share the same limitations that arise from uncertainty in the values of the model parameters. A major challenge to taking full advantage of the capabilities of Pareto optimization is the development of accurate multidrug dose‐response models, which depend on informative experimental data from nonclinical and clinical sources. Such model development may benefit from experimental studies that incorporate methods of optimal design, ⁴⁷ , ⁴⁸ with additional dosage arms, and sample sizes and timings, chosen to minimize error in the PK‐PD model parameter estimates. Additionally, oral drug delivery with only a few fixed tablet sizes presents a practical barrier to implementing individualized or fine‐grained dosage regimens. However, emerging tablet printing technologies ⁴⁹ offer a promising companion to the computational framework described here, to identify and implement complex dosage regimen designs.

CONFLICT OF INTEREST

The author declared no competing interests for this work.

AUTHOR CONTRIBUTIONS

M.A.L. wrote the manuscript, designed the research, performed the research, and analyzed the data.

Supporting information

Supplementary Material