Risk Analysis of Unruptured Aneurysms Using Computational Fluid Dynamics Technology: Preliminary Results

Abstract

BACKGROUND AND PURPOSE:

The decision as to the treatment of incidental IAs is complex. There are no certain quantitative methods that can be used to evaluate the risk of rupture in IAs. In recent years, CFD technology has been recognized as a potential risk-analysis tool. The aim of this article was to propose a hemodynamic parameter, EL, to determine the effects of stable unruptured aneurysms and of those that ruptured during the subsequent observation period.

MATERIALS AND METHODS:

Four incidentally found ICA-PcomA aneurysms ruptured during the period of observation (ruptured-IAs). Another 26 unruptured aneurysms (stable-IAs) with similar location, size, and morphology were compared for the differences in hemodynamic factors, such as EL and WSS.

RESULTS:

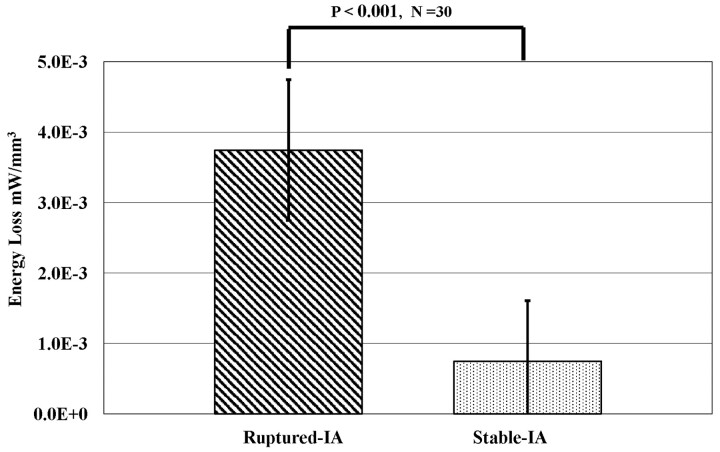
The EL calculated at the ruptured-IAs was nearly 5 times higher on average than that at the stable-IAs (ruptured, 0.00374 ± 0.0011; stable, 0.000745 ± 0.0001 mW/mm³, P < .001). However, there was no difference between the ruptured and stable groups according to the results of time-averaged WSS (P = .8) for ruptured- and stable-IAs. According to flow visualization, though the mean average inflow speed of ruptured-IAs was 2 times higher than that of the stable-IAs, the flow inside ruptured-IAs appeared to undergo longer resident tracks, with stronger impact on the aneurysm wall. On the contrary, the flow inside stable-IAs passed smoothly through the aneurysms.

CONCLUSIONS:

These preliminary results indicated that EL may be a useful parameter for the quantitative estimation of the risks of rupture for IAs.

Implications for the treatment of incidentally found IAs have been discussed for many years.^1–4 Reported risk factors for aneurysm rupture include size, geometry, location, arterial hypertension, smoking, and family medical histories.^5–7 Although the size of the aneurysm is one of the important risk factors for rupture, treatment decisions are complex and sometimes controversial, especially for aneurysms around 5 mm. To date, no reliable methods for the prediction of rupture risk for IAs have been developed. Thus, additional parameters would be necessary to evaluate this risk.

Recently, computational hemodynamic technologies have been introduced to simulate blood flow within cerebral aneurysms; the relationship between flow parameters and WSS has been proposed for the flow characterization of cerebral aneurysms.^8–10 The influence of parent vessel geometry was reported by Hassan et al.¹¹ Castro et al¹² highlighted the importance of proper modeling for the proximal portions of the parent vessel, a procedure that can strongly influence the results on the basis of the aneurysm orifice and parent artery shape. Hoi et al¹³ demonstrated the effect of arterial geometry on the growth of the aneurysm: More tortuous arteries and wide-neck aneurysms were subjected to higher hemodynamic stresses, particularly on the distal parts of the neck. Cebral et al⁸ performed computational hemodynamic simulations for a total of 62 cerebral aneurysms (25 ruptured, 34 unruptured, and 3 with unknown histories of hemorrhage) in various locations. They found that high-speed narrow jet flows were commonly observed in ruptured aneurysms. Shojima et al¹⁴ studied 20 MCA aneurysms (3 ruptured and 17 unruptured, 7 male and 12 female patients). Spatial average WSS within the aneurysm at the peak systole was found to be lower than that within the parent artery and higher within ruptured aneurysms. However, Shojima et al also indicated that the WSS was markedly reduced at the top of the aneurysm or within a bleb area.

All these findings, in addition, have no quantitative expression and are difficult to use in the prediction of rupture. WSS is forced in the tangential direction along the surface of the aneurysm. WSS is a vector described by scale and direction. Therefore, it is essential to estimate the alteration of the direction of WSS (pulls and shrinks) during blood flow pulsation. However, to our knowledge, almost all previous literature focused solely on the WSS value, disregarding the alteration of the direction of WSS.

Hence, to evaluate the role of flow−arterial wall interaction in the pathogenesis of aneurysms, we introduced a hemodynamic parameter—the EL—to thoroughly and more accurately estimate the pressure variation and kinetic energy transformations within the aneurysm. This demonstrated the value of collision power from hemodynamic forces. We assumed that the EL may assess the risk of aneurysmal growth and rupture. This concept of EL has been applied in cardiovascular surgical applications to estimate the transformation of blood flow power and to evaluate the outcome of cardiovascular surgery and optimization.¹⁵ We analyzed several hemodynamic parameters such as WSS and a new concept, EL, between stable unruptured aneurysms and those that ruptured during the observation period that followed.

Materials and Methods

Patients

Between March 2003 and March 2009, 258 incidental IAs of the PcomA were referred to our institution. All patients underwent a 3D CTA, performed by using 16-section CT (Somatom; Siemens, Erlangen, Germany). We devised a prospective protocol for the management of the IAs, which was approved by the university institutional review board. This protocol was defined on the basis of the low annual rupture rate of small-sized aneurysms described in previous reports.¹ For IAs <5 mm (small), we recommended conservative observation. When the size of the aneurysm ranged between 5 and 9.9 mm (medium), we discussed potential treatment procedures with the patient. For those with medium-sized aneurysms, the final decision for treatment depended on the patient. If the size of the aneurysm was >10 mm (large), we strongly recommended treatment.

As a result, 113 IAs were treated, while 145 IAs were conservatively observed. During follow-up, 4 medium-sized untreated IAs ruptured (ruptured-IA group in this study). To compare the differences of hemodynamic performance between the ruptured-IAs and the stable-IAs under the same conditions (as a control group), we matched 26 stable-IAs observed for >12 months by location (ICA-PcomA) and size (medium).

For the ruptured-IAs, the images were obtained during 5 months on average before the occurrence of rupture, generally at the time of the patient's last clinical visit. These 4 patients who had subsequent aneurysmal rupture (age range, 62–71 years; average, 66.7 years; aneurysm size range, 5.3–7.7 mm; mean, 6.05 mm) are cases A–D in this study. The other 26 patients (cases E-AD) are stable IAs. Their age range was between 40 and 78 years (average, 60.1 years), with aneurysms of 5.0–9.5 mm in diameter (mean, 7.07 mm). In the control group, 3D CTA studies from the first examination were used, with the observational period of their unruptured history being an average of 12 months, longer than the period undergone (from angiography to rupture) by the ruptured-IA group (5 months). All patients were women. The images scanned after aneurysm rupture were not selected for this study because the force of blood flow within the aneurysm would subsequently be reduced after bleeding, along with alterations in the geometry of the aneurysm following rupture.

Image Processing

Medical visualization software Real INTAGE (http://www.fanhow.com/real-i/real-intage-vintage-download) was introduced to transfer and extract DICOM-formatted clinical CT images into 3D angiography, allowing its export in geometric data format (STL format, http://www.sgi.com/tech/stl/) for the purpose of numeric modeling. The STL format geometry was meshed by using ICEM (ANSYS, Lebanon, New Hampshire). This process of image transfer has been intentionally developed in a compact manner, for the rapid conversion of data.

Numeric Modeling, Simulation Methods, and Boundary Conditions

The fluid in this study was assumed as an incompressible Newtonian fluid, while the flow was assumed to be laminar (Reynolds number <1000). The vessels were modeled as rigid, with the omission of the roughness of the inner vessel surfaces. Transient Navier-Stocks governing equations were solved through the use of CFX (ANSYS) on the basis of the finite volume method. Pulsatile flow conditions were introduced as inflow conditions in the ICA, with an average flow set at 0.254 L/min and pulse, at 70 beats per minute.

To simulate the peripheral capacitance, we extended the outlet of the patient ICA at the distal end in the normal downstream direction to 100 times the size of the vessel diameter, sufficient for the recovery of blood pressure at the ICA. A zero pressure gradient in the flow direction was used at the outlets. This boundary condition ensured that the length of the extended domain would not further influence the flow in the patient's domain. To form a fully developed flow boundary layer at the proximal inlet, we extended the inlets of the domains in an upstream direction to 20 times the size of the ICA so that fully developed velocity profiles were formed in the boundary layer. At the extended inlet boundary, uniform velocity, which was calculated from the average of ICA flow ratios (measured by echocardiography),¹⁶ was introduced as the ICA inlet boundary condition. The extended domains at the inlet and outlet were only for the purpose of the simulation and were not included in the analysis of flow characteristics.

We have previously performed in vitro validation processes to confirm the accuracy and effectiveness of our simulation system in clinical settings.^17,18 The system was able to efficiently convert the imaging data from MR imaging/MR angiography and CTA/conventional angiography (DICOM format) to computationally available vessel-shape geometries (STL format). This process took 10–20 minutes. The ANSYS package software, ICEM, was used to generate the mesh, a process that took approximately 5–10 minutes. The pulsatile simulation was performed with 500 time-steps for each cycle. The pulsatile calculation of 3 cardiac cycles took 1 hour on a PC with a 2-CPU, 3.3-GHz processor, and 32-Gb RAM memory. The entire process, including data transfer and instantaneous simulation with readily available information for the clinician, took approximately 2 hours.

Mesh Generation

The domain of the aneurysm and parent artery was meshed by using unstructured grids. To accurately calculate the WSS from the surface of the vessel, we meshed 7 layers of growth mesh (prism mesh) at constant distances, gradually moving them away from the aneurysm and vessel. The distance of the first layer to the vessel surface was fixed at 0.01 mm. The mesh and boundary conditions were independently evaluated in previous validation processes¹⁸; the meshes used in this study ranged from 700 000 to 800 000 cells in total, including the extended domain. To save calculation time, we generated the mesh size of the extension domain to increase gradually. Considering that the extended domain was only designed for pressure recovery, the coarse mesh of the extended domain did not have any influence on the final results.

EL

The EL of flow is caused by the loss of power (ie, when the flow must pass through complicated units). Generally, the main reasons for EL are flow separation, turbulence, surface friction, and flow attachment. From observations of the flow within aneurysms, the flow pattern appeared very complex, with the occurrence of jet flow, swirling and separating flows, and flow attachment. The interior flow of the aneurysm was highly dependent on the location and geometry of the parent artery. Part of this EL was considered to be transferred into other types of energy, such as heat and energy to wear away aneurysm surfaces. This hemodynamic EL is assumed to be one of the major factors in the development, growth, and final rupture of aneurysms.

Furthermore, the flow patterns inside the aneurysm were not only dependent on the aneurysm itself but also highly influenced by the conditions within the proximal artery. To calculate the EL created by the effect of aneurysm formation, we assumed a situation before aneurysmal formation (ie, the conditions occurring before aneurysm formation). This was called a “nonaneurysm” condition in this study. In nonaneurysm cases, the aneurysm was removed on-screen by visualization software (Fig 1 ). The EL of aneurysms in this study was characterized by the difference between the results of “with-aneurysm” (the original patient image) and nonaneurysm cases. The EL was calculated by equation 1. The simulations of the nonaneurysm cases were carried out with the same flow conditions as that of the with-aneurysm cases. The results from equation 1 indicated that the total increase of EL is due to aneurysmal formation:

where by using the Bernoulli equation, E (W) is energy calculated from total pressure in the artery domain inlet and outlet at each time- step:

where P (Pa) is pressure, v (m/s) is velocity, g (m/s²) is gravity acceleration, and i and o indicate the inlet and outlet of artery. Pressure, P, is a form of energy created by hemodynamic forces. The term ρ½v² is a form of kinetic energy; ρgh is acceleration owing to gravity. The time-averaged EL was calculated by an average of the instantaneous EL at each pulse:

where n is time-steps at each pulse.

Fig 1.

The method of EL calculation.

To allow the various sizes of the aneurysms to be comparable by using a standard method, we divided the EL by its volume. The EL_v was calculated by equation 4:

WSS

Any real fluid moving along the solid boundary will cause shear stress on that boundary. Because a no-slip boundary condition is assumed in this study, the speed of the fluid at the vessel surface is zero. Because flow was assumed to be incompressible and a Newtonian fluid, at any distance inside the vessel from the surface, the flow speed must equal that of the fluid. Hence, the flow variation in the vertical direction created a tangential shear force on the vessel surface, defined as WSS; τ_w was imparted onto the boundary as a result of this velocity reduction. WSS is given by

where y is the distance from the vessel surface, and μ is viscosity. The distance y is one of the important factors for obtaining accurate WSS. Thus in this study, for the first layer to the vessel surface, y, was constantly fixed at 0.01 mm.

Results

Flow Visualization

Typical cases featuring blood streamlines and the velocity vectors within the central area of the aneurysms at peak systole are shown in Fig 2, to compare flow patterns between ruptured-IAs and stable-IAs. The blood flow patterns in ruptured-IAs were more complex than those inside the stable-IAs. In addition, recirculation streams were observed in the vicinity of a bleb in the ruptured-IAs. A comparatively high-speed jet flow existed at the inlet of ruptured-IAs. The jet flows interacted at the top of the aneurysms, and high pressure was created at the site of collision between the jet flow and the opposing aneurysm walls. The flows in the ruptured-IAs were not only separated but strong swirls also occurred. In cases A, B, C, and D (ruptured-IAs), swirling vortexlike streams around the center of aneurysmal cavities (secondary flows) were observed. Contrarily, there were no such streams found in stable-IAs. The results indicated that the blood had circulated for a longer track within the ruptured aneurysms, presumably resulting in the consumption of greater energy. Although there were blebs in cases I, O, and S, these blebs were all located away from the proximal edge and near the flow distal to the neck. While flows passed close to these blebs, the speed was significantly reduced. In ruptured-IA case A, however, the jet flow was projected to the bleb.

Fig 2.

The color represents the magnitude of speed: Red indicates the highest speed and blue, the lowest. Streamlines and velocity are vectors on the center section of each aneurysm. A high-flow jet is observed at the ruptured-IAs, and the flows pass smoothly through the stable-IAs.

In the other ruptured-IA cases, B, C, and D, there was direct flow interaction at the aneurysm surface near the neck area, resulting in the distribution of high-speed flow into the aneurysm. The zones of the flow inlet for the 4 ruptured-IAs were much narrower than the flow outlet at the neck of these aneurysms. The results indicated that the inlet speeds were higher than the outlet speeds. The average inflow speed recirculation inside the ruptured-IAs was computed at the inlet zone of the aneurysmal neck section: 14.0, 16.3, 16.7, and 17.5 cm/s for A, B, C, and D, respectively (mean, 16.1 cm/s). Although the streams in some stable-IAs, such as those in cases G and I, had relatively high speeds near the proximal edge of the aneurysm, the flows inside the aneurysm passed almost smoothly through and around the surface of the aneurysm, an observation seen in all stable unruptured IAs. In addition, contrary to the results seen in ruptured-IAs, the flow-inlet areas in stable-IAs were large. There were no jet flows found. The average inflow speeds of stable-IAs had a mean of 8.03 cm/s. The mean average inflow speed of ruptured-IAs was 2 times higher than that of the stable-IAs. We assumed that all flow must pass out from the aneurysm at each heart pulse, meaning, therefore, that the high inflow speed would cause the flow to experience a longer track to pass through ruptured-IAs. Differences in inflow speeds were also an indication of EL.

EL for Rupture-Risk Quantitative Estimation

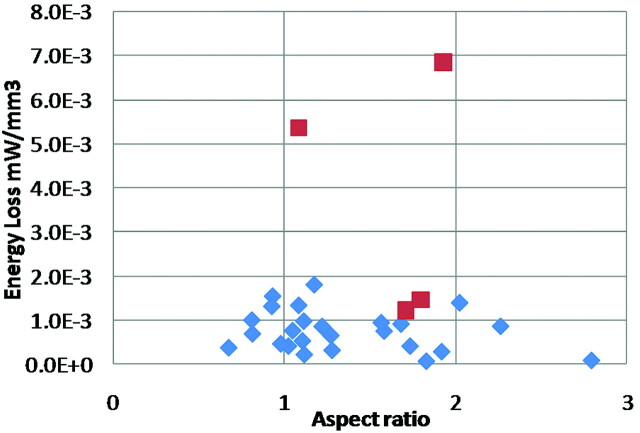
In Fig 3, AR^5,6 calculated by dividing the aneurysm size by its maximum neck length is compared with the EL_v of each aneurysm. We found that the AR of 75% of ruptured aneurysms was >1.6, while the AR of 76.2% of unruptured aneurysms was <1.6. The results coincided with the reports of Ujiie et al.^5,6 The EL_v for ruptured-IAs had a mean of 0.00374 ± 0.0011 mW/mm³, and for stable-IAs, a mean of 0.000745 ± 0.0001 mW/mm³. The EL_v for ruptured-IAs was 5.02 times (P < .001) higher than that of stable-IAs (Fig 4 ). Five cases of stable-IA aneurysms were found to possess a high range of EL (Fig 3). The results indicated that these 5 patients might already be experiencing a high risk of aneurysmal rupture. Because these patients were treated before rupture, these 5 aneurysms were included in the stable-IA group. From observation of the flows within aneurysms, there was an occurrence of jet flows, swirling and separating flows, and so forth, which were considered some of the major causes of EL. Flow separation originated from changes in fluid momentum, and this type of EL was generally proportional to the square of the flow rate—such losses appear as kinetic energy in the Bernoulli equation. Inside the aneurysm, such separation occurred in the bleb and with sudden pressure variation as the flow attached to the vessel surface. This EL may have converted into physical stimulus, force, and stress on the pathologic aneurysm surfaces.

Fig 3.

EL against AR (red, ruptured-IAs; blue, stable-IAs).

Fig 4.

The difference of EL from the ruptured-IAs and stable-IAs. The results show that the EL_v of the ruptured-IAs is 5.02 times (P < .001) higher than that in the stable-IAs.

WSS Analysis

The average WSS on aneurysms at heart peak systolic condition is shown in Fig 5 . There was little significant difference in magnitude and gradient in WSS between the 2 groups of aneurysms. The time averages of WSS calculated at the surface of the aneurysms were 2.77 ± 0.11, and 2.86 ± 0.63 N/m² for ruptured- and stable-IAs, respectively, without any statistically significant differences (P = .8 > 0.1) (Fig 6 ).

Fig 5.

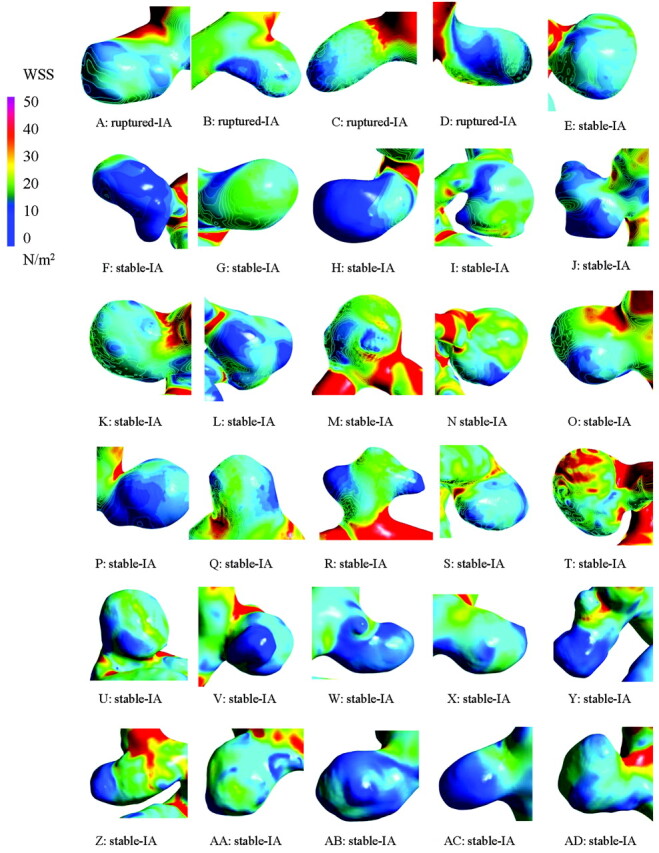
WSS distributions on each aneurysm surface. There were no significant differences between aneurysms.

Fig 6.

The average WSS on the aneurysm surface did not have a statistically significant difference between Ruptured-IA and Stable-IA aneurysms (P = .8 > 0.1).

Discussion

EL was originally proposed in industry to calculate the transmission of flow power. Recently, EL has been introduced into clinical applications (eg, to estimate the outcomes of artery anastomosis in cardiovascular surgery).^15,19 In this study, we have introduced the EL concept to predict the risk of aneurysmal rupture. The results demonstrated that the EL created when flow passes through the aneurysm was significantly higher in ruptured-IAs than in unruptured-IAs.

The blood flow patterns in ruptured-IAs were more complex, with jet flows observed in these aneurysms. The blood has circulated for a longer track within the ruptured aneurysms, presumably resulting in a greater consumption of energy. The mean average inflow speed of ruptured-IAs was 2 times higher than that of stable-IAs. Clinically, contrast stagnation could be observed during angiography in the ruptured aneurysms. The circulation track of blood flow and streamlines may also be used as potential parameters for the rupture of aneurysms.

In this study, variations in WSS were also analyzed within ruptured- and stable-IAs. The WSS is an important factor for the “wearing” of the aneurysm parent vessel. WSS represents the tangential force of blood flow on the vessel wall, and its interaction with the wall is expressed by flow retardation. Thus, predictably, higher WSS will indicate that greater kinetic energy would be required for the circulation of a certain volume through the aneurysm. It is well known that aside from WSS, a factor that leads to eventual aneurysmal rupture is a force that pushes vertically on the internal aneurysmal surface. It has long been suggested that WSS contributes to aneurysm initiation and development.²⁰ Contrarily however, low WSS found in the aneurysm plays an important role in reorganization of the significantly altered vessel.²¹ Considering that WSS was measured through the use of a flow gradient near the vessel surface (equation 5), the WSS was dependent on main flow speed. Generally, the flow decelerated at locations far from the aneurysmal neck (eg, the top of large aneurysms and in the bleb area). From a hemodynamic point of view, we considered the low WSS to be a result of aneurysm growth and not caused by the enlarged size of these aneurysms.

Currently, there are no quantitative standards to associate hemodynamic forces and markers of vascular initiation with remodeling; the most important shortcoming of previous researchers was their almost complete disregard of WSS as a vector function. WSS alters not only in magnitude but also in its spatial temporal direction, changing frequently during each cardiac cycle. Therefore, further discussion of both the magnitude and direction of WSS under time-dependent pulsatile conditions will be necessary.

Numeric Methods and Geometry (Rigid and Elastic)

In this study, the boundary condition of the vessel was assumed as a rigid surface. Until now, the elasticity of cerebral arteries has not been clearly understood,²¹ though the distribution of WSS has indicated an association between the aneurysm and the deformation of its parent artery.²² Some previous studies were performed under a constant Young modulus and Poisson ratio.^21,23 Comparisons made for a range of wall moduli with elasticity (25–100 MPa) showed that the WSS was dependent on the modulus, only when the elasticity of the modulus was <25 MPa.²³ The results indicated that hypertension and a lower modulus of elasticity would likely affect the flow patterns within aneurysms. From our in vivo observations, there was a significant difference between the wall elasticity of the aneurysm and its parent artery. Hence, the hemodynamic calculations including elasticity will be considered as an FSI calculation. The process of FSI simulation, by using various elastic moduli, requires a long calculation time, with the additional difficulty of result validation. Considering the above reasons, the vessels were assumed to be a rigid surface in this study. The evaluation of the results and ASI between rigid and elastic boundaries will be performed in further in vitro and in vivo studies. Furthermore, the aim of our study was to develop a system that can be directly applied in clinical practice. The system should be operated by medical staff, with clinical data transfer and hemodynamic simulation completed as rapidly as possible; our target is 1 hour at the longest. Therefore, accuracy and efficiency are both essential issues in this system.

Limitations

There were several limitations to this study. We had only 4 ruptured PcomAs for observation. This was due to the low likelihood of rupture; “risky aneurysms” such as multilobular ones are usually treated. A randomized study of IAs is ethically difficult. We selected 26 stable PcomA IAs that were similar in size range to the ruptured cases, acting as the control. Although the geometry was similar, it was impossible to match completely identical aneurysms with ruptured ones. In addition, we were not able to obtain 3D CTA data for all patients immediately after aneurysm rupture. The applied images were obtained at a preceding date. Therefore exact morphologic changes of ruptured cases remain unknown. To limit the influence from the uncertainty of flow distribution in PcomAs, we selected only simple sidewall-type aneurysms in this study; the flow influence from the PcomA was disregarded and 1 inlet and 1 outlet were considered for all cases at the parent artery of the aneurysms. Other types (such as MCA bifurcation) and sizes of aneurysms will be analyzed in future studies.

We supposed that vessel compliance was limited due to the small space around the reconstructed ICA-PcomA. However, we believe that the elasticity of vessels is an important issue influencing hemodynamics. One of the major characteristics of elastic arteries is their ability to stretch and store additional volumes of blood when subjected to increased pressure. Considering that the characteristics of vessel elasticity are still uncertain, however, the simulation involving patient-specific vessel elasticity and vessel thickness will be a challenge.

Another limitation is that both WSS and flow visualization were analyzed for the instantaneous flow at systolic peak in this preliminary analysis, while the EL was calculated as an average with time. We will compare the difference in results between transient and instantaneous calculations in future analyses.

Conclusions

A new approach by using EL to estimate the risk of aneurysm rupture was performed under hemodynamic simulation. Flow EL in aneurysms was significantly different between ruptured-IAs and stable-IAs. The preliminary study found that greater EL occurred when flow passed through ruptured-IAs, compared with unruptured-IAs. This new concept of EL may become a useful tool for the prediction of aneurysm rupture.

Abbreviations

AR

aspect ratio

IA

intracranial aneurysm

CFD

computational fluid dynamics

CTA

CT angiography

EL

energy loss

EL_v

energy loss per unit volume

FSI

fluid-structure interaction

ICA

internal carotid artery

MCA

middle cerebral artery

PcomA

posterior communicating artery

STL

stereolithography file format

WSS

wall shear stress