Influence of Hemodynamic Factors on Rupture of Intracranial Aneurysms: Patient-Specific 3D Mirror Aneurysms Model Computational Fluid Dynamics Simulation

Abstract

BACKGROUND AND PURPOSE:

Hemodynamics factors play an important role in the rupture of cerebral aneurysms. The purpose of this study was to evaluate the impact of hemodynamic factors on the rupture of the MANs with 3D reconstruction model CFD simulation.

MATERIALS AND METHODS:

RDSA was performed in 9 pairs of intracranial MANs. Each pair was divided into ruptured and unruptured groups. The hemodynamic factors of the aneurysms and their parent arteries were compared.

RESULTS:

There was a significant difference in the WSS at peak systole between the regions of the aneurysms and their parent arteries in the ruptured group (ie, 6.49 ± 3.48 Pa versus 8.78 ± 3.57 Pa, P =.015) but not in the unruptured group (ie, 9.80 ± 4.12 Pa versus 10.17 ± 7.48 Pa, P =.678). The proportion of the low WSS area to the whole area of the aneurysms was 12.20 ± 18.08% in the ruptured group and 3.96 ± 6.91% in the unruptured group; the difference between the 2 groups was statistically significant (P =.015). The OSI was 0.0879 ± 0.0764 in the ruptured group, which was significantly higher than that of the unruptured group (ie, 0.0183 ± 0.0191, P =.008).

CONCLUSIONS:

MANs may be a useful disease model to investigate possible causes linked to ruptured aneurysms. The ruptured aneurysms manifested lower WSS compared with their parent arteries, a higher proportion of the low WSS area to the whole area of aneurysm, and higher OSI compared with the unruptured aneurysms.

IAs are pathologic dilations of cerebral arteries, usually arising on the circle of Willis or from arterial bifurcations. The reported prevalence of unruptured cerebral aneurysms ranges from 2% to 5%.^1,2 For a variety of reasons, an increasing number of asymptomatic unruptured IAs has been discovered recently. Acute aneurysm rupture, resulting in subarachnoid hemorrhage, is often a devastating clinical event; thus, a more active policy of endovascular treatment of unruptured aneurysms is warranted in some circumstances. The investigation of the natural history of unruptured aneurysms remains controversial. According to the International Study of Unruptured Intracranial Aneurysms Investigators, unruptured IAs that were <10 mm in diameter had an exceedingly low risk of rupture (approximately 0.05% per year).³ They estimated that only approximately 5% of IAs ever rupture. While the risk of postoperative sequelae is >10%,³ in some groups of patients, the treatment risks may outweigh the aneurysm rupture rate. Therefore, it is desirable to predict aneurysm outcome and select those lesions with high rupture risk for further treatment.

We defined “intracranial MANs” as bilateral saccular aneurysms at roughly the same location on each side of the IAs in the same patient without considering the size of the aneurysms. The mechanisms responsible for rupture of aneurysms are not well understood as yet. Previous studies displayed a number of causes that may be related to ruptured aneurysms, such as location, blood pressure, and sex.^4,5 Because MANs occur in the same patient, they provide an ideal internal control for such variables as location, blood pressure, collagen genetics, and so forth. In addition, with MANs located at symmetric anatomic positions, hemodynamic parameters of parent arteries are also balanced, so we can presume that the different clinical signs of MANs contribute to the aneurysms hemodynamic factors.

Blood flow dynamics plays an important role in the pathogenesis and treatment of cerebral aneurysms. A number of specific hemodynamic factors—notably WSS, vorticity, flow impingement, pressure, and so forth—may be implicated in aneurysm growth and rupture. However, currently there are not reliable imaging techniques to quantify intra-aneurysm blood flow patterns in the human body, and hemodynamic parameter measurement in vivo is very difficult. In recent years, CFD has become a powerful and desirable tool in the investigation of cardiovascular diseases. Patient-specific hemodynamic computations, embodied as fluid dynamics computations by using patient-specific information for geometry, will enhance our ability to predict aneurysm rupture.

WSS not only acts directly on the vascular endothelium that modulates the endothelial function but also is presumed to have profound effects on rupture of aneurysms indirectly.⁶ In this study, we performed patient-specific pulsatile CFD simulation on 9 pairs of the intracranial MANs. OSI and the distribution of WSS from computational regions of the MANs model were obtained and compared between the ruptured group and the unruptured group to explore the impact of hemodynamic factors on the ruptured ICAs.

Materials and Methods

Patients and Imaging

We defined 2 aneurysms in the same patient and at roughly the same anatomic location as MANs. From January 2008 to July 2010, 13 patients with the intracranial MANs were diagnosed by RDSA. Four pairs of the MANs without ruptured aneurysms were excluded from this study. The remaining 9 pairs of the MANs were included and divided into 2 groups (ie, ruptured and unruptured groups). The common conditions were sex, age, and the location of the aneurysms; and the ruptured sides of 9 included patients are summarized in Table 1.

Table 1:

The common conditions of 9 patients with MANs

Patient No.	Sex	Age (yr)	Location	Ruptured Side
1	M	55	MCA	Right
2	F	54	C2	Right
3	M	61	C2	Right
4	F	61	C3	Left
5	F	52	ACA	Left
6	F	44	C3	Right
7	F	64	C2	Left
8	M	42	C3	Right
9	M	66	C3	Right

The images of the MANs were obtained from Integris Allura Flat digital subtraction angiography (Philips Healthcare, Best, the Netherlands). RDSA was performed on the bilateral ICAs by using 6-second constant injection of contrast agent and 270° rotation with imaging at 13.3 frames per second, for a total of 8 seconds. The corresponding 106 images were reconstructed on the Philips Allura FD20 workstation into the 3D modeling.

The maximum and minimum velocities of the IA blood flow frequency spectra were obtained by transcranial Doppler. Using Matlab 7.0 software (MathWorks, Natick, Massachusetts), we then captured the flow spectrum envelope to obtain average blood flow velocity curves in a whole cardiac cycle.

Patient-Specific Modeling of MANs

All of the RDSA images were reconstructed on the Allura FD20 workstation (Philips Healthcare). The 3D data can produce a virtual reality modeling language format and then convert it to a standard template library format. The surface data were imported into ICEM CFD 11.0 (ANSYS, Lebanon, New Hampshire) to create volume grids for fluid computation. Finite-element grids were generated by a commercial mesh generator (ICEM-CFD). An unstructured grid was generated by using tetrahedral elements with a 0.02-mm minimum mesh resolution, which resulted in grids containing between 1 and 1.7 million. The grid-dependency on the average value of WSS has been confirmed.

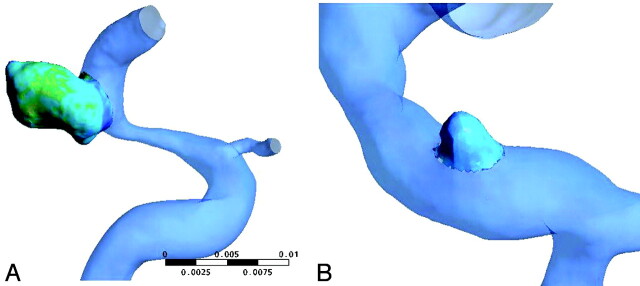
Blood was modeled as an incompressible fluid with attenuation of ρ=1060 kg/m³ and viscosity of μ=0.004 Pa·s, and the blood flow in the cerebral artery was assumed to be laminar. Because non-Newtonian effects in large arteries are usually regarded as the second order,⁷ we treated blood as a Newtonian fluid. CFX 11.0 (ANSYS) was used to perform the simulation. The governing equations for blood flow were the Navier-Stokes formulations. The vessels were modeled as rigid with no-slip boundary conditions. A pulsatile velocity profile was imposed into the inlet. The outlet had an opening boundary condition with zero static pressure. A whole cardiac cycle of 0.8 seconds was discretized by a time-step of 0.01 seconds for numeric simulation. We performed 2 cardiac cycle simulations, and the second cardiac cycle result was used to confirm the numeric stability. We separated the aneurysms from their parent arteries, as seen in Fig 1. The results of these simulations were then postprocessed and visualized by CFX 11.0 (ANSYS).

Fig 1.

The aneurysm is divided from the parent artery by spheres.

The OSI was formulated to account for cyclic departure of the WSS vector from its predominant axial alignment. We defined the mean shear stress (τ_mean) as the magnitude of time-averaged surface traction vector as

and magnitude shear stress (τ_mag) as the time-averaged magnitude of the surface traction vector was

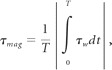where τ_w is the WSS vector and T is the duration of the cardiac cycle. Following He and Ku,⁸ we computed the OSI, a measure of variation in the direction of shear vector during the cardiac cycle, as

Statistical Analysis

The size of the aneurysms was expressed as median and range. The proportion of the low WSS area to the whole area of the aneurysms, WSS and OSI, was expressed as mean ± SD. The differences between the unruptured and ruptured groups were analyzed by a paired nonparametric Wilcoxon test. A P value < .05 was considered statistically significant, and all tests were 2-sided. Statistical analysis was performed with the Statistical Package for the Social Sciences, Version 16.0 (SPSS, Chicago, Illinois).

Results

Overall, 18 patient-specific aneurysm models in the 9 included patients were constructed. The size of the MANs is displayed in Table 2. In patient 1, the unruptuerd aneurysm was much larger than the ruptured aneurysm. In patient 9, the bilateral aneurysms had similar sizes. In other cases, especially in patients 3, 4, and 5, the unruptured aneurysms were smaller than the ruptured aneurysms. The median size of the aneurysms was 112.32 mm³ (range, 42.59–392.94 mm³) in the ruptured group and 32.39 mm³ (range, 4.16–1211.31 mm³) in the unruptured group. However, the size of the aneurysms in the 2 groups was not statistically significantly different (P = .139).

Table 2:

The size of the included MANs

Patient No.	Ruptured Group (mm3)	Unruptured Group (mm3)
1	392.94	1211.31
2	58.22	15.40
3	158.94	6.92
4	92.38	4.16
5	106.54	4.92
6	112.32	46.87
7	199.44	52.63
8	42.59	32.39
9	121.56	123.39

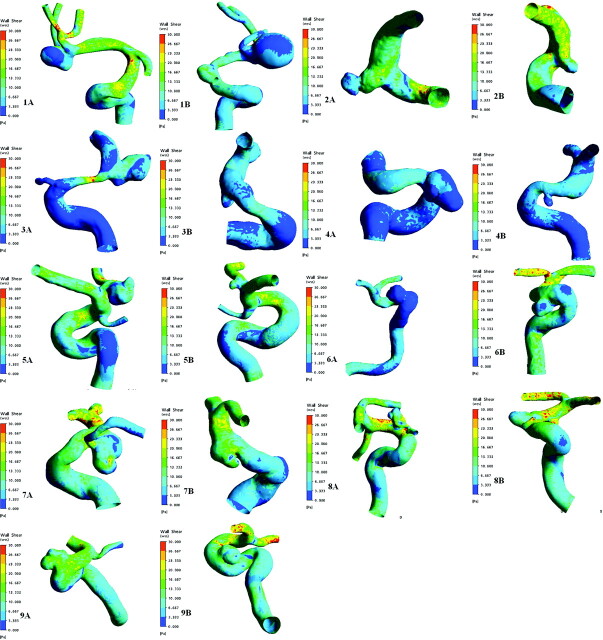
CFD analysis enables computation of the pulsatile shear stress vector, including direction and magnitude on the luminal surface of the aneurysms as a function of time. The mean WSS at end systolic time of the parent arteries was 8.78 ± 3.57 Pa in the ruptured group and 9.80 ± 4.12 Pa in the unruptured group. The mean WSS of the aneurysm regions was 6.49 ± 3.48 Pa in the ruptured group and 10.17 ± 7.48 Pa in the unruptured group. The difference in WSS between the aneurysms and their parent arteries was significant (P =.015) in the ruptured group, but not in the unruptured group (P = .678). The distribution of WSS in 9 pairs of MANs is shown in Fig 2.

Fig 2.

Distribution of WSS in 9 pairs of MANs at the systolic peak time (t =0.2 seconds). A, The ruptured group. B, The unruptured group. The numbering is annotated. The same color scale is selected for each pair of MANs.

More irregular distribution of aneurysmal WSS was observed in the ruptured group. WSS of the ruptured aneurysms was much lower than that in their parent arteries, especially at the daughter cysts or the domes of the aneurysms (Fig 2). Previous research indicated that WSS can change the biologic signals of the pressure receptors of the ECs to adjust the function of the ECs, and a WSS of ≈2.0 Pa is suitable for maintaining the structure of arterial vessels, while a WSS <1.5 Pa will degenerate ECs via apoptotic cell cycles.⁶ Therefore, we defined the place where WSS is <1.5 Pa at the systolic peak time (t =0.2 seconds) as the low WSS area. The distribution of WSS at the systolic peak time (t =0.2 seconds) and OSI in the 9 pairs of the MANs are summarized in Table 3. In the ruptured group, the proportion of the low WSS area to the whole area of the aneurysm was more than zero without exception. However, in the unruptured group, this proportion was zero in patients 2 and 9. This proportion was 12.20 ± 18.08% in the ruptured group and 3.96 ± 6.91% in the unruptured group. There was a statistically significant difference in this proportion between the ruptured and the unruptured groups (P =.015).

Table 3:

WSS and OSI in MANs and their parent arteries

Group/Patient No.	Mean WSS of Aneurysms (Pa)	Proportion of Low WSS Area to Whole Area of Aneurysms (%)	Mean WSS of Parent Arteries (Pa)	OSI of Aneurysms
Ruptured
1	4.52	10.66	11.51	0.1472
2	7.80	2.75	11.32	0.0188
3	4.07	3.00	4.19	0.0797
4	2.37	38.19	3.44	0.0998
5	7.28	2.70	11.82	0.0150
6	1.54	48.49	4.71	0.0149
7	9.84	2.35	10.63	0.2062
8	10.89	0.91	11.36	0.1854
9	10.06	0.75	9.81	0.0244
Unruptured
1	4.37	7.46	8.16	0.0485
2	18.04	0	15.91	0.0071
3	5.33	2.84	4.23	0.0022
4	2.30	21.31	3.97	0.0542
5	9.67	1.40	9.36	0.0053
6	6.92	1.38	8.41	0.0132
7	26.08	0.10	13.66	0.0094
8	8.42	1.11	13.22	0.0137
9	10.45	0	11.32	0.0117

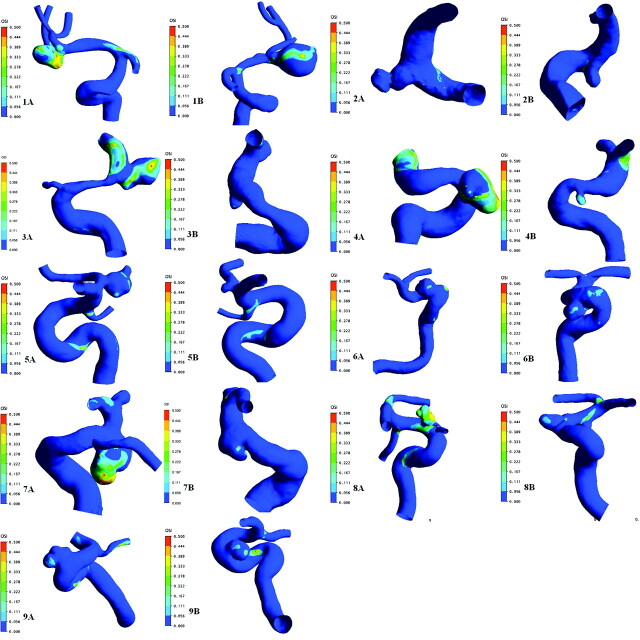
The OSI defined by He and Ku⁸ is a normalized parameter that identifies regions undergoing relatively increased changes of WSS direction compared with the temporal mean. It is an important parameter for the prediction of arterial disease. Figure 3 depicts the spectrum of OSI distribution of 9 patients, with regions of increased OSI corresponding to regions of rapid WSS directional changes. OSI was 0.0879 ± 0.0764 in the ruptured group and 0.0183 ± 0.0191 in the unruptured group; the former was significantly higher than the latter (P = .008). In patient 7, OSI of the daughter cysts was 0.2120, which was 11.58 times higher than that of the unruptured group.

Fig 3.

Distribution of OSI into 9 pairs of MANs. A, The ruptured group. B, The unruptured group. The numbering is annotated. The same color scale is selected for each pair of MANs.

Discussion

The prevalence of aneurysms was 0.4% in retrospective postmortem studies, 3.6% in prospective postmortem studies, 3.7% in retrospective angiographic studies, and 6.0% in prospective angiographic studies.² The treatment strategies of unruptured aneurysms are still controversial. When determining surgical clipping, one must weigh the natural history of the disease against the risks of operative intervention. Because the natural history of intracranial aneurysms has still not been fully investigated, it is desirable to predict aneurysm outcome and select those lesions with high rupture risk for further treatment.

MANs Model

Multiple aneurysms are discovered in approximately 20%–30% of patients with cerebral aneurysms.^9,10 Among multiple aneurysms, MANs account for approximately 20%–30%.¹¹ MANs were defined as bilateral saccular aneurysms at roughly the same locations on each side in a patient, without considering the size of the aneurysms. The most common site of MANs is the MCA and posterior communicating artery, or they may occur symmetrically.¹⁰ The MANs model may be extremely useful for appreciating the pathogenesis and end result of IAs. As an ideal internal control model, MANs can offer a condition in which most variables are equal, such as anatomic positions, hemodynamic parameters of parent arteries, blood pressure, collagen genetics, and so forth. For patients with MANs, the distinctions of shapes and hemodynamic factors in aneurysms per se were the best possible contributions to different clinical outcomes. Therefore, we combined the clinical observations with the patient-specific 3D models to describe differences in hemodynamic variables in MANs, 1 group with ruptured aneurysms and another with unruptured aneurysms.

WSS

Conventional studies had focused on many hemodynamic factors that are contingent on aneurysm geometry; the relation of the aneurysm to its parent vessel, size, and aspect ratio may be linked to rupture of aneurysms.^5,12 CFD of aneurysms has gradually become a hot topic in this realm.^6,13–20 Among various hemodynamic indices, WSS has been investigated for a long time as a cause of aneurysm rupture. Acevedo-Bolton et al¹⁴ reported an individual who presented with a giant aneurysm growing very rapidly; a striking feature found in this individual was that there was systematic growth in the region of low WSS. Valencia et al¹⁵ found linear correlations between mean WSS on the aneurysmal sac at peak systole for lateral unruptured and ruptured aneurysms with an area index. Using CFD analysis, Shojima et al¹⁶ reported that low-flow and/or low-pressure conditions might induce aneurysm rupture; low WSS on the aneurysmal wall promoted growth and eventual rupture via degeneration of ECs of saccular IAs. The findings of our research also demonstrated that the regions of low WSS at the inner surface of the aneurysm were larger in the ruptured than in the unruptured group. The difference between the WSS spatial mean at peak systole of the parent arteries and the mean WSS of the aneurysm regions in the ruptured group was statistically significant (P =.015), but not in the unruptured group (P =.678).

Low WSS has been shown to correlate with disease-inducing phenotypes in ECs of vascular lumens.¹⁷ Kataoka et al,¹⁸ who observed histologic evaluations by using scanning electron microscopy of IAs, noted that the inner surfaces of asymptomatic and unruptured aneurysms were covered with normally structured ECs; in contrast, the inner surfaces of several ruptured or symptomatic unruptured aneurysms were fragile. Dardik et al¹⁹ pointed out that ECs exposed to low magnitudes of orbital shear stress correspond to “activated” ECs compared with those exposed to laminar shear stress. It was assumed that WSS equivalent to 2 Pa was suitable for maintaining the structure of aneurysmal walls, whereas lower WSS resulted in the degeneration of ECs.⁶ Radaelli et al²⁰ found that pairs of MANs presented differences in WSS distributions around aneurysms, in intra-aneurysmal flow patterns, and in parent vessel flow divisions between side branches and the aneurysm sac.

In this study, we defined the area of WSS <1.5 Pa as the low WSS area. The proportion of the low WSS area to the whole area of the aneurysm at systolic peak time was 3.96 ± 6.91% in the unruptured group and 12.20 ± 18.08% in the ruptured group. The low WSS area in the ruptured group was much larger than that of the unruptured group, and there was a statistically significant difference between the 2 groups (P = .015). The reasons behind this difference may be high flow and/or elevated WSS protecting ECs from apoptosis; however, in the low WSS area where WSS was <1.5 Pa in the entire cardiac cycle, apoptosis of ECs is prone to develop and would eventually induce rupture of the aneurysms. Moreover, from the WSS contour, we found the low WSS area concentrated in the top of aneurysms or the daughter cyst regions.

OSI

Oscillatory flow, characterized by a low mean component and an important amount of flow in the reverse direction, has been widely studied. Although OSI can identify regions of flow reversal, it is insensitive to shear stress magnitude. Low shear can result from flow expansion without any local flow reversal beyond that which may follow from pulsatility alone. Similarly, strong oscillatory flows can exhibit the same OSI as very slow flows with the same waveform.²¹ In our study, the ruptured group always had lower WSS and higher OSI than the unruptured group. Site oscillatory shear stress may contribute to endothelial dysfunction by inducing increased Endothelin-1 and decreased NO production, thus leading to cellular toxicity.²² Oscillatory shear stress and cyclic strain increase vascular oxidative stress and enhance the vascular production of reactive oxygen species, which impairs endothelium-dependent vasodilation, NO bioavailability, and anti-inflammatory response.^23,24 During the augmented beats, the increased mean WSS reversal and oscillatory components would have shifted the relaxing/activating endothelial factor equilibrium, increasing the basal or resting VSM tone. High reversal, oscillatory mean WSS levels, and VSM tone-dependence enlarge the biomechanical and functional changes of arteries. Consequently, it was postulated that at medium and long term, oscillatory mean WSS exerts deleterious effects on the arterial wall, establishing a connection between reversal flow and vascular diseases.²⁵

In 9 pairs of the MANs that we explored, OSI was much higher in the ruptured group compared with the unruptured group. The mean OSI of the ruptured group was 0.0766 ± 0.0630, which was 4 times higher than that of the unruptured group (0.0139 ± 0.0168). Moreover, the high OSI regions usually occurred at the dome or the daughter cyst of aneurysms where rupture emerged. In patient 7, OSI of the daughter cysts was 0.2120, which was 11.58 times higher than the mean OSI of the unruptured group.

Study Limitations

Although some studies have shown that the increasing size of the aneurysm was related to an increased risk of rupture, Tremmel et al²⁶ considered that high aneurysm-to-parent-vessel size ratios may affect the hemodynamics of IAS. In our study, the unruptured aneurysms seemed smaller, especially in the patients 3, 4, and 5; the median size of the aneurysms was 112.32 mm³ (range, 42.59–392.94 mm³) in the ruptured group and 32.39 mm³ (range, 4.16–1211.31 mm³) in the unruptured group, but there was a statistically significant difference in the size of the aneurysms between the 2 groups (P = .139). Therefore, this question merits further investigation.

Blood behaves as a Newtonian fluid, and the dynamic viscosity μ is constant when it flows in arteries that are greater than approximately 1 mm in diameter⁷; however, Ohta et al²⁷ pointed out that blood inside cerebral aneurysms behaves more like non-Newtonian fluid because the blood flow is very slow inside the aneurysm sac. In our study, blood was only presumed to be a Newtonian fluid.

Furthermore, our CFD approach assumed rigid walls and did not take into account the viscoelasticity of the vessel wall because of the limited availability of physical information of arterial wall properties such as elasticity, thickness, and so forth.

Conclusions

Multiple factors may be related to rupture of IAs, and MANs are a useful disease model in which many factors are balanced to investigate the possible causes of ruptured aneurysms. The ruptured aneurysms had lower WSS compared with their parent arteries and a wider range of the low WSS area compared with the unruptured aneurysms. Meanwhile, the mean OSI was much higher in the ruptured group, and the maximum OSI customarily appeared at the dome or the daughter cyst of ruptured aneurysms.

Abbreviations

ACA

anterior cerebral artery

CFD

computational fluid dynamics

EC

endothelial cell

IA

intracranial aneurysms

MAN

mirror aneurysm

MCA

middle cerebral artery

NO

nitric oxide

OSI

oscillatory shear index

RDSA

rotation digital subtraction angiography

VSM

vascular smooth muscle

WSS

wall shear stress