In Vitro Study of Near-Wall Flow in a Cerebral Aneurysm Model with and without Coils

Abstract

BACKGROUND AND PURPOSE:

Coil embolization procedures change the flow conditions in the cerebral aneurysm and, therefore, in the near-wall region. Knowledge of these flow changes may be helpful to optimize therapy. The goal of this study was to investigate the effect of the coil-packing attenuation on the near-wall flow and its variability due to differences in the coil structure.

MATERIALS AND METHODS:

An enlarged transparent model of an ACA aneurysm was fabricated on the basis of CT angiography. The near-wall flow was visualized by using a recently proposed technique called Wall-PIV. Coil-packing attenuation of 10%, 15%, and 20% were investigated and compared with an aneurysmal flow without coils. Then the flow variability due to the coil introduction was analyzed in 10 experiments by using a packing attenuation of 15%.

RESULTS:

A small packing attenuation of 10% already alters the near-wall flow significantly in a large part of the aneurysmal sac. These flow changes are characterized by a slow flow with short (interrupted) path lines. An increased packing attenuation expands the wall area exposed to the altered flow conditions. This area, however, depends on the coil position and/or on the 3D coil structure in the aneurysm.

CONCLUSIONS:

To our knowledge, this is the first time the near-wall flow changes caused by coils in an aneurysm model have been visualized. It can be concluded that future hydrodynamic studies of coil therapy should include an investigation of the coil structure in addition to the coil-packing attenuation.

GDC embolization was introduced for the treatment of cerebral aneurysms in 1991 as an alternative to surgical clipping.¹ Some studies² found no significant differences between patient outcomes after surgical and endovascular treatment; other studies^3,4 reported lower morbidity and mortality rates for GDC embolization. The choice of the optimal treatment procedure depends on the patient's age and the site and size of the aneurysm.¹ The primary goal of the GDC embolization treatment is to prevent blood flow in the aneurysm by filling the aneurysm sac with coils that should initiate thrombus formation. In 20%–40% of patients, however, blood-flow recanalization after coil embolization was reported.^5,6 A basic review of endovascular techniques for the treatment of intracranial aneurysms was published by Lanzino et al.⁷

Different aspects of the GDC embolization procedure have been investigated and reported in the literature. Canton et al⁸ reported changes in the intra-aneurysmal pressure due to coiling. Piotin et al⁹ studied attenuated packing and aneurysmal circulation exclusion. Boecher-Schwarz et al¹⁰ investigated the physical effects of coils on pressure and flow dynamics in experimental aneurysms created in rabbits. They also studied the effect of coils on the aneurysmal wall pulsation. The study of aneurysmal hemodynamics after coiling is challenging due to the optical distortions caused by the coils. Therefore, most of these studies^9,11–13 used an experimental dye washout technique (cine angiography) to visualize flow. Only a few numeric studies^14–16 of the aneurysmal flow after coiling are known. Most of these studies modeled coils by simply assuming that the aneurysm sac volume was a porous medium. Sorteberg et al¹⁷ investigated whether the aneurysmal flow changes could be assigned to the hydrodynamic effect of the coils themselves or to a compound effect of coils plus thrombus formation. They concluded that GDCs indicate a pure hydrodynamic effect.

The present study investigated near-wall flow hydrodynamics after coiling in an in vitro model of a cerebral anterior aneurysm. The aneurysmal near-wall flow is of great interest because this flow defines WSS. WSS and its derivatives, including WSS time and space gradients, the oscillating shear stress index, and WSS angular deviations, are the major hydrodynamic parameters linking blood flow and vessel wall remodelling related to aneurysm initiation, growth, and rupture.^18–20 Knowledge of the near-wall flow changes caused by coils may help us to optimize endovascular treatment by using coils.

The study included, primarily, an investigation of the near-wall flow for different coil packing attenuation. The second study goal was an examination of flow variability resulting from the variability of a 3D coil structure. The hydrodynamic impact of a 3D coil structure, which is unknown, has not, to our knowledge, been studied until now. Both investigations were performed by using a novel visualization technique based on Wall-PIV.^21,22

Materials and Methods

Patient Data, Reconstruction Procedure, and Experimental Model

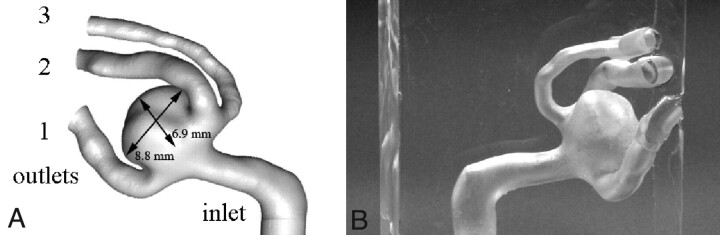
A standard CT angiography of a woman (55 years of age, body-mass index = 27.3) with a nonruptured aneurysm was performed in the Helios Hospital, Berlin-Buch. The CT was performed in sections of 1.8-mm thickness with a 0.9-mm distance in a 512 × 512 pixel (0.26 × 0.26 mm²) matrix with a 16-bit gray-scale. These data were used for the 3D reconstruction of a trifurcation aneurysm of the ACA by using the program ZIB-Amira (Zuse Institute Berlin, Berlin, Germany). Thresholding and semiautomatic image segmentation were performed by using voxel labeling with subvoxel accuracy. On this basis, a 3D isosurface of the aneurysm was generated. After applying smoothing algorithms, a solid geometric model was constructed and an STL data file was created (Fig 1A). The aneurysm sac had an 8.86-mm diameter (0.268-mL volume) with a neck area of 33.6 mm². The diameters of outlet branches 1, 2, and 3 (Fig 1B) at the trifurcation were 2.5. 2.55, and 1.9 mm, respectively. The aneurysm surface could be virtually divided into the following 2 approximated half-spheres: the half-sphere between branches 1 and 2 (HS1), which is visible in Fig 1A, and the opposite half-sphere located between branches 1 and 3 (HS2) seen in Fig 1B.

Fig 1.

A, Computer model of the reconstructed aneurysm with in vivo aneurysm dimensions. B, Three-fold enlarged transparent silicone model of the reconstructed aneurysm.

Using the STL file, we fabricated a 3-fold scaled-up aneurysm rubber mold by using the rapid prototyping technique with an STL device (SLA 250/50; 3D Systems, Darmstadt, Germany) with a resolution of 0.1 mm. The mold was then filled with Wood's metal (melting temperature, 70°C) to produce a cast. The Wood's cast was used to fabricate a nearly rigid transparent silicone block model (Fig 1A) by using the 2-component silicone rubber, ELASTOSIL RT 601 (Wacker-Chemie, Munich, Germany) with a refraction index of n = 1.4. The inner-duct diameter of the enlarged model was D = 14 mm (4.66 mm in vivo size).

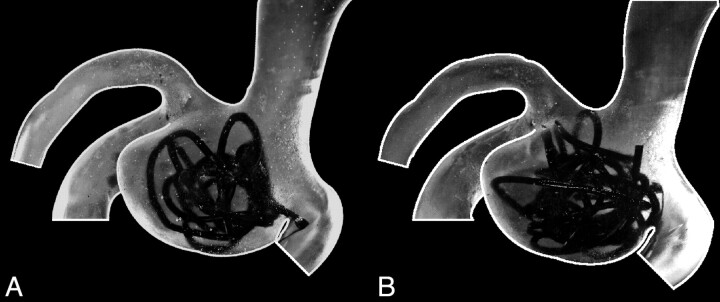
The coil model was fabricated from polyamide cord with a 1.2-mm diameter, corresponding to the 0.4-mm diameter in vivo coil wire. To obtain a 10% volume-packing attenuation in the 3-fold enlarged silicone model, a 650-mm cord length was necessary. The major goal of the coil model was to mimic the complex random coil structure in the aneurysm as it is known from angiography.¹² Furthermore, the resulting coil structure needed to be stable to allow reproducible experiments. Both goals were achieved with the coil model used. During the coiling procedure, attention was paid to avoid coil parts protruding into the parent vessel lumen, and this was achieved for all coil fillings. Figure 2 shows photographs of the investigated aneurysm model with 2 coil models with 10% and 15% volume filling.

Fig 2.

A, Photo of the model with a 10% coil-packing attenuation. B, Photo of the model with a 15% coil-packing attenuation. The coil winding that seems to protrude into the parent vessel is located completely in the aneurysm lumen.

Wall-PIV Visualization Technique

The Wall-PIV method potentially allows the evaluation of all 3 velocity components of flows within the range of a few 100 μm or less adjoining a transparent curved wall.²² The term “Wall-PIV” is used because of the similarity of the proposed technique to PIV. The basic principles of the PIV technique are well described by Adrian.²³ In this study, we used Wall-PIV as a pure visualization technique, and the principles are briefly described below. A more detailed description of the proposed technique can be found in Kertzscher et al²² and Berthe et al.²⁴

The Wall-PIV technique uses reflecting particles, which are added to the fluid as tracers, then illuminated, and recorded with a digital camera. The illumination is realized with diffuse monochromatic light illuminating the model from the camera side. A molecular dye is added to the test fluid, and this dye causes the exponential absorption of light (Beer-Lambert law), allowing the depth of the light penetration to be adjusted by varying either the incoming light intensity or the dye concentration. The intensity of the light reflected by the particles and acquired by the camera gives information about particle-to-wall distance. The recorded intensity of the reflected light from the particle closer to the wall is higher than that of the particle farther away from the wall.

Although the algorithm for the 3D 3-component near-wall flow assessment is still under development,^24,25 the Wall-PIV technique may be used for flow visualization of the near-wall path lines. The visualization of path lines in the trifurcation ACA aneurysm without coils was recently published by our group.²⁶ This study was, however, repeated because a new camera and an improved light source allowed us visualization with a higher quality.

Experimental Setup

Steady laminar flow, with the Reynolds number = V * D / ν = 300, based on the dynamic viscosity of blood with ν = 0.0035 Pa·s, the inlet diameter of the aneurysm model D = 14 mm, and a flow rate of 600 mL/min, was simulated. The flow rate in the model was calculated on the basis of the Reynolds similarity for the 3-fold enlarged model and the known mean flow rate of the inlet artery (arteria carotis interna) of 200 mL/min in humans according to published data.^27,28 The flow was generated by using the self-developed computer-controlled piston pump described in an earlier publication.²⁶ The 3 outlets of the model were connected to the 3 separate collecting reservoirs, which were used to prove the flow-rate ratio volumetrically. The flow-rate ratio between the 3 outlet branches was regulated by using throttles mounted at the outlet tubes. The flow ratio was set according to Murray's law, which is known to be valid for cerebral arteries.²⁹

The test fluid was a glycerin−distilled water mixture (37.5% of the 99.5% pure glycerin), which has the same refractive index as the silicone model (n = 1.4), to which was added 0.3 g/L of the molecular dye Patent Blue V (Schumann and Son, Karlsruhe, Germany). The measured attenuation of the test fluid was 1.1038 g/cm³. The experimentally measured kinematic viscosity of the test fluid was 3.47 · 10⁻⁶ m²/s at the temperature T = 24°C. The kinematic viscosity was measured with the Ubbelohde-Viscosimeter type 50101/0a (Schott Glaswerke, Mainz, Germany) with a measurement accuracy of 1%. To generate a well-defined velocity profile at the inlet, we connected the silicone model to the pump with a rigid duct of 14-mm diameter and 650-mm length. The test fluid was seeded with nearly monodisperse Conduct-o-fil AGSL 150–30 TRD particles (Potters Industries, Carlstadt, New Jersey) with diameters of between 71 and 75 μm and an attenuation of 1.1 g/cm³.

The model was illuminated by 2 panel sets of 56 Luxeon light-emitting diodes (Philips Lumileds Lighting, San Jose, California) powered with 3 W each and an emitted wavelength of λ = 627 nm (red). Matrix light-shaping LSD Luminit diffuser sheets (BFi OPTiLAS, Munich, Germany) were used to obtain an evenly distributed light front. According to our experimentally obtained calibration curve, the particles were seen up to a depth of 140 μm. Image sequences were acquired with the high-speed 8-bit camera Redlake MotionPro X3 (Imaging Solutions, Hannover, Germany) with a resolution of 1280 × 1024 pixels and 125 frames per second. Each image of the sequence represents an instant mapping of light-reflecting tracers, which follow the fluid flow. Particles are represented in images by bright speckles of 2–4 pixels in diameter.

On the basis of the 25-second sequences (3125 images), we generated max-min images. A max-min image is obtained by subtracting the min-image from the max-image. The max-image is generated by calculating the maximal gray values for each pixel of the image over a defined sequence, whereas the min-image is generated by calculation of the minimal gray values. Max-min images allow visualization of path lines formed by moving tracers in an image. Moving tracers can be visualized by sequential displaying of images. This enables our eyes to appreciate the apparent temporal movement of tracers, which are then interpreted by our brain as path lines. These path lines are visualized by calculating the max-images, which provide overlapping images of tracers acquired at different time steps. Subtraction of the min-image removes optical artifacts because calculated min-images correspond to images acquired by the camera without moving tracers. However, the resulting max-min images do not represent the flow direction. The information about local flow directions in the resulting max-min images is indicated by arrows.

Altogether 14 experimental sets were performed. Each experimental set was repeated 3 times to prove an intraexperimental variability. The first 4 experimental sets represent an aneurysmal flow without coils and with 10%, 15%, and 20% coil-packing attenuation. One coil (650-mm length) was used to achieve a 10% coil-packing attentuation. One additional coil with 325-mm length was added to achieve a 15% coil-packing attenuation, and 2 additional coils (each with a 325-mm length) were added for the 20% coil-packing attenuation. Furthermore, 10 experimental sets were performed with a 15% coil-packing attenuation. For each experimental set, the coil model was completely removed from the aneurysm and reinserted. This was done to investigate the impact of random 3D coil structures formed during the coil-placing procedure. No control of coil distribution in the aneurysm was possible during the coil-placement procedure.

Results

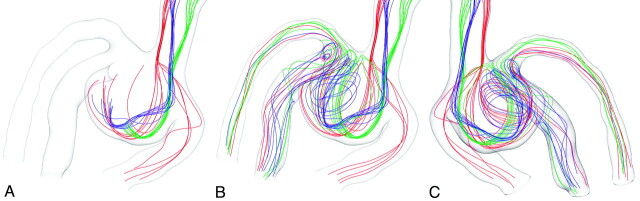
Figure 3 shows the 3D complex flow field in the ACA aneurysm, visualized by path lines. This visualization is based on the CFD study of the steady laminar flow, presuming rigid motionless walls, that was presented in our earlier publication.²⁶ The article describes, in detail, flow conditions, mesh generation, convergence criteria, and other aspects of the CFD study. Visualization based on CFD simulation was included in this article for a better understanding and description of the 3D aneurysmal flow governing the investigated aneurysm without coils. The 3D aneurysmal flow cannot be assessed by Wall-PIV.

Fig 3.

Steady-flow field in the aneurysm visualized by path lines separated into 3 colors representing the 3 visualized streams. A and B, Two images show the formation of the aneurysmal flow structure. B and C, Two views are shown for a better 3D representation of the complex flow field.

Three separated flow streams were visualized by using 3 bundles of path lines (red, blue and green, Fig 3A) generated from 3 spots of approximately 0.4 mm in diameter selected in the inlet vessel. This visualization was based on the streamline visualization proposed by Steinman et al.³⁰ Due to the asymmetric aneurysm formation relative to the inlet vessel, the blood stream enters the aneurysm mainly along the HS1 wall, turns 180° at the aneurysm dome, and flows mainly along the HS2 wall to the 3 outflow branches. Only a small part of the flow directly enters outlet 1 (see red bundle of path lines), forming saddle and node critical points at the apex of the aneurysm and the outlet 1 branch (Fig 4A). A critical point is one with zero WSS.³¹ Critical points were automatically detected by the ZIB-Amira software based on the CFD solution.

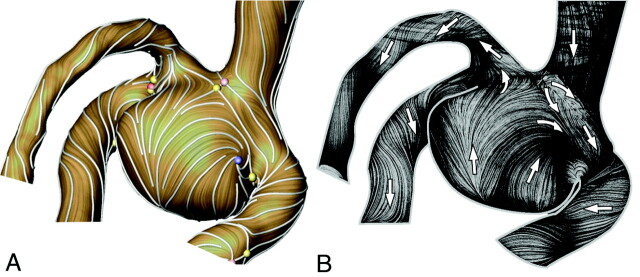
Fig 4.

A, Flow visualization of the WSS surface vector field with stream lines (white) and critical points (yellow, saddle; blue, repelling or attracting node; red, source or sink stagnation point). B, Experimental flow visualization of surface path lines in the respective model by using the Wall-PIV technique. Arrows show flow directions.

The turned stream meets the inlet flow stream, which forms another saddle critical point at the neck area of HS2 near the outlet branch 3 (Fig 4A). That part of the flow leaves the aneurysm immediately through the outlet branches 2 and 3 after 1 turn, forming an S-shaped stream (green bundle in Fig 3B). Another part of the flow (the blue stream in Fig 3B) generates a strong vortex in the aneurysm, filling the major part of the aneurysm volume.

Finally, Fig 4 shows a good agreement between the CFD-based WSS vector field (Fig 4A) visualized by a LIC and the near-wall path lines visualized experimentally with Wall-PIV (Fig 4B). The LIC technique shows the streamlines of the WSS vector field as visually attenuated. This is achieved by smearing a white-noise pattern along the directions of the vector field.³² As shown in Fig 4, the resulting pattern on the surface clearly reveals important flow phenomena such as recirculations, stagnations, and saddles. The LIC visualization was realized by using the software ZIB-Amira.

Figure 5A shows max-min images with path lines visualizing the flow in the investigated aneurysm model and showing the near-wall flow observed from 3 different directions. The left image shows HS2; the right image shows HS1 with the bifurcation of the outlet branches 2 and 3. The middle image shows the dome of the aneurysm. This flow is a result of the 3D flow structure described above.

Fig 5.

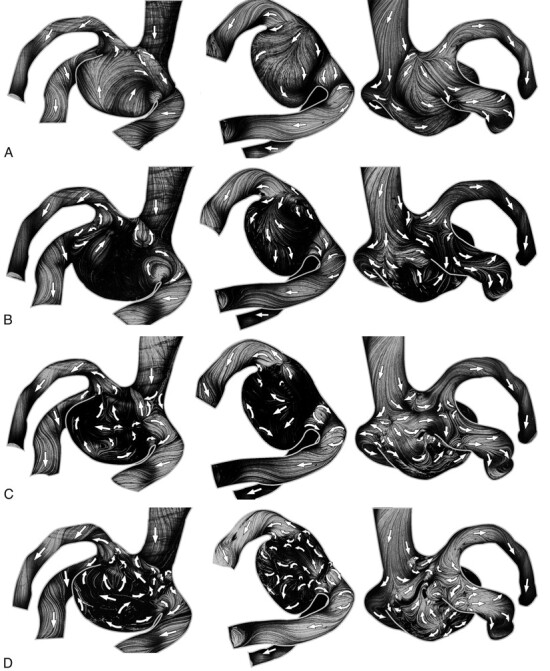
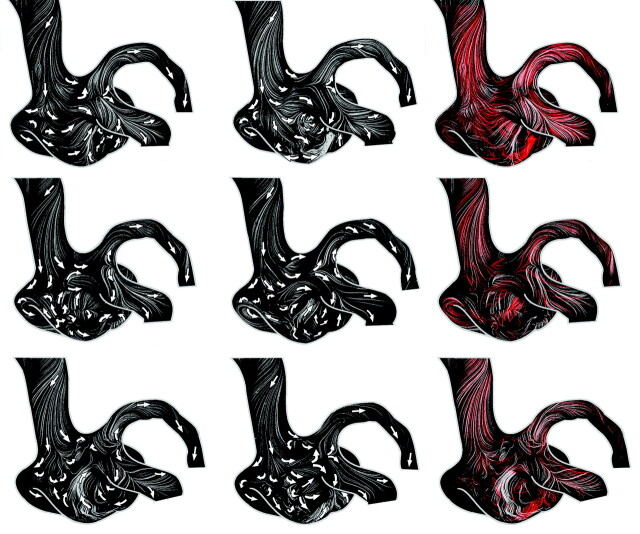
Max-min images of path lines assessed over the 25-second period in the ACA aneurysm model without coils (A) and with coils of different volume-packing attenuations of 10% (B), 15% (C), and 20% (D). Arrows show local flow directions.

Figure 5B–D shows max-min images with path lines visualizing the aneurysmal flow after the coiling, with 10%, 15%, and 20% volume-packing attenuation, respectively. Already a 10% coil-packing attenuation has a significant impact on the near-wall flow (Fig 5B). The major part of HS2 has a nearly stagnant flow. The dome part, however, indicates a stronger flow by the existence of long path lines. In contrast, the 15% coil packing reduced significantly the flow in the dome, whereas the near-wall flow of the HS1 was higher than that in the 10% coil-packing attenuation. The 20% coil packing further reduced the near-wall flow. Note that all 3 investigated cases show that the coils also alter the flow at the proximal part of outlet branches (eg, bifurcation between outlet 2 and 3 branches). An additional saddle critical point can be identified (Fig 5). Furthermore, coils may change completely (rotate by 90°) the direction of the near-wall flow stream lines when compared with the original flow features (Fig 5A).

Figure 6 represents only 1 view of the near-wall flow variability (HS1 and outlets 2 and 3 branch bifurcations) generated by different coil-placing procedures. The reduction of the near-wall flow, estimated by the path-line lengths, is generally the same in the assessed cases. Different coil structures, however, produce flows with different flow directions in the same aneurysm areas (Fig 6). These flow diversities are illustrated by overlaying different flow fields (Fig 6, right column). The flow alterations caused by coils are also propagated up to the proximal parts of outlet branches and show different flow features (bifurcation area of outlets 2 and 3 in Fig 6).

Fig 6.

Six different flow fields (2 left columns) show near-wall flow variability in the near-wall fluid layer (<150 μm) generated by different coil structures with a 15% coil-packing attenuation. Arrows show flow directions. In the right column, the overlays of the 2 max-min images from the same row are shown.

As was noted above, each of the 14 experimental sets was repeated 3 times. No intraexperimental variability, however, was observed.

Discussion

The results of the present study correspond very well with published flow investigations reporting significant flow slowing in coiled aneurysms and a better flow blockade (stagnation) with higher coil-packing attenuation.^9,17 It was also reported that a higher coil-packing attenuation allows a lower recanalization rate.^12,33 There is, however, no lower limit for the packing attenuation above which the aneurysm occlusion will be effective.³⁴ Recently, Goddard et al³⁵ reported that for a limited series of 25 small aneurysms (<7-mm diameter) treated with a single coil, satisfactory stability was achieved with time despite a low-average packing of 8%. Piotin et al³⁴ concluded that an attenuated coil mesh is not the sole prerequisite to ensure that the aneurysm occlusion will be effective. The study of the near-wall flow also revealed significant local alterations in the flow directions in comparison with the original flow (Fig 5A). The path lines over the whole visible aneurysm surface (Fig 5A, left) have nearly the same direction. In contrast, different parts of the aneurysmal surface show different flow directions after the coiling (Fig 5D, left).

The local changes in flow direction depend, however, on the structure of the coil, as was shown in 10 experiments with the same coiling attenuation. These flow-direction changes may be 1 of the additional mechanisms responsible for effective aneurysm occlusion. The control of flow changes due to coiling should be 1 of the major goals in the effort to optimize this treatment procedure. This effort should include a reduction in variability of the flow changes due to random coil structures at a constant coil volume filling. Furthermore, an attempt should be made to avoid near-wall regions with distinct (pronounced) flow patterns (Fig 5B, middle, and Fig 5C, left). Both goals can be achieved by using the proposed Wall-PIV visualization technique. Note that the flow changes caused by coils and observed in our experiments cannot be assessed by using simple CFD models simulating coils by a porous medium evenly filling the aneurysmal sac.^14–16

The present in vivo aneurysm had a wide neck with an area of 33.6 mm². We were concerned that the coils might dislocate into the aneurysm-bearing vessel and, thereby, occlude it. Therefore, the neuroradiologist and the neurosurgeon decided to clip this aneurysm. In the proposed in vitro study, the coil dislocation risk was avoided by both the model scaling, resulting in lower hydrodynamic forces, and the use of the stiffer coil model, allowing a fixed location of the coil in the aneurysmal sac. Note that these differences between the in vivo situation and in vitro model did not affect our findings of the near-wall aneurysmal flow with and without coils. In clinical practice, either a combined use of stents and coils or the sole use of stents with a low porosity (smaller distance between struts) is an option for treating aneurysms with a large neck area.³⁶ These therapy options should be researched intensively in the future. The impact of stents on the near-wall aneurysmal flow is also of interest for our future studies.

Study Limitations

The study presented here has some limitations. The maximal investigated packing attenuation was 20%. The coil model has a relatively large in vivo corresponding wire diameter of 0.4 mm. All investigations were performed under steady-flow conditions. The first 2 limitations were caused by requirements of the Wall-PIV technique. The technique required the use of an enlarged phantom model; the use of particles with a smaller diameter would generate optical distortions (Mie scattering), which would hamper the use of Wall-PIV. Following the Reynolds similarity, the 3-fold enlarged model means, however, a 3 times lower velocity field compared with the in vivo situation. Lower velocities, however, result in the improved ability of the particles to follow the flow. Furthermore, an enlarged model means a relatively long coil model (650-mm length for 10% attenuated packing). It was difficult to introduce the coil for the 20% packing attenuation. Note that this procedure also risked the possibility of model destruction. A higher packing attenuation (> 20%) with further flow slowing would result in a near-wall flow field that is challenging to assess with the proposed technique.

The coil-packing attenuation investigated in this study, however, is also clinically relevant. Piotin et al³⁴ reported a clinical study with a mean coil-volume packing attenuation of 27% (median, 25%; range, 6%–55%), which correlates well with the experience in our Helios Hospital. A desire to reduce the length of the coil model forced us to use a relatively thick wire of 0.4-mm in vivo diameter. White et al³⁷ reported coils with diameters between 0.254 and 0.381 mm. A separate study question would be the following: which is the better option for the coiling therapy, a shorter wire with a larger diameter or a longer wire with a smaller diameter; which would generate a more complex 3D coil structure in the aneurysmal sac? To solve the above-mentioned problems, we plan, in the future, to work with 2-fold enlarged models and use a test fluid with a viscosity lower than that of blood. This would allow us to investigate coil packing densities up to 35%.

Note that the in vitro coil model used does not have the secondary microstructure of modern coils. The coils used now in clinical practice are made of stock wire (0.044- to 0.076-mm diameter), which is wound around a mandrel to form a secondary tubular structure (spring) with a diameter of between 0.254 and 0.381 mm. This tubular shape is generated to increase the volume packing, which is calculated with this secondary diameter, and to control the softness of the coil. The spring microstructure does not affect the hydrodynamic impact of the coil. The stock wire used in our experiments mimics this secondary diameter. The coil model is stiffer than coils used in clinical practice. This was done to achieve stable coil structures, which are necessary for the reproducibility of the experiments. The study of the pure hydrodynamic effect of coils on the near-wall flow was the major goal of our study and was not affected by physical coil properties. Our coil model, however, does not allow the investigation of the effect of the aneurysm recanalization due to soft coils resulting in unstable coil structures. Therefore, the modified material properties of, for example, Matrix coils (Boston Scientific, Natick, Massachusetts) or HydroCoils (MicroVention Terumo, Aliso Viejo, California)⁷ were also not investigated here. These modifications are done either to improve the ability of the coils to generate thrombi or to increase the possible coil-volume packing attenuation and do not primarily affect the aneurysmal hydrodynamics.

The use of steady flow conditions in our experiments does not have any significant impact on our findings. In 1 experiment, we compared max-min images acquired under steady and pulsatile flow conditions in the aneurysm model without coils (Fig 7). No significant differences were found between characteristic flow features. This means that the flow in the investigated aneurysm was stable. Note that the Wall-PIV technique allows only a visualization of path lines assessed for a longer period, which means a time averaging of the flow. The image sequences of >25 seconds, which were presented here, represent nearly 3 heart cycles. Due to the Strouhal number similarity, 1 second of in vivo time corresponds to 9 seconds in our experiments. Furthermore, stable aneurysmal flow was reported for a large number of investigated aneurysms. Cebral et al¹⁸ studied numerically the stability of the impingement jet in 62 cerebral aneurysms. Only in 3 aneurysms was an unstable flow reported. Hence, stable aneurysmal flow is a common finding.

Fig 7.

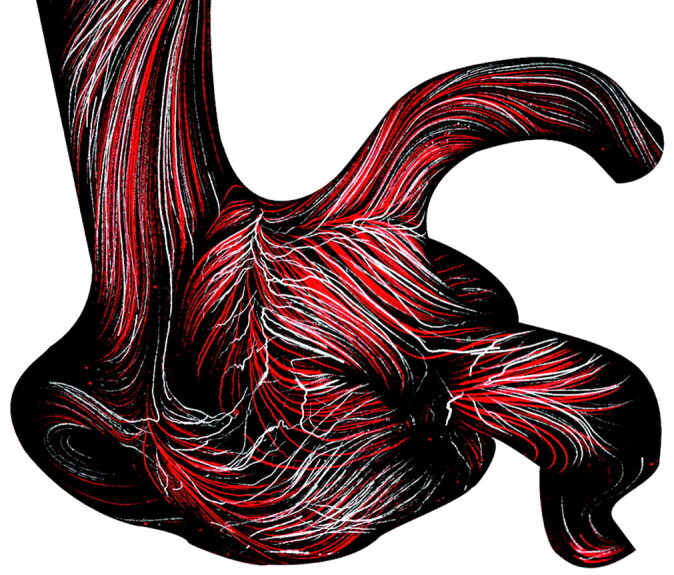
Two overlapped max-min images for comparing results of the Wall-PIV visualization under steady and pulsatile flow conditions in the aneurysm without coils. Red-colored path lines represent results for steady flow conditions.

Conclusions

The near-wall flow features were visualized in the enlarged in vitro model of the ACA aneurysm with and without coils by using max-min images acquired with the novel Wall-PIV visualization technique. The Wall-PIV technique allowed qualitative assessment of the flow in a near-wall fluid layer of approximately 150-μm thickness, corresponding to 50-μm in vivo dimensions. Flow disturbances caused by coils with a volume packing attenuation of 10%, 15%, and 20% were observed and compared with an original flow in the aneurysm. Furthermore, the variability of flow disturbances due to the variability of randomly generated coil structures was investigated. GDCs significantly reduce near-wall flow already at low packing densities. As expected, a higher coil-packing attenuation has a greater impact on flow alteration. Furthermore, coils may also affect the flow in vessel segments proximal to the aneurysm. The random coil structure, however, may have a random local effect on the near-wall flow direction. Control of the flow alteration (flow reduction and direction) mechanisms could be very important for the success of the coil embolization therapy and should be investigated further. The ability to control these flow changes should be a well-investigated design goal for 3D coil structures, which should allow control of the coil-attenuation distribution in the aneurysmal sac. Further development of the Wall-PIV technique, allowing an assessment of WSS distribution is planned to quantify these flow changes.

Abbreviations

ACA

anterior cerebral artery

CFD

computational fluid dynamics

GDC

Guglielmi detachable coil

HS1 and HS2

half-spheres 1 and 2

LIC

line integral convolution

PIV

particle image velocimetry

STL

stereolithography

Wall-PIV

wall particle image velocimetry

WSS

wall shear stress