Computer-Aided Diagnosis Improves Detection of Small Intracranial Aneurysms on MRA in a Clinical Setting

Abstract

BACKGROUND AND PURPOSE:

MRA is widely accepted as a noninvasive diagnostic tool for the detection of intracranial aneurysms, but detection is still a challenging task with rather low detection rates. Our aim was to examine the performance of a computer-aided diagnosis algorithm for detecting intracranial aneurysms on MRA in a clinical setting.

MATERIALS AND METHODS:

Aneurysm detectability was evaluated retrospectively in 48 subjects with and without computer-aided diagnosis by 6 readers using a clinical 3D viewing system. Aneurysms ranged from 1.1 to 6.0 mm (mean = 3.12 mm, median = 2.50 mm). We conducted a multireader, multicase, double-crossover design, free-response, observer-performance study on sets of images from different MRA scanners by using DSA as the reference standard. Jackknife alternative free-response operating characteristic curve analysis with the figure of merit was used.

RESULTS:

For all readers combined, the mean figure of merit improved from 0.655 to 0.759, indicating a change in the figure of merit attributable to computer-aided diagnosis of 0.10 (95% CI, 0.03–0.18), which was statistically significant (F_1,47 = 7.00, P = .011). Five of the 6 radiologists had improved performance with computer-aided diagnosis, primarily due to increased sensitivity.

CONCLUSIONS:

In conditions similar to clinical practice, using computer-aided diagnosis significantly improved radiologists' detection of intracranial DSA-confirmed aneurysms of ≤6 mm.

Intracranial aneurysms are abnormal dilations of the cerebral arteries that may rupture and result in subarachnoid hemorrhage, a condition associated with high morbidity and mortality. The estimated prevalence of unruptured intracranial aneurysms in the population varies between 0.2% and 9% according to different postmortem and angiographic studies,¹ with most estimates in the 2%–3% range. The estimates of the risk of rupture of aneurysms are controversial,^2–5 but two-thirds of patients with aneurysm rupture either die or have serious morbidity.⁶

While DSA remains the criterion standard for the detection of intracranial aneurysms, MRA is widely accepted as a noninvasive diagnostic tool. In recent years, due to the increasing use and availability of MRA, incidental unruptured aneurysms are detected more frequently than in the past.^1,7 Older studies specifically evaluating the detectability of untreated aneurysms by using MRA compared with DSA showed a sensitivity from 67%–89%,^8,9 but only 35%–56% for aneurysms <5 mm^9–11; more recent studies have shown a sensitivity as high as 96.7%, which is comparable with that of DSA.^12–14

It is often difficult to detect small (<5–7 mm) or very small (<3 mm) aneurysms^15–17on maximum-intensity-projection images due to overlap of the aneurysm with adjacent arteries and to flow patterns that reduce signal. Aneurysms often occur at arterial branch points, where there is greater likelihood of vessel overlap. Additionally, TOF-MRA, the most common technique in clinical practice, is often limited by low signal intensity within the aneurysm due to irregular or slow flow.

We have developed an algorithm that is capable of identifying regions that are suspicious for intracranial aneurysms on TOF-MRA with high sensitivity.¹⁸ It can be considered automated because no human input is required to produce its results. Previous computer-aided diagnosis (CAD) algorithms were evaluated on a few cases from a single MR imaging scanner, or they were not fully automatic.^19,20 In other studies, CAD did not detect small or fusiform types of aneurysms,²¹ or its effectiveness was not tested with a proper reader performance study.²² Although there have been several performance studies on CAD schemes described by Arimura et al^19,23 by using receiver operating characteristic curve analysis,^20,24 none of these studies used DSA as a standard of reference for the presence or absence of aneurysms; therefore, the true CAD accuracy remains unknown.

We examined the practical use of our automated CAD scheme for detecting aneurysms by using DSA as the reference standard. We performed a retrospective multireader observer performance study by using MRA data from a variety of clinical sites with variable image quality.

Materials and Methods

Design of the Present Study

After review by the institutional review board, the present study was determined to be of minimal risk, and the requirement for consent was waived. We queried the radiology information system to find all TOF-MRA examinations of the brain that were performed for clinical purposes 0–30 days before DSA. This short time span increased the diagnostic reliability. Fifty cases were randomly chosen from the 312 cases in our data base, with the only requirements being that aneurysms must be ≤7 mm and the patients have no previously treated aneurysms. The cases were retrieved from the image archive, with protected health information removed and subject identifiers inserted. Ninety-one percent of these examinations were performed on 1.5T scanners: Signa Excite MR imaging (46%) (GE Healthcare, Milwaukee, Wisconsin); Genesis Signa (25%) (GE Healthcare); Magnetom Espree (10%) (Siemens, Erlangen, Germany); Signa HDx (8%) (GE Healthcare); Magnetom Avanto (2%) (Siemens). Six percent of examinations were performed on 3T scanners (Signa Excite MR imaging [4%]; Signa HDx [2%]). For all the examinations, standard protocols were used with gradient-echo TOF-MRA sequences (short TR, 512 × 512 in-plane resolution).

Two neuroradiologists then reviewed all MRAs and confirmed the number and location of aneurysms by using DSA as the reference standard for the presence and size of aneurysms. The location from DSA for each aneurysm was then mapped to a location in the MRA dataset by a radiologist.

CAD Algorithm

In a previous article, we described in detail the fully automatic CAD scheme for detecting aneurysms on 3D TOF-MRA images.¹⁸ Briefly, it applies an automatic-segmentation algorithm based on global thresholding and region-growing schemes that generate separate 3D regions (representing a group of connected vessels). Next, it calculates the centerline of each 3D region, resulting in 3D thinned vessel representations, which are later transformed into vector representations, which we refer to as “trunks.” It uses an inner tangent sphere-testing method to calculate the radius of the vessel at each trunk. Subsequently, it applies a single-point seeded distance transformation algorithm and radius-fitting to detect the change in the radii of vessels. On the basis of these calculations, initial points of interest are created.

The algorithm also uses 2 other supplementary methods we found useful in case of incomplete segmentation to collect initial points of interest. One is based on subtracting the segmented vessels from the raw image and collecting the points of interest from the difference image (floater points of interest); in the other method, we apply a dot-enhancement filter to the raw image and collect points of interest from the filtered images (dot points of interest). These steps are necessary because of signal drop-out sometimes seen on 3D TOF images. The series of empirically predetermined filtering rules remove most (about 99%) of the initial points of interest, and the remaining points of interest are then assigned a score (ranging from 0 to 1) and are output as aneurysm suspects. Clusters of suspect points of interest are combined to eliminate overlapping detections.

Image Review

The CAD algorithm was applied to all 50 cases, and the results were represented as a DICOM-structured report that was sent to a 3D viewing system used in our clinical practice (Aquarius iNtuition; TeraRecon, San Mateo, California). The algorithm allowed a configurable number of suspicious regions, or hits, per examination. In this study, we limited that number to a maximum of 10, and for this set of 50 cases, the mean number of hits was 7.2. The study used a multireader, multicase, double-crossover, free-response design. Six experienced radiologists (hereafter referred to as readers) participated in this study, including 5 Certificate of Added Qualification–certified neuroradiologists and 1 general radiologist (range of 4–22 years on staff), trained on the TeraRecon system and the CAD algorithm. All cases were presented to readers twice, once with CAD and once without CAD, with 5 weeks' separation. Half of the cases (determined by random selection) were presented first without CAD. Each presentation used a unique identifier, so the readers were blinded to all other imaging studies and clinical data for each subject.

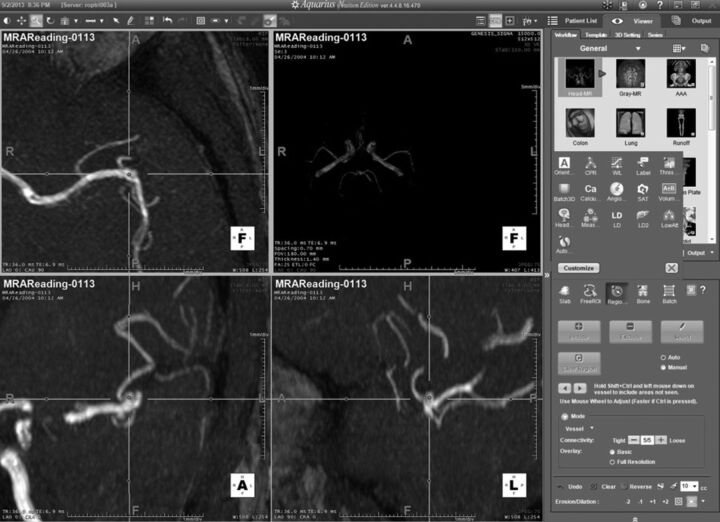
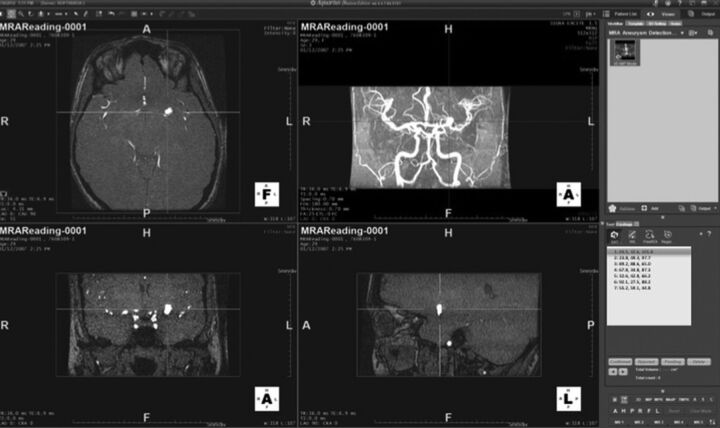
The 50 cases of the first set were made available to readers for 5 weeks. The readers were aware neither of the number of DSA-confirmed aneurysms nor of the size range. Readers were allowed to freely mark suspected regions, recording the coordinates (x, y, z in millimeters) and assigning a level of certainty (from 1 to 5) to all suspected regions that might represent an aneurysm for each dataset. The certainty scale used reflected clinical decision-making as follows: 1) no aneurysm detected; 2) probably not, follow-up MRA in 6 months; 3) probably, use CTA to confirm; 4) likely, use DSA to confirm, and possibly treat; 5) unequivocal. Readers were able to view the study images by using interactive multiplanar, maximum-intensity-projection, and volume-rendering methods, according to their preferences. The actual CAD results were depicted as blue dots on the rendering (they could be hidden if preferred) (Fig 1). Each suspicious point could be centered in the rendering view by using a clickable list (Fig 2). In the final step, an independent adjudication (I.L.Š.B. and B.J.E.) determined whether marked regions of interest were correct, denoted as lesion localization, or incorrect, denoted as nonlesion localization. A mark within 1 cm of the true location was considered a correct localization.

Fig 1.

Example of examination visualization in a patient without an intracranial aneurysm. The CAD outputs are depicted as blue dots on different MRA projections (shown here as gray dots).

Fig 2.

Rendering showing the algorithm implemented in a 3D viewing system with the suspicious point centered in the rendering view by using a clickable list.

Statistical Analysis

Of the 50 cases selected, 2 were rejected after ratings were obtained but before statistical analysis: 1 with 9 aneurysms, which made confident identification of reader markings too challenging; and another in which the DSA did not include injection of 1 of the carotid arteries. The remaining 48 cases (39 with no aneurysm; 9 with ≥1 aneurysm) were included for analysis.

The lesion localization and nonlesion localization ratings were combined to produce the alternative free-response receiver operating characteristic curve with the figure of merit (FOM), which is the area under the alternative free-response receiver operating characteristic curve.^25,26 The marked-pair data were analyzed by using jackknife alternative free-response operating characteristic curve analysis software (Version 4.1a; http://www.devchakraborty.com).^25–27 The nonlesion localizations on cases with at least 1 aneurysm were not used in the analysis. The Dorfman-Berbaum-Metz mixed-model method²⁸ was used for significance testing. A fixed-reader random-case model was used for the primary analysis because the selected radiologists were not considered a random sampling of radiologists.

Sensitivity, specificity, and accuracy rates were computed for CAD and no CAD for each reader; SAS 9.3 (SAS Institute, Cary, North Carolina) was used for this analysis. For these calculations, a rating of ≥3 on any case was considered a detection (the highest rating a reader assigned for each case was used, regardless of location). Because the goal was to improve clinical care, any patient with at least 1 suspected aneurysm would typically go to DSA; therefore, we collapsed cases with at least 1 rating of 3, 4, or 5 into positive cases.

Results

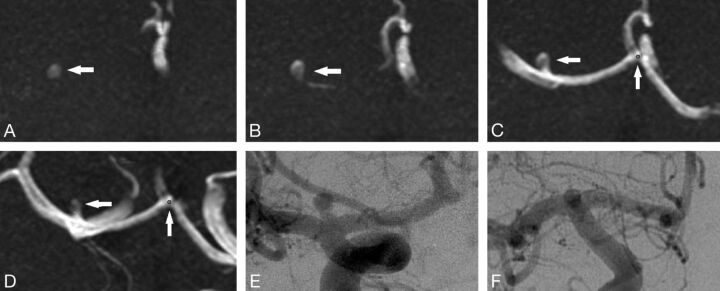
For the 48 cases analyzed, there were 9 cases with aneurysms (11 aneurysms) and 39 cases without aneurysm. Table 1 highlights the size and location of the 11 aneurysms. The mean aneurysm size was <5 mm (mean = 3.12 mm, median = 2.50 mm, minimum = 1.1, maximum = 6). Ninety-one percent of the aneurysms (10/11) were detected by our CAD algorithm, including the 1.1-mm aneurysm (Fig 3). The aneurysm that was not detected was actually larger than average (4.2 mm) but had a rather vessel-like appearance, which likely accounts for the false-negative (Fig 4).

Table 1:

Location and size of 11 aneurysms^a

No.	Size (mm)	Location
1	3.6	Left middle cerebral artery (M1)
2	2.5	Right posterior communicating artery
3	4.2	Right internal carotid artery terminus
4	2.1	Right distal anterior cerebral artery (A1)
5	2.1	Right supraclinoid internal carotid
6	2.2	Left pericallosal artery aneurysm (A2)
7	1.1	Left middle cerebral artery (M1)
8	6.0	Right proximal cavernous internal carotid artery
9	4.0	Left superior cerebellar artery
10	4.0	Left internal carotid artery proximal to ophthalmic
11	2.5	Left middle cerebral artery (M1)

^aThe sizes shown are the greatest dimension based on the DSA images.

Fig 3.

The smallest aneurysm (1.1 mm).

Fig 4.

This aneurysm was missed by the CAD algorithm. We believe that the error was because the aneurysm had a relatively consistent diameter up to the dome, thus not meeting the curvature criteria. This was detected by all radiologists with and without CAD.

Impact of CAD on Reader Figure of Merit

The mean number of suspicious regions per patient was 7.2 when using CAD. Overall there were 393 lesion localizations and 237 nonlesion localizations among the 6 readers. Of true-negative cases (cases in which DSA showed no aneurysm), 20.5% were correctly marked as negative for aneurysm by all readers without CAD, and 20.5%, by all readers with CAD.

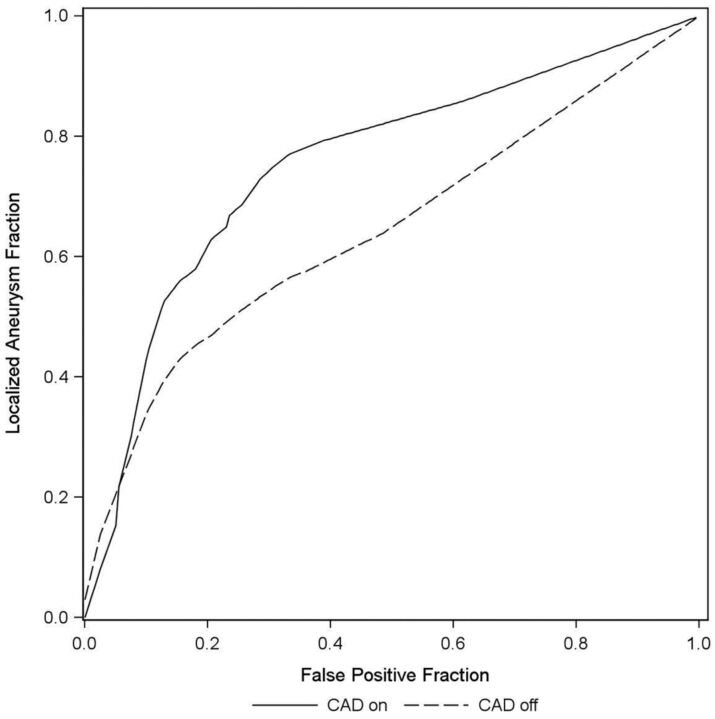
No aneurysm was missed by all readers with CAD. Five aneurysms (45.5%) were found by all readers only when CAD was used (mean size = 3.59 mm, median = 4 mm). Every aneurysm was missed by at least 1 reader without CAD. Five of the 6 readers achieved higher FOMs by using CAD, whereas 1 reader did not. For each of those 5 readers, the FOM improved. For 1 reader (reader 6), the FOM decreased. For all readers combined, the mean FOM improved from 0.655 to 0.759, a mean change in the FOM attributable to using CAD of 0.10 (95% CI, 0.03–0.18). This improvement was statistically significant (F_1,47 = 7.00, P = .011). These results are depicted in Table 2 and Fig 5.

Table 2:

Estimated figure of merit by reader and method^a

	Estimated FOM
	CAD−	CAD+	Difference	95% CI	P Value
Reader 1	0.667	0.726	0.060	(−0.184–0.304)	.62
Reader 2	0.660	0.842	0.182	(0.021–0.344)	.028
Reader 3	0.789	0.892	0.103	(−0.071–0.276)	.24
Reader 4b	0.594	0.746	0.152	(−0.042–0.347)	.12
Reader 5	0.514	0.717	0.203	(−0.158–0.564)	.26
Reader 6	0.707	0.630	-0.077	(−0.371–0.217)	.60
Overall	0.655	0.759	0.104	(0.025–0.183)	.011

^aFor all except reader 6, there was a definite increase in the FOM when CAD results were available, though the difference was statistically significant for only 1 reader (reader 2).

^bGeneral radiologist; all other readers are neuroradiologists.

Fig 5.

A free-response receiver operating characteristic curves aneurysm fraction.

Impact of CAD on Reader Sensitivity, Specificity, and Accuracy

The mean sensitivity value for all readers without CAD was 70.40 ± 10.47%, and this improved to a mean of 83.35 ± 8.48% with CAD. Five of 6 readers demonstrated higher sensitivity with CAD, and 1 reader improved the sensitivity from 77.8% to 100%. The mean specificity without CAD was 79.50 ± 3.31% and 75.65 ± 4.37% with CAD. The mean accuracy without CAD was 77.78 ± 3.94% and 77.10% ± 4.64% with CAD. Sensitivity, specificity, and accuracy for each reader are depicted in Table 3.

Table 3:

Individual reader performance results

	Sensitivity (95% CI)	Specificity (95% CI)	Accuracy (95% CI)
Reader 1
CAD−	55.6% (5/9) (26.7%–81.1%)	76.9% (30/39) (61.7%–87.4%)	72.9% (35/48) (59.0%–83.4%)
CAD+	77.8% (7/9) (45.3%–93.7%)	66.7% (26/39) (51.0%–79.4%)	68.8% (33/48) (54.7%–80.1%)
Reader 2
CAD−	66.7% (6/9) (35.4%–87.9%)	74.4% (29/39) (58.9%–85.4%)	72.9% (35/48) (59.0%–83.4%)
CAD+	88.9% (8/9) (56.5%–98.0%)	79.5% (31/39) (64.5%–89.2%)	81.3% (39/48) (68.1%–89.8%)
Reader 3
CAD−	77.8% (7/9) (45.3%–93.7%)	84.6% (33/39) (70.3%–92.8%)	83.3% (40/48) (70.4%–91.3%)
CAD+	100% (9/9) (70.1%–100.0%)	79.5% (31/39) (64.5%–89.2%)	83.3% (40/48) (70.4%–91.3%)
Reader 4a
CAD−	66.7% (6/9) (35.4%–87.9%)	82.1% (32/39) (67.3%–91.0%)	79.2% (38/48) (65.7%–88.3%)
CAD+	77.8% (7/9) (45.3%–93.7%)	76.9% (30/39) (61.7%–87.4%)	77.1% (37/48) (63.5%–86.7%)
Reader 5
CAD−	88.9% (8/9) (56.5%–98.0%)	79.5% (31/39) (64.5%–89.2%)	81.3% (39/48) (68.1%–89.8%)
CAD+	77.8% (7/9) (45.3%–93.7%)	74.4% (29/39) (58.9%–85.4%)	75% (36/48) (61.2%–85.1%)
Reader 6
CAD−	66.7% (6/9) (35.4%–87.9%)	79.5% (31/39) (64.5%–89.2%)	77.1% (37/48) (63.5%–86.7%)
CAD+	77.8% (7/9) (45.3%–93.7%)	76.9% (30/39) (61.7%–87.4%)	77.1% (37/48) (63.5%–86.7%)

^aGeneral radiologist, all other readers are neuroradiologists.

Discussion

This report studies the value of CAD in an image-viewing environment that is similar to that in clinical practice. The performance in detecting intracranial aneurysms was significantly improved with CAD. Most important, in comparison with previous studies, we used DSA as a criterion standard for all cases, and we included cases that had multiple and small aneurysms (mean size = 3.2 mm).

In the present study, the overall performance of the pool of 5 neuroradiologists and 1 general radiologist was significantly improved when using the CAD algorithm because the mean FOM increased from 0.655 to 0.759. The absolute numbers (both with and without CAD) were lower than analogous data seen in previous studies. In the 2-reader performance studies evaluating the algorithm of Arimura et al,^19,23 the average areas under the receiver operating characteristic analysis curve were improved from 0.931 to 0.983 (sensitivity and specificity values were not given)^20,29 and from 0.851 to 0.903 (with a sensitivity of 82.7% and a specificity of 88.6%).²⁴ However, in previous studies, readers were informed that there was either zero or 1 aneurysm per case (making false-positives less likely), DSA was not used as the criterion standard imaging method, the mean aneurysm size was larger, and the non-CAD images were presented first with CAD presented after them.

We tested using the criterion standard of DSA, which is important because 3D TOF can have artifacts causing signal to be lost in the region of an aneurysm. In cases in which there might be signal loss on the 3D TOF, the prior studies might conclude that an MRA is negative for aneurysm. Similarly, artifacts on MRA that falsely gave the appearance of an aneurysm might have been incorrectly counted as an aneurysm without DSA to deny its presence.

In the present study, we did see overall sensitivity increased significantly (from the range of 55.6%–88.9% to the range of 77.8%–100%), suggesting that with proper interpretation of the CAD results, 100% sensitivity is possible and was achieved by 1 individual. We noted also a mild decrease in specificity from the range of 74.4%–84.6% to 66.7%–79.5% and a slight decrease in accuracy from 77.78% to 77.10%. This was seen in other CAD reports^30,31 and was not surprising because the improved sensitivity is typically accompanied by an increase in the average number of false-positive results. We designed our study to be like clinical practice, and the higher number of negative cases may account for the lower apparent performance.

Other reports suggest that CAD increases the performance of nonspecialists, approaching that of specialists but with no significant benefit to specialists,^20,24 but we did not observe that. Tables 1 and 2 show the improved performance of the general radiologist (marked with a footnote). This is contrary to the results of Kakeda et al²⁴ but similar to those of Hirai et al.²⁰ Unlike the above-mentioned observer performance studies, our readers did not know a priori how many aneurysms were present in each case and therefore searched for any suspicious areas and marked them together with the confidence level. Conventional receiver operating characteristic analysis with the FOM as the area under the receiver operating characteristic curve has limited value, with the rating of the highest rated mark in the image only, without taking into account the aneurysm locations. In contrast, free-response operating characteristic analysis is considered more sensitive and enables more precise evaluation of the performance of radiologists (with greater statistical power) by using multiple responses, each with information on both the confidence level and location.³² The estimated FOM is, therefore, interpretable as the probability that the rating of the highest rated and correct detection on an aneurysm case exceeds the rating of the highest-rated detection mark on a normal case. The higher statistical power for this approach is an important issue in observer performance studies because it determines the probability of detecting a true difference between modalities/groups while controlling the probability of detecting nonexisting differences.³³

Our CAD algorithm turned out to be efficient in terms of the workflow; though we did not specifically focus on measuring the time of reader evaluations, the algorithm implemented in a clinical rendering viewing system enabled them to efficiently review the regions of concern. Therefore, the overall time spent on the evaluation did not change.

Improved CAD-attributable efficiency at aneurysm detection has clinical impact when making further diagnostic and management decisions. Most interesting, treatment guidelines are different worldwide, and this difference is valid particularly for smaller aneurysms (early invasive treatment after detection versus follow-up). The higher detection rate would, therefore, directly influence the decision-making process. Increasing the level of reader confidence for equivocal cases would also provide better guidance with further diagnostic possibilities (CTA versus DSA).

Our study had a number of limitations. We had only 1 general radiologist in the study group, which limits our ability to determine whether there is a difference in the value of CAD for specialists versus nonspecialists. In many CAD applications, there is a much greater benefit to general radiologists than specialists, but in this study, we found a benefit for both specialists and generalists. Additionally, the cases in this study were randomly selected and were of variable quality. Only 6% of examinations were conducted on a 3T scanner. Some MRA examinations, particularly older ones, had lower signal-to-noise and more intensity variation. It is possible that the CAD algorithm could see through these problems and that the benefit may be greater with older technologies than with current MR imaging scanners. It is also possible that CAD does better with newer examinations where more vessels are visualized, increasing the superimposition problem.

Conclusions

A CAD algorithm significantly improved the performance of radiologists (specialists and general) in detecting intracranial aneurysms ≤6 mm in conditions that are similar to those in clinical practice.

ABBREVIATIONS:

CAD

computer-aided diagnosis

FOM

figure of merit