Intracranial Aneurysmal Pulsatility as a New Individual Criterion for Rupture Risk Evaluation: Biomechanical and Numeric Approach (IRRAs Project)

Abstract

BACKGROUND AND PURPOSE:

The present study follows an experimental work based on the characterization of the biomechanical behavior of the aneurysmal wall and a numerical study where a significant difference in term of volume variation between ruptured and unruptured aneurysm was observed in a specific case. Our study was designed to highlight by means of numeric simulations the correlation between aneurysm sac pulsatility and the risk of rupture through the mechanical properties of the wall.

MATERIALS AND METHODS:

In accordance with previous work suggesting a correlation between the risk of rupture and the material properties of cerebral aneurysms, 12 fluid-structure interaction computations were performed on 12 “patient-specific” cases, corresponding to typical shapes and locations of cerebral aneurysms. The variations of the aneurysmal volume during the cardiac cycle (ΔV) are compared by using wall material characteristics of either degraded or nondegraded tissues.

RESULTS:

Aneurysms were located on 6 different arteries: middle cerebral artery (4), anterior cerebral artery (3), internal carotid artery (1), vertebral artery (1), ophthalmic artery (1), and basilar artery (1). Aneurysms presented different shapes (uniform or multilobulated) and diastolic volumes (from 18 to 392 mm³). The pulsatility (ΔV/V) was significantly larger for a soft aneurysmal material (average of 26%) than for a stiff material (average of 4%). The difference between ΔV, for each condition, was statistically significant: P = .005.

CONCLUSIONS:

The difference in aneurysmal pulsatility as highlighted in this work might be a relevant patient-specific predictor of aneurysm risk of rupture.

Intracranial aneurysms kill about 15,000 people in Europe each year. Most are young, between 40 and 60 years old. New medical imaging techniques are now able to clearly depict intracranial aneurysm, but no systematic screening of this disease exists at the moment. The main reason is that 2%–6% of the general population lives with an aneurysm,¹ but only 0.5% of these will rupture. Screening for intracranial aneurysm is not justified unless it is capable of detecting vulnerable aneurysms. Subarachnoid hemorrhage is the consequence of aneurysm rupture and approximately 12% of patients with SAH die before receiving medical attention, 40% of patients will die within the first month, and 30% will present with a severe permanent disability. Nevertheless, with brain imaging being more frequently and widely used, a growing number of intracranial aneurysms are being diagnosed, introducing the question of which aneurysms harbor a sufficiently high risk of rupture to merit a prophylactic repair. This question remains unsolved at the moment and the therapeutic decision for an unruptured aneurysm is still a challenging point discussed by the neurosurgeon/neurointerventionist based on sparse epidemiologic clinical data that cannot represent the specific individual risk of the patient.

Recent publications have addressed this issue and have demonstrated that, among other variables affecting the natural history of aneurysms, size and location represent independent predictors of both risk of rupture and surgical/endovascular repair outcomes.^2,3 Other parameters, such as irregular aneurysm shape and the presence of blebs are recognized as markers of weak wall structure and high risk of rupture. Rapid aneurysm growth is also likely a risk factor for rupture.⁴

From a mechanical point of view, the rupture of an aneurysm occurs when wall tension exceeds the strength of the wall tissue. Because these quantities cannot be assessed via conventional medical imaging, a natural approach is to compute the wall tension and set a rupture threshold.

Few studies consider the coupled fluid-structure interaction (FSI) problem, where the flow equations for blood are solved together with the structural equations for the tissue.⁵ The problem is the lack of data on mechanical properties of cerebral arteries and aneurysms; most of the studies based on an FSI^6–10 framework do not use experimental mechanical behavior of the aneurysm wall as input. A few exceptions exist for abdominal aorta aneurysms^11,12 but not for intracranial aneurysms until recently when, in a study by Costalat et al,¹³ the aneurysm wall properties were characterized and a classification of aneurysm wall behavior was carried out. One of the main conclusions of this work was that the clinical status of the aneurysm (unruptured, preruptured, and ruptured) was strongly correlated with the mechanical behavior of the aneurysm wall and, hence, a classification was proposed (stiff, intermediate, and soft).

This was followed with FSI computations by Sanchez et al,¹⁴ who demonstrated for 1 specific aneurysm that the different mechanical properties of the aneurysm wall (stiff or soft) are responsible for significantly different variations in aneurysm volume over the cardiac cycle (pulsatility). A parametric study was also achieved in this work and demonstrated that uncertainties did not change the main conclusion.

The further application of these results to the in vivo setting and in particular to cerebral aneurysms arising from the circle of Willis is an additional important step.

The aim of this work was to investigate and verify the correlation between wall biomechanical properties (stiff and soft) and aneurysmal volume variation during the cardiac cycle for a variety of aneurysms that differ in shape and location in the circle of Willis.

This study was conceived and carried out as part of the Individual Risk of Rupture Assessment consortium, which is a research project dedicated to the evaluation of patient-specific risk of rupture of cerebral aneurysms. The consortium brings together neurosurgeons, neuroradiologists, and researchers in biomechanical engineering in a common translational research project.

Materials and Methods

Identification of Mechanical Behavior of Aneurysm Wall

The details of the study establishing the correlation between the aneurysm status and tissue mechanical properties are given in the work of Costalat et al.¹³ The methodology and main results are briefly given for the sake of completeness. A similar study was conducted by Duprey et al¹⁵ for thoracic aortic aneurysms.

Each sample was studied as appropriate for biomaterials.^16–19 Only the meridional axis of the aneurysm was chosen to preserve maximum length of the aneurysmal tissue in the sample, given the very small size of each specimen and the fragility of the tissue. Using these measurement series, a model of the tissue behavior was proposed for large displacements to represent the evolution of the stress in the materials.²⁰ For this purpose, the assumption that the material is isotropic and noncompressible was made and the hyperelastic model of Mooney-Rivlin with 3 parameters was selected.¹ It reads:

where W is the strain energy potential, I₁ = tr(C) and I₂ = $\frac{1}{2}$(tr²(C) – tr(C²)) are the first and second strain invariants of the right Cauchy-Green deformation tensor C, and C₁₀, C₀₁, and C₁₁ are the material coefficients.

All unruptured aneurysms presented as stiffer tissue than the ruptured aneurysms.

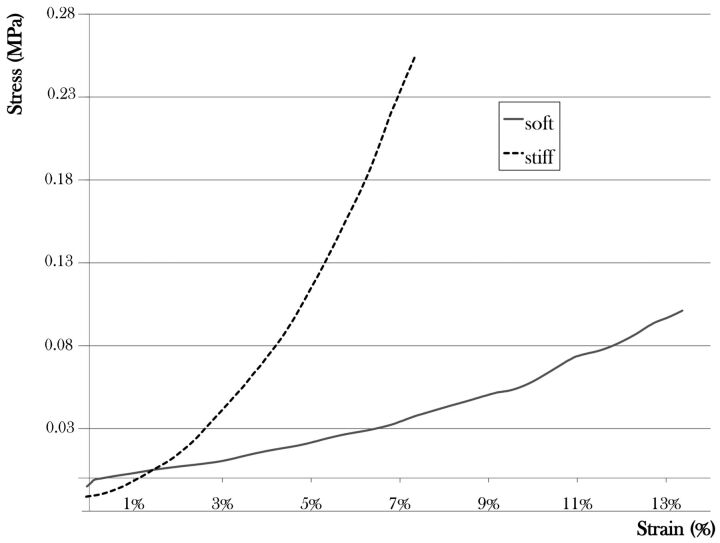
Their mechanical behavior was either stiff or intermediate. Conversely, all ruptured aneurysms correspond to a soft tissue. The corresponding parameters are given in Table 1 while the strain/stress curves are displayed in Fig 1.

Table 1:

Material coefficients of the aneurysm walls used in the present study

Aneurysm	C10 (MPa)	C01 (MPa)	C11 (MPa)
Soft	0.024	0.026	0.42
Stiff	0.39	0	22.14

Fig 1.

Nominal stress/engineering strain curves representing the average mechanical properties of the soft and the stiff classes.

Numeric Method

Aneurysmal Geometry.

Aneurysm geometry was obtained from 3D rotational angiography. Using dedicated software ScanIP (Simpleware, Exeter, United Kingdom), the aneurysmal geometries were cleaned up by keeping only the aneurysms and the parent vessels to reduce the region of interest. A low-pass filter was applied on the geometries to reduce noise-to-signal ratio. The results were exported as stereolithography files to proceed to numeric analysis.

Simulation Parameters.

The flow boundary conditions imposed were obtained from specific patient examinations by using phase-contrast MR imaging for each aneurysm location (3T Skyra; Siemens, Erlangen, Germany). The velocity profiles were considered as uniform. Outlet pressure was computed by computational fluid dynamics and used as boundary conditions at the outlet of the computational domain. The pressure was obtained by resolving the 1D equations in the arterial network with boundary flow conditions from the imaging measurement.²¹

An intracranial pressure of 20 mm Hg²² was applied on the external surface of the geometries to recreate the in vivo conditions.

Physical Modeling.

The blood flow within the computational domain is described by the incompressible Navier-Stokes equations (2) and (3)

where v_f is the time dependent flow velocity vector, ρ_f is the attenuation of blood, and σ^f is the stress tensor for the fluid part. The flow is assumed to be laminar, a reasonable assumption given the moderate value of the Reynolds number (Re ≈ 300). Blood is modeled as a Newtonian fluid,⁴ of attenuation of ρ_f = 1050 kg/m³ and dynamic viscosity of μ = 0.004 Pa × s.^9,23–25

where p is the pressure, I is the identity tensor, and D is the rate of deformation tensor.

For the parent artery, a linear elastic model was selected to focus the attention on the aneurysmal sac and to reduce the computational time. The structural equation solved for both the artery and aneurysmal sac reads⁵:

where σ^s is the Cauchy strain for the structural part and v_s stands for the structural velocity vector.

The aneurysm wall is modeled as an isotropic incompressible hyperelastic material⁶:

where F is the transformation gradiant tensor, E is the Green Lagrangian strain tensor, and W is the strain energy potential defined in Eq. (1).

The material used for the parent artery has the following properties: Young modulus E = 3 MPa, Poisson ratio ν = 0.49, specific mass ρ_s = 2300 kg/m³, and thickness e_pa = 0.6 mm.^24,26 The thickness of the aneurysm wall is e = 0.38 mm. A linear model was used for the arterial wall because the deformations are small enough in all cases (<5%) to stay in the small deformation theory.

Furthermore, the edge nodes of the arterial extremities are taken away from the displacement in the longitudinal direction.

FSI Computations.

Computations were performed by using Workench version 13 (ANSYS, Canonsburg, Pennsylvania). The fluid motion equations were solved with the software CFX, which uses the finite volume approach and the Newton-Raphson method for solving the subsequent nonlinear system. For the structural part, Mechanical software employed the finite-element method and the Newton-Raphson algorithm. The wall pressure resulting from the fluid was imported as boundary conditions in the structural analysis while wall displacement calculated by the structure solver was imported as a boundary condition for the fluid solver; this procedure was carried out in an iterative manner within each time-step. It was an iterative implicit coupling. At the interface of the 2 physical domains, the element type differs and the nodes of the 2 meshes did not coincide, so surface interpolation was carried out.²⁷ For each FSI computation, a time-step of 0.004 seconds was used. The structural meshes were composed by 2500 to 5000 shell elements and the fluid meshes by 100,000 to 300,000 tetrahedral elements. These meshes were fine enough to ensure the convergence of the computations. The 2 FSI computations of the reference case from Sanchez et al¹⁴ were performed for mesh refinements multiplied by 10 (about 30,000 elements for structural mesh and 1,000,000 elements for fluid mesh). Despite a significant increase of the computation time, the results were similar. For example, in the soft case, the maximal mesh displacement was 0.78 instead of 0.77 mm (variation of 1.3%) and the volume variation was 44.3 mm³ instead of 44 mm³ (variation of 0.7%).

A structural computation was performed before the FSI computation to determine the stress state of the acquired geometry. All the details about the initial stress of the aneurysm geometry are given in Sanchez et al.¹⁴

Wall Motion Analysis.

For each aneurysmal geometry, 2 FSI computations were performed by using the 2 different biomechanical properties (stiff and soft) defined in the Identification of Mechanical Behavior of Aneurysm Wall section. Volume variations and wall motions were calculated for each aneurysm. For each case, the systolo-diastolic variation of the volume of the aneurysm (ΔV) was computed from the results. The maximal mesh displacement on the aneurysm sac D_max was also calculated. ΔV represents global information about the aneurysmal sac behavior whereas D_max provides local information (maximal displacement of a point of the aneurysm boundary).

To compare ΔV and D_max between soft and stiff material for different aneurysms, we defined the following ratio:

A pulsatility index was also defined as: Pulsatility = ΔV/V, where V is the diastolic volume of the aneurysmal sac.

Statistical Analysis

A statistical analysis was performed to evaluate the influence of ΔV and D_max in soft and stiff cases. The comparison was made by using a nonparametric Wilcoxon rank test for continuous variables and a Fisher exact test for categoric ones. Statistical significance threshold was set at 5%. Statistical analyses were performed by using SAS version 9.1 (SAS Institute, Cary, North Carolina).

Results

Aneurysm Population

Twelve aneurysms from 12 different patients were computed with the stiff and the soft materials. These aneurysms were located on 7 different arteries: left and right middle cerebral arteries (4 cases), anterior cerebral artery (3 cases), ICA (1 case), vertebral artery (1 case), ophthalmic artery (1 case), and basilar artery (2 cases). These had a variety of shapes: simple (uniform) or complex (multilobulated). The volume varied from 18 mm³ to 392 mm³. Geometric information is displayed in Table 2.

Table 2:

Aneurysm geometry information

Aneurysm	Location	V (mm3)	Shape	D (mm)	N (mm)	D/N
1	MCA R	61	Simple	4.8	4	1.2
2	MCA L	51	Complex	3.4	3.75	0.91
3	ACA	161	Simple	5.25	5.6	0.94
4	MCA R	188	Complex	5.5	6.5	0.85
5	ICA	392	Complex	9.2	5	1.84
6	VA	45	Simple	4	2.3	1.74
7	MCA L	212	Complex	7.8	6.6	1.18
8	ACA	232	Complex	8	4.5	1.78
9	ACA	79	Complex	6.85	2.9	2.36
10	OA	138	Simple	6.1	4.3	1.41
11	BA	68	Complex	4.4	3.9	1.13
12	BA	18	Simple	3	3	1

Note:—V indicates diastolic volume; D, the dome size; N, the neck size; D/N, the ratio of dome/neck; ACA, anterior cerebral artery; VA, vertebral artery; OA, ophthalmic artery; BA, basilar artery; R, right; L, left.

Wall Motion Results

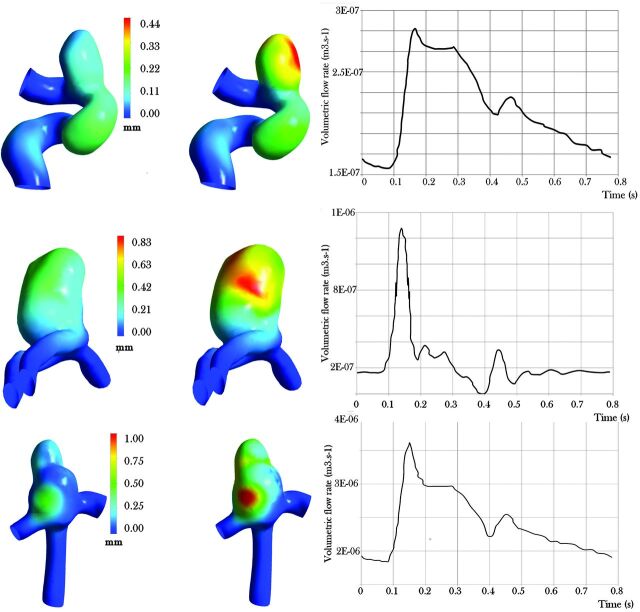
Figure 2 gives an example of the FSI results for 3 different cases by displaying maximum displacement for the simulations with soft or stiff materials. All results of the patient-specific FSI computations are displayed in Tables 3 and 4. Two aneurysms (5 and 6) show unusual results. For aneurysm 5, the volume variation is 149 mm³. The important initial volume of the aneurysm sac, almost 400 mm³, can explain this important variation. This aneurysm could be considered as a giant aneurysm. Nevertheless, the pulsatility ratio is still in the range of 30% in comparison to an overall mean of 25% for the cases. For aneurysm 6, the pulsatility is much more important than in the other cases. That is the result of a volumetric flow rate more important in this location (vertebral artery) for this specific patient compared with the others (Table 4); this due to the particularity of this cerebral arterial network.

Fig 2.

FSI maximal mesh displacement results for the systolic pressure for aneurysms 10 (top), 8 (middle row), and 7 (bottom row) with the volumetric flow rate imposed at the inlet (on the left for the stiff material and on the right for the soft material).

Table 3:

Results of FSI computations for 12 different aneurysms for stiff and soft materials

Aneurysm	Material	V (mm3)	ΔV (mm3)	Pulsatility = ΔV/V (%)	>Dmax (mm)
1	Soft	61	10	16	0.35
	Stiff		1	2	0.12
2	Soft	51	8	16	0.32
	Stiff		0.5	1	0.09
3	Soft	161	44	27	0.7
	Stiff		6	4	0.26
4	Soft	188	37	20	0.71
	Stiff		7	4	0.15
5	Soft	392	149	38	1
	Stiff		18	5	0.45
6	Soft	45	33	73	1.8
	Stiff		4	9	1.2
7	Soft	212	60	28	1.05
	Stiff		14	7	0.48
8	Soft	232	54	23	0.84
	Stiff		10	4	0.4
9	Soft	79	15	19	0.48
	Stiff		3	4	0.15
10	Soft	138	26	19	0.47
	Stiff		5	4	0.17
11	Soft	68	11	16	0.42
	Stiff		2.5	4	0.12
12	Soft	18	4	22	0.27
	Stiff		0.5	3	0.14

Table 4:

Comparison between volumetric flow rate variation and volume variation of soft aneurysmal sacs

Aneurysm	Systole Flow Rate (m3·s−1)	Flow Rate Variation (m3·s−1)	ΔV (mm3)
1	3.21 × 10−06	1.78 × 10−06	10
2	3.10 × 10−06	1.75 × 10−06	8
3	2.85 × 10−06	1.95 × 10−06	44
4	3.36 × 10−06	1.84 × 10−06	37
5	4.21 × 10−06	2.15 × 10−06	149
6	3.55 × 10−06	4.454 × 10−05	33
7	3.12 × 10−06	1.77 × 10−06	60
8	1.28 × 10−06	1.27 × 10−06	54
9	1.62 × 10−06	7.94 × 10−07	15
10	2.92 × 10−07	1.36 × 10−06	26
11	5.07 × 10−06	3.34 × 10−06	11
12	5.07 × 10−06	3.34 × 10−06	4

A significant difference was observable between ΔV for a stiff material and for a soft material (P = .005). Consequently, the pulsatility index (ΔV /V) was obviously more important for a soft aneurysmal sac (average of 26%) than for a stiff aneurysmal sac (average of 4%), despite the relatively small number of aneurysms considered.

Naturally, we found the same difference for the ratio R_v: R_v varies from 4 (aneurysm 7 and 10) to 16 (aneurysm 2) for an average of 7. R_d also showed differences between stiff and soft materials but to a lesser extent: the minimum was 1.5 (aneurysm 6) and the maximum was 5 (aneurysm 4) and the average was 3 (Table 5). The difference between ΔV and D_max for each condition was statistically significant: P = .005 for ΔV and P = .02 for D_max.

Table 5:

Results for R_v and R_d for the 12 cases

Aneurysm	Volume (mm3)	Rv = ΔVsoft/ΔVstiff	Rd = Dmaxsoft/Dmaxstiff
1	61	10	2.9
2	51	16	3.5
3	161	7.3	2.7
4	188	5.3	4.7
5	392	8.3	2.2
6	45	8.25	1.5
7	212	4.3	2.2
8	232	5.4	2.1
9	79	5	3.2
10	138	5.2	2.8
11	68	4.4	3.5
12	18	8	1.9

Discussion

Our results clearly suggest that the wall displacement provides information about the level of degradation of the aneurysm wall and, thanks to the findings of Costalat et al,¹³ about the rupture risk of the aneurysm sac. Our study shows that whatever the location of the aneurysm on the circle of Willis, the aneurysmal pulsatility was about 7 times higher for soft/ruptured aneurysms in comparison with stiff/unruptured aneurysms (26% versus 4%). That is the result of a volumetric flow rate more important in this location (vertebral artery) compared with the others (Table 4). These observations are consistent with our previous work (the study from Sanchez et al,¹⁴ using FSI computations) where a significant difference between the displacements and volume variations corresponding to the soft (close to the rupture) and stiff (undegraded) tissues was observed in a particular case. This result is generalized to the entirety of the circle of Willis in this paper.

Interestingly, in an observational study on 51 patients, Hayakawa et al,²⁸ using 4D CT angiography, highlighted that the pulsation of the aneurysm sac (or volume variation) between ruptured aneurysms and unruptured aneurysms was significantly different. In their study, 12/51 cerebral aneurysms were ruptured. Among these 12 ruptured cerebral aneurysms, a pulsation was observed in 9 cases (75%). Thirty-nine cerebral aneurysms were unruptured; among these 39 unruptured cerebral aneurysms, a pulsation was observed in 12 cases (30%). Two of these 12 pulsating unruptured cerebral aneurysms were treated by surgery because of the clinical background of the patients. They came to the conclusion that the detection of pulsation in an unruptured aneurysm could therefore be a clue of an important risk factor. Our results confirm this point of view.

Furthermore, the precision needed to identify the aneurysmal wall motion variation between unruptured/ruptured aneurysm would be about 0.1 mm (D_max) or 0.5 mm³ (ΔV) according to our study. New imaging techniques may approach this high resolution level in recent literature (for example Ishida et al²⁹ and Zhang et al³⁰).

To date, the most relevant solution has been proposed by Karmonik et al³¹ who used 2D phase contrast MR imaging (1.5T MR imaging) to observe wall displacement over the cardiac cycle on 7 patients (7 aneurysms) and 3 different locations (anterior communicating artery, basilar artery, and ICA). This noninvasive technique was accurate enough to measure wall displacements as small as 0.04 mm, in the range of the expected wall displacement reported in our study. New generation MR imaging at 3T could offer a more accurate depiction of the wall motion in the next future.

As already stated, D_max gives local information about the wall displacement and in some cases, this parameter is not accurate enough to clearly demonstrate a difference between degraded/ruptured and nondegraded/unruptured aneurysms. The variation of the maximal mesh displacement measured by the software depends strongly on the displacement of the artery. The deformation of the artery induces an additional displacement of the mesh of the aneurysmal sac. Then, the bulge of the artery is added to the displacement of the sac in relation to the artery to obtain the total maximal mesh displacement.

As shown in Table 4, the value of the ratio R_v is more important than R_d and allows us to better characterize aneurysm status. Furthermore, ΔV is a global indicator and is less sensitive to the uncertainties of the input parameters of the computations.¹⁴ ΔV is thus thought to be a better parameter to evaluate the risk of rupture.

A limitation of this study was the simplification of the aneurysmal environment in the FSI computations, by assuming that the aneurysm lies in a fluid of a given pressure. This environment would probably influence the geometric variations of the aneurysm depending on the location; friction and contact of the wall with other structures (bone, meninges, arachnoid trabeculae, cerebrospiral fluid) will certainly impact the wall motion.^32,33 The assumptions made regarding the aneurysm wall are another limitation. In the present study, the aneurysm wall was considered as isotropic and homogeneous, but the anisotropy of this kind of biologic material is well known.³⁴ Nevertheless, isotropy and homogeneity were assumed because they most probably do not change the trends observed when comparing soft and stiff materials in this range of physiologic solicitation. To characterize the behavior of blood, more sophisticated models can be used to account for non-Newtonian effects, especially in the aneurysmal sac (Cebral et al³⁵ and Sforza et al³⁶). However, these effects are expected to be prevalent only when dealing with local quantities like wall shear stress. This is not the case in the present study where the aneurysmal volume, which is primarily influenced by the pressure forces generated by the blood flow, was analyzed.

Numerous parameters are not known precisely when computing the FSI problem for a specific patient: wall thickness, fluid boundary conditions, artery properties, and intracranial pressure.

Despite these last limitations, the parametric study achieved in previous work¹⁴ showed a positive consistency with our results regarding the numerous sources of uncertainty involved in such FSI computations. Therefore, the uncertainties of the input parameters did not change the main conclusion: whatever the values of the parameters (in a range of physiologic variations), the soft/ruptured aneurysms deform more than the stiff/unruptured ones.

CONCLUSIONS

The difference in aneurysmal pulsatility as highlighted in this work might be a relevant patient-specific predictor of aneurysm rupture. These results are consistent with recent observational data in the literature to date. Development of a new imaging technique in the near future would allow for the accurate measurement of wall motion and therefore characterize the intracranial aneurysm vulnerability for any given patient.

ABBREVIATION:

FSI

fluid-structure interaction