Intracranial Aneurysm Neck Size Overestimation with 3D Rotational Angiography: The Impact on Intra-Aneurysmal Hemodynamics Simulated with Computational Fluid Dynamics

Abstract

BACKGROUND AND PURPOSE:

3DRA is considered the reference standard for the assessment of intracranial aneurysm morphology. However, it has been shown that 3DRA may overestimate neck size compared with 2D DSA. The purpose of this study was to determine the impact of neck size overestimation with 3DRA on intra-aneurysmal hemodynamics.

MATERIALS AND METHODS:

In a series of 20 patients, 20 intracranial aneurysms were analyzed for aneurysm neck size overestimation with 3DRA compared with 2D DSA. 3DRA-derived vascular models were modified to agree with 2D DSA. Geometric and hemodynamic variables of the original and modified vascular models were compared.

RESULTS:

In 8 of the 20 evaluated cases, 3DRA-derived aneurysm models showed neck size overestimation compared with 2D DSA images. The average neck diameter reduction after modification was 19%, which was, on average, 0.85 mm (±0.32 mm). Modification of the neck resulted in differences in location of inflow jet (2/8), impingement zone (3/8), and low WSS area (4/8). In 1 case, the maximal WSS increased by 98% after modification. The change of impingement zone location resulted in a different classification of the impingement zone region in 2 cases.

CONCLUSIONS:

Neck size overestimation on 3DRA can have non-negligible consequences for hemodynamic features determined with CFD.

Rupture of an intracranial aneurysm is a devastating event, with high morbidity and mortality rates.¹ Intra-aneurysmal hemodynamics have been associated with an increased risk of aneurysmal rupture. Several studies showed an association of aneurysm rupture with specific hemodynamic patterns and local variations in wall shear stress.^2–4

CFD is increasingly used to simulate hemodynamics in intracranial aneurysms.^2–4 CFD consists in the numeric solution of the Navier-Stokes equations to simulate fluid flow. In these calculations, an accurate 3D geometric vascular model of the aneurysm and parent arteries is required as the definition of the computational domain over which Navier-Stokes equations are solved.^5,6 These vascular models are commonly based upon high-resolution image data. In general, intracranial aneurysms measure between 2 and 25 mm. This size makes it difficult to image small details in aneurysm geometry, which potentially affect hemodynamics. Intracranial aneurysms can be imaged with CT, MR imaging, conventional angiography (2D DSA), and 3DRA. Because of the high resolution of approximately 0.25 mm and high image contrast, 3DRA is considered the reference standard for generating these vascular models.^5,6 Although the resolution of 2D DSA is, in general, higher than 3DRA, 2D DSA cannot directly be used for the generation of vascular models because of the lack of 3D information of the vascular geometry. A study by Brinjikji et al⁷ showed a difference in the dome-to-neck ratio of intracranial aneurysms between 3DRA and 2D DSA and that, in some cases, the 3DRA overestimates the aneurysm neck size compared with 2D DSA. Intra-aneurysmal blood flow velocity is highest within the neck of the aneurysm. Therefore, it can be expected that differences in the geometry of the neck affect the distribution of intra-aneurysmal hemodynamics.

The aim of this study is to assess the degree of aneurysm neck size overestimation with 3DRA compared with 2D DSA and determine the hemodynamic consequences of this overestimation. We collected 3DRA and corresponding 2D DSA images of intracranial aneurysms to identify aneurysm neck size overestimation in 3DRA. In the cases in which 3DRA clearly differed from the 2D DSA images, 3DRA-derived vascular models were modified to resemble the 2D DSA visualization of aneurysm necks. For both the original and the modified models, CFD simulations were performed and differences in intra-aneurysmal hemodynamics were assessed.

Materials and Methods

Patient Population

We retrospectively evaluated 20 intracranial aneurysms in 20 patients for which both 2D DSA and 3DRA image data were available. The 20 patients were selected from a population of 264 consecutive patients used in an ongoing study on the relation between hemodynamics and aneurysm recurrence after coiling. Permission of the medical ethics committee was given for this retrospective analysis of anonymous patient data. Informed consent was waived because no diagnostic tests other than routine clinical imaging were used in this study.

Imaging Protocols

All images were acquired during endovascular treatment procedures under general anesthesia using a single-plane angiographic unit (Integris Allura Neuro; Philips Medical Systems, Best, the Netherlands) following institutional protocol. There was no difference in the 3DRA acquisition for the 20 patients. All imaging parameters were constant with an image intensifier field-of-view of 22 cm for all cases. A guide catheter (5F or 6F) was placed in the internal carotid artery or vertebral artery. Anteroposterior and lateral views were obtained followed by a “working projection” DSA based on views identified on 3DRA. The working projection was the 2D DSA image that showed the optimal view of the aneurysm neck separated from the parent artery.

The 3DRA was acquired during a 6-second run, with 21 mL of contrast (Visipaque; GE Healthcare, Cork, Ireland), which was administered at 3 mL/s. During the rotational run, 100 isocentric images were generated during a 180° rotation (240° including start and calibration), resulting in a 256³ isotropic image volume. The angiographic unit was calibrated according to manufacture maintenance schedules, was performed by qualified Philips personnel. The 2D DSA images were acquired on the same angiographic unit using a mechanically administered bolus of 8 mL of contrast, infused at 4 mL/s, or a manually administered bolus of contrast, resulting in images of 1280 × 1024 pixels.

Vascular Models

The 3DRA volume datasets were imported in VMTK (www.vmtk.org). The aneurysm and its parent arteries were segmented by using a gradient-based level set method, as available in VMTK, using its standard settings (propagation and curvature scaling set to 0, advection scaling set to 1, and 1000 iterations).⁸ The gradient-based level set method uses a user-generated initialization as a starting point for the automated iterative segmentation. The segmentations were converted into a vascular model. These vascular models were represented by triangular surface meshes consisting of 9901 to 36,936 triangles.

Comparison of 3DRA and 2D DSA

An experienced neuroradiologist (C.B.M.) and an observer experienced with level set segmentation (J.J.S.) compared the aneurysm neck region of the 3DRA-derived vascular models with 2D DSA images for neck size overestimation. The comparison was based mainly upon working projection DSA. The vascular models were rotated such that they had the same projection angle as the 2D DSA images using Paraview 3.6 (Kitware; Los Alamos National Laboratory, Los Alamos, New Mexico). The 2D DSA images were displayed using ImageJ (National Institutes of Health, Bethesda, Maryland).⁹ Neck size overestimation on 3DRA was defined as an aneurysm neck that (as judged by an experienced neuroradiologist) appeared larger on the working projection of the 3DRA vascular model compared with the corresponding projection on 2D DSA. For the models with observed neck size overestimation, instructions for correction were provided by the neuroradiologist.

Vascular Model Correction

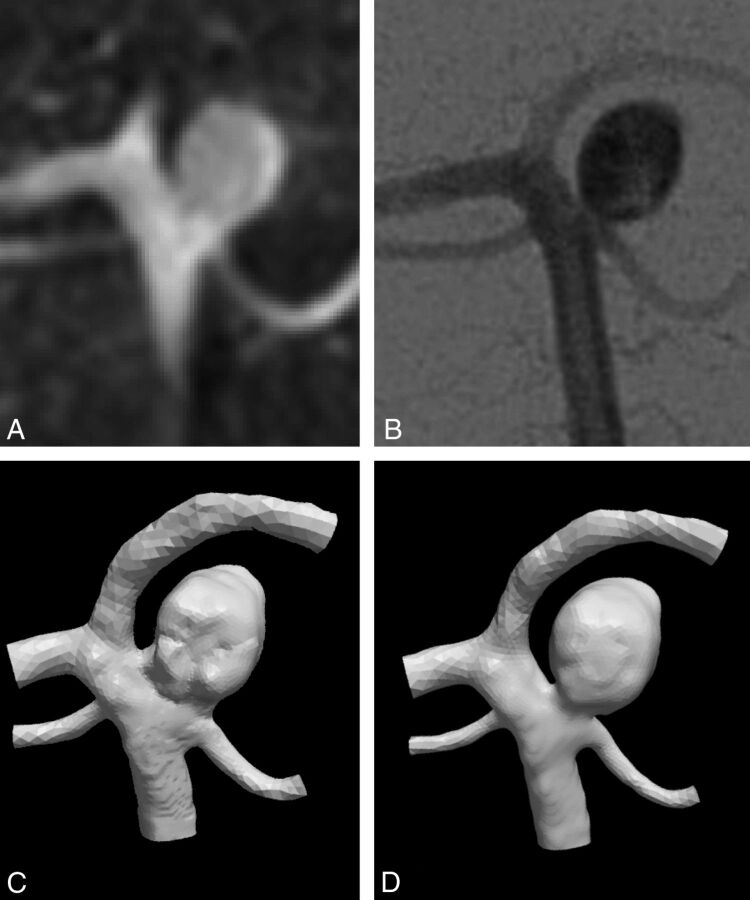
Correction of the models with neck size overestimation was performed using the image volume editor ITK-SNAP (www.itksnap.org)¹⁰ to manually modify the shape of the aneurysm neck to match the corresponding 2D DSA. All modified 3DRA-based vascular models were independently inspected for accuracy in visualizing neck size compared with 2D DSA by 2 neuroradiologists. With the approval of both, the modified aneurysm necks were considered consistent with 2D DSA (Fig 1). From this point on, we refer to “original” and “modified” models for the models without and with manual adjustments of the aneurysm neck, respectively.

Fig 1.

Comparison of the aneurysm neck as imaged by 3DRA (A) and 2D DSA (B). The 3DRA image suggests a wider neck than 2D DSA, which is expressed in the original 3DRA-derived vascular model (C). D, The vascular model after modification.

Hemodynamic Modeling

Both the original and modified vascular models were converted into tetrahedral meshes. A radius-adaptive method was applied to determine the element size. The parameter ‘edge length factor’ was set to 0.1 and to create mesh sized of approximately 1,000,000 tetrahedral cells (range 837,997 to 1,724,594 cells) using VMTK. CFD simulations were performed using Fluent 6.3 (ANSYS, Lebanon, New Hampshire). The calculations assumed rigid walls, no-slip boundary conditions at the wall, a fluid with a constant viscosity of 0.004 kg · m⁻¹ · s⁻¹, and a blood attenuation of 1060 kg · m⁻³. An inlet extension was added to the vascular models for the imposition of inlet boundary conditions. A continuous flow of 0.6 m · s⁻¹ was set as inflow velocity. Zero pressure boundary conditions were prescribed at all outlets.

Image Analysis

The original and modified diameters of the aneurysm neck in the vascular models were measured on a view that offered the best separation of the aneurysm neck and parent artery. Subsequently, the absolute and relative diameter reduction was determined.

Hemodynamic features for the original and the modified models were qualitatively compared by 2 neuroradiologists independently. Before the comparison, a joint meeting was arranged in which the 2 observers agreed upon the method of measuring and classification. During this session, models that were not included in this study were used to illustrate potential differences in flow patterns. The compared hemodynamic features were the location and size of the inflow jet, the number of vortices, the location and size of the impingement zone, and the location and size of the low WSS zone.

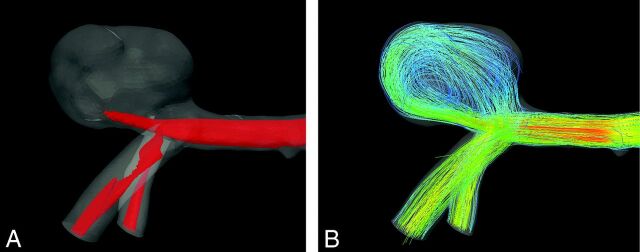
The inflow jet was defined as the maximum 25% of the flow magnitude within the aneurysm; it was visualized with an isosurface of the flow velocity (Fig 2A). We identified vortices with a minimal diameter of approximately half the diameter of the aneurysm (Fig 2B). The impingement zone was defined as the maximum 20% of the WSS in the aneurysm associated with the inflow jet, thus excluding high WSS areas at the aneurysm neck. The area of low WSS was defined as the lowest 10% of the WSS in the aneurysm. The WSS of the aneurysm was visualized in a 10-color scale.

Fig 2.

Illustration of the hemodynamic features displayed for comparison of case 7. A, Isosurface of the maximal 25% of the flow magnitude within the aneurysm as used in the assessment of the inflow jet. B, Streamlines of the flow used in the assessment of the main vortices.

The observers assessed whether there was a difference in position of the inflow jet, impingement zone, and the area of low WSS (yes/no). Change in size was classified as smaller, larger, or no change. A 5-point scale was used to classify the significance of change (1, little significance; 5, great significance).

The observers were blinded to all clinical information. To avoid observer-expectancy effect, 4 cases with 2 identical hemodynamic features were included in the scoring series. The order of the cases was randomly varied for every hemodynamic feature. Furthermore, for each case, the order of original and modified model was randomly varied such that the observers did not know which model was the original model and which was modified. Differences between the results of the 2 observers were discussed in an additional meeting to reach consensus.

For a number of hemodynamic features, the differences were quantified; the relative increase in inflow jet, the relative increase in maximal WSS in the aneurysm, and distance between the impingement zone in the original and modified vascular models. Furthermore, the impingement zone locations were classified by using the impingement region classification by Cebral et al.¹¹ This classification identifies 4 regions in an aneurysm: neck, body, dome, and lobulation.

Statistical Analysis

The interobserver variability of the 2 observers was calculated using weighted κ statistics of the dichotomized and trichotomized results. The interobserver variability was calculated twice. First, the decisions were compared where the significance scoring was excluded. Second, the significance was included and used as an ordinal value making the values negative for a reduction in size. No change in size was given to the value 0. The κ value was interpreted according to the method of Landis and Koch¹²: poor (0 to 0.20), fair (0.21 to 0.40), moderate (0.41 to 0.60), good (0.61 to 0.80), and perfect (0.81 to 1) agreement.

Results

Eight of 20 evaluated 3DRA-derived vascular models showed neck size overestimation compared with 2D DSA images. The demographic and clinical data of these 8 patients are given in Table 1. This table also contains the diameter reductions of the aneurysm neck. The mean diameter reduction was 0.85 mm, ranging from 0.34 to 1.20 mm. The average ratio of the modified diameter and the original diameter in the coiling projection was 19%, ranging from 8% to 32%. The approved modified vascular models are presented in Fig 3.

Table 1:

Demographic and clinical data of the 8 patients with aneurysm neck size overestimation in the 3DRA-derived vascular models

Case	Location	Age/Sex	Aneurysm Size (mm)	Original Neck Diameter (mm)	Absolute Neck Diameter Reduction (mm)	Relative Neck Diameter Reduction
1	AcomA	56/F	5.9	5.24	0.77	15%
2	AcomA	27/M	6.9	4.28	0.34	8%
3	BA	53/F	11.0	6.86	0.54	8%
4	MCA	41/M	4.5	2.86	0.82	29%
5	PcomA	57/F	17.9	6.66	1.20	18%
6	BA	50/F	6.0	3.86	1.19	31%
7	MCA	58/M	12.8	6.79	0.70	10%
8	PA	39/F	6.1	3.76	1.20	32%
Average		48	8.9	5.04	0.85	19%
Minimum		27	5.9	2.86	0.34	8%
Maximum		58	17.9	6.86	1.20	32%
Standard deviation		11	4.6	1.58	0.32	10%

Note:—Aneurysm size is the largest aneurysm diameter. Neck diameters were measured in the working projection. AcomA indicates anterior communicating artery; BA, basilar artery; PA, pericallosal artery; PcomA: posterior communicating artery.

Fig 3.

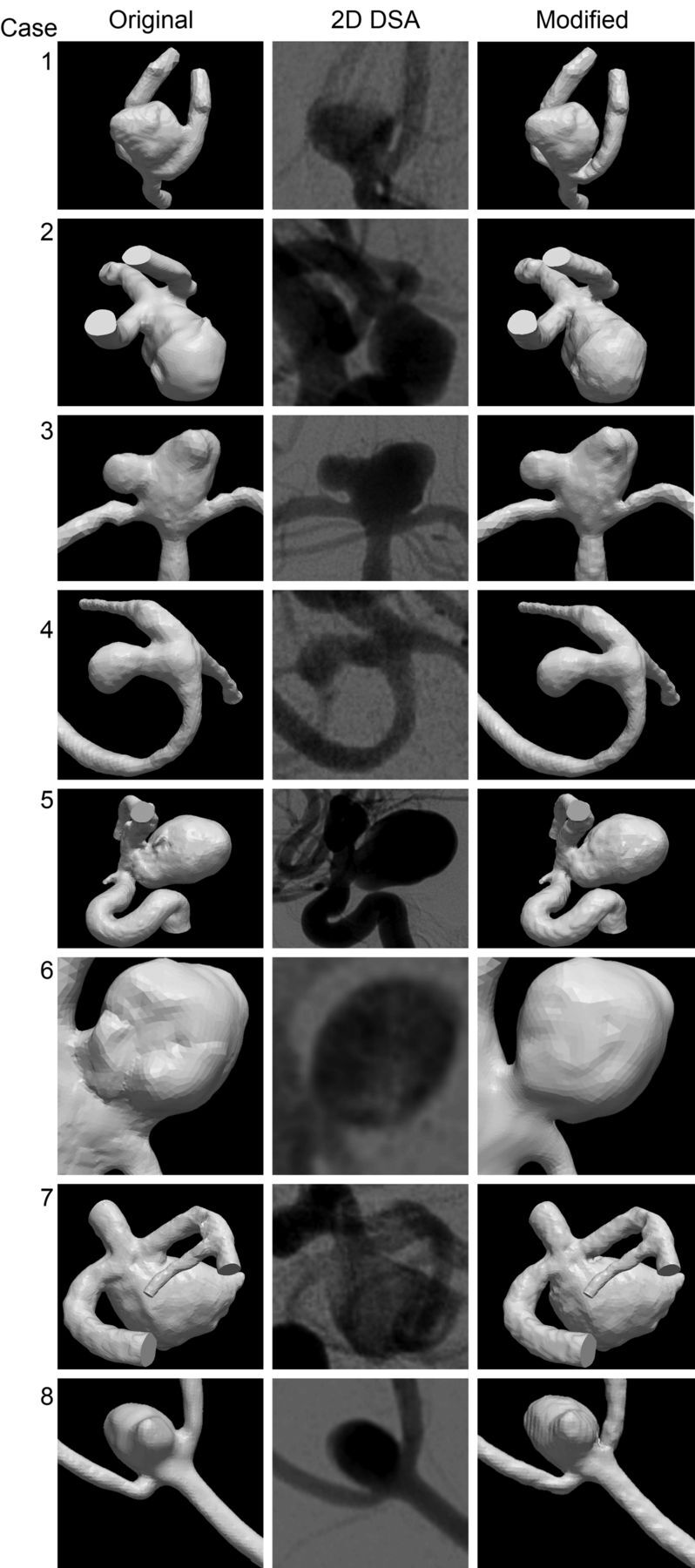
Eight cases in which the 3DRA-derived vascular models were considered to disagree with 2D DSA. From left to right: the original vascular model; the working projection DSA; the modified 3DRA-derived vascular model.

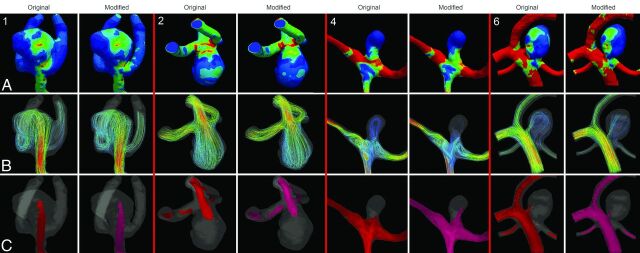
The results of the qualitative comparison of the hemodynamic patterns of the original and modified vascular models are presented in Table 2. This table shows that neck size overestimation has a considerable effect on the size of impingement zone, inflow jet, and low WSS area. Differences were also detected in location of inflow jet (2 cases), impingement zone (for 3 cases), and low WSS (4 cases). The number of vortices was not changed in the 8 models. Fig 4 shows 4 exemplary cases with WSS, streamlines, and an isosurface of the flow velocity for original and modified vascular models.

Table 2:

Consensus measurements of hemodynamic changes as a result of a correction of the 3DRA surface neck

Case	Inflow Jet		Impingement Zone		Low WSS Zone		Vortices Change
	Change in Position	Change in Size	Change in Position	Change in Size	Change in Position	Change in Size
1	No	Narrower (2)	No	Smaller (3)	No	Larger (1)	No
2	No	Narrower (2)	No	Smaller (5)	No	Larger (4)	No
3	No	Wider (2)	Yes (3)	Larger (3)	Yes (4)	No	No
4	Yes (2)	Wider (2)	No	Larger (5)	Yes (4)	Smaller (5)	No
5	No	Narrower (2)	Yes (5)	Smaller (5)	No	Larger (5)	No
6	Yes (2)	Narrower (3)	Yes (5)	Larger (5)	Yes (4)	Larger (5)	No
7	No	Narrower (5)	No	Smaller (2)	Yes (5)	Larger (5)	No
8	No	Wider (1)	No	Smaller (2)	No	Larger (3)	No

Note:—The significance scoring is given in brackets (1 = little significance; 5 = great significance).

Fig 4.

Hemodynamic features in original (left) and modified vascular models (right). Case 1 shows a similar impingement zone and WSS distribution, flow velocity, and direction of the inflow jet. Case 2 shows an increase in maximal WSS, unchanged flow velocity, and direction of the inflow jet. Case 4 shows an increased maximal WSS, an increased impingement zone, an increased maximal flow velocity, and a change in inflow jet position. Case 6 shows a decrease in maximal WSS, a change in impingement zone, and a change in the maximal flow velocity and the position of the inflow jet.

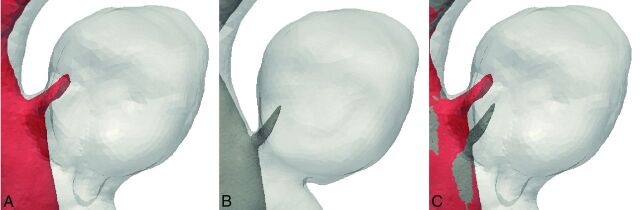
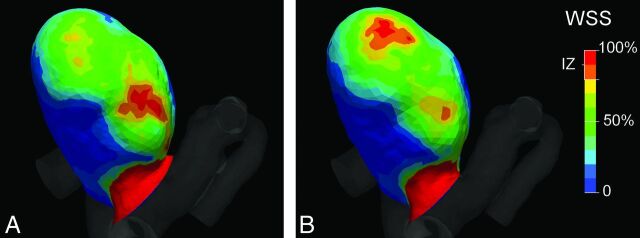
Table 3 shows the quantitative differences in hemodynamic patterns between original and modified vascular models. For most cases, the maximal velocity of the inflow jet was similar for both vascular models. However, for some cases, large differences were observed; for example, the maximal WSS in the aneurysm for case 4 increased by 98% as a result of the alteration of the inflow jet after the modification of the aneurysm neck (Fig 4). In some cases, there was a profound difference in inflow jet position after modification (Fig 5). The geometric distance between the impingement zone of the original and modified vascular model was, on average, 1.2 mm and ranged from 0.2 to 6.5 mm (Fig 6). For 2 cases, the region classification of the impingement zone changed from “body” to “dome” classification and from “dome” to “lobulation” classification, respectively (Table 3).

Table 3:

Quantitative differences in hemodynamic patterns of the original and modified vascular models

Case	Relative Increase in Maximal Inflow Velocity	Relative Increase in Maximal WSS	Distance Between Impingement Zones (mm)	Region Classification of Impingement Zone (Original/Modified)
1	−2.7%	+0.7%	0.25	Body/Body
2	−5.4%	−17.7%	0.27	Neck/Neck
3	2.6%	+22.0%	1.14	Dome/Lobulation
4	8.3%	+98.0%	0.46	Body/Body
5	−0.3%	+1.5%	6.51	Body/Dome
6	9.3%	−18.4%	0.47	Neck/Neck
7	−1.6%	−4.5%	0.27	Neck/Neck
8	3.8%	+6.3%	0.23	Dome/Dome

Fig 5.

Inflow jet in the original model (A) and modified model (B) showing a considerable difference in the inflow jet position of case 6. Both inflow jets are shown in superposition in image C.

Fig 6.

A change in position of the impingement zone (IZ) between the original (A) and modified (B) vascular model after modification of case 5.

The interobserver variability of the scoring of hemodynamic features, including the significance of change, was considerably lower than the interobserver variability without the significance of change (Table 4).

Table 4:

Interobserver agreement on the scoring of the hemodynamic patterns

	κ	Weighted κ
Inflow jet position	0.63 (0.36)	0.16 (0.11)
Inflow jet size	NA	0.67 (0.22)
Impingement zone position	1	0.89 (0.06)
Impingement zone size	1	0.62 (0.12)
Visible change in low WSS	1	NA
Change in low WSS position	0.67 (0.20)	0.50 (0.16)
Change in low WSS size	1	0.63 (0.23)
Number of vortices	1	NA

Note:—The weighted interobserver agreement is measured including the significance of a reported change in a hemodynamic feature. Standard error is given between parentheses. NA indicates not available.

Discussion

In 8 of the 20 evaluated cases, the 3DRA-derived vascular models showed a neck size overestimation compared with the working projection DSA. Correction of this overestimation resulted in a mean neck diameter reduction of 19%. Such neck size overestimation affected intra-aneurysmal hemodynamic features as computed with CFD. We observed a shift of the impingement zone of up to 6.5 mm (Fig 6), which resulted in a different impingement region classification in 2 cases. The change of the maximal inflow velocity was modest after modification; however, changes in inflow jet location were observed (Fig 5). Additional changes were found in size of the impingement zone, size of inflow jet, and the area of low WSS in almost all cases. The current study thus indicates that aneurysm neck size overestimation is an important limitation for accurate intra-aneurysmal hemodynamics as simulated with CFD.

3DRA is currently considered the reference standard imaging technique for 3D acquisitions of intracranial aneurysms because of its higher spatial resolution and image contrast compared with CTA and MRA (approximately 0.5 mm). As a result of the lower resolution of the latter imaging modalities, certain geometric details can be missed.⁶ In a phantom study, it was shown that volume measurements for 3DRA were more accurate than for CTA and MRA.¹³ It was also shown that segmentation of aneurysm structures is better for 3DRA than CTA.⁵ For example, models based on CTA image data resulted in larger aneurysm necks than those based on 3DRA data.⁶ Consequently, hemodynamic variables based on CTA and 3DRA models showed significant differences. In time-of-flight MRA, turbulent and slow residual flow may result in signal loss because of intravoxel dephasing and spin saturation, which may particularly occur in larger aneurysms. Contrast-enhanced MRA requires the administration of contrast material to shorten T1 of flowing blood. Its drawbacks are increased cost, possible superimposition of veins,¹⁴ and the possibility of peripheral contrast enhancement of subacute or organized thrombus within the adventitial layer of the aneurysm wall because of the short T1.¹⁵ 3DRA is, however, invasive and has a small risk of complications.¹⁶

As has been addressed by Kallmess,¹⁷ 3DRA may be considered the standard of reference in CFD modeling, but it should not be considered as the “truth.” We showed considerable differences in aneurysm neck size between 2D DSA imaging, which is the imaging technique with the highest spatial resolution, and 3DRA-derived vascular models. In a study by Brinjikji et al,⁷ discrepancies between conventional 2D DSA and 3DRA, with regard to neck-to-dome ratio measurements, were found. In that study, the researchers considered 2D DSA as more reliable for the calculation of the dome-to-neck ratio due to the higher spatial resolution. We believe that, in the absence of interference from other opacified arteries, 2D DSA provides more accurate visualization of the aneurysm neck. This is generally the case for the working projection images that neurointerventionalists use during endovascular treatment of intracranial aneurysms. However, overprojection as a consequence of projection imaging generally results in an overestimation of the dimensions of vascular structures. Furthermore, in a 2D DSA image, pixels are dimensionless and thus contain no size information. Therefore, it is not possible to measure absolute neck sizes unless special setups are adopted.

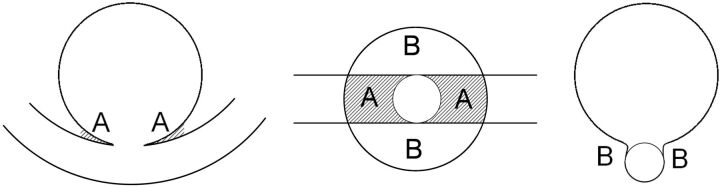
Although we have not studied this explicitly, we observed a relation between aneurysm neck size overestimation and proximity of adjacent arteries. With a small distance between the aneurysm sac and adjacent arteries, the neck size overestimation of the 3DRA-derived vascular models was larger. Figure 7 shows a typical working projection in which the parent artery is adjacent to the aneurysm (area A), making it sensitive for blurring artifacts. In our series, there were no arteries adjacent to the aneurysm perpendicular to the imaging plane (area B in Fig 7). Therefore, in the perpendicular direction, only a limited amount of neck size overestimation was expected and, consequently, the aneurysm neck was not edited. Because of the lack of reliable information on the neck size in this direction, we measured the change in neck diameter rather than neck area. The relation between neck size overestimation and presence of adjacent arteries should be studied in more detail in the near future to predict whether an adjustment of the aneurysm neck is required.

Fig 7.

Schematic front view (left), bottom view (middle), and side view (right) of an idealized aneurysm and its parent artery. The front view would be chosen as the working projection. This figure shows that the parent artery is closer to the artery in the front view (area A) than perpendicular to the working projection (area B), suggesting that the blurring of the neck is more severe in this direction.

In a theoretic, simplified aneurysm model, Hoi et al¹⁸ have shown that an increase in neck size results in an increase in impingement zone. As such, it is expected that our reduction of the neck sizes would result in smaller impingement zones. However, this was only observed in 5 of 8 cases. For the other 3 vascular models, the reduction of the neck size resulted in a larger impingement zone (Fig 4, case 4). It therefore appears that the findings of Hoi et al¹⁸ cannot be directly extrapolated to more realistic and complex aneurysm geometries.

Our results are in agreement with the study of Geers et al,⁶ who showed that the larger aneurysm neck areas on CTA compared with 3DRA have a profound impact on aneurysmal WSS. In their study, the mean WSS differed by as much as 44% between the 2 modalities. Nevertheless, the visual categorization of flow characteristics in this study was mostly similar for both modalities.⁶

The VMTK segmentation method used to create the original models is based on finding image intensity gradients representing the lumen boundary and is therefore not dependent on absolute intensity thresholds. To ensure equal aneurysm volume for both modified and original models, we only corrected the vascular models at the neck area. These models were inspected by experienced neuroradiologists. The manual nature of modification toward 2D DSA resemblance limits the reproducibility of this method. In addition, we could not compare absolute size of the vascular structures, as imaged with 2D DSA and the 3DRA model, because the former contains dimensionless pixels. These limitations justify reproducibility studies and further research on automated methods for aneurysm neck adjustments.

The current study is explorative, aiming to understand neck geometry overestimation and the hemodynamic consequences. The 20 patients were selected from a population of 264 consecutive patients used in an ongoing study on the relation between hemodynamics and aneurysm recurrence after coiling. Because all of these patients had an aneurysm recurrence after coiling, our results may reflect a selection bias. However, we do not expect a relation between aneurysm recurrence and neck size overestimation. Due to the rather small sample size, the occurrence of neck size overestimation in intracranial aneurysms may not be representative of its prevalence in a larger population. The prevalence and severity of the neck overestimations of 3DRA-derived vascular models should be studied in larger and more general patient populations than presented here.

The limitations of CFD included the lack of patient-specific information on blood viscosity, attenuation, and notably constant blood flow velocities at the inflow boundary of the model. We have kept these properties identical for all cases before and after neck correction. Results of CFD simulation may depend on the applied volumetric element type and mesh size. In a recent comparative study, the effects of polyhedral- versus tetrahedral-based meshes and mesh size (5119 to 258,481 volume elements) appeared to be small, with changes of 0.84% to 6.3% in WSS and blood velocities.¹⁹ Cebral et al¹¹ also studied the influence of mesh size on the hemodynamic CFD result and concluded that the effect of mesh size is small on the major hemodynamic patterns. Because we have used a fine mesh size of approximately 1,000,000 elements, we do not expect that this had a negative influence on our results. As a final limitation, we modeled vascular walls as rigid. Although this is common in CFD research, cerebral arteries are known to be distensible. Previous studies have shown that using rigid walls can result in unrealistic pressure gradients.²⁰ However, the effect of wall movement on estimated intra-aneurysmal hemodynamic patterns was shown to be minimal.²¹ We are aware that the mentioned parameters all influence the final CFD simulations. We chose to keep these parameters constant for all cases to study the effects of neck size overestimation solely.

The technical limitations warrant some caution in interpretation of the predicted hemodynamic patterns. In particular, absolute values for local velocity and shear stress depend on the specific choices indicated here. For that reason, the calculation of impingement zones and areas of low WSS was based on a relative definition of WSS. Despite the limitations, clear effects of neck morphology on intra-aneurysmal hemodynamic patterns were shown. It leaves little doubt that such profound effects, though quantitatively somewhat different, are also expected for other CFD parameters.

In retrospective studies, specific hemodynamic patterns based on CFD have been associated with intracranial aneurysm rupture.^3,22 Knowledge of patient-specific hemodynamic patterns therefore has the potential to improve rupture risk assessment. Currently, the role of CFD is the subject of preclinical research and it still has to be decisively demonstrated what accuracy is needed to predict rupture. In this study, we have shown that the current reference standard imaging technique, 3DRA, has limitations with regard to the imaging and modeling of the aneurysm neck, which can, in turn, lead to effects on specific intra-aneurysmal hemodynamics. This study contributes to the overall accuracy of the CFD simulations through optimization of the geometric parameters involved. Furthermore, 3DRA-based neck size overestimation may have implications in daily clinical practice, as the aneurysm neck plays an important role in clinical decision making with respect to the feasibility and strategy of coiling.

Conclusions

In 8 of 20 evaluated cases, we observed aneurysm neck size overestimation in 3DRA-derived vascular models compared with 2D DSA. For specific cases, this overestimation has non-negligible consequences for hemodynamic parameters as determined by CFD. Future studies are needed to assess the clinical impact of these consequences.

ABBREVIATIONS:

3DRA

3D rotational angiography

CFD

computational fluid dynamics

VMTK

Vascular Modeling Toolkit

WSS

wall shear stress