Abstract
The layered chalcogenide Ta2NiSe5 has been proposed to host an excitonic condensate in its ground state, a phase that could offer a unique platform to study and manipulate many-body states at room temperature. However, identifying the dominant microscopic contribution to the observed spontaneous symmetry breaking remains challenging, perpetuating the debate over the ground state properties. Here, using broadband ultrafast spectroscopy we investigate the out-of-equilibrium dynamics of Ta2NiSe5 and demonstrate that the transient reflectivity in the near-infrared range is connected to the system’s low-energy physics. We track the status of the ordered phase using this optical signature, establishing that high-fluence photoexcitations can suppress this order. From the sub-50 fs quenching timescale and the behaviour of the photoinduced coherent phonon modes, we conclude that electronic correlations provide a decisive contribution to the excitonic order formation. Our results pave the way towards the ultrafast control of an exciton condensate at room temperature.
Subject terms: Electronic properties and materials, Phase transitions and critical phenomena, Quantum fluids and solids
The dominant mechanism of the excitonic insulator transition in Ta2NiSe5 and the nature of its high-temperature phase are debated. The authors report transient reflectivity measurements indicating a significant electronic contribution to the transition and a gapped state of preformed excitons at high temperatures.
Introduction
Ultrafast optical spectroscopy has emerged in recent years as a crucial technique for the study and control of correlated electron phases in solid state materials1–14 due to its few-femtosecond time resolution, ability to investigate phenomena on a rather wide energy scale, and superior signal-to-noise ratio15. This technique allows one to separate structural, spin, and charge contributions to the emergence of these systems’ exotic behaviour by studying the timescales required to relax from an out-of-equilibrium state. This information is critical for engineering and manipulating these quantum phases16. For example, in the study of the properties of superconductors (SCs), ultrafast spectroscopy has been essential to uncover the microscopic origin of Cooper pair condensation14.
The proposed excitonic insulating (EI) phase of matter shares numerous similarities in its theoretical treatment with the superconducting phase17,18. Below a critical temperature (Tc), an excitonic insulator undergoes a spontaneous symmetry breaking resulting in the formation of a macroscopic population of condensed electron–hole pairs in its ground state. Concurrently, a bandgap opens at the Fermi level, which mirrors the order parameter of the collective phase19. Interestingly, as a result of the strong Coulombic nature of the fermion-pair binding, this phase can appear at or above room temperature, providing a unique platform for the investigation of many-body effects. In addition, EIs could manifest superfluidity and share features with other strongly correlated materials. One example is vanadium dioxide, where an insulating state emerges below a certain temperature as a result, at least partially, of electronic correlations. The insulator-to-metal photoinduced transition observed in this material has been proposed as a platform to obtain ultrafast Bragg switches2.
Here, we investigate the properties of Ta2NiSe5, a layered van der Waals compound believed to be an EI17,18 with Tc ~ 328 K and an excitonic bandgap of ~150 meV at cryogenic temperatures. The stabilisation of the bound electron–hole pairs in this material has been attributed to its quasi-1D nature (see inset of Fig. 1b), with alternating chains of tantalum and nickel atoms in each of the stacked atomic planes20. A number of studies that support the hypothesis of an EI phase in Ta2NiSe5 have emerged in the past few years21–26, and very recently the first detection of collective excitations in this system was reported27 and explained theoretically28,29. However, the existence of a simultaneous structural phase transition at Tc20 still calls into question the effective contribution of electronic correlations to the low-temperature behaviour of this material, and further efforts are required to directly study the properties of the EI order parameter and to develop a complete microscopic description of the interactions that govern this phase.
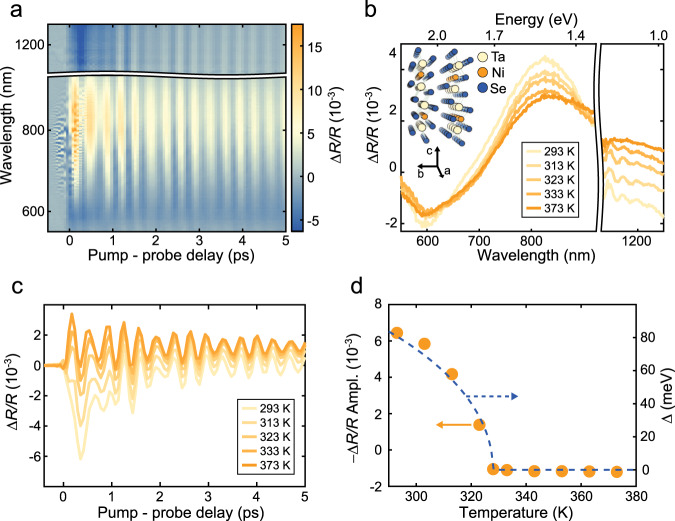
Fig. 1. Temperature dependence of the transient reflectivity signal of Ta2NiSe5.
a ΔR/R signal measured at room temperature as a function of pump-probe delay and probe wavelength for Φpump = 50 µJ/cm2. b Spectra of ΔR/R averaged between 1 and 2 ps for a series of temperatures and Φpump = 50 µJ/cm2. The range between 930 and 1130 nm is removed in panels (a, b) to eliminate the noise due to residual spectral components of the laser pulses used to generate the probe beam. c ΔR/R kinetic at 1200 nm corresponding to the data in panel (b). d Temperature dependence of the signal amplitude (orange dots, left y-axis) and of a BCS-like order parameter calculated using37 , valid for (blue dashed line, right y-axis). The amplitudes are extracted from a fit of the incoherent component of the signal (see Supplementary Information Note 2 for more details). In the inset of panel (b) we show the crystal structure of TaNiSe (figure generated with the software Vesta68).
In this work, through a combination of temperature-dependent, fluence-dependent, and multi-pulse ultrafast broadband spectroscopy, we address these open questions. First, we demonstrate that the optical response of Ta2NiSe5 in the near-infrared (NIR) range maps that of an order parameter. This result does not in itself provide information on the nature of the ordered phase, but rather means that we can use this response to track the out-of-equilibrium evolution of the system. In particular, we establish that a strong photoexcitation can completely suppress the ordered phase at room temperature. This result is confirmed through the study of the phononic degrees of freedom, which also manifest the response expected at high temperature. Using a two-pump technique, we can show that the evolution of the phonon response occurs on the same femtosecond timescale of the ultrafast electronic response. Notably, the timescale of the order melting and its dependence on the excitation fluence allows us to conclude that electronic correlations play a key role in driving the formation of the EI phase. Finally, above Tc, we observe a transient optical signal typical of systems with an energy gap at the Fermi level. We ascribe this behaviour to the existence of an insulating state of preformed excitons, as recently theoretically proposed30.
Results and discussion
We begin by characterising the transient optical response of Ta2NiSe5 using pump-probe spectroscopy at room temperature. Figure 1a shows the transient reflectivity (ΔR/R) signal of this material obtained using 12 fs, 1.8 eV, low-fluence (Φpump = 50 µJ/cm2) pump pulses and probed using broadband (550–1250 nm) pulses. We observe an incoherent component to the signal, which quickly grows after time zero and then decays exponentially, and that is associated with the excitation of quasi-particles (QPs) across the bandgap. The oscillations are instead associated with coherent phonon modes, which are excited through resonant impulsively stimulated Raman scattering or displacive excitation processes31. Contrary to previous reports23, the ΔR/R signal does not depend on the pump polarisation, but it significantly changes with the orientation of the probe polarisation (see Supplementary Note 1). We determine that the response to a polarisation oriented parallel to the atomic chains is more directly related to the status of the condensate (as suggested in previous equilibrium measurements32,33) and limit our measurements to this probe configuration. This behaviour, together with the wavelength dependence described below, is in close analogy with that reported for superconducting systems34–36, and can be ascribed to the difference in the initial and final states for the probe-induced transitions as a function of polarisation and wavelength. A detailed knowledge of the interband selection rules, which is beyond the scope of this work, is required to further investigate this aspect.
To identify the signatures of the proposed phase transition, we investigate the temperature dependence of the material response. In Fig. 1b, we present the spectrum of ΔR/R averaged between 1 and 2 ps for a series of temperatures and Φpump = 50 µJ/cm2. While the signal shows a negligible change in the visible range (particularly at the shortest wavelengths), a more significant effect appears in the NIR, where the ΔR/R even flips sign as the temperature is increased above Tc. This behaviour becomes even clearer when we plot ΔR/R from this wavelength region as a function of time (Fig. 1c). Here, we see that the overall signal dynamics profoundly change as a function of temperature. At room temperature, the signal magnitude increases over ~300 fs and subsequently decays over a time scale of a few hundred femtoseconds, while the oscillations continue over a much longer timescale. As we approach Tc the signal amplitude rapidly decreases until it is completely replaced by a component of opposite sign that does not significantly decay on the timescale of our measurements. In Fig. 1d, we plot the signal amplitude extracted from a fit of the data (see Supplementary Note 2) as a function of temperature. Interestingly, the amplitude follows remarkably well the behaviour of an order parameter with a zero temperature gap of 150 meV37 (dashed line), changes sign close to Tc, and remains almost constant as the temperature is further increased. This behaviour is different from that previously observed at shorter probe wavelengths38 (see also Supplementary Note 3). The exact temperature at which the signal crosses zero depends weakly on the probe wavelength and it is sensitive to its polarisation, which again reflects the details of the transition matrix elements involved. However, the overall behaviour is clear at all wavelengths in the NIR range (see Supplementary Note 3). This result exposes a connection between the low-energy physics of the excitonic condensate and the high-energy electronic transitions probed by NIR light, in analogy with observations reported in high-temperature superconducting systems and other strongly correlated electron materials36,39–41. This interpretation is supported by previously reported results on the equilibrium response as a function of temperature42. Indeed, we can recognise a feature in the equilibrium optical conductivity at ~1 eV that maps the behaviour of the low-energy gap. Therefore, we interpret the drastic change in ΔR/R as the result of a shift in the spectral weight of the NIR electronic transition into the energy range of the excitonic bandgap when we increase the temperature above Tc (see Supplementary Note 4 for a more detailed explanation).
Focusing now on the NIR wavelength range, we investigate the effect of changing Φpump on the system’s response at room temperature (Fig. 2a). In the low-fluence regime, as expected, a stronger excitation results in a larger (negative) amplitude of ΔR/R. However, as Φpump is further increased, the signal is progressively suppressed, until it becomes positive at early times, and then decays until reaching the level of the low-fluence signal in ~1.5 ps. A closer inspection of the signal rise (Fig. 2b) reveals that the ΔR/R negative transient progressively becomes shorter as Φpump is increased, and it is absent at the highest fluences.
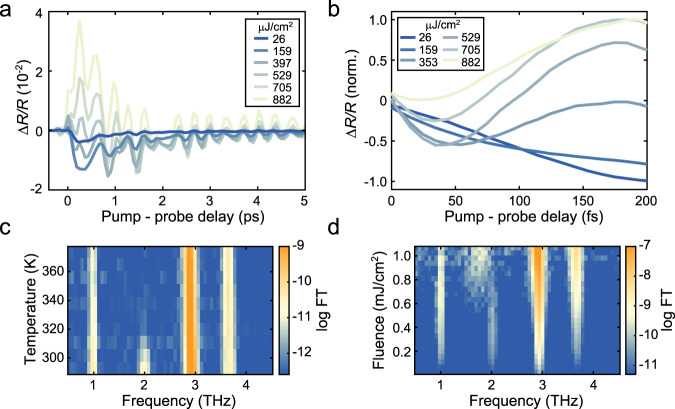
Fig. 2. Photoinduced suppression of the excitonic order.
a ΔR/R kinetic at 1200 nm for different values of Φpump. b Normalised signal collected with smaller time steps to better resolve the behaviour at early times. Data are cut after the coherent artefact for clarity (see Supplementary Note 4). c, d Natural logarithm of the Fourier transform (FT) of the oscillatory component of ΔR/R as a function of temperature (c) and Φpump (d).
The behaviour of the coherent phonon oscillations can be studied performing a Fourier transform (FT) of the oscillatory component of the signal. At room temperature, the FT shows the well-known phonon resonances at 1, 2, 2.9, and 3.6 THz (Fig. 2c). As previously reported23,43, the 2 THz oscillation becomes strongly suppressed as we approach Tc and is then almost completely quenched up to ~400 K44. In Fig. 2d, we present instead the FT as a function of Φpump. We see that while the 1, 2.9, and 3.6 THz phonon modes have a rather straightforward monotonic behaviour, the 2 THz mode is strongly modified at high Φpump, where its resonance is shifted towards lower frequencies and is significantly broadened. Interestingly, recent works have suggested that the 2 THz phonon is the most strongly coupled to the electronic bands closest to the EI gap, and therefore could be the most influenced as the system is perturbed45.
From these results, we develop a microscopic description of the material response. At temperatures below Tc, the pump pulse excites highly energetic QPs across the single-particle excitation gap. At low values of Φpump, the QP population promptly starts to thermalise through electron–electron scattering events. As a part of this process, further QP excitations can be created through a cascade mechanism in which the QPs transfer some of their kinetic energy to carriers in the valence band. The rise of the ΔR/R amplitude reflects this carrier multiplication process. Within a few hundred femtoseconds, the QPs relax to the edge of the single-particle excitation gap through electron–phonon scattering processes. Subsequently, the QPs recombine across the single-particle excitation bandgap and reform bound electron–hole pairs by emitting gap-energy bosons (amplitude or Higgs mode of the excitonic condensate46). This relaxation process occurs in ~2 ps, after which only the oscillations associated with the coherent phonons remain visible. This behaviour is different from that observed in SCs, where at temperatures below Tc a bottleneck mechanism involving the re-breaking of Cooper pairs by the gap-energy bosons prolongs the QPs’ population lifetime beyond the intrinsic recombination rate47,48. We believe that this difference is the result of a crucial distinction between SCs and EIs in the low-energy range of the excitation spectrum. While in SCs the phase or Nambu–Goldstone mode of the condensate is pushed at energies above the Higgs mode due to the Anderson–Higgs mechanism49, this is not the case in Ta2NiSe5, where we recently detected the phase mode signature at energies below the excitonic bandgap27. The presence of this low-energy mode provides a channel for the rapid relaxation of the amplitude mode into pairs of phase modes, in analogy with the relaxation of optical phonons into pairs of acoustic ones50. These low-energy modes can quickly propagate away from the photoexcited region in addition to progressively relaxing into even lower-energy excitations. This mechanism can prevent the bottleneck effect seen in SCs and allows for a fast relaxation of the QPs.
This result is in sharp contrast with the behaviour observed for temperatures above Tc, where the signal relaxation is drastically slowed down. The absence of a significant decay (see Supplementary Note 2 for additional information) suggests that the system transitions to a gapped phase at high temperatures, with an energy gap larger than the available bosonic excitations in the system. In this context, the QPs quickly relax to the bottom of the respective energy bands, but their lifetime is then limited by the intrinsic electron–hole recombination time across the bandgap, which can be of the order of nanoseconds in insulating systems51. In agreement with recent theoretical30,52 and experimental21 work, we propose that this insulating state is characterised by the existence of preformed excitons, but no long-range order. While the debate over the nature of the high-temperature phase of Ta2NiSe5 is still ongoing24,53–56, this result clearly points to the existence of a gapped phase.
Considering now the data in Fig. 2, we can conclude that in the presence of a strong photoexcitation, the system undergoes a transient collapse of the EI phase associated with a sign inversion of ΔR/R at short pump-probe delays. As expected, the threshold fluence required for this collapse becomes smaller as the temperature is increased towards Tc, reflecting the presence of a weaker order (see Supplementary Note 6). We attribute the duration of the negative transient seen in Fig. 2b to the time required for the complete melting of the excitonic order. This allows us to conclude that this process becomes progressively faster as we increase Φpump until the full quench of the excitonic order happens faster than our time resolution (see Supplementary Note 5 for more details). The femtosecond timescale of this process excludes the possibility of a thermally driven transition, and, instead, we can associate this fluence-dependent, ultrashort rise time to the existence of key electronic contribution to the ordered phase57,58. In addition, the very rapid relaxation of the ΔR/R signal towards negative values, which occurs on the timescale of the QPs’ relaxation processes, also hints at the electronic nature of the driving force that restores the excitonic condensate. We note that, at long delay times, the signal for high Φpump acquires a small positive baseline, which we associate to bolometric heating as concluded in previous works38.
The previous conclusions are well supported by our study of the phonon modes. In particular, the shift in frequency and increased linewidth of the 2 THz mode can be associated with an ultrafast transition to the high-temperature lattice response that the system would present in the absence of stable electron–hole pairs44. Alternatively, this could be the result of the suppression of long-range phase coherence upon photoexcitation10,15,59,60. This result further justifies associating the sign reversal of ΔR/R to a melting of the ordered phase.
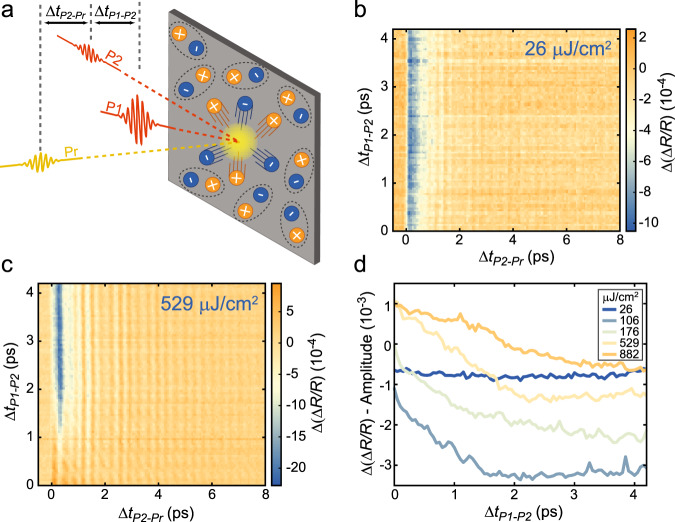
The pump-probe measurements are key in uncovering the existence of a photoinduced phase transition, as evidenced both in the incoherent and coherent response of the system, and in studying the timescale of the order suppression. To gain more information on how the out-of-equilibrium state evolves over time, we can instead utilise a three-pulse scheme, equivalent to a pump-probe measurement on the out-of-equilibrium state of the system10. In particular (see Fig. 3a), we use a first laser pulse (pump1, P1) of varying fluence (ΦP1) to prepare the system into a perturbed state. After a delay ΔtP1–P2, a second weak pulse (pump2, P2, 50 µJ/cm2) further excites the material before a final pulse (Pr) is used to probe the state of the system after ΔtP2–Pr (again we focus on the response of the system in the NIR). By subtracting the signal obtained in the presence of P2 and that collected with only the P1 excitation (we identify this signal as Δ(ΔR/R)), we can isolate the effect of the weak excitation on the perturbed state. By changing ΔtP1–P2 we can therefore study how the excitations induced by the second pump evolve in time (for more details on the implementation of this technique, see ref. 61).
Fig. 3. Recovery of the EI phase measured with multi-pulse ultrafast spectroscopy.
a Schematic of the multi-pulse experiment. b, c Δ(ΔR/R) signal at 1200 nm as a function of the P2–Pr and P1–P2 delays for ΦP1 = 26 µJ/cm2 (b) and ΦP1 = 529 µJ/cm2 (c). d Evolution of the Δ(ΔR/R) amplitude as a function of the P1–P2 delay for different values of ΦP1.
To further clarify this technique, in Figs. 3b, c we show Δ(ΔR/R) as a function of ΔtP1–P2 for low (26 µJ/cm2) and high (529 µJ/cm2) values of ΦP1, respectively. In the presence of low P1 fluence, the ΔtP2–Pr traces are identical for all ΔtP1–P2 delays (and are similar to those seen at low fluence in Fig. 2a). However, when ΦP1 is increased, Δ(ΔR/R) becomes positive for short ΔtP1–P2 delays. Only after ~1 ps of ΔtP1–P2 delay do the kinetics recover the low-fluence lineshape. To better illustrate this, in Fig. 3d, we plot the amplitude of the Δ(ΔR/R) for a series of ΦP1 (we extract the amplitude using a fit process analogous to that discussed in Supplementary Note 2). We emphasise again that this signal shows us the effect of P2 on the out-of-equilibrium response induced solely by the P1 pulse. Considering the data in Fig. 2a, b, this effect can be easily anticipated for low and high values of ΦP1. In these conditions, we know that an additional excitation results in a more negative and more positive transient reflectivity response, respectively. More complex is the interpretation of the data for medium values of ΦP1. Here, we expect the Δ(ΔR/R) signal to become positive as soon as the additional photoexcitation induced by P2 reduces the negative transient reflectivity value. Indeed, in Fig. 3d we see that the amplitude of Δ(ΔR/R) becomes positive for values of ΦP1 much lower than the fluences needed to reverse the sign of ΔR/R (see Fig. 2a). As a consequence of this interpretation, we note that we do not expect to observe a rise time for a positive Δ(ΔR/R) signal in the same way that we do in Fig. 2b. For instance, for all the four highest fluences used there, we expect the Δ(ΔR/R) signal to be positive even at the shortest ΔtP1–P2 values. In principle, there could be very specific values of ΦP1 for which the Δ(ΔR/R) signal would be positive for short values of ΔtP1–P2 and ΔtP2–Pr, but this would not have the same meaning as a change of sign in the transient reflectivity.
We can now interpret the behaviour of the Δ(ΔR/R) amplitude for ΦP1 = 106, 176, and 529 μJ/cm2 as that associated with a progressively stronger suppression of the excitonic order (all these curves decay with a similar recovery time τcond, see Supplementary Note 7). For ΦP1 = 882 μJ/cm2, instead, the amplitude decay is clearly slowed down, which could signify the complete suppression of the condensate and the onset of bottleneck processes that delay the electron–hole recombination rate and drives the system to the gapped phase. The value that the signal amplitude reaches at long delays depends on the number of long-lived QPs that can absorb the incoming P2 pulse, and is additionally influenced by the bolometric contribution.
So far, we have focused on the incoherent component of the Δ(ΔR/R) signal, which confirms the conclusions reached from the data in Fig. 2 and provides additional insights on the recovery processes of the perturbed excitonic condensate. The three-pulse technique can give us further understanding of the behaviour of the perturbed system when we look at the coherent component of the signal. At each ΔtP1–P2 delay, we perform a FT of the ΔtP2–Pr to characterise how the lattice response evolves in time after P1. Figure 4a shows the result of this calculation for ΦP1 = 26 µJ/cm2.
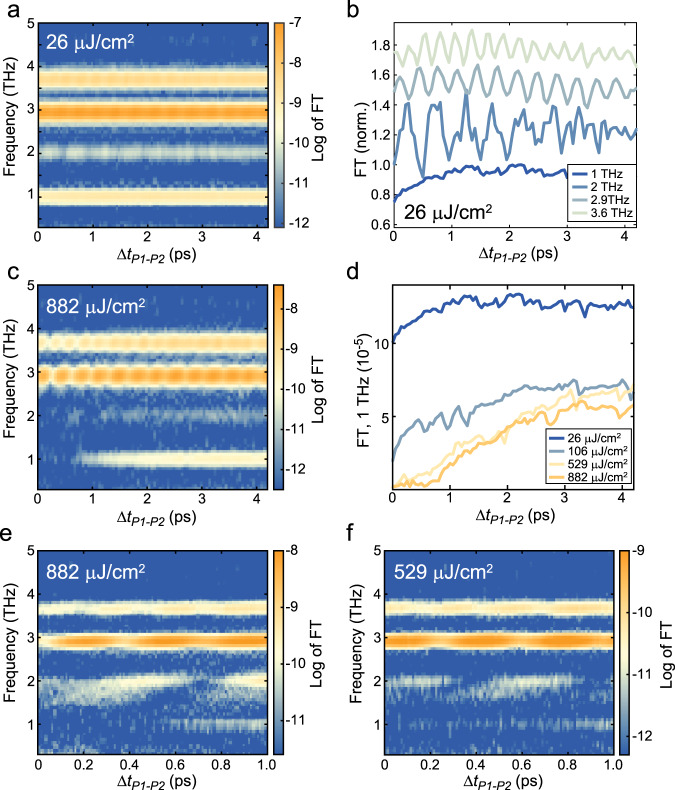
Fig. 4. Effect of ΦP1 on the coherent phonon oscillations excited in the system.
a, c Natural logarithm of the FT of Δ(ΔR/R) oscillatory component at 1200 nm as a function of the P1–P2 delay for ΦP1 = 26 µJ/cm2 (a) and ΦP1 = 882 µJ/cm2 (c). b Normalised linecuts at 1, 2, 2.9, and 3.6 THz of the data in panel (a). d FT amplitude for the 1 THz resonance as a function of the P1–P2 delay for a series of ΦP1 values. e, f Data analogous to panels (a, c) but collected with higher temporal resolution for ΦP1 = 882 µJ/cm2 (e) and ΦP1 = 529 µJ/cm2 (f).
The interpretation of the coherent component is simpler as it describes the phonon modes that P2 can excite at each ΔtP1–P2 delay. Oscillations in the 2, 2.9, and 3.6 THz phonon amplitude are present, as it is clear in Fig. 4b where we present the linecuts along the resonance frequencies. Nodes and antinodes of these oscillations occur as P2 coherently amplifies or suppresses the phonons excited by P162,63, and are an indication of these modes’ coherence. Interestingly, the 1 THz mode is only very weakly modulated, and instead appears partially suppressed at early delays. When we increase ΦP1 (see Fig. 4c), while the 2.9 and 3.6 THz modes are not significantly affected, a drastic change is observed for the other two modes. As evidenced in Fig. 4d, the 1 THz mode is progressively quenched at early times, until it is completely suppressed at the highest ΦP1, where it starts recovering only after a delay of ~0.8 ps. We associate this behaviour with a saturation of the 1 THz mode excitation, which can be also deduced from the two-pulse results (see Supplementary Note 8). As ΦP1 is increased, the perturbed, photoexcited state of the system cannot support the excitation of additional 1 THz phonons, and therefore the Δ(ΔR/R) signal does not contain any signature of this mode at short P1–P2 delays. In addition, the 1 THz phonon mode exhibits a temperature-dependent saturation (see Supplementary Note 8): at high temperatures, the amplitude of the oscillations are nearly independent of Φpump. Moreover, we note that the recovery time of the 1 THz amplitude closely mirrors τcond.. This suggests that the saturation of the 1 THz mode is associated with the depletion of the excitonic condensate, but further studies are required to unveil this connection. These results add important insights into the behaviour of this phonon mode, suggesting a possible different interpretation of its role from what was previously reported23,27.
Even more important, for what concerns our analysis, is the response of the 2 THz phonon oscillations. As seen in Fig. 2d, this mode provides information on the evolution in the lattice properties. In Fig. 4c we see that this mode is strongly affected at early times, but it still shows a coherent oscillation induced by P2 before reaching a constant value, which signals the return to the weakly perturbed state. A better understanding of the quenching process can be gained by taking finer P1–P2 delay steps and achieving a higher signal-to-noise ratio (Fig. 4e). Here, we observe that the 2 THz mode is promptly shifted to lower frequencies and broadened, while still showing a modulation induced by P2, signalling a residual coherence of the oscillations excited by P1. At intermediate values of ΦP1 (Fig. 4f), a signal indicative of a partial collapse of the EI phase is observed as expected. We, therefore, conclude that the lattice transitions to its high-temperature response44 on a femtosecond timescale, before relaxing back to the typical room temperature behaviour in ~1.5 ps. This supports our interpretation that, upon strong photoexcitation, the excitonic order can be completely suppressed and recovered on timescales compatible with the presence of strong correlation driven by electronic interactions. We stress that all the results obtained from the incoherent and coherent components of the signal, both with the pump-probe and the three-pulse experiments, are important pieces of evidence that were used to construct our interpretation.
Previous measurements on Ta2NiSe5 have suggested that structural degrees of freedom play an important role in the formation of the EI phase, raising questions about the nature of the symmetry breaking transition. In particular, it is crucial to determine the relative strength of the electronic and structural contributions to the phase transitions. In other words, we want to determine if the electronic contribution is strong enough that, if we were able to suppress the structural phase transition, we could still obtain the excitonic order, possibly manifesting superfluidic behaviour. In this work, we used a combination of temperature- and fluence-dependent, ultrafast spectroscopy techniques to address this question and to provide a more complete picture of the femtosecond dynamics of Ta2NiSe5. In analogy with the case of high-temperature SCs, we find that high-energy electronic transitions track the low-energy physics of the system, allowing us to use the response in the NIR as a marker of the EI order parameter.
Through the study of both the electronic and lattice out-of-equilibrium response, we find evidence that the excitonic long-range order can be transiently melted under strong photoexcitation. Crucially, the timescale of the EI phase suppression supports the hypothesis of an excitonic order driven substantially by electronic interactions.
Nonetheless, our work also showcases the existence of strong electron–phonon interactions in Ta2NiSe5 and could guide the development of experimental and theoretical efforts aimed at uncovering the nature of the connections between these degrees of freedom. In particular, the relationship between the possible state with short-range order and the behaviour of the 1 and 2 THz phonon modes would be an area of great research interest.
We have also accessed the out-of-equilibrium dynamics of the high-temperature phase of Ta2NiSe5, believed to host a state of preformed excitons. Further investigations of this insulating phase could shed more light on the properties of this and other systems characterised by strong electronic interactions. Intriguingly, the discovery of a photoinduced, ultrafast sign reversal and recovery of the material reflectivity also showcases the possibility of using Ta2NiSe5 as a platform for the development of ultrafast optical switches and more in general for quantum devices based on the control of correlated phases64.
Methods
Sample growth and preparation
The sample was grown with the procedure outlined in ref. 65. To prepare samples for optical measurements, flakes were exfoliated onto glass coverslips and subsequently encapsulated with a second glass slide while in a nitrogen glove box.
Ultrafast spectroscopy measurements
Pump-probe measurements are carried out using a Nd:YAG laser system (PHAROS, Light Conversion), which delivers a 14.5 W output of 1025 nm light, 200 fs pulse duration, and with a repetition rate of 38 kHz. Part of the output further seeds a commercial OPA (ORPHEUS, Light Conversion). The second harmonic of the Nd:YAG laser, generated by the OPA, is combined with the fundamental laser beam in a noncollinear OPA to generate broadband pulses centred around 1.8 eV, which are compressed to ~12 fs using a wedge prism and chirp mirrors. The compressed beam was split to generate P1 and P2, whose time delay relative to each other are controlled with mechanical delay stages. The broadband probe pulses (550–1250 nm) are generated from the fundamental of the Nd:YAG laser using a sapphire crystal, and their delay with respect to the pump pulses is controlled with a mechanical delay stage. Pump and probe beams are then combined in a boxcar geometry on the sample. Reflected pump pulses are discarded, while the reflected probe pulses are collected with a collimating lens and split using a dichroic mirror with a 960 nm cutoff to separate the visible and NIR components of the beam, which are then detected by an InGaAs and Si photodiode array, respectively. Both arrays are synchronised and read out at the repetition rate of the laser, using a chopping scheme of 38/4 kHz for P1 and 38/8 kHz for P2. For further details, see refs. 66,67.
Supplementary information
Acknowledgements
We thank Alexander Boris for kindly sharing data of the equilibrium optical conductivity of Ta2NiSe5. We would like to thank Yuta Murakami, Denis Golež, Selene Mor, Daniele Fausti, Vikas Arora, and Edoardo Baldini for many fruitful discussions. We are also grateful to the Engineering and Physical Science Research Council (EPSRC) and the Winton Programme for the Physics of Sustainability for funding. We acknowledge the financial support from the Department of Science and Technology (DST), India [Grant No. SR/WOS-A/PM-33/2018 (G)] and IISER Pune for providing the facilities for crystal growth and characterisation. We acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement 758826). We also thank the Department of Science and Technology, India for support under Nanoemission and Year of Science Professorship.
Author contributions
H.M.B. and P.A. performed measurements and analysed data. P.T., A.S., and L.H. worked on the growth and characterisation of the material. P.A., A.K.S., and A.R. conceived the experiments. H.M.B., P.A., and A.R. wrote the paper with input from all authors.
Data availability
The data underlying all figures in the main text are publicly available at 10.17863/CAM.63831.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Hope M. Bretscher, Paolo Andrich.
Contributor Information
Paolo Andrich, Email: pa343@cam.ac.uk.
Akshay Rao, Email: ar525@cam.ac.uk.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-21929-3.
References
- 1.Demsar J, Biljaković K, Mihailovic D. Single particle and collective excitations in the one-dimensional charge density wave solid K0.3MoO3 probed in real time by femtosecond spectroscopy. Phys. Rev. Lett. 1999;83:800–803. doi: 10.1103/PhysRevLett.83.800. [DOI] [Google Scholar]
- 2.Cavalleri A, et al. Femtosecond structural dynamics in VO2 during an ultrafast solid-solid phase transition. Phys. Rev. Lett. 2001;87:237401. doi: 10.1103/PhysRevLett.87.237401. [DOI] [PubMed] [Google Scholar]
- 3.Mitrano M, et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature. 2016;530:461–464. doi: 10.1038/nature16522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kogar A, et al. Light-induced charge density wave in LaTe3. Nat. Phys. 2020;16:159–163. doi: 10.1038/s41567-019-0705-3. [DOI] [Google Scholar]
- 5.Lian C, Zhang S-J, Hu S-Q, Guan M-X, Meng S. Ultrafast charge ordering by self-amplified exciton–phonon dynamics in TiSe2. Nat. Commun. 2020;11:43. doi: 10.1038/s41467-019-13672-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhang MY, et al. Light-induced subpicosecond lattice symmetry switch in MoTe2. Phys. Rev. X. 2019;9:021036. [Google Scholar]
- 7.Demsar J, Forró L, Berger H, Mihailovic D. Femtosecond snapshots of gap-forming charge-density-wave correlations in quasi-two-dimensional dichalcogenides 1T−TaS2 and 2H−TaSe2. Phys. Rev. B. 2002;66:041101. doi: 10.1103/PhysRevB.66.041101. [DOI] [Google Scholar]
- 8.Cavalleri A, Dekorsy T, Chong HHW, Kieffer JC, Schoenlein RW. Evidence for a structurally-driven insulator-to-metal transition in VO2: A view from the ultrafast timescale. Phys. Rev. B. 2004;70:161102. doi: 10.1103/PhysRevB.70.161102. [DOI] [Google Scholar]
- 9.Kübler C, et al. Coherent structural dynamics and electronic correlations during an ultrafast insulator-to-metal phase transition in VO2. Phys. Rev. Lett. 2007;99:116401. doi: 10.1103/PhysRevLett.99.116401. [DOI] [PubMed] [Google Scholar]
- 10.Yusupov R, et al. Coherent dynamics of macroscopic electronic order through a symmetry breaking transition. Nat. Phys. 2010;6:681–684. doi: 10.1038/nphys1738. [DOI] [Google Scholar]
- 11.Fausti D, et al. Light-induced superconductivity in a stripe-ordered cuprate. Science. 2011;331:189–191. doi: 10.1126/science.1197294. [DOI] [PubMed] [Google Scholar]
- 12.Wall S, et al. Ultrafast changes in lattice symmetry probed by coherent phonons. Nat. Commun. 2012;3:721. doi: 10.1038/ncomms1719. [DOI] [PubMed] [Google Scholar]
- 13.Stojchevska L, et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science. 2014;344:177–180. doi: 10.1126/science.1241591. [DOI] [PubMed] [Google Scholar]
- 14.Giannetti C, et al. Ultrafast optical spectroscopy of strongly correlated materials and high-temperature superconductors: a non-equilibrium approach. Adv. Phys. 2016;65:58–238. doi: 10.1080/00018732.2016.1194044. [DOI] [Google Scholar]
- 15.Zong A, et al. Evidence for topological defects in a photoinduced phase transition. Nat. Phys. 2019;15:27–31. doi: 10.1038/s41567-018-0311-9. [DOI] [Google Scholar]
- 16.Mihailovic D, et al. Femtosecond data storage, processing, and search using collective excitations of a macroscopic quantum state. Appl. Phys. Lett. 2002;80:871–873. doi: 10.1063/1.1447594. [DOI] [Google Scholar]
- 17.Jérome D, Rice TM, Kohn W. Excitonic insulator. Phys. Rev. 1967;158:462–475. doi: 10.1103/PhysRev.158.462. [DOI] [Google Scholar]
- 18.Halperin BI, Rice TM. Possible anomalies at a semimetal-semiconductor transistion. Rev. Mod. Phys. 1968;40:755–766. doi: 10.1103/RevModPhys.40.755. [DOI] [Google Scholar]
- 19.Pekker D, Varma CM. Amplitude/Higgs modes in condensed matter physics. Annu. Rev. Condens. Matter Phys. 2015;6:269–297. doi: 10.1146/annurev-conmatphys-031214-014350. [DOI] [Google Scholar]
- 20.Kaneko T, Toriyama T, Konishi T, Ohta Y. Orthorhombic-to-monoclinic phase transition of Ta2NiSe5 induced by the Bose-Einstein condensation of excitons. Phys. Rev. B. 2013;87:035121. doi: 10.1103/PhysRevB.87.035121. [DOI] [Google Scholar]
- 21.Seki K, et al. Excitonic Bose-Einstein condensation in Ta2NiSe5 above room temperature. Phys. Rev. B. 2014;90:155116. doi: 10.1103/PhysRevB.90.155116. [DOI] [Google Scholar]
- 22.Mor S, et al. Ultrafast electronic band gap control in an excitonic insulator. Phys. Rev. Lett. 2017;119:086401. doi: 10.1103/PhysRevLett.119.086401. [DOI] [PubMed] [Google Scholar]
- 23.Werdehausen D, et al. Coherent order parameter oscillations in the ground state of the excitonic insulator Ta2NiSe5. Sci. Adv. 2018;4:eaap8652. doi: 10.1126/sciadv.aap8652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lu YF, et al. Zero-gap semiconductor to excitonic insulator transition in Ta2NiSe5. Nat. Commun. 2017;8:14408. doi: 10.1038/ncomms14408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wakisaka Y, et al. Excitonic insulator state in Ta2NiSe5 probed by photoemission spectroscopy. Phys. Rev. Lett. 2009;103:026402. doi: 10.1103/PhysRevLett.103.026402. [DOI] [PubMed] [Google Scholar]
- 26.Wakisaka Y, et al. Photoemission spectroscopy of Ta2NiSe5. J. Supercond. Nov. Magn. 2012;25:1231–1234. doi: 10.1007/s10948-012-1526-0. [DOI] [Google Scholar]
- 27.Andrich, P. et al. Imaging the coherent propagation of collective modes in the excitonic insulator candidate Ta2NiSe5 at room temperature. Preprint at arXivhttp://arxiv.org/abs/2003.10799 (2020). [DOI] [PMC free article] [PubMed]
- 28.Murakami Y, et al. Collective modes in excitonic insulators: effects of electron-phonon coupling and signatures in the optical response. Phys. Rev. B. 2020;101:195118. doi: 10.1103/PhysRevB.101.195118. [DOI] [Google Scholar]
- 29.Remez B, Cooper NR. Effects of disorder on the transport of collective modes in an excitonic condensate. Phys. Rev. B. 2020;101:235129. doi: 10.1103/PhysRevB.101.235129. [DOI] [Google Scholar]
- 30.Sugimoto K, Nishimoto S, Kaneko T, Ohta Y. Strong coupling nature of the excitonic insulator state in Ta2NiSe5. Phys. Rev. Lett. 2018;120:247602. doi: 10.1103/PhysRevLett.120.247602. [DOI] [PubMed] [Google Scholar]
- 31.Zeiger HJ, et al. Theory for displacive excitation of coherent phonons. Phys. Rev. B. 1992;45:768–778. doi: 10.1103/PhysRevB.45.768. [DOI] [PubMed] [Google Scholar]
- 32.Larkin, T. I. Excitonic Fano resonances in Ta2NiSe5 and Ta2NiS5. Online Publ. der Univ. Stuttgart10.18419/opus-8843 (2016).
- 33.Seo Y-S, et al. Temperature-dependent excitonic superfluid plasma frequency evolution in an excitonic insulator, Ta2NiSe5. Sci. Rep. 2018;8:11961. doi: 10.1038/s41598-018-30430-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Giannetti C, et al. Revealing the high-energy electronic excitations underlying the onset of high-temperature superconductivity in cuprates. Nat. Commun. 2011;2:353. doi: 10.1038/ncomms1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gedik N, et al. Abrupt transition in quasiparticle dynamics at optimal doping in a cuprate superconductor system. Phys. Rev. Lett. 2005;95:117005. doi: 10.1103/PhysRevLett.95.117005. [DOI] [PubMed] [Google Scholar]
- 36.Dvorsek D, et al. Femtosecond quasiparticle relaxation dynamics and probe polarization anisotropy in YSrxBa2-xCu4O8 (x = 0,0.04) Phys. Rev. B. 2002;66:020510. doi: 10.1103/PhysRevB.66.020510. [DOI] [Google Scholar]
- 37.Tinkham, M. Introduction to Superconductivity (McGraw-Hill, 1980).
- 38.Werdehausen D, et al. Photo-excited dynamics in the excitonic insulator Ta2NiSe5. J. Phys. Condens. Matter. 2018;30:305602. doi: 10.1088/1361-648X/aacd76. [DOI] [PubMed] [Google Scholar]
- 39.Han SG, Vardeny ZV, Wong KS, Symko OG, Koren G. Femtosecond optical detection of quasiparticle dynamics in high-Tc YBa2Cu3O7-δ Superconducting Thin Films. Phys. Rev. Lett. 1990;65:2708–2711. doi: 10.1103/PhysRevLett.65.2708. [DOI] [PubMed] [Google Scholar]
- 40.Meinders MBJ, Eskes H, Sawatzky GA. Spectral-weight transfer: breakdown of low-energy-scale sum rules in correlated systems. Phys. Rev. B. 1993;48:3916–3926. doi: 10.1103/PhysRevB.48.3916. [DOI] [PubMed] [Google Scholar]
- 41.Basov DN, Averitt RD, van der Marel D, Dressel M, Haule K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 2011;83:471–541. doi: 10.1103/RevModPhys.83.471. [DOI] [Google Scholar]
- 42.Larkin TI, et al. Giant exciton Fano resonance in quasi-one-dimensional Ta2NiSe5. Phys. Rev. B. 2017;95:195144. doi: 10.1103/PhysRevB.95.195144. [DOI] [Google Scholar]
- 43.Mor S, et al. Inhibition of the photoinduced structural phase transition in the excitonic insulator Ta2NiSe5. Phys. Rev. B. 2018;97:115154. doi: 10.1103/PhysRevB.97.115154. [DOI] [Google Scholar]
- 44.Kim, K. et al. Direct observation of excitonic instability in Ta2NiSe5. Preprint at arXivhttps://arxiv.org/abs/2007.08212 (2020).
- 45.Suzuki, T. et al. Detecting electron-phonon couplings during photo-induced phase transition. Preprint at arXivhttp://arxiv.org/abs/2002.10037 (2020).
- 46.Coleman, P. Introduction to Many-Body Physics (Cambridge University Press, 2015).
- 47.Rothwarf A, Taylor BN. Measurement of recombination lifetimes in superconductors. Phys. Rev. Lett. 1967;19:27–30. doi: 10.1103/PhysRevLett.19.27. [DOI] [Google Scholar]
- 48.Mihailovic D. Optical experimental evidence for a universal length scale for the dynamic charge inhomogeneity of cuprate superconductors. Phys. Rev. Lett. 2005;94:207001. doi: 10.1103/PhysRevLett.94.207001. [DOI] [PubMed] [Google Scholar]
- 49.Shimano R, Tsuji N. Higgs mode in superconductors. Annu. Rev. Condens. Matter Phys. 2020;11:103–124. doi: 10.1146/annurev-conmatphys-031119-050813. [DOI] [Google Scholar]
- 50.Klemens PG. Anharmonic decay of optical phonon in diamond. Phys. Rev. B. 1975;11:3206–3207. doi: 10.1103/PhysRevB.11.3206. [DOI] [Google Scholar]
- 51.Klingshirn, C. Semiconductor Optics (Springer, 1995).
- 52.Kadosawa M, Nishimoto S, Sugimoto K, Ohta Y. Finite-temperature properties of excitonic condensation in the extended Falicov–Kimball Model: cluster mean-field-theory approach. J. Phys. Soc. Jpn. 2020;89:053706. doi: 10.7566/JPSJ.89.053706. [DOI] [Google Scholar]
- 53.Di Salvo FJ, et al. Physical and structural properties of the new layered compounds Ta2NiS5 and Ta2NiSe5. J. Less Common Met. 1986;116:51–61. doi: 10.1016/0022-5088(86)90216-X. [DOI] [Google Scholar]
- 54.Watson MD, et al. Band hybridization at the semimetal-semiconductor transition of Ta2NiSe5 enabled by mirror-symmetry breaking. Phys. Rev. Res. 2020;2:013236. doi: 10.1103/PhysRevResearch.2.013236. [DOI] [Google Scholar]
- 55.Tanabe T, Sugimoto K, Ohta Y. Nonequilibrium dynamics in the pump-probe spectroscopy of excitonic insulators. Phys. Rev. B. 2018;98:235127. doi: 10.1103/PhysRevB.98.235127. [DOI] [Google Scholar]
- 56.Okazaki K, et al. Photo-induced semimetallic states realised in electron–hole coupled insulators. Nat. Commun. 2018;9:4322. doi: 10.1038/s41467-018-06801-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Petersen JC, et al. Clocking the melting transition of charge and lattice order in 1T-TaS2 with ultrafast extreme-ultraviolet angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2011;107:1–5. doi: 10.1103/PhysRevLett.107.177402. [DOI] [PubMed] [Google Scholar]
- 58.Hellmann S, et al. Time-domain classification of charge-density-wave insulators. Nat. Commun. 2012;3:1069. doi: 10.1038/ncomms2078. [DOI] [PubMed] [Google Scholar]
- 59.Lee WS, et al. Phase fluctuations and the absence of topological defects in a photo-excited charge-ordered nickelate. Nat. Commun. 2012;3:838. doi: 10.1038/ncomms1837. [DOI] [PubMed] [Google Scholar]
- 60.Mertelj T, et al. Incoherent topological defect recombination dynamics in TbTe3. Phys. Rev. Lett. 2013;110:156401. doi: 10.1103/PhysRevLett.110.156401. [DOI] [PubMed] [Google Scholar]
- 61.Menke SM, et al. Order enables efficient electron-hole separation at an organic heterojunction with a small energy loss. Nat. Commun. 2018;9:277. doi: 10.1038/s41467-017-02457-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hase M, et al. Optical control of coherent optical phonons in bismuth films. Appl. Phys. Lett. 1996;69:2474–2476. doi: 10.1063/1.117502. [DOI] [Google Scholar]
- 63.Cheng Y-H, Gao FY, Teitelbaum SW, Nelson KA. Coherent control of optical phonons in bismuth. Phys. Rev. B. 2017;96:134302. doi: 10.1103/PhysRevB.96.134302. [DOI] [Google Scholar]
- 64.Cotleţ O, Zeytinoǧlu S, Sigrist M, Demler E, Imamoǧlu A. Superconductivity and other collective phenomena in a hybrid Bose-Fermi mixture formed by a polariton condensate and an electron system in two dimensions. Phys. Rev. B. 2016;93:054510. doi: 10.1103/PhysRevB.93.054510. [DOI] [Google Scholar]
- 65.Pal S, et al. Destabilizing excitonic insulator phase by pressure tuning of exciton-phonon coupling. Phys. Rev. Res. 2020;2:043182. doi: 10.1103/PhysRevResearch.2.043182. [DOI] [Google Scholar]
- 66.Hinrichsen TF, et al. Long-lived and disorder-free charge transfer states enable endothermic charge separation in efficient non-fullerene organic solar cells. Nat. Commun. 2020;11:5617. doi: 10.1038/s41467-020-19332-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Stern HL, et al. Vibronically coherent ultrafast triplet-pair formation and subsequent thermally activated dissociation control efficient endothermic singlet fission. Nat. Chem. 2017;9:1205. doi: 10.1038/nchem.2856. [DOI] [PubMed] [Google Scholar]
- 68.Momma K, Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011;44:1272–1276. doi: 10.1107/S0021889811038970. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data underlying all figures in the main text are publicly available at 10.17863/CAM.63831.