Assessing Combinability of Phylogenomic Data Using Bayes Factors

Abstract

With the rapid reduction in sequencing costs of high-throughput genomic data, it has become commonplace to use hundreds of genes to infer phylogeny of any study system. While sampling a large number of genes has given us a tremendous opportunity to uncover previously unknown relationships and improve phylogenetic resolution, it also presents us with new challenges when the phylogenetic signal is confused by differences in the evolutionary histories of sampled genes. Given the incorporation of accurate marginal likelihood estimation methods into popular Bayesian software programs, it is natural to consider using the Bayes Factor (BF) to compare different partition models in which genes within any given partition subset share both tree topology and edge lengths. We explore using marginal likelihood to assess data subset combinability when data subsets have varying levels of phylogenetic discordance due to deep coalescence events among genes (simulated within a species tree), and compare the results with our recently described phylogenetic informational dissonance index (D) estimated for each data set. BF effectively detects phylogenetic incongruence and provides a way to assess the statistical significance of D values. We use BFs to assess data combinability using an empirical data set comprising 56 plastid genes from the green algal order Volvocales. We also discuss the potential need for calibrating BFs and demonstrate that BFs used in this study are correctly calibrated.

Introduction

Until recently, common practice for inferring multigene phylogenies involved concatenation of all available genes with an assumption that the evolutionary histories of all sampled genes were identical. However, phylogenetic trees for different genes (gene trees) can differ from each other, from the tree inferred from the concatenated data, and from the true species tree, due to evolutionary events/processes such as incomplete lineage sorting (ILS), horizontal transfer, and hybridization (Maddison 1997; Degnan and Rosenberg 2009; Edwards 2009; Mallet et al. 2016). Further, even if the sampled genes share the same evolutionary history, estimated trees can differ because of: 1) insufficient phylogenetic information in the sampled genes (stochastic or sampling error) or 2) model misspecification (systematic error) leading to, for example, long edge attraction in some gene trees and not in others (Swofford et al. 1996; Philippe et al. 2005; Philippe et al. 2011).

With the recent surge of large-scale genomic DNA data from high-throughput sequencing methods, the issue of phylogenetic incongruence has become even more important in phylogeny reconstruction. Inferring species trees by addressing these challenges has become an area of active research in phylogenetics. Several species tree methods already available (reviewed in Liu et al. 2015) are effective in correcting incongruences due to deep coalescence (e.g., Song et al. 2012; Jarvis et al. 2014; Xi et al. 2014; Tang et al. 2015). These methods estimate a species tree either from multiple sequence alignments (e.g., *BEAST, Heled and Drummond 2010; BEST, Liu et al. 2008; SVDquartets in PAUP* v.4a137+, Swofford 2003; Chifman and Kubatko 2014; Chifman and Kubatko 2015) or summary statistics calculated from estimated gene trees (e.g., STEM, Kubatko et al. 2009; MP-EST, Liu et al. 2010; BUCKy, Ané et al. 2007; ASTRAL, Mirarab et al. 2014). Methods such as *BEAST and BEST simultaneously estimate gene trees and the species tree by using MCMC to integrate over trees and substitution model parameters; however, coestimation of species and gene trees under a multispecies coalescent model is computationally intensive and cannot be applied to large scale genomic data. On the other hand, fast and efficient summary statistic methods (e.g., Mirarab et al. 2016) that completely rely on estimated gene trees (partial data) for the downstream species tree estimation may be prone to systematic bias as they do not incorporate uncertainty in the gene tree estimation process. SVDQuartets stands out as a method that is computationally tractable, infers species trees from sequence data directly rather than depending on accurately estimated gene trees, and explicitly models ILS. However, even if methods exist that accurately estimate species trees in the face of deep coalescence, there is still a need for methods that identify incongruent data subsets resulting from processes that cause conflict among genes but which are not explicitly modeled.

Tests for Phylogenetic Congruence using Bayes Factors

The only direct tests of phylogenetic congruence from the multiple sequence alignments and explicitly through the model testing approach proposed to date are likelihood ratio tests (LRTs). Huelsenbeck and Bull (1996) proposed a parametric bootstrapping approach in which the null hypothesis constrained all data subsets to have the same tree topology, while the alternative (unconstrained) hypothesis allowed each subset to have a potentially different tree topology. The distribution of the test statistic was generated by simulating data sets under the null hypothesis using maximum likelihood estimates of all model parameters and computing the test statistic under each simulated data set.

Nonparametric boostrapping, in conjunction with LRTs, was used by Leigh et al. (2008) to test the same null hypothesis. Leigh et al. (2008) also proposed clustering of data subsets based on pairwise LRT results to generate compatible sets. Separate LRTs were also proposed by Leigh et al. (2008) to test for heterotachy: in this case, the null hypothesis constrains edge lengths to be proportionally identical across subsets, while the alternative hypothesis allows each subset to potentially have different edge lengths. The software CONCATERPILLAR (Leigh et al. 2008) may be used to carry out these nonparametric bootstrapping LRTs.

These LRTs are well justified and are the best available means to assess congruence when there are no priors involved in the tree estimation process. However, when the phylogeny estimation involves Bayesian methods, then evaluation of congruence should properly account for the effects of the assumed prior distributions. We propose a Bayesian approach to testing phylogenetic congruence (or, equivalently, dissonance) by comparing the marginal likelihoods of competing models. When only two models are compared, the ratio of marginal likelihoods is termed the Bayes factor (BF). Our approach is comparable to that of Leigh et al. (2008), but instead of comparing maximized log-likelihoods of competing models using LRTs, we use marginal likelihoods and their ratio (BF) for model comparison. Our approach is made possible by recent improvements in marginal likelihood estimation for phylogenetic model selection (stepping-stone, SS: Xie et al. 2010; Fan et al. 2011; path-sampling, PS: Lartillot and Philippe 2006; partition weighted kernel estimator: Wang et al. 2018). The SS and PS estimators substantially outperformed other approaches [e.g., harmonic mean estimator, and a posterior simulation-based analog of the Akaike information criterion through Markov chain Monte Carlo (MCMC)] for comparing models of demographic change and relaxed molecular clocks (Baele et al. 2012). Recently, Brown and Thomson (2016) also used BF to analyze sensitivity in clade resolution to the data types used to infer the topology.

Quantifying Topological Dissonance Through Entropies of Posterior Tree Distributions

Lewis et al. (2016) introduced Bayesian methods for measuring the phylogenetic information content of data and for measuring the degree of phylogenetic informational dissonance among data subsets. Phylogenetic dissonance is relevant to the problem of identifying congruent subsets of loci. When data are partitioned into subsets (corresponding to, for example, genes or codon positions), such tools yield insight into which data subsets have the greatest potential for producing well supported estimates of phylogeny. Conflict between different subsets with respect to tree topology can lead to paradoxical results with respect to both information content and estimated phylogeny. For example, a tree topology minimally supported by all data subsets may be given maximal support in a concatenated analysis if each subset is highly informative and effectively rules out the trees most supported by other subsets (Lewis et al. 2016). The information measure 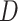(phylogenetic dissonance) was introduced by Lewis et al. (2016) to specifically identify such anomalies. Phylogenetic dissonance is defined as

(1)

 

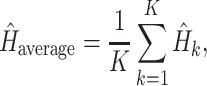(2)

where 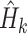is the entropy of the marginal tree topology posterior distribution for data subset 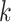(of subsets), and 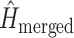is the entropy of the distribution estimated from a merged tree sample. Posterior tree samples from separate analyses of each data subset are combined to form the merged tree sample. (Note that this merged tree sample is not the same as a tree sample obtained from a concatenated analysis.) If different data subsets strongly support mutually exclusive tree topologies, then the average entropy of marginal tree topology posterior distributions (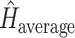) will be small while the merged entropy (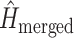) will be relatively large due to the fact that topology frequencies are more evenly distributed in the merged sample compared to samples from individual subsets, which are each dominated by one tree topology. Lewis et al. (2016) defined and estimated phylogenetic dissonance using this entropy-based measure, but how to evaluate the statistical significance of a given level of phylogenetic dissonance remains an open question.

BF Calibration

It is standard practice to use the value 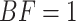as the critical value determining whether the null model (e.g., CONCATENATED) or the alternative model (e.g., SEPARATE) wins. This makes sense when the prior predictive error probabilities of BF under both models are equal; however, in cases where models differ substantially in their effective dimensions, the distributions of the BF for the two models being compared may not be symmetrical. For example, it is possible that the probability that the BF favors the CONCATENATED model when the SEPARATE model is true may not equal the probability that BF favors the SEPARATE model when the CONCATENATED model is true. Under such circumstances, a different threshold value (other than 1) can be selected such that the probability of choosing the incorrect model under both hypotheses is equal. Subtle, nonintuitive behavior of BFs, especially with respect to models that differ with respect to the size of tree topology space (Bergsten et al. 2013), made us wary of using BF tests right out of the box, so to speak. García-Donato and Chen (2005) provided an example of a model comparison in which calibration was needed and suggested a method for calibrating the BF (adopted here) that makes the prior predictive error probabilities symmetrical.

Aims of this Study

The primary aim of our study is to evaluate the effectiveness of BFs in uncovering phylogenetic discordance and in assessing the significance of the phylogenetic dissonance measure 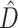(1). We explore the behavior of BFs using simulations designed to create a spectrum of 10-gene data sets ranging from low to high information content and from complete topological concordance to extreme discordance (due to deep coalescence and subsequent ILS). We provide an empirical example involving concordance of plastid genes in the green algal order Volvocales which demonstrates that LRTs carried out using CONCATERPILLAR can differ from conclusions based on marginal likelihoods when analyses are performed in a Bayesian context.

We investigate whether BFs are correctly calibrated in our particular application: that is does the standard BF=1 cutoff tend to (a priori) favor the SEPARATE model over the CONCATENATED mode, or vice versa?

Finally, we investigate the use of BFs for identifying heterotachy by fixing topology but allowing edge lengths to vary across gene subsets, and also under what circumstances the heterotachy model (hereafter HETERO model) detects true heterotachy versus other phenomena, such as topological discordance (Mendes and Hahn 2016) and heterobathy (different coalescent times rather than rate heterogeneity).

Materials and Methods

Parameters and Prior Distributions

Parameters of the models and the priors used in the GTR+G models employed in this article are:

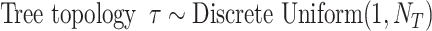(3)

 

(4)

 

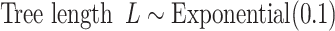(5)

 

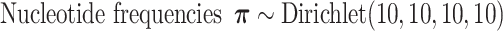(6)

 

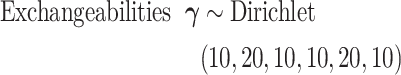(7)

 

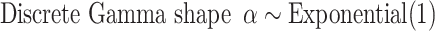(8)

 

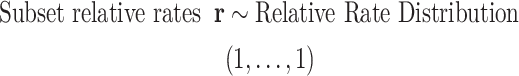(9)

 

(10)

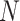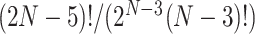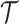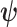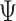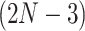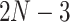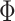equals the total number of distinct unrooted, binary, labeled tree topologies for taxa. There are such topologies comprising tree topology space . The space of edge length proportions is , which is the -simplex, where is the number of edge lengths in any tree topology in . The space of all other parameters is , which in this article includes the 6-simplex for GTR exchangeabilities, the 4-simplex for nucleotide frequencies, and for both tree length and the discrete gamma shape parameter quantifying the amount of among-site rate heterogeneity. Nucleotide frequencies were ordered 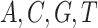and exchangeabilities were ordered . The Relative Rate Distribution is a transformed Dirichlet distribution and was described in Fan et al. (2011).

Bayes Factors

In Bayes’ Rule,

(11)

the denominator represents the marginal likelihood conditional on model 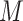, 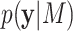. The marginal likelihood is the total probability of data 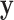, averaged over tree topology 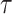, a multivariate parameter vector of edge length proportions, and a multivariate parameter vector comprising all other model parameters (including tree length). Data is a vector comprising observed patterns of states for all taxa for individual characters (sites in the case of sequence data). Considering two models, (, 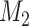), and their marginal likelihoods, and 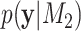, respectively, the BF 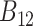is the ratio 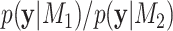. The BF on the log-scale is calculated as:

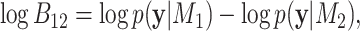(12)

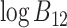
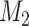where   0 signifies that model is preferred over . By preferred, we mean that model 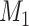fits the data better on average than model 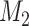over the parameter- and tree-space defined by the prior. Applying this approach to the problem of phylogenetic congruence, consider data from a set of loci 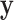(, ,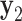...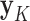), and two models, CONCATENATED and SEPARATE. The CONCATENATED model represents the marginal likelihood of the concatenated set (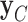) in which all loci are forced to have the same topology (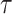) and edge length proportions (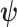), but allowed to differ in other model parameters ():

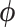(13)

In contrast, the SEPARATE model represents the marginal likelihood for a model in which each individual locus 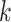() is allowed to have its own topology (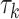), edge length proportions (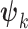), and model parameters (),

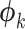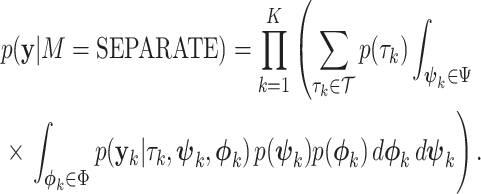(14)

The BF for CONCATENATED against SEPARATE is defined

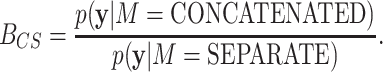(15)

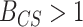(or equivalently ) indicates that the CONCATENATED model (numerator) is preferred over the SEPARATE model (denominator), whereas 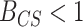(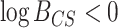) indicates the reverse (i.e., SEPARATE model is the preferred model).

A third, intermediate model HETERO links topology across subsets but allows edge lengths to vary between single-gene data sets:

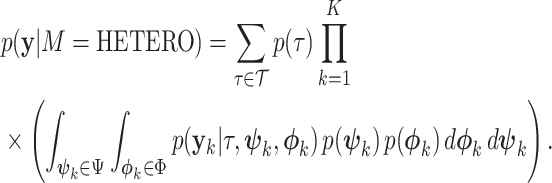(16)

Data Simulation

Gene trees were simulated within species trees using parameter combinations chosen to yield differing levels of phylogenetic incongruence. Using a Python script (source code provided in Supplementary Materials available on Dryad at http://dx.doi.org/10.5061/dryad.gt81779), one thousand 6-taxon species trees were generated under a pure-birth (Yule) process in which the tree height 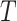(expected number of substitutions along a single path from root to tip) was drawn from a Lognormal(0.05, 0.22) distribution (mean 1.08, 95% of samples between 0.68 and 1.62). Ten gene trees were simulated within each species tree using coalescent parameter 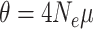, where 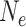is the effective (diploid) population size and is the mutation rate per generation. For each species tree, the ratio 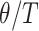was drawn from a Lognormal(0.60, 0.77) distribution (which has mean 2.45 with 95% of samples between 0.40 and 8.24) and was determined by multiplying this ratio by the value of 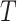used for a specific species tree. Increasing relative to results in a higher number of deep coalescences, causing increased discordance among the gene trees.

The gene trees thus generated were subsequently used to simulate DNA sequence alignments of length 2000 sites using SEQ-GEN (Rambaut and Grass 1997) under the GTR+G model (equal nucleotide relative frequencies, exchangeabilities 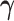= Dirichlet(1,2,1,1,2,1), discrete Gamma shape parameter 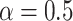). Individual single-gene data sets and the concatenated data set were used to compute marginal likelihoods using the Stepping-stone method (Xie et al. 2010) implemented in MrBayes (Ronquist et al. 2012). For the concatenated data set, two marginal likelihoods were estimated by enforcing: 1) the same topology and edge lengths for all sites (CONCATENATED model) and 2) the same topology but allowing edge lengths to vary among single-gene data subsets to account for nontopological gene tree variation (HETERO model). The fact that the marginal likelihood for the separate model (14) involves the product of 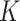independent terms (each corresponding to a different locus and each integrating out all unobserved quantities, including the tree topology), means that each term can be estimated using an analysis of one locus in isolation. The total log marginal likelihood for the SEPARATE model can be obtained as a sum of log marginal likelihoods from each locus analyzed separately.

The BF results were evaluated with respect to the phylogenetic information content () and phylogenetic dissonance (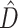) values computed using Galax v1.0.0 (Lewis et al. 2016). Estimation of 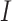and uses conditional clade probabilities (Larget 2013) to estimate Shannon entropy (Shannon 1948), from which is calculated simply as a difference between the entropies of the marginal prior and marginal posterior distributions of tree topology (Lindley 1956). The phylogenetic dissonance is defined as in equation (1), and thus 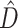is computed as the entropy of the merged tree sample minus the average entropy of tree samples from individual genes. Phylogenetic dissonance is expected to be zero for comparisons of independent MCMC samples from the same posterior distribution, and thus provides a sensitive measure of MCMC convergence with respect to tree topology (Lewis et al. 2016). We replicated each single-gene and concatenated MCMC analysis and computed 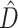for these paired samples as a way of ensuring that post burn-in MCMC sample size was sufficient for convergence.

Example from the Green Algal Order Volvocales

We tested phylogenetic congruence among 56 protein-coding plastid genes used in Fučíková et al. (2016), focusing on one of the most topologically consistent parts of the tree, the green algal order Volvocales. The Volvocales data set consisted of a subset of the Sphaeropleales, Vovocales, and OCC (Oedogoniales-, Chaetopeltidales-, and Chaetophorales) clades studied in Fučíková et al. (2016). We included four of the five Volvocales members from the study: Chlamydomonas reinhardtii, Gonium pectorale, Pleodorina starrii, and Volvox carteri. These four genomes were originally published by Smith et al. (2013). The length of the plastid genes ranged from 93 sites (psbT) to 2259 sites (psaA) after trimming portions with a high proportion of missing data at the ends. We conducted BF tests for all possible pairs from the 56 genes (by estimating marginal likelihoods under the CONCATENATED, HETERO, and SEPARATE models) used in the study with the aim to detect possible outlier genes that may be present among the sampled genes for the concatenated phylogeny. In order to compare our results with the likelihood-based approach, we also tested congruence among these 56 genes using CONCATERPILLAR (Leigh et al. 2008) using its topological congruence test (-t) option.

BF Calibration

To apply the method of García-Donato and Chen (2005), we simulated 1000 replicate 6-taxon, 10-gene data sets (2000 sites/gene) from the joint prior distribution of each model (CONCATENATED and SEPARATE). For the CONCATENATED model, data for all 10 genes were simulated from a single topology sampled from the discrete uniform topology prior. For the SEPARATE model, data for each of the 10 genes was simulated from topologies separately sampled from the discrete uniform topology prior. All other model parameters were simulated from their respective prior probability distributions.

For each simulated data set, 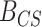was computed, yielding a sample of 1000 values from the prior predictive BF distributions for both the CONCATENATED and SEPARATE models. The 2000 sampled BF values were combined into a single vector and sorted, and we observed whether the nominal critical value 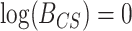was inside the interval defined by the 1000th and 1001th values in the sorted vector. If this cutoff interval spans 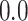, then the following desirable equality holds:

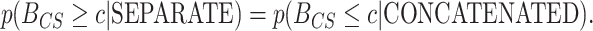(17)

The simulations needed for BF calibration were carried out using PAUP* 4a161 (Swofford 2003). The process was identical for calibrations done for the Volvocales analyses except that there were only 4 taxa and 2 genes, and the lengths of the two genes differed. Because the lengths of genes varied considerably, three separate calibrations were performed using the following pairs of sequence lengths: 1) 2259 sites for gene 1 and 93 sites for gene 2; 2) 2259 sites for gene 1 and 2205 sites for gene 2; and 3) 93 sites for gene 1 and 96 sites for gene 2. These numbers corresponded to the lengths of the largest (2259 for psaA), next largest (2205 for psaB), smallest (93 for psbT), and next smallest (96 for petL) genes in the genome.

Results and Discussion

Assessing Phylogenetic Dissonance Using Bayes Factors

In the 1000 simulated gene sets (10 genes/set) representing various degrees of topological and edge length congruence, the SEPARATE model won in a majority of replicates when 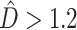or when the number of deep coalescences exceeded 1.8 per gene (Fig. 1). Also, in general, more deep coalescences yielded higher 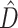and a greater chance of the SEPARATE model winning. The presence of deep coalescence does not guarantee that different genes will have different tree topologies, but the fact that lineages are joined randomly when there is deep coalescence means that greater incongruence is the expected result of increasing the frequency of deep coalescence. Therefore, as expected, estimated phylogenetic dissonance () was correlated with number of deep coalescences (Fig. 1). The number of deep coalescences varied from the minimum possible number (0) to the maximum possible number (50). The maximum number of deep coalescences is 5 per gene because there are 5 internal nodes in a rooted tree of 6 taxa. When SEPARATE failed to have the largest log marginal likelihood, CONCATENATED usually won, with HETERO only achieving the largest log marginal likelihood if 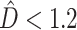and the number of deep coalescences was less than 3.2 per gene. Because a single simulation study can only suggest appropriate cutoff values for for the limited range of parameter combinations explored, we argue that a BF approach provides a sensible general approach for determining when values of 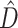are too high to be compatible with phylogenetic congruence.

Figure 1.

Plot of 1000 replicates simulated under conditions that yielded varying levels of deep coalescence (x-axis) and phylogenetic dissonance 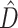values (y-axis). Blue circles indicate Bayes Factor support for the CONCATENATED model over both HETERO and SEPARATE. Green squares indicate support for the HETERO model over both CONCATENATED and SEPARATE. Red triangles indicate support for SEPARATE model over both CONCATENATED and HETERO. Filled symbols represent 90% average information content across genes, with closed symbols indicating 90%. Numbers indicate particular replicates mentioned in the text.

It is informative to examine some outliers in the simulation results presented in Figure 1. In few cases, SEPARATE was the winning model even when the number of deep coalescences was less than 1 per gene on average. For example, consider replicate 532, for which the SEPARATE model won despite a high average information content (94% of maximum information), relatively low 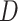, and a single topological conflict among 10 genes. Removing the gene that conflicted (gene2) from the concatenated set, followed by re-estimation of marginal likelihoods, resulted in a win for the CONCATENATED model, suggesting that a single incongruent subset out of 10 total can be enough to give the SEPARATE model victory.

In cases of multiple deep coalescences (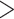3.2/gene) or high dissonance , the CONCATENATED model won only when average information content was low, while HETERO never won under these circumstances. Low phylogenetic signal can result in a preference for the CONCATENATED model despite a high number of deep coalescences (e.g., Fig. 1, replicates 19, 56, 70, 97, 251, 292, 339, 533). In some extreme cases, when phylogenetic information content is very low (approaching zero information), 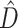can also be low (Fig. 1, replicates 19, 56, 70, 251). In such cases, posterior samples of individual gene subsets visit every possible tree topology (of the 105 possible unrooted binary tree topologies for 6 taxa) in roughly equal proportions. Phylogenetic dissonance is zero if all subset posterior distributions are equal, and this is true whether these posterior distributions are concentrated or flat, so low 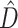in the face of low information content for all gene subsets is not surprising. It is also unsurprising that the marginal likelihood would favor the CONCATENATED model in such cases because one tree topology is about as good as any other tree topology in explaining the data, and the marginal likelihood implicitly punishes models providing access to additional dimensions of parameter space that do not appreciably increase the likelihood.

Detecting Phylogenetic Outliers in Volvocales

The results of the pairwise tests of congruence are illustrated in Figure 2a. Marginal likelihoods indicated topological congruence (i.e., the HETERO model fits better than the SEPARATE model) for all gene pairs with the exception of petD and rpl36, each of which was topologically incongruent with every other gene (but congruent with each other). Both petD and rpl36 favor Gonium + Pleodorina (Fig. 2b) while all other genes favor Volvox + Pleodorina (Fig. 2c). However, when the SEPARATE model was compared with the CONCATENATED model, the SEPARATE model was the winner in nearly 50% of the gene pairs from the 54 topologically congruent genes. This suggests that topological congruence for many gene comparisons is only possible when edge lengths are allowed to differ, implying that heterotachy or heterobathy is common.

Figure 2.

Pairwise BF test for phylogenetic congruence for all possible pairs among 56 protein coding plastid genes where the colors represent the information content present in the gene and the lines between the genes indicate phylogenetic incongruence (i.e., support for SEPARATE over HETERO) suggested by the BF test (a). In the 56 gene sets, petD and rpl36 show support for Gonium + Pleodorina relationship (b), whereas the other 54 genes support Volvox + Pleodorina relationship (c).

The CONCATERPILLAR analysis, however, indicated that all 56 genes were topologically congruent. The two genes found to be incongruent using BF analysis (petD and rpl36) were not contiguous in the chloroplast genomes of the four taxa, suggesting that they were not the result of a single horizontal transfer event. In the case of petD, there is a single variable amino-acid site (amino-acid position 106) that determines the Gonium + Pleodorina relationship: excluding site 106 removes support for this relationship. Despite the incongruence of rpl36 to the other genes, this particular gene is short (total nucleotide length =114) and it contains relatively less information relevant to estimating topology compared to the other genes analyzed. We also used PhyloBayes (Lartillot et al. 2009) to estimate phylogeny for the petD data (including all the sequences from Chlorophyceae available on Dryad: http://dx.doi.org/10.5061/dryad.q8n0v) under the CAT model (Lartillot and Philippe 2004). The CAT model accommodates sites with distinct state frequency profiles, unlike standard models that assume state frequencies are homogeneous across sites. The CAT model can potentially avoid long-branch attraction due to the model assuming a wider range of available amino acids at particular sites than are actually available. However, even under the CAT model, resolved sister to .

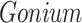Our empirical example involved a reanalysis of a subset of four taxa from a more inclusive study of green algal phylogeny. In that former study, Fučíková et al. (2016) found strong support for a single tree topology relating these four taxa using a concatenated data set, but reported very low internode certainty (IC: Salichos et al. 2014) values for all but one edge in the estimated tree. This suggests some conflict exists among genes, and thus it is not surprising that our BF analyses identified two genes (rpl36 and petD) that preferred a different tree topology than the majority (54/56) of genes. What is perhaps surprising is that LRTs conducted using CONCATERPILLAR found no conflict, concluding that all 56 genes should be concatenated. The fact that our BF approach and CONCATERPILLAR’s LRT approach provides conflicting advice highlights a major difference between the Bayesian and frequentist statistical approaches to phylogenetics. For the petD gene, we found that a single amino acid site (site 106) determines the preference of this gene for Gonium + Pleodorina. Bayesian analyses do not take into consideration (either implicitly or explicitly) any data other than what was observed, and thus take the evidence from site 106 at face value. Assuming a site appears (to the model) to be a reliable reporter (i.e., substitution is rare and the site is not contradicted by any other site), then even one site may have a strong impact on a Bayesian phylogenetic analysis. Frequentist approaches involving bootstrapping, however, take additional sources of uncertainty into consideration. Bootstrapping evaluates many data sets, each different than the observed data set, and thus accounts for uncertainty in the observed data. This is one possible explanation for why bootstrap support values for clades tend to be smaller than posterior probabilities: the Bayesian analysis assumes that there is no uncertainty in the observed data and never considers the possibility that the observed data could be atypical in some way. If support for a clade depends critically on a single site, then the bootstrap support for that clade depends on the probability that the site will be included at least once in a particular bootstrap replicate. The probability that a particular site (out of 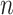total sites) will be omitted from any given bootstrap data set is 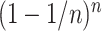, which, by definition, approache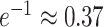s as 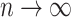. The probability that a single critical site will be included at least once in any given bootstrap data set is thus approximately 63% for a reasonably large number of sites. We should therefore not expect strong bootstrap support for a clade if that clade is supported only by a single site, even if that site appears to be reliable indicator of history. Such a site may, however, have a strong impact on a Bayesian analysis because data sets excluding that site are never considered. For this reason, frequentist tests of data combinability that use bootstrapping to evaluate the significance of likelihood ratios are not appropriate when Bayesian approaches are used for estimating phylogeny.

Bayes Factor Calibration

BF calibration for the 6-taxon, 10-gene simulation study resulted in a critical interval that bracketed zero: the 1000th element in the combined, sorted vector of prior predictive 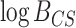values from CONCATENATED and SEPARATE models was 407.29 and the 1001th element was 73.23 (Fig. 3a). Using the standard cutoff (0.0) would thus result in the SEPARATE model winning exactly as often when CONCATENATED is the true model as the CONCATENATED model wins when the SEPARATE model is true.

Figure 3.

Kernel density estimates of 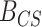under CONCATENATED (solid line) and SEPARATE (dashed line) models for the data sets with 6 taxa, 10-genes (3a), 4 taxa 2-genes (2259 sites, 93 sites) (3b), 4 taxa 2-genes (2259 sites, 2205 sites) (3c), and 4 taxa 2-genes (96 sites, 93 sites) (3d). The densities were each estimated using 1000 prior predictive replicates.

The results of the calibration for the 4-taxon, 2-gene case were more interesting due to overlap in the distribution of BF values generated under competing model. We performed calibrations for the extremes of sequence length encountered in the real (Volvocales chloroplast DNA) data. For all comparisons, whether they involved roughly equal sample sizes (2259 vs. 2205 or 96 vs. 93 sites) or quite unequal sample sizes (2259 vs. 93 sites), the cutoff interval had zero width and was close to zero: (0.15,0.15) for 2259 vs. 93 (Fig. 3b); (0.08,0.08) for 2259 vs. 2205 (Fig. 3c); and (0.05,0.05) for 96 vs. 93 (Fig. 3d). Bootstrapping the 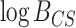values produced intervals that overlapped zero in only about 1–3% of the replicates, but were nearly equally distributed on either side of zero, indicating that these minor deviations from zero are not statistically significant. Specifically, 51.6%, 41.2%, and 46.4% of the interval midpoints were less than zero for 2259 vs. 93, 2259 vs. 2205, and 96 vs. 93 sites, respectively.

The 4-taxon, 2-gene case is extreme in that there are only three possible tree topologies, so even under the SEPARATE model prior, there is a probability of 1/3 that both genes will have the same tree topology. In these cases, it is thus understandable that the BF cutoff might be shifted to the right because the CONCATENATED model should win all of its own simulations as well as up to 1/3 of the simulations under the SEPARATE model. The fact that the cutoff values are not significantly greater than zero even in this case is due to the fact that even when the separate model chooses the same tree for both genes, it nevertheless selects quite different edge lengths for these two trees, with the result that the SEPARATE model still wins over the CONCATENATED model because the CONCATENATED model assumes that edge lengths are proportionally scaled across genes.

The Case of Mistaken Heterotachy

An interesting phenomenon was observed as a result of using phylogenetic dissonance to assess MCMC convergence with respect to tree topology. Most replicate MCMC analyses in our simulated data exhibited 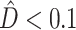, indicating that the posterior samples from replicate analyses were essentially identical (as they should be if both Markov chains mixed well and were sampled only after converging to the stationary distribution); however, many analyses exploring the HETERO model produced unexpectedly high replicate phylogenetic dissonance values. The reason for this turns out to be the completely understandable result of a model making the best of a bad situation, and offers a warning for those who might be tempted to use a HETERO model win as an evidence for heterotachy.

Consider a case of two data subsets (genes) in which the true tree topology differs (Fig. 4). The HETERO model assumes that the same tree topology applies to both genes (which is not true in this case), but allows each gene to have its own set of edge lengths. The HETERO model can choose to focus on the true tree topology for gene 1 and attempt, using edge lengths, to explain the data for gene 2 as best it can. Alternatively, it can focus on the true tree topology for gene 2 and attempt, using edge lengths, to explain the data for gene 1 to the extent possible. How does a model fit data when assuming an incorrect tree topology? The answer is that it increases the lengths of edges for some taxa that are sister taxa in truth but not in the assumed tree, leaving other closely related taxa connected by relatively short paths. Thus, the fact that some taxa are more similar than the tree topology suggests can be explained by the model using evolutionary convergence (the long edged taxa), while similarities between other taxa that seem far apart on the assumed tree topology are explained by a lowered rate of substitution. In replicate analyses, it is possible for one run to choose the tree topology for gene 1 and the other replicate to choose the tree topology for gene 2, yielding posterior distributions that are concentrated on conflicting tree topologies, which in turn produces high estimated phylogenetic dissonance. The lesson to be learned from this study is that a win by the HETERO model may not mean the presence of heterotachy in data, but may simply reflect a model doing its best to explain data generated on a different tree topology.

Figure 4.

Explanation of paradoxical high dissonance for samples from independent replicate MCMC analyses exploring the same posterior distribution under the HETERO model.

This crafty use of spurious edge lengths by models to explain away topological discordance among genes was explored in detail by Mendes and Hahn (2016). In their study of simulated and empirical data, Mendes and Hahn (2016) found that the topological discordance between gene trees due to ILS can cause multiple apparent substitutions on the focal tree (e.g., species tree) on one or more of its branches that uniquely define a split on the discordant gene tree that is absent in the species/focal tree. It is interesting that measuring phylogenetic dissonance among replicate analyses under the HETERO model alone can potentially be used to detect incongruence in gene tree topologies.

The presence of true heterotachy is suggested by low phylogenetic dissonance combined with HETERO model being the winning model. None of our simulations imparted true heterotachy; however, some results (e.g., replicate 942) did combine = 0 with a winning HETERO model. The explanation is that the HETERO model is actually detecting heterobathy (a new term) rather than heterotachy. Heterobathy may be defined as differences in coalescence depth across genes when the gene tree topologies are identical. The HETERO model is, in this case, detecting differences in coalescence times instead of differences in rate of substitution across data subsets.

Summary

Marginal likelihoods provide a straightforward way of assessing the statistical significance of phylogenetic dissonance (Lewis et al. 2016). We simulated data sets with varying levels of deep coalescence and found, as expected, that larger numbers of deep coalescence events led to higher estimated phylogenetic dissonance and also to preference for the SEPARATE model over the CONCATENATED and HETERO models based on estimated marginal likelihoods. Exceptions mainly involved data sets with low information content due to small tree lengths, which can show low dissonance and preference for the CONCATENATED model despite a relatively large number of deep coalescence events. We calibrated BF comparisons between CONCATENATED and SEPARATE using the method of García-Donato and Chen (2005) to determine the critical value that balances the prior predictive error probabilities of competing models, finding that the standard cutoff (1.0 or 0.0 on the log scale) is valid for this application of BF. Our results also show that conflict among gene tree topologies may masquerade as heterotachy in combined analyses, as shown previously by Mendes and Hahn (2016). Finally, heterobathy (differences among genes in the depth of coalescence events) can lead to preference for the HETERO model over the CONCATENATED model even when all genes have equal substitution rates and identical tree topologies.

Supplementary Material

Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.gt81779.

Funding

This material is based upon work supported by the National Science Foundation [Grant Numbers DEB-1354146 to P.O.L., M.H.C., L.K., and L.A.L.; DEB-1036448 (GrAToL) to L.A.L. and P.O.L.]; National Institutes of Health (NIH) [Grant Numbers GM 70335 and P01 CA142538 to M.H.C.] (in part).