Causal inference in the face of competing events

Abstract

Purpose of review:

Epidemiologists frequently must handle competing events, which prevent the event of interest from occurring. We review considerations for handling competing events when interpreting results causally.

Recent findings:

When interpreting statistical associations as causal effects, we recommend following a causal inference “roadmap” as one would in an analysis without competing events. There are, however, special considerations to be made for competing events when choosing the causal estimand that best answers the question of interest, selecting the statistical estimand (e.g. the cause-specific or subdistribution) that will target that causal estimand, and assessing whether causal identification conditions (e.g., conditional exchangeability, positivity, and consistency) have been sufficiently met.

Summary:

When doing causal inference in the competing events setting, it is critical to first ascertain the relevant question and the causal estimand that best answers it, with the choice often being between estimands that do and do not eliminate competing events.

Introduction

Epidemiologists study the occurrence of health events and the relationship between exposures and those events. We frequently run into scenarios where some of the participants in our study experience an event that prevents them from experiencing the outcome under study. Such events are referred to as competing events. In fact, unless the outcome is all-cause mortality, there will always be a potential competing event for the outcome, namely death (or death from a different cause).

There exist well-established statistical methods for time-to-event analyses that allow us to estimate a range of measures of association between an exposure and an outcome, while carefully considering the occurrence of competing events [1-3]. However, interpreting those exposure-outcome associations causally requires a causal inference framework that formalizes conditions under which such a causal interpretation might hold. Counterfactuals (or potential outcomes) form the basis of the modern approach to causal inference [4]. We consider what our outcome might have been had we, say, exposed all individuals in our target population to a particular level of the exposure. When applying this framework to any analysis (regardless of whether competing events are present), several steps should be considered, for example [5, 6]:

1. Define the research question and target population of interest

2. Choose the counterfactual estimand that corresponds best to the question

3. Review identification conditions, to guide estimation choices

4. Choose a statistical estimand that reflects the above 3 steps

5. Estimate the chosen estimand, carefully selecting the data and estimator

6. Consider whether we can interpret the estimated association causally, based on whether relevant identification conditions were met

When an analysis includes competing events, there are additional considerations added to each of these steps. Here, we describe some of the relevant causal and statistical estimands when competing events are present and summarize one set of causal identification conditions extended for the competing events setting. We end with a discussion of causal interpretations to clarify the distinction between the statistical handling of competing events and inferring causal relations in the presence of competing events. Determining causality requires a more holistic causal framework that ought to be rooted in the research question being asked and in which the choice of target estimand and estimator is only one consideration.

This paper further highlights the recent advances in the area of causal inference with competing events. We define “recent” as papers published since 2010, which roughly coincides with the papers by Lau et al. and Andersen et al. that described for an epidemiologic audience the concept of competing events and the statistical methods to handle them [1, 7].

Defining the research question and the appropriate counterfactual contrast

Formulating an informative epidemiologic research question requires both methodological and substantive expertise, and counterfactuals can play a central role in helping to clarify these questions. Suppose in a given study we were interested in a treatment A = a (here using the standard notation that denotes lower case a to be a realization or actual value of the random variable A), which has been hypothesized to be related to a health outcome Y with time-to-event T. For example, we might be interested in assessing how taking low dose aspirin (A = a) affects time to live birth (Y), as was assessed in the Effects of Aspirin on Gestation and Reproduction trial [8]. Assume, for a moment, that live birth has no competing events. We can then define the expected (average) outcome that would be seen if all individuals in our population were (contrary to fact) exposed to aspirin: P(T^a ≤ t) or E[Y^a(t)]. We use superscript a to denote the counterfactual probability of the outcome Y through a given time t (equivalently, that time-to-event was less than or equal to t) had all individuals in the population received a. This expected outcome can still be defined in the presence of right censoring, which occurs when we do not observe an individual’s event time but we assume the event could still occur (as might happen if a pregnant woman withdrew from the study).

When the outcome can be precluded by ≥1 competing events, we can additionally define a variable J = {1, …, k} that indexes the k possible, mutually exclusive events. In our example, such a competing event might be pregnancy loss. Fundamentally, for a given pregnancy, if someone experiences a pregnancy loss, they cannot at a later time experience live birth (and vice versa). T is then the time to any event j ∈ J. Cole et al. provided a formulation for counterfactual risk when there are competing events, in which both a counterfactual time to event and a counterfactual event type are specified: F_a(t,j) = P(T^a ≤ t,J^a = j) [9, 10]. In words, this is the probability, under treatment a, that an event would occur by time t and that it would be of type j. This counterfactual risk could also be written using the expectation, E[Y^a(t), J^a(t)], which is the equivalent to Pr(Y^a(t) = 1, J^a(t) = j) when the outcome is binary [11]. We could then define a second counterfactual scenario, where our same population was now exposed to $a^{\prime }$ (in our example, $a^{\prime }$ might be placebo), and contrast that scenario to the one above, e.g. by taking a difference in the expected outcomes: $E\left[Y^a\right(t),J^a(t\left)\right]-E\left[Y^{a^{\prime }}\right(t),J^{a^{\prime }}(t\left)\right]$.

A framework formalizing causal effects in the presence of competing events has been proposed by Young et al [12]. In their work, competing events are defined as a random variable D(t), which is a causal mediator between baseline exposure A and the outcome of interest Z(t). This formulation would, of course, not hold if A did not affect D(t). Figure 1 shows how this framework represents competing events on a directed acyclic graph [13, 14, 11]. In this mediator-based competing events formulation, the authors describe two possible counterfactual contrasts that might be of interest: the total and controlled direct effect. The total effect for the primary event of interest is defined as a contrast of E[Z^a(t)] and $E\left[Z^{a^{\prime }}\right(t\left)\right]$, which is equivalent to the contrast above. The controlled direct effect for the event of interest is then defined as a contrast of $E[Y^{a,\overline{d}=\overline{0}}(t)]$ and $E[Y^{a^{\prime },\overline{d}=\overline{0}}(t)]$ where the superscript $\overline{d}=\overline{0}$ implies an intervention that eliminates competing events [15]. This contrast has also been referred to as a contrast in conditional risks. In our example, we would be contrasting the counterfactual risk of live birth had all EAGeR participants been assigned to aspirin and we eliminated pregnancy losses versus the risk had they been assigned to placebo and we eliminated pregnancy losses. Whether the total effect or direct effect will be of more interest primarily comes down to the question being asked.

Figure 1.

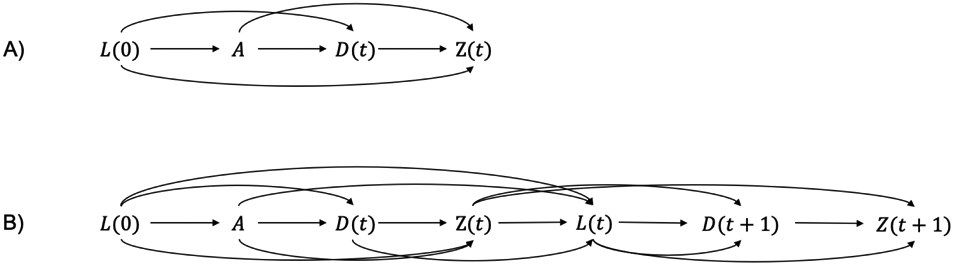
Potential directed acyclic graphs for competing events analyses that treat the competing event as a mediator. In panel A, we provide the time-fixed case, where A is a point exposure, L(0) is a baseline confounder, D(t) is occurrence of the competing event by time t, and Z(t) is occurrence of the event of interest by time t. In panel B, we expand to the time-varying case. Now, we must consider L(t) a time-varying confounder which affects the occurrence of the competing event and the event of interest by time t + 1. This case could be expanded even further if our interest was not in a baseline exposure A but rather a time-varying exposure A(t).

Statistical estimands and estimators

Two fundamental measures of the incidence of Y in standard time-to-event analyses (in the absence of competing events) are the hazard and survival (and by extension, risk). The hazard is the probability of Y occurring in a small timespan, conditional on not having already had the event. Survival is the probability of experiencing Y at some point beyond time t, S(t) = P(T > t), and is often estimated using the Kaplan-Meier survival estimator [16]. We further define the cumulative density function (equivalently, risk function) as the complement of survival, F(t) = 1 – S(t).

In the presence of competing events, these statistical estimands are expanded into two categories: cause-specific and subdistribution. These approaches target different counterfactual estimands: cause-specific measures are linked to the direct effect while subdistribution measures are linked to the total effect. As with choosing the counterfactual estimand, the approach one takes will be dependent on the research question.

Cause-specific survival S_j(t) and cause-specific risk F_j(t) target the counterfactual risks under a hypothetical intervention that eliminates competing events. Cause-specific risk is equivalent to so-called “conditional risk,” or risk under elimination of competing events. That is, even in single-sample estimation problems (i.e., ignoring any hypothetical interventions on an exposure), the interpretation of cause-specific survival or risk involves a counterfactual scenario (elimination of competing events). Consequently, estimation of the cause-specific risk or survival function requires the independent competing risks assumption. In our example, this assumption implies that whatever hypothetical intervention would eliminate pregnancy losses would have no impact on the hazard of live birth. Estimating S_j(t) usually involves plugging the h_j(t) into an estimator for all-cause survival, such as the Kaplan-Meier estimator, which will treat all other outcomes as right censored (implying that individuals who experienced a pregnancy loss could have a live birth for the same pregnancy sometime beyond their “censoring” time). While this can be done, it leads to an overestimate of the observable risk of the event and leads to unintuitive properties like the sum of the risks for each event type summing to more than one [7]. The magnitude of this overestimation will depend on the risk of the competing event.

The cause-specific hazard, h_j(t), is defined as the probability of an event occurring and it being type J = j in a short time window, conditional on not having experienced event type j or any other event. The total hazard at time t is then a simple sum of the cause-specific hazards: h(t) = Σ_j h_j(t) [12]. The cause-specific hazards can be compared using a hazard ratio, often estimated using a Cox or accelerated failure time model. We can use h_j(t) to target the hazard analog of the counterfactual risk under elimination of competing events (compared in the direct effect above). As with the cause-specific risk, this approach censors competing events and requires the independent competing events assumption. A nuanced point raised in Young et al is that, if we instead target the counterfactual hazard of the event of interest conditional on no competing events having occurred, $P(Y_t^a=1\mid D_{t-1}^a=Y_{t-1}^a=0)$, we do not censor competing events and do not have to make the independent competing events assumption because we are not intervening to eliminate competing events [12]. For our example, it might be easier to interpret the hazard of live birth among those who had not experienced pregnancy loss than it is to interpret the hazard had we eliminated pregnancy losses. However, in general, one should be cautious about interpreting any hazard estimand causally [17, 12].

On the other hand, the subdistribution approach is centered around estimating the cumulative incidence (risk) function, $F_j^{\ast }(t)=P(T\le t,J=j)$, interpreted as the probability of having an event by time t and having it be of type j. The cumulative incidence function is commonly estimated using the Aalen-Johansen estimator, which is a generalization of the Kaplan-Meier estimator [18]. The cumulative incidence function has also been referred to as the “cause-specific cumulative incidence;” [12, 19, 20] however, we believe use of this term could lead to confusion of $F_j^{\ast }(t)$ with F_j(t) Whereas cause-specific risk is linked to conditional risk, subdistribution risk is linked to unconditional risk, i.e. the observable risk without elimination of competing events. An essential property of survival under the subdistribution approach is that the probability of having the event by a given time point is a function of both the cause-specific hazard for event j and the hazards of events J ≠ j. In our example, women who experience a pregnancy loss are not censored but can conceptually be thought of as remaining in the risk set for live birth. This means that, unlike the cause-specific approach, the sum of the event-specific risks will not exceed one. When interested in a contrast, cumulative incidence functions under each treatment arm can be estimated and then contrasted using a difference or ratio.

The subdistribution hazard, $h_j^{\ast }(t)$, is derived from the subdistribution survival function and is defined as the probability of the event of interest in a small timespan, given one had not experienced an event or one had in the past experienced a different event type. Contrasts of subdistribution hazards can be estimated using the Fine-Gray model [21]. Subdistribution hazards are challenging to interpret because they condition on having experienced a competing event. However, they are considered useful because they allow for a hazard ratio estimand that will always be consistent with a contrast of cumulative incidence functions. This is not the case for cause-specific hazard ratios, which in some cases will be on the opposite side of the null from a subdistribution risk or hazard ratio. The misalignment between a cause-specific hazard ratio and subdistribution risk or hazard ratio depends on how common the competing events are and how strongly the exposure affects the competing events (and the direction of that effect) [1].

Very little has changed in these approaches to competing events or the target estimands over the last two decades, since the cumulative incidence function was developed in 1978-1980 and the Fine-Gray model in 1999 [18, 22, 21]. However, new models have been proposed to estimate the traditional statistical estimands [23-26]. Additionally, both approaches have been integrated with g-methods like inverse probability weighting and g-computation, which make it easier to explicitly link the statistical estimand to the targeted counterfactual estimand [27, 10, 28]. Work has also been done to better understand the results of competing event approaches in more complex data structures (e.g., a Cox or Fine-Gray model with competing events and time-varying covariates) [29, 30].

Causal identification

Identification in the formal sense is the ability to write the observed outcome (or contrast of outcomes) under an observed exposure as the corresponding counterfactual outcome (or contrast), e.g. that E[Y^a(t),J^a(t)] = E[Y(t),J(t) ∣ A = a]. Causal identification is not something that can be done using the data alone; we must make additional assumptions [31, 4]. One common set of identification conditions includes exchangeability, positivity, and counterfactual consistency, and there have been several recent papers that have discussed the special considerations that must be made when in the presence of competing events. Identification in the presence of competing events and how the assumptions differ depending on the target counterfactual contrast has also been explored in depth by Young et al [12].

When estimating the total effect on the unconditional risk of the outcome (i.e., a contrast of subdistribution risks), we need to meet an intuitive extension of the usual conditional exchangeability assumption ($A\coprod Y^a(t),J^a(t)$), in that we must also say the exposure is independent of the counterfactual event type [12]. If one were instead interested in estimating the direct effect with elimination of competing events, one has to additionally assume that occurrence of the competing event is independent of the counterfactual outcome, which is essentially the independent competing events assumption. In this case, the exchangeability assumption is similar to exchangeability for other mediation effects.

When estimating cumulative incidence functions or subdistribution hazard ratios, Lesko et al. demonstrated in simulation that one needs to control for all of confounders of the exposure and competing event relationship(s) in addition to the standard confounders for the main outcome [11]. In contrast, the cause-specific hazard ratios were unbiased if only the confounders for the main outcome were included. These findings are consistent with the conclusions one would make regarding the adjustment set from the causal diagrams included in Young et al [12].

Exchangeability might be broken when records with missing data are removed from the analysis, i.e. when a complete case analysis incurs selection bias. While complete case analyses can be unbiased (when data are missing completely at random), often there are fundamental reasons why the data are missing and, if those factors are related to the outcome, there could be bias. In a recent paper, Lau et al. summarized the available analytic methods that can be used when the variable with missing data was event type [32]. Like most approaches for missing data, these methods assume that event type is missing at random, i.e. conditional on the observed variables [33-37, 24].

Positivity changes little from the case when there are no competing events but there is right censoring (in that we assume for any level exposure, there remain uncensored individuals through t). Counterfactual consistency must be extended to account for the counterfactual event type J^a(t), e.g. as such: E[Y^a(t),J^a(t)∣A = a] = E[Y(t),J(t)∣A = a][38]. If using a framework treating the competing event as a mediator, we would need to be able to make a similar statement regarding D^a(t) and Z^a(t). While most of the attention on the estimation of effects under elimination of competing events has focused on the implications of the independent competing risks assumption for exchangeability, there could be interesting implications for counterfactual consistency as well. It is quite possible that an intervention to remove competing events would result in one being unable to assume that the observed time to event can be interpreted as the counterfactual time to event.

To interpret results causally, we typically make several other assumptions. We assume no measurement error. Methods have been developed to handle misclassification of event type [39, 40]. We also assume that both our causal and statistical models are correctly specified [41]. If we use any parametric (or semiparametric) models to estimate the target estimand, we must assume that the specified form of our statistical model is correct. For example, if we choose to estimate subdistribution hazard ratios using a Fine-Gray model, we assume that the subdistribution hazards for the two exposures were proportional.

Interpretations

When seeking to make causal inferences, it is important to consider not just what estimands we can quantify but what those estimands mean. We ought to ask ourselves: will the estimand inform public health action or lead to greater understanding of biological mechanisms? This is easiest when one starts with the research question and then chooses the appropriate estimation approach (whether it be cause-specific or subdistribution, alternatively the direct or total effect) – rather than the other way around. In terms of choosing the appropriate question in the presence of competing events, there are many factors to consider.

Recall that the cause-specific approach treats competing events as right censored. Sometimes censoring competing events is referred to as “ignoring” competing events, although it is more accurate to say that one is assuming that cause-specific measures occur in a counterfactual world in which the competing event did not occur. One has to make the judgement call of whether this is realistic. In our example of aspirin and pregnancy outcomes, it is unrealistic to imagine a scenario where we could entirely remove pregnancy loss. However, this will not be the case for all research questions.

Censoring competing events generally divorces estimates of risk or survival for the event of interest from what is or might be observed in reality. This is because the usual estimator (e.g., Kaplan-Meier) redistributes that mass of persons who are censored onto future events, upweighting those events in the calculation of survival or risk to account for the unobserved events that censoring implies occurred [16]. That is, someone who has a competing event is assumed to remain biologically at risk for the event of interest but to merely be unobserved (not methodologically at risk) following their competing event. As discussed previously this requires the independent competing risks assumption, in addition to the other causal assumptions.

Whether the cause-specific hazard as commonly used in the statistical literature treats competing events as censored events is less clear than for cause-specific risk. It has been well established that estimating cause-specific hazards does not require the independent competing event assumption, but uncertainty remains on how we are to interpret this estimand. The uncertainty would likely be cleared if the literature had been clearer on the question that was being asked, via the specification of the target counterfactual contrast. Young et al showed that the cause-specific hazard can be used to target a causal estimand that does not treat competing events as censored (but simply conditions on them having not occurred), but there seems to be a long-standing interest in using cause-specific hazards to say something about how an exposure affects the hazard of an outcome, when any competing events have been removed [3, 42]. As was mentioned previously, this latter interpretation requires strong assumptions related to the elimination of the competing events. Further note, though, that even if we are not attempting to say the cause-specific hazard applies to the world that has eliminated competing events, we can still say that the hazard and its contrasts only apply to those who have not experienced any event at a given moment in time.

There is an oft-repeated statement that the cause-specific hazards are more fundamentally “causal,” while the subdistribution approach to handling competing events is more “predictive” [1, 7, 43]. This sentiment appears to be linked to an interest in studying underlying biological mechanisms [44], where a “signal” that the exposure influences the outcome in whomever happens to remain under study could be regarded as evidence of a causal mechanism at work. With such a goal in mind, one might prefer an effect that seems to remove any influence of the effect of the exposure on competing events, even if that effect is not one that reflects the impact one would see in any real population subject to multiple competing outcomes. However, despite this statement being repeated across the literature [43, 45, 1, 7, 44], we have yet to find a clear explanation as to why cause-specific hazard ratios reflect etiology better or what causal framework is underlying such an opinion. Furthermore, it may be misleading to ignore the impact of the exposure on the population that remains under study, in whom cause-specific hazards are being estimated. The built-in potential for selection bias when estimating hazards and the associated perils have been well-described [17, 12].

Moreover, the viewpoint that cause-specific hazard ratios are more fundamentally causal than contrasts of subdistribution measures seems to be at odds with the more population intervention oriented causal inference framework (not to mention the expressed opinions that hazards and hazard ratios are inappropriate estimands for causal analyses) [46, 9,17, 12]. In causal inference, we imagine counterfactual scenarios produced by potential interventions and consider how well we can approximate such counterfactuals using the observed data. However, relying on cause-specific measures raises the question: could we ever find an intervention that would somehow remove a competing event like pregnancy loss or, even more extreme, death? There could be rare cases in which we remove a competing event that is death due to a particular cause (e.g., death due to an infectious disease with a highly effective and well implemented vaccine). However, even in such cases, it is unlikely that we could estimate the cause-specific hazards that would be observed if the competing events were removed [47, 11].

In contrast, the term “predictive” to describe the subdistribution risk was used in the literature to say that these estimands are useful for informing policy or predicting resource requirements for interventions [1, 48]. While predictive was meant in a traditional sense, subdistribution risk is useful for causal prediction, i.e. prediction of counterfactual outcomes under a particular policy relative to a second policy. In other words, it is useful for causal effect estimation. Some have suggested that one of the essential goals of causal inference and indeed of epidemiology ought to be examining the population impacts of interventions or policies [46]. For such causal analyses, subdistribution risk seems to be the natural estimand. Returning to our example, if we were to implement an intervention aiming to reduce early term pregnancy loss, we might also wish to know whether that intervention would affect time to live birth. Subdistribution risk mirrors what we actually observe in the real world, allowing us to make decisions based on all available evidence about the true risk of the outcome and the related resource needs and costs.

Conclusions

Over the past decade, applied analyses that explicitly account for competing events, whether they adopt the cause-specific or subdistribution approaches, have become more commonplace. Much work has also been done to extend the theory of counterfactual outcomes and identification conditions to the competing event scenario. However, there remains debate over which approach is more “causal.”

Fundamentally, before researchers attempt to make causal inferences in the presence of competing events, they will need to specify concretely their causal question and then choose the target estimand and estimation approach which will best answer that question. If unsure of the most important question to ask, researchers can always present results from both approaches, especially the cause-specific hazards and cumulative incidence functions, as they may convey different information [49, 7, 11].