Pentagalloyl glucose (PGG) partially prevents arterial mechanical changes due to elastin degradation

Abstract

Background:

Elastic fibers are composed primarily of the protein elastin and they provide reversible elasticity to the large arteries. Degradation of elastic fibers is a common histopathology in aortic aneurysms. Pentagalloyl glucose (PGG) has been shown to bind elastin and stabilize elastic fibers in some in vitro studies and in vivo models of abdominal aortic aneurysms, however its effects on native arteries are not well described.

Objective:

Perform detailed studies of the biomechanical effects of PGG on native arteries and the preventative capabilities of PGG for elastin degraded arteries.

Methods:

We treated mouse carotid arteries with PGG, elastase (ELA), and PGG+ELA and compared the wall structure, solid mechanics, and fluid transport properties to untreated (UNT) arteries.

Results:

We found that PGG alone decreased compliance compared to UNT arteries, but did not affect any other structural or biomechanical measures. Mild (30 sec) ELA treatment caused collapse and fragmentation of the elastic lamellae, plastic deformation, decreased compliance, increased modulus, and increased hydraulic conductance of the arterial wall compared to UNT. PGG+ELA treatment partially protected from all of these changes, in particular the plastic deformation. PGG mechanical protection varied considerably across PGG+ELA samples and appeared to correlate with the structural changes.

Conclusions:

Our results provide important considerations for the effects of PGG on native arteries and a baseline for further biomechanical studies on preventative elastic fiber stabilization.

Introduction

Elastin is a polymer consisting of highly crosslinked tropoelastin subunits that imparts elasticity to the large arteries. Elastin is organized by smooth muscle cells (SMCs) in the medial layer into a three-dimensional interconnecting lamellar network of elastic fibers designed to transfer stresses throughout the arterial wall. The elastic fiber network is essential for proper cardiac function in a closed circulatory system, serving as an elastic reservoir and enabling the arterial tree to undergo substantial volume changes with little change in pressure.

Genetic defects in elastic fiber components are associated with thoracic aortic aneurysms (TAAs) [1]. TAAs are also associated with mutations in genes related to other extracellular matrix (ECM) proteins, SMC function, or growth factor signaling pathways. TAAs have a common histopathology including progressive disruption and loss of elastic fibers in the aortic wall [2], suggesting that despite different molecular mechanisms that cause TAA, there are commonalities in disease pathology that may be targeted for treatment options. Degradation of elastic fibers in the TAA wall allows aortic dilation [3], releases inflammatory peptides [4], and affects porosity that may alter advection of soluble plasma molecules important for disease progression and treatment [5,6].

Pentagalloyl glucose (PGG) is the core structure of tannic acid and acts as an elastin-stabilizing agent [7]. PGG has been used in abdominal aortic aneurysm (AAA) models in rats [8] and pigs [9] to protect elastic fibers, inhibit inflammation, and reduce or prevent aneurysm growth. PGG has also been used to stabilize elastin scaffolds for vascular graft applications [10]. PGG studies have focused on degenerated ECM tissues in aneurysm models and decellularized tissues for vascular grafts, but the biomechanical effects of PGG on native arteries have not been investigated [11]. Patnaik et al. [12] characterized the biomechanical restoration potential of PGG after arterial elastin degradation in vitro, but did not investigate the preventative effects of PGG or its effects on native arteries. Cocciolone et al. [13] showed that elastic fiber degradation alters hydraulic conductance of the arterial wall, but how PGG treatment affects arterial wall fluid transport is not known.

The goal of the current study was to quantify the effects of preventative PGG treatment on native arteries and on arteries with mild elastin degradation. We quantified circumferential mechanical behavior, hydraulic conductance, and wall structure in mouse carotid arteries. Our results show that PGG partially prevents structural and mechanical changes in the arterial wall due to elastin degradation, but also changes the solid mechanical behavior of the native arterial wall. Our results are important for advancing treatments to prevent elastic fiber degradation.

Experimental Procedure

Animals and tissue preparation

Common carotid arteries were removed from 3–5 month old, C57BL6/J male mice (000664, Jackson Labs) euthanized by carbon dioxide inhalation in compliance with the Institutional Animal Care and Use Committee. Males were used as carotid artery diameter varies with sex [14]. Tissues were stored at 4 °C in phosphate-buffered saline (PBS) for 1–3 days before use [15]. 39 total carotid arteries from 20 total mice were used. There were four treatment groups: untreated controls (UNT), pentagalloyl glucose (PGG) only, elastase (ELA) only, and PGG+ELA.

PGG treatment

Penta-O-galloyl-β-D-glucose hydrate (PGG, G7548, Millipore Sigma) was diluted to 0.3% (w/w) concentration in PBS [8]. For PGG and PGG+ELA groups, the artery was mounted on a blunted 27 gauge needle attached to a syringe containing the PGG solution. The PGG solution was dispensed through the arterial lumen, then the artery was removed and left in the PGG solution for 15 minutes on an orbital shaker. Arteries were then rinsed in phosphate-buffered saline (PBS).

Elastase treatment and mechanical test preparation

All arteries were mounted in a pressure myograph system (114P, Danish Myotechnology). They were secured to metal cannulae with 7–0 suture and surrounded by a 10 mL bath of PBS maintained at 37 °C. Unloaded length and outer diameter were noted. The artery was stretched to an axial stretch ratio of 1.4, which is near the in vivo stretch ratio for a mouse carotid artery [16]. For ELA and PGG+ELA groups, the PBS in the bath and within the arterial lumen was then replaced with 7.5 U/mL high-purity porcine pancreatic elastase (EC134, Elastin Products Company) in PBS. The outlet port was closed and the artery was manually pressurized with a syringe to 100 mmHg for 30 seconds. The elastase solution in the bath and arterial lumen was removed and replaced with a stop solution of 100 mM NaCl PBS [17] and the artery was held at 100 mmHg for 30 min. The stop solution was rinsed out and replaced with PBS in the bath and arterial lumen.

As elastase treatment causes arterial lengthening, a new unloaded (not buckled) length was determined if required. The ratio of the new unloaded length to the unloaded length before treatment is termed the unloaded length ratio and is only applicable to elastase treated arteries. The elastase-treated arteries were then stretched back to an axial stretch ratio of 1.4 with respect to the new unloaded length, when possible, before continuing experimentation. In some cases, the artery could not be stretched to 1.4 after elastase treatment without significantly increasing the axial force and a lower axial stretch ratio was used. For the ELA group, the average axial stretch ratio for the mechanical tests was 1.32 ± 0.09. For all other groups, including the PGG+ELA group, the average axial stretch for the mechanical test protocols was 1.4. For UNT and PGG treatment groups, the arteries were mounted in the myograph with PBS only.

Mechanical behavior and hydraulic conductance

For characterization of circumferential mechanical behavior, the artery was inflated with PBS from 0 – 175 mmHg in steps of 25 mmHg with 12 seconds/step for three cycles while recording the outer diameter and lumen pressure (Myoview, Danish Myotechnology) [16]. The myograph inlet was then attached to a static 100 mmHg pressure column for hydraulic conductance measurements [13]. Using an air-filled syringe and a three-way stopcock, an air bubble was introduced into the tubing leading to the arterial lumen. Displacement of the bubble was measured by taking an image every minute for 10 minutes of the bubble versus a ruler for scale.

After treatment and testing, 200 – 300 μm thick rings were cut from the artery and imaged. The inner and outer border of three rings per artery were manually traced and the average unloaded outer diameter and thickness were determined by fitting an ellipse in Image J software. The remaining arterial segment was processed for examination of the wall structure.

The treatment groups and experimental procedures are summarized in Fig. 1.

Fig. 1.

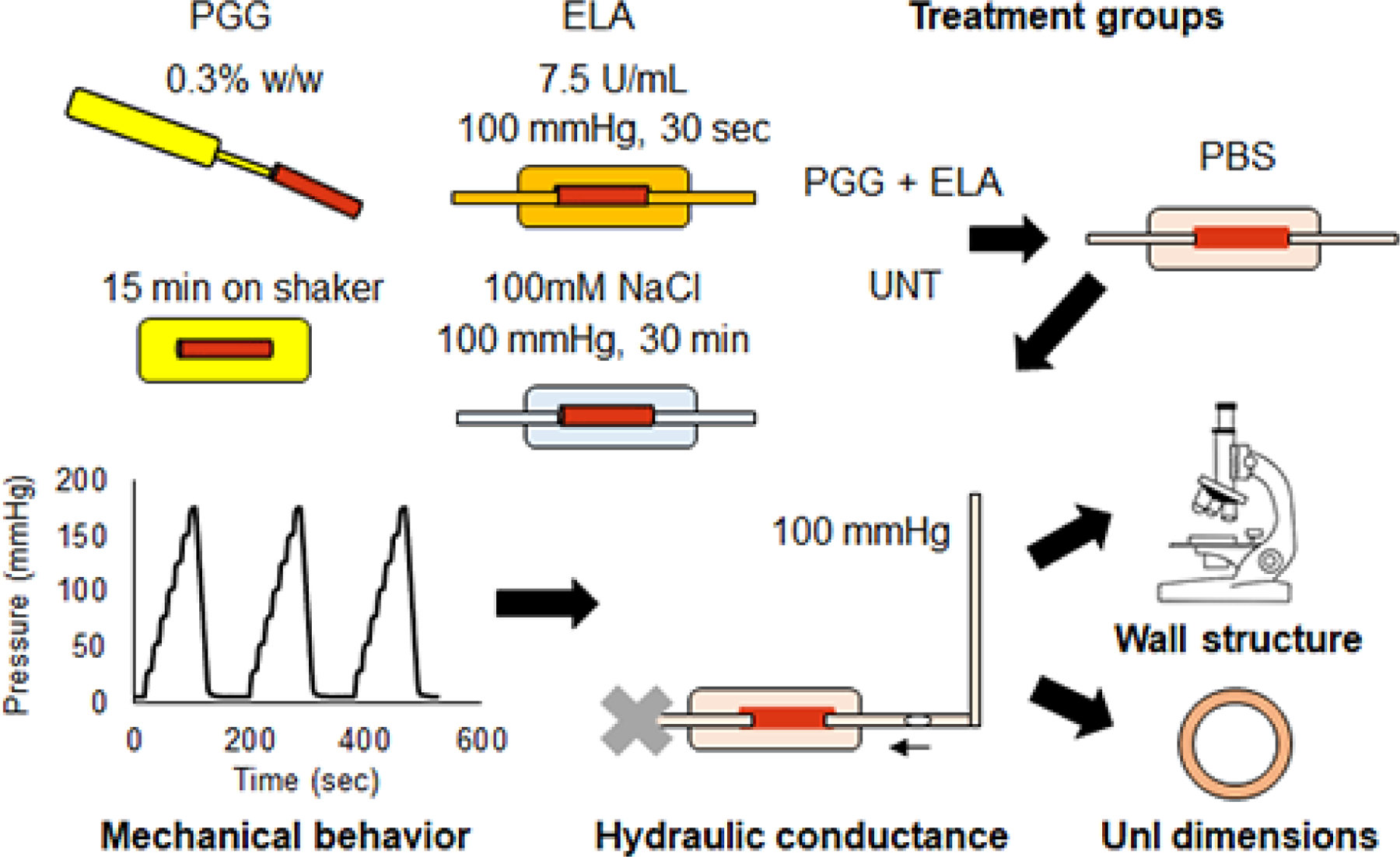
Diagram of the treatment groups and experimental procedures. Mouse carotid arteries were treated with PGG, ELA, PGG+ELA, or UNT. They were then mounted in a pressure myograph and cyclically inflated for three cycles under in vivo axial stretch. Next, a static pressure of 100 mmHg was applied and the movement of a bubble was recorded to measure fluid transport across the arterial wall. The arteries were then removed from the myograph. Small rings were cut to measure unloaded dimensions after treatment and testing and the remaining arterial tissue was processed for imaging the wall structure.

Data analysis

The loading portion of the third inflation cycle was used to determine the diameter-pressure curve and diameter compliance. The diameter compliance was calculated as the average change in diameter for each pressure step, and is an inverse measure of arterial stiffness. The unloaded dimensions after treatment, axial stretch ratio, and diameter-pressure data were used to determine the average circumferential stretch ratio (λ_θ) and stress (σ_θ), assuming no shear and an incompressible material [18],

$${\lambda }_{\theta }=\frac{1}{2}\left(\frac{d_i}{D_i}+\frac{d_o}{D_o}\right),$$ (Eqn. 1)

$${\sigma }_{\theta }=\frac{P{d}_i}{d_o-d_i},$$ (Eqn. 2)

where d is the loaded diameter, D is unloaded diameter, i is the inner wall, o is the outer wall, and P is the applied pressure. The stretch-stress curve was fit to an exponential equation,

$${\sigma }_{\theta }=b_1+b_{2}exp\left(\frac{{\lambda }_{\theta }^{b_3}}{b_4}\right),$$ (Eqn. 3)

where b_i are constants determined by regression in Matlab. The tangent modulus (E_P) was determined at a specific pressure P by differentiating Eqn. 3,

$$E_p={\frac{\partial {\sigma }_{\theta }}{\partial {\sigma }_{\theta }}|}_P.$$ (Eqn. 4)

The outer surface area of the artery (A_A) available for fluid transport across the wall was calculated from the suture-to-suture length and outer diameter. The volumetric flowrate of the bubble in the tubing was calculated using the known tubing inner diameter and average velocity determined from the distance traveled for each minute interval. By continuity, the volumetric flowrate of the bubble is equal to the volumetric flowrate (Q) of PBS across the arterial wall. Hydraulic conductance (L_p) across the arterial wall can be calculated by

$$L_p=\frac{Q}{A_A*\Delta P},$$ (Eqn. 5)

where ΔP is the pressure difference between the arterial lumen and the bath (approximately equal to 100 mmHg with the pressure column) [13].

Wall structure

Artery segments were fixed in 4% paraformaldehyde for 24 hours at 4 °C. Arteries were sequentially dehydrated in ethanol in 5 minute increments (30%, 50%, and 70% by volume). In preparation for imaging, samples were rehydrated with PBS containing 0.02% (w/v) sodium azide. En face and cross-sectional slides were prepared from three arteries for each group.

En face slides were prepared by performing a longitudinal incision the length of the artery and laying it flat such that the adventitia rested on the slide. Cross-sections were prepared by cryosectioning. Samples were first transferred to a solution of PBS containing 30% w/v sucrose to aid in tissue structure preservation. Once the tissue had sunk to the bottom of the tube (approx. 6 hrs.) they were embedded in OCT cryostat media and quick frozen on an aluminum block submerged in liquid nitrogen. Using a cryostat (Leica CM1860), 10 μm thick sections were made and placed on adhesive slides (TruBond 360 #0380W, Masunami). Once the OCT had thawed and dried, the slides were washed in deionized water before adding a drop of hydromount and a coverslip.

Two-photon microscopy was performed using a Zeiss LSM 880 Airyscan microscope and a non-descanned detector. A 63x oil immersion (Plan-Apochromat 63x/1.40 Oil DIC M27) and 40x water immersion objective (C-Apochromat 40x/1.2 W Korr FCS M27) were used for en face and cross-sectional images, respectively. Using an excitation wavelength of 800 nm, collagen second harmonic generation (SHG) was imaged through a 380–430 nm filter. Elastin auto fluorescence was imaged through a 500–550 nm and 575–610 filter for en face and cross-sections, respectively. For the en face slides, a z-stack was captured in 0.270 nm increments.

Statistics

The PGG+ELA pressure diameter data showed a large standard deviation, so the number of samples was doubled (from N = 8 to 16) for that group to increase statistical power. Outliers were identified using the ROUT method with Q = 1%. One outlier was identified in the PGG+ELA circumferential mechanical test data at 0 mmHg and was removed from all subsequent analyses. Seven outliers (1 UNT, 1 PGG, 2 ELA, 3 ELA+PGG) were identified in the hydraulic conductance data, five of which were noted during the hydraulic conductance protocols as likely having leaks. The hydraulic conductance experiments are especially sensitive to fluid leaks due to the assumption of volume conservation. These specimens were not removed from the circumferential mechanical test data as there was no indication of pressure leaks during the circumferential mechanical test protocols and they were not identified as outliers. After outlier removal, all groups were compared by one-way ANOVA with Tukey’s multiple comparisons test. P < 0.05 was considered significant and Graphpad Prism software was used for outlier and ANOVA analyses.

Histograms of the PGG+ELA pressurized diameters suggested a bimodal distribution. We used Hartigan’s Dip Test [19] calculated using Matlab scripts [20] combined with the Bimodality Coefficient [21] to assess multimodality of the pressure-diameter data for each group. A quadratic relationship was used to calculate the appropriate significance level of the Hartigan’s Dip Test for a given Bimodality Coefficient to determine multimodality [22].

Results

PGG partially protects from solid and fluid mechanical changes induced by elastase

Fig. 2a shows the diameter-pressure data for all four treatment groups. There is a large standard deviation for the PGG+ELA group, especially at 25 mmHg (Fig. 2b). Complete statistical comparisons between groups are in Online Table 1. One PGG+ELA sample was indicated as an outlier at 0 mmHg and was removed from all subsequent analyses. Examination of the remaining PGG+ELA data at 25 mmHg suggests a bimodal distribution (Fig. 2b inset). Hartigan’s Dip Test combined with a quadratic relationship for the Bimodality Coefficient [22] confirms that the PGG+ELA diameter data at 25 mmHg is multimodal (Online Table 2). The PGG+ELA data shows that some arteries appear “protected” from elastase-induced changes and resemble UNT behavior at low pressures and some appear “semi-protected” and resemble ELA behavior soon after the pressure begins to increase (Fig. 2b). Hence, we split our PGG+ELA group into two sub-groups (1 and 2) at the center of the bimodal distribution at 25 mmHg. All further data analyses were performed on the split PGG+ELA groups.

Fig. 2.

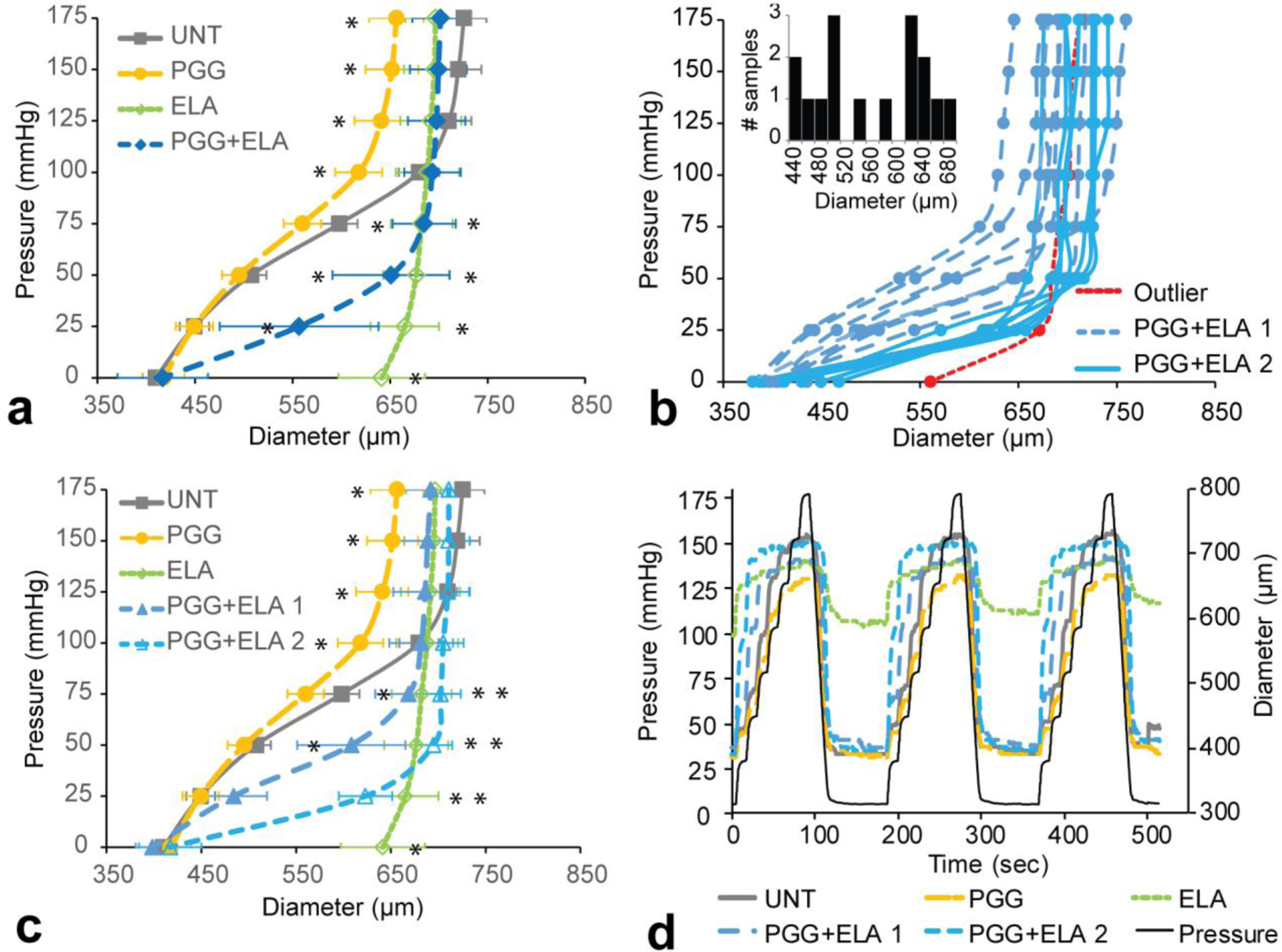
Diameter-pressure behavior of mouse carotid arteries for different treatment groups. a) Average UNT, PGG, ELA, and PGG+ELA behavior. N = 7 – 8 for all groups except N = 16 for PGG + ELA. Mean ± SD. * indicates P < 0.05 compared to UNT by ANOVA followed by Tukey’s posthoc test. All individual comparisons and P values are in Online Table 1. b) Individual curves for all arteries in the PGG+ELA group. One outlier was removed for subsequent analyses. The rest of the arteries were split into two groups for subsequent analyses, PGG+ELA 1 and 2, based on the apparent bimodal distribution of the diameters at 25 mmHg (inset) (Online Table 2). c) Average UNT, PGG, ELA, PGG+ELA 1, and PGG+ELA 2 behavior. N = 7 – 8 for all groups. Mean ± SD. * indicates P < 0.05 compared to UNT by ANOVA followed by Tukey’s posthoc test. All individual comparisons and P values are in Online Table 3. d) Representative pressure and diameter versus time behavior for each group.

Average diameter-pressure curves for the third loading cycle for the five groups are shown in Fig. 2c. Complete statistical comparisons between groups are in Online Table 3. PGG treatment leads to lower maximum diameters at the highest pressure values (100 – 175 mmHg) compared to UNT. ELA treatment causes a large increase in diameter at low pressures (0 – 75 mmHg) compared to UNT. In both PGG+ELA groups, the pressure-diameter behavior is similar to UNT and PGG at 0 mmHg and similar to ELA at high pressures (75 – 175 mmHg). The PGG+ELA 1 group also has similar diameters to UNT at 25 mmHg. To better examine the diameter-pressure behavior at 0 mmHg, we plotted the time-diameter and time-pressure behavior over all three loading cycles. Representative curves for each group are shown in Fig. 2d. Despite the steep increase in diameter with increasing pressure, the PGG+ELA groups always come back to minimum diameters that are near UNT values, while the ELA group is dilated at 0 mmHg and cannot return to minimum diameters near the UNT values. The minimum diameter for the ELA group is almost 50% larger than all other groups.

Compliance was calculated as the average change in diameter for each 25 mmHg pressure step (Fig. 3a). PGG treatment decreases the compliance compared to UNT at 75 and 100 mmHg. ELA treatment causes a sharp decrease in compliance at all pressures ≥ 25 mmHg compared to UNT. The PGG+ELA 1 group has similar compliance behavior to UNT at 50 and 175 mmHg, but divergent compliance behavior at all other pressures. The PGG + ELA 2 group has significantly different compliance compared to UNT at all pressures. Complete statistical comparisons between groups are presented in Online Table 4. To compare physiologic compliance across groups, we calculated the average compliance at 75 mmHg, which represents the peak compliance of the UNT artery (Fig. 3a) and the diastolic pressure in the mouse. The compliance at 75 mmHg highlights the small drop in compliance with PGG treatment, the large drop in compliance in the ELA group, and the partial rescue in the protected PGG+ELA 1 group (Fig. 3b).

Fig. 3.

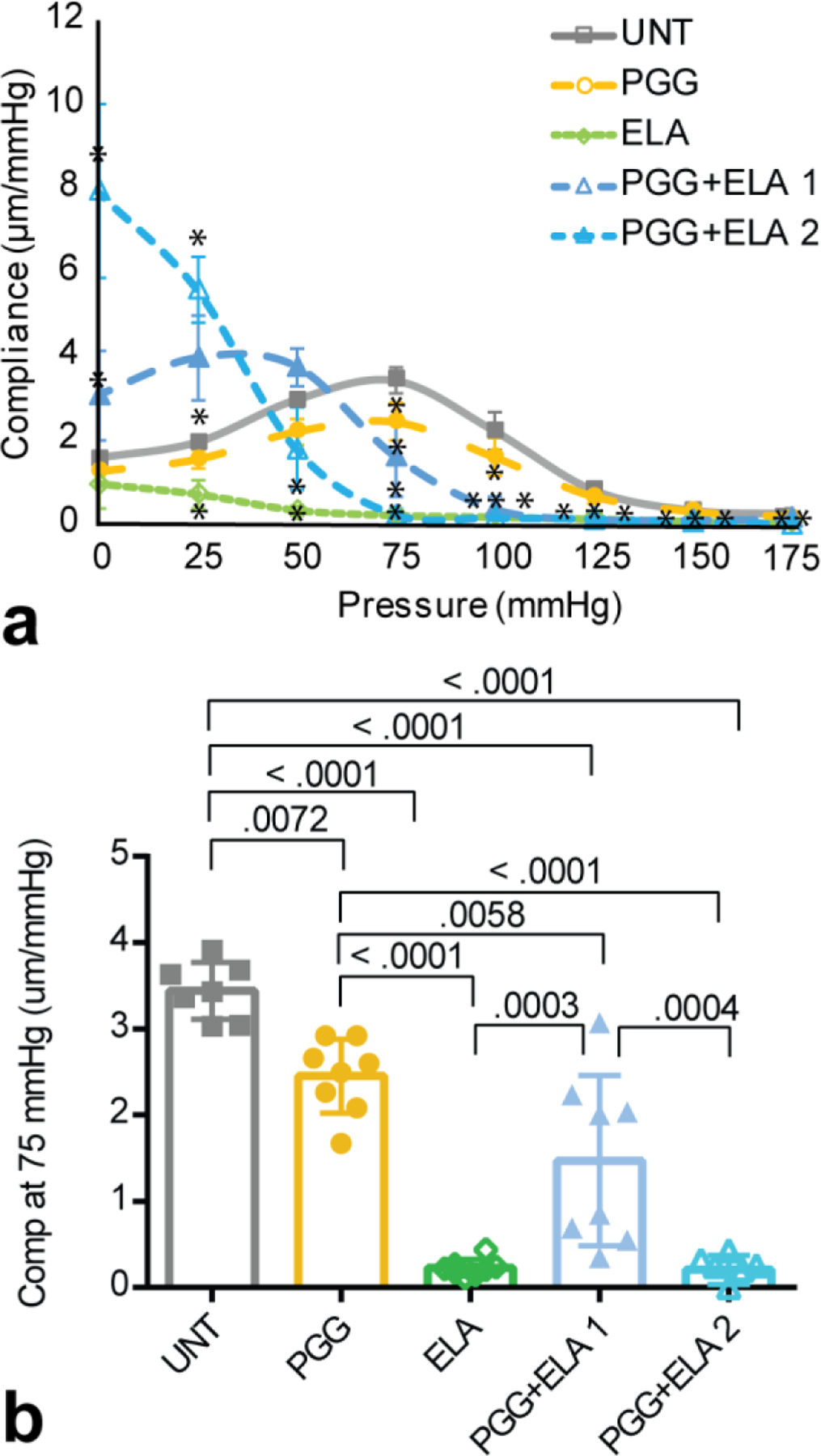
Compliance of mouse carotid arteries for different treatment groups. a) Average pressure-compliance behavior for UNT, PGG, ELA, PGG+ELA 1, and PGG+ELA 2 groups. N = 7 – 8 for all groups. Mean ± SD. * indicates P < 0.05 compared to UNT by ANOVA followed by Tukey’s posthoc test. All individual comparisons and P values are in Online Table 4. b) Compliance at 75 mmHg with individual statistical comparisons for significant P-values. Individual data points and mean ± SD are shown.

The unloaded outer diameters after treatment are similar except between the PGG and ELA groups (Fig. 4a). The unloaded outer diameters of all groups except ELA are near the recorded myograph values from the cyclic inflation cycles at 0 mmHg (Fig. 2c), as expected. For the ELA group, the unloaded outer diameter is 25% lower than the 0 mmHg myograph value. This is because ELA arteries are so compliant in the unloaded state that slight positive pressures cause large diameter increases and slight negative pressures cause artery collapse, so we cannot capture a true unloaded diameter in the myograph. The unloaded thickness values are not different between groups (Fig. 4b). The unloaded length ratio is the amount that the artery had to be stretched after elastase treatment to return to an unloaded (not buckled) length and is only applicable for the elastase treated groups. PGG treatment prevents the increase in unloaded length observed with ELA treatment (Fig. 4c). Note that because of the additional axial stretch needed to bring ELA arteries back to an unloaded length after treatment, these arteries were tested in a different configuration than all other groups, which complicates comparison of the results.

Fig. 4.

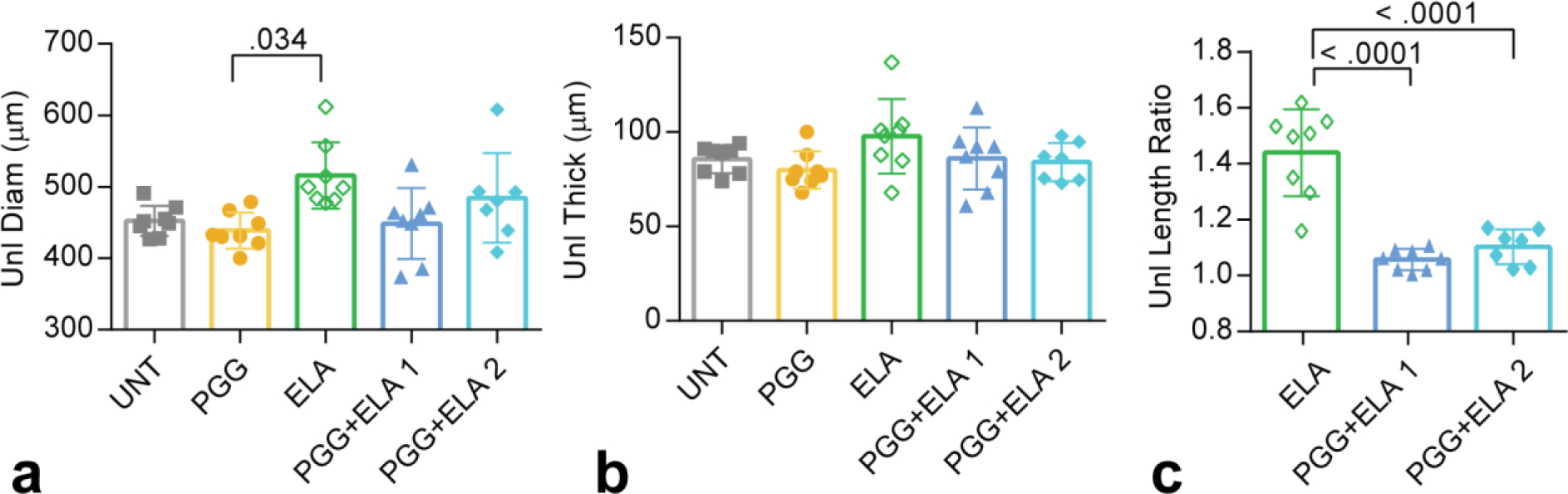
Unloaded dimensions after treatment of mouse carotid arteries for different groups. a) Unloaded diameters and b) unloaded thicknesses were measured from cut rings after treatment and testing. c) Ratio of the unloaded artery length after elastase treatment to the original unloaded artery length before elastase treatment. N = 7 – 8 for all groups. Individual data points and mean ± SD are shown. Significant P values are shown from ANOVA followed by Tukey’s posthoc test.

Average circumferential stretch versus stress curves are shown in Fig. 5a. The expected nonlinear behavior is observed in the UNT group, with a slight shift to the left for the PGG group. The ELA group starts at a high stretch ratio, consistent with the inability to return to the unpressurized diameters in the myograph and then has an almost vertical slope. The PGG+ELA groups have almost vertical slopes at high stretch, like ELA, but return to near the unpressurized diameters like UNT. To compare physiologic modulus values across groups, we calculated the tangential modulus at 75 mmHg which is near the diastolic pressure in the mouse (Fig. 5b). The physiologic modulus values demonstrate the large increase in modulus with ELA treatment and the partial rescue in the protected PGG+ELA 1 group.

Fig. 5.

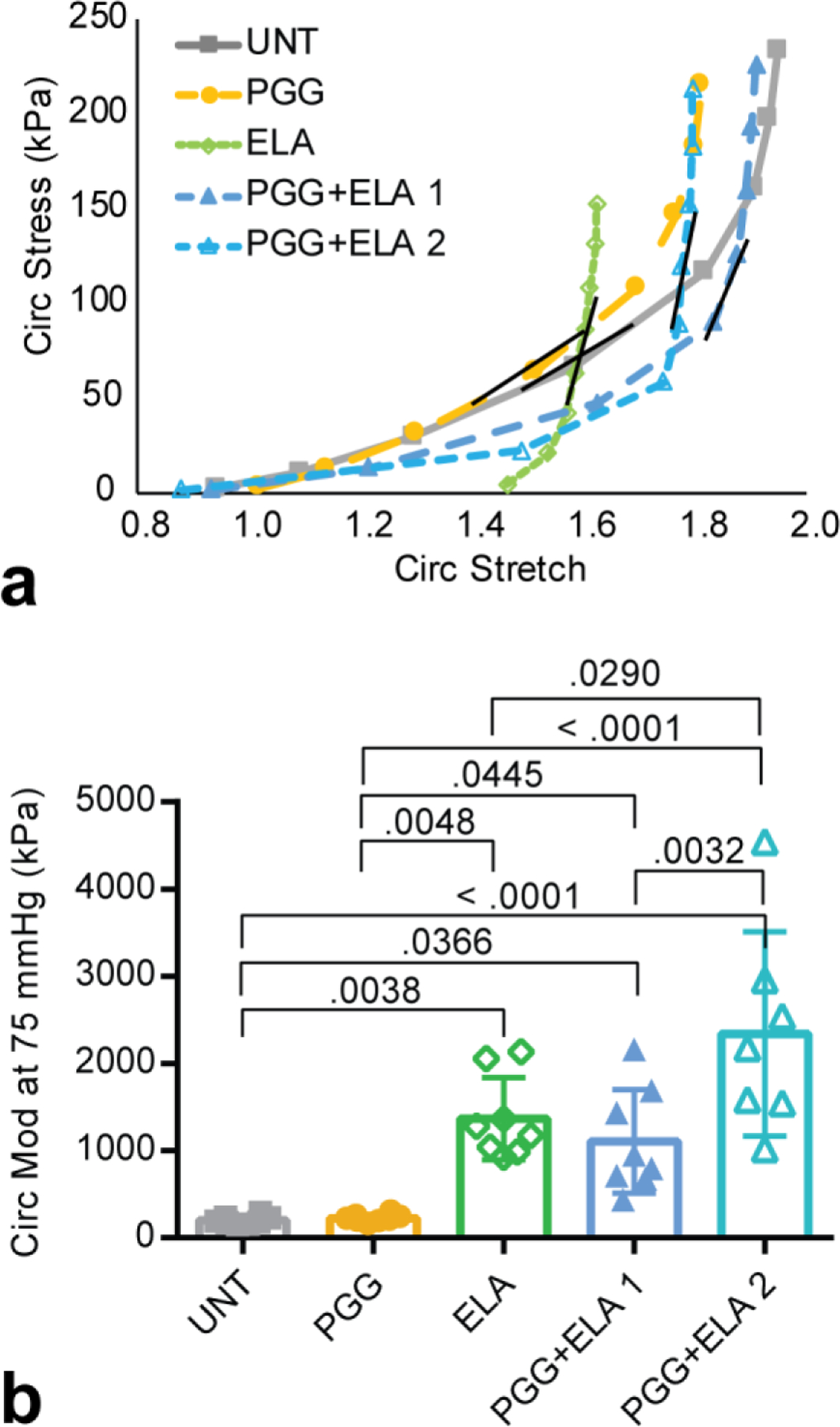
Stretch-stress behavior and tangent modulus of mouse carotid arteries for different treatment groups. a) Average circumferential stretch versus stress. Error bars were removed for clarity. The short black line on each curve represents the approximate location where the tangent modulus was calculated at a pressure of 75 mmHg. b) Tangent modulus at 75 mmHg. N = 7 – 8 for all groups. Individual data points and mean ± SD are shown. Significant P values are shown from ANOVA followed by Tukey’s posthoc test.

Hydraulic conductance, which is a measure of pressure-driven fluid transport across the arterial wall is shown in Fig. 6. ELA causes a 13x increase in hydraulic conductance compared to UNT and is significantly different from the other groups except for PGG+ELA 2. The PGG+ELA groups were split based on the circumferential mechanical behavior, but the “protected” and “semi-protected” labels for groups 1 and 2, respectively, appear to apply to hydraulic conductance, as well.

Fig. 6.

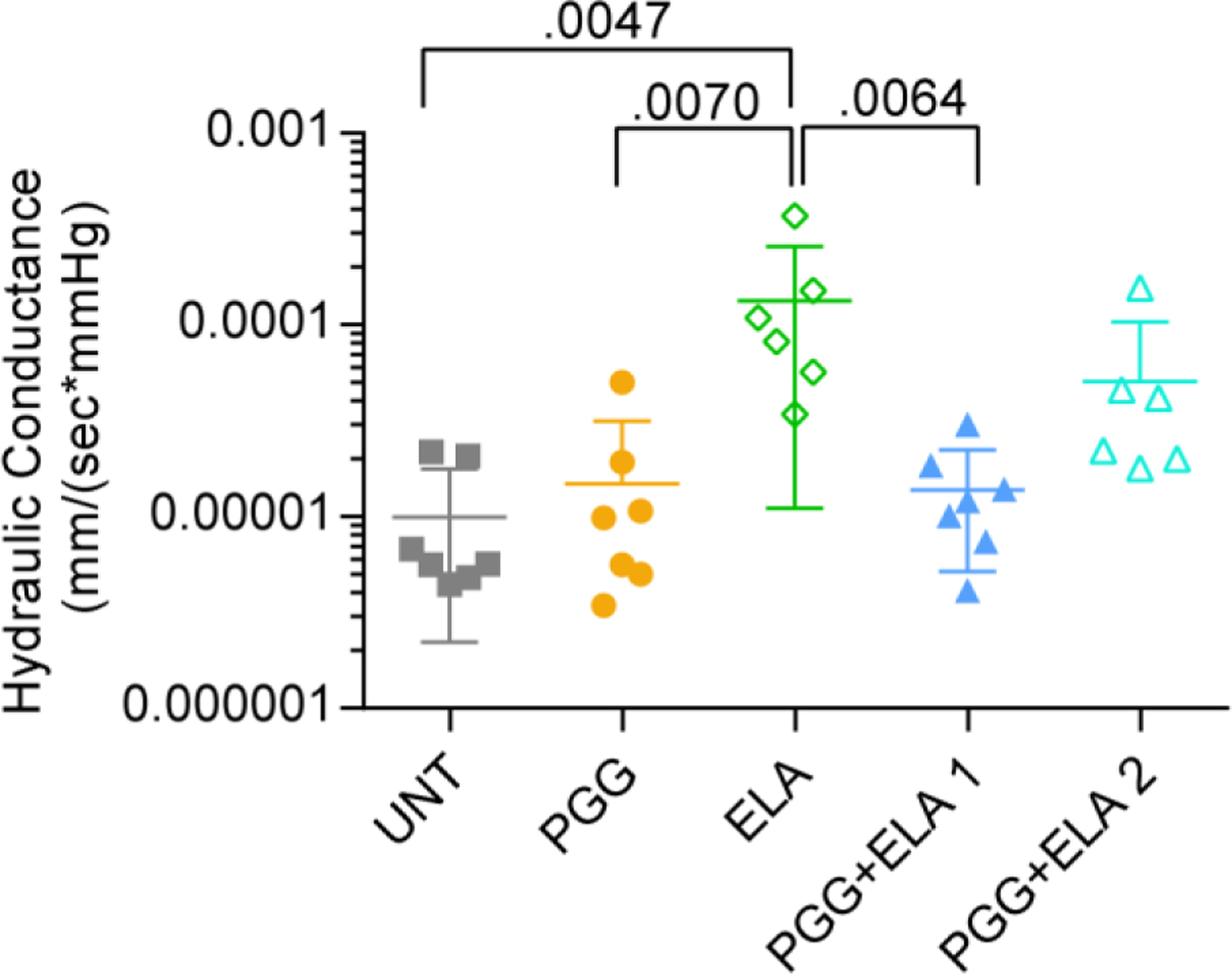
Hydraulic conductance (pressure-driven fluid transport) across the wall of mouse carotid arteries for different treatment groups. Y-axis is on a log scale. N = 6 – 7 for all groups. Individual data points and mean ± SD are shown. Significant P values are shown from ANOVA followed by Tukey’s posthoc test.

PGG partially prevents elastase induced changes in the arterial wall microstructure

Representative cross-sectional images from each group are shown in Fig. 7. Elastic fibers are organized in layers called elastic laminae throughout the arterial media. UNT and PGG elastic laminae are indistinguishable from each other. ELA treatment causes thinning, fragmentation, and collapse of the elastic laminae. Part of the thinning and collapse must occur during fixation, dehydration, and freezing of the samples for the wall structure analyses, because there were no significant decreases in thickness of the ELA samples as measured from the cut rings (Fig. 4b). PGG+ELA treatment appears to partially prevent the changes observed in the ELA group. There is less noticeable collapse of the space between elastic laminae in the PGG+ELA groups. However, there are missing segments in the elastic laminae in the PGG+ELA arteries, especially in the inner and outer layers where the tissue was exposed to ELA. The PGG+ELA 2 group appears to have thinner elastic laminae, more fragmentation, and more artery-artery variation in the wall structure than the PGG+ELA 1 group, consistent with the solid and fluid mechanical data.

Fig. 7.

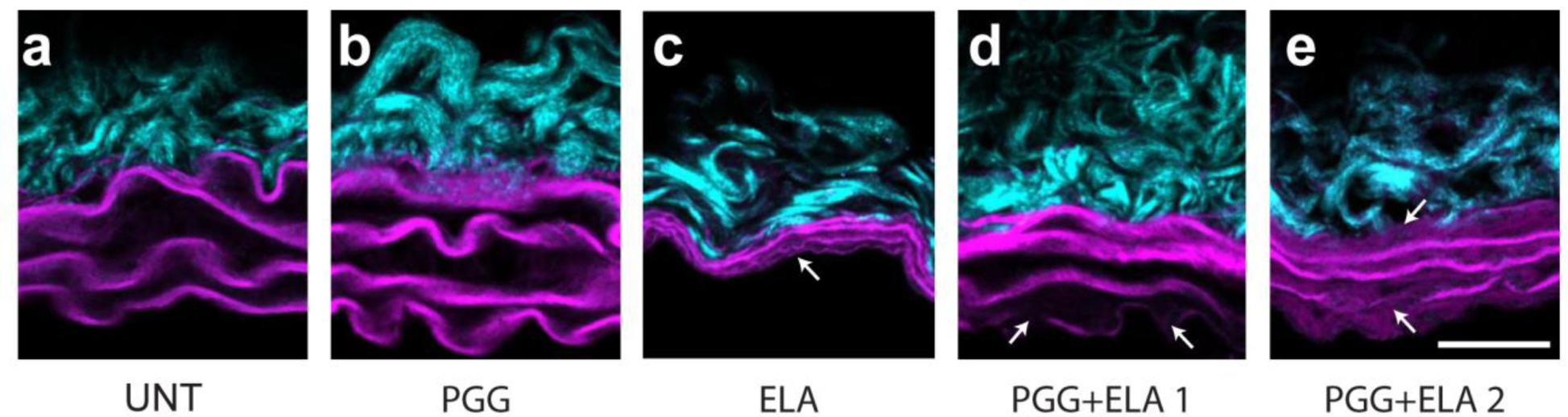
Representative cross-sectional views of mouse carotid arteries from different treatment groups (a – e). The arterial lumen is at the bottom of the image. Collagen in the adventitia is visible at the outer wall. Elastic laminae are visible as 3 – 4 wavy layers starting at the inner wall. Arrows point to fragmented or absent elastic laminae. Scale bar = 20 μm.

Representative en face images of the internal elastic lamina (IEL) closest to the lumen are shown in Fig. 8. The IEL in UNT and PGG arteries is made up of a dense mat of elastic fibers with small fenestrae. The IEL in ELA arteries appears to have a loose network of elastic fibers with large tears. Qualitatively, the IEL in PGG+ELA arteries looks intermediate between UNT and ELA arteries, with a decreased density of the elastic fiber mat and some tears.

Fig. 8.

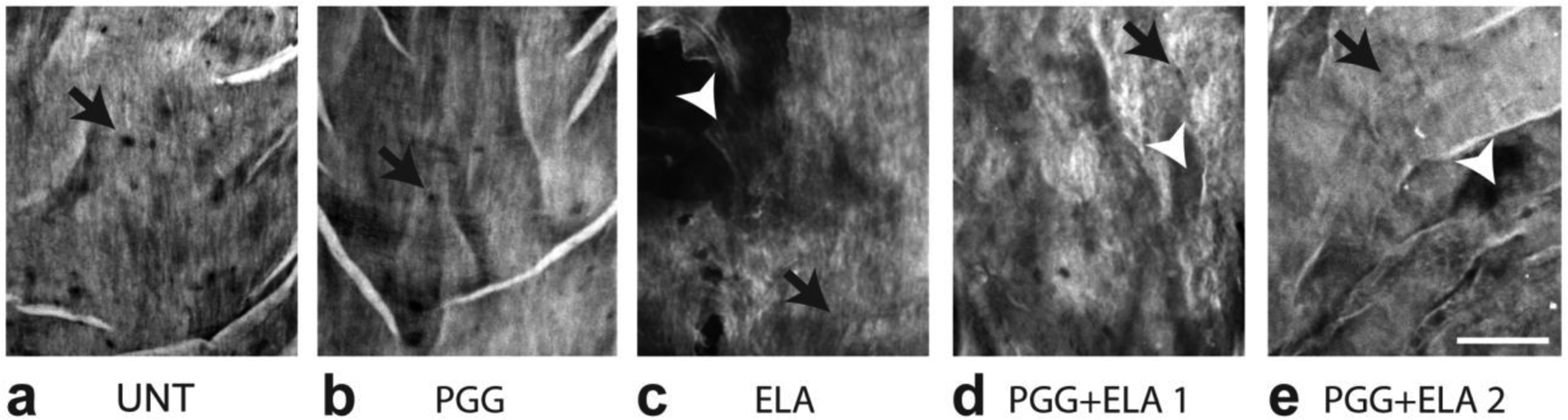
Representative en face views of mouse carotid arteries from different treatment groups. The circumferential direction is horizontal and the axial direction is vertical. Maximum z-projections were constructed through the internal elastic lamina (IEL) nearest the arterial lumen. All groups have fenestrations (black arrows) in the IEL. A dense mat of elastic fibers can be seen in UNT (a) and PGG (b) groups. A loose network of elastic fibers with large tears (white arrowheads) can be seen in the ELA group (c). PGG+ ELA groups (d and e) appear to have an intermediate structure between UNT and ELA with a slightly less dense elastic fiber network and some tears Scale bar = 20 μm.

Discussion

We present effects of PGG on native mouse arteries and on the prevention of structural and mechanical changes due to elastin degradation by a mild elastase treatment. Elastin degradation is a hallmark of aneurysmal disease and elastin stabilization through PGG treatment may represent a viable option to prevent aneurysm progression [11].

Mechanism of action of PGG

PGG has significant elastase inhibitory activity with a half-maximal inhibitory concentration of 57 μg/ml [23]. We used 0.3% w/w PGG in PBS, which is equal to 3.36 mg/ml and should be near 100% elastase inhibition. PGG inhibits elastase activity through substrate binding and not through direct enzyme inhibitory effects [7]. PGG binds to proline-rich proteins, such as collagen and elastin [24], through hydrophobic stacking of the polyphenol ring against the pro-S face of proline [25]. Presumably, binding of PGG to elastin blocks access to elastase cleavage sites, preventing degradation. Additionally, binding of PGG to elastin and/or collagen may alter mechanical behavior of the individual proteins at multiple length scales (i.e. molecule, fibril, fiber, tissue).

PGG reduces the compliance of native mouse arteries in the physiologic pressure range

PGG arteries have reduced compliance in the 75–100 mmHg (physiologic) pressure range, suggesting that binding of PGG to native elastin and/or collagen proteins alters their individual mechanical behavior and the subsequent behavior of the composite tissue. There were no observable differences in wall structure at the light microscope level for the PGG group. Quantitative light microscopy or studies at higher resolution (i.e. electron microscopy) may demonstrate structural differences in the elastic laminae or collagen fibers with PGG treatment. Biochemical studies may also provide explanations for the observed reduction in compliance with PGG treatment. Isenburg et al. [8] showed a dose dependent effect of PGG on elastase inhibition for in vitro studies on rat abdominal aorta and we chose the highest concentration from that study for maximal efficacy. It is possible that the PGG dosage could be optimized for minimal effects on native arterial mechanics while still providing elastin stabilization. There were no significant differences in unloaded dimensions, circumferential stretch-stress behavior, or hydraulic conductance with PGG treatment, so the overall mechanical changes were minimal. As decreased arterial compliance, or increased stiffness, is associated with an increased risk for a first cardiovascular event [26], care must be taken to balance the beneficial effects of elastin stabilization with the detrimental effects of increased arterial stiffness for any clinical application.

PGG partially prevents arterial wall changes with elastase treatment

Brief elastase treatment causes collapse and fragmentation of elastic laminae within the arterial wall. The structural changes are associated with a decrease in arterial elasticity, as the artery can no longer return to the unloaded state within the allotted time for mechanical testing and it shows plastic deformation (cannot return to the unloaded diameter after pressurization). This behavior is consistent with the role that elastic fibers play in arterial mechanics [27]. ELA arteries have decreased compliance [28], axial lengthening [29], increased modulus [30], and increased hydraulic conductance [13], consistent with previous studies on elastase treated arteries.

All of the structural, solid mechanical, and fluid transport changes are partially prevented by pretreatment with PGG. PGG showed a wide variation in preventative capability, which appears to correlate with the degree of elastic laminae degradation. For example, the PGG+ELA 1 group had solid and fluid mechanical behavior more similar to the UNT group than the PGG+ELA 2 group and had correspondingly less apparent fragmentation and thinning of the elastic lamellae. Mechanisms for the wide variation in PGG+ELA behavior need to be further studied. The individual ELA and PGG groups had relatively consistent mechanical behavior between arterial samples, so there must be variation in the level of protection that PGG provides when combined with ELA. It may be that small changes in PGG accessibility to elastin binding sites lead to large changes in elastase inhibitory ability and the resulting mechanical behavior. Schrader et al. [31] recently demonstrated heterogeneity in elastin crosslinking that may alter available PGG binding sites.

Our PGG+ELA data suggest a multimodal distribution of PGG preventative effects. We eliminated one outlier at 0 mmHg that did not have the same starting diameter as others in the group, but this single artery may represent a third PGG+ELA group with even less protective effects. Variation in the PGG+ELA data did not correlate with storage time of the arteries before treatment or differences between the left and right carotid arteries. Additionally, PGG+ELA data was collected by two different individuals on two different test systems and did not segregate by experimentalist or test system.

Comparison to previous studies using PGG for elastin stabilization in arteries

In 2006, Isenburg et al. [7] showed that PGG possesses the same elastin stabilizing properties as tannic acid, but is less cytotoxic. In aggressive elastase treatments that digested 83% of the porcine aorta, PGG pretreatment reduced the digestion to 58% of the porcine aorta. Mechanical studies (uniaxial stretch and residual stretch) in Isenburg et al. [7] were done for porcine aortae treated with glutaraldehyde in addition to PGG, as the authors were looking for suitable fixation procedures for cardiovascular tissues. They observed a decrease in distensibility for aorta treated with glutaraldehyde + PGG compared to aorta treated with glutaraldehyde alone, consistent with our observation that PGG binding to elastin and/or collagen fibers decreases compliance of the native arterial wall. In 2007, Isenburg et al. [8] showed that rat abdominal aorta treated with 0.3% w/w PGG retained 15x more desmosine (an elastin specific crosslink) than saline treated aorta after a 24 hour elastase treatment. 0.3% w/w PGG treatment decreased the opening angle (a measure of residual stretch) by 65° compared to saline treated aorta [8], consistent with our results that PGG alone affects some aspects of arterial mechanical behavior.

Patnaik et al. [12] investigated the restorative capability of PGG on arterial biomechanical behavior after a 1 hour elastase treatment for porcine aorta, rather than the preventative capability before elastase treatment as in our study. They found that the circumferential tensile moduli at the highest biaxial stretch ratios (about 1.5) went in descending order from native aorta (196 kPa) to ELA+PGG (82 kPa) to ELA alone (47 kPa). We found the exact opposite trend. The moduli in our study are similar to Patnaik et al. [12] for the native aorta (mean = 201 kPa), but are much higher for PGG + ELA (means = 1107 and 2339 kPa for groups 1 and 2, respectively) and ELA (mean = 1370 kPa). Our moduli were calculated at the circumferential stretch ratio at 75 mmHg, which ranged from a mean of 1.6 for UNT and ELA to 1.8 for PGG + ELA 1 and 2 groups, slightly higher values than Patnaik et al. [12]. We also used mouse arteries, while they used porcine aorta. The order of treatment (ELA+PGG or PGG+ELA) is a likely explanation for the differences in moduli between studies for those groups. The calculated stretch ratios are likely explanations for the differences in the moduli between studies for the ELA groups. The maximum stresses for the ELA group in Patnaik et al. [12] for 1.5 biaxial stretch are only 10 kPa in each direction. The unloaded dimensions change considerably after elastase treatment and it is unclear if this was taken into account by the authors. Using stretch controlled biaxial testing, it may be that they never loaded the ELA tissue into the nonlinear range. Using pressure controlled inflation and calculating stretch ratios with respect to the unloaded dimensions after elastase treatment, our ELA arteries show highly nonlinear behavior and a large modulus. Regardless of these differences, both studies show that PGG can bring biomechanical properties of ELA treated arteries back toward native values.

There have been several in vivo studies to investigate the use of PGG in stabilizing elastin in chemically-induced AAA models. Isenburg et al. [8] showed that periadventitial application of PGG interfered with early AAA formation and hindered later AAA growth in a rat CaCl₂ model. Thirugnanasambandam et al. [32], using a similar application procedure and rat CaCl₂ model, showed a trend toward AAA wall stress reduction and a significant decrease in matrix metalloproteinase (MMP)-activated fluorescent signal with PGG treatment. Nosoudi et al. [33] incorporated the PGG into targeted nanoparticles that hindered AAA growth in the rat CaCl₂ model. Nosoudi et al. [34] extended this work to show that the PGG targeted nanoparticles could also reverse late stage AAA expansion in the rat CaCl₂ model. Kloster et al. [9] showed that intraluminal delivery of PGG prevented AAA growth in a porcine elastase model. Interpretation of these studies is complicated by the extensive anti-inflammatory, anti-oxidant, anti-thrombotic, MMP inhibitory, and vasodilatory properties of PGG [11] that may contribute to its beneficial effects on AAAs. However, these studies show the promise of PGG treatment for elastin stabilization in aneurysmal disease.

Limitations and future directions

We presented circumferential mechanical data, but arteries are loaded in the circumferential and axial directions in vivo. We presented data on male mice; future work is needed to determine if the results apply to female mice. We measured hydraulic conductance, but the different treatments may also affect solute transport through the arterial wall. We chose a PGG concentration for maximal effects on elastase inhibition. Additional work is needed to determine if lower PGG concentrations are effective for elastase inhibition, while minimizing the effects on native arterial wall mechanics. Additional investigation is also needed to better understand how PGG interacts with elastin and collagen in the arterial wall, how the interactions change with degradation of elastic fibers in aneurysmal disease, and how the PGG preventative effects can be made more consistent across samples. Future work should include PGG as a treatment option in chemical and genetic animal models of TAA, in addition to AAA [11]. Preventative PGG treatment may someday be a viable option for expectedly severe TAA cases, especially in young children where aneurysm failure risk is high and replacement grafts do not grow with the children. Delivery of PGG must be optimized for long term treatment [11]. It remains to be seen whether the small decrease in arterial compliance is worth the trade-off for stabilization of the elastic fibers in the wall.

Conclusions

We showed that PGG treatment alone decreases compliance of the native arterial wall, without changing any other observed structural features or measured biomechanical properties. PGG pretreatment partially prevents changes in wall structure and solid and fluid mechanical behavior observed with mild elastase treatment in mouse arteries. Our work provides a baseline for future studies using PGG to stabilize elastic fibers in mouse models of vascular disease.