The impact of sampling patients on measuring physician patient‐sharing networks using Medicare data

Abstract

Objective

To investigate the impact of sampling patients on descriptive characteristics of physician patient‐sharing networks.

Data Sources

Medicare claims data from 10 hospital referral regions (HRRs) in the United States in 2010.

Study Design

We form a sampling frame consisting of the full cohort of patients (Medicare enrollees) with claims in the 2010 calendar year from the selected HRRs. For each sampling fraction, we form samples of patients from which a physician (“patient‐sharing”) network is constructed in which an edge between two physicians depicts that at least one patient in the sample encountered both of those physicians. The network is summarized using 18 network measures. For each network measure and sampling fraction, we compare the values determined from the sample and the full cohort of patients. Finally, we assess the sampling fraction that is needed to measure each network measure to specified levels of accuracy.

Data Collection/Extraction Methods

We utilized administrative claims from the traditional (fee‐for‐service) Medicare.

Principal Findings

We found that measures of physician degree (the number of ties to other physicians) in the network and physician centrality (importance or prominence in the network) are learned quickly in the sense that a small sampling fraction suffices to accurately compute the measure. At the network level, network density (the proportion of possible edges that are present) was learned quickly while measures based on more complex configurations (subnetworks involving multiple actors) are learned relatively slowly with relative rates of learning depending on network size (the number of nodes).

Conclusions

The sampling fraction applied to Medicare patients has a highly heterogeneous effect across different network measures on the extent to which sample‐based network measures resemble those evaluated using the full cohort. Even random sampling of patients may yield physician networks that distort descriptive features of the network based on the full cohort, potentially resulting in biased results.

1. What is already known on this topic

• The use of network methods in health services research is becoming increasingly common and holds the promise of revealing new insights about important problems in health care and medicine.

• Network analyses frequently are based on data collected for a sample of individuals from the population of interest, rather than the full cohort, and unlike standard surveys, the complexity of network topology can result in the sample network differing substantially from the full‐cohort network it is intended to represent.

2. What this study adds

• A compendium of findings concerning the relationship of the patient sampling fraction to the relative and absolute accuracy of the descriptive measures for the patient‐sharing physician network based on the sample in relation to the full cohort of patients.

• A much smaller sampling fraction suffices for physician‐level network centrality measures, including physician degree, but less so for network‐level measures based on complex configurations of actors such as transitivity, clustering coefficient, and number of network communities.

1. INTRODUCTION

With the growing use of network analysis methods in health and other areas of research, ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ various limitations on data availability frequently result in the need to perform such research based on samples rather than using data from the entire population. Many systems of interest can be represented as bipartite networks, where the network nodes can be divided into two disjoint subsets, and each tie connects a node in one subset with a node in the other subset. ¹⁶ There are several ways in which bipartite data may be sampled: The actors of one type (eg, patients), the other type (eg, physicians), or individual encounters of patients with physicians can each be sampled. The fee structure or requirements for purchased health data necessitate certain forms of sampling. For example, utilizers of claims data from the US Medicare program often are limited to a 20% random sample of data on physician encounters. Even without such a limitation, users are charged a fee determined by the number of patients (eg, Medicare enrollees or diagnosis or procedure‐based subgroup thereof) sampled and thus often specify a fraction of patients to be sampled from the full patient cohort that ideally would be used to form a patient‐sharing network. The impact of the patient sampling probability on the resulting “patient‐sharing” network of physicians—the projected unipartite network of physicians with edges determined by the number of times each pair (“dyad”) of physicians encounter the same patients ¹⁷ , ¹⁸ —is of critical importance to the trustworthiness of studies involving such networks. ¹⁹

The sequence of patient‐physician encounters in claims data lends itself to the use of network measures based on patient‐sharing networks to study the utilization, quality, cost, and clinical outcomes of health care treatments and procedures. In one type of analysis, the general approach is to describe the structure of the patient‐sharing network for each health unit being studied using various summary measures of the network as a whole (eg, the relative prominence of PCPs to specialists) or reflecting the position of physicians or organizations within the network. Outcomes (eg, cost) can then be regressed on the summary network measures and physician positional network measures along with any other covariates. ² , ⁶ , ⁷ Another common analysis encompasses the study of peer‐effects and the diffusion of treatments or procedures. Following formation of the patient‐sharing network, community detection may be used to partition the patient‐sharing network into mutually exclusive groups of actors. ¹³ , ²⁰ , ²¹ The analysis then evaluates whether nonadopter physicians who are grouped in communities with a greater extent of adoption or use at baseline are more likely to adopt or have greater utilization in the follow‐up time period.

This research is motivated by the fact that little is known about the sensitivity of network features to the sampling fraction of the nodes of one type in a bipartite network. While the challenges posed by sampling have been investigated for studies of directly measured (unipartite) networks, ²² , ²³ , ²⁴ , ²⁵ a study investigating the impact of sampling observations in the bipartite space prior to forming a projected unipartite network has not to our knowledge been performed. A study of bipartite network sampling is timely given their growing use in studying physician, hospital, and health organization patient‐sharing networks. In patient‐sharing networks, it is common for data to be sampled at the patient level. Yet, the extent to which such sampling results in inaccurate network projections of physician‐physician networks is unknown. Although we focus on this specific application, our results generalize to other settings that sample one type of actor prior to forming the bipartite network, which is then projected to form the unipartite network of the other actor type. We assume that global information about the network based on the full cohort is unavailable, and so, we cannot strategically sample actors in order to best estimate a particular feature of the network. Therefore, we focus on evaluating the consequences of simple random sampling across many network measures.

The general graph sampling problem has been assessed in terms of the ability to recover topological characteristics often focusing on a single characteristic or objective; for example, degree (the number of other physicians to which a particular physician is connected). ²⁶ , ²⁷ , ²⁸ However, there is a multitude of other aspects of the topology of the network that may be used as metrics against which to evaluate the impact of sampling. ²⁹ In the relatively scant literature on sampling bipartite network data, the sampling of nodes and edges has both been considered and compared. ³⁰ We focus on sampling one type of node in the bipartite space to mirror the handling of administrative health insurance claims data purchases.

The remainder of this paper is structured as follows. The Methods section begins with relevant background material pertaining to networks. We then describe some important theoretical results derived in the Appendix S1 (in the supplemental materials) that provide insights into the relationship between the probability of sampling each patient and the likelihood of sampling various configurations of actors. We then describe a simulation study that evaluates the relationship between the distribution of 18 network features derived from regional samples of patients in the Medicare database and from the full cohort of patients in a region in relation to the sampling probability. The results of the simulation study and their connection to the theoretical derivations are described in the Section 3, including a set of recommendations of what a minimum sampling fraction should be in order to measure each network measure with a desired level of accuracy, before the Conclusion.

2. METHODS

A patient‐sharing network is generated from a data set of patient‐physician encounters that summarize whether and the extent to which each patient encountered each physician. The bipartite network has two sets of nonoverlapping nodes, one for patients and one for physicians. Edges only exist between nodes in different sets. Bipartite network data may be projected to form a network in which physicians are nodes and the number of shared patients is derived for each physician pair (“dyad”). We assume that the simplest bipartite projection strategy of multiplying the adjacency matrix by its transpose is used to form the physician network (see Appendix S1). In this study, we consider a weighted and a binarized (0‐1) version of each network, allowing the computation of both binary‐valued and weighted network measures. The latter is obtained by making all nonzero edge weights equal to 1.

We compare an extensive range of network measures between the networks formed from the full 100% patient cohort (or the “population”) and the sampled data (Table 1). Each measure has been frequently used in network applications, and so, the extent to which its value in the full network is expected to be captured in a sample has direct applicability to research involving patient‐sharing and other networks generated from bipartite data.

TABLE 1.

Network measures for a bipartite network of physicians connected via shared patients

Network measures	Definition
(Number of) Nodes	Size of network measured in terms of number of physicians
(Number of) Ties	Number of physician dyads sharing at least one patient
Degree Distribution	Distribution of number of degree (number of ties to other physicians) across physicians in the network
Proportion of isolates	Proportion of physicians with no ties
Density	Proportion of ties out of the total possible for network; proportional to average physician degree
Strength	Average number of shared patients per physician dyad
Centralization	Variance of degree across physicians
Triadic averages	Extent to which closure occurs in triads and higher‐order configurations
Transitivity	Proportion of 2 stars (triads with at least two ties) that are closed
Weighted clustering coefficient	Extent to which nodes who share high numbers of patients with common actors share high numbers of patients among themselves
Triad census	Frequency counts of the different types of triads
Proportion with 0 ties	Proportion of triads with 0 ties
Proportion with 1 tie	Proportion of triads with 1 tie
Proportion with 2 ties	Proportion of triads with 2 ties (open triads or 2 stars)
Proportion with 3 ties	Proportion of triads with 3 ties (closed triads)
Centrality	The structural importance of a node in the network
Degree	Number of ties in the network
Weighted closeness	The inverse length of the shortest path from a given node to another node through the network averaged over each other node
Weighted betweenness	Proportion of shortest paths through a node
Weighted eigenvector	Centrality capturing the notion that you have high (low) centrality if the nodes you are tied to have high (low) centrality

In addition, we also run a community detection algorithm on the whole network for each geographic region. This algorithm seeks to partition the nodes in the network into groups such that modularity, a quality function that is proportional to the number of edges among a group of nodes less the expected number of edges among the group of nodes under random assignment of edges, such that the degree distribution of the network is conserved, is maximized. ³¹ As a way of summarizing the extent to which community structure exists in the network, we compute the number of communities for each health referral region ³² (the geographic region of interest) and sampling fraction. We also compute the average number of physicians per community.

2.1. Theory: Patient‐level sampling

To gain general insights into the impact of sampling one node type in a bipartite network on the resulting projected network for the other node type, in the Appendix S1, we derive expressions for the probability distributions and related summary measures of various quantities evaluated on the network constructed from the sampled data. Calculations are performed under independent and equal probability sampling without replacement as this emulates the sampling of patients in data from the Center for Medicare and Medicaid Services (CMS). The summary measures include the number of shared patients between two providers, the likelihood of a tie in the full‐cohort network being in the π‐sample network (the network based on sampling patients with probability π), the likelihood of a physician in the full‐cohort network being in the π‐sample network, and the likelihood of a closed triad being in the π‐sample network.

2.2. Simulation experiment

We illustrate the impact of sampling patients on the resulting projected physician networks using the following 10 health referral regions (HRRs) in the United States in 2010: Bend, OR; Alexandria, LA; Duluth, MN; Lubbock, TX; Bakersfield, CA; Eugene, OR; Harrisburg, PA; San Bernardino, CA; New Haven, CT; and Manhattan, NY. In order to visually represent our results, we selected 10 HRRs from a nationally representative set of 50 HRRs for which we had full Medicare claims data. To select the HRRs, we arranged the 50 HRRs by the number of Medicare enrollees (size) and then selected every 5th one in order to be certain to capture HRRs of vastly different sizes. The resulting networks were also diverse in location and urbanicity. See Appendix S1: Section A.3 for a fuller description of the 10 HRRs.

For each of the regions, we sample patients using sampling fractions ranging from π = 0.05 to 0.9 and evaluate the measures in Table 1. We compute the Pearson correlation ρ between the network measure evaluated on the network obtained from the full cohort and the π‐sample network. The extraction of the sample and subsequent calculations are performed multiple times to reduce Monte Carlo sampling error. The results, presented graphically, quantify relative performance in that they reveal the extent to which the pattern across the HRRs in the sample reflects that based on the full cohort; the attainment of a high ρ at a small π for a given network measure implies that it is learned quickly with respect to π. To evaluate the absolute relationship between the measure evaluated on the sample for each π and that evaluated on the full cohort, we also plot the correlation profiles for each network measure for each of the 10 HRRs.

In addition to examining the occurrence of specified network microstructures, such as closed triads (a common network measure examining the extent to which two physicians already connected to another physician are also connected to each other), we also investigated groupings of network nodes (physicians) into so‐called network communities. ³³ This clustering of network nodes into mutually exclusive subgroups of nodes (in our case physicians) is often carried out using modularity maximization. ³⁴ , ³⁵ Modularity maximization is challenging as there are no algorithms that will in general find the global optimum in finite time. Therefore, community detection algorithms tend to accept solutions as good enough when a local optimal solution has been found. Thus, rerunning the algorithm may lead to a different solution even with the full patient cohort. We ran the community detection algorithm multiple times on both the sampled and the full networks, estimating the correlation coefficient for each network measure in Table 1 at each π, averaging over the physician dyads to obtain the average estimated correlation coefficient.

3. RESULTS

We first plot the correlation between each network measure on the π‐sampled network and that based on the full cohort of patients as a function of π (the sampling fraction). We then present the value of each network measure across the 10 HRRs for each value of π. The former evaluates the extent to which the relative value of the network measures across the HRRs is able to be learned, while the latter reflects the absolute accuracy under sampling and the heterogeneity in these relationships across different regions. Finally, recommendations are made for the minimal π to use in order to measure each feature of a network such that its correlation with the feature's value in the network based on the full cohort is sufficiently high. The threshold at which a correlation is considered to be sufficiently high is not a normative global quantity. Rather, it ought to reflect the role of that measure in the problem at hand and the extent to which sampling error can be accommodated. In our case, we consider two thresholds, 0.95 and 0.99, as corresponding to a minimal level and a desired level, respectively.

3.1. Correlations of network measures at given sampling fraction to whole network

The correlation of all measures derived from the π‐sampled patient data with their corresponding value under the full cohort increases with π (Figure 2). However, there is notable heterogeneity in the comparative rates of increase. We will use the terms “rapid learning” and “slow learning” to group the measures into those whose correlation with the full network value approaches 1 very quickly and those that require larger sampling fractions to be learned (eg, <0.95 correlation at a sampling probability of 0.2).

FIGURE 2.

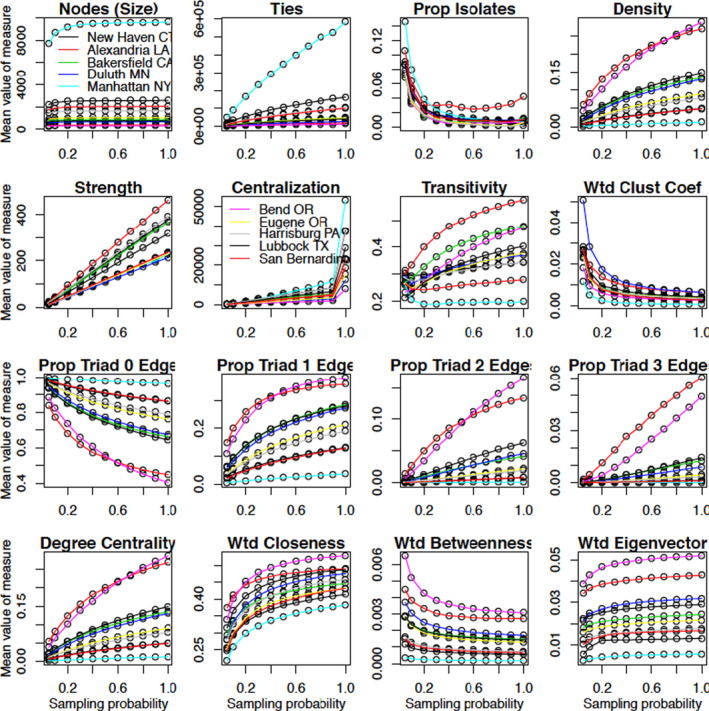
Values of network measures for the 10 health referral regions (HRRs). Clustering coefficient and closeness, betweenness, and eigenvector centrality are all evaluated on the weighted network, whereas the other measures are for the binarized version of the network. Notable HRRs for their extremity are colored as follows: Manhattan (NY) = light blue, Bend (OR) = pink, San Bernardino (CA) = orange [Color figure can be viewed at wileyonlinelibrary.com]

The correlation functions for the number of nodes (network size) and the number of ties both depict rapid learning. However, the gradient of the correlation function for network size is steeper than for the number of ties, indicating that network size is more conducive to being learned quickly. The theoretical results in the Appendix S1 predict these findings because there is a much greater opportunity to sample a given node than a specific edge in which it is involved (see Equations 1 and 3 and Figure A in the Appendix S1).

While the comparative number of nodes and ties in one network versus another is learned rapidly, the proportion of isolates is the slowest quantity to be learned (Figure 1). The contrast is due to the higher prevalence of isolates at small values of π leading to a low correlation with the proportion in the network determined from the full cohort.

FIGURE 1.

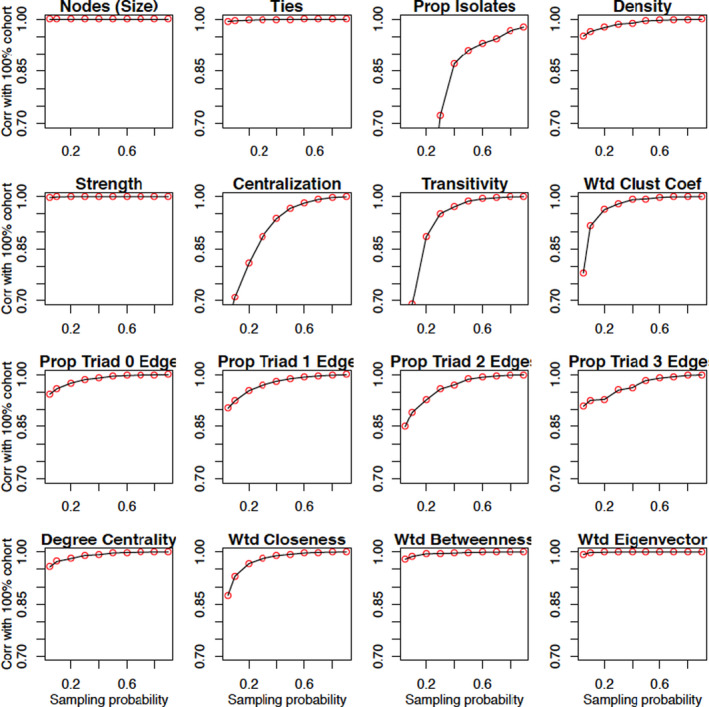
Plots of the Pearson correlation coefficient between network measures evaluated on the network derived from a 100 π% sample of patients and that based on the full cohort of patients (the full cohort). The plotted points are the correlations of the network measures for the networks built on the $\pi$‐sampled data and the full cohort across the 10 HRRs. Clustering coefficient and closeness, betweenness, and eigenvector centrality are all evaluated on the weighted network [Color figure can be viewed at wileyonlinelibrary.com]

Density, which is equivalent to normalized mean degree, is learned slower than the number of ties. Centralization, as measured by the heterogeneity of the node degrees, is learned at a yet slower rate than density (eg, at a 90% sampling fraction, the value for Manhattan is about one‐fifth of its value for the 100% cohort). Because the sample variance is more sensitive to outliers than the sample mean, a greater proportion of the network must be sampled in order for centralization to be learned accurately.

Despite both being learned quickly, the rate of increase in the correlation for total strength (the sum of the number of shared patients across all edges in the network) exceeds that of the total number of ties (the total number of instances of at least one shared patient). This result implies that edges with more patient sharing are more likely to be sampled and have more influence on a summary measure than when each edge is treated equally, such as for density. In the weighted projected network, edges are weighted in proportion to the observed number of shared patients, not the number of selected edges, and so are less impacted by edges involving a small number of shared patients than the total number of distinct edges.

Transitivity has a yet slower rate of learning than density. Under dyadic independence, the probability of a triad being closed is a product of three edge existence probabilities (Appendix S1: Equation (4)). The correlation function for the (weighted) clustering coefficient, computed as the geometric average of the subgraph edge weights, ³⁶ , ³⁷ increases relatively slowly with π due to its dependence on edges between pairs of actors both connected to the focal actor, as opposed to the actor themselves. The correlations for the proportion of triads of each type also increase slowly, especially in the case of the closed triangle, but generally are faster than transitivity and the clustering coefficient.

The results for the measures of centrality (mean degree, weighted closeness, weighted betweenness, and weighted eigenvector) are shown on the fourth row of Figure 1. Degree centrality is the most local measure in that it only depends on edges involving the focal node. Closeness and betweenness both involve geodesic (shortest) paths through the network and are distinguished by whether the focal node is at the start or is a midpoint of the path. These centrality measures involve varying proportions of the network. At the opposite end of the spectrum to degree is eigenvector centrality, which is a function of the entire network. A comparison of the correlation trajectories for these four measures reveals that closeness is learned the slowest, followed by degree, betweenness, and then eigenvector centrality. The disparate learning rates for closeness and betweenness are explained by closeness depending on path lengths from the focal node to other nodes, whereas betweenness is a count of all pairwise shortest paths through the focal node. The former relies on a greater sampling proportion of patients to be measured accurately and is sensitive to long paths involving weak connections. In contrast, betweenness is learned quickly from the preferential sampling of well‐connected nodes and of paths involving them being captured. Eigenvector centrality measures the extent to which a node is connected to nodes with high centrality. Because the most connected nodes have a higher likelihood of being sampled, the key nodes underlying the infrastructure of the network based on the full cohort are preferentially sampled and eigenvector centrality is the most rapidly learned centrality measure.

3.2. Values of network measures for the 10 HRRs

The closer the HRR‐specific plots of the network measure against π are to a horizontal line, the closer the π‐sampled value is to the value based on the full cohort. The number of nodes (physicians), betweenness centrality, and eigenvector centrality have fairly flat trajectories, whereas strength increases linearly, degree increases nonlinearly, and the number of isolates decreases nonlinearly.

Centralization has one of the most interesting trajectories across π. For every HRR, it increases linearly over $\pi \in \{0.05,0.90\}$ but then jumps substantially to the value for the full cohort. This may be a consequence of centralization being hard to learn because a number of the weakest edges are often only captured using the full cohort. The presence of these low degree nodes substantially changes the spread of the degree distribution.

A standout feature of the HRR‐specific sampling plots is that network size has a substantial impact. Manhattan, the largest HRR, typically has a trajectory that is the highest or the lowest across the HRRs (Figure 2). For example, network size and the number of ties have much higher values in the Manhattan network due to the large number of physicians, whereas density is the lowest in Manhattan, a reflection of the phenomenon that density typically dissipates with network size.

The proportion of isolates is an exception in that Manhattan is not an extreme HRR. The reason is that a physician is only included in the sampled network if a patient seeing that physician was sampled. Hence, the numerator and denominator of the proportion of isolates both change with π, lowering the correlation with its value for the full cohort (physicians in the original bipartite network that are not sampled are not considered isolates in the sampled network).

The network measures with the trajectories that vary the most between the HRRs are eigenvector centrality and other measures based on the status of configurations involving three or more edges, such as transitivity, clustering, and the proportions of the remaining types of triads.

3.3. Results based on community structure

The correlation plot for the number of communities obtained from the community detection algorithm suggests that a point of inflection occurs at $\pi =0.30$ (Figure 3, upper segment). Community structure thus appears harder to learn than most other measures. The correlation for the number of communities is approximately 0.96 when using the full cohort, implying that the results across all sampling probabilities might be penalized downwards by an amount of around 0.04 due to the failure of the community detection algorithm to find the global optimal partition of physicians.

FIGURE 3.

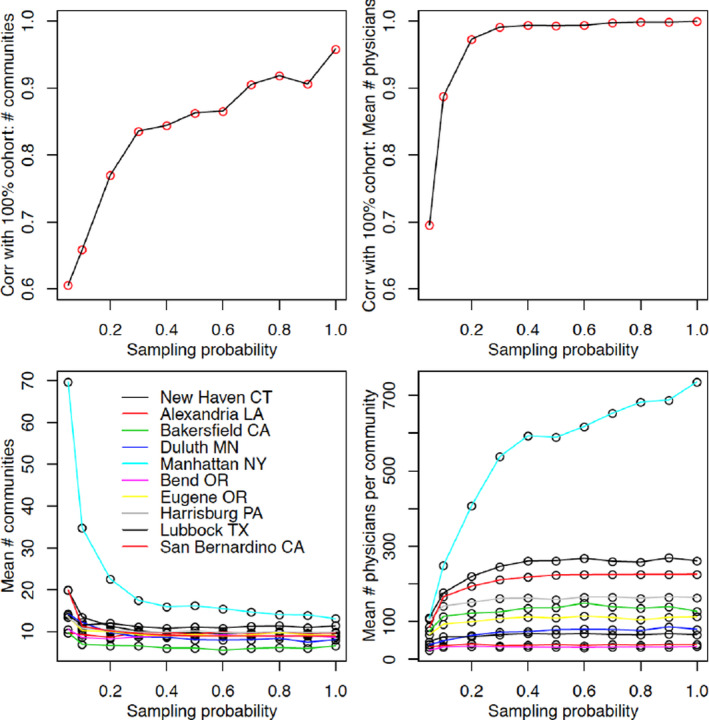
Plots of the Pearson correlation coefficient of the number and the mean size of the communities detected in the network evaluated on a 100 π% sample of patients and the corresponding measures evaluated on the 100% cohort (upper plots). In addition, the number of communities and the mean number of physicians per community are presented for the 10 HRRs (lower plots). Values at $\pi =1$ do not exactly emulate those of the full network due to the nonoptimality of the community detection algorithm [Color figure can be viewed at wileyonlinelibrary.com]

The number of communities and the mean number of physicians per community attain flat trajectories for $\pi >0.2$ implying that the actual value in the network based on the full cohort is learned quickly. A slight exception is the Manhattan HRR, whose trajectory increases more quickly than that for the other HRRs.

The number of communities decreased with π especially for the Manhattan HRR (lower segment of Figure 3). For small π, community detection algorithms will tend to find many communities with several of the communities being small in size, likely because some linking ties that would have strengthened the bridge between those communities were not sampled. As π increases, the community detection algorithm stabilizes due to the network being larger and thus more difficult to break into communities, resulting in a structure close to that obtained when the full cohort of patients is analyzed. The number of physicians per community is again quicker to learn and increases with π.

3.4. Practical considerations: what sampling fraction is sufficient?

Researchers may wonder about the extent to which a sampling fraction of 20% or 5% influences the physician network since CMS often provides Medicare data using a patient sampling fraction of 20% or 5% ³⁸ or, conversely, of knowing what value of π is needed in order for a certain correlation between the sample and full‐cohort measures to be attained. We evaluated which measures can be measured with sufficient accuracy for the four combinations of the use of a 20% and a 5% sample crossed with the requirement of a 0.95 and a 0.99 minimum correlation with the value of the network measure in the full‐cohort network. Results are summarized by grouping the measures into the 5‐tiered hierarchical categorization: those that meet the 0.99 correlation standard using a 5% sample (category I), those who fail this but meet the 0.95 correlation standard (category II), those who miss category II but meet the 0.99 correlation standard with a 20% sample (category III), those who miss category III but meet the 0.95 correlation standard with a 20% sample (category IV), and those who fail to meet the 0.95 correlation standard with a 20% sample (category V).

The category I network measures are the number of nodes, the number of ties, average strength, and eigenvector centrality (Table 2). Betweenness centrality is the only measure in category II. Category III consists of average degree (or equivalently density), while category IV consists of most elements of the triad census, weighted clustering coefficient, and closeness centrality. The two other elements of the triad census were very close to satisfying the criteria for category IV. Finally, the proportion of isolates, transitivity, and the community measures failed to attain the lowest standard and so comprise category V.

TABLE 2.

Threshold attainment by network measures

Measure	p20	p05	q95	q99	Cat
Attained 0.99 correlation on 5% sample
(Number of) Nodes	1.000	1.000	<0.001	<0.001	I
Strength	0.999	0.997	<0.001	0.001	I
Weighted eigenvector centrality	0.999	0.994	<0.001	0.022	I
(Number of) Ties	0.998	0.994	<0.001	0.015	I
Attained 0.99 correlation on 20% sample
Weighted betweenness centrality	0.993	0.979	0.003	0.147	II
Attained correlation between 0.95 and 0.99 on 5% sample
Degree centrality	0.983	0.957	0.034	0.319	III
Density	0.978	0.951	0.047	0.394	III
Attained correlation between 0.95 and 0.99 on 20% sample
Proportion of triads with 0 edges	0.977	0.943	0.065	0.383	IV
Weighted closeness centrality	0.963	0.881	0.156	0.386	IV
Proportion of triads with 1 edges	0.956	0.901	0.172	0.562	IV
Weighted clustering coefficient	0.953	0.803	0.193	0.335	IV
Did not attain 0.95 correlation on 20% sample
Mean physicians per community	0.943	0.732	0.212	0.314	V
Proportion triad 3 edges	0.942	0.908	0.258	0.683	V
Proportion triad 2 edges	0.935	0.847	0.262	0.604	V
Transitivity	0.833	0.167	0.286	0.336	V
Centralization	0.830	0.615	0.490	0.709	V
Number of communities	0.764	0.598	1.000	1.000	V
Proportion of isolates	0.554	−0.025	0.692	0.853	V

Key: In order, the four numerical columns contain the estimated correlation with the truth when using a 20% (p20 column) and a 5% sample (p05 column) and the estimated sampling fraction needed to obtain a correlation with the truth greater than 0.95 (q95) and 0.99 (q99). The separate regions of the table show the measures that attain a correlation above 0.99 with a 5% sample; above 0.99 with a 20% sample; above 0.95 but below 0.99 with a 5% sample; and that fail to be above 0.95 with a 20% sample.

Based on the above, we propose the following normative rules for investigators planning network studies to use in order to compute the network measures of interest with sufficient accuracy:

1. Measures of network size such as the number of nodes and the number of ties are learned very quickly, and they accurately reflect the full cohort with π as small as 0.001 (a 0.1% sample).

2. Average strength is more robust than density or average degree. Its measurement is aided through preferential measurement of the edges with the highest values enabling it to be accurately measured (above 0.99 correlation) using a 5% sample, whereas degree is only just above the 0.95 threshold.

3. Eigenvector centrality followed by betweenness centrality is learned more rapidly than degree centrality and closeness when $\pi <0.2$.

4. Degree and density can be learned modestly accurately with a sample as low as 5% but are learned precisely with a sample of 20%.

5. Closeness centrality is learned the slowest of the centrality measures.

6. While the triad census is partially measured above a 0.95 correlation with a 20% sample, transitivity is more challenging to learn and so a sampling fraction greater than 20% is needed. Estimates based on this analysis suggest using a 30% sample.

7. Centralization requires a 50% sample to be learned with 0.95 accuracy. It is a measure of spread that is not robust to outliers.

8. Measures that partition the network such as the number of communities and the proportion of outliers are learned very slowly, and it may be necessary for the full cohort to be analyzed in order to be confident in the measured values.

The above recommendations may vary depending on the number of patients available to sample as well as the number of distinct physicians that they can encounter. This point is evidenced by the plots in Figure 3 that reveal differences between the HRRs in the value of the network measures at the same sampling probabilities. The differences are largely proportional but not perfectly. However, the substantial differences between the rapid‐learning and slow‐learning measures make the above recommendations universal in their applicability.

4. CONCLUSION

Because bipartite networks have complicated topologies, it is perilous to assume that sampling will not affect results of analyses based on these networks. In fact, for measures like density and even more so transitivity, the sampled network will underestimate the true value as the probability that a given physician is sampled far exceeds the probability that one of its edges is sampled. To extend the applicability of this work, the theoretical results in Appendix S1 Section A.2 are presented for the sampling of patients and for the sampling of patient episodes.

We found support for the hypothesis that degree and the centrality measures are more robust to sampling (ie, are learned more quickly) than community‐based metrics. We also found that eigenvector centrality is learned most quickly followed by betweenness centrality and degree. All centrality measures are learned substantially more quickly than the number of communities in the full network.

We have made recommendations on the sampling fraction needed to be needed for the value of a network measure determined from a sample of patients to be sufficiently highly correlated with the corresponding quantity in the full network. However, a limitation of basing this on Medicare fee‐for‐service claims is that even the 100% sample misses Medicare advantage and privately insured individuals. Because these missed claims pertain to different types of claims and patients, an addition concern is whether the sample of individuals is representative of the entire population of claims and persons.

A consideration for future work concerns whether certain network measures for the network as a whole can be recovered by utilizing sampling probabilities. Weighting (dividing) each sampled edge by its probability of being sampled yields an unbiased estimator of the network density in the full network, whereas biased estimates will be obtained for higher‐order network measures. However, a weighting‐based remedy relies on the full network being known in order to determine the sampling probabilities for each edge or higher‐order configuration.

The results presented in this paper provide a warning to network analysts and researchers on the types of bias that occur when sampling from one type of node before constructing a bipartite network. Inaccuracies evaluating network measures on samples of patients may manifest in both measurement error and confounding bias in subsequent analyses of the relationship of network measures to outcomes (see Appendix S1 Section A.4 for full description). Network‐based studies that involve some form of sampling should pay allegiance to these results before drawing firm conclusions from their network analyses.

Supporting information

Author matrix

Appendix S1

O'Malley AJ, Onnela J‐P, Keating NL, Landon BE. The impact of sampling patients on measuring physician patient‐sharing networks using Medicare data. Health Serv Res 2021;56:323–333. 10.1111/1475-6773.13568