Abstract
With the coronavirus pandemic wreathing havoc around the world, power industry has been hit hard due to the proposal of lockdown policies. However, the impact of lockdowns and shutdowns on the power system in different regions as well as periods of the pandemic can hardly be reflected on the foundation of current studies. In this paper, a prediction-based analysis method is developed to point out the electricity consumption gap resulted from the pandemic situation. The core of this method is a novel optimized grey prediction model, namely Rolling IMSGM(1,1) (Rolling Mechanism combined with grey model with initial condition as Maclaurin series), which achieves better prediction results in the face of long-term emergencies. A novel initial condition is adopted to track data with various characteristics in the form of higher-order polynomials, which are then determined by intelligent algorithms to realize accurate fitting. Historical power consumption data in China are utilized to carry out the monthly forecasts during COVID-19. Compared with other competitive models’ prediction results, the superiority of IMSGM(1,1) are demonstrated. Through analyzing the gap between predicted consumption values and the actual data, it can be found that the impact of the pandemic on electricity varies in different periods, which is related to its severity and the local lockdown policies. This study helps to understand the impact on power industry in the face of such an emergency intuitively so as to respond to possible future events.
Keywords: Electricity consumption gap; Prediction-based analysis; IMSGM(1,1); COVID-19
1. Introduction
1.1. Background
Increasing fluctuations in energy consumption has become a basic problem that draws attention worldwide [1], [2]. To understand the influence of emergencies on power industry as well as arrange energy distribution appropriately, it’s crucial to investigate the industry [3]. Scale of power industry in China has expanded continuously in the past few decades, which now ranks the second around the world. For the sustainable development of national economy, China will continue to develop power industry as the basic industry in the coming decade. Generally, accurate forecast helps to determine electricity scheduling as well as methods of power storage, and the layout of facilities can thus be improved [4], [5]. However, due to the sudden outbreak of COVID-19, power consumption shows a downward trend in 2020. In current situation, the consumption of electricity has been given new connotations that help to evaluate the impact of COVID-19 on power system at different stages, and can also be regarded as a reference indicator for the resumption progress of production.
As the most commonly used energy resources, there are plentiful of determinants that affect electricity consumption such as economy, demography, climate, public emergencies and other factors. In terms of economy, influential elements include National Gross Product, price fluctuations and the organization of market [6], [7]. The trend of economic development is proved to be consistent with electricity consumption, which especially prompts the increasing variety of power generation approaches [8]. Factors pertinent to electricity consumption from the aspect of demography involve population in rural and city areas [9]. In practice, the optimization of economic structure and implementation of energy conservation policies to reduce emission also have an impact on power industry [10]. Factors such as industrial structure adjustments, technological progress, and changes from generating capacity also play their part in electricity consumption [11]. As for whether the consumption level can return to normal after disasters, factors such as people's attitude towards energy saving consciousness and residents' income are vital [12]. Therefore, prediction of electricity consumption through the establishment of an overall model is complex as many factors need to be considered and the model is tied with unknown possibilities, while mathematical methods are more succinct to be conducted.
As an unprecedented challenge faced by mankind, governments worldwide are doing their utmost to contain the spread of COVID-19. In view of the fact that vaccines haven’t been promoted successfully by now, many countries have adopted stringent measures such as nationwide lockdowns or partial lockdowns in certain areas. In China, where the lockdown policies are carried out at the earliest, restrictions including individual isolation, blockade of high-risk areas and movement of personnel in non-epidemic areas have effectively prevented the spread of the disease [13]. However, due to these policies, there are also adverse effects such as the increased cost of pandemic control and impediments on social and economic development, which have certain influence on China's power supply, grid operation and market transaction. Restricted operations of industries and mobilities of residents lead to electricity consumption decline in 2020 in China compared with the same period in previous years. To understand the impact on power industry during the pandemic, this paper proposes a prediction model that can precisely forecast power consumption gap caused by the pandemic so as to better grasp the influences owing to lockdown policies and industry downtime.
1.2. Literature review
Based on the need to estimate the impact under current situation, forecast energy consumption accurately is significant to make full arrangements of energy industry [14]. The selection criteria of apropos forecasting method include the inherent abilities of historical data, correlation of variables in prediction, and how the predictions are carried out. In the field of energy consumption forecast, various methodologies have been put forward, including Time Series [15], [16], support vector regression [17], Markov model [18], Artificial Neural Networks (ANNs) [19], [20], Fuzzy Systems [21] and other advanced methodologies. Each method has its own characteristics and performs differently in diverse research contexts.
For the above methods, predictions can be carried out only when there are enough training data, while for problems related to uncertainty and lack sufficient input information, Professor Julong Deng proposed grey theory, whose mechanism is on the basis of grey generating function and differential fitting that directly converts time series into differential equations to establish the dynamic model of an abstract system.
Though the prediction results of the traditional GM(1,1) model can reach certain degree of accuracy, they are not satisfying enough. To enhance forecast performance, many scholars have made efforts in three aspects to optimize the original grey model:
-
1.
Adjustments to optimize the initial condition;
-
2.
Applying intelligent algorithms to optimize parameters or to construct hybrid models;
-
3.
Consideration of circumstances with multivariate or non-linear problems.
The initial condition in grey model has been modified in diverse ways. Traditionally, the initial condition adopts the first number in historical data sequence as the coefficient, which does not correspond with the computational disciplines that use accumulated generating operation (AGO) data. Therefore, some studies are implemented on this issue. Dang et al. [22] choose as the initial condition in grey differential equation. The improved initial conditions is generated by the original sequence through accumulation process, therefore, the information of data sequence can be fully reflected. Xiong et al. [23] present an original grey model that optimizes the initial value by giving preference to more timely data. Song et al. [24] come up with a model that involves uneven influential level of each individual element to the AGO sequence by inserting a dynamic weighted coefficient that further improves the initial condition. These modifications overcome the shortage in grey model as they avoid the problem that the initial conditions are not concerned with the growth trend of the data sequence, which are in line with new information principle.
Meanwhile, different intelligent algorithms have been employed to optimize parameters or to construct hybrid models. Lee et al. [25] come up with a model combining genetic programming symbol evaluation with residual correction in the case of small original data set. To reduce the simulation error and improve the model adaptability to different data features, Xu et al. [26] construct a nonlinear model with an optimized time response function (TRF) on the basis of particle swarm optimization (PSO). Yuan et al. [27] put forward a hybrid model composed of GM(1,1) and ARIMA by giving equal weights to both methods. Li et al. [29] integrate regression models with GM(1,1) aiming at compensating for the residual sequence, and Markov chain has been utilized in improving predictive performance. Considering the research background of these studies, the prediction accuracy is enhanced to some extent by hybrid grey models.
Multivariate and non-linear prediction problems are taken into consideration due to the complexity under real circumstances. Wang et al. [30] analyze the advantages of linear and nonlinear models and make a combination of nonlinear grey model and ARIMA model appropriate for predicting shale gas production in the U.S. Liu et al. [31] deal with multivariate prediction problems through GM(1,n) model which includes n − 1 input and single output of the sequence number in the grey system. Li et al. [32] propose a second-order univariate improved dynamic model, and the cubic spline function and Taylor approximation method are applied to compute background values. Wang [33] proposes a method combining grey model with technologies in multivariate statistics, in which the sample data are divided into different categories through hierarchical clustering analysis and discriminant analysis.
Studies related to prediction have made contributions in many fields and have improved our understanding of prediction mechanism. Through analyzing the updated electricity consumption data in China as well as studying previous prediction models in depth, grey prediction models proposed in former researches turned out to have some limitations since the specific impact of COVID-19′s on the reduction of electricity consumption is not clear yet.
Whether it is due to the COVID-19 pandemic or other major disasters that have occurred in the past, many scholars have studied their impact on power system. WAKASHIRO [34] uses the ordinary least squares model to analyze 276 days of electricity consumption data in 10 Japanese regions, and estimates its reduction in electricity demand in the emergency state of COVID-19. Gillingham et al. [35] assume that the impact of COVID-19 is temporary, and the trend before the pandemic would continue after a brief interruption, including investments in green technologies such as wind and solar power generation capacity and energy efficiency investments. Narajewski [36] uses the high-dimensional time series change point model to analyze the power load of European countries, and the load forecast model is applied to analyze the structural changes in power demand due to shutdowns. Wang et al. [37] study Black Marble's artificial satellite night lighting products, which are used to monitor the scope and restoration of power outage space at the community level, and have been successfully used to monitor disaster-related power outages. Ruan et al. [38] quantify the “delay” effect of COVID-19 cases, social distance, and retail liquidity on electricity consumption, and develope a cross-domain open access data center to track and measure COVID-19′s impact on the US power industry. Chen et al. [39] develop a load forecasting method, discussing the load change brought by home isolation and the transformation of people's travel patterns, and respond to the load forecast challenge during COVID-19 pandemic in a timely manner.
Although previous works have made it clear for us to understand the impact of such emergencies, there are still some gaps in the existing studies on the impact on power industry due to the different severity of the pandemic in different regions. When energy growth trend changes, existing models seem not capable of making timely adjustments to predict the future situations. To fill this research vacancy, this paper considers public health data such as COVID-19 cases and deaths, and put forward a new prediction model to analyze the consumption gap resulted from the pandemic. The model establishes its basic form by virtue of grey model. From the perspective of optimizing initial condition, innovative coefficients are introduced to better reveal the deviance from normal growth trend due to the pandemic situation.
1.3. Contributions of this work
Main contributions of this work are shown as below:
-
(1)
A prediction-based framework is proposed to study the consumption gap of electricity caused by long-term emergencies.
-
(2)
The Rolling IMSGM(1,1) whose prediction goal is the power consumption gap is proposed. Initial condition of the model is in the form of Maclaurin series and is resolved by intelligent algorithms, which better concludes the long-term laws of data and predicts more accurate under long-term emergency.
-
(3)
Predictions using other grey models are carried out with the same sample data, and the comparison results demonstrate the superiority of the new model.
-
(4)
The proposed framework is validated by the case in China after COVID-19. In the first two months of this year, total electricity consumption in Chine decreased by 7.8% year-on-year. On the fundamental of the difference between the forecasted and actually reported values of China's electricity consumption achieved through the new model, combined with the severity of the outbreak, the impact of the outbreak on the power sector in 2020 is discussed in this paper.
1.4. Paper organization
The organization of the remainder of this article is described hereinafter. A succinct demonstration of the electricity prediction problem is given in Section 2. Section 3 introduces the newly proposed IMSGM(1,1). Section 4 contains the modelling steps and solution methods of the new model in detail. Empirical cases are carried out to testify the performance and effectiveness of Rolling IMSGM(1,1) in Section 5, and monthly predictions in 2020 are conducted to appraise the pandemic influence. The last part gives the conclusions of this paper.
2. Problem description
Pandemic caused by the coronavirus continuously spreads across China. In order to fight against the pandemic and safeguard the lives of the people, the State Council of China issued the Notice on extending the Spring Festival Holiday in 2020 and many corporations postponed the resumption of work according to the actual situation. Under this circumstance, forecasting the gap between the normal electricity consumption values and the real data during the pandemic helps to indicate the influence of lockdown policies as well as industry shutdowns, and further judges the resumption of each industry. Constructing an overall prediction model for electricity industry contains many difficulties, including thorough surveys of local infrastructures and the acquisition of plentiful of historical data during different periods. Given this complex structure of the model, it is more convenient and accurate to make predictions through mathematical models which can avoid errors caused by the defects of incomplete information. According to data released by the National Energy Administration of China, the newly established model is applied to analyze the impact of this pandemic on electricity consumption.
At present, most of the existing forecast models set their research period as annual forecasting or short-term forecasting (generally within a day or so). Considering that dynamic lockdown policies have been carried out in different stages of the pandemic, the research period in this study should be reconsidered as well. In China, some regions have already arranged to permit residents to return to work step by step. In response to the impact of COVID-19 and to stimulate the recovery of consumption, more than 30 cities have recently issued policies to raise domestic consumption.
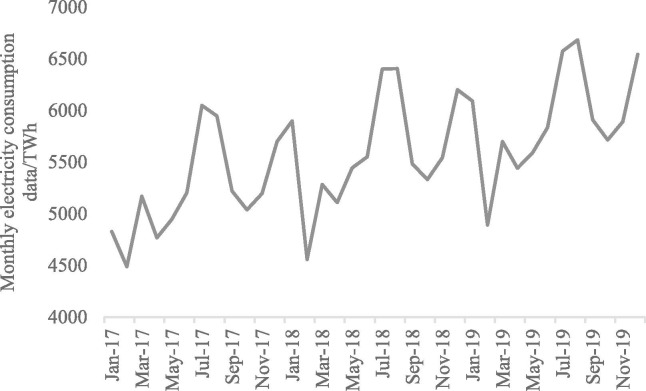
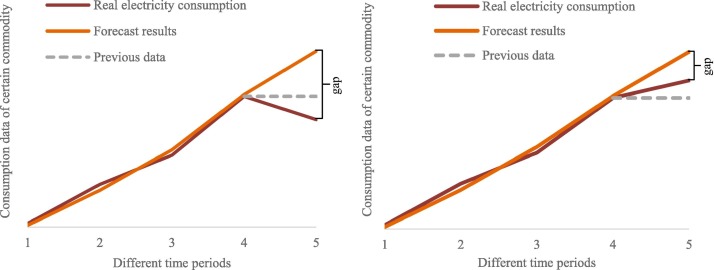
The lockdowns and shutdowns have reduced power consumption to a lower level than in previous years. Different from the annual consumption data of electricity, the consumption in each month fluctuates greatly within a year as shown in Fig. 1 , while for each month, the consumption shows an overall growth trend with regularity. Therefore, taking time intervals by month can better reflect the actual impact in different stages of the pandemic. Meanwhile, if the historical consumption data of previous years are used as the benchmark with the actual consumption data, the thwarted development momentum of the power industry is thus ignored. This paper develops a suit of monthly electricity consumption gap forecast model, which is applied to the analysis of China's electricity consumption in the most severe months of the pandemic. As depicted in Fig. 2 , in the case of unknown severity of an emergency,using data from previous years for analysis cannot fit the original development trend of the power industry. The figure on the left in Fig. 2 indicates that if the impact is not enough to bring power consumption back to the previous year's level, using data of previous years will even come to a conclusion that there is only slight impact, which is inconsistent with the reality. In the figure on the right side, when using real consumption data rather than forecast results to discuss the consumption gap, the discrepancy is underestimated as the ignorance of growth trend. Therefore, it is more appropriate to analyze the gap by using the predicted results. It can be seen that gap analysis based on predicted results is more practical than that based on the data of previous years since it can better reflect the original development trend.
Fig. 1.
Monthly electricity consumption data in China from 2017 to 2019.
Fig. 2.
Power consumption gap analysis with different benchmark.
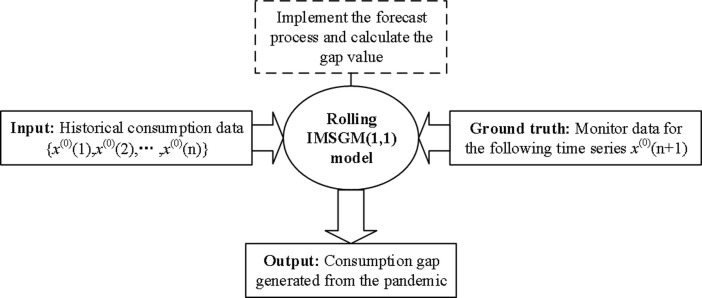
Conventional sequential forecasting method is applied to the forecast and its basic idea is shown in Fig. 3 . We arrange the known data to be the input of the model, then, coefficients in prediction are formulated by mining the internal discipline of historical data sequence. Through the modelling procedures of IMSGM(1,1) model, the predictive values can be obtained. Periodic and rolling predictions can be made continuously according to the latest acquired data.
Fig. 3.
Simplified structure of electricity consumption gap prediction.
3. Methodology
In this section, the construction of GM(1,1) is introduced in section3.1. Then, extensions of GM(1,1) with optimized initial condition are introduced. Lastly, Section 3.2 gives a systematic introduction to the new Rolling IMSGM(1,1) model. Details of these models are described below.
3.1. GM(1,1) and its extensions
Among various prediction models, GM(1,1) is one of the most frequently applied first-order single-variate models used in predicting problems with uncertain factors and incomplete information. As the theory of grey model describes, the basic grey model does not consider the background of the research problem. Raw data are processed by means of accumulation, and then the law of potential trend derives from the discrete equation. Afterwards, a continuous differential equation which possesses undecided coefficients is utilized as the reflection equation. Data are mapped to an adjustable function and simplified into TRF as the prediction fundament.
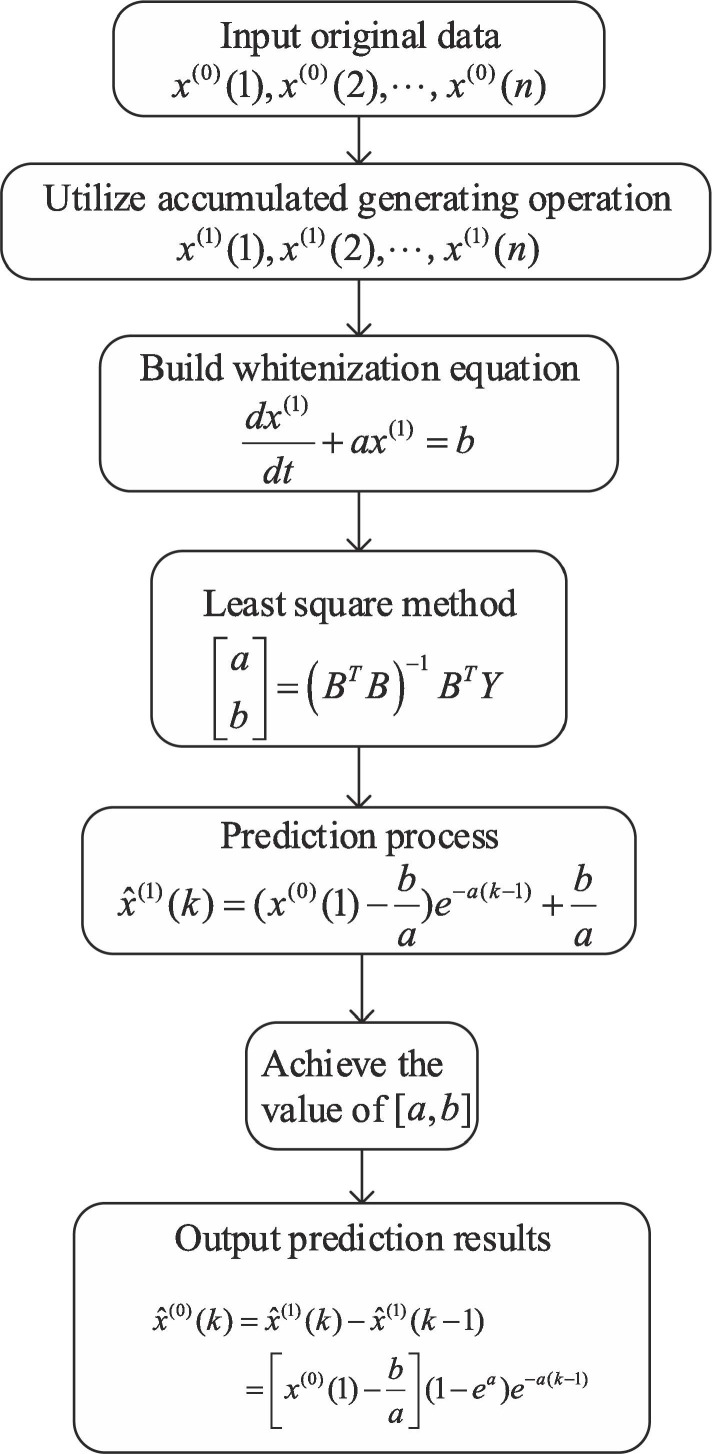
Considering that many studies have explained the mechanism of GM(1,1) in detail, we only outline its steps briefly in this paper. Flowchart of GM(1,1) is given in Fig. 4 to present the model in a clearer way.
Fig. 4.
Procedures of basic GM(1,1).
Step 1: Define the original data (which require the value to be positive) as
Achieve the one-time accumulated generating operation (abbreviated as 1-AGO) sequence
in which .
Later, calculate background values through getting the average values of consecutive neighbors by Eq. (1):
| (1) |
Step 2: Define grey differential equation of GM(1,1) by the formula
| (2) |
where , is the development coefficient and is the grey driving coefficient.
Step 3: Whitened equation in GM(1,1) is defined as
| (3) |
Least square method is utilized as a tool to acquire the parameters:
| (4) |
where and .
Therefore, calculating results of and can be obtained.
Step 4: At time point , the winterization equation possesses solution:
| (5) |
Step 5: Restored response function is achieved through reverse procedures of AGO. Then the predictive values can be obtained through extrapolating conditions
| (6) |
When , and the subsequent values represent the predictive values.
Among various approaches to optimize the basic grey model, many scholars choose to improve the initial values, which are among the most significant elements that influence forecast performance. As the basis of the IMSGM(1,1) method, extensions of GM(1,1) related to optimized initial condition are introduced in the rest of this section.
Newly priority grey model (NP-GM(1,1)) is an extended grey model that adopts the law of new information principal. Traditional solutions of grey models appoint to be the initial condition in prediction model while the process of building GM(1,1) are not associated with directly. This disadvantage can be overcome by taking as coefficient in the model.
The TRF of whitened equation adopts as initial value [31] is presented as follows:
| (7) |
To exploit more timely information, Dang et al. [40] substitute with in the GM(1,1) to build GM(1,1)-x(1)(n). The corresponding TRF turns out to be:
| (8) |
Taking every item in as influential factors of predictive values, Xiong et al. optimize the GM(1,1) by inserting weight coefficients to each element, and the new model is named OICGM(1,1).
| (9) |
in which , and is time parameter.
TRF function of whitened equation with this initial condition is transformed to be:
| (10) |
In view of different influential level of each element in 1-AGO sequence of the prediction results, the initial condition of the whitening equation is modulated by a newly imported weight coefficient, in which data of more recent years are more influential to the predictive value of the next year. Such an initial condition is able to enhance overall timeliness of the model. Data in 1-AGO sequence can be computed by Eq. (11) as below [24]:
| (11) |
where denotes the dynamic weight coefficient and is the time input.
3.2. The Rolling IMSGM(1,1) model
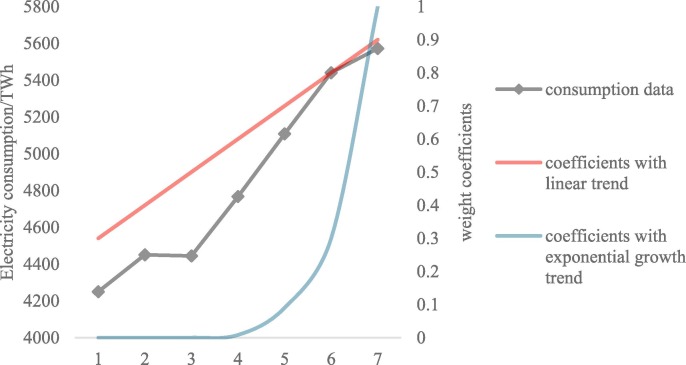
The so-called initial condition in grey prediction includes the dynamic weight coefficients, whose impact on the forecasting performance is reflected in different influential levels of historical data onforecast results. Although many scholars have made adjustments to these coefficients, we can see from Fig. 5 that results obtained by different initial condition determination methods are still fixed values. In the newly proposed IMSGM(1,1) model, the result from ant colony algorithm (ACO) makes the initial coefficient be a dynamic parameter, which is not bounded by exponential or linear trend and can be better modulated when the trend changes.
Fig. 5.
Common forms of initial conditions in grey models.
According to the initial condition put forward in Section 3.1, coefficients can be expanded into higher-order polynomials for the purpose of converting the fixed coefficient in the initial condition of TRF to dynamic coefficients.
As a special form of the Taylor series, the Maclaurin series depicts the given function with information on certain points to describe its value near the formula. If the function is smooth enough, derivative values of coefficients of Taylor’s formula in a known function of certain points can be used to build a polynomial approximation function, which can help obtain value of this field with a polynomial function to approximate a given function. To avoid fixed initial condition that might bring about grey model's inner errors, we assume that the relationship between the t th accumulated value at time namely and each original accumulated value of given data namely is appointed to grow at the same exponential. Then, the novel coefficient can be folded into the Maclaurin series expansion.
In line with the Taylor mean value theorem, if function has a derivative up to in some open interval which contains , then for , there is:
| (12) |
where is the residual terms and , is between and . There are several ways to express the residual terms of Taylor's formula, and we employ the Lagrange residue term of Taylor's order expansion in which the remainder of the order Taylor's formula is further expanded in to .
When , the function is denoted as Maclaurin series. Therefore, the formula is substituted as:
| (13) |
By applying the value from the novel grey model, is substituted into Maclaurin formula, whose expansion can be obtained as:
| (14) |
In this form, uneven influential levels of each individual element to the AGO sequence are reflected by inserting a dynamic weighted coefficient.
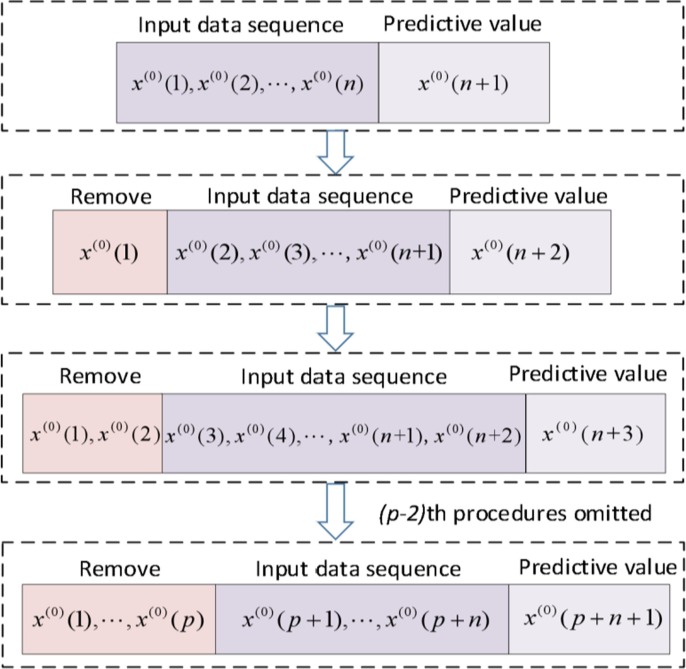
Rolling mechanism (also known as Metabolic mechanism, whose theory is identical) is an efficiency technique to enhance forecast accuracy of grey model with exponential and chaotic data and use up-to-date data with good timeliness, which closely follows the rule of new information priority that recommend selecting recent data. In this way, data can be utilized to a large extent. In existing works, Rolling mechanism has been applied to various forecast models in different domains [28], [41], [42], [24], [43]. In Fig. 6 , the principle of RM utilized in prediction models is expressed.
Fig. 6.
Diagram of the operating principle of Rolling mechanism.
Through methodologies introduced above, optimal results of the higher-order polynomial can be obtained. Coefficients and are calculated by reversing the Maclaurin series formula. The prediction process progresses through the time response function.
4. Modeling steps and solution methods
4.1. Framework of the Rolling IMSGM(1,1) model
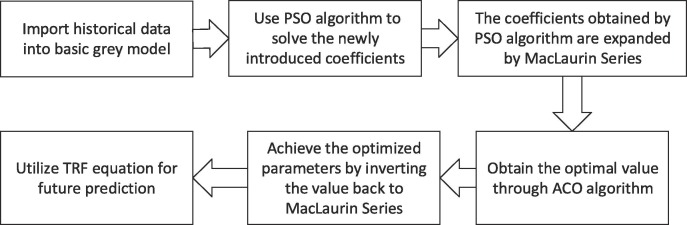
Given that data for the object to be predicted is generally of little regularities, it is not an easy task to figure out its future growth trend. Grey prediction looks for the inner law of historical data andbuilds a model accordingly, and the predict procedures can be implemented to obtain the solution of the model. Previous studies investigated factors associated with the accuracy of forecast models and found that grey models with fixed initial conditions possess limited applicability to data of various features. Inspired by the small amount of data required for grey model, Rolling IMSGM(1,1) is established on the basis of GM(1,1) for electricity consumption gap forecast during the coronavirus pandemic. In this article, we present a novel model with an initial condition in the form of Maclaurin series for the purpose of raising precision in the original GM(1,1). Framework of the IMSGM(1,1) is presented in Fig. 7 .
Fig. 7.
Flowchart of methodologies utilized in IMSGM(1,1).
Traditional grey model uses least square estimation to solve the parameters, which is far less accurate than other optimization algorithms. In this study, PSO algorithm is adopted to preliminarily determine the parameters which can reduce the computing time in subsequent processes. The optimal results from PSO are taken as the initial input of Maclaurin expansion. Since the operation of polynomials permits only addition, subtraction and multiplication, polynomials are generally utilized in terms of numerical calculation. To obtain higher accuracy, the function must be approximated by polynomial of higher degrees, and the error formula should be given at the same time. Afterwards, an intelligent bionic algorithm known as ACO is combined to help adjust the coefficients of higher order polynomials in the Maclaurin's expansion by taking the minimum fitting deviation from the actual values as the fitness function to obtain better results. Specific solutions to each parameter and the application of intelligent algorithms will be introduced in detail in the following section.
4.2. Calculation of grey coefficients
In order to obtain parameters involved in Rolling IMSGM(1,1), two intelligent algorithms namely PSO and ACO, are selected to solve these parameters. Firstly proposed by Kennedy and Eberhart [44], PSO has the traits of well robustness, search proficiency and can avert unreasonable convergence, and has been widely used in many fields [45]. With the accumulation of iterations, the optimal individual in the group can be found and the parameters are determined accordingly. ACO algorithm is designed for simulating ant foraging behavior which abstract the characteristics of the ant colony foraging into mathematical descriptions to solve optimization problems [46]. ACO algorithm has the advantage of positive feedback mechanism that makes the probe procedures converge continuously and approximate the optimal path. Traditional ACO algorithm has a slow convergence rate and is prone to local optimum while PSO is easy to prematurely converge while its local search ability is not satisfying [32]. After evaluating the pros and cons of the two algorithms, Rolling IMSGM(1,1) model utilizes PSO algorithm to acquire the initial value of vector and ACO algorithm to conduct path optimization under the action of pheromone to obtain the optimal coefficients in Maclaurin series. How these two algorithms are used in this model is presented below.
PSO algorithm first assumes that a bunch of random particles exists, then initialize their velocities and positions within a certain searching space.
where represents the maximum value of particles’ position, represents the upper bound of speed of particle, which can be estimated within range.
The position and velocity of each particle updates as follows:
where , are acceleration factors, is a random variable within the range .
The function to evaluate fitness value in PSO adopts minimal Mean Absolute Percentage Error (MAPE), whose construction is expressed as:
| (15) |
Each particle updates its location through following two optimal values: one is determined by each particle, which is denoted as personal best (abbreviated as ) and the other by the whole population (abbreviated as ). Each particle updates its value when individual fitness value conforms to the comparison expression [47].
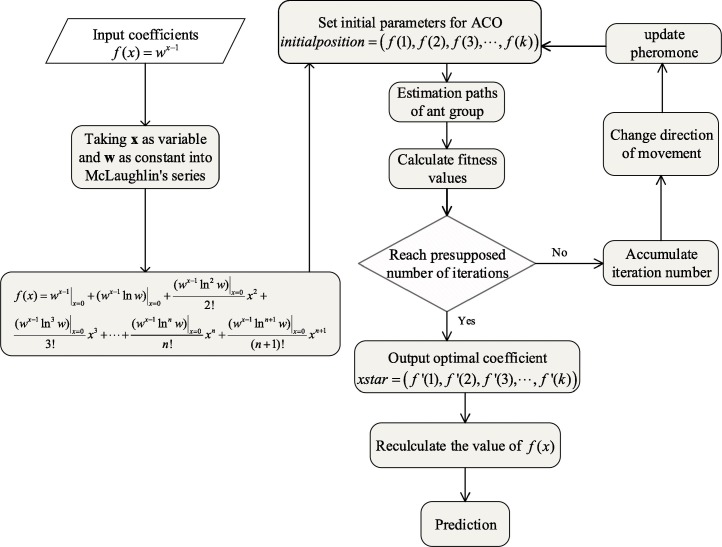
Analogies to other intelligent algorithms such as GA (genetic algorithm) and PSO, ACO also has its own optimization strategy. The basic idea of ACO is to use the paths of ants on behalf of available methods for the unsolved problem. Individuals with shorter paths release more pheromone and all paths by the whole group make up for solution set of the problem. According to the principal to track the shortest path, the number of ants that choose the shorter path and the concentration of pheromones accumulate simultaneously, thus finding the optimized path.
Before calculation, relevant parameters should be initialized, including colony size (), maximum iteration number (), limitation of maximum step () and the number of iterations (). The initial position of the ant colony is from the extended results of Maclaurin's formula which is expressed as .
During iterations, the location of each individual in the colony is recorded as a two-dimensional variable , which composes rows as and columnsas . Best position in history of the whole group is denoted as . The calculation process of the position of each particle is denoted as and is defined as a matric of the same dimension as , which depicts the specific procedure to estimate path of particles. The entire process of the model proposed in this paper is shown in Fig. 8 , including how the introduced intelligent algorithms adjust the coefficients in the grey model.
Fig. 8.
Structure of the newly proposed IMSGM(1,1) model.
Fitness function of ACO method adopts the minimal MAPE results the same as PSO as presented in the equation below:
| (16) |
The iteration number updates from 1 to after each iteration.
The history best position takes the minimal fitness value of position in the previous iteration, and updates the optimal position of each individual by
Change the position of particle in each iteration, and constrain its moving step size. Random movement in each direction is carried out to achieve this iteration by the following equation:
Compute the distance of each ant’s path and record the optimal solution (shortest path) in the current iteration number. At the same time, the pheromone concentration in the connection path of each position is updated. After the iteration is completed, account the iteration number, and let . is the fitness value obtained by procedure , if then let
To illustrate the method, value of is assumed to be the minimal.
Define as the optimal result of the algorithm:
When iteration time is smaller than the presupposed maximum number, the number of iterations increases by one and go back to the steps of constructing the solution space; otherwise, the calculation is terminated and output the optimal solution.
In this way, coefficients in front of higher-order polynomials are adjusted to minimize the errors, so as to obtain more accurate fitting equations and increase the prediction accuracy. Replace the coefficients in Maclaurin's formula expansions with ACO achieved results, we can attain a more precise conclusion of vector .
In the form of grey prediction models, we insert and into the whitened GM(1,1) formula, then TRF is transformed as:
| (17) |
Depending on the results of winterization function mentioned above, we attain the restored function as follows:
| (18) |
5. Case study
5.1. Model accuracy analysis
In this section, monthly electricity consumption in the first quarter of 2019 in China is predicted to testify the precision of Rolling IMSGM(1,1). To appraise the performance of different models, we select three performance evaluation indicators namely PE (percentage error), RMSE (root mean square error), and MAPE. PE is the relative error multiplied by 100%. RMSE utilizes the average error to sensor aberrant points, if values at some points are abnormal, the error will increase largely and in turn affect RMSE results. The MAPE criterion is proposed for evaluating prediction model, taking the numerical value of errors as well as the deviation proportion into consideration [21]. The three frequently-used error metrics mentioned above are as Eq. (19) to Eq. (21). Test results have been compared with other forecasting methodologies put forward in previous researches. Same testing data is applied to GM(1,1), GM(1,1)-x(1)(n) [22], OICGM(1,1) [23], IRGM(1,1) [26] and Rolling NOGM(1,1) [24] to achieve competitive results.
The definitions of the three criteria are as follows:
| (19) |
| (20) |
| (21) |
where is the total time series number; represents real data at time ; represents the predictive value at time .
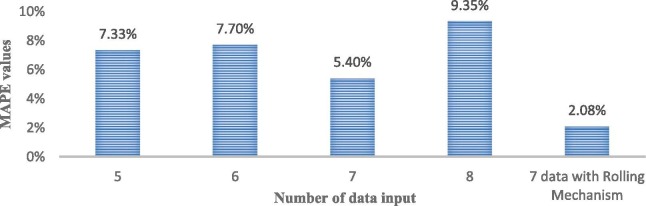
Before the prediction, multiple cases have been organized to select the amount of input data. Considering the number of input data commonly used in the field of energy forecast by grey models, we sequentially use 5 to 8 historical data as input. Then, data in the following years are selected to verify the prediction accuracy. Based on the existing data, MAPE values are calculated. As shown in Fig. 9 , when 7 historical data are selected as input, the error is the smallest.
Fig. 9.
Comparison of the prediction errors of different input data number.
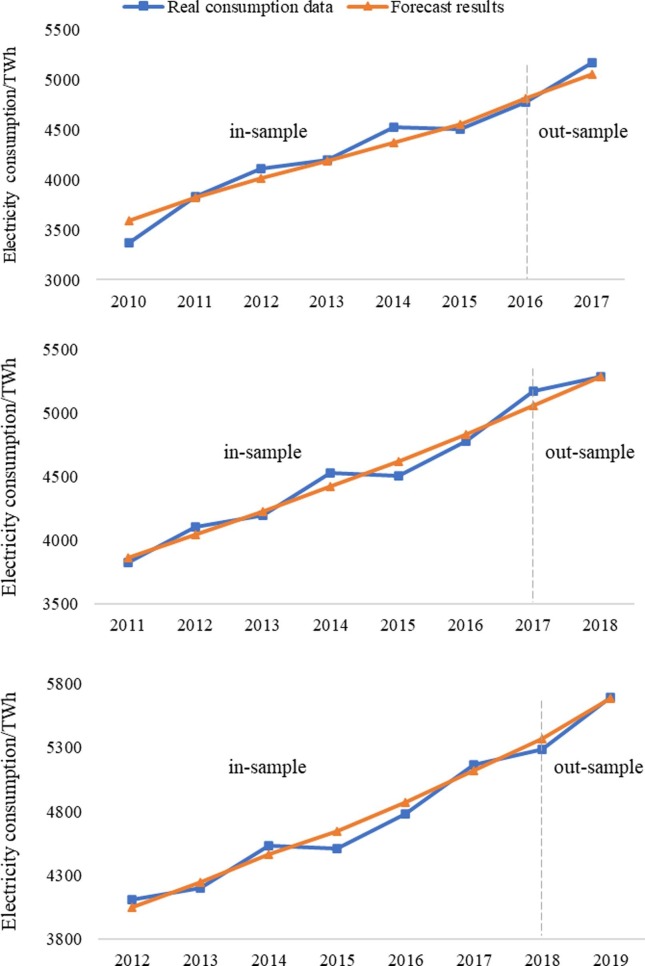
Results in Fig. 9 are obtained by accounting the MAPE in the following four years. As can be seen from the figure, when the same data are used for prediction, using seven historical data as the model input leads to smaller prediction error than using other input data number. Though Rolling Mechanism has been widely used in many areas, this study applies electricity consumption data to the model combined with rolling mechanism, which turns out to achieve smaller error than the original model. Prediction results of annual power consuption are given in Table 1. Additionally, fitting graphs are presented as Fig. 10 to directly display the results of Rolling IMSGM(1,1).
Table 1.
Comparison results of rolling mechanism combined model (100 million kwh).
| 2017 | 2018 | 2019 | |
|---|---|---|---|
| IMSGM(1,1) | 5061.34864 | 5274.6981 | 5497.0408 |
| Rolling IMSGM(1,1) | 5061.34864 | 5286.51501 | 5684.84949 |
| Real | 5168.9 | 5283.4 | 5697.9 |
Fig. 10.
Fitting curves of Rolling IMSGM(1,1).
To further illustrate the progress of the prediction, electricity consumption data from 2012 to 2018 in China are selected as model input. By unfolding coefficient achieved through PSO algorithm into Maclaurin series, the initial position for ant colony in ACO algorithm are obtained. In this study, we expand the coefficient to a seventh-order polynomial. Coefficients and of grey model are obtained by least square method, and then by PSO, is calculated as shown in Table 2 . The expanded form in this case is obtained as shown in Table 2. Substitute the expanded coefficient optimized through ACO algorithm into Maclaurin expansion formula, assign the result to , and also conduct predicting process through TRF. All parameters in Table 2 are non-dimensional.
Table 2.
Parameter achieved from Rolling IMSGM(1,1).
| Years | |||||
|---|---|---|---|---|---|
| Jan-20 | −0.06599 | 3,923.26 | 0.208727 | 7.997181 | [−0.0005856,0.0064261,−0.0149236,−0.0076881,−0.0079772,−0.012396,−0.0073472] |
| Feb-20 | −0.05995 | 3,290.47 | 0.294207 | 8.796217 | [−0.0001080,0.0008382,−0.000523,0.0022754,−0.0134055,−0.0090861,0.0040955] |
| Mar-20 | −0.04948 | 4,081.00 | 0.210646 | 8.167102 | [−0.0001231,0.0013373,−0.0037269,0.0011311,0.0149984,0.0021661,−0.012713874] |
| Apr-20 | −0.05040 | 3,859.10 | 0.153986 | 7.678601 | [−-0.000376056, 0.004126913,−0.010150526, −0.001144183,−0.005941807,0.0073773,0.0032196] |
The optimized results by ACO are named . When the ACO algorithm accesses the minimum fitness value, it is then accumulated in turn to obtain a fitting value as the optimal value of . Other related models are selected including traditional grey model and models that optimize the initial conditions. Forecast results are listed in Table 3 .
Table 3.
Forecasted results by different forecasting models (100 million kwh).
| Real data | GM(1,1) | GM(1,1)-x(1)(n) | OICGM(1,1) | NOGM(1,1) | Rolling IMSGM(1,1) | |
|---|---|---|---|---|---|---|
| Jan-19 | 6090.9 | 5934.02 | 6146.68 | 5874.64 | 5850.66 | 6065.69 |
| Feb-19 | 4891 | 4829.83 | 4903.56 | 4905.60 | 4832.70 | 4872.36 |
| Mar-19 | 5697.9 | 5556.93 | 5630.06 | 5570.64 | 5533.02 | 5684.85 |
Rolling IMSGM(1,1) can detect fluctuations through rolling mechanism so as to be more accurate in the phase of predicting for the following years. Models with rolling mechanism take advantage of newly achieved data to calibrate the orientation for energy growth, which can better control the latest growing tendency of power consumption.
It can be directly seen from Table 4 that error analysis by the three indicators proves the performance of Rolling IMSGM(1,1), with percentage errors at the values of 0.41, 0.38 and 0.23 for the first three months in 2019 separately. In aspect to criteria MAPE and RMSE, Rolling IMSGM(1,1) obtains 0.34 and 19.61 by the computational outcome, which is less than other models.
Table 4.
PE, MAPE and RMSE calculated for each model(%).
| Evaluation index | GM(1,1) | GM(1,1)-x(1)(n) | OICGM(1,1) | NOGM(1,1) | Rolling IMSGM(1,1) |
|---|---|---|---|---|---|
| PE of forecast results in Jan-19 | 2.58 | 0.92 | 3.55 | 3.94 | 0.41 |
| PE of forecast results in Feb-19 | 1.25 | 0.26 | 0.30 | 1.19 | 0.38 |
| PE of forecast results in Mar-19 | 2.47 | 1.19 | 2.23 | 2.89 | 0.23 |
| MAPE | 2.10 | 0.79 | 2.03 | 2.68 | 0.34 |
| RMSE | 126.79 | 51.22 | 145.12 | 171.56 | 19.61 |
For the initial condition proposed in this paper, IMSGM (1,1) outperforms other non-rolling models in the monthly electricity prediction tests. Although GM(1,1)-x(1)(n) is generally referred to as a grey model with optimized initial condition, in the case study, OICGM(1,1) and NOGM(1,1) does not provide forecast results as good as GM(1,1).
Such accurate predictions with small errors have much to do with the optimal initial conditions of dynamic weighting coefficients that can be expanded into higher order polynomials. Therefore, the Rolling IMSGM (1,1) can judge the features in power system based on the data growth trend and provide the best behaviors in the competition models. Moreover, the Rolling IMSGM (1,1) possesses higher prediction precision than other grey prediction models, indicating that coefficients calculated before the expansion of the high-order polynomial using the ACO algorithm is optimized. Prediction accuracy plays an important role. The rolling mechanism is an important factor in optimizing the success of the initial conditions. Therefore, Rolling IMSGM(1,1) is the optimal method for forecasting power consumption.
5.2. Electricity consumption gap research in China during COVID-19
Since the accuracy of the model has been verified, the impact of COVID-19 on power consumption is analyzed to comprehend the process of the resumption work under the current situation.
Through the observation of monthly historical power consumption data listed in Table 5, it can be found that power consumption of each month within a year is not very much the same, such as the low ebb in February and peaks in summer. Power consumption data in the past few years are selected as the model input to achieve the predictive consumption gap under the COVID-19 situation, whose results are shown in Table 6.
Table 5.
Historical monthly power consumption data in the first quarter of a year in China (100 million kwh).
| Month | Year |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | |
| January | 3485.6 | 4199.2 | 4328.1 | 4907 | 4889.7 | 4827.3 | 5897.5 | 6090.9 | 5805 |
| February | 3701.7 | 3374 | 3833.6 | 3653.9 | 3812 | 4488 | 4557 | 4891 | 4398 |
| March | 4109.2 | 4194.3 | 4527.7 | 4510.6 | 4778.8 | 5168.9 | 5283.4 | 5697.9 | 5493 |
| April | 3718.2 | 3994.4 | 4250.2 | 4450.3 | 4444.5 | 4767.2 | 5107.8 | 5440.2 | 5572 |
Table 6.
Prediction results of electricity consumption in the first quarter of 2020 (100 million kwh).
| Month | Forecast results of Rolling IMSGM(1,1) | Consumption gap | Decline proportion (%) |
|---|---|---|---|
| January | 6234.95 | 429.95 | 6.90 |
| February | 5032.04 | 634.04 | 12.60 |
| March | 5807.09 | 314.09 | 5.41 |
| April | 6234.95 | 60.83 | 0.98 |
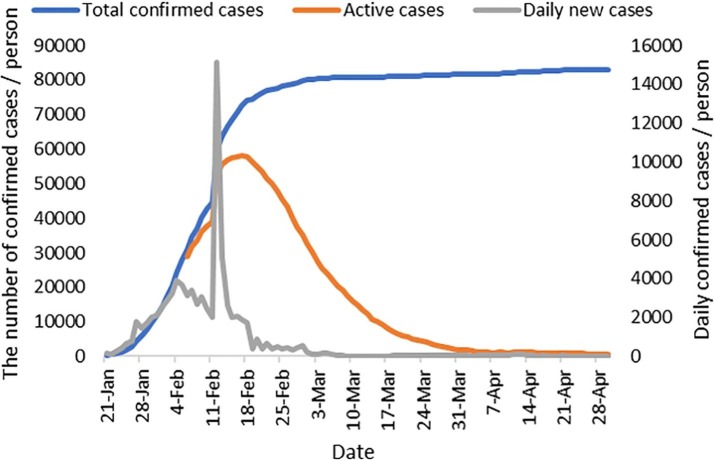
According to data released by the Office of Health Emergency of China, the number of new and cumulative diagnosed with COVID-19 since January 20th and existing cases since February 6th are plotted above as shown in Fig. 11. As can be seen from the figure, sincethe novel coronavirus was confirmed in China in late January, the number of daily confirmed cases peaked in February. Since March, the situation in China leveled off which is consistent with the trend of power consumption differences. Owing to the pandemic, many parts of China have been sealed off since January, and residents are self-quarantine at home. With the improvement of the situation, these lockdowns are gradually lifted, and the emergency response levels nationwide are reduced, travels are no longer restricted, and the return to work and production proceed gradually. Data of newly confirmed COVID-19 cases is readily available, while it may not have a direct impact on changes in electricity consumption. To determine whether there is a strong relationship between the number of confirmed cases and the reduction in power consumption, Pearson correlation coefficient (PCC) is used to analyze the correlation of gap prediction results and the confirmed cases. PCC is a measure of the degree of correlation between two variables. It is a value between −1 and 1, while 1 means the variable is completely positive correlation, 0 means nothing, and −1 means completely negative correlation. This coefficient is widely used to measure the degree of correlation between two variables. Results of PCC between the number of confirmed active cases from January to April and the consumption gap predicted by Rolling IMSGM(1,1) are shown in Table 7 as below.
Fig. 11.
The number of daily confirmed cases of COVID-19 in China.
Table 7.
Prediction results of electricity consumption in the first quarter of 2020 (100 million kwh).
| Pearson correlation coefficient | 0.846 |
|---|---|
| significance (two-tailed test) | 0.154 |
| number of cases | 4 |
The PCC value reaches 0.846, indicating a strong positive correlation between electricity consumption gap and the number of active COVID-19 cases. COVID-19 outbreak began in Wuhan, China, in mid-to-late January and peaked in February in nearly all provinces. With improved detection capabilities and better response to the outbreak, the epidemic has been well under control since March. As a result of the outbreak, many people work from home or do not work at all, making less use of productive capacity, office buildings and electrified public transport. Since the implement of lockdown policies, more people cook or use electricity for entertainment at home. Table 8 shows a growth in the proportion of urban and rural residents’ electricity consumption due to the lockdown, and the proportions are higher from January to March. As the main content of electricity consumption in the secondary industry, industrial electricity consumption, including the production and supply of light industry, heavy industry, power and heat industry, chemical raw material and chemical products manufacturing, petroleum processing and construction industry, has been greatly reduced due to the pandemic blockade. In line with our prediction results, there has been a gap in electricity consumption nationwide since January, which is consistent with the increasing trend of the number of COVID-19 cases and also reached its maximum value in February. As the outbreak was brought under control, the electricity shortfall steadily declined in March and April.
Table 8.
The proportion of electricity consumption of different industries in the whole society in China in 2020.
| Primary industry | Secondary industry | Tertiary industries | Urban and rural residents’ consumption | |
|---|---|---|---|---|
| January | 1.05% | 63.70% | 18.86% | 16.40% |
| February | 1.21% | 57.37% | 18.94% | 22.46% |
| March | 0.95% | 68.27% | 12.78% | 17.99% |
| April | 1.11% | 70.06% | 14.29% | 14.54% |
| May | 1.16% | 70.47% | 15.02% | 13.35% |
As the pandemic in China has gradually become under control, industrial enterprises have speeded up the resumption of work and production. Residents are now allowed to return to their work as the lockdown policies eased, thus weakened its impact on electricity consumption. Compared with February, the worst period of the pandemic, electricity consumption in March fell by 5.41%, which is 7.19 percentage points less than that in February. The gap fell 4.43% in April from March. It is expected that the growth rate of electricity consumption in the whole society in the second quarter will pick up further than the first quarter.
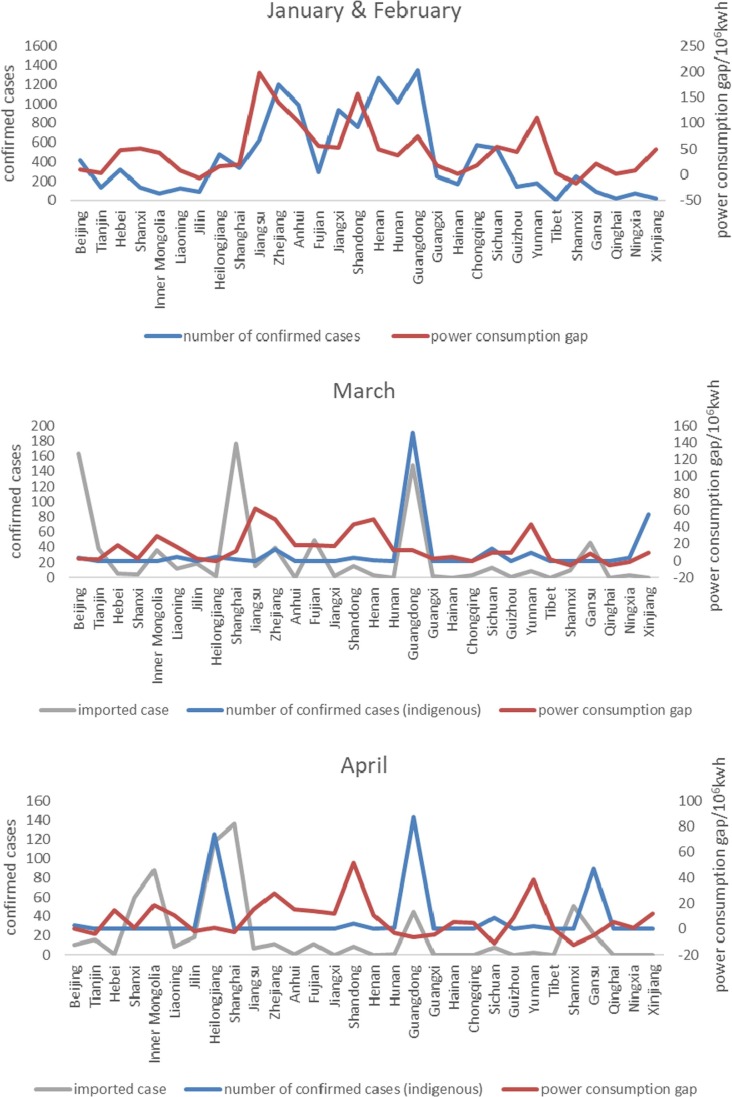
Based on the historical data of electric power production and the existing gap analysis model, this paper analyzes the influence of electric power production capacity by provinces. As shown in Fig. 12 , the influence of COVID-19 on power industry is not exactly the same in different areas in China, but the overall trend turns out to be the same as mentioned in the disease severity in timeline. For instance, in the in the northeastern region, provinces like Jilin, Liaoning and Heilongjiang, where a large number of imported cases have been reported, March becomes the period with the largest proportion of electricity production gap values.
Fig. 12.
Power consumption gap caused by the COVID-19 and the number of confirmed cases in provinces of China Mainland.
For most provinces in China, January and February are the worst months of the pandemic. For example, the number of confirmed cases in Zhejiang province in these two months is 1205, resulting in a gap of 1.4 × 108 kwh in electricity consumption. In March, there were 13 new local cases in Zhejiang province, including 39 imported cases from abroad. The gap value of electricity consumption was 4.89 × 107 kwh. In April, there were 0 new local cases and 11 imported cases in Zhejiang province, and the gap value of electricity consumption was 2.77 × 107 kwh.
In Northeast China's Heilongjiang Province, a total of 480 cases were confirmed in January and February, resulting in a decrease in electricity consumption of 1.62 × 107 kwh. In March, there were 4 confirmed cases and 2 imported cases. In April, 74 local cases were confirmed in Heilongjiang province, and 118 imported cases were confirmed, resulting in a reduction in power consumption of 0.934 × 107 kwh. As the province rich in tourism resources, Yunnan suffered from a large drop in the volume of passengers due to the blockade policy, resulted in a large consumption gap. As the number of confirmed cases in Hubei province is relatively large compared with other provinces, it is not listed in the figure, and its trend is roughly similar to that of other provinces: in the first two months of 2020, 66,907 cases were confirmed accumulatively, resulting in 9.25 × 107 kwh consumption gap, while in March, 895 cases were confirmed, and the consumption gap was 4.70 × 107 kwh; in April, 326 patients were diagnosed with the power consumption gap of 8.08 × 106 kwh.
From the figure above, it can be concluded that the power system in China is gradually being restored, and the power production capacity in some areas has exceeded the expected level by 2020. In order to ensure the safe and stable supply of energy and power, it is necessary to accelerate the establishment and improvement of auxiliary services such as peak-regulating and frequency modulation, continuously improve the peak-regulating capacity of the power system, and ensure the power infrastructure supply chain.
6. Conclusion
In the current situation, forecasts of power consumption gap have obtained new significance, revealing the process of resumption and analyzing the severity of the epidemic in different periods. Unlike other natural disasters such as earthquake and tsunami, the outbreak of COVID-19 has little impact on power infrastructure, so it remains to be seen whether electricity consumption will recover to pre-pandemic levels.
This paper proposes a new type of forecast model for evaluating the impact on electricity consumption due to lockdown measures under the COVID-19 epidemic. According to the principle of new initial condition that can be expanded into the Maclaurin series, GM(1,1) has been improved by using weight coefficients to all elements in 1-AGO sequence to illustrate the influential level of each element to the predictive result. Parameters in the new model are preliminarily evaluated by PSO algorithm, which is expanded through Maclaurin series to obtain a high-order polynomial in the following step. The optimized model overcomes the deficiency in previous works by substituting for the fixed initial condition, uses more precise fitted curve to grasp the growth trend and outputs the electricity consumption gap generated from the pandemic.
Results show that in China, the largest consumption gap occurs in January and February. As the number of confirmed cases stabilizes and active cases reduced to less than 1000, electricity consumption in April 2020 has exceeded the number in 2019, while the consumption level in April is still affected by the pandemic as there is certain gap according to our research results. It can be concluded that the deviation of the overall electricity consumption depends on the severity of the pandemic and the degree of lockdown policies. The increase in the number of diagnoses and the implement of hard lockdown policies have led to a large decline in consumption data. Model proposed in this study reflects the stage of the pandemic in China by predicting the consumption gap, so that preparations for the design of new strategies to help reduce the impact of COVID-19 can be carried out appropriately.
At the same time, for future emergencies or other severe public health threats, model established in this paper can also be used for impact analysis. Although this paper is discussing the scenario of COVID-19 pandemic in China, model proposed in this paper can also be extended to analyze the impact in other countries. Moreover, power consumption habits and the attitudes of the public toward energy usage may have changed due to the long lockdown period. Factors like that haven’t been taken into account in this paper. Potential changes in the user behavior concerning power consumption caused by COVID-19 can be explored further in future studies.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was partially supported by the National Natural Science Foundation of China (51874325) and the Grant-in-Aid for Early-Career Scientists (19K15260) from the Japan Ministry of Education, Culture, Sports, Science and Technology.
References
- 1.Xing X., Yan Y., Zhang H., Long Y., Liang Y. Optimal design of distributed energy systems for industrial parks under gas shortage based on augmented ε-constraint method. J Cleaner Prod. 2019;218:782–795. [Google Scholar]
- 2.Dong L, Lao L, Yang Y, Luo J. Probabilistic load flow analysis considering power system random factors and their relevance.
- 3.Ranaweera D.K., Karady G.G., Farmer R.G. Economic impact analysis of load forecasting. IEEE Trans Power Syst. 2002;12:1388–1392. [Google Scholar]
- 4.Luo X., Wang J., Dooner M., Clarke J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl Energy. 2015;137:511–536. [Google Scholar]
- 5.Zhang H., Xuan S., Xia T., Meng Y., Liang Y. Battery electric vehicles in Japan: Human mobile behavior based adoption potential analysis and policy target response. Appl Energy. 2018;220:527–535. [Google Scholar]
- 6.Al-Bajjali S.K., Shamayleh A.Y. Estimating the determinants of electricity consumption in Jordan. Energy. 2018;147:1311–1320. [Google Scholar]
- 7.Mohamed Z., Bodger P. Forecasting electricity consumption in New Zealand using economic and demographic variables. Energy. 2005;30:1833–1843. [Google Scholar]
- 8.Ferguson R., Wilkinson W., Hill R. Electricity use and economic development. Energy Policy. 2000;28:923–934. [Google Scholar]
- 9.Damm A., Köberl J., Prettenthaler F., Rogler N., Töglhofer C. Impacts of +2°C global warming on electricity demand in Europe. Clim Serv. 2017;7:12–30. [Google Scholar]
- 10.Yan Y., Zhang H., Meng J., Long Y., Zhou X., Li Z., et al. Carbon footprint in building distributed energy system: an optimization-based feasibility analysis for potential emission reduction. J Cleaner Prod. 2019;239:117990. [Google Scholar]
- 11.Crompton P., Wu Y. Energy consumption in China: past trends and future directions. Energy Econ. 2005;27:195–208. [Google Scholar]
- 12.Otsuka A. Natural disasters and electricity consumption behavior: a case study of the 2011 Great East Japan Earthquake. Asia Pacific J Reg Sci. 2019 [Google Scholar]
- 13.Lin Q., Zhao S., Gao D., Lou Y., Yang S., Musa S.S., et al. A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int J Infect Dis. 2020;93:211–216. doi: 10.1016/j.ijid.2020.02.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Long Y., Yoshida Y., Meng J., Guan D., Yao L., Zhang H. Unequal age-based household emission and its monthly variation embodied in energy consumption – a cases study of Tokyo, Japan. Appl Energy. 2019;247:350–362. [Google Scholar]
- 15.Zheng J., Zhang H., Dai Y., Wang B., Zheng T., Liao Q., et al. Time series prediction for output of multi-region solar power plants. Appl Energy. 2020;257:114001. [Google Scholar]
- 16.Wang Q., Li S., Li R. Forecasting energy demand in China and India: Using single-linear, hybrid-linear, and non-linear time series forecast techniques. Energy. 2018;161:821–831. [Google Scholar]
- 17.Fonseca J.G.D.S., Oozeki T., Takashima T., Koshimizu G., Uchida Y., Ogimoto K. Use of support vector regression and numerically predicted cloudiness to forecast power output of a photovoltaic power plant in Kitakyushu, Japan. Prog Photovoltaics Res Appl. 2012;20:874–882. [Google Scholar]
- 18.Jafarzadeh S., Fadali S., Evrenosoglu C.Y., Livani H. Hour-ahead wind power prediction for power systems using Hidden Markov Models and Viterbi Algorithm. Power Energy Soc Gen Meet. 2010 [Google Scholar]
- 19.Ekonomou L. Greek long-term energy consumption prediction using artificial neural networks. Energy. 2010;35:512–517. [Google Scholar]
- 20.Kavaklioglu K., Ceylan H., Ozturk H.K., Canyurt O.E. Modeling and prediction of Turkey’s electricity consumption using Artificial Neural Networks. Energy Convers Manage. 2009;50:2719–2727. [Google Scholar]
- 21.Pai P.-F. Hybrid ellipsoidal fuzzy systems in forecasting regional electricity loads. Energy Convers Manage. 2006;47:2283–2289. [Google Scholar]
- 22.Dang Y., Liu S., Chen K. The GM models that x(n) be taken as initial value. J Xiamen Univ (Natl Sci) 2002;33:247–254. [Google Scholar]
- 23.Xiong P-p, Dang Y-g, Yao T-x, Wang Z-x. Optimal modeling and forecasting of the energy consumption and production in China. Energy. 2014;77:623–634. [Google Scholar]
- 24.Ding S., Hipel K.W., Dang Y.G. Forecasting China's electricity consumption using a new grey prediction model. Energy. 2018;149:314–328. [Google Scholar]
- 25.Lee Y.-S., Tong L.-I. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers Manage. 2011;52:147–152. [Google Scholar]
- 26.Xu N., Dang Y., Gong Y. Novel grey prediction model with nonlinear optimized time response method for forecasting of electricity consumption in China. Energy. 2017;118:473–480. [Google Scholar]
- 27.Yuan C., Liu S., Fang Z. Comparison of China's primary energy consumption forecasting by using ARIMA (the autoregressive integrated moving average) model and GM(1,1) model. Energy. 2016;100:384–390. [Google Scholar]
- 28.Zhao H., Guo S. An optimized grey model for annual power load forecasting. Energy. 2016;107:272–286. [Google Scholar]
- 29.Li G.-D., Masuda S., Nagai M. The prediction model for electrical power system using an improved hybrid optimization model. Int J Electr Power Energy Syst. 2013;44:981–987. [Google Scholar]
- 30.Wang Q., Li S., Li R., Ma M. Forecasting U.S. shale gas monthly production using a hybrid ARIMA and metabolic nonlinear grey model. Energy. 2018;160:378–387. [Google Scholar]
- 31.Liu S., Forrest J.Y.L. Springer; Berlin Heidelberg: 2010. Grey systems: theory and applications. [Google Scholar]
- 32.Kong Z., Wang L., Wu Z. Application of fuzzy soft set in decision making problems based on grey theory. J Comput Appl Math. 2011;236:1521–1530. [Google Scholar]
- 33.Qi W. Grey prediction model and multivariate statistical techniques forecasting electrical energy consumption in Wenzhou, China. In: International symposium on intelligent information technology & security informatics; 2009.
- 34.Yasunobu W. Impact of COVID-19 on electricity demand in Japan. EnerarXiv. 2020 [Google Scholar]
- 35.Kenneth T., Gillingham C.R.K., Li Jing, Ovaere Marten, Reguant Mar. The short-run and long-run effects of Covid-19 on energy and the environment. Joule. 2020 doi: 10.1016/j.joule.2020.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Michał Narajewski FZ. Changes in electricity demand pattern in Europe due to COVID-19 shutdowns; 2020.
- 37.Wang Z, Román MO, Sun Q, Molthan AL, Schultz LA, Kalb VL. Monitoring disaster-related power outages using NASA black marble nighttime light product; 2018.
- 38.Guangchun R., Dongqi W., Xiangtian Z., Sivaranjani S., Haiwang Z., Chongqing K., et al. A cross-domain approach to analyzing the short-run impact of COVID-19 on the U.S. Electricity Sector. EnerarXiv. 2020 doi: 10.1016/j.joule.2020.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chen Y, Yang W, Zhang B. Using mobility for electrical load forecasting during the COVID-19 pandemic; 2020.
- 40.Yaoguo D. The GM models that x(n) be taken as initial value. Kybernetes. 2004;33:247–254. [Google Scholar]
- 41.Akay D., Atak M. Grey prediction with rolling mechanism for electricity demand forecasting of Turkey. Energy. 2007;32:1670–1675. [Google Scholar]
- 42.Kumar U., Jain V.K. Time series models (Grey-Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy. 2010;35:1709–1716. [Google Scholar]
- 43.Şahin U. Forecasting of Turkey's greenhouse gas emissions using linear and nonlinear rolling metabolic grey model based on optimization. J Cleaner Prod. 2019;239:118079. [Google Scholar]
- 44.Kennedy J, Eberhart R. Particle swarm Optimization. In: Icnn95-international conference on neural networks; 2002.
- 45.Zheng J., Zhang H., Yin L., Liang Y., Zhang Y. A voyage with minimal fuel consumption for cruise ships. J Cleaner Prod. 2019;215:144–153. [Google Scholar]
- 46.Lee Z.-J., Su S.-F., Chuang C.-C., Liu K.-H. Genetic algorithm with ant colony optimization (GA-ACO) for multiple sequence alignment. Appl Soft Comput. 2008;8:55–78. [Google Scholar]
- 47.Zhang H., Yuan M., Liang Y., Liao Q. A novel particle swarm optimization based on prey–predator relationship. Appl Soft Comput. 2018;68:202–218. [Google Scholar]