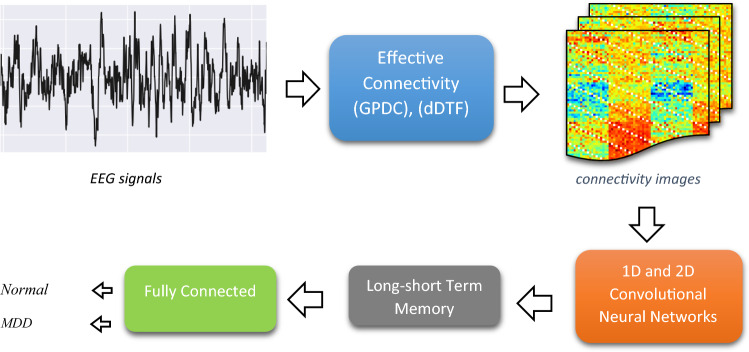
Abstract
Deep learning techniques have recently made considerable advances in the field of artificial intelligence. These methodologies can assist psychologists in early diagnosis of mental disorders and preventing severe trauma. Major Depression Disorder (MDD) is a common and serious medical condition whose exact manifestations are not fully understood. So, early discovery of MDD patients helps to cure or limit the adverse effects. Electroencephalogram (EEG) is prominently used to study brain diseases such as MDD due to having high temporal resolution information, and being a noninvasive, inexpensive and portable method. This paper has proposed an EEG-based deep learning framework that automatically discriminates MDD patients from healthy controls. First, the relationships among EEG channels in the form of effective brain connectivity analysis are extracted by Generalized Partial Directed Coherence (GPDC) and Direct directed transfer function (dDTF) methods. A novel combination of sixteen connectivity methods (GPDC and dDTF in eight frequency bands) was used to construct an image for each individual. Finally, the constructed images of EEG signals are applied to the five different deep learning architectures. The first and second algorithms were based on one and two-dimensional convolutional neural network (1DCNN–2DCNN). The third method is based on long short-term memory (LSTM) model, while the fourth and fifth algorithms utilized a combination of CNN with LSTM model namely, 1DCNN-LSTM and 2DCNN-LSTM. The proposed deep learning architectures automatically learn patterns in the constructed image of the EEG signals. The efficiency of the proposed algorithms is evaluated on resting state EEG data obtained from 30 healthy subjects and 34 MDD patients. The experiments show that the 1DCNN-LSTM applied on constructed image of effective connectivity achieves best results with accuracy of 99.24% due to specific architecture which captures the presence of spatial and temporal relations in the brain connectivity. The proposed method as a diagnostic tool is able to help clinicians for diagnosing the MDD patients for early diagnosis and treatment.
Keywords: Major depression disorder, Electroencephalography, Effective connectivity, Deep learning, Convolutional neural network, Long short-term memory
Introduction
Major depressive disorder (MDD) is a mental illness that drastically interferes with the quality of life. It includes symptoms such as feelings of severe despondency and hopelessness, loss of interest in normal daily activities, extensive changes in appetite and recurrent thought of suicide (World Federation for Mental Health 2012). According to the World Health Organization (WHO), more than 350 million people of all ages are affected by depression worldwide (World Health Organization 2017). The exact cause of depression is not fully understood, but it is associated with an imbalance in neurotransmitters, hormonal abnormalities, genetic vulnerability, and stressful environmental conditions. About half of depressed people are unaware of their illness or their disorder is misdiagnosed (World Health Organization 2017). For the diagnosis of mental disorders such as depression, electroencephalogram (EEG) is a powerful tool due to high temporal resolution, low cost, noninvasive technique and easy setup. EEG is also widely used in clinical applications (Afshani et al. 2019; Shalbaf et al. 2017; 2019).
Traditionally, a number of EEG-based machine learning methods have been used for automated detection of depression. Puthankattil et al. (2012) used relative wavelet energy, entropy and Artificial neural network (ANN) on the 5-min EEG signal of 30 subjects. Ahmadlou et al. (2012) analyzed 12 depressed patients and 12 normal persons with Higuchi and Katz Fractal measurements (HFD, KFD) of the frontal brain signals. Ahmadlou et al. (2013) experimented with 22 MDD subjects and presents a new non-linear method: spatial temporal analysis of relative convergence (STARC) of EEG signals. Hosssinifard et al. (2013) worked on 45 subjects (Depressed and healthy) using various non-linear methods such as detrended fluctuation analysis (DFA), Higuchi fractal dimension (HFD), largest Lyapunov exponent (LLE) to characterize the amount of complexity of the signal. They also used correlation dimension and Welch’s power spectral density for estimating power in certain frequency bands. Faust et al. (2014) used combination of the two-level wavelet packet decomposition and various entropies aiming to extract significant features on 15 healthy controls and 15 depressed patients. Acharya et al. (2015) have used non-linear approaches including fractal dimension, LLE, Sample entropy, DFA analysis, Hurst’s exponent, Higher order spectra and recurrence quantification analysis (RQA) on 30 subjects. Li et al. (2016) used an event-related potential method to diagnose depression among 37 university students. Different feature selection methods were used, consisting of Greedy stepwise and Genetic search (GS) to identify the most efficient features to distinguish between the two classes. Mumtaz et al. (2017) used linear characteristics from EEG signals; band power and alpha inter-hemispheric asymmetry with ranked the features based on classification accuracy on data of 33 MDD patients and 30 normal participants. Finally, Bachmann et al. (2017) used spectral asymmetry index (SASI), and DFA methods for differentiating depressive and healthy subjects on 34 subjects. But, as it can be concluded from the literature, most of the studies focused on feature engineering and classification optimization with moderate success and ultimately, finding a solution for this mental disorder accurately remains a challenging task.
In recent years, with developments in neural network architecture design and training, there has been a developing interest in the utilization of deep learning methods as the state-of-the-art in machine learning especially the Convolutional neural network (CNN) in a wide range of computer vision studies especially in medical applications (Bachmann et al. 2017; Sun et al. 2017; Litjens et al. 2017; Esteva et al. 2017; Roy et al. 2019) and also for processing EEG signals with very success. (Faust et al. 2018; Zhang et al. 2019; Chaudhary et al. 2019; Acharya et al. 2018). Recently, Acharya et al. (2018) tried to automatically detect depression using deep machine learning methods. They have used CNN for discrimination of 30 normal and depressed patients. They have also indicated that signals in the right hemisphere were more effective for deep learning classification. Sharma et al. (2018) developed a new method bandwidth-duration-localized, three-channel orthogonal wavelet filter bank for depression diagnosis. The study included 30 subjects using the least square support vector machine (LS-SVM) classifier. Ay et al. (2019) used raw signals from 30 subjects (15 normal, 15 depressed) to develop a deep learning model using a CNN to extract features and reduce variance, then feeding the CNN maps directly to a LSTM cell and using fully-connected layers for classification. Then, Mumtaz et al. (2019) used CNN with long short-term memory (LSTM) architecture for automatically learn patterns in the EEG data that were useful for classifying the 33 depressed and 30 healthy controls. Raghavendra et al. (2019) in comprehensive review presents state-of-the-art artificial intelligence automated techniques for diagnosis of neurological disorders.
The main novelty of this paper is to provide a more generalized approach to model the brain dysfunction by using insights from the connectivity concept. We have used brain effective connectivity method to convert 1-D EEG signal into 2-D image. Then, we have developed a classifier using state of the art deep learning methods (CNN-LSTM) as a novel approach for automated diagnosis of the depression patients from EEG signals. The effectiveness of the proposed approach is tested on dataset recorded of from 33 MDD patients and 30 normal participants.
Materials and methods
Participants
The dataset used in this study is provided by Mumtaz et al. in (2017), with open access (https://figshare.com/articles/EEG_Data_New/4244171). The Methodology was accepted by the ethics committee in Hospital University Sains Malaysia (HUSM). 34 MDD patients with age ranging from 27 to 53 (mean = 40.3 ± 12.9) and 30 normal subjects with age ranging from 22 to 53 (mean = 38.3 ± 15.6) were recorded. The depressed group qualified for the experiment based on the Diagnostic and Statistical Manual-IV (DSM-IV) (Association 2000).
Data acquisition and preprocessing
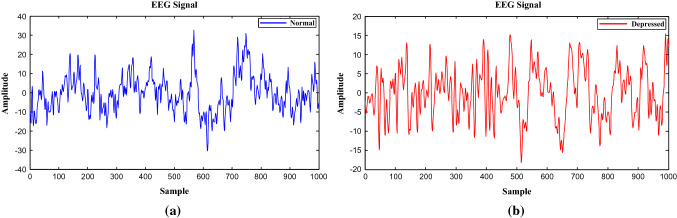
The EEG data recording involved 19-channel EEG cap placed on the scalp according to the 10–20 international standard electrode position system was obtained with eyes closed for 5 min. The EEG sampling frequency was set to 256 Hz. Notch filter was applied to reject 50 Hz power line noise. An amplifier was simultaneously used to magnify weak signals. All EEG signals were band-pass filtered with cutoff frequencies at 0.1 Hz and 70 Hz. Sample of EEG signals from normal and depressed subjects are demonstrated in Fig. 1.
Fig. 1.
EEG signals from a normal and b depressed subjects
Effective connectivity
Effective connectivity has become a popular analysis method in modern neuroscience because of its potential to represent information flow between different channels (Astolfi et al. 2007). The most famous method for estimating effective connectivity is Granger causality (GC) which is a model-based approach (Granger 1969). If a signal can be predicted by previous information from another signal better than from its own information, then the second signal is considered to be the cause of the first signal. GC measures can be computed in the frequency domain which allows the analysis of EEG frequency bands (Geweke 1984). To achieve this, the estimation of parameters of Multi-Variable Auto-Regressive (MVAR) model for an individual signal data is required. Suppose is a vector representing m channels at time t. The MVAR model can be written as
| 1 |
where p is the model order, Ak is an matrix and ut is a white noise process with as covarince matrix which will be used later. By rearranging Eq. (1), it can be written as follows:
| 2 |
By performing Fourier transform Eq. (2) can be written as:
| 3 |
where A(f), U(f) and X(f) spectral representation of vectors in Eq. 2 and and can be written as:
| 4 |
Equation (3) can be written as:
| 5 |
Also, Spectral density matrix S(f) is defined as
| 6 |
The matrices A(f), H(F) and S(f) can be used to define various effective connectivity measures. Most used quantitative spectral measures are: Generalized Partial Directed Coherence (GPDC) (Baccalá and Sameshima 2001, 2007), and Direct directed transfer function (dDTF) (Kaminski et al. 2001) which have been used in this study and can be defined as follows:
| 7 |
| 8 |
where and shows the information flow from channel j to channel i. is the component [i,i] of , aij is the component [i,j] of A(f) and .
We extract each frequency range for each measure by averaging as follows: delta (1–4 Hz), theta (4–7 Hz), alpha or mu (8–12 Hz), beta1 (12–15 Hz), beta2 (15–22 Hz), beta3 (22–30 Hz), Beta (12–30 Hz) and gamma (30–70 Hz). All calculations were done in MATLAB (The Mathworks, Inc., Natick, MA, USA) via the open-source SIFT toolbox (Mullen 2010).
Proposed deep learning scheme
In this paper, five famous deep learning algorithms were presented. The first and second algorithms were based on one and two-dimensional convolutional neural network (1DCNN–2DCNN). The third method is based on long short-term memory (LSTM) model, while the fourth and fifth algorithms utilized a combination of 1DCNN and 2DCNN with LSTM models namely, 1DCNN-LSTM and 2DCNN-LSTM. The spatial and temporal characteristics of the EEG signal are captured by combination of CNN with LSTM models.
Convolutional neural networks (CNN)
CNN is a specific type of neural networks which widely used in image processing and classification tasks. It is the state-of-the-art deep learning methodology consisting of many stacked convolutional layers. This network contains a convolutional layer, pooling layer, and finally fully connected layers (Chauhan et al. 2018).
Convolutional layers
In this layer, a linear transformation is performed on the data using a particular filter. Filters are a way of extracting important patterns from the prototypes. This operation can be defined as follows:
| 9 |
| 10 |
where the filter is a matrix in which each element corresponds to a weight in . denotes a single output element from the current layer l, and is calculated with the filter sliding over the last layer’s output . After convolution operation, a sigmoid activation function is applied to introducing non-linearity, demonstrated in Eq. (10). During the training phase, filter coefficients are updated based on error back propagation to derive the most distinct features. Thus, filters can have different count, length, or striding and padding size depending on the input characteristics.
Pooling layers
Like convolutional layers, pooling plays an important role in CNNs. A pooling layer has a fixed kernel size and strides over the feature map resulted from convolutional layers, whereas it reduces the dimensionality by selecting only a number of elements. In a convolutional layer, the input size is reduced from to , whereas in pooling operation it’s reduced to with a pool size of as only one element is chosen in every iteration. Depending on the layer type, a mean, max or summation operation can be chosen. What this operation does is that it lets the computations proceed faster, and also by reducing parameters and making the network less vulnerable to every single element in feature map, helps to prevent overfitting.
Fully-connected layers
Ultimately the feature map is flattened to a single column vector and is fed to fully-connected layers. They allow non-linear summation of features to be used to maximize discrimination. The whole action is done as follows:
| 11 |
| 12 |
where is the input from the earlier layer i, which is then multiplied by the jth layers weights , resulting in , in the end goes through a desirable activation () to produce .
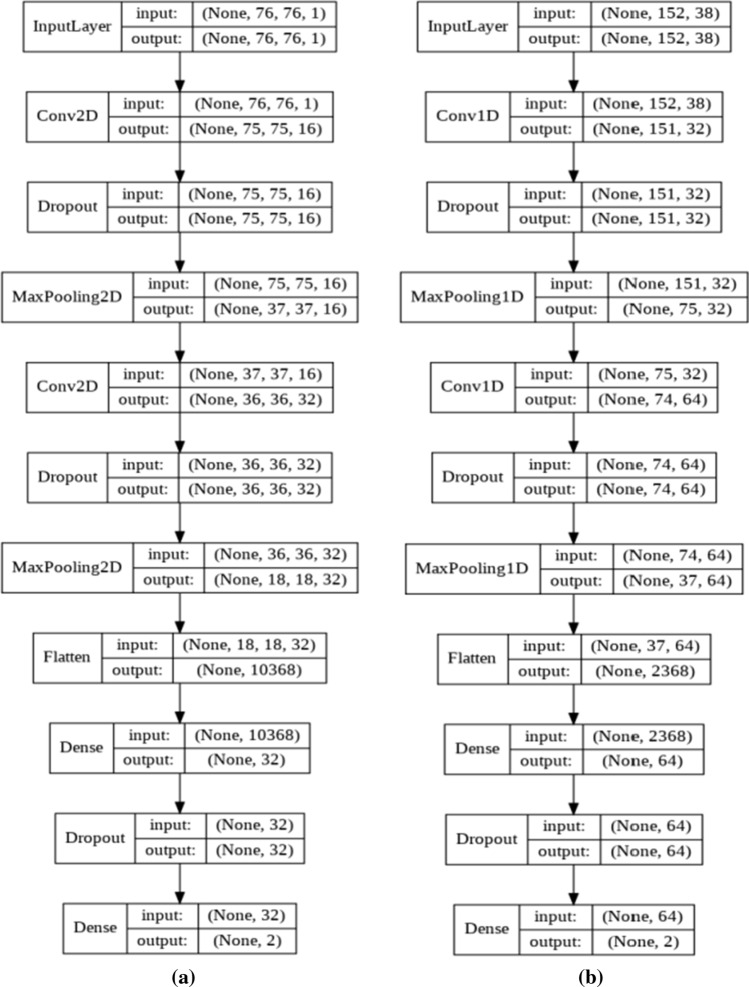
CNNs used here are shown in Table 1. They have two convolutional layers of small and bigger filters to derive both high and low scale features. These layers were then accompanied by 50% dropouts. In a dropout layer, the neuron weights are randomly discarded to reduce variance from training to testing. After each dropout, a max pooling layer with pool sizes and strides of 2 were applied. In the end flattened, features mapped by a dense layer will be used for the final decision. Figure 2 demonstrates the one and two dimensional CNNs that were used in this study.
Table 1.
Parameter descriptions for the one and two dimensional CNNs
| Layer-model | 1D CNN | 2D CNN |
|---|---|---|
| Convolution | 32 − 1 * 1 strides | 32 − 1 * 1 strides |
| Dropout | 50% | 50% |
| Pooling | 2 − 1 * 2 strides | 2 * 2 − 2 * 2 strides |
| Convolution | 64 − 1 * 1 strides | 64 − 1 * 1 strides |
| Dropout | 50% | 50% |
| Pooling | 2 − 1 * 2 strides | 2 * 2 − 2 * 2 strides |
| Fully-connected | 64 | 32 |
| Dropout | 50% | 50% |
| Output | 2 | 2 |
Fig. 2.
Block representations of the a one and b two dimensional CNNs
Long short-term memory (LSTM)
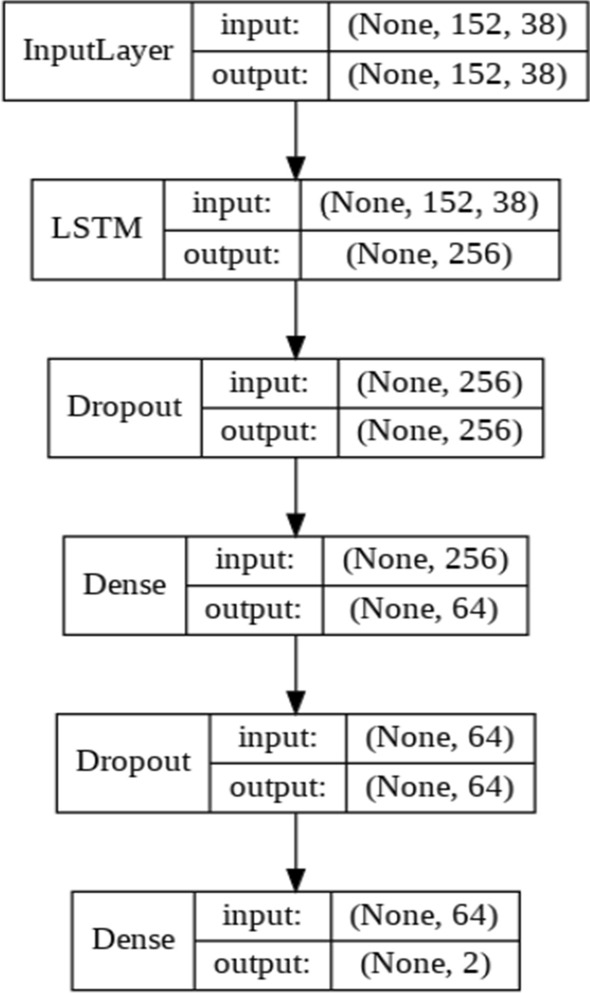
LSTM is an extension of Recurrent neural networks (RNN) (Hochreiter and Schmidhube 1997). These types of networks have the ability to transfer a hidden state as a representation of what’s been through the network. LSTMs have been linked to many sequence classification problems with huge success (Nagabushanam et al. 2019). LSTMs have been introduced because of the problem of gradient loss in RNNs (Hochreiter 1998), which prevents the starting layers of the RNN to be updated with gradient vector. The problem is that the local gradient will get close to zero as it approaches the first layers and the learning effect becomes minimal. With LSTM, a number of gates are developed to be able to carry important information for larger sequences and provide control over information flow. Just like RNNs, each LSTM cell passes a hidden state to the next layer. But the procedure in which the hidden state is calculated is very different. Three gates are used for this purpose which is explored below. The architecture of the proposed LSTM is shown in Fig. 3.
Fig. 3.
Block representation of the LSTM network
Forget gate
This gate decides to keep the information from the previous cell status. Cell state plays an invaluable role in forwarding the information through the LSTM cells. This procedure can be expressed as below:
| 13 |
where is the specific input gets concatenated with last layers hidden state . Then a linear transformation is done using layer weights and a bias . The output value is between 0 and 1, where a higher means keeping a larger proportion of the cell state.
Input gate
The input gate determines the exact data to be passed to the current cell state. Equation 6 shows this procedure.
| 14 |
It’s a result of product between the previous hidden state and this cells input , which then goes through the linear transformation with , and ultimately a sigmoid activation resulting . The calculations for the input gate and forget gate may seem the same but the difference is in the information flow that they are able to control. With forget gate, the cell state output is changed, although the input gate affects the information that is to be provided by the candidate gate, which will be explained shortly. The network used in this study had a LSTM layer with 256 neurons, following a 50% dropout and a deep layer with 64 neurons (Table 2).
Table 2.
Parameter descriptions for the LSTM model
| Layer-model | LSTM |
|---|---|
| Long short-term memory | 256 |
| Dropout | 50% |
| Fully-connected | 64 |
| Dropout | 50% |
| Output | 2 |
Candidate gate
Candidate layer has an activation function and serves as the main source to the current cells’ contribution to the cell state. This gate can be expressed as below.
| 15 |
This gate is also a simple dot product between and , which then goes through the linear transformation with , , featuring unique weights and bias. In the end, next cell state can be computed as:
| 16 |
Output gate
In this layer, we decide on the next cells hidden state and the final output of current cell. The expression can be simplified as below.
| 17 |
This gate is also a simple dot product between input and hidden state , which then goes through the linear transformation with , , and will be passed to a sigmoid function to produce the cell output. The next hidden state, which will be sent to the upcoming cell will also be calculated by using a activation on the cell state which is then multiplied by the cell output .
| 18 |
Convolutional neural network-long short-term memory (CNN-LSTM)
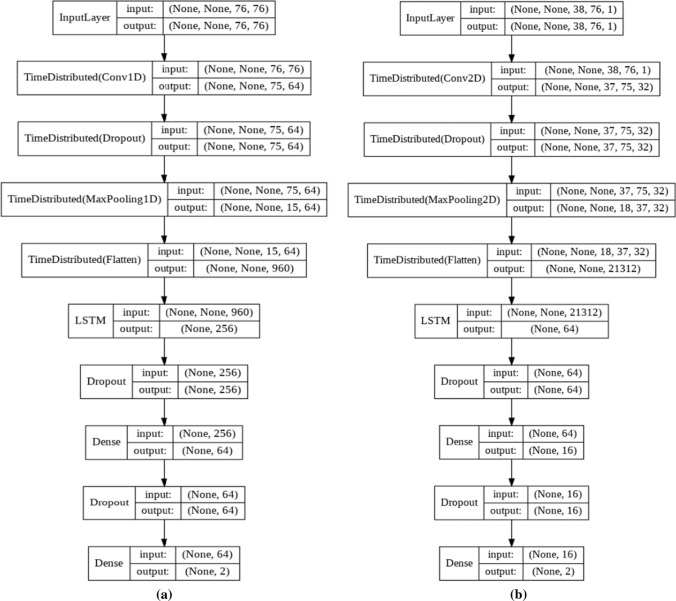
A newly issued method, named CNN-LSTM which was first used on text classification (Luan and Lin 2019) tries to find spatiotemporal relations in the data. In CNN-LSTM, the input first goes through a series of convolutional layers to provide a satisfactory feature map. Then, these features will be fed to a number of LSTM layers to inspect possible temporal information. The classification in CNN-LSTM is also done by using fully-connected layers. The CNN-LSTM evaluated in this work consisted of three main layers and two time-steps with a length of 76 samples. First, a conventional layer with 64 filters and a kernel and stride of size of 2 and 1 are used, respectively, followed by a 50% drop of neuron weights to reduce variance from training to testing. Then a max pooling with size 2 and a stride of 2 is performed. Secondly, the resulting features are flattened and fed to a LSTM cell with 2 neurons which is then followed by another 50% dropout. Ultimately, the LSTM output is forwarded to 64 fully-connected layers to evaluate classification. Activations were all RELU except for output layer that used the sigmoid function. Better interpretation of the CNN-LSTM can be seen on Fig. 4 and Table 3.
Fig. 4.
Block representations of the a one and b two dimensional CNN-LSTM
Table 3.
Parameter descriptions for the one- and two-dimensional CNN-LSTM
| Layer-model | 1D CNN-LSTM | 2D CNN-LSTM |
|---|---|---|
| Convolution | 64 − 1 * 1 strides | 64 − 1 * 1 strides |
| Dropout | 50% | 25% |
| Pooling | 5 − 1 * 2 strides | 2 * 2 − 2 * 2 strides |
| LSTM | 256 − 1 * 1 strides | 64 − 1 * 1 strides |
| Dropout | 50% | 25% |
| Fully-connected | 64 | 64 |
| Dropout | 50% | 50% |
| Output | 2 | 2 |
Evaluation
Independently, 4 versions of the proposed models were trained on 70% of data and then evaluated from the residual data. This procedure was then repeated ten times and the results were averaged to derive the mean and standard deviation of the metrics for each model. The accuracy, sensitivity and specificity measures are computed in this study as follow.
| 19 |
| 20 |
Results
19 channels of EEG signals from each subject were preprocessed using the EEGlab toolbox in Matlab software (version 2019a). The EEG data were segmented with a window length of one second. The selection of a one second window size was based on the evaluation of the proposed models. Then, two measures of effective connectivity named GPDC and dDTF methods based on parameters of calculated MVAR model are extracted on each signal frequency band ranges [Delta, theta, alpha, beta1, beta2, beta3, beta and gamma]. The parameters for MVAR model fitting were selected according to autocorrelation function and portmanteau tests. The optimized parameters are: 1 s of window length, and model order of 5.
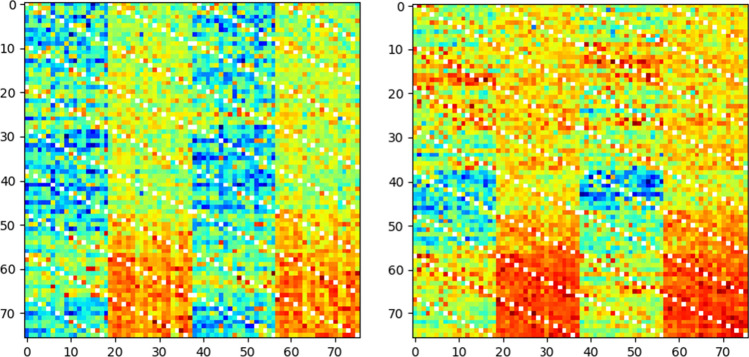
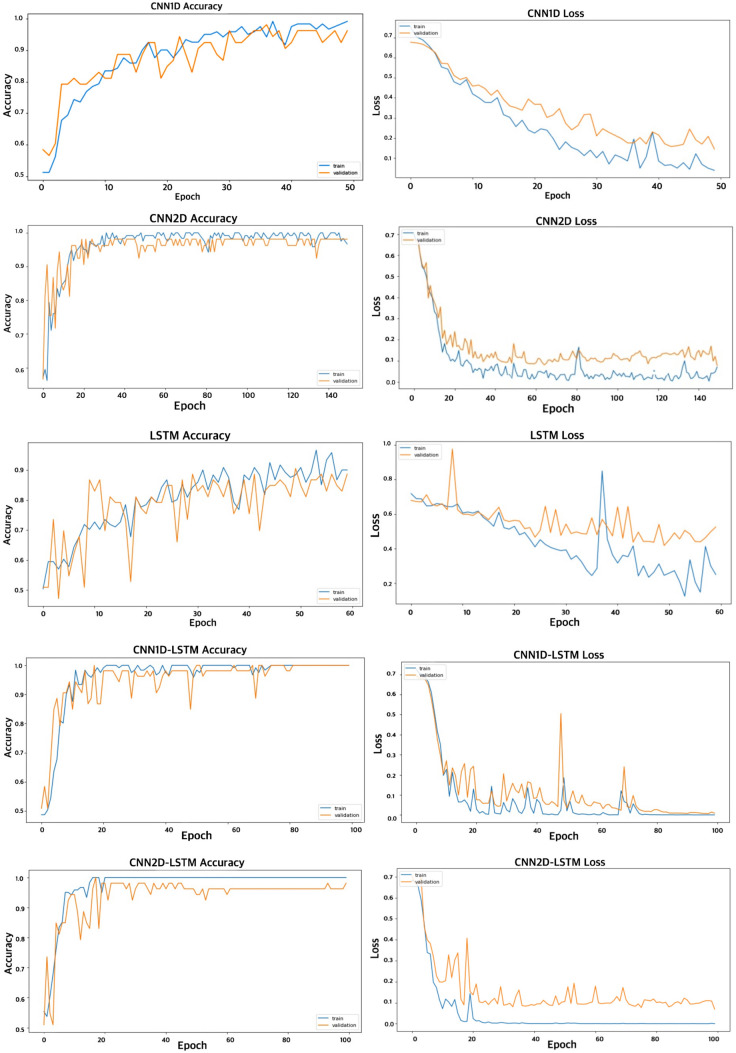
Since the input of CNN is an image, a process to convert 1D EEG signal to image is required. To do this, effective connectivity method has been used which yields in 19*19 image (19 channels). Then, this image must be resized to match the size of the input layer and then feed it to the CNN. However, one should notice that the input layer size is usually large and resizing and up-sampling might deteriorate the quality of the image. That’s the reason we chose to build an image which does not need resizing to be fed to CNN. Having 19-channel EEG, 19*19 effective connectivity image between channels was extracted for each method. Since there are 2 connectivity measures (GPDC and dDTF) and eight frequency bands (Delta, theta, alpha, beta1, beta2, beta3, beta and gamma), 16 images with size of 19*19 can be estimated. These images are combined in the way shown in Fig. 5 to provide the image input (76*76) for the deep learning networks. Also, it should be noted that we hypothesized that the order of image grouping should not have considerable impact on the performance, since the spatial filters in convolutional layers are powerful enough to learn patterns in an image regardless of the exact location of the pattern (for example Googlenet is able to recognize an apple given the apple is at the center or corner of the image, i.e. it is translation invariant). We also tested this hypothesis and formed different images with different groupings and no meaningful change in the performance was observed. Figure 6 shows a sample image for healthy subject and MDD patient. Then, constructed images from EEG signals were fed as input to each deep learning method and the parameters of these models were trained. It should be noted that the images were resized to match the acceptable dimension for each deep network architecture. Independently, five versions of deep methods, 1DCNN, 2DCNN, LSTM, 1DCNN-LSTM, and 2DCNN-LSTM were trained. For model training, a batch size of 4 was selected and each network was trained for five hundred epochs. Cross Entropy was chosen as the loss function and in optimization phase, ADAM algorithm was chosen due to superior results and shorter run-time. An early stopping criterion was used, if the validation loss wouldn’t improve after 125 consecutive epochs. Classifier tuning parameters were shown in Table 4. Training was performed on 70% of data for classification of MDD patients and healthy subjects and then the residual data used to evaluate the performance of the classifier using various metrics (accuracy, Sensitivity, Specificity). All computations were done using a single NVIDIA Tesla k80 chip provided for free by Google Colaboratory, and two reliable deep learning frameworks Keras and Tensorflow, available in python. Figure 7 shows an overview of the proposed method. Training and validation accuracy and loss curves for CNN 1D, CNN 2D, LSTM, CNN 1D-LSTM and CNN 2D-LSTM methods are demonstrated in Fig. 8. Table 5 shows the classification results for these methods for MDD detection from healthy controls. Maximum accuracy was achieved for 1DCNN-LSTM with 99.245%, followed by 2DCNN-LSTM with accuracy of 96.415%. Worst accuracy was achieved by to the LSTM (89.057%). Highest sensitivity was acquired with the 1DCNN-LSTM and 2DCNN-LSTM, having a lower standard deviation with 2DCNN-LSTM. Considerable specificity was seen in 1DCNN-LSTM (100% specificity). Based on the training times, 2DCNN had the 262 s times and 1DCNN took the 1030 s due to the need to use more fully-connected layers. The 2DCNN-LSTM also showed a lower training time (296 s) compared with the 1DCNN-LSTM (405 s), which can be related to the higher number LSTM cells in the 1DCNN-LSTM. The LSTM needed the longest time, although that is consistent with Keras’ GPU problem when compiling LSTM models only.
Fig. 5.
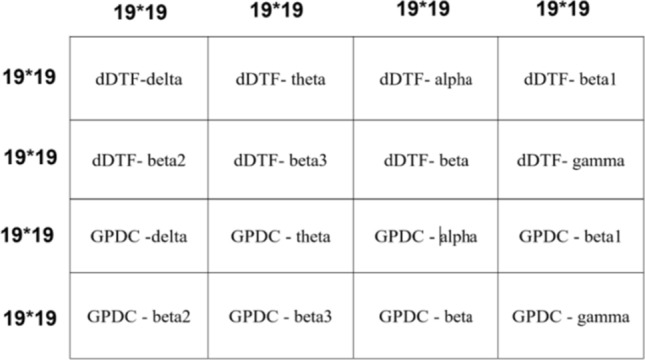
Constructed connectivity image with 2 connectivity measures (GPDC and dDTF) and eight frequency bands (Delta, theta, alpha, beta1, beta2, beta3, beta and gamma) for input of deep learning networks (each block is comprised of a 19*19 connectivity image)
Fig. 6.
A sample constructed connectivity image. Left) MDD patient, Right) healthy subject
Table 4.
Classifier tuning parameters
| Parameters | CNN 1D | CNN 2D | LSTM | CNN 1D-LSTM | CNN 2D-LSTM |
|---|---|---|---|---|---|
| Batch size | 4 | 4 | 4 | 4 | 4 |
| Loss function | Cross entropy | Cross entropy | Cross entropy | Cross entropy | Cross entropy |
| Optimizer | Adam | Adam | Adam | Adam | Adam |
| Learning rate | 0.001 | 0.001 | 0.001 | 0.001 | 0.001 |
| Epochs | 50 | 150 | 60 | 100 | 100 |
Fig. 7.
Block diagram of the proposed method which summarizes the process of the entire work
Fig. 8.
Training and validation accuracy and loss curves for CNN 1D, CNN 2D, LSTM, CNN 1D-LSTM and CNN 2D-LSTM methods
Table 5.
Classification comparison between the proposed models
| Model-metrics | Accuracy | Sensitivity | Specificity | F1 Score | Precision | Training time |
|---|---|---|---|---|---|---|
| CNN 1D | 95.283% ± 2.109 | 91.481% ± 4.074 | 97.170% ± 1.538 | 95.23 ± 1.23 | 97.37% ± 2.40 | 1030.78 |
| CNN 2D | 96.226% ± 1.208 | 94.815% ± 2.457 | 98.846% ± 1.763 | 96.57% ± 1.41 | 97.37 ± 2.25 | 262.508 |
| LSTM | 89.057% ± 1.849 | 84.815% ± 4.521 | 93.462% ± 7.102 | 88.75% ± 1.92 | 89.31 ± 1.77 | 3253.17 |
| CNN 1D-LSTM | 99.245% ± 1.152 | 98.519% ± 2.457 | 100% | 99.05% ± 0.94 | 98.14 ± 1.85 | 405.52 |
| CNN 2D-LSTM | 96.415% ± 3.422 | 98.519% ± 1.814 | 94.231% ± 7.740 | 96.55% ± 1.80 | 97.73 ± 2.77 | 296.89 |
Discussion
Screening of depressed patients is important for early diagnosed and treated. Artificial intelligence methods (Subhani et al. 2018; Wang et al. 2019; Čukić and Stokić 2020; Yao et al. 2020) like this paper can overcome this limitation and can be utilized everywhere with no need to highly-trained experts. In this research, we have used deep learning and effective connectivity methods for automated detection of MDD patients and healthy controls with very success. Accuracy value of 99.245% is achieved for applying the 1DCNN-LSTM architecture in images of GPDC and dDTF methods on 19 channels of EEG signals.
One of the main novelties of this work is using brain effective connectivity method to convert 1-D EEG signal into 2-D image to be fed to CNN Architecture. There are number of ways to convert 1-D signal to 2-D image namely, classical ways based on time–frequency distribution (STFT, wavelets etc.) (OzalYildirim et al. 2019); or techniques based on dynamical system view point such as RQA. However, we have used effective connectivity method which represents information flow between different EEG channels in different frequencies. Also, the combination of effective connectivity methods over different frequencies has been used to form the image needed for CNNs. Also, we have exploited different deep learning schemes which are fundamentally different, i.e. convolutional neural networks which search for patterns in images vs LSTMs which tries to classify based on time dependencies between frames. Also, the combinations of these deep techniques are used to achieve the highest possible performance.
According to Table 5, the CNN-LSTM models showed higher accuracy compared to other techniques, which are also extremely popular and powerful. This is due to a higher-level representation of the data with less variance provided by convolutional layers which aid the LSTM in finding relations in the time domain case (Luan and Lin 2019). The LSTM itself is unable to analyze the EEG connectivity image due to lack of spatial resolution. While, the CNNs themselves get great results. LSTM is built in order to operate differently from a CNN and generally is used to interpret arbitrary input sequences and it’s not appropriate for spatial data. Since the connectivity matrix image is an image consisting of spatial relations between different EEG channels, a local interpretation is needed. This indicates that most of the role played in the modeling is done by CNNs and the remaining important minority by LSTMs giving the desired performance enhancement on the derived features by keeping a memory of the past features, which were simplified by the CNN. The LSTM itself was unable to analyze the EEG connectivity efficiently to extract local features. The less efficiency in modeling brain connectivity from LSTM itself can be observed from Table 5. Moreover, as it was clear from the results, the one-dimensional CNN-LSTM performed better than its two-dimensional version. It can be suggested that, two-dimensional filtering on the proposed connectivity image might loss temporal information, which prevents a faster model like 2DCNN-LSTM achieve remarkable results even with more parameters compared to 1DCNN-LSTM.
In Table 6, results of this study are compared with new best related studies that used EEG signals of the same database (Mumtaz et al. 2017; Mumtaz and Qayyum 2019) and different database (Acharya et al. 2015; Bachmann et al. 2017; Acharya et al. 2018; Sharma et al. 2018; Ay et al. 2019; Čukić and Stokić 2020). As it is observed, accuracy achieved in this study is higher than those studies with the traditional machine learning methods of extraction of linear and non-linear features and proves the preference of the proposed method. Moreover, our results with 1DCNN-LSTM and image constructed with effective connectivity has higher accuracy compared other deep learning methods on time-series data of EEG signals. So, compared to other similar studies, this work has the advantage of comparing the deep learning models, and inspecting the importance of temporal and spatial information mutually and jointly with CNN-LSTM. The authors did not just use a powerful model like CNN-LSTM, but evaluated such model on brain effective connectivity image converted from EEG signals. Consequently, according to the Table 6, this study acquired the best results so far in automated detection of depressed patients and healthy controls. The main drawback of the research can be considered the dataset size to train the networks. By performing regularization terms and simplifying deep models, we were able to overcome this problem. Our aim in the future is to further expand the experimental space by collecting more samples and employing the developed methodology on other types of EEG data.
Table 6.
Overview of previous studies on automated EEG-based depression diagnosis
| Authors year | Methods | Samples | Classification methods | Sensitivity (%) | Specificity (%) | Accuracy |
|---|---|---|---|---|---|---|
| Acharya et al. (2015) | Non-linear features |
15 depressed 15 normal |
SVM | 97.00 | 98.50 | 98.00% |
| Mumtaz et al. (2017) | Alpha asymmetry |
33 depressed 30 normal |
Naive Bayes, logistic regression, SVM | 96.60 | 100.00 | 98.40% |
| Bachmann et al. (2017) | SASI, DFA |
17 depressed 17 normal |
LDA | 94.10 | 88.20 | 91.20% |
| Acharya et al. (2018) | 13-layer CNN |
15 Depressed 15 normal |
1D-CNN | 94.99 | 96.00 | 95.96% |
| Sharma et al. (2018) |
BDL_TCOWFB LE |
15 Depressed 15 normal |
LS-SVM | 98.66 | 99.38 | 99.54% |
| Ay et al. (2019) | – |
15 Depressed 15 normal |
CNN-LSTM | 98.55 | 99.70 |
99.12%(Right) 97.66%(Left) |
| Mumtaz and Qayyum (2019) | – |
33 Depressed 30 normal |
CNN-LSTM, 1D-CNN | 98.34 | 99.78 | 98.20% |
| Čukić and Stokić (2020) | HFD, SampEn |
23 Depressed 20 normal |
Naïve Bayes | – | – | 97.56% |
| Current study | Effective Connectivity (GPDC, dDTF) |
33 Depressed 30 normal |
IDCNN, 2DCNN, 1DCNN-LSTM, 2DCNN-LSTM | 98.52 | 100 | 99.25% |
Conclusion
In this paper a comprehensive study was done using effective brain connectivity methods (GPDC, dDTF) and a number of famous deep learning algorithms (CNN, and LSTM). The best accuracy of 99.24% in classifying MDD patients and healthy controls was achieved via 1DCNN-LSTM. The spatial and temporal characteristics of the EEG signals are captured by this deep learning model. Relying on the results, newly issued deep learning model is capable of effectively analyzing the brain connectivity and produces the best results compared to all studies in recent years. So, the current technique can help health care professionals to identify the patients with MDD for early identification and intervention.
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
The dataset was approved by the ethics committee in Hospital University Sains Malaysia (HUSM), Kelantan, Malaysia.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Acharya UR, Sudarshan VK, Adeli H, Santhosh J, Koh JE, Puthankatti SD, Adeli A. A novel depression diagnosis index using nonlinear features in EEG signals. Eur Neurol. 2015;74(1–2):79–83. doi: 10.1159/000438457. [DOI] [PubMed] [Google Scholar]
- Acharya UR, Oh SL, Hagiwara Y, Tan JH, Adeli H. Deep convolutional neural network for the automated detection and diagnosis of seizure using EEG signals. Comput Biol Med. 2018;100:270–278. doi: 10.1016/j.compbiomed.2017.09.017. [DOI] [PubMed] [Google Scholar]
- Acharya UR, Oh SL, Hagiwara Y, Tan JH, Adeli H, Subha DP. Automated EEG-based screening of depression using deep convolutional neural network. Comput Methods Programs Biomed. 2018;161:103–113. doi: 10.1016/j.cmpb.2018.04.012. [DOI] [PubMed] [Google Scholar]
- Afshani F, Shalbaf A, Shalbaf R, Sleigh J. Frontal–temporal functional connectivity of EEG signal by standardized permutation mutual information during anesthesia. Cogn Neurodyn. 2019;13(6):531–540. doi: 10.1007/s11571-019-09553-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmadlou M, Adeli H, Adeli A. Fractality analysis of the frontal brain in major depressive disorder. Int J Psychophysiol. 2012;85:206–211. doi: 10.1016/j.ijpsycho.2012.05.001. [DOI] [PubMed] [Google Scholar]
- Ahmadlou M, Adeli H, Adeli A. Spatiotemporal analysis of relative convergence of EEGs reveals differences between brain dynamics of depressive women and men. Clin EEG Neurosci. 2013;44:175–181. doi: 10.1177/1550059413480504. [DOI] [PubMed] [Google Scholar]
- Association AP . Diagnostic and Statistical manual of mental disorders: DSM-IV-TR®. Washington, DC: American Psychiatric Publishing; 2000. [Google Scholar]
- Astolfi L, Cincotti F, Mattia D, Marciani MG. Comparison of different cortical connectivity estimators for high-resolution EEG recordings. Hum Brain Mapp. 2007;28(2):143–157. doi: 10.1002/hbm.20263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ay B, Yildirim O, Talo M, Baloglu UB, Aydin G, Puthankattil SD, Acharya UR. Automated depression detection using deep representation and sequence learning with EEG signals. J Med Syst. 2019;43(7):205. doi: 10.1007/s10916-019-1345-. [DOI] [PubMed] [Google Scholar]
- Baccalá LA, Sameshima K. Partial directed coherence: a new concept in neural structure determination. Biol Cybern. 2001;84:463–474. doi: 10.1007/PL00007990. [DOI] [PubMed] [Google Scholar]
- Baccalá LA, Sameshima K (2007) Generalized partial directed coherence. In: 15th International conference on digital signal processing, pp 163–166. IEEE
- Bachmann M, Lass J, Hinrikus H. Single channel EEG analysis for detection of depression. Biomed Signal Process Control. 2017;31:391–397. doi: 10.1016/j.bspc.2016.09.010. [DOI] [Google Scholar]
- Chaudhary S, Taran S, Bajaj V, Sengur A. Convolutional neural network-based approach towards motor imagery tasks EEG signals classification. IEEE Sens J. 2019;19(12):4494–4500. doi: 10.1109/JSEN.2019.2899645. [DOI] [Google Scholar]
- Chauhan R, Ghanshala KK, Joshi RC (2018) Convolutional neural network (CNN) for image detection and recognition. In: 2018 First international conference on secure cyber computing and communication (ICSCCC), Jalandhar, India, pp 278–282
- Čukić M, Stokić M, Simić S, Pokrajac D. The successful discrimination of depression from EEG could be attributed to proper feature extraction and not to a particular classification method. Cogn Neurodyn. 2020;14(4):443–455. doi: 10.1007/s11571-020-09581-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017;542(7639):115–118. doi: 10.1038/nature21056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust O, Ang PCA, Puthankattil SD, Joseph PK. Depression diagnosis support system based on EEG signal entropies. J Mech Med Biol. 2014;14(3):1450035. doi: 10.1142/S0219519414500353. [DOI] [Google Scholar]
- Faust O, Hagiwara Y, Hong TJ, Lih OS, Acharya UR. Deep learning for healthcare applications based on physiological signals: a review. Comput Methods Programs Biomed. 2018;161:1–3. doi: 10.1016/j.cmpb.2018.04.005. [DOI] [PubMed] [Google Scholar]
- Geweke JF. Measures of conditional linear dependence and feedback between time series. J Am Stat Assoc. 1984;79(388):907–915. doi: 10.1080/01621459.1984.10477110. [DOI] [Google Scholar]
- Granger CW. Investigating causal relations by econometric models and cross-spectral methods. Econometrica. 1969;37:424–438. doi: 10.2307/1912791. [DOI] [Google Scholar]
- Hochreiter S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int J Uncertain Fuzziness Knowl Based Syst. 1998;6(02):107–116. doi: 10.1142/S0218488598000094. [DOI] [Google Scholar]
- Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- Hosseinifard B, Moradi MH, Rostami R. classifying depression patients and normal subjects using machine learning techniques and nonlinear features from EEG signal. Comput Methods Programs Biomed. 2013;109:339–345. doi: 10.1016/j.cmpb.2012.10.008. [DOI] [PubMed] [Google Scholar]
- Kaminski M, Ding M, Truccolo WA, Bressler SL. Evaluating causal relations in neural systems: Granger causality, directed transfer function and Statistical assessment of significance. Biol Cybern. 2001;85:145–157. doi: 10.1007/s004220000235. [DOI] [PubMed] [Google Scholar]
- Li X, Hu B, Sun S, Cai H. EEG-based mild depressive detection using feature selection methods and classifiers. Comput Methods Programs Biomed. 2016;136:151–161. doi: 10.1016/j.cmpb.2016.08.010. [DOI] [PubMed] [Google Scholar]
- Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, Sánchez CI. A survey on deep learning in medical image analysis. Med Image Anal. 2017;42:60–88. doi: 10.1016/j.media.2017.07.005. [DOI] [PubMed] [Google Scholar]
- Luan Y, Lin S (2019) Research on text classification based on CNN and LSTM. In: 2019 IEEE international conference on artificial intelligence and computer applications (ICAICA), pp 352–355. IEEE
- Mullen T (2010) An electrophysiological information flow toolbox for EEGLAB theoretical handbook and user manual
- Mumtaz W, Qayyum A. A deep learning framework for automatic diagnosis of unipolar depression. Int J Med Inform. 2019;132:103983. doi: 10.1016/j.ijmedinf.2019.103983. [DOI] [PubMed] [Google Scholar]
- Mumtaz W, Xia LK, Ali SSA, Yasin MAM, Hussain M, Malik AS. Electroencephalogram (EEG)-based computer-aided technique to diagnose major depressive disorder (MDD) Biomed Signal Process Control. 2017;31:108–115. doi: 10.1016/j.bspc.2016.07.006. [DOI] [Google Scholar]
- Mumtaz W, Xia L, Mhod Yasin MA, Azhar Ali SS, Malik AS. A wavelet-based technique to predict treatment outcome for Major Depressive Disorder. PLoS ONE. 2017;12(2):e0171409. doi: 10.1371/journal.pone. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagabushanam P, George ST, Radha S. EEG signal classification using LSTM and improved neural network algorithms. Soft Comput. 2019;24:9981–10003. doi: 10.1007/s00500-019-04515-0. [DOI] [Google Scholar]
- Puthankattil SD, Joseph PK. Classification of EEG signals in normal and depression conditions by ANN using RWE and signal entropy. J Mech Med Biol. 2012;12:1240019. doi: 10.1142/S0219519412400192. [DOI] [Google Scholar]
- Raghavendra U, Acharya UR, Adeli H. Artificial intelligence techniques for automated diagnosis of neurological disorders. Eur Neurol. 2019;82(1–3):41–64. doi: 10.1159/000504292. [DOI] [PubMed] [Google Scholar]
- Roy Y, Banville H, Albuquerque I, Gramfort A, Falk TH, Faubert J. Deep learning-based electroencephalography analysis: a systematic review. J Neural Eng. 2019;16(5):051001. doi: 10.1088/1741-2552/ab260c. [DOI] [PubMed] [Google Scholar]
- Shalbaf A, Saffar M, Sleigh JW, Shalbaf R. Monitoring the depth of anesthesia using a new adaptive neurofuzzy system. IEEE J Biomed Health Inform. 2017;22(3):671–677. doi: 10.1109/JBHI.2017.2709841. [DOI] [PubMed] [Google Scholar]
- Shalbaf A, Shalbaf R, Saffar M, Sleigh J. Monitoring the level of hypnosis using a hierarchical SVM system. J Clin Monit Comput. 2019;15:1–8. doi: 10.1007/s10877-019-00311-1. [DOI] [PubMed] [Google Scholar]
- Sharma M, Achuth PV, Deb D, Puthankattil SD, Acharya UR. An automated diagnosis of depression using three-channel bandwidth-duration localized wavelet filter bank with EEG signals. Cogn Syst Res. 2018;52:508–520. doi: 10.1016/j.cogsys.2018.07.010. [DOI] [Google Scholar]
- Subhani AR, Kamel N, Mohamad Saad MN, et al. Mitigation of stress: new treatment alternatives. Cogn Neurodyn. 2018;12:1–20. doi: 10.1007/s11571-017-9460-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun W, Tseng TL, Zhang J, Qian W. Enhancing deep convolutional neural network scheme for breast cancer diagnosis with unlabeled data. Comput Med Imaging Graph. 2017;57:4–9. doi: 10.1016/j.compmedimag.2016.07.004. [DOI] [PubMed] [Google Scholar]
- Wang Y, Xuying X, Zhu Y, Wang R. Neural energy mechanism and neurodynamics of memory transformation. Nonlinear Dyn. 2019;97:697–714. doi: 10.1007/s11071-019-05007-4. [DOI] [Google Scholar]
- World Federation for Mental Health (2012) Depression: a global crisis, Occoquan, VA, USA
- World Health Organization (2017) Depression. http://www.who.int/mediacentre/factsheets/fs369/en/
- Yao D, Zhang Y, Liu T, Xu P, Gong D, Lu J, Xia Y, Luo C, Guo D, Dong L, Lai Y, Chen K, Li J. Bacomics: a comprehensive cross area originating in the studies of various brain–apparatus conversations. Cogn Neurodyn. 2020;14(4):425–441. doi: 10.1007/s11571-020-09577-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yildirim O, Talo M, Ay B, Baloglu UB, Aydin G, Acharya R. Automated detection of diabetic subject using pre-trained 2D-CNN models with frequency spectrum images extracted from heart rate signals. Comput Biol Med. 2019;113:103387. doi: 10.1016/j.compbiomed.2019.103387. [DOI] [PubMed] [Google Scholar]
- Zhang X, Yao L, Wang X, Monaghan J, Mcalpine D (2019) A survey on deep learning based brain computer interface: recent advances and new frontiers. arXiv preprint arXiv:1905.04149 [DOI] [PubMed]