Systems dynamics and the uncertainties of diagnostics, testing and contact tracing for COVID-19

Abstract

The current COVID-19 pandemic contains an unprecedented amount of uncertainty and variability and thus, there is a critical need for understanding of the variation documented in the biological, policy, sociological, and infrastructure responses during an epidemic to support decisions at all levels. With the significant asymptomatic spread of the virus and without an immediate vaccine and pharmaceuticals available, the best feasible strategies for testing and diagnostics, contact tracing, and quarantine need to be optimized. With potentially high false negative test results, infected people would not be enrolled in contact-trace programs and thus, may not be quarantined. Similarly, without broad testing, asymptomatic people are not identified and quarantined. Interconnected system dynamics models can be used to optimize strategies for mitigations for decision support during a pandemic. We use a systems dynamics epidemiology model along with other interconnected system models within public health including hospitals, intensive care units, masks, contact tracing, social distancing, and a newly developed testing and diagnostics model to investigate the uncertainties with testing and to optimize strategies for detecting and diagnosing infected people. Using an orthogonal array Latin Hypercube experimental design, we ran 54 simulations each for two scenarios of 10% and 30% asymptomatic people, varying important inputs for testing and social distancing. Systems dynamics modeling, coupled with computer experimental design and statistical analysis can provide rapid and quantitative results for decision support. Our results show that widespread testing, contacting tracing and quarantine can curtail the pandemic through identifying asymptomatic people in the population.

1. Introduction

Natural biological variation in pathogen impacts and responses, in addition to the uncertainty in disease parameters, can greatly affect the outcomes of modeling the impacts of a pandemic infectious disease. Some examples of these uncertain parameters include transmission, infectivity rate, incubation time, mortality, recovery rate, and the stage of the greatest infectivity. Completing sensitivity analyses can elucidate the role of uncertainties and enable the extrapolation of the results to support decision makers. The objective of this work is to use our mature and calibrated infectious disease and health care model to make sense of this biological and behavioral variability to forecast with probabilities and likely outcomes from different scenarios with a specific focus on diagnostics and testing.

Rapidly changing and relatively novel infectious diseases, such as coronaviruses, have strong elements of uncertainty due to viral evolution as well as geographic, population level, and individual differences in how the host and virus interact in an outbreak and possibly a pandemic. During an epidemic, viruses and hosts continue to evolve, adapting and altering their contagiousness and virulence. Human populations are diverse with differences in immune function, underlying morbidities, genetics, and age groups for responses, as well as exposure to infectious diseases. The current COVID-19 pandemic in 2020 contains an unprecedented amount of uncertainty [1], [2]. With this uncertainty, there is a critical need for understanding the variation documented in the biological, policy, sociological, and infrastructure responses during an epidemic to support decisions at all levels.

The Modeling Epidemics for Decision Support and Infrastructure Analysis System (MEDIAN) project was used to assess potential impacts of a range of testing and diagnostics strategies on the COVID-19 pandemic. The suite of system dynamics models that comprise the MEDIAN platform were previously used and validated for the pandemic response for H1N1 influenza in 2009 [3]. A simulation-based uncertainty analysis uses repeated evaluations of a model, using different combinations of key model input variables, to estimate the range of potential outcomes and most important factors for driving an epidemic. Key model inputs, such as mitigations for controlling the epidemic, are varied using a computer experimental design structure and identified through a sensitivity analysis, which determines how the outcomes vary through a range of values of model input parameters. Information about the distribution of likely outcomes, which needs to account for these outcomes as well as exposure to low-probability, high-consequence events, is important in a risk-informed decision-making environment.

There are many sources of uncertainty in a local or global infectious disease outbreak. The sources of variability can be grouped into four categories: biological, policy, sociological response, and infrastructure responses [3]. The biological uncertainty of the SARS-2 coronavirus is unprecedented. Since the SARS-2 coronavirus (SARS-2 COV) is a newly emerged disease, almost the entirety of the population is not immune to the virus, however, the range of impacts to individuals is from completely asymptomatic to death and everything in between [4]. Until vaccines were readily available to the population, the intervention strategies for fighting the SARS-2 COV included testing and tracing potentially exposed individuals, social distancing, quarantining infectious and susceptible persons, and respiratory protection, such as masks. Each of these strategies decreases the transmission of the disease. Medical interventions continue to help reduce mortality in COVID-19 patients, but there remains no clear drug therapies for targeting viral replication and its multiplication in patients [5]. Particularly for the COVID-19 pandemic where state health departments are largely autonomous of federal control, their approaches to containing the pandemic, such as school closures, vary immensely [6], [7]. Sociological uncertainties include the behavioral responses of the populations to adhering to the policy guidance while infrastructure uncertainties include impacts on labor and supply chain interruptions, particularly for personal protective equipment.

The analyses described here identify key uncertain input variables in three of these four uncertainty categories and assesses the variability in outcomes due to uncertainty in the inputs for testing and diagnostics. In particular, we focus on modeling the uncertainties for testing and diagnostics (biological, sociological, and policy), contact tracing (sociological and policy), and social distancing through quarantine (sociological and policy). As pointed out by Ribeiro da Silva et al. [8], laboratory diagnosis is “crucial for the clinical management of patients and the implementation of disease control strategies to contain SARS-CoV-2 at the clinical and population level”.

The objectives of this analysis are to (1) describe the application of a systems dynamics approach, coupled with a computer experimental design of the COVID-19 pandemic, (2) assess the range of consequences of the pandemic COVID-19 given the uncertainty about its disease characteristics for the asymptomatic population, (3) assess the uncertainties and strategies for testing and diagnostics on the outcome of the pandemic, and lastly, (4) identify high utility and robust strategies, especially with regard to testing and diagnostics.

2. Model Overview

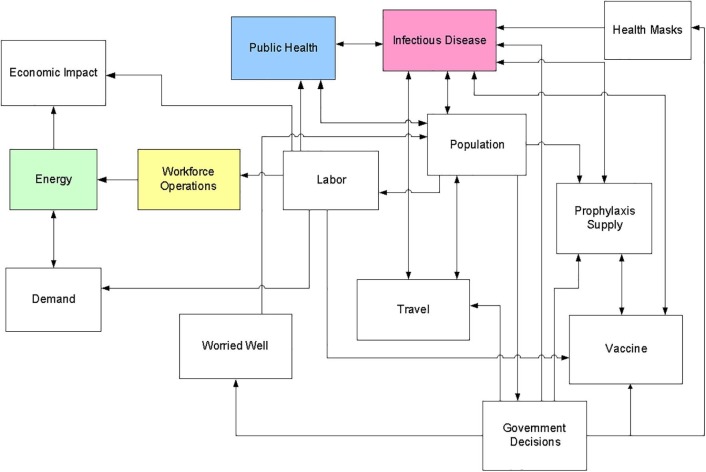
The model used to perform these analyses is a subset of the suite of Modeling Epidemics for Decision Support and Infrastructure Analysis (MEDIAN) models described elsewhere [3], [9]. The set of models used represents infectious disease propagation and possible interventions, population, travel, labor, and infrastructure operations as shown in Fig. 1 . Important sub-models include a general infectious disease (GID) model, a population model used to track inter-region travel and labor availability, a public health model, and an economic impact estimation model.

Fig. 1.

Major elements of the Modeling Epidemics for Decision Support and Infrastructure Analysis models that can be used in a pandemic COVID-19 impacts analysis.

The population and infectious disease models interact to introduce the pandemic COVID-19 strain into the population and spread the disease across the region. The population developing symptoms and needing treatment place a demand on the public health sector. The use of various intervention strategies, such as vaccination, affects the spread of the disease and alters the impacts on the public health system and on the overall population. The population model also tracks which members of the ill population are also members of the workforce and estimates absenteeism due to illness, care for ill family members, or other reasons.

2.1. Model architecture

The MEDIAN architecture uses the system dynamics method to model the dynamics of disease and infrastructure behavior and a Java-based program to manage model integration and experiment design and execution. System Dynamics (SD) is a methodology and mathematical modeling approach designed to visualize a ‘system’s structure and behavior, analyzing the system both qualitatively and quantitatively’. Originally developed in the 1950′s by Jay Forrester of the Massachusetts Institute of Technology [10], [11] to help corporate managers improve their understanding of industrial processes, SD is currently being used throughout the public and private sector for policy analysis and design. System dynamics software with a graphical user interface (GUI), such as the commercially available Vensim™ package [12] used in the MEDIAN project, was developed in the 1990's and has been applied to a diverse set of systems.

In the SD methodology, a problem or a system (e.g., ecosystem, political system or mechanical system) may be represented as a causal loop diagram - a map of a system with all its constituent components and their interactions. By capturing interactions and feedback loops, a causal loop diagram can help reveal the structure of a system, evaluating a system’s behavior dynamically. A causal loop diagram is then transformed in software to a stock and flow model to study and analyze the system quantitatively [13], [14]. In the MEDIAN suite of models, the stocks and flows are used to represent such things as stocks of hospital patients, beds, ICU units, masks, and infected persons in different stages of a disease, and flows of patients in and out of a hospital, infection rates, and death and recovery rates. SD with its representation of feedback loops is also a natural choice for representing the interdependencies amongst the infrastructures and disease behavior in MEDIAN.

The MEDIAN modeling process uses a Los Alamos National Laboratory-written, Java-based program, Conductor tool, to create and manage input for Vensim™. The Conductor tool allows us to merge multiple Vensim^TM sub-models into a single comprehensive model and then fully explore the model parameters, in Monte-Carlo fashion, by running many separate instances of the model on a high-performance parallel computer. Using the Conductor, the modeler chooses the experimental design (described below), statistical distribution functions to sample each parameter, the number of processors on which to run, and the variables to output. The models are considered proprietary at this point and while this does lead to challenges with reproducibility of the results, the burden is on researchers to show appropriate validation and parameterization of epidemiological models [15]. We use experimental design to understand the uncertainty and the variation in the results, but the models are entirely deterministic.

2.2. The infectious disease model

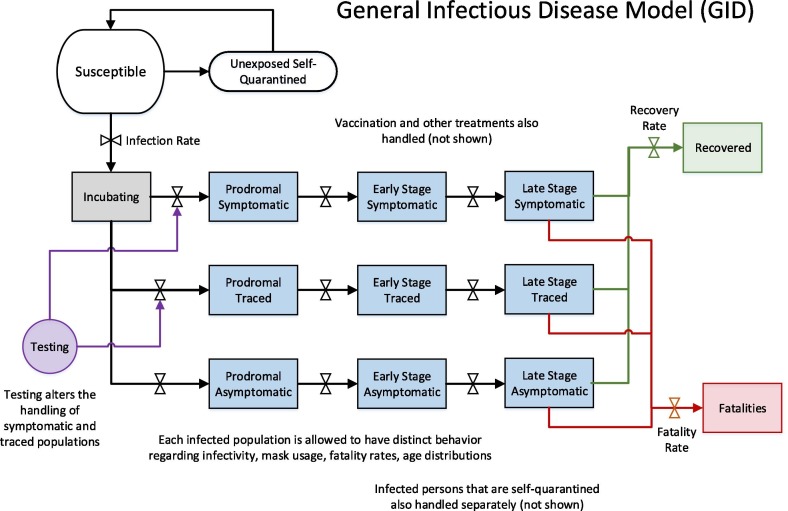
The infectious disease model is a systems dynamics model that uses the core susceptible-exposed-infected-recovered (SEIR) epidemiological approach with a set of disease stages [16]. The GID model includes demographic groupings; an integrated model for testing and diagnostics, contact tracing, quarantine, and isolation. As a form of the SEIR model, this application represents a selected population, such as a metropolitan area, as homogeneous with exponentially distributed residence times in each stage. The use of additional stages and demographic groupings also adds heterogeneity where it is useful in capturing key differences between subpopulations for disease spread.

The infectious diseases stages are represented generically so that the model can be used for any infectious pathogen by adjusting the input parameters appropriately (Fig. 2 ).

Fig. 2.

Representation of the multi-stage susceptible-exposed-infected-recovered general infectious disease model.

The demographic groups used in the model are as follows:

• •Young (ages 0–19)
• •Young Adults (ages 20–49)
• •Adults (ages 50–69)
• •Older adults (ages 70–79)
• •Elderly (ages 80 + )
• •Responders

Responders are the health and emergency-services workers who are drawn primarily from the two adult groups (young adults and adults). The populations of these groups are thus reduced by the number of responders in each group. Responders are treated separately in the model to allow modeling of an increase in exposure to SARS-2 COV compared to the general population and to be able to model different policies for response to the pandemic. The demographic groups are very different for SARS-2 COV than for influenza due to the different impacts to age groups for COVID-19 [17].

The basic reproductive number (R₀) is the average number of people infected by a typically infectious individual in an otherwise susceptible population. If the basic reproductive number is greater than 1, the disease has the potential to spread. If it is less than 1, the disease will die out after only a few generations. The parameters that affect R₀ include the ease of transmission of disease, survivability in the ecosystem, and the contact rates among the populations. The MEDIAN infectious disease model can use R₀ as an input into the model or it can calculate it as an output of the model based on input contact rates by demographic group. For this study, R₀ was used as an input to the model.

2.3. Metropolitan population model

The focus of this analysis is on the Metropolitan Statistical Area for Albuquerque, New Mexico as an example metropolitan area that includes the four counties of Bernalillo, Sandoval, Torrance, and Valencia. The cases and fatalities in the metropolitan four county region is governed by the three concurrent processes: detection and control of the disease, movement of infected people out of the initial exposure region, and the overall rate of disease propagation. The relative values of the time constants associated with these processes determine whether the outbreak is effectively contained within the metro region or instead causes a significant number of cases outside the metro region. For small values of the reproduction number and low travel rates, the conventional process of detecting the infection and mobilizing the response can react in time to keep the number of extra-metro cases small. However, for large values of the reproduction number or higher travel rates, the disease can spread outside the targeted region before effective control is established and possibly lead to hundreds of fatalities.

The population model keeps track of the number of people in different health statuses for each region. It drives the visitation rates for the public health model in three categories: normal afflictions, pandemic COVID-19 afflictions, and “worried-well” afflictions. Worried, but clinically healthy, people are those who think they might have the pandemic COVID-19, but do not. The population model also outputs the fractional labor availability for each infrastructure category. In addition to normal, pandemic COVID-19, and worried well people, it also considers the number of quarantined and self-isolating people. Parents of infected children that stay home from work to care for them can be tracked by the model. A sub-model tracks emergency responders separately, so the labor availability for emergency services can be different than for other infrastructures. All other infrastructures have essentially the same level and time history for labor availability.

2.4. Public health model

The public health model is a coupled, but separate, systems dynamics model, that represents treatment of patients by physicians’ offices and clinics, emergency medical services, emergency rooms, and hospitals. Within the selected metropolitan area, average values are used for patient-treatment capacities and number of hospital beds. Three types of patients are tracked in the model: “normal” patients (numbers based on historical data), patients who have pandemic COVID-19 (denoted “special” within the model), and worried-well patients (people who think they might have the pandemic COVID-19, but who do not). As the numbers of patients increase over normal conditions, backlogs and long waits result, causing a reduction in the quality of care. In addition, if large numbers of healthcare workers are sick or in isolation, the capacity to treat patients is reduced, further exacerbating the overloading of the healthcare system. In a situation like this, it is possible that additional healthcare workers would be brought in (for example, healthcare workers from other locations and the armed services, retirees, and volunteers) to relieve the overloading, but the ability to add healthcare workers is not included in the model at present. It is worth noting, however, that the usual methods of bringing in additional healthcare workers might not work well in a pandemic because the entire country is affected.

2.5. Normal hospital care

The ongoing rates of medical treatment under normal conditions are based on data for the year 2017 from the “National Hospital Ambulatory Medical Care Survey” [18]. Key data are summarized in Table 1 . Visit rates are given per year in the table, but the model uses units of hours. Weekdays and weekends are not differentiated in the model, so annual totals were divided by the number of hours in a year to get the hourly values used by the model. The numbers listed in the table are all national averages. The last two numbers (hospital beds and hospital occupancy rate) are available for New Mexico hospitals [19]. The hospital occupancy rate is based on appropriate occupancy rates for the southwest region obtained by specifying the number of staffed beds per person and the average length of stay for the southwest region.

Table 1.

Summary of medical care in 2016 and 2017.

Quantity	Value
Rate of visits to physicians’ offices and hospital outpatient departments	85.1% saw any physician 2016
Rate of visits to hospital emergency departments	0.43–2017 visits per year per person
Rate of admissions to community hospitals	8.7% admitted to hospital 2016
Fraction of emergency department patients arriving by ambulance	39% − 2017
Fraction of emergency department patients requiring hospital admission	8.7% 2016
Fraction of emergency department visits dead on arrival or dying in the emergency department	1.8% − 2017
Fraction of hospital inpatients dying	0.2% in ED 2016
Average time spent in emergency department	2–4 h (most patients spent) 2016
Average hospital length of stay	3–4 days (most patients stayed) 2016
Number of staffed community hospital beds	0.0028 beds per person
Occupancy rate for community hospital beds	66%

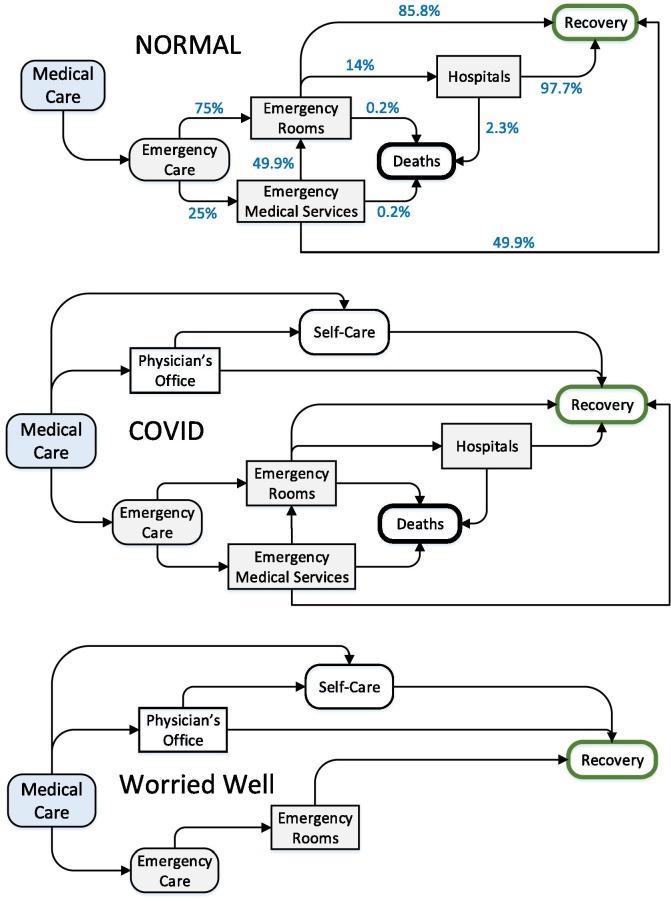
A flow diagram illustrating the major patient flows for “normal” emergency care in the model is shown in Fig. 3 . Several of the fractions are unknown, but they have been chosen to be consistent with the data in Table 1. For example, a 75-% to 25-% split between emergency patients going directly to an ER versus being treated in the field by EMS, coupled with the assumption that half of the patients treated by EMS are then taken to ER by ambulance, results in approximately 14% of patients arriving at the ER by ambulance, as shown in Table 1. A total mortality rate of 0.3% is derived by combining the mortality rates of the EMS and ER patients.

Fig. 3.

Flow diagram for normal emergency care in the public health model, flow diagram for pandemic COVID-19 patients in the public health model, and flow diagram for worried-well patients in the public health model.

The demand for “normal” care continues even during an COVID-19 pandemic; therefore, the team made several adjustments in the model:

• •When there is a long waiting time for visits, up to 20% of the patients who would have gone to a physician’s office are assumed to go instead to a hospital ER because of an urgent problem. Up to 40% of the patients who would have gone to a physician’s office are assumed to cancel if there is a long waiting time for visits.
• •If the waiting time for EMS response gets too long, more people will go directly to the ER rather than wait.
• •When hospital beds are full, nonemergency patients are not admitted to hospitals, but the patients who would have been admitted wait and are admitted later when the hospital crowding subsides.
• •When demand exceeds normal capacity for treatment, the time it takes to treat a patient goes up and quality of care goes down, which can cause an increase in the mortality rates.

2.6. Treatment of pandemic COVID-19 patients

People becoming ill with the pandemic COVID-19 are added to the normal load on the healthcare system. The rates at which people get sick and recover or die from the pandemic COVID-19 are calculated by the epidemiological model discussed above. The fractional splits in the model are variable, depending on the average case fatality rate and the degree of crowding in the healthcare system. A higher case fatality rate indicates a more severe variant of the disease and so the fractions of patients seeking healthcare, requiring emergency care, and requiring admission to hospital are higher.

Overcrowding in the healthcare system can have several effects including more people self-treating because waiting times are so long, more people going directly to an ER rather than waiting for EMS, and, if wait time for hospital admission is long enough, people starting to recover before getting into the hospital. Further, as mentioned above, overcrowding can cause quality of care to decline and mortality rates to increase. In Fig. 3, the hospital “box” includes temporary alternative-care facilities that are assumed to be set up when hospitals are full. The calculated healthcare cost includes a reduced cost per patient per day. For these simulations, MEDIAN assumed that there are enough alternative beds (for example, in gyms, convention centers, or elsewhere). MEDIAN also assumed that some patients are sent home for care because there is no room in hospitals or temporary facilities

MEDIAN assumed the time spent in an ER would be the same for pandemic patients as for normal patients, but the time in hospital would be longer. MEDIAN also assumed the average hospital stay for pandemic COVID-19 patients would be the same as the COVID-19 recovery time (the amount of time spent in the last disease stage in Fig. 2).

2.7. Worried well

The number of worried-well patients is highly uncertain, but it could be large enough to cause a significant additional load on physicians’ offices and ERs. For the analyses discussed here, MEDIAN assumed the number of worried-well patients would be 20% larger than the number of people who have pandemic COVID-19 symptoms (that is, the number of worried-well patients would be 1.2 times the number of pandemic COVID-19 patients). The worried-well rate has been much higher for many past incidents; for example, there were five times as many worried well patients as actual patients afflicted after the Sarin attack in Tokyo [20]. However, because a large fraction of the population is assumed to become ill in the COVID-19 pandemic if there is no mitigation, the worried-well multiplier could not be too much higher. If mitigation measures successfully reduce the fraction of the population becoming ill, then there would be less reason for the fear response that leads to people becoming worried well. Furthermore, while worried-well patients can have an important impact on crowding in parts of the healthcare system, the uncertainty in the number of worried-well patients has less impact than many other uncertainties on the quantities of greatest concern (such as number of deaths and economic impact). Therefore, for this analysis, the worried-well multiplier was fixed at 1.2.

The flow of worried-well patients through the healthcare system is simpler than for normal or pandemic-COVID-19 patients because, by definition, worried-well patients are not seriously ill, but are only afraid they might be. Therefore, MEDIAN assumed that not one person is treated by EMS, admitted to the hospital, or dies. This simplified patient flow is illustrated in Fig. 3.

The split of patients seeking care at a physician’s office versus an ER is variable, depending on the average case fatality rate. MEDIAN assumed that if the disease is more severe (as indicated by a higher case fatality rate), then worried-well patients would be more likely to seek emergency care instead of going to a physician’s office. Also, if the waiting time for an appointment at a physician’s office is too long, some patients may end up self-treating and bypassing the healthcare system as they start to recover from their COVID-19-like symptoms.

3. Sensitivity and uncertainty analysis

Uncertainty analysis is estimating the distributions of outcome metrics of interest so that probability estimates can be made on the consequences of the simulated pandemic. In this context, sensitivity analysis is identifying which input variables cause the most variation in the outputs. The relative sensitivity of an output to an input variable is often given as a ratio of variance measures, referred to as the R² metric later in this section.

The analysis team selected an initial set of uncertain input variables to study, including biological variation, policy options, and sociological response differences, based on the team’s experience. An initial sensitivity analysis identified key input variables that are important in determining the variation in the outcomes. The team then used the resultant variables as the basis for a subsequent uncertainty analysis to characterize the uncertainty in the outcomes.

3.1. Experimental Design

In the design and modeling of complex systems, designed experiments are frequently the only practical approach to obtaining a solution. Typically, a simulation model of system performance is constructed based on knowledge of how the system operates, and sampling via experiments may be employed to estimate the number of possible outcomes. If the simulation model is computationally expensive, then the optimization of the possible outcomes may instead rely on a sampling methodology to adequately cover all the possible ranges of inputs that contain uncertainty or variability.

This uncertainty analysis employed an experimental design approach to pandemic scenario simulations to obtain information for statistical estimates and correlation in the most efficient manner possible. The goal of the experiment design was to improve the understanding of the correlation between mitigations or the variation in the virus infection and the propagation of the pandemic. The design is based on a fractional factorial experiment, which allows an experiment to be conducted with only a fraction of all the possible experimental combinations of parameter values and it used orthogonal arrays to aid in the design of an experiment. The orthogonal array specifies the combinations of inputs for each run of the simulation experiment. This process for designing and conducting an experiment to determine the effect of design factors (parameters) and noise factors give statistical power for both an uncertainty analysis and sensitivity analysis.

The statistical method of Latin hypercube sampling (LHS) was developed to generate a distribution of plausible collections of parameter values from a multidimensional distribution. Orthogonal-array based LHS is in common use for computer experiments [21], [22], [23]. The sampling method is often applied in uncertainty analysis. The LHS technique was first described by McKay [24] and see Iman et al. [25] for a review. In the context of statistical sampling, a square grid containing sample positions is a Latin square if (and only if) there is only one sample in each row and each column. A Latin hypercube is the generalization of this concept to an arbitrary number of dimensions, whereby each sample is the only one in each axis-aligned hyperplane containing that sample.

Latin hypercube design samples input parameters based on stratification of the specified marginal distributions of the parameters. This approach to designing and conducting an experiment to determine the effect of design factors (parameters) and noise factors make this method useful for both uncertainty analysis and sensitivity analysis [26]. For the pandemic COVID-19 sensitivity study, the experimental design was an orthogonal array-based LHS plan (strength three, allowing evaluation of main effects without interference from two factor interactions), varying nine input variables based on their input distributions for two different scenarios (10% and 30% fraction asymptomatic) for a total of 108 runs. For this study, we identified nine input variables as potential influential variables on the estimated consequences. The input variables and associated ranges are listed in Table 2 and were identified based on expert opinion and literature review. Input variables that are grouped together were varied together (i.e., 100-% correlation among the variables).

Table 2.

Input variables distributions (normal) used for orthogonal Latin hypercube design for testing, contact tracing and quarantine. There are three types of diagnostic testing flow strategies, Cohort (e.g. school district or neighborhood), random (broader surveillance), and symptomatic testing. The lowest values and highest values are within three standard deviations of the mean.

Variable	Normal Distribution Values				Units
	Mean	Stand. Dev.	Lowest	Highest
Fraction Contact Traced and Quarantined	0.5	0.1	0.20	0.8	Dimensionless (rate)
Cohort Testing Outcome Probabilities [False Negative]	0.275	0.075	0.05	0.50	Dimensionless (rate)
Random Testing Outcome Probabilities [False Negative]	0.275	0.075	0.05	0.50	Dimensionless (rate)
Symptomatic Testing Outcome Probabilities [False Negative]	0.275	0.075	0.05	0.50	Dimensionless (rate)
Cohort Testing Time	60	13	21	99	Hours
Random Testing Time	60	13	21	99	Hours
Symptomatic Testing Time	60	13	21	99	Hours
Fraction Traced Tested	0.56	0.14	0.14	0.98	%
Nominal Random Testing Rate	80	23	11	149	Tests per hour

Even with varying only nine input parameters, there can be a high degree of variability in the epidemic curves of the pandemic. A past study on pandemic influenza show that the output variability of the model due to uncertainty in the parameters of the infectious disease model can be remarkably large [3]. R² correlation coefficients are a standard metric for evaluating goodness of fit of a model to a statistical response, in either an analysis of variance (ANOVA) or modeling a polynomial regression framework [22], [26], [27], [28]. For the sensitivity evaluation, the team used R² as a heuristic tool to rank inputs with respect to relative importance. In analysis, R² was calculated and compared for two-way interactions as well as main effects. The (strength three or higher) orthogonal-array-based LHS experiment design supports identification of main effects with reduced potential bias from two-way interactions. In the end, sensitivity based on R² analysis was a tool to focus attention on effects (main and two-way interaction) that arise as having relatively larger sensitivity metric. A common assumption for the use of R² as a sensitivity metric can be considered, that includes a sparsity and hierarchy of effects. Interaction effects may not be then, be considered important, if at least one of the main effects was not and it is assumed that high order polynomial terms are less likely. In computer experiments using an LHC experimental design, a large R² for an interaction effect without either main effect being important would require additional analyses. In the analyses, here this situation did not occur.

Mitigation responses for testing, quarantine and contact tracing were based on potential interventions for pandemic COVID-19 and the New Mexico Department of Health response during the first six months of the pandemic. These included two scenarios for the fraction of asymptomatic infected people of 10% and 30%, with no vaccine or antiviral mitigation measures.

3.2. Contact tracing and Social Distancing

Contact tracing is identifying and diagnosing persons who may have encountered an infected person. Public health workers are given the names of people that test positive for COVID-19, interview them for their contacts, and tell them to isolate or quarantine themselves and their contacts for two weeks which is the general guidance for COVID-19 so they can’t infect others. The fraction of actual contacts identified and traced varied in the study, ranging from 0.025 to 0.75. These lower values are appropriate because the disease is assumed to be contagious prior to the appearance of symptoms. The upper limit for contact tracing is based on average rates completed by the New Mexico Department of Health and then based around that average. The number of contacts per afflicted case varied between 5 and 40 people.

There are many ways to achieve social distancing, including measures to limit person-to-person interactions such as canceling events involving large gatherings and closing buildings or schools. These restrictions are sometimes called “focused measures to increase social distance” and decrease the rate of contact between individuals, thereby slowing the spread of the disease. Closing office buildings, stores, schools, and public transportation systems may be feasible community containment measures that could be employed during a pandemic. Because MEDIAN does not have the resolution to closely model specific social distancing measures, MEDIAN approximated social distancing by varying the self-quarantine behavior in the models. People self-quarantine by voluntarily limiting their contacts with others, thus achieving social distancing. Self-quarantined individuals may remain home for a variety of reasons, including school closures, child or afflicted persons care, fear, telecommuting, or extended leave policy, but the reason for their self-quarantine is not explicitly represented in MEDIAN.

The MEDIAN model for social distancing begins by estimating what is called the nominal rate of self-quarantine, which is the rate if this quarantine behavior were unaffected by competing model behaviors such as getting sick or being contact traced. This nominal rate is based on a multiplier of the rate that people are entering the prodromal stage. This multiplier can be varied by demographic group and is delayed from the prodromal rate by a user-defined time reaction delay. Thus, the self-quarantine behavior is linked to the observed progression of the disease; that is, as more people get sick the tendency for self-quarantine increases. Time reaction delay allows strengthening or weakening of coupling between the disease progression and social distancing.

This nominal rate of self-quarantine won’t be the actual rate because the model must account for the fact that people would be getting sick and not self-quarantining. MEDIAN also wants to allow for some user control to cap the self-quarantine behavior based on data or judgment. Therefore, the model calculates an “otherwise occupied rate” that accounts for vaccinations, contact tracing (with quarantine), and people entering prodromal. Only the population not otherwise occupied is available to be self-quarantined. Thus, the model estimates the actual self-quarantine rate as the nominal self-quarantine rate (based on prodromal rate) times a power law damping factor that accounts for the fraction of the population available for self-quarantine and the user-defined maximum fraction self-quarantined. MEDIAN incorporated this maximum relative tendency of the different demographic groups to self-isolate during a crisis to represent demographic differences in quarantine behavior. For example, infants and the elderly will be much more likely to self-isolate than working-age people who need to continue work-related tasks. In addition, school-age children may stay home at a higher rate due to school closures. So, as the nominal rate approaches either the fraction available for self-quarantine or the desired maximum self-quarantine rate, it is damped down smoothly so that it never exceeds these values.

The infectious disease model applies this self-quarantine rate to the unexposed population. A user-defined multiplier determines the rate people leave self-quarantine on the characteristic time of the disease (the time from infection to recovery or death). The result is that early in the disease progression, the self-quarantine rate looks like a straight multiplier on the sick rate; however, as things progress, it becomes altered below this nominal rate. In many cases, the self-quarantine rate gets damped down much lower than this nominal rate as the population gets depleted and the maximum behavior is reached.

The reaction delay is an important parameter that regulates how closely tied the population’s self-quarantine behavior is to the progression of the disease. The smaller the delay, the closer it is tied to disease progression and the more oscillations it creates in the self-quarantine and disease progression behavior. People lower their self-quarantine behavior as soon as the disease starts to let up, allowing for the disease to grow again, and so on. The longer the delay, the more these behaviors are decoupled and the oscillations are damped out.

The model calculates a number of metrics that provide useful representations of the overall social distancing behavior in a scenario, including the cumulative number of persons self-quarantined, the cumulative number of person-days spent in self-quarantine, a population-weighted overall fraction self-quarantined (taking into account the different behaviors of the demographic groups), the peak self-quarantine fraction, and the time during the scenario when the peak self-quarantine behavior is achieved.

3.3. Variable ranges

For this study, MEDIAN identified nine input variables as likely in COVID-19 entail variables on the estimated consequences for testing, diagnostics, contact tracing and quarantine. The team reviewed these selected variables and associated reasonable ranges with each input (Table 2) based on the published and archived (MEDRx) literature and other sources for the COVID-19 pandemic and data specific for the Albuquerque Metropolitan Statistical Area (MSA). Each input varied within the specified ranges for every simulation run. Normal distributions were assumed for the input variables for a closer resemblance to the true distributions prior to the data from around the world being published. Table 3 lists the output variables of interest. Input variables that are together in a box were varied together (that is, with 100% correlation). The team describes the significance of some of the inputs in a subsequent section of this report.

Table 3.

Output variables of interest.

Output Response Variable	Description
Total cumulative deaths	Cumulative deaths caused by event
Maximum outbreak duration	The maximum over all regions of the outbreak duration; based on a threshold of 25 people remaining in the exposed stage that determines when the outbreak is considered over
Overall total cases	Number of pandemic cases, irrespective of treatment
Total attack rate	The total attack rate (ratio of cumulative cases to population) in%age terms
Total cumulative deaths	Total fatalities
Total cumulative symptomatic	Total symptomatic cases
Total number hospitalized	Hospitalizations
Cumulative cases demographically	Cases by age groups
Cumulative deaths demographically	Deaths by age groups

Generating reliable estimates of the reproductive number (R ₀) for COVID-19 is difficult to estimate because R ₀ is a dynamic number based on the behavior of people in the community. An example of the former is the profound emerging diversity of COVID-19 impacts of different people and the consequent effect of population immunity on transmission. Population age structure, contacts, and density are factors that need to be incorporated. The doubling time for a pandemic curve is a function of the reproductive number. The magnitude of R ₀ also determines the intensity of control measures needed to bring the pandemic to a halt.

3.4. Asymptomatic and Pre-Symptomatic Infection

To understand the sources of new infections, knowing the age of the population that is asymptomatic and pre-symptomatic and how many of these individuals contribute to new infections is critical. The evidence supporting the transmission of SARS-CoV-2 prior to symptoms or asymptomatically includes data from multiple sources, and estimates have been wide ranging. Several studies suggest that transmission can occur in people that are asymptomatic (i.e. no symptoms) [29], [30], [31], and those that are pre-symptomatic (i.e. are asymptomatic at testing, but later develop symptoms [32], [33]. Transmission from asymptomatic and pre-symptomatic individuals may contribute to many new cases.

Asymptomatic cases may be more common in middle-aged people [34], [35]. Studies have found that asymptomatic individuals may be just as infectious as those that are symptomatic based on viral shedding [36], [37]. Likewise, Yin et al. [38] found no difference in transmission rates between asymptomatic and symptomatic patients. Asymptomatic individuals have been estimated to be infectious for a median of 9.5 days [35]. More recently, the duration of viral shedding in asymptomatic patients was shown to be 19 days (median interquartile range: 15–25 days) and this viral shedding period was significantly longer than symptomatic individuals [39].

Given that asymptomatic individuals can transmit the virus, estimating the number of asymptomatic individuals in the population is critical. Studies and surveys show wide-ranging estimates of asymptomatic cases, with estimates ranging from 43% to 95% of the population [40]. To try and estimate the fraction of asymptomatic cases, using capturerecapture methods, Böhning et al. [41] estimated that ratio of the total cases to the observed cases is around 2.3. Researchers in Italy found that approximately 50% of people positive for the virus were asymptomatic at the time of testing [42]. However, in a metanalysis of fraction of asymptomatic people, 79 studies in a range of different settings, 20% (95% confidence interval) 17%–25%, of people with SARS-CoV-2 infection remained asymptomatic during follow-up [43]. Children have also been shown to be asymptomatic with 21 children being asymptomatic at the time of sampling out of 100 tested [44]. On the other hand, other studies have suggested that as much as 50–75% of cases may be asymptomatic [42].

Initially, it was estimated that 12% of new cases are caused by pre-symptomatic transmission [45]. However, additional studies suggest that between 23% and 44% of cases may be from pre-symptomatic transmission [46], [47]. In a meta-analysis, Casey et al. [48] report that the proportion of pre-symptomatic transmission ranged from 42.8% to 80.6% using data from 13 individual estimates. The average estimate of these studies was 56.4%. Pre-symptomatic individuals may be infectious up to 3 days prior to showing symptoms [48]. Similarly, Yuki et al. [49] found that 56% of patients were asymptomatic or pre-symptomatic at the time of transmission events.

While the spread of SARS-CoV-2 by infected but asymptomatic and pre-symptomatic individuals is known, knowledge gaps for SARS-CoV-2 regarding asymptomatic and pre-symptomatic cases include the following:

• 1.Narrowing down the number of asymptomatic individuals.
• 2.More accurately determining the percentage of new infections caused by asymptomatic individuals
• 3.Determining how many individuals that are asymptomatic at testing eventually develop symptoms and those that never develop symptoms
• 4.Finding the proportion of undetected positive cases in populations

3.5. Diagnostics and Testing

We focused on three areas of uncertainty for testing and diagnostics for SARS-2 and COVID-19 infections. First is the error rate (particularly the false negative rate) of existing COVID-19 diagnostic tests. Second is the number of tests administered per capita of population, usually reported usually as numbers of tests per million people. Lastly, the number of hours that it takes to receive back test results which can vary from within 24 h to over a week.

Several factors make this task a difficult one: (1) There remains a lack of information on test reliability, and just as important is the ubiquity of conflicting information concerning reliability (due in part to differences in testing protocols, the time the test was administered relative to the onset of infection, as well as innate properties of the tests themselves); (2) Terminological and conceptual issues can be confusing; and (3) There are a variety of different classes of tests, with a multiplicity of tests by different manufacturers for each type. Moreover, the information concerning testing accuracy changes on a near-daily basis. Finally, there are differences of opinion concerning the implications of test reliability on public health policy. Performance estimates, even for a specific diagnostic test, can vary widely. There is a consistent pattern for manufacturers’ estimates of performance to be superior to estimates from independent evaluators. There need be no intentional (or even unintentional) bias within either set of numbers: it is likely (in some cases certain) that manufacturers use near-ideal sampling and test conditions, whereas outside evaluators generally use conditions more representative of the “real-world.”

Kucirka et al. [50] describes the false-negative rate (FNR) for RTPCR-based assays as a function of day after infection. The authors looked at nasopharyngeal, oropharyngeal and unspecified upper respiratory tract assays separately, but their results do not vary much between these types. The FNR is 100% for the first day and drops to 67% by day 4. The minimum FNR is about 20% and occurs on day eight and then rises back to 66% by day 21. Most of the literature states that the false negative rate is very important for COVID-19 tests, because even a small false negative rate means that many infected people will be missed, and therefore not be identified and contact traced, researchers have been working to improve diagnostic methodologies [51], [52]. In an unpublished analysis, it was shown that even false negative error rates of 20–40% makes a difference by putting infectious people into quarantine [53].

3.6. Isolation and quarantine

Isolation refers to separating persons who have a specific infectious illness from those who are healthy and restricting their movement to stop the spread of that illness. Quarantine refers to separating and restricting movement of persons who, while not yet ill, have been exposed to an infectious agent and therefore, may become infectious. Both isolation and quarantine are public health strategies that have proven effective in stopping the spread of infectious diseases. Quarantine of a person exposed to pandemic COVID-19 would last a total of 14 days to cover for the incubation + prodromal period. For annual COVID-19, the incubation period is 2–5 days and the prodromal period after that is when the person could be infectious and it could be from 4 to 14 days post exposure [54], [55]. Without varying this parameter, we used a set value of five days for the period prior to symptoms [55]. We separated out incubation and the prodromal period in the GID model to separate out the potentially infectious period of the infection prior to showing symptoms. The simulation scenarios for pandemic COVID-19 used a general quarantine factor that varied by age class and by public health responders that correspond to the four types of social distancing suggested by previous pandemic plans and researchers [56], [57], [58]. These included, but were not limited to:

• •Voluntary isolation of the sick at home or in a hospital
• •Voluntary home quarantine of potentially exposed family members of the sick
• •Child social distancing, including dismissing students from schools, closing childcare programs, and reducing out-of-school social contacts and community mixing
• •Adult social distancing, including canceling large public gatherings and altering work environments and schedules

The fraction of people who self-quarantine is dependent on age group, correlated to the rate that people become ill, and restricted to those who are not already affected by the outbreak (such as the sick or vaccinated). Individuals may self-quarantine either as a result of their own preferences (for example, fear reaction to media coverage) or in response to guidance from government officials. There is a delay in the model between changes in the progress of the outbreak and changes in self-quarantining behavior. This delay decouples the disease progression and self-quarantine behavior to some degree, with delays of a week or more producing reasonable results.

Due to demographic differences in quarantine behavior, the study incorporated a maximum relative tendency of the different demographic groups to isolate themselves during a crisis. For example, infants and the elderly will be much more likely to self-isolate than working-age people who need to continue work-related tasks. In addition, school-age children may stay home at a higher rate due to school closures.

The self-quarantine sick-rate modifier is a multiplier of the rate that people are becoming ill, which is used as the initial estimate of the rate at which people self-quarantine. The team assumed that the people that self-quarantine will be a multiple of the infected people. They then modified the rate to reflect limitations imposed by the availability of people to self-quarantine and the maximum fraction of the population subset that engages in the self-quarantine activity (self-quarantine tendency is 0.95 for infants and elderly, 0.9 for school-age children, 0.4 for adults, and 0.25 for responders). A range of 2 to 10 was used for the sick-rate modifier, loosely based on survey results from the SARS outbreak in Hong Kong. The team believes that the resulting range of self-quarantine behavior in the simulations is reasonable.

3.7. Base fraction of afflicted seeking healthcare

This parameter is the fraction of people who would be symptomatic with the pandemic COVID-19 and who would seek healthcare of some kind (at a physician’s office, clinic, or ER or by calling for EMS) if the case fatality rate were 0.02 (the 1918 pandemic case mortality rate). MEDIAN used a case fatality rate of 0.02 for the point-case analyses earlier in this study and assumed the fraction of afflicted seeking healthcare to be 0.6, with the other 40% of people with pandemic COVID-19 self-treated. The team based this choice for the earlier part of this study on the planning assumptions in the U.S. Department of Health and Human Services (HHS) Pandemic Plan, which were that 50% of ill people would seek outpatient medical care and 11% would be hospitalized in a severe (1918-like) pandemic [58]. This study took the fraction seeking medical care to be 60% rather than 50% because the HHS plan is unclear about whether the fraction hospitalized is a subset of those patients seeking outpatient medical care or a separate fraction.

In setting an appropriate range of values for the uncertainty analysis, MEDIAN considered it unlikely that 100% of COVID-19 victims, compared to influenza, would seek medical care, so they set the upper limit to 50%. The team set the lower limit to 10% because, in preliminary simulations, unrealistic results would sometimes occur if the fraction was lower. For example, if over 60% of COVID-19 cases were mild enough that the people would simply self-treat, there might not be enough severe cases to account for the assumed death rate. The model is currently structured so that anyone sick enough to be at risk of dying is assumed to seek healthcare. In reality, some people might die without having sought care, but the current model neglects that possibility.

MEDIAN incorporated a number of adjustments to this fraction in the model. Most notably, for case fatality rates higher than 0.02, MEDIAN assumed the fraction of afflicted seeking healthcare to be higher than the base fraction that is sampled. Thus, at the upper end of the case fatality rates considered (that is, near 0.15), the model assumes that almost all COVID-19 victims would seek care even if the sampled value of base fraction of afflicted seeking healthcare is well below 1.0. In addition, the model allows for the possibility that some people will seek healthcare and then cancel their request for care if the healthcare system is heavily overloaded and the waiting time is so long that their health starts to improve.

3.8. Maximum mortality enhancement multiplier

This parameter considers a decline in the quality of treatment if the healthcare system is overloaded. If waiting times for emergency care or to gain admission to hospital are too long, the mortality rate in the model will increase, up to the maximum mortality enhancement multiplier. In the earlier analyses, this effect was not included, so the mortality enhancement multiplier was left at 1.0. For the uncertainty analyses, inclusion of this effect was desired, but the amount of increase in mortality that could occur is not really known. There have been a number of studies (usually relating to particular illnesses) that have found increases in mortality when care is delayed, but how the increase in mortality might average out over all patients in an emergency room or a hospital is not known. Thus, the range of 1 to 2 for the maximum effect is somewhat speculative, although it does have some support in the literature.

3.9. Pre-symptomatic and Asymptomatic Spread

The evidence supporting the transmission of COVID-19 prior to symptoms includes data from many sources. First, experimental and observational studies of viral excretion usually find that infected people start excreting COVID-19 viruses at low levels from their respiratory tracts a short time before they develop symptoms [39], [46], [59]. Second, serological studies of levels of population immunity to COVID-19 often find people who show antibodies from prior infection but have no recollection of symptoms [60]. Modeling analyses have suggested that many more people have been infected during the COVID-19 pandemic and cases have been greatly underestimated [61]. However, as there are few field reports of infections from asymptomatic or pre-symptomatic persons, the quantification of asymptomatic and pre-symptomatic transmission remains unclear [62]. The first clinical analysis of asymptomatic SARS-CoV-2 infection was for the Diamond Princess cruise ship, where an estimated 17.9% of cases on board were asymptomatic [63]. Reports of asymptomatic or pre-symptomatic patients excreting high levels of virus are rare and it is possible that any infections resulting from such transmissions are mild or asymptomatic, although they could be important in maintaining chains of transmission [64].

Because the spread of viruses by infected, but asymptomatic people, is one of the largest biological uncertainties, it has long been described as the top research priority for understanding epidemics [65]. Knowledge gaps for COVID-19 continue to include the following questions: (1) What is the true infectiousness length of the asymptomatic incubation period? (2) What are the quantifiable contributions to COVID-19 transmission from pre-symptomatic and asymptomatic spread?

3.10. Reduction in early symptom contagion due to limited quarantine

This parameter captures the effect of the assumption that 50% of remaining cases are isolated per day after symptoms become apparent; for example, 15% of cases slip through due to delayed recognition. This study assumed this fraction of persons isolating themselves to be 0.82 based on the idea of isolating 50% of the remaining symptomatic infections each day for 3 days. The assumption would work as follows: If the duration of the early (contagious) stage is 5 days, 20% of the possible transmission (without any isolation) would occur each day. If 50% of those people were isolated at the beginning of the first day (with the initial onset of symptoms), only 10% of the possible transmissions would occur. If 50% of the remaining people were isolated at the beginning of the second day, only 5% of the possible transmissions would occur that day. Again, isolating 50% of the remaining symptomatic infections at the beginning of the third day would result in 2.5% of the possible transmissions occurring. Assuming everyone else is isolated by the beginning of the fourth day, the total transmission would be 0.1 + 0.05 + 0.025 = 0.175 of the possible transmissions and the reduction multiplier would be 0.825. The model set this variable at 0.82 for all runs. This value may be optimistic for pandemic COVID-19.

3.11. Effective Reproductive Number

The effective reproductive number, R, for disease transmission is defined as the average number of secondary infectious cases produced in a population where a fraction X is susceptible over the lifetime of one infectious individual [66], [67]. The effective reproductive number, R, is related to the basic reproductive number, R₀, by the equation

$$R=R_{0}X$$ (1)

The basic and effective reproductive numbers are good indicators of the severity of a pandemic and the effectiveness of control [68]. In general, estimation of these parameters from actual disease outbreak data is limited because the process of infection is not observed, data are often incomplete, and the rate of infection in an epidemic is non-linear [69]. An effective reproductive number is calculated to integrate the impacts of asymptomatic transmission and effects of individuals who isolate themselves early in the disease progression due to being ill. Self-isolation of infected and symptomatic persons greatly affects the transmission of the disease to new individuals. In terms of the parameters used in the MEDIAN infectious disease model, the effective reproductive number is given by the following formula:

$$R=R_0\left\{f_t+(1-f_t)(1-f_i)+f_a{C}_a\right\}$$ (2)

Where:

R₀ is the basic reproductive number,

f_t is the fraction of transmission prior to clear symptoms,

f_a is the additional fraction asymptomatic,

C_a is the relative contagion of asymptomatic, and

f_i is the reduction in early symptom contagion due to limited quarantine.

4. Results

The ranges are quite large for each of the two scenarios for fraction asymptomatic, ranging from complete control of the pandemic to much higher than the actual number of cases documented in the Albuquerque metropolitan area from March to October 2020. The average is sometimes significantly higher than the median. The highest values in these figures represent extremely severe consequences for the Albuquerque metropolitan area. This shows the great impact that the policies and social compliance for mitigations has had on the pandemic in the region. The wide ranges of the consequence of the pandemic is, of course, from the large amount of uncertainty in the sampled input parameters. The previous discussion based on the average values would still be generally valid if maximum values were used instead, but the differences among the maxima are not as strong as the differences among the averages.

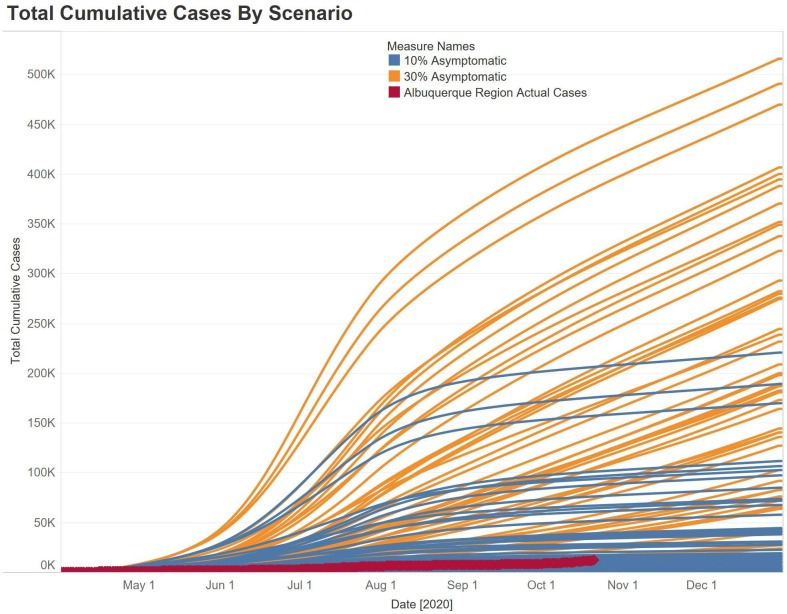
For the small set of nine inputs that we varied for testing, contact tracing, and quarantine, we found significant variation in the outcomes of the epidemic within each experiment spread up to two orders of magnitude (Fig. 4 ). The difference between 10% and 30% asymptomatic infections was 2.5 orders of magnitude for the highest number of cases for each scenario (Fig. 4). For the actual cases in the Albuquerque area in New Mexico (red line, Fig. 4), we can see the impact of the community doing social distancing, testing and contact tracing, and all of the other myriad of mitigations such as wearing masks to lower transmission. We can also see that 55% of simulation runs of the 10% asymptomatic assumption are better than the pandemic outcome in New Mexico, while only 5% of the runs have fewer overall cases for 30% asymptomatic. The same pattern of variability was seen for total deaths and hospitalizations.

Fig. 4.

Epidemic curves for 54 runs per the two scenarios (Orange = 30% fraction asymptomatic, Blue = 10% asymptomatic), red epidemic curve is four county area of Albuquerque, New Mexico. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

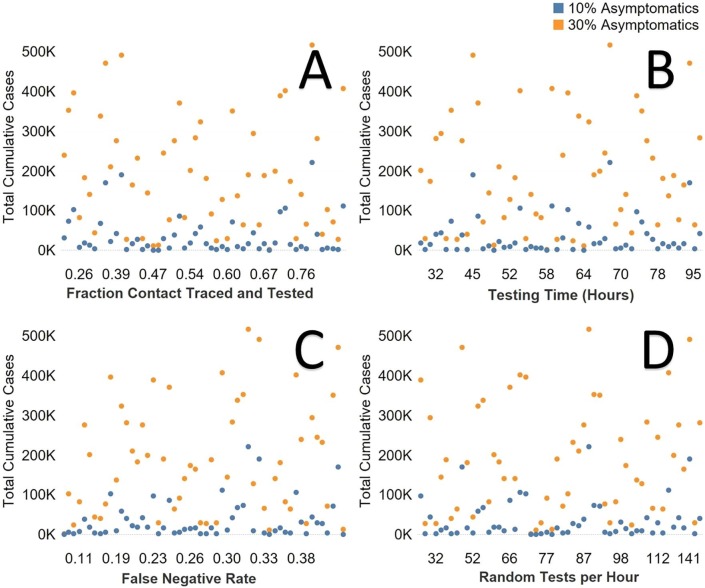
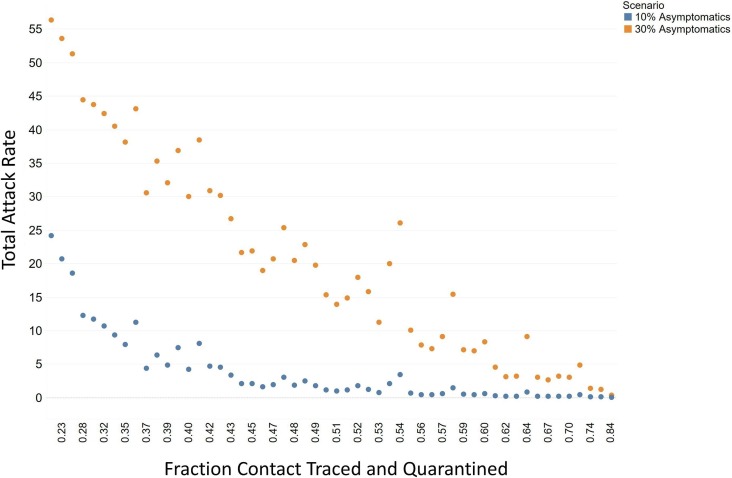
There was not as much of an impact on the local epidemic for the fraction contact traced and tested without the resulting quarantine (Fig. 5 A). The value of the contact tracing and testing comes from the identified infections socially distancing themselves. When including the varied social distancing inputs, testing time of hours to hear back test results, did not impact the outcome of the local epidemic (Fig. 5B). This was also true for the false negative rate and total test ran per hour for the broader “random” disease surveillance (Fig. 5C and 5D). However, the correlation of contact tracing and quarantine on the overall attack rate of the epidemic was strong for all age groups (average R² = 0.83). The overall attack rate can be decreased by over 82% when contact tracing and quarantine is implemented in this case and the relationship is almost linear (Fig. 6 ).

Fig. 5.

A. Fraction of contacted, traced and tested and total cases for both asymptomatic scenarios. B. Testing time from test to reporting (hours). C. False negative rate for diagnostics. D. Diagnostic tests per hour for random testing. (Orange = 30% fraction asymptomatic, Blue = 10% asymptomatic). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Fraction contacted, traced, and quarantined and attack rate for the COVID-19.

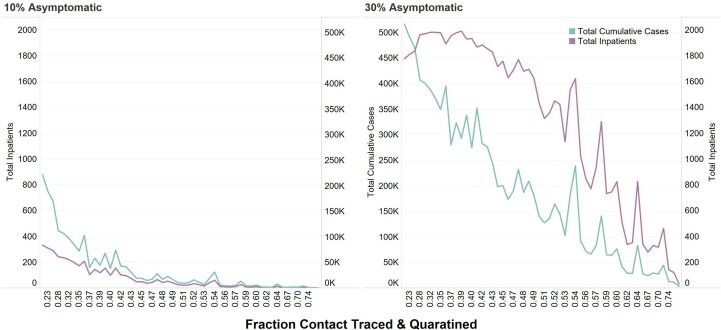
The fraction of people that are asymptomatic greatly impacts the outcome of the epidemic and the ability to curtail the number of cases (Fig. 7 ). The greater the number of fraction asymptomatic people impacted the hospitalizations. With more asymptomatic people and more cases, hospitalizations remain high until around 50% of people are contact traced and quarantined.

Fig. 7.

Fraction contacted, traced and quarantined and total inpatient hospitalizations and total cases for 10% and 30% fraction asymptomatic.

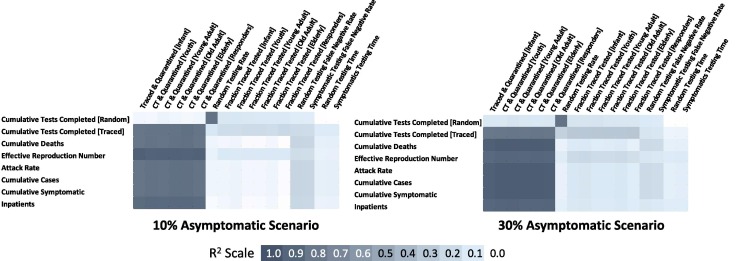
The most sensitive variable inputs related to the outcomes of the COVID-19 pandemic was (e.g. cases, hospitalizations, deaths, effective reproductive number) the Fraction Contact Traced and Quarantined for all age groups (R² 0.83–0.87 for 10% Asymptomatic; R² 0.88–0.94 for 30% Asymptomatic) (Fig. 8 ). The sensitivity test also revealed that mitigations, in general, impacted the pandemic more greatly with increasing asymptomatic infections. Overall, the diagnostic testing rate did not have significant impact on the number of cases. However, the false negative test rate was slightly significant for the broader, more random testing strategy (R² 0.22–0.29).

Fig. 8.

Correlation coefficients for all input varied and outputs for 10% and 30% fraction asymptomatic.

5. Discussion

Results show that the overall uncertainty in the parameters of the infectious disease model can be remarkably large. In a previous study we showed that variability can be great for multiple scenario runs that cover the range of biological, sociological, and mitigation options for affecting the cumulative number of illnesses [3]. In Fair et al. [3], we found that the top variables related to overall epidemic attack rate and number of cases included (1) Fraction transmission prior to clear symptoms (infectious asymptomatic), (2) Reproductive number, and (3) Disease stage duration (all stages).

A major limitation of models for pandemic COVID-19 is the uncertainty inherent in many of their assumptions. This uncertainty and the differences in the assumptions used in each model make model comparison difficult. Overall, the infectiousness of the COVID-19 estimated by R ₀ was the most investigated uncertain parameter (ranging from 0.5 to 21). Most models were in the range for R ₀ of 2 to 3.5. In comparison, this study investigated R₀ up to 14.4 to examine where impacts begin to degrade the critical infrastructure and public health. However, for runs with R₀ between 2 and 2.5, the average attack rate is 30.8% for our baseline scenario, which compares favorably with other published model attack rates for baseline scenarios., Three important biological parameters can be identified from the results of all previous pandemic COVID-19 models: the basic reproductive number (R ₀) that corresponds to the number of secondary infections generated by primary infectious in a susceptible population, the disease generation or stage time that is the time interval between one person and the people they infect, and the proportion of transmission occurring prior to the onset of symptoms and the related fraction of persons that are asymptomatic.

A primary social response to a contagious disease is to voluntarily modify one’s behavior, by any number of means, to reduce the rate of contact with other potentially infectious individuals. While it is reasonable to assume that some degree of social distancing occurs in a pandemic, in this study social distancing is modeled as “on” or “off.” When social distancing is on, the degree of social withdrawal is assumed to be proportional to the rate of infection. The rate of social distancing is mildly decoupled from the rate of infection by introducing a delay to account for individual perception of the risk of infection and any preparation needed for entering a social distancing behavior.

The effect of social distancing is two-fold. First, it tends to reduce morbidity and mortality. Second, it tends to increase the fraction of workers unavailable and, hence, increases the fraction of lost GDP [3]. These results rely on assumptions about gross social distancing behavior, as it is very difficult to get reliable data upon which to base the model.

In summary, the R² for a model based on input parameter x1 has a larger R² for a model based on input parameter x2, then x1 is judged more influential than x2 for that response. Also, the evaluation of correlation coefficients was based the heuristic significance value for R² from goodness of fit evaluation in the regression modeling for random data and by inclusion of a phony input column that is included in the experiment design but is not actually a simulation input. If R² for a particular response is below a threshold determined by one of these strategies, then that parameter is judged likely less important. The analysis computed the R² values for the five varied inputs for each of several output metrics. The results served as a filter to eliminate less important variables for the propagation of the pandemic.

Using the R² criterion in the final sensitivity analysis for each of the outputs listed below, the highest-ranking variables that affect that pandemic scenario outputs are given. In addition to looking at R² within each scenario, the model can identify other inferences on the relative importance of each parameter by using the aggregate data for all scenarios. Overall, most epidemiological models agree when using similar infectiousness parameters. However, different mitigation results occur when the biological parameters differ significantly. This is particularly true for COVID-19, where different ages, social classes, other phenotypic differences have been documented, such as increased susceptibility with blood type or nutrition [70], [71]. Other differences in the transmission and susceptibility for COVID-19 can be modeled using a systems dynamics and computer experimental design, as described here.

For COVID-19 or other similar epidemics, the false negative is the worst-case situation. A person with the pathogen in his/her lungs will go untreated and be sent home. As Sarkar [51] writes, “if this (false negative) happens for someone in the high-risk cohort, then a tragic (and possibly avoidable) loss of life can ensue with a high enough possibility”. However, the bigger cost is that the person will not be contact traced and quarantined. If the person does not have symptoms, they may continue to socialize because they do not believe they are positive and will not take the precautions necessary to reduce transmission.

Ultimately, the successful control and containment of a pandemic will depend on using a variety of mitigation measures that include both pharmaceutical and nonpharmaceutical interventions (NPIs). In 2017, the CDC released updated guidance for the use of NPIs during an influenza pandemic [56]. These guidelines document the objectives of NPIs during a pandemic to include: (1) Delaying the exponential growth in illnesses and shifting the pandemic curve to the right to ‘buy time’ for production and distribution of a well-matched pandemic strain vaccine. (2) Decreasing the pandemic peak. (3) Reducing the total number of incident cases and reducing community morbidity and mortality

NPIs have been shown to be effective in controlling a pandemic in our previous study on pandemic influenza [3] and other simulation studies [72], [73], as well as past pandemics [74]. However, it has also been pointed out that the worst outcome may arise when control is attempted through social distancing, but not cautiously enough to cause the epidemic to be suppressed [75]. Social distancing can also be the costliest in terms of lost wages and workers available.

6. Conclusions

The impact of any pandemic is highly sensitive to how infectious the virus is for infected people not showing symptoms. As with the COVID-19 pandemic, the importance and role of asymptomatic transmission is documented, but it remains unknown the actual fraction of people that are asymptomatic spreaders of the SARS-2 COV [76]. The MEDIAN model predicts that transmission through asymptomatic infections of the COVID-19 virus is critical for the propagation of the disease, the number infected, and the resulting impacts. Household-based interventions can significantly reduce pandemic spread. While MEDIAN did not model household transmission, MEDIAN results show social distancing interventions that reduce the number of daily interactions can reduce the severity of the pandemic (although at significant economic cost). Individual and community-based behavioral modifications, such as school closures, fear-based home isolation, and social distancing, have a significant effect on slowing COVID-19 spread and reducing morbidity and mortality. MEDIAN modeled a uniform self-quarantine (social distancing) strategy. Because MEDIAN did not model schools, it could not represent the infection waves caused by reopening.

National pandemic preparedness plans currently focus on reducing the impacts associated with a constant attack rate in addition to reducing transmission. MEDIAN model results build on previous modeling studies of pandemic COVID-19 that have focused on the possibility of containment through mitigation strategies. Understanding and predicting the effectiveness of different mitigation strategies in controlling a pandemic will depend on the range of virulence, transmissibility, age-effects, public response, and response of the public health infrastructure. Mitigation strategies and combinations of responses may vary with the reality of the pandemic scenario presented, while maintaining a cost-effective and appropriate response that does not affect critical infrastructure and maintains continuity of our nation’s business operations and economy.

The most important variables related to the total number of afflicted people in our pandemic system dynamics simulation are the fractions of the transmission that occur prior to symptoms (infectious presymptomatic), fraction asymptomatic, and the fraction that quarantine. The most important aspect of COVID-19 transmission is the limited window of time before symptoms appear when a person is able to transmit the virus to other people. The ability to effectively find and contact people that may have been exposed to an infected person and then have them be quarantined greatly reduced the continued transmission of the COVID-19 virus and thus, reduced the total numbers of illnesses and deaths. Contact tracing alone reduced the impact of the pandemic significantly. The use of the NPI of social distancing reduced the pandemic outcomes for both of the asymptomatic scenarios.

When combining all mitigation strategies available, it was found that the overall pandemic impact can be dramatically reduced. The more infective overall, and asymptomatic and infective, the virus is, the more it will limit the effectiveness of any or even a combination of mitigation strategies. All scenarios within the simulation runs contained a significant amount of variation. However, even for a 30% fraction of asymptomatic using the combination strategy on high testing rate, contact tracing, and social distancing can reduce the pandemic significantly. Containing a pandemic that is highly infective is possible with a combination of NPI strategies. However, the simulations here have shown that although uncertainty and variability is large, coordinated efforts for response and can reduce the impacts felt by potentially millions of people. For the other NPI of wearing masks, we did not model the variation of mask wearing in this analysis. Overall, large variability was observed in the outcomes using possible biological (fraction asymptomatic and false negative diagnostic rate), sociological (quarantine), interventions (contact tracing), and policy uncertainty (number of tested per capital).

The impact of the current COVID-19 pandemic is highly sensitive to how infectious the virus will remain throughout the pandemic and how infectious the disease is prior to an infected person showing symptoms. The majority of the above variables deal with biological variability of the behavior of the SARS-2 Coronavirus, with the exception of the effectiveness of contact tracing and testing rate. With novel virus pandemics, until there is a vaccine or pharmaceutical measures that limit transmission and not just reduce mortality rates, NPI strategies for pandemic COVID-19 that identify infections and quarantine the infected people and all recent contacts will be the most effective. This was the case for early on in the COVID-19 pandemic and would be the case for future pandemics as well until vaccines are developed and disseminated to the population. The results show that all of the interventions considered provide reduction in the number of cases and deaths caused by the pandemic, but social distancing and contact tracing with quarantine give the best results in this analysis.

Here, we show that systems dynamics modeling of multiple sub-systems can be both a flexible and rapid approach for understanding the behavior of epidemics and pandemics. Coupled with computer simulation experimental designs of orthogonal Latin hypercube sampling, the uncertainty of the system can be better understood, and with the correlation analysis the sensitivity of mitigations can be quantified quickly. With the systems dynamics approach, thousands of simulations can be run and rapidly analyzed.

CRediT authorship contribution statement

JMF, RL, LD, DP, & ME: conceptualization, formal analysis, methodology, validation, and writing original draft. TC, DP, LD, and DP: conceptualization and formal analysis of Conductor Tool. WR, LD, & TC: software, formal analysis, methodology and visualization. JMF: funding acquisition, project administration, writing original draft and editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.