Predictive Global Models of Cruzain Inhibitors with Large Chemical Coverage

Abstract

Chagas disease affects 8–11 million people worldwide, most of them living in Latin America. Moreover, migratory phenomena have spread the infection beyond endemic areas. Efforts for the development of new pharmacological therapies are paramount as the pharmacological profile of the two marketed drugs currently available, nifurtimox and benznidazole, needs to be improved. Cruzain, a parasitic cysteine protease, is one of the most attractive biological targets due to its roles in parasite survival and immune evasion. In this work, we compiled and curated a database of diverse cruzain inhibitors previously reported in the literature. From this data set, quantitative structure–activity relationship (QSAR) models for the prediction of their pIC₅₀ values were generated using k-nearest neighbors and random forest algorithms. Local and global models were calculated and compared. The statistical parameters for internal and external validation indicate a significant predictability, with q_loo² values around 0.66 and 0.61 and external R² coefficients of 0.725 and 0.766. The applicability domain is quantitatively defined, according to QSAR good practices, using the leverage and similarity methods. The models described in this work are readily available in a Python script for the discovery of novel cruzain inhibitors.

1. Introduction

Chagas disease affects 8–11 million people in 21 Latin American countries; there is an estimation of 70–150 million people at risk of infection.^1,2 Migration phenomena have contributed to the spread of the parasite into nonendemic areas such as the United States, Europe, New Zealand, and Australia.¹ Chagas disease is a vector-borne parasitic infection caused by Trypanosoma cruzi and it is transmitted by the three main genera of triatomine bug, Triatoma, Rhodnius, and Panstrongylus. World Health Organization has recognized this infection as a neglected tropical disease (NTD) because of its persistence in developing countries, being a major economic and social problem in these regions, and one of the main causes of premature death for heart failure.²⁻⁴ It was previously reported that this disease causes an estimated loss of 752,000 working days in southern American countries,⁴ which implies an economic burden of about US$1.2 billion in productivity.⁴ Globally, this parasitic infection has an estimated annual cost of $627.46 million, and 10% of this affects nonendemic countries.⁴ Currently, there are only two approved drugs for the treatment of Chagas disease: nifurtimox (NFX) and benznidazole (BZ). Both NFX and BZ have similar efficacy during the acute phase of infection, with 88–100% of negative parasite detection after treatment with NFX and up to 80% for BZ.⁵ However, in the chronic phase, the rate of negative tests for the disease after treatment falls to 7–8%,⁵ and there are significant side effects, including anorexia, weight loss, paresthesia, nausea, and vomiting, among others.^3,5 Recent therapeutic research is focused on specific biological targets, including cysteine proteases, enzymes in trypanothione metabolism, enzymes in ergosterol biosynthesis, and the kinetoplastid proteasome.⁵

Cruzain is a cathepsin L-like cysteine protease present in all stages of the parasite life cycle. It plays significant roles in the trypanosomal growth, survival, and evasion from the host immune response. Plasma membrane-anchored cruzain degrades the Fc fraction of antibodies, overcoming the classic path of complement activation.^3,6 In the amastigotic intracellular stage, this cysteine protease degrades transcription factors, such as NFkB, and thus prevents the activation of macrophages.³ Cruzain generates the bloodstream pro-inflammatory peptide Lys-bradykinin, which activates host immune cells, promoting the parasite uptake and spread by phagocytosis.⁶ The use of cruzain inhibitors in animal models has shown to be effective in clearing the parasite burden, even in the chronic phase. The vinyl-sulfonic compound known as K777 was one the first proof-of-concept studies about the antitripanosomal activity of cruzain inhibitors in animal models.⁷⁻⁹ Parasite death induced by cruzain inhibitors is attributed to the accumulation of a peptide precursor in the Golgi complex. Therefore, this in vitro and in vivo evidence has validated cruzain as a potential biological target for Chagas disease.^3,6 A variety of chemotypes for cruzain inhibition have been explored through structure–activity relationship (SAR) analysis, high-throughput screening, and docking methods. The most potent molecules belong to the vinyl-sulfone derivatives, oxadiazoles, nitrile-containing peptidomimetics, and thiosemicarbazones, with a broad range of biological activities among chemical families.^2,10,11 These molecules should be further optimized by increasing their selectivity toward parasite vs human cathepsins, and they should be neutral at physiological pH to avoid concentration in lysosomes and off-target effects.²

Quantitative structure–activity relationship (QSAR) models mathematically correlate structural properties of molecules with their biological activity. There are two distinctive goals in the practice of QSAR modeling: the use of mathematical tools to describe the trends in the data, providing interpretations that could be useful in the understanding of an inherent mechanism, and the use of these methods to achieve predictions with high accuracy, irrespective of the interpretability of the generated models.^12,13 These mutually complementary approaches are often called “descriptive QSAR” and “predictive QSAR.”¹³ The advances in QSAR modeling led to its acceptance as a prediction tool of toxicity endpoints for the risk assessment of new chemical entities¹⁴ or as a preliminary step in drug development to identify compounds with potential toxic or mutagenic profiles.¹⁵ The Organization for Economic Cooperation and Development (OECD) established guidelines for the use of QSAR in regulatory settings, and these principles became gold standards in the general QSAR practice.¹⁴ The OECD principles for the validation of QSAR models for regulatory purposes are (1) a defined endpoint, (2) an unambiguous algorithm, (3) a defined domain of applicability, (4) appropriate measures of goodness of fit, robustness, and predictability, and (5) a mechanistic interpretation, if possible. For regulatory purposes, the prediction of a toxicity endpoint must have a high degree of reliability. Importantly, the external validation criteria must be strict regarding the numerical precision of the model since this is a crucial step in decision-making about risk assessment of new compounds.^12,16

In drug discovery, QSAR modeling is a valuable tool for the prioritization of possible hits for experimental validation and to explain the relationships between structural modification and biological activity from a mechanistic basis.¹⁷ Interestingly, QSAR models have often been used to guide the synthesis of new molecules;¹⁸ thus, the descriptive approach is predominant. More recent studies focus on the use of QSAR for virtual screening (VS), and this application has been successful in finding novel chemotypes against important drug targets in diseases such as malaria,^18,19 schistosomiasis,^18,20 tuberculosis,^18,21 cancer,^22,23 and inflammation, among others.²² Notably, despite the exponential growth in the development of deep learning (DL) algorithms and their applications in many areas such as image and voice recognition, most of the successful QSAR case studies still use classical machine learning algorithms like multiple linear regression, partial least squares, k-nearest neighbors, support vector machines, random forest, and even shallow neural networks. It is a matter of debate if, in the field of QSAR modeling, the advanced DL algorithms offer a better performance over the classical approaches. Several published reviews find that DL models do not have significant improvements over simpler models.^17,24,25 One of the main reasons for this behavior is that DL algorithms require high amounts of data,^24,25 which is feasible in many areas where these methods have been applied, but in drug research, the data is often “limited, expensive, and resource-intensive”.¹⁷ However, advanced DL algorithms still offer advantages for a variety of purposes like modeling multiple endpoints, for the generation of novel chemical features or in inverse QSAR, where structures can be generated from the model.¹⁷

QSAR modeling has also been used in the study and design of cruzain inhibitors. A summary of some recently published models is presented in Table 1. Most of these studies are built upon data sets with a single chemical family, producing local models and following the descriptive approach. CoMFA and CoMSIA analyses are widely used in these studies, mainly because the results are fully interpretable, since the interaction maps can easily show which fragments of the molecules are correlated with the biological activity. However, this method requires the 3D coordinates of the molecules and, thus, it is dependent on their conformation and alignment. The procedures required to generate conformations and alignments may not be suitable if the model is intended to be used in virtual screening. In turn, 2D QSAR only requires the 2D structure of the molecules. The generation of 2D descriptors is usually fast and easy; nonetheless, their interpretation is often difficult. The main purpose of this work is to generate QSAR predictive models of structurally diverse cruzain inhibitors. Models calculated by means of machine learning algorithms describe the behavior of biological activity in terms of the molecular descriptor space. From the trends identified, the effects of structural modifications on cruzain inhibition become predictable, making QSAR models a useful tool in the search and rational design of cruzain inhibitors.

Table 1. Summary of QSAR Models of Cruzain Inhibitors^a.

data set	algorithm	validation summary	reference
27 benzimidazoles	HQSAR (PLS)	q2 = 0.77, R2 = 0.65	(26)
	CoMFA	q2 = 0.71, R2 = 0.94
	CoMSIA	q2 = 0.75, R2 = 0.82
41 peptides	HQSAR (PLS)	q2 = 0.77, R2 = 0.88	(27)
55 thiosemicarbazones and semicarbazones	CoMFA	q2 = 0.78, R2 = 0.81	(28)
	CoMSIA	q2 = 0.73, R2 = 0.79
57 dipeptidyl nitriles	HQSAR (PLS)	q2 = 0.70, R2 = 0.62	(29)
61 semicarbazones	MLR	q2 = 0.801, R2 = 0.906	(30)
32 triazine nitriles	CoMFA	q2 = 0.736, R2 = 0.762	(31)
	CoMSIA	q2 = 0.627, R2 = 0.806
41 ketones	HQSAR (PLS)	q2 = 0.794, R2 = 0.954	(32)
55 thiosemicarbazones and semicarbazones	HQSAR (PLS)	q2 = 0.75, R2 = 0.95	(33)
	2D QSAR (PLS)	q2 = 0.72, R2 = 0.83
46 ketones	BRANN	q2 = 0.749	(34)

^aq², coefficient of determination for leave-one-out cross-validation; R², coefficient of determination of external set; PLS, partial least squares; MLR, multiple linear regression; BRANN, Bayesian regularized artificial neural networks.

2. Computational Methods

2.1. Data Compilation and Curation

Cruzain inhibitors were collected from the ChEMBL database, searching by the molecular target using the keyword cruzain. Molecules annotated with IC₅₀ values were retrieved as the initial data set. The uncurated database has a total of 840 inhibitors. From this set, 118 molecules with activity missing values and 211 that could not be determined (reported with a relation of “>”) were excluded. Since the modeling approach was 2D QSAR, the presence of molecules with chiral atoms was verified in the original sources. In most of the cases, the activity data reported for those compounds does not specify the activity for each enantiomer. The structures and biological activities were kept as stated in the original publications, and a single case where both enantiomers were reported with a significant difference in activity was excluded from the database. For the removal of duplicates, the original papers were consulted and the selection was based on the experimental protocol. A strong criterion for selection was the inclusion of detergent in the assay because colloidal aggregation is one of the main causes of false positives in exploratory and high-throughput screens.^2,35 Moreover, after reviewing the original publications, molecules reported in refs (36) and (37) were excluded because they are classified as aggregators. The main focus of these studies is the search of aggregation, autofluorescence, and reactivity artifacts in screening assays using cruzain as the biological target. After this filter, the final data set for modeling consisted of 344 inhibitors. The IC₅₀ values were converted to pIC₅₀, and this was used as a dependent variable. Lastly, the structures and activities were compared to those in the original sources³⁶⁻⁷² and discrepancies were fixed. The molecular structures, originally retrieved as SMILES strings, were converted to their 2D representation, and tautomers and protonation states at pH 7.0 were assigned using ChemAxon. The curated database is available as cruzain_dataset.xlsx in the Supporting Information.

The molecules in the final database were classified based on chemical families. The set was divided by the assigned molecular types, and those with at least 20 compounds were used to build local models. The structural fragments of the molecules in the local sets are presented in Figure 1. The total data set was also used to build global models, and their performances were compared.

Figure 1.

Functional groups used for the classification of the molecules into chemical families for the development of local models. The amide group includes peptidic and nonpeptidic inhibitors with a central amide group.

2.2. QSAR Modeling

2.2.1. Descriptor Calculation and Feature Selection

Molecules in the database were loaded and standardized using the RDKit package in Python.⁷³ 2D molecular descriptors were calculated in the Mordred package for Python.⁷⁴ This library contains 1613 1D and 2D descriptors, including atomic counters, topological indices, adjacency matrix-derived values, autocorrelation weighted by atomic properties, subdivided van der Waals surface areas, and physicochemical properties including logP and polarizabilities.⁷⁴ For the local models, the data was used separately by family type. Each of these sets was randomly split into training, validation, and test sets. Training and validation sets were used together in feature selection and hyperparameter optimization of the machine learning algorithms, whereas test sets were reserved for the final evaluation. Table 2 shows the number of molecules in the partition for each group.

Table 2. Number of Molecules in Each Family Type for the Generation of Local Models.

group	training set	validation set	test set
amides	68	17	22
N-acylhydrazones	16	5	6
thiazolylhydrazones	20	6	7
thiosemicarbazones	49	13	16
triazine nitriles	22	6	7

The initial set with all the molecules was used for the generation of global models. The training sets for the local models were merged to build the global training set, and the same was done for the test sets. Molecules not used in the local models (those with less than 20 molecules per family) were included in the generation of global models. The final partition contains a training set with 223 molecules, a validation set of 53 molecules, and an external test set of 70 inhibitors. Descriptors were scaled to the [0,1] range using eq 1, where X_i^′ is the scaled descriptor, X_i,min is the minimum value, and X_i,max is the maximum value. Molecular descriptors in the test and validation groups were scaled according to the training set.

1

Feature selection was first performed by discarding those descriptors with zero variance and with less than three different values (semiconstant variables). After excluding highly correlated descriptors, i.e., those with a correlation coefficient higher than 0.9, the final set contained 558 variables. The selection of the best subset of features was made using a combination of genetic algorithm (GA) and three different machine learning algorithms: multiple linear regression (MLR), k-nearest neighbors (KNN), and random forest (RF). A simple genetic algorithm was built using DEAP in Python,⁷⁵ with a crossover probability of 0.6, an individual probability of mutation of 0.3, and a gene mutation probability of 0.02,^76,77 where an individual refers to a candidate model and each gene refers the presence or absence of a certain descriptor in the model. A population of 150 individuals was evolved during 10,000 generations and the best 20 observed individuals were saved for further selection. The multi-objective function was the 10-fold cross-validated q² together with the R² value for the validation set, with a penalization for models with more than 10 variables. The GA was performed five times for each regression algorithm, generating a total of 300 models. The machine learning suite used for modeling was the scikit-learn library for Python.⁷⁸ In the GA runs, the hyperparameters for the KNN algorithm were the default values,⁷⁹ with a weighting scheme based on the inverse of the distance: closer neighbors have a greater influence than distant neighbors.⁷⁹ The number of estimators of RF was reduced to 10 for performance reasons, and the values for the remaining hyperparameters were left as defaults.⁸⁰ The number of nearest neighbors for KNN and the number of estimators in the RF were further optimized using cross-validation with the GridSearchCV tool of scikit-learn.⁸¹

2.2.2. Model Validation

After feature selection, the internal performance and stability of the model were assessed with leave-one-out cross-validation, and the coefficient of determination q² was reported. The y-scrambling method was used to verify the absence of chance correlation. The order of the pIC₅₀ values was randomized 100 times and the models were recalculated for each new independent variable. The q² coefficients of the randomized models were evaluated. Since a high value of q_loo² is not related to a good predictability,⁸² the external evaluation was performed using the selected models to predict the pIC₅₀ of the molecules in the test set, which were never used in model generation. The coefficient of determination for the test set, R_ext, is often used as a measure of external predictability. However, this coefficient is a measure of the fit for the experimental and predicted values to a straight line and this may not be the ideal identity relation.⁸² One of the best practices is to compute several statistics for the external validation, compare the diagnostics between them, and in this way, achieve more confident conclusions.^83,84 Thus, we evaluated the root-mean-squared error (RMSE) for the external prediction, the concordance correlation coefficient (CCC), and the Q_F² family of parameters.^83,84Equations 2–7 were used to calculate the external validation criteria.

2

3

4

5

6

7

In the above equations, y_i is the experimental pIC₅₀ of molecule i, ŷ_i is the predicted activity for molecule i, y̅_TR and y̅_EXT are the means of pIC₅₀ values for the training and test sets, respectively, and n_TR and n_EXT are the numbers of molecules in the training and external test sets, respectively. In the CCC formula, x_i refers to the experimental pIC₅₀ value for the i molecule, y_i is the predicted activity for molecule i, and x and y̅ are the mean values for the respective experimental and predicted activities.

2.2.3. Applicability Domain

The predictability of a QSAR model is framed by the nature of the molecules in the training set. The applicability domain is the quantitative delimitation of the descriptor and activity space where predictions are reliable. In this work, the applicability domain was defined using the leverage method.⁸⁵ Leverage values, h_i, are computed using eq 8, where X is the descriptor matrix of the training set and x_i is the descriptor vector for a query molecule.

8

Basically, leverage values are proportional to the distance of the molecule from the centroid of the training set. Thus, compounds above a threshold are far from the explored descriptor–activity space and, therefore, their predicted biological activity will be unreliable. Typically, the threshold, h_max, is computed with eq 9, where p is the number of features and n is the number of molecules in the training set.

9

Leverage and limit values were computed in Python, and the results are presented in a Williams plot. In this representation, molecules with high leverages or large residuals can be easily detected for further examination.

Along with the leverage method, molecular similarity was used as a criterion for belonging to applicability domain. The molecular fingerprints using the public MACCSKeys implementation in RDKit were calculated for every molecule in the training and test sets. Then, a similarity matrix of the query test molecules against the training set was computed using the Tanimoto index. The highest similarity value of each molecule is presented together with the corresponding leverage score. The methodology for QSAR modeling is summarized in Figure 2.

Figure 2.

Flowchart with the summary of the methods for QSAR model generation. MLR, multiple linear regression; KNN, k-nearest neighbor regression; RF, random forest regression; GA, genetic algorithm.

3. Results and Discussion

This work consists of two main parts, the development of global and local models. For the global models, we prepared and analyzed a diverse set of cruzain inhibitors annotated with pIC₅₀ values. The distributions of the biological activity values of the training and test sets are shown in Figure 3. The pIC₅₀ values range from 3.48 to 10.0 units, from nanomolar to micromolar scale. It is noteworthy that the biological activity values of the test set lie within those of the training set as shown in the histogram of Figure 3, there are no gaps within bins, and activity outliers are not present, following the general recommendations in QSAR modeling.^12,22 The functional groups of the subsets divided by the chemical family resemble those in the previously reported local models shown in Table 1. Moreover, current efforts in the search for cruzain inhibitors focus on the design and optimization of particular chemotypes, including imidazoles and benzimidazoles,^9,86,87N-acyldhydrazones,⁸⁸ imides,⁸⁹ vinyl peptidomimetics,^2,11,90 oxadiazoles,^2,11,91 and triazoles,¹⁰ among others. Molecules that belong to these chemical groups are part of our curated modeling database. Figure 4 shows selected compounds from our data set. Therefore, the chemical space defined by these molecules resembles the current knowledge about cruzain inhibitors.

Figure 3.

Distribution of pIC₅₀ values for cruzain inhibitors. Molecules in the training set are shown in dark gray, and molecules in the test set are shown in light gray. The inhibitory potency of the test set falls within the interval of pIC₅₀ values of the training set.

Figure 4.

Selected molecules from the modeling data set.

The performance of the global models is summarized in Table 3. This table shows the top 5 models obtained after the evolution of the GA for each of the machine learning approaches. The number of variables selected for most of the models is 9; thus, the ratio of molecules per descriptor is around 24. This ratio is critical for the correct generalization of trends between the chemical structure and biological activity and to avoid overfitting. Except for the MLR algorithm, the selected feature subsets have determination coefficients between experimental and predicted values for the molecules in the test set above 0.7, which is a generally accepted value for external predictability. The best models were obtained using the KNN and RF algorithms, and they will be discussed further in this paper.

Table 3. Results of the Top 5 Models after GA Feature Selection for Every Machine Learning Algorithm^a.

algorithm	nd	qloo2	Rext2	RMSE	CCC	QF12	QF22	QF32
MLR	9	0.604	0.506	0.906	0.701	0.506	0.506	0.534
MLR	9	0.604	0.496	0.924	0.688	0.496	0.496	0.525
MLR	9	0.608	0.495	0.925	0.689	0.496	0.495	0.524
MLR	9	0.601	0.491	0.934	0.685	0.491	0.491	0.520
MLR	9	0.601	0.490	0.935	0.683	0.490	0.490	0.519
KNN	9	0.664	0.725	0.504	0.842	0.725	0.725	0.741
KNN	9	0.649	0.705	0.542	0.826	0.705	0.705	0.722
KNN	9	0.665	0.704	0.542	0.821	0.704	0.704	0.721
KNN	9	0.674	0.703	0.544	0.830	0.703	0.703	0.720
KNN	9	0.661	0.701	0.549	0.822	0.701	0.701	0.718
RF	9	0.608	0.766	0.445	0.841	0.757	0.757	0.771
RF	9	0.687	0.741	0.474	0.842	0.741	0.741	0.756
RF	9	0.604	0.730	0.494	0.821	0.730	0.730	0.745
RF	9	0.656	0.698	0.554	0.821	0.698	0.698	0.715
RF	8	0.597	0.716	0.520	0.813	0.716	0.716	0.733

^aMLR, multiple linear regression; KNN, k-nearest neighbor regression; RF, random forest regression; n_d, number of descriptors in the model; q_loo², coefficient of determination for the leave-one-out cross-validation; R_ext, coefficient of determination for the external data set; RMSE, root-mean-squared error for the external set; CCC, concordance correlation coefficient; Q_Fn², Q² family of external validation parameters (see Section 2).

The results of the best models using the local data sets for MLR and KNN algorithms are presented in Tables 4 and 5, respectively. The external coefficients of determination are higher for some of the groups in comparison with the global models, and the best values are around the same magnitude of the previously reported models. The amide and N-acylhydrazone groups are satisfactorily modeled even with the MLR approach. According to the similarity-property principle, on the basis of the classical QSAR analysis, gradual changes in structure lead to gradual changes in activity.¹⁷ In a database of congeneric compounds, the variation of chemical structures tends to be moderate, generating a continuous structure–activity space, which is often capable of being modeled with linear methods. Increasing the molecular diversity in a set of molecules also increases the complexity of the modeled property. Changes in structure are more abrupt and multiple mechanisms involved in activity tend to coexist, making the linearity between the structural modifications and activity not hold.^13,17 This is clearly shown in the comparison between Tables 3, 4, and 5, where the MLR algorithm was able to predict the activity values in the external set for some of the local models, but in the global set, this was not the case.

Table 4. Results for the Best MLR Models for Each Chemical Group^a.

group	nd	qloo2	Rext2	RMSE	CCC	QF12	QF22	QF32
amides	4	0.784	0.805	0.371	0.885	0.805	0.805	0.855
N-acylhydrazones	4	0.617	0.780	0.307	0.850	0.831	0.780	0.682
thiazolylhydrazones	4	0.588	0.555	0.293	0.755	0.622	0.555	0.729
thiosemicarbazones	4	0.532	0.760	0.231	0.854	0.767	0.760	0.764
triazine nitriles	4	0.593	0.571	0.776	0.685	0.583	0.571	0.363

^an_d, number of descriptors in the model; q_loo², coefficient of determination for the leave-one-out cross-validation; R_ext, coefficient of determination for the external data set; RMSE, root-mean-squared error for the external set; CCC, concordance correlation coefficient; Q_Fn², Q² family of external validation parameters (see Section 2).

Table 5. Results for the Best KNN Models for Each Chemical Group^a.

group	nd	qloo2	Rext2	RMSE	CCC	QF12	QF22	QF32
amides	4	0.822	0.809	0.363	0.892	0.809	0.809	0.858
N-acylhydrazines	4	0.378	0.834	0.231	0.891	0.873	0.834	0.761
thiazolylhydrazines	4	0.547	0.918	0.054	0.961	0.931	0.918	0.950
thiosemicarbazones	4	0.653	0.725	0.265	0.814	0.732	0.725	0.730
triazine nitriles	2	0.724	0.879	0.220	0.924	0.882	0.879	0.820

^an_d, number of descriptors in the model; q_loo², coefficient of determination for the leave-one-out cross-validation; R_ext, coefficient of determination for the external data set; RMSE, root-mean-squared error for the external set; CCC, concordance correlation coefficient; Q_Fn², Q² family of external validation parameters (see Section 2).

Consensus diversity plots (CDPs),⁹² cyclic system retrieval curves (CSRs),⁹² and pairwise similarity matrices were calculated to compare chemical diversity between databases. Results of similarity analysis are depicted in Figure 5. As expected, the complete database has the lowest mean similarity value, and quartile distributions show that 75% of these values are not higher than 0.44. Among local groups, amides have the largest diversity with a mean similarity value of 0.48. The blocks in the matrix suggest that this group could be further divided into subsets, indicating that side chains have a strong influence on the group diversity. However, this set has also the best performances using MLR and KNN algorithms. These results show that sudden changes in structure are accompanied by proportional changes in activity, maintaining linearity within the group. N-Acylhydrazones, thiazolylhydrazones, and thiosemicarbazones have comparable similarity distributions and their model performances are also similar. Lastly, triazine nitriles share the highest similarity between other molecules in their group, with a mean value of 0.64. It is notable that this model, using the KNN algorithm, has a good performance, comparable to the amide model, with only two descriptors.

Figure 5.

Pairwise Tanimoto similarity matrices for compounds in each global and local data set based on MACCSKeys fingerprints.

Figure 6 shows the CDP and CSR results for the global and local sets. It is interesting that the area under the CSR curve for the complete set is higher than the area for amides and N-acylhydrazones. The CSR curve is calculated from a scaffold decomposition of the molecules in the database. Then, the fraction of scaffolds is plotted on the X-axis and the fraction of compounds that contains those scaffolds is plotted on the Y-axis.⁹² This result implies that there are more molecules in the complete database that share the same scaffold than those in the amide and N-acylhydrazone sets. In other words, there is an overlap in the scaffolds between local databases. However, this analysis focuses on the core structure of the molecules, ignoring side chains or substituents. In the CDP depicted in Figure 6, the complete database lies in an area with the highest fingerprint-based diversity but with middle scaffold-based diversity. Therefore, the main differences between the molecules in the complete database come from the side chains.

Figure 6.

(A) Cyclic system retrieval curve for the global and local models. (B) Consensus diversity plot comparing the global (complete) and local data sets. Marker size is proportional to the number of molecules in each database.

Applicability domain is a concept as important as the external validation in the QSAR modeling practice. The reliability of a prediction will also depend on the extent a new molecule is near the set used for the generation of the model. In this context, local models tend to have more restrictive applicability domain and their predictability will be framed by the same mechanism of action of those molecules in the training set.¹² The complete data includes cruzain inhibitors comprising several of the chemical groups reported in the literature to afford a more general model. Global models are more appropriate than local ones in virtual screening because their wider applicability domain may exert a larger coverage of the chemical space in a diverse database.¹² However, compared with larger databases, the chemical space of the model can still be very narrow. Since there is no QSAR model that can be applied universally, any QSAR-based virtual screening round must have a quantitative measure to identify which molecules are within the applicability domain. The trends in structure–activity relationships are only valid in the region of the chemical space covered by the molecules in the training set. The KNN and RF global models with the best statistical parameters will be discussed in more detail, including the limitations imposed by their applicability domain.

Molecular descriptors codify the structural information relevant to the activity. Although some descriptor definitions are rather complex and their interpretation is difficult, a closer look into these features may provide insights into the qualitative structure–activity relationships. Molecular descriptor definitions for KNN and RF models are presented in Tables 6 and 7, respectively. Scatter plots showing the intercorrelation between descriptors and with the biological activity are presented in Figures S1 and S2 of the Supporting Information. Most of the molecular descriptors used by the KNN models, depicted in Figure S1, are related to atomic partial charges and their topological distribution. These properties are relevant in the formation of intermolecular interactions that could describe the binding of inhibitors in the cruzain active site. In turn, descriptors in the random forest regression include counters of atom types along with partial charges and logP contributions. The matrix of scatter plots in Figure S2 shows that counters are able to divide the molecules into groups with different ranges of activity values. For example, high counts of acidic groups correlate with low values of pIC₅₀ (but the opposite is not true), and a high number of double-bonded nitrogen atoms gives a narrow range of activity in the middle potency region. It is also interesting to note that the descriptor BCUTd-1l separates the set in two groups of high and low potency inhibitors. A closer look into the results of this descriptor reveals that molecules with the lowest values belong to the class of peptidyl nitriles, which are also one of the most potent chemical families. The eigenvalues of the Burden matrix are recognized as a molecular descriptor with high discrimination power,⁹³ as shown in this observation.

Table 6. Definition of Molecular Descriptors Used by the KNN Model^a.

descriptor name	definition
MATS5z	Moran coefficient of lag 5 weighted by atomic number
GATS3c	Geary coefficient of lag 3 weighted by Gasteiger charge
GATS8s	Geary coefficient of lag 8 weighted by intrinsic state
BCUTc-1h	first highest eigenvalue of Burden matrix weighted by Gasteiger charge
NsssCH	number of sssCH atoms
CIC0	0-ordered complementary information content
PEOE_VSA4	sum of VSA for atoms with Gasteiger charge in [−0.20,–0.15)
JGI4	4-ordered mean topological charge
JGI8	8-ordered mean topological charge

^asssCH, carbon atoms single-bonded to three heavy atoms; VSA, van der Waals surface area.

Table 7. Definition of Molecular Descriptors Used by the RF Model^a.

descriptor name	definition
nAcid	acidic group count
nF	number of F atoms
AATSC1c	averaged and centered Moreau–Broto autocorrelation of lag 1 weighted by Gasteiger charge
AATSC1dv	averaged and centered Moreau–Broto autocorrelation of lag 1 weighted by valence electrons
BCUTd-1l	first lowest eigenvalue of Burden matrix weighted by sigma electrons
NdsN	number of dsN atoms
NdO	number of dO atoms
PEOE_VSA5	sum of VSA for atoms with Gasteiger charge in [−0.15,–0.10)
SlogP_VSA2	sum of VSA for atoms with SlogP atomic contribution in [−0.20,–0.15)

^adsN, nitrogen atoms with a single bond and a double bond to other heavy atoms; dO, oxygen atoms with a double bond; SlogP refers to the atomic contribution to calculate the logP using the Wildman and Crippen algorithm.⁹⁴

The regression plots of experimental versus predicted values are depicted in Figure 7 for both models. From this figure, it is clear that the models are correctly describing the trends in activity of cruzain inhibitors, even in the test set. The external validation parameters for these models, presented in Table 3, are above the generally accepted thresholds, except for the concordance correlation coefficient. The selected models have CCC values of 0.842 and 0.845, slightly below the proposed limit of 0.85.¹⁶ Notably, these models are able to capture the hierarchical relationships of the inhibitors regarding their biological activity. In descriptive QSAR modeling, identification of trends in the data is useful for the prioritization or identification of molecules with desirable properties, even if the predictive value is not very accurate.⁸⁴ Although previously reported models have similar or better performances, our data set comprises a wider chemical diversity.

Figure 7.

Regression plots of the best generated models. The first plot shows the predicted values by the KNN model for the training and test sets, and the plot below shows the results for the RF forest model. Q_loo² and R_ext are presented inside the graphs.

The analysis of residuals is presented along with the discussion of applicability domain. A new molecule can be reliably predicted only if its structural features resemble those of the molecules used to calculate the model. This is because, outside the explored chemical space, the structure–activity landscape may be unpredictable. This must be taken into consideration if the model is going to be used for the search of new molecules from databases. The residual histograms for the discussed models are presented in Figure 8. The external test residuals are distributed in a range similar to those of the training set. For both models, residuals follow a nearly normal distribution. Although, for nonlinear and nonparametric methods, the normal distribution of residuals is not mandatory, it is useful to make inferences about the prediction error and to identify biases that could indicate the presence of systematic errors. In this case, all the residuals are approximately centered around 0, which is the expected value for the prediction error, and distribute almost symmetrically above and below this value.

Figure 8.

Histograms of the distribution of model residuals. The upper plots show the residuals for the KNN model, and the lower histograms plot these results for the RF model.

The leverage values are proportional to the Mahalanobis distance of the molecules to the center of the group.⁸⁵ This distance metric is used in multidimensional spaces of random variables to detect the presence of outliers, and it is particularly useful in spaces where the feature space is not orthogonal. High leverage values are related to molecules with structural features far from the general trends in the data. The Williams plots for the considered models are shown in Figure 9. This graph represents the leverage values versus the standardized residual; thus, it gives a visual representation of both the structural and activity domains. For both models, most of the molecules in the test set are distributed along the space defined by the training molecules. Vertical lines in the plots represent the calculated limit according to eq 9. The KNN group has four molecules in the training set slightly after the limit, and the RF group has one molecule with a very high leverage in comparison with the others. This molecule is identified as CHEMBL409024 and its structure is depicted in Figure 10. It has relatively extreme values of the AATSC1c, AATSC1dv, and BCUTd-1l descriptors in comparison with the general trends of the rest of the compounds in the set. This inhibitor is a nonstandard amino acid with two aromatic rings and a phosphate group. The presence of the phosphate group is a unique feature of this compound and may be the cause of the difference with the rest of the molecules. However, deletion of this molecule did not modify significantly the performance of the model.

Figure 9.

Williams plots for the calculated models. In the upper graph, leverages and residuals are shown for the KNN model, whereas the lower graph shows the results for the RF model.

Figure 10.

Structure of CHEMBL409024. This molecule has a high leverage in the RF group.

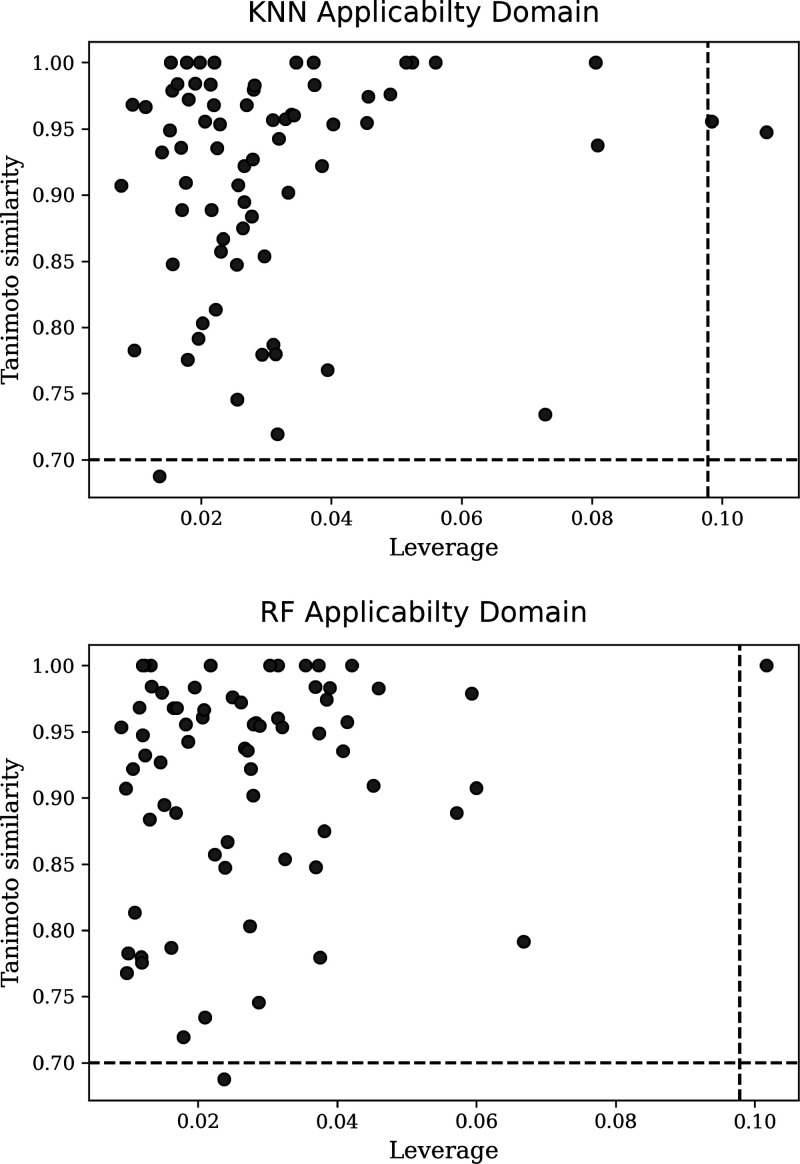
The leverage method for applicability domain definition is based on the values of descriptors. However, these features may not capture some effects related to out-of-target phenomena, like the potential of a molecule to cause aggregation. For this reason, an analysis based on molecular similarity was also assessed. Fingerprints, using MACCSKeys implementation of RDKit, were used to compute Tanimoto similarity values between the molecules of the test set and those in the training set. The maximum similarity values for each compound in the test set are plotted against leverage values in Figure 11. The graphs show that most molecules have at least one congener whose similarity value is greater than 0.7. In general, molecules with low leverage values tend to have higher similarities with the training set. Thus, predictions made by the models are considered reliable if the predicted molecules have leverages and maximum similarity values inside the box depicted in Figure 11.

Figure 11.

Maximum Tanimoto similarity values for each molecule in the test set. MACCSKeys were used to generate molecular fingerprints. Similarities are plotted against leverage values.

The analysis of the possibility of chance correlation was tested using the Y-randomization method. The results of the q² values for 100 randomized models are presented in Figure 12. The scatter plot shows the q² values for each iteration followed by the value of the nonrandomized model. Histograms represent the distribution of the calculated q² coefficients together with the values of the true model. This figure reveals that for the randomized models, the determination coefficient falls to unacceptable levels. Moreover, the distribution of the randomized coefficients does not overlap with the values for the true models. This behavior indicates that the probability of chance correlation is very low. Although the predictability of the models is not outstanding, the relationships of molecular features captured by the descriptors with the biological activity are significant since the randomization of pIC₅₀ values alters considerably the stability and performance of the models.

Figure 12.

Results of the q² values for randomized models in comparison with the q² of the true model.

The statistical parameters of internal and external validation for the selected models indicate a satisfactory performance. The models can be used to predict the pIC₅₀ on cruzain in the search or prioritization of molecules to be tested as antitripanosomal agents. For this purpose, a Python script is provided in the file cruzain_qsar_models.zip of the Supporting Information, together with the trained models. A detailed explanation on the use of the script is provided in section S3 of the Supporting Information and in the ACS LiveSlides. Briefly, the program takes as input an sdf file with the 2D structures of the query molecules, internally calculates the molecular descriptors, and predicts the pIC₅₀ values using the RF and KNN models. It also computes the leverage and Tanimoto similarity values with respect to the training set to test if the molecules are within the applicability domain of the models. Results are saved in a csv file, and details on its contents and interpretation can be found in Table S1 of the Supporting Information.

The Python script provided in this work is intended for scientists working on research and development of anti-Chagas agents. The availability of the training set and descriptors used, the use of open-source software, and the easiness for nonexperts make this tool readily used for a broad scientific audience. As a result, the models will be useful in virtual screening campaigns that, in combination with molecular modeling studies, such as docking, will help with the design and prioritization of experimental studies.

4. Conclusions

Quantitative structure–activity relationship models were developed for the calculation of pIC₅₀ values of cruzain inhibitors using multiple machine learning algorithms. The statistical parameters describing the performance of the best selected models agree with the general recommendations for QSAR modeling. The data set used in the model includes several of the chemotypes already explored in the literature as well as those not previously modeled, comprising a wider chemical space than local models. External validation results show that the models are able to reproduce the trends and hierarchical relations of the experimental pIC₅₀ values. The reliability of predictions is framed by the applicability domain of the model, which is quantitatively defined by descriptor and molecular similarity methods. Therefore, the OECD principles for QSAR practices and applications are fulfilled. The generated models reproduce the biological activity values, indicating that structural trends are well captured by nonlinear correlations in terms of molecular descriptors. Using these relationships, a molecule can be predicted as a cruzain inhibitor based solely on its chemical structure. This is useful for the prioritization of molecules to be tested experimentally from a database. The models can also be used to ascertain structural modifications likely to improve or decrease cruzain inhibitory activity, if the change in pIC₅₀ is higher than the expected error of prediction. The calculated models are made publicly available and its use could guide the search, development, and rational design of cruzain inhibitors as possible pharmacological treatment of Chagas disease.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c05645.

• File with the curated database of cruzain inhibitors, along with biological activities (cruzain_dataset.xlsx); file with additional figures depicting pairwise scatter plots between model descriptors and detailed instructions on the use of the script provided (supporting_information.pdf); Python script and related files ready to use for prediction of pIC₅₀ values of molecules using the models described in the paper (cruzain_qsar_models.zip) (ZIP)

The authors declare no competing financial interest.