Uncertainty in collocated mobile measurements of air quality

Abstract

Mobile mapping of air pollution has the potential to provide pollutant concentration data at unprecedented spatial scales. Characterizing instrument performance in the mobile context is challenging, but necessary to analyze and interpret the resulting data. We used robust statistical methods to assess mobile platform performance using data collected with the Aclima Inc. mobile air pollution measurement and data acquisition platform installed on three Google Street View cars. They were driven throughout the greater Denver metropolitan area between July 25, 2014 and August 14, 2014, measuring ozone (O₃), nitrogen dioxide (NO₂), nitric oxide (NO), black carbon (BC), and size-resolve particle number counts (PN) between 0.3 μm and 5.0 μm diameter. August 6, 2014 was dedicated to parked and moving collocations among the three cars, allowing an assessment of measurement precision and bias. We used the median absolute deviation (MAD) to estimate instrument precision from outdoor, parked collocations. Bias was assessed by measurements obtained from parked cars using the standard deviation of median values over a collocated measurement period, as well as by Passing-Bablok regression statistics while the cars were moving and collocated. For the moving collocation periods, we compared the distribution of 1-σ standard deviations among the 3 cars to the estimated distribution assuming only measurement uncertainty (precision and bias). The distribution of mobile measurements agreed well with the theoretical uncertainty distribution at the lower end of the distribution for O₃, NO₂, and PN. We assert that the difference between the actual and theoretical distributions is due to real spatial variability between pollutants. The agreement between the parked car estimates of uncertainty and that measured during the mobile collocations (at the lower quantiles) provides evidence that on-road collocation while parked could be sufficient for estimating measurement uncertainties of a mobile platform, even when extended to the moving environment.

1. Introduction

Measurements form the basis of our understanding of air pollution; scientists, regulators, and the public use these measurements to understand atmospheric chemistry, determine air quality levels, link concentrations to health effects, and evaluate advanced air quality models. Conventional measurement programs, including regulatory programs, are typically developed around one or more central monitoring sites within a given geographical area. These measurement networks provide regional (tens to hundreds of kilometers) to neighborhood (half a kilometer to 4 km) scale pollution information, although a limited network of micro scale (several meters to about one hundred meters) near-road air quality monitoring sites exist as well (40 C.F.R. 58, 2018). In the United States, local, state, and tribal air quality agencies measure air quality using well characterized regulatory grade instruments, typically with 1-hr to 24-hr time resolution. These measurements are spatially limited, and to some extent temporally limited, and do not capture the full variability of pollutant concentrations that exist in urban environments over fine spatial and temporal scales.

Size, cost, and power requirements associated with stationary monitoring sites prohibit widespread deployment of laboratory or regulatory grade air pollution measurement instrumentation to study spatial variability on sub-kilometer scales. New monitoring approaches, especially the use of mobile monitoring platforms, have the potential to fill this data gap by expanding spatial and temporal coverage of air pollution measurements across urban environments (Apte et al., 2017). On-road mobile monitoring studies have been used for computing on-road emission factors from vehicles (Park et al., 2011), studying the impacts of traffic interventions or roadside barriers (Wang et al., 2009; Hagler et al., 2012), identifying local sources (Apte et al., 2017), and general air quality surveying of urban areas (Wallace et al., 2009; Hu et al., 2012), including environmental justice neighborhoods (Apte et al., 2017). One efficient approach is to leverage existing fleet-based mobile platforms, such as public transit systems (Hagemann et al., 2014; Mitchell et al., 2018), Google Street View cars (Apte et al., 2017; Messier et al., 2018), or other fleet vehicles (Castell et al., 2015; Kaivonen and Ngai, 2019).

The evolving capability for fleet-based mobile measurements requires researchers to determine the amount of data necessary, and the appropriate statistical methods needed, to extract spatially representative trends from mobile monitoring data. Studies have tackled this challenge by performing multiple mobile passes for each spatial location and using robust spatial or temporal aggregation techniques to reduce the data and reveal spatial trends (Brantley et al., 2014). The uncertainty of the resulting spatial patterns is assessed statistically using the distribution of statistical parameters obtained from ensemble Monte Carlo subsampling of the dataset (Apte et al., 2017; Li et al., 2018; Van Poppel et al., 2013). Apte et al. (2017) found that, with 30 m median spatial aggregation, only 10–25 repetitions over a particular area generate reproducible results (with high precision and low bias) for nitric oxide, nitrogen dioxide, and black carbon.

Mobile monitoring data consists of a complex series of pollutant concentration data, with contributions from neighborhood-scale and regional background concentrations punctuated by spikes of pollution from nearby sources. Layered under the complexity of the actual concentrations is the instrument precision and, when comparing 2 or more platforms, potential measurement biases between platforms. Characterizing instrument performance in the mobile context is challenging. However, it is necessary to define quality assurance requirements for robust spatial data collection. Researchers must assess the uncertainty in the measurements, both in stationary and mobile environments, to routinely confirm platform comparability between different units (i.e. vehicles).

In this paper, we approach the mobile monitoring data analysis problem from a quality assurance perspective. Like previous studies, we use robust (outlier-resistant) data reduction techniques to simplify the datasets. However, we use these techniques to specifically isolate the uncertainty (i.e. precision and bias) between and among measurements obtained by the mobile platforms. Although most mobile monitoring studies perform some level of quality assurance, it is generally limited to laboratory-based calibration or collocation between parked cars and well-characterized stationary monitors. Measurements in a moving environment produce additional complications that are not necessarily addressed using these traditional methods but are necessary to assess instrument performance under on-road mobile conditions.

We analyzed data from a pilot study in July and August of 2014. This study used 3 identical mobile monitoring platforms integrated into fleet-based (Google Street View) cars. The study was performed in the Denver, CO metropolitan area to leverage the enhanced monitoring for the NASA-led DISCOVER-AQ field study (Crawford and Pickering, 2014). Science goals included understanding the performance of the mobile monitoring platforms, as well as exploring methods for assessing data quality and platform comparability. We focus on data from August 6, 2014, which was dedicated to stationary and driving collocated comparisons between the three mobile platforms. Through analysis of this data, we assess different statistical methods to understand mobile platform performance.

2. The summer 2014 measurement campaign in denver, Colorado

2.1. Mobile measurement platform

Three Google Street View cars (gasoline-powered Subaru Imprezas) were equipped with the Aclima mobile measurement and data acquisition platform (Aclima Inc., San Francisco, CA; https://aclima.io). The Aclima platform provides data management, quality control, and real-time visualization functions to facilitate extensive, routine mobile air quality measurements. In this study, the cars were equipped with high time resolution (0.5 hz or 1 hz data reporting rate) laboratory-grade air pollution monitors that measured ozone (O₃), nitrogen dioxide (NO₂), nitric oxide (NO), black carbon (BC), and size-fractionated particle numbers (PN). The instruments pulled from a common manifold. Total flow through the manifold was between 7.0 and 7.5 L per minute (Table 1). The manifold’s inlet was centered several inches over the top of the windshield and faced towards the front of the car. O₃, NO₂, and NO concentrations are reported in parts per billion volume (ppbv), BC concentrations are reported in micrograms per cubic meter (μg m⁻³), and PN number concentrations are reported in number of particles per liter (L⁻¹). PN was measured in six size classes based on aerodynamic diameter: PN_0.3–0.5 (0.3–0.5 μm), PN_0.5–1.0 (0.5–1.0 μm), PN_1.0–2.0 (1.0–2.0 μm), PN_2.0–5.0 (2.0–5.0 μm), PN_5.0–10.0 (5.0–10.0 μm), and PN_10.0+ (10.0 μm and larger). Only the smaller four fractions (PN_0.3–0.5, PN_0.5–1.0, PN_1.0–2.0, PN_2.0–5.0) are analyzed in this paper. Due to instrument issues, BC was only measured on 2 of the 3 cars (Cars 1 and 2). Instruments and methods are summarized in Table 1 and described in greater detail in the Supplemental Text (Sect. S1). A brief discussion of the differences between instrumental reporting rate and instrumental response time is also given in the Supplemental Information (Sect. S1).

Table 1.

Performance specifications for the instruments deployed in the vehicles. All values are obtained from manufacturer’s performance specifications unless otherwise noted.

Pollutant	Manufacturer and Model	Measurement Principle	Resolution	Range	Precision	Response Time	Nominal Flow Rate (mL/min)
O3	2B Technologies 211	UV absorption	0.1 ppbv	1–2000 ppbv	1% or 0.5 ppbv	4 s	2000
NO2	Teledyne T500U	Cavity attenuated phase shift	0.010 ppbv	0–1000 ppbv	0.5% (above 5 ppbv)	a< 8 s	900
NO	Ecophysics CLD64	O3 chemiluminescence	1 ppbv	0–1000 ppbv	2%	<1 s	1000
PN	MetOne GT-526S	Light scattering (laser)		0–105,900 L~1	10%	1 s	2830
BC	Droplet Measurement Technologies Photoacoustic Extinctometer	Photoacoustic extinctometry	0.2 m–3	<1 Mm−1 – 10000 Mm−1 (60 sec)	10%	<5 s	1000

^aManufacturer’s quoted response time is < 30 s. However, analysis of instrument response consistently suggests the response time is < 8 s in our system.

2.2. Quality assurance of mobile monitoring data

We evaluated gas-phase instruments (O₃, NO₂, and NO) daily in the field and after the study in the Aclima laboratory. Flow rates were checked and remained within specifications throughout the study. Instrument responses to zero air were measured using a zero air cylinder and recorded. Daily span checks were performed for NO (360 ppbv) and O₃ (80 ppbv) using a dilution gas calibrator with a certified NO cylinder or a certified O₃ generator, respectively. NO₂ instruments relied on pre- study and post-study zero and single point calibrations, with only zero checks in the field. Daily calibrations (zero and span) were performed “through the probe” by connecting the calibration system to the sample inlet with a vented tee configuration. Internal instrument span and zero parameters were not adjusted in the field. Instead, a single study-wide zero offset value for each instrument (on each car) was determined and applied after the study. No post-hoc adjustment to instrument span values was necessary as the span values did not drift outside the manufacturer’s specifications over the course of the study.

Based on the span checks, the daily biases of the O₃ instruments varied between 3% and 6% with a standard deviation of 5%. The daily biases of the NO instrument varied between 3% and 8% with a standard deviation of 6%. The NO gas standard had a concentration uncertainty of ±2% (EPA certified grade). Mass flow controllers in the dilution calibrator had a specified accuracy of ±3.6% at the conditions used. The O₃ generator had a specified accuracy of ±1%. All gas cylinders were within date, and flow controllers and O₃ generators had been certified less than three months prior to the study. Daily NO₂ biases were not calculated due to technical problems performing NO₂ span checks during the study. Thorough NO₂ calibrations were performed at the beginning and end of the study. No drift was observed between these two calibrations.

The PN and BC instruments relied on the manufacturer’s calibrations; no additional span checks were performed in the field. A high-efficiency particulate air (HEPA) filter was placed at the sampling inlet daily to monitor for and correct leaks in the particulate sampling manifold. The total flow rate at the inlet was measured daily and remained stable throughout the course of the study.

Aclima used an algorithm to calculate daily time shifts for individual instrument data streams, accounting for the differences between instrument sample transport times. The instruments’ responses were all aligned to the NO instrument, which had the fastest response time, and corrected to account for any delay in the sampling line. The response times of the instruments, sample flow rate, and relative positions in the sampling manifold were consistent with the degree of time-shifting. Daily time shifts for individual instruments ranged from 0.1 s to 12 s and were generally correlated with the flow rate of each instrument from the common manifold. Daily time shifts were consistent over the month-long study. Timestamps in the final, processed data reflect the time at which the sample air entered the inlet.

Aclima screened and removed invalid data from the final database. They flagged and removed periods when instruments were performing internal process operations (e.g. auto-zeroing) or operating outside of instrument specifications. They monitored instrument diagnostics and invalidated data when the instrument reported anomalous diagnostic values or other flags or warnings. Research staff reviewed the data daily during the study and in depth afterwards. Data corresponding to periods when obvious issues were noted in field notes (such as a leak in the sampling manifold) were also removed from the final dataset. For the mobile collocated periods on August 6, 2014, over 95% for the 1-s data were considered valid for the PN variables, O₃, and NO₂. Over 90% of 1-s data were valid for NO and over 85% were valid for BC. The missing data for BC and NO₂ is largely explained by the instrument’s internal zero routine, which accounts for about 15% and 3.3% of potential timepoints for BC and NO₂, respectively.

We did not exclude data points reported outside the manufacturer’s specified range of the instruments. This accounted for a small fraction (<1%) of the total data. We consider this data essential to properly assessing the statistical distribution of the measurements. The analyses we present are based on either entire statistical distributions, in which case the higher end of the distribution can influence the rest of the distribution, or outlier-resistant robust statistics, in which the values of the high outliers (data above the calibration range of the instrument) do not impact the resulting statistics. Data points that lie outside the calibration range of the instruments have a lower accuracy than data within the calibration range, but still represent valid measurements of real concentrations. Exclusion of this data would artificially bias the resulting statistical distribution of the data. The inclusion of this data did not impact any of our results or interpretations.

2.3. Mapping region, study design, and sampling protocol

The three cars drove through the Denver, CO greater metropolitan area between July 25^th, 2014 and August 14th, 2014. Research staff gave route assignments to the professional drivers each day. Drivers drove with the normal flow of traffic. On August 6, 2014, the three cars remained near each other while driving, focusing on coordinated driving patterns. These patterns included side-by-side driving and one-behind-the-other driving. We designed the coordinated drives as a mobile collocation experiment to provide data for assessing platform performance. Drivers also parked the cars next to each other throughout the day as part of these driving patterns. Over the course of the day, the cars traversed diverse environments, including parks (Cherry Creek State Park), residential neighborhoods, arteries, and highways (Interstate 25 and Interstate 225). Maps of the routes are shown in the Supplemental Information (Fig. S1).

August 6, 2014 was a typical, partly cloudy summer day in Denver, CO. Meteorological data from the La Casa regulatory monitoring site (latitude: 39.77943°, longitude: 105.0052°) in Denver had temperatures that ranged from 15.5 °C (immediately before sunrise) to 29.5 °C (in the early afternoon). Mean windspeeds were 4.8 m s⁻¹, with 1^st quartile, median, and 3^rd quartile windspeed values of 3.2 m s⁻¹, 4.3 m s⁻¹, and 5.8 m s⁻¹. Wind direction fluctuated throughout the day. Additional meteorological information is available via the United States Environmental Protection Agency’s Air Quality System (AQS) database (https://www.epa.gov/aqs) or on the 2014 DISCOVER-AQ Denver data archive (https://www-air.larc.nasa.gov/missions/discover-aq/discover-aq.html).

3. Statistical analysis methods

The measurement platform recorded 1 hz data for NO₂, NO, BC, PN_0.3–0.5, PN_0.5–1.0, PN_1.0–2.0, and PN_{2.0 −5.0}, and 0.5 hz data for O₃. We extracted and processed the data using the R statistical computing environment (R Core Team, 2017) and we used the ggplot2 R library (Wickham, 2016) to produce visualizations. The GPS coordinates were used to calculate car-versus-car distances for every 1 s data point using the algorithm of Karney (2013), as implemented in the geosphere R library (Hijmans, 2017).

We subdivided the dataset for August 6, 2014 into three categories: stationary collocated (SC), mobile collocated (MC), and other. We only evaluate the SC and MC periods in this paper. We visually assessed the car speed, latitude and longitude, and car-versus-car distances, as well as changes in those parameters, to determine which category to group sampling periods into. Periods were classified as SC if the car speed was less than or equal to 0.1 m s⁻¹ for a period of 5 min or longer and car-versus-car distances were within 30 m and constant. We identified 14 SC periods on August 6, 2014 (Table S1). Six of these periods were near 2265 South Kalamath Street, Denver, Colorado, two were in Cherry Creek State Park (Englewood, Colorado), two were near 970 Yuma Street, Denver, Colorado, and the remaining 4 were at various locations in Denver, Colorado and Englewood, Colorado (Table S1). We classified periods when the distances were varying but generally within 100 m and the speed was varying as mobile collocation (MC) periods. We identified seven MC periods on August 6, 2014 (Table S2, Fig. S1), with the first one starting at 6:55 local time (Mountain Daylight Time, MDT) and the last one ending at 22:27 local time.

3.1. Method for assessing platform uncertainty from stationary collocation periods

We used the data from the 14 SC periods on August 6, 2014 (Table S1) to assess measurement uncertainty. We decomposed the measurement uncertainty into two components: a random component termed precision and a systematic component termed bias. The precision component is comprised of all factors that cause random variations in the measurements about a mean value (e.g. instrument noise) and is directly measured for each instrument and each period. Bias, on the other hand, is estimated by the differences between measurements obtained by the three identical platforms and the mean value of the three platforms. We also calculate the uncertainty due to bias, which we estimate as the standard deviation of the car-specific biases for all three cars.

Consider the case where an instrument measures a constant pollutant concentration for an extended period. In this situation, the standard deviation of the measurement over that period provides a measure for the 1 s instrument precision. Because the concentration is assumed to be constant, the instrument’s response time (Table 1) will not impact the 1 s precision, which will be dominated by factors such as electronic noise or random thermal fluctuations. Assuming no bias, we expect the measured values to be normally distributed around the mean concentration. Now, put that same instrument on a car, and put that car on a road. The variations measured by that on-road instrument now includes both the instrument precision as well as variability in ambient concentrations. Assessing precision in an on-road environment may overestimate the true precision if there is variability in ambient concentrations during the measurement period.

To reduce the impact of ambient variability on our precision estimates, we calculated the precision using a robust, median-based estimator for standard deviation, the median absolute deviation (MAD). We apply a scale factor of 1.4826 to the MAD values (Leys et al., 2013), where 1.4826 is the ratio of the standard deviation and the median absolute deviation for a normal distribution. This scaling factor assumes that the instrument precision is normally distributed. The scaled MAD value (σ-_MAD) is sensitive to the center (roughly 50%) of the distribution and robust against extreme values. Using σ-_MAD instead of the standard deviation removes the influence of occasional pollution spikes and reduces, but does not eliminate, the impact of high frequency and low frequency variability in external concentrations during the measurement period. As a robust estimator for standard deviation, σ-_MAD values provide a reasonable estimate for 1 s (or 2 s for O₃) instrument 1σ precision. The combination of 3 cars and 14 SC periods produced 42 σ-_MAD values for each measured species (28 for BC and 39 for O₃). Some of the stationary collocation periods occurred on busy roads or near other potential sources, so even a robust estimator such as MAD may overestimate the instrument precision. To further insulate our estimate from high-variability cases, we use the median of the set of σ-_MAD values for each species as the study-wide estimate for the instrument precision, σ_precision, for that species.

To calculate car-specific biases, we first calculated the median measurement value of each species for each car and period. We then took the difference between the median value for that car (for that period) and the mean of the median values for all three cars (for that period). This gave us a period-specific estimate of bias for each car. We obtained a study-wide estimate of bias for each car (Bias₁ for car 1, Bias₂ for car 2, Bias₃ for car 3) by taking the median of the period-specific biases for that car. Differences in instrumental response time will not impact the bias calculations, since they are made under the assumption of a constant concentration and rely on a statistical measure of central tendency for a long measurement time period.

To obtain the estimated uncertainty due to the biases (for all three cars) for each period, we computed the standard deviation of the 3 car-specific, period-specific biases for each period. A study-wide estimate of the uncertainty due to bias (σ_bias) was computed as the median of the 14 period-specific uncertainties due to bias.

We thus reduced the data to a single estimate of measurement precision (σ_precision) and a single uncertainty due to bias (σ_bias) for each species. We estimated our total measurement uncertainty (σ_total) as the square root of the sum of the squared random (σ_precision) and systematic (σ_bias) uncertainties. Calculated mean, median, standard deviation, and scaled MAD values for each parameter, car, and SC period are given as a supplemental table (Table S3).

3.2. Regression for assessing bias during mobile collocation periods

We evaluated systematic differences between measurements from each pair of cars for the mobile collocation (MC) periods using regression analysis. The 7 MC periods range in duration from 40 min to 75 min (Table S2). Typical regression analyses, including ordinary least squares, orthogonal, and Deming regressions, are strongly influenced by outliers. Preliminary analyses using these techniques gave poor results, especially for species with highly skewed distributions (such as NO). Many outlier points are due to near source ambient concentration variability on the scale of car-versus-car distances rather than systematic measurement differences. Therefore, we decided to use a robust, median-based regression method for assessing potential car-versus-car biases during the MC periods.

The Passing-Bablok regression (Passing and Bablok, 1983) provides a robust, symmetric, and non-parametric method for assessing instrument comparability in the presence of high degrees of random variations. We used this method to assess systematic variations between pairs of cars in the presence of ambient spatial variability in the measurements. The validity of this approach assumes (1) collocated cars will measure the same background concentrations in the absence of hyperlocal pollution plumes, and (2) the influence of the hyperlocal pollution plumes will be randomly distributed between the cars over the course of the 366 min (21960 s) of mobile collocated data. Assumption (1) is supported by the observation that pollutants tend to deviate from consistent baseline (background) values. Assumption (2) is assumed to be true based on the large number of data points and the pseudo-stochastic nature of the on-road environment. Drivers intentionally switched relative positions (i.e. which car was in front) regularly to prevent a consistent bias in measurements during the drives. For a given pollutant, the statistical distribution of each car had a similar shape (i.e. a similar statistical distribution), which supports the assumption (2), that one car was not always closer to primary pollutant sources than the other car (which would result in a skewed distribution for that car relative to the others). If these two assumptions hold true, the resulting regression statistics represent systematic differences (i.e. bias) between measurements obtained by the cars, even in the presence of occasional ambient concentration differences. Passing-Bablok regressions used the deming R library (Therneau, 2018).

3.3. Separating measurement uncertainty and ambient variability while driving

Analysis methods described up until this point have focused on assessing uncertainty, reducing data to estimates of precision and bias during SC periods (Section 3.1) and bias during the MC periods (Section 3.2). To understand the relationship between measurement uncertainty and on-road variability of pollutants during the MC periods, we took the standard deviation (σ_1sec,MC) and the coefficient of variation (CV, standard deviation divided by the mean) of the measurements from the 3 cars for each time-paired 1 s period in the mobile collocated dataset (approximately 21960 data points) that had at least two valid measurements. Each time-paired 1 s period may have ≤3 valid measurements depending on the number of cars and instruments with valid data for any specific 1 s period. 2 s periods were used for O₃ due to the 2 s data reporting time of the O₃ instruments.

We use σ_{1sec, MC} and CV rather than robust estimators because we are interested in assessing the whole variability (versus just the central tendency), and because the dataset for each σ_{1sec, MC} or CV is small (N = 2 or 3). We calculated the normalized distribution and the complementary cumulative distribution functions (CCDF) for the σ_1sec,MC and CV values for each parameter. The standard deviation provides an assessment of the absolute variability in concentrations in the region covered by the 3 cars at that point in time, whereas the CV provides an assessment of the relative variability.

Measured distributions of σ_1sec,MC are compared to distributions assuming only normally-distributed uncertainty equal to σ_total (Section 3.1). We computed 3 sets of 22,000 normal random variables (with a mean of 0 and a standard deviation of σ_total) for each parameter and calculated the standard deviation of each set of 3 variables (i.e. calculated 22,000 standard deviations of 3 normal random variabls each). 22,000 is the approximate number of 1 s data points in the MC dataset, and is a large enough value that the resulting distributions approximate a normal distribution well. We only used 2 sets for BC, as only 2 cars had valid BC measurements. The distribution of the standard deviation values represent the expected distribution of σ_1sec,MC values assuming all cars were measuring the same concentrations and that all differences between the cars were due to measurement uncertainty (σ_total) rather than real concentration differences. Comparison of the expected uncertainty distribution to the measured σ_1sec,MC distribution allows us to compare the σ_1sec,MC distributions to those predicted from uncertainty alone, and by extension better understand the ambient variability on car-to-car distance scales.

Uncertainty distributions are displayed as CCDFs. The value of the CCDF at a given uncertainty value (σ_X on the horizontal axis) is the empirical probability that a randomly chosen point from the generating dataset will have an uncertainty value less than σ_X. If the empirical σ_1sec,MC CCDF distribution matches that of σ_total, the differences in measured values between the cars can be attributed to measurement uncertainties. However, if the empirical distribution is higher than the σ_total distribution, this suggests that some fraction of the measured differences are greater than that predicted by the measurement uncertainty alone and are likely due to spatial variability in pollutant concentrations between the cars.

4. Results and discussion

4.1. Range and distribution of pollutants during mobile measurements on aug 6, 2014

Although our focus is on the differences between the collocated measurements, the distribution of the measurements themselves provides an important context. Table 2 lists quantile distributions of pollutants during the MC periods. The middle 90% of measurements (Q₀₅ to Q₉₅, where Q_xx is the 0.xx quantile or xx^th percentile) have scale factors (Q₉₅/Q₀₅) of about 36, 104, 9, and 18 for BC, NO, NO₂, and O₃, respectively. BC and NO vary more than NO₂ and O₃ on a relative scale and are skewed towards higher values. The middle 90% of PN measurements scale with particle size, with Q₉₅/Q₀₅ = 3, 5, 8, and 17 for PN_0.3–0.5, PN_0.5–1.0, PN_1.0–2.0, and PN_2.0–5.0, respectively. We have found Q₀₅, Q₅₀, and Q₉₅ to be more useful summary descriptors of the data distribution than minimum, mean, and maximum values due to the small number of extreme outlier points in most species distributions.

Table 2.

Quantile distribution of pollutants during MC period, with data from all 3 cars combined (i.e. we concatenated the datasets from all 3 cars without distinguishing between the cars). The distribution of car-to-car distances is also given.

Parameter	Q05	Q25	Q50	Q75	Q95	Q99
BC (μg∙m3)	0.21	0.73	1.41	2.72	7.54	23.9
NO (ppbv)	1.80	9.60	26.6	58.8	188.0	424.8
NO2 (ppbv)	5.10	12.7	21.1	29.1	44.6	64.7
O3 (ppbv)	2.90	9.7	25.6	42.5	53.5	57.4
PN0.3–0.5 (L−1)	12163	15702	19305	24116	35243	57844
PN0.5–1.0 (L−1)	720	1123	1575	2098	3751	7206
PN1.0–2.0 (L−1)	63	127	190	275	506	996
PN2.0–5.0 (L−1)	21	63	105	169	359	741
Distance, 1–2 (m)	6.3	12.8	23.2	38.0	75.4	108.4
Distance, 1–3 (m)	10.2	21.7	42.7	66.8	108.1	176.1
Distance, 2–3 (m)	6.8	14.0	24.8	38.5	72.3	155.0

Table 2 also lists the distributions of car-versus-car distances, which provides a reference for the length scales used in the MC comparability analysis (Sections 4.4–4.6). For the 1–2 and 2–3 car pairs, 1 s car-to-car distances are <25 m over 50% of the time and <75 m over 95% of the time. Car 1–3 distances were slightly larger, but still <45 m over 50% of the time and <110 m over 95% of the time. Given the difficulty with staying close together while driving with traffic, we consider the cars to be collocated for the entirety of the MC periods, even with a small number (<1%) of car-to-car distances > 200 m. Collocation generally refers to measurements taken within meters of each other, but such strict constraints were impossible in a moving environment. Recognition of the possibility for real spatial variability on the order of the car-to-car distances, especially in the dynamic on-road environment, drove our decision to focus on robust statistical measures (e.g. median, MAD, Passing-Bablok regression, quantile distributions). Previous studies (Brantley et al., 2014) demonstrated that simple robust statistics, such as medians or rolling medians, can provide results equivalent to (or superior to) more complex statistical measures.

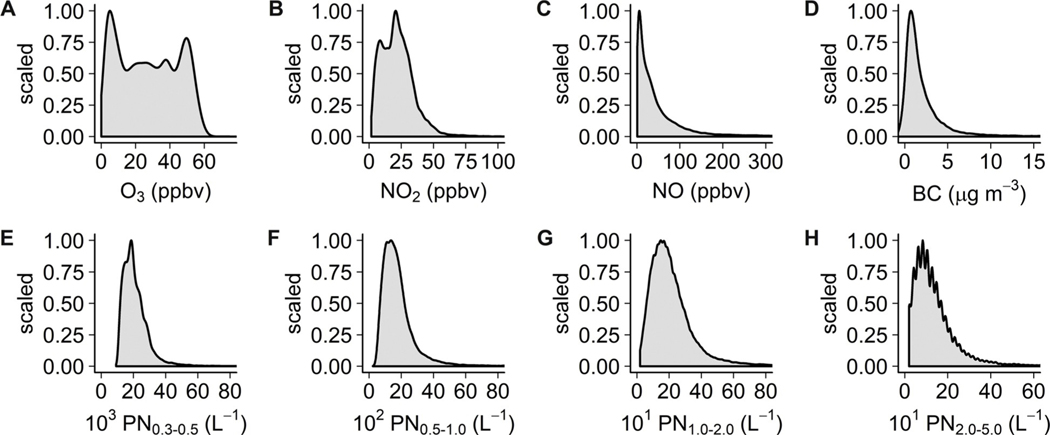
Fig. 1 illustrates the distribution of the pollutant measurements during the combined MC periods. O₃ (Fig. 1A) and NO₂ (Fig. 1B) both have a polymodal distribution, reflecting the diurnal variability in regional O₃ and NO₂ concentrations, although the O₃ distribution appears relatively uniform in the 0 ppbv–60 ppbv range, with several peaks at lower (0–20 ppbv) and higher (40–60 ppbv) values. The NO (Fig. 1C) and BC (Fig. 1D) distributions appear to be lognormal, with peak density towards the low end of the distribution and long tails at the higher end of the distribution. This reflects lower background levels for NO and BC, with significant primary (peak) values from local or mobile source emissions. This contrasts with NO₂ and O₃, which have diurnally varying background values and less pronounced peak values.

Fig. 1.

Relative distribution of pollutant concentration measurements from the mobile collocation period. The upper <1% of the distributions are trimmed from the figures to better illustrate the lower 99% of the distributions. All values are scaled to the maximum value.

The four PN size fractions (Fig. 1E – H) have similar distribution shapes, which appear somewhat normal at lower concentrations but with long, lognormal-like tails towards higher concentrations. This distribution reflects background concentrations at the lower end of the distribution with contributions from primary emission plumes at the upper end. PN_0.3–0.5 values begin above 0 (at approximately 10⁴ L⁻¹), suggesting significant background levels of PN_0.3–0.5 even under clean conditions. The lower tail of the PN_0.5–1.0 distribution also indicates non-zero background values of PN_0.5–1.0. With the PN_1.0–2.0 and PN_2.0–5.0 distributions, the main hump of the distribution terminates close to (or intersects with) 0 L⁻¹, indicating that under clean conditions the background concentrations of PN_1.0–2.0 and PN_2.0–5.0 are relatively small compared with peak concentrations. This is consistent with the size-scaling of Q₉₅/Q₀₅ ratios for PN that was noted above.

The apparent “sawtooth” pattern in the PN_2.0–5.0 distribution (and, to a lesser degree, the PN_1.0–2.0 distribution) is an artifact of the reporting resolution of the PN instrument compared to the scale at which the figure is plotted. The instrument only reports particle number counts at a specific, size-dependent resolution. For the smaller size fractions, the range of particle counts (hundreds to thousands of counts per liter) is large relative to the reporting resolution (between one and ten counts per liter). However, for larger size fractions, the reporting resolution (on the order of ten counts per liter) is similar to the range of measured particle counts (about 100 counts per liter or less for most of the measurements). This causes a quantized or pixelated (versus continuous) distribution, which causes the jagged shape shown in Fig. 1.

4.2. Temporal variability and pollutant relationships

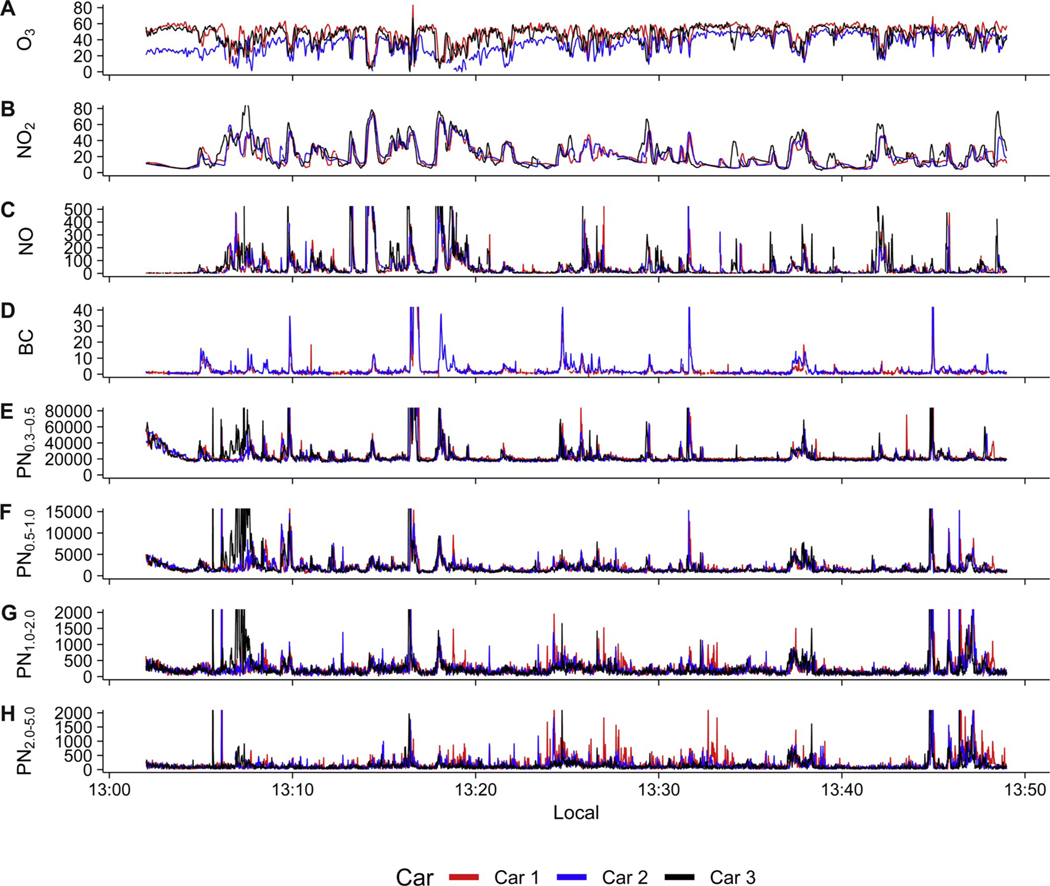
Pollutant distributions (Section 4.1) provide context for assessing measurement uncertainty; the structure of those distributions in time reveals additional insight into the nature of the measurements. Time series of all seven MC periods (Fig. 2, Fig. S2 – S7) were assessed visually. Period MC-05 (Fig. 2) demonstrates several observations about the dataset. There are periods of both low variability and high variability, with the latter generally associated with roads having higher traffic volumes. NO, BC, and PN vary significantly on short timescales (less than 10 s), but also show more persistent elevations in concentration (e. g. 13:15–13:20). These patterns reflect the observation that NO, BC, and PN can be emitted from or produced by mobile sources in the highly dynamic traffic environment.

Fig. 2.

Representative pollutant timeseries from period MC-05, showing (A) O₃, (B) NO₂, (C) NO, (D) BC, (E) PN_0.3–0.5, (F) PN_0.5–1.0, (G) PN_1.0–2.0, and (H) PN_2.0–5.0, for the three cars (two cars for BC). The y axis is truncated arbitrarily to enable a better representation of baseline variations in pollutants rather than focusing on a few minor high-lying outlier points.

Peaks in NO₂ and O₃ variations tend to be broader in time, consistent with NO₂ and O₃ concentrations being due predominantly to secondary formation chemistry, although direct emissions of NO₂ occur from diesel engines. The O₃ and NO₂ instruments have a slower response time than the other instruments (several seconds versus less than 1 s, Table 1), which could cause temporal smoothing of the O₃ and NO₂ data. NO₂ and O₃ do vary on timescales of several seconds, however, and demonstrate how dynamic the on-road environment is for pollutants that have relatively stable concentrations in clean ambient environments (e.g. O₃). Peaks in NO and NO₂ usually correspond to decreases in O₃ of similar magnitude and duration, highlighting the importance of rapid NO titration of O₃ (NO + O₃ → NO₂ + O₂) in the on-road environment.

The NO₂ and NO pairing provide information about NO_X on different time scales. NO₂ displays broad trends, likely reflective of a slower removal rate than NO and the longer response time of the NO₂ monitor. In contrast, NO is often a series of sharp peaks on top of a low and stable baseline. NO peaks are due to short-duration emissions and are quickly removed by dilution and oxidation. The quick response time (<1 s) of the NO instrument and the high degree of NO variability provides a highly dynamic picture of the local environment. Together, the simultaneous measurement of NO and NO₂ can provide details on NO_X partitioning and reactivity on different spatial and temporal scales.

PN_0.3–0.5 is elevated from 13:00–13:05, suggesting a source or accumulation of smaller particles into that size range, although increases in other PN size ranges are observed concurrently. In contrast, 13:45–13:50 shows significant elevations of the larger PN size fractions (PN_1.0–2.0 and PN_2.0–5.0) relative to baseline noise compared to the smaller size fractions (PN_0.3–0.5). There are several NO and BC peaks in the latter event. This could be a pollution plume from heavy duty diesel traffic, with possible contributions from road dust or other environmental factors. Although we could not unambiguously distinguish unique sources based on the concentration data alone, these timeseries indicate the contributions from a variety of different sources that vary in relative emissions of NO, BC, and the different PN size fractions.

4.3. Measurement uncertainty in pollutant concentrations derived during stationary collocation periods

Collocation of instruments in the ambient environment is a standard practice for assessing comparability of different methods, or even the internal precision for replicates of the same method. Collocation is based on the premise that the instruments measure from the same airmass, and thus observe the same concentrations. We used robust analysis methods to allow for a collocation experiment under near-road and on-road conditions. The nature of collocation in near source environments, particularly on road environments, does not comply with the “collocation = same concentration” assumption. This is especially true at the large inlet-to-inlet distances (meters to tens of meters) that measuring in moving traffic necessitated. We chose to use the median absolute deviation as a robust estimator for standard deviation, although other robust estimators (such as the interquartile range) likely work as well.

Period and car specific median and σ_MAD values from stationary collocated measurements (Table S3) are used to calculate study-wide estimates for the random (σ_precision) and systematic (σ_bias) measurement uncertainties for each species (Table 3). These are conservative estimates of the uncertainty within each measurement (σ_precision) and between collocated measurements (σ_bias) and do not assess the absolute accuracy of the measurements. Unlike the signed car-specific biases (Bias₁, Bias₂, Bias₃), which provide the direction (positive or negative) of the bias for each car, σ_bias is a positive value that estimates the magnitude of the measurement uncertainty due to the systematic biases for all 3 cars.

Table 3.

Estimate of uncertainty in 1 s (2 s for O₃) measurements due to random (σ_precision) and systematic (σ_bias) uncertainties during the 14 stationary collocation periods.

Parameter	σprecision	Bias1	Bias2	Bias3	σbias	σtotal
O3 (ppbv)	2.3	1.8	−2.5	1.5	2.8	3.6
NO2 (ppbv)	2.3	−0.5	−0.9	1.4	1.5	2.7
NO (ppbv)	5.9	0.2	−0.5	0.0	2.0	6.2
BC (μg∙m−3)	0.52	−0.11	0.11		0.21	0.56
1BC* (μg∙m−3)	0.42	0.05	−0.05		0.08	0.43
PN0.3–0.5 (L −1)	1300	925	−752	−87	991	1635
PN0.5–1.0 (L−1)	251	14	3	−24	31	253
PN1.0–2.0 (L−1)	93	9	1	−6	11	94
PN2.0–5.0 (L−1)	64	13	−7	−7	12	65

¹BC* is black carbon after correction for the systematic bias in Car 2 (Section 4.4).

With all of the pollutants except O₃, the uncertainty due to measurement precision is a larger fraction of the total measurement uncertainty than that from measurement bias. Bias between the cars, caused by factors such as calibration errors, are smaller than the precision of the individual measurements (i.e. σ_precision > σ_bias), boosting our confidence in the comparability of the data obtained from the three cars. The instruments and cars are identical, interchangeable, and effectively indistinguishable for the purposes of mobile air pollution measurement. Confirmation of car comparability is critical for creating a scalable system of mobile measurements but has been limited in previous studies (e.g. Apte et al., 2017). The precision and bias during the SC analysis provides a foundation for exploring the comparability in the mobile environment (Section 4.6).

Ozone is the exception to the observation that σ_precision > σ_bias. A potential issue can be seen visually in Fig. 2, where O₃ from Car 2 appears systematically low during part of MC-05. This was observed to a lesser extent in MC-01, MC-02, and MC-03, but not significantly during the other periods. Car 2 also has a systematic negative bias relative to the other cars during the SC periods (Table 3). It is possible that the ozone concentrations observed during some of the SC and MC periods were adversely affected by reduced reagent gas (N₂O) flow supplied to the analyzer (Supplemental Information). Although efforts were made to flag and remove affected data, we only screened data when justified by specific notes or other instrument-specific indicators. For quality assurance reasons, we did not remove data that looked suspicious or incorrect without specific documentation justifying the removal of that data. Following the Denver study, improvements to the reagent gas supply system has essentially eliminated this issue for all future studies.

4.4. Systematic differences between cars during combined mobile collocations

Although we assessed instrument performance under stationary conditions (Section 4.3), we are most interested in ensuring that the measurements from different cars are comparable in a mobile environment. To do that, we assessed the bias between the cars during the combined mobile collocation periods using robust (Passing-Bablok) regression analysis. Table 4 shows the slope and intercept for each car pair and pollutant, as well as the Pearson correlation (r). Comparison of regression lines with the distribution of points (shown as a density of points) is shown in Fig. S8 for several species. Slopes for O₃, NO₂, NO, PN_0.5–1.0, and PN_1.0–2.0 are all within 10% of 1.0, and the intercepts are smaller in magnitude than the stationary estimates of uncertainty due to bias (σ_bias, Table 3). We consider a slope variation of up to 10% to be a reasonable criteria for comparability in this situation given the high variability in concentrations and the potential for meter-scale concentration variability in the collocated mobile measurements. For these five pollutants, the cars meet this comparability criteria in the mobile environment.

Table 4.

Slope and intercept from Passing-Bablok regressions of each parameter and car pair. r is the Pearson correlation coefficient. Slopes that differ from 1.0 by more than 10% and intercepts larger than the associated σ_bias value (Table 3) are in bold face.

Car Pair	2 vs 1			3 vs 1			3 vs 2
Parameter	Slope	intercept	r	Slope	Intercept	r	Slope	Intercept	R
O3	1.07	1.14	0.95	1.04	1.04	0.93	0.98	− 2.25	0.94
NO2	1.01	− 0.85	0.87	1.10	−1.29	0.76	1.09	− 0.38	0.84
NO	1.08	− 0.13	0.55	1.00	− 0.80	0.38	0.97	−1.04	0.53
PN0.3–0.5	0.87	766.54	0.73	0.85	1661.43	0.60	0.98	875.43	0.69
PN0.5–1.0	1.00	− 5.28	0.57	0.96	−10.97	0.25	0.97	−17.93	0.31
PN1.0–2.0	1.00	2.00	0.37	0.93	− 5.20	0.20	0.99	0.49	0.36
PN2.0–5.0	0.88	0.75	0.27	0.72	9.51	0.28	0.87	5.55	0.67
BC	1.56	− 0.04	0.73

PN_0.3–0.5 and PN_2.0–5.0 have slopes that deviate up to 15% and 28% from 1.0, respectively. In addition, the 3–1 car pair had a PN_0.3–0.5 intercept larger than the estimated intercar bias (σ_bias, Table 3). Visual inspection of the pollutant timeseries (Fig. S2 – S7) does not reveal significant systematic variability between the different cars. Scatterplots of Car 1 PN_0.3–0.5 versus that of Car 2 (Fig. S8J) and Car 3 (Fig. S8K), however, show deviations from the 1:1 line in the highest density trend region. Therefore, it is possible that a 13%–15% systematic bias does exist for Car 1 relative to Cars 2 and 3 for PN_0.3–0.5. This is consistent with the bias estimate from the SC periods (bias₁ in Table 3), which suggest that Car 1 is systematically low. We were unable to determine the source of the potential systematic bias. The PN instrument was calibrated by the manufacturer and we did not have sufficient equipment on-site to confirm the calibration except for the zero. It is possible that one instrument was calibrated on the low end of the manufacturer’s specification range (10%), whereas the other two were on the higher end. It is also possible that minor differences in the inlets might also have caused one to have higher wall losses than others. Given the large range of measurements and the difficulty with accurate size-fractionated particle number measurements, we do not consider a 15% discrepancy to have significant impact on our results.

Several factors make it challenging to assess the PN_2.0–5.0. These factors include the high degree of baseline noise, low precision relative to signal (Tables 2 and 3), and large “step size” between subsequent measurements (discussed in Section 4.1).

BC shows a large (>50%) systematic bias, with Car 2 reading about 56% higher than Car 1 (Table 4). Continued use of these same instruments post-Denver showed a 52% difference between the instruments, which was corrected by reducing the higher-reading instrument by 52% to be consistent with the lower-reading instrument (Apte et al., 2017). The two BC instruments used in this study are the same two instruments used in Apte et al. (2017), where the higher reading instrument (in Car 2 in this study) was determined by the manufacturer to be biased high, whereas the lower reading instrument was determined to be accurate. We choose to scale the Car 2 BC to be consistent with Car 1 for the remainder of the paper (Sections 4.5 and 4.6) by dividing all Car 2 value by 1.56. The scale factor of 1.56 is based on the Passing-Bablok slope between BC measurements in Car 2 versus Car 1 (Table 4). We repeated the SC analysis with the scaled value and show that scaling the Car 2 BC measurements significantly reduces the car-versus-car bias (σ_bias) by almost a factor of 3 (BC* in Table 3). The scaled BC value is denoted BC* to distinguish it from the raw BC measurement.

4.5. Car-versus-car measurement relative variability

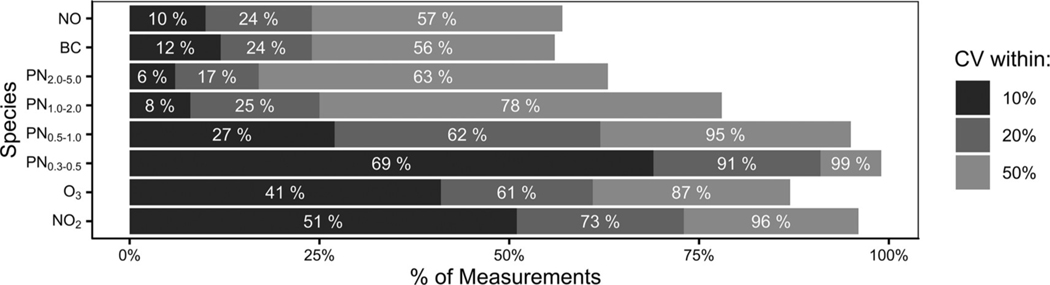
To explore the car-versus-car measurement variability of the different pollutants, we computed the coefficient of variation (CV) for each set of time-paired 1 s measurements during the MC periods where at least 2 cars reported data. The percentage of time-paired 1 s measurements with CVs below 10%, 20%, and 50% for each pollutant are shown in Fig. 3. NO, BC*, and the larger PN size classes (PN_1.0–2.0 and PN_2.0–5.0) had the highest degree of relative variability (i.e. highest fraction of CV pairs above 50%). NO, BC (and BC*), PN_1.0–2.0, and PN_2.0–5.0 all have low baseline concentrations (e.g. Fig. 2), and NO and BC have higher Q₉₅/Q₀₅ ratios than NO₂ and O₃, indicating a larger relative range of variability in pollutant concentrations.

Fig. 3.

Percentage of mobile collocated data points with a coefficient of variation below 0.1 (10%), 0.2 (20%), and 0.5 (50%), showing the relative degree of variability for different measured pollutants.

The large difference in relative variability between NO and BC* versus NO₂ and O₃ is consistent with the expected pollutant behavior between these two groups. NO and BC both have low background concentrations and are emitted as primary emissions from mobile sources. This results in sharp peaks in the pollutant measurements as the car and the mobile source pass near each other, providing the potential for a large range of concentrations. O₃ is predominantly a secondary species formed from photochemical reactions of NO_X and VOCs, but is titrated quickly near combustion sources by NO. NO₂ can be both a primary and a secondary pollutant but has a significantly longer lifetime than NO in the presence of O₃. Evidence for the different behavior of NO and BC versus NO₂ and O₃ comes from Fig. 1, with NO and BC having approximately lognormal distributions, whereas NO₂ and O₃ are closer to a uniform distribution. O₃ and NO₂ have higher background concentrations and lower peak concentrations than NO and BC. Combined with the longer response time of the O₃ and NO₂ instruments, this explains why most (>60%) of the CV values for O₃ and NO₂ are less than 20%, whereas only about 24%–26% of NO and BC* CV values are below 20%.

The shape of the absolute PN distributions are similar for all four PN size fractions (Fig. 1). However, the PN_0.3–0.5 and PN_0.5–1.0 size fractions never read values of zero – there is always some background concentration of PN_0.3–0.5 and PN_0.5–1.0. In contrast, both PN_1.0–2.0 and PN_2.0–5.0 have measured values at or near 0 L⁻¹. This means that the relative variability in PN (compared against a lower quantile, such as Q₀₅) will be higher for larger size fractions than smaller size fractions, scaling similarly to the Q₉₅/Q₀₅ ratios. Differences in relative variability between the smaller and larger PN size fractions could be due to higher inherent variability in larger size fractions than smaller size fractions (due to the influence of source factors such as road dust or brake or tire wear) but may also be due to differences in background concentrations and low concentrations in these size ranges.

4.6. Car-versus-car variability during MC periods

We have summarized the pollutant distributions from the MC periods (Section 4.1), derived insight from a visual inspection of the timeseries (Section 4.2), and computed estimates of precision and bias from SC periods (Section 4.3). Robust regression analysis (Section 4.4) provided some constraints on biases among the cars while moving. While providing a useful screening tool for assessing potential bias, additional insights were needed to understand the performance of the measurements while the cars were moving relative to the variability in ambient pollutant concentrations.

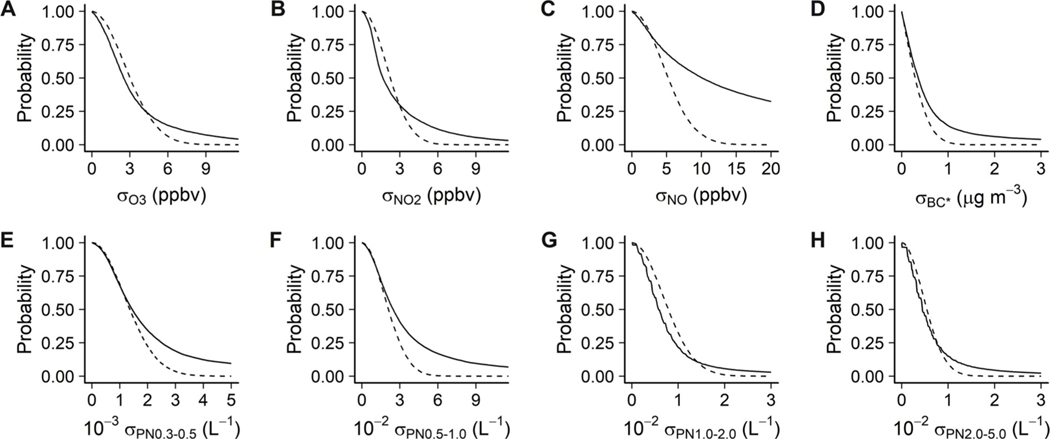
We assessed the distribution of pollutant variability for the MC periods through the CCDFs, which are presented in Fig. 4 as solid lines. These distributions are shown alongside a theoretical distribution assuming no ambient variability, with only measurement uncertainty. We assume that the theoretical distribution of the measurement uncertainty for each car is normally distributed around the true concentration, with a standard deviation of σ_total (Table 3).

Fig. 4.

Complementary cumulative distribution function (CCDF) of standard deviation values from 1 s (2 s for O₃) measurements of the three collocated cars during MC periods, for (A) ozone, (B) nitrogen dioxide, and (C) nitric oxide, (D) BC, (E) PN_0.3–0.5, (F) PN_0.5–1.0, (G) PN_1.0–2.0, and (H) PN_2.0–5.0. Dashed lines represent theoretical values assuming that all the variability was caused by the uncertainties calculated in Section 4.3.

We interpret the portion of Fig. 4 where the empirical CCDFs overlap with the theoretical distribution as periods when the variability in the measurements among the cars could be attributable to uncertainty in the measurements. This represents about 70% of the variability for O₃, 65% for NO₂, 15% for NO, and essentially none for BC*. For PN size fractions, the overlapping regions range from 30% (PN_0.5–1.0) to 90% (PN_1.0–2.0), with no apparent relationship between the particle size and the associated variability due to uncertainty. The region above this overlap region represents measured variability larger than what can be explained by σ_total, and thus represents ambient spatial variability on car-to-car distance scales.

If we consider that all the variability is caused by measurement uncertainties and that our estimates of measurement uncertainties from the stationary environment (Section 4.3) extend into the mobile environment, the empirical CCDF should line up exactly with the theoretical distribution. Any actual differences in true values between collocated measurements (i.e. ambient variability) will cause the CCDF to lie above the theoretical distribution.

In general, the empirical distributions agree reasonably well with the theoretical distributions at lower values, which provides confidence for our estimates of uncertainty based on the stationary collocated periods (σ_total). For PN_1.0–2.0 (and, to a lesser degree, O₃ and NO₂), the theoretical distribution predicts larger uncertainties at lower quantiles than the empirical distribution. Assuming the overlapping values reflect periods when the cars were measuring the same concentrations, the theoretical distribution appears to be overestimating the empirical distribution. This may indicate that our method for assessing the uncertainty for the stationary collocated periods is overestimating the uncertainty observed in the mobile environment.

The lack of overlap for BC* could suggest that our stationary estimate of uncertainty for black carbon underestimates the uncertainty in the mobile environment. Although there is generally strong correspondence between the theoretical and empirical distributions at lower values, they diverge at higher values for all species. The divergence is faster for NO, but even more spatially homogeneous species (O₃ and NO₂) show divergence over 30% of the time. We interpret the region of divergence as periods when the cars were measuring ambient variability in pollutant concentrations due to localized pollution sources (i.e. plumes from mobile sources). Our interpretation of the relationships between the empirical and theoretical distributions is consistent with the expectation that ambient variability will be highest for the predominantly primary pollutants (BC and NO) and lowest for the predominantly secondary pollutants (O₃ and NO₂), with PN having intermediate values (except for PN_1.0–2.0, in which the uncertainty may be overestimated).

The CCDF figures plots (Fig. 4) should not be over-interpreted. We use this comparison to assess the high-level relationship between the stationary uncertainty estimates, the uncertainty while the cars are moving, and the measured ambient variability, but are cautious to not over-interpret the data. However, a first-order analysis suggests that stationary estimates of measurement uncertainty are overly conservative for O₃, NO₂, and PN when extended to the mobile environment. Possible reasons for this are discussed in the following section (Section 4.7).

4.7. Sensitivity of measurement uncertainty to assumptions and methodology

There are several factors that would lead to an overly conservative estimate of measurement uncertainty from the stationary collocated periods using our methodology. The first is bias that arises from the nature of the collocation. When two or three cars are stationary and collocated, any positional biases between the cars will be carried through the collocation period. Examples of possible biases are relative position of the cars compared to a busy street or intersection, or the relationship between the car positions and eddies formed by the local urban microenvironment. When the cars are moving during the MC periods, any position biases are averaged out by the constant motion of the cars through space. Because all the collocated cars are in motion, they are all sampling a much larger volume of air during the same sample period, and their relative positions in space are constantly shifting. There will be positional biases for individual (or groups of) 1 s sampling periods during the mobile collocation periods, such as when one sampling car passes closer to a high-emitting vehicle than the other sampling cars. However, such intermittent biases will average out towards a typically less biased comparison in a mobile setting, versus the stationary collocations, where any positional biases are likely to be persistent throughout the entire sampling period.

Another possible explanation for the SC-based overestimate of the MC uncertainty is that the statistical methods used to estimate the SC uncertainties are overly conservative. The median, MAD, and Passing-Bablok regression statistics are all based heavily (or entirely) on the median, or 50^th percentile. In a balanced distribution, such as when we are comparing two cars, we expect outliers or near-source events to be distributed equally between the two cars. Thus, by focusing on the center of the distribution (i.e. the median), we ignore the outliers on both sides and zero in on the region where the cars should be measuring the same values. This allows us to use the median-based Passing-Bablok regression to compare car pairs even in the presence of a high degree of random scatter (or, in this case, extreme near-source pollutant measurements for one car but not the other).

The impact of the assumptions made in Section 4.3 to use σ-_MAD to calculate the SC uncertainties are complex. The σ-_MAD values were similar to the typical standard deviation values in most cases, especially for less variable pollutants (such as O₃ and NO₂), with several exceptions in each case due to ambient variability during the collocation period (Table S3). In terms of σ-_MAD as a robust estimator for precision, it will be most immune to short-duration spikes in pollution over a constant background, which would have a large impact on standard deviation but would not impact σ-_MAD. σ-_MAD is more sensitive to slowly varying background levels, which may be expected in ambient air over a 20–60 min measurement period. If ambient levels of the pollutant being measured vary during the measurement period, that will inflate the time-integrated σ-_MAD value over the idealized 1 s estimates. Because the MC car comparisons are 1 s car-versus-car comparisons, differences will be isolated to measurement uncertainties and spatial variability. For the time-integrated σ-_MAD values calculated in Section 4.3, differences can be due not only to measurement uncertainties and spatial variability, but also time-varying ambient concentrations during the measurement period.

The additional decision we made in Section 4.3 that impacted our estimated theoretical distributions in Fig. 4 was to use the median σ-_MAD value for the 14 SC periods (times 2 or 3 cars). The median was again chosen to be a robust estimate for the central tendency of the group of measurements. In this case, however, perhaps the choice of the median was biasing the estimate high. If we are considering just the measurement uncertainty due to instrument precision, the minimum σ-_MAD value may have been a better estimate. If we accept the assertion that σ-_MAD provides a good estimate for instrument precision under ideal circumstances, it would be challenging for the instrument to produce results better than its inherent precision (and thus to produce σ-_MAD value below the precision). Therefore, all measured σ-_MAD values must be greater than or equal to the precision. It is possible, however, for σ-_MAD to be higher than the inherent precision, such as in the case of a time-varying background concentration during the measurement period. Although choosing the minimum σ-_MAD value for each parameter would have increased the sensitivity to potential errors on the low end, choosing a lower percentile (such as the 10^th or 25^th percentile) instead of the 50^th percentile may have provided a more realistic estimate of the measurement uncertainty that would transfer better to the MC periods.

We choose to retain the median-σ-_MAD based estimate for the present purposes because it is conservative. For quality assurance purposes, we consider reporting a conservative estimate of uncertainty to be superior to underestimating errors and forming erroneous conclusions. Based on our results, it appears that measurement uncertainty estimates from collocated mobile monitoring platforms while stationary extend conservatively into the mobile environment. Although we cannot generalize beyond the current study, this finding has the potential to simplify quality assurance for future multi-platform and fleet-based mobile air quality monitoring studies. Stationary collocated analyses appear to be sufficient to estimate the uncertainty in measurements in the mobile environment, even when the concentration ranges in the mobile environment is significantly larger.

5. Conclusions

We report results from a mobile monitoring study in Denver, Colorado during the summer of 2014. Quality assurance considerations were included as part of study design, instrument selection, data collection, and data analysis. Air pollutants were measured using accurate, high time resolution (1 hz, or 0.5 hz for O₃), research grade instrumentation. Daily zero checks (and span checks for O₃ and NO) ensured that the instruments remained with the manufacturer’s specification, with resulting zero values and instrument-specific biases within EPA-recommended guidelines for air quality measurement. In addition, our statistical peak alignment method, essential to ensure data points have accurate timestamps, were consistent with values calculated based on the manifold specifics providing confidence in our methodology. The quality assurance practices resulted in a robust dataset of collocated measurements for evaluating statistical techniques for assessing precision, bias, and variability in a mobile environment.

The uncertainty was evaluated under collocated stationary conditions and then applied to car-versus-car variability in measurements during the mobile collocated driving periods. We found that O₃, NO₂, PN_0.3–0.5, PN_0.5–1.0, PN_1.0–2.0, and PN_2.0–5.0 all produced absolute variability distributions similar to estimates based on precision and bias alone for lower values, suggesting that the lower 40%–80% of the observed variability can be partially attributed to measurement or instrument uncertainty. The stationary collocated estimates of uncertainty were based on medians and median absolute deviations and seemed to overestimate the uncertainty observed in the mobile collocation periods. We hypothesize that this overestimate could be due to differences between the stationary and mobile environments, differences between the way the two uncertainty estimates were evaluated, or choices made in estimating the stationary uncertainty.

Periods when the mobile variability distribution reflects the stationary uncertainty likely represent local on-road and near-road background conditions with some influence from regional background or from diffuse pollution emission plumes measured simultaneously by instruments in all three cars. The upper 20–60% of the distribution showed a divergence between estimates of variability due to measurement uncertainty and the observed ambient variability in pollutant concentrations. These points cannot be attributed to measurement uncertainties and likely represent true ambient variability over car-to-car distance length scales, such as near-source short-duration plume sampling.

The correspondence between the stationary uncertainty estimates and mobile distributions at lower values provides evidence that uncertainty estimates derived from stationary performance evaluations transfer well to the mobile environment under the conditions tested. Robust statistical measures that account for the occasional (~20%) outlier points are especially powerful in separating the uncertainty statistics from measurements containing ambient variability. This observation, once evaluated under a larger range of conditions, may provide a method to simplify quality assurance approaches for future fleet-based (or other multi-platform) mobile monitoring campaigns. Appropriate instrument selection, a well-planned experimental design, a solid quality assurance project plan, and the use of appropriate statistical techniques are all important components of a successful mobile monitoring study. The use of robust statistical metrics for constraining uncertainty can provide a powerful technique for assessing mobile monitoring data. As mobile fleet-based monitoring advances in the future, it will provide regulators and the community extensive data about hyperlocal air quality. This data, if interpreted with the appropriate statistical techniques, will be used to improve air quality and exposure modeling, as well as providing the public with real-time, actionable information to lower exposure and reduce health-based risk to air pollution.