Abstract
The development of fluid-structure interaction (FSI) software involves trade-offs between ease of use, generality, performance, and cost. Typically there are large learning curves when using low-level software to model the interaction of an elastic structure immersed in a uniform density fluid. Many existing codes are not publicly available, and the commercial software that exists usually requires expensive licenses and may not be as robust or allow the necessary flexibility that in house codes can provide. We present an open source immersed boundary software package, IB2d, with full implementations in both MATLAB and Python, that is capable of running a vast range of biomechanics models and is accessible to scientists who have experience in high-level programming environments. IB2d contains multiple options for constructing material properties of the fiber structure, as well as the advection-diffusion of a chemical gradient, muscle mechanics models, and artificial forcing to drive boundaries with a preferred motion.
Keywords: fluid-structure interaction, biomechanics, immersed boundary, math biology
1. Introduction
Fully coupled fluid-structure interaction problems (FSI) is a rapidly growing discipline across all the sciences, ranging from engineering to biology [1]. Fully coupled FSI is different from models in which the motion or bending of a structure is prescribed. The action of the aortic valve is a good example of fully coupled FSI, since the motion of the valve is governed by the motion of the fluid, and in turn, the valve alters the underlying blood flow. Note that in a fully coupled simulation, the movement of the valve would not be prescribed.
The immersed boundary (IB) framework was first published in 1972 to study blood flow around valve leaflets of the heart by Charles Peskin [2]. It has been applied to a plethora of biomechanics problems which involve the interaction of a flexible structure immersed in a viscous, incompressible fluid. The method has been successfully applied to study fluid dynamics in a variety of biological settings within the intermediate Reynolds number range, defined here as 0.01 < Re < 1000, where
| (1) |
μ and ρ are the dynamic viscosity and density of the fluid, respectively, and L and V are a characteristic length and velocity of the problem. Some of these applications include cardiovascular dynamics [3, 4], aquatic locomotion [5, 6], insect flight [7-9], muscle-fluid-structure interactions [10-12], and plant biomechanics [13].
The strength of this method is that it can be used to model fully coupled fluid-structure interaction problems involving complicated time-dependent geometries using a regular fixed Cartesian discretization of the fluid domain, while the elastic fibers describing the structure are discretized on a Lagrangian mesh. The fluid and elastic fibers constitute a coupled system in which the structure moves at the local fluid velocity and the structure applies a singular force to the fluid.
Beyond fully-coupled fluid-structure interaction models, many scientists have successfully coupled other constitutive equations within the IB framework [10, 14-20]. For example, in [15], Fogelson and Guy modeled platelets suspended in an incompressible fluid to study blood clotting and included chemical reaction equations modeling the mechanisms for binding-unbinding, platelet stimulus-response, and chemistry on the platelets surfaces. Moreover, in [10], Tytell et al incorporated calcium dynamics, which governed the muscle contraction dynamics that were responsible for force generation in a swimming lamprey.
Many implementations of the immersed boundary method (IBM) exist in compiled programming languages, including a few open source and freely available packages, e.g. IBIS [21] and IBAMR [22]. IBIS is IB software written in FORTRAN that includes its own graphical user interface, ibisview, to visualize the simulations. IBAMR is an adaptive and parallelized implementation of the IBM in C++, with extensions to a hybrid implementation of IB which uses a finite element discretization of the immersed structure [23]. It depends on many open source libraries, including PETSc [24], SAMRAI [25], libMesh [26], and OpenMPI [27] which make it robust and very efficient to run but at the cost of a steep learning curve for anyone inexperienced at high performance computing. Moreover installation of IBAMR is non-trivial, as it requires installing the above open source libraries and coupling them with the IBAMR framework. Furthermore, without multi-processor computational resources available, IBAMR cannot run at its full potential.
IBAMR was developed for highly resolved computational grids and specifically designed to include adaptive mesh refinement (AMR) capabilities. AMR allows for more computational speedup; it dynamically adapts the computational grid for higher resolution near regions of interest, e.g. boundaries and regions of vorticity above a user-prescribed threshold, while solving at lower resolution in other areas. Because of IBAMR’s AMR and parallelization capabilities, it can be used for 3D applications unlike previous open source IB software, such as IBIS, which was strictly developed for 2D applications.
IBIS AND IBAMR, having been written in lower level programming languages, e.g. FORTRAN and C++ respectively, require familiarity with these languages. For students and scientists from disciplines that are not typically trained in rigorous programming, these languages are often inaccessible and necessitate a steep learning curve.
Recently there have been a few open source 2D IB codes available on GitHub, such as matIB [28] and pyIBM [29], which are a MATLAB and Python 3.5 implementation, respectively. Charlie Peskin also has a MATLAB 2D IB implementation available on his website [30]. All these implementations use the standard immersed boundary framework [31] but do not include a breadth of fiber models or examples and are not as robust or efficient in comparison to their 3D counterparts, such as IBAMR. However, implementations in these high-level programming languages offer many powerful advantages, perhaps foremost being that they are more readable and familiar to a broad audience of scientists and engineers.
In this paper, we present IBM software called IB2d with full implementations in both MATLAB [32] and Python 3.5 [33] that is capable of modeling a broad array of problems in biomechanics including (but not limited to) locomotion, physiological processes, and plant biomechanics. Even for skilled programmers, IB2d represents a nice option for preliminary tests of new models. For example, one may add new muscle models to the software quite easily for testing before attempting an implementation in a more challenging software framework such as IBAMR.
IB2d is an extension of the preliminary code found in [11]. It extends the capabilities of this code by introducing a full implementation in Python, numerous additions in functionality, such as more fiber-structure modelling options, advection-diffusion, electrophysiology models, and artificial forcing, as well as visualization output and data analysis options. The package also contains 30+ examples, which illustrate the breadth of the software.
2. IBM framework
IB2d models the fluid motion in two dimensions using the Navier–Stokes equations in Eulerian form, given as
| (2) |
| (3) |
where u(x, t) = (u(x, t), v(x, t)) is the fluid velocity, p(x, t) is the pressure, and f(x, t) is the force per unit volume (area in 2D) applied to the fluid by the immersed boundary. The independent variables are the position, x = (x, y), and time, t. Equation (2) is equivalent to the conservation of momentum for a fluid, while equation (3) is the condition mandating that the fluid is incompressible. IB2d also assumes a periodic and square fluid domain. Future implementations will incorporate non-square domains as well as the inclusion of a projection method solver to enforce Dirichlet and Neumann boundary conditions [34, 35].
The interaction equations between the fluid and the immersed structure are given by
| (4) |
| (5) |
where X(r, t) gives the Cartesian coordinates at time t of the material point labeled by Lagrangian parameter r, F(r, t) is the force per unit area imposed onto the fluid by elastic deformations in the immersed structure as a function of the Lagrangian position, r, and time, t. The force density, F(r, t), is a functional of the current immersed boundary’s configuration. Moreover, we write the force density as
| (6) |
where is a combination of all the fiber components modeling the desired material properties of the immersed structure. The fiber models implemented in IB2d are described in subsequent sections.
Equation (4) applies a force from the immersed boundary to the fluid through a delta-kernel integral transformation. Equation (5) sets the velocity of the boundary equal to the local fluid velocity, to satisfy the no-slip condition.
Upon discretizing equations (4) and (5), regularized delta functions, δh, are implemented,
| (7) |
where h is the fluid grid width and
| (8) |
where r is the distance from the Lagrangian node. This regularized delta function has compact support. Other compactly supported discrete delta functions may be easily incorporated into the code as well. More details on regularized delta functions and their discretizations may be found in [31, 36].
The coupled equations (2)-(5) are solved using the algorithm described in Peskin’s IB review paper [31] with periodic boundary conditions imposed on both the fluid and immersed boundary. Details on the discretization used in IB2d are found in appendix.
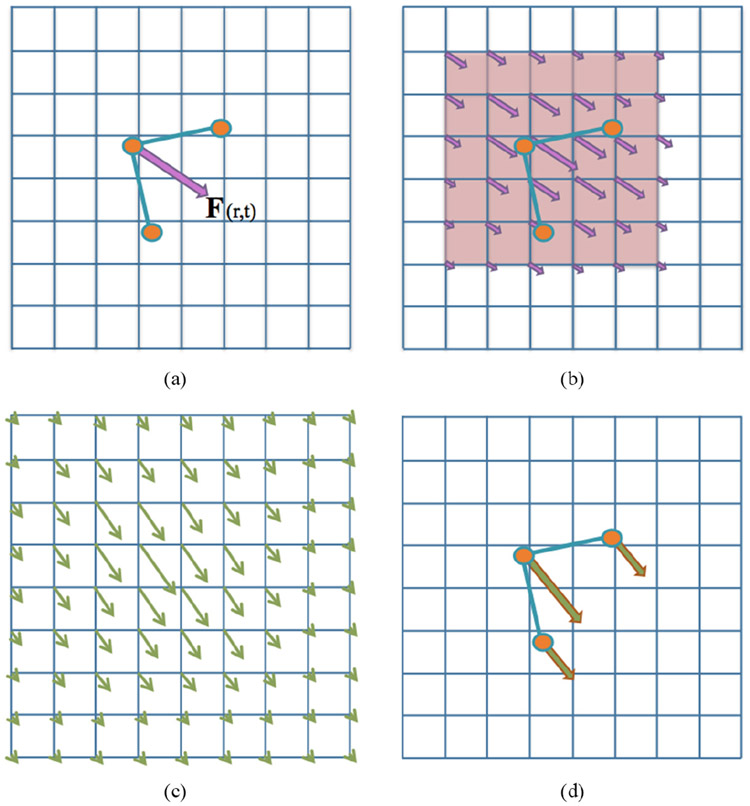
The standard numerical algorithm for immersed boundary [31], illustrated in figure 1, is as follows:
Figure 1.
A visual guide to the standard steps in Peskin’s immersed boundary method. (a) The elastic deformation forces are computed from the current configuration of the immersed structure. (b) Those deformation forces are spread to neighboring fluid grid points, via equation (4). (c) The fluid velocity is updated everywhere in the domain using equations (2) and (3). (d) The immersed boundary is moved at the local fluid velocity by equation (5). Note that the deformation force vectors in (b) and velocity vectors in (c) are not parallel, as the fluid already may have some underlying non-zero velocity field, which gets perturbed due to the presence of the deformation forces.
Step 1: Compute the force density Fn(r, t) on the immersed boundary from the current boundary deformations, Xn, where n indicates the nth time-step.
Step 2: Use equation (4) to spread these deformation forces from the Lagrangian nodes to the fluid lattice points nearby.
Step 3: Solve the Navier–Stokes equations, equations (2) and (3), on the Eulerian domain. e.g. update un+1 and pn+1 from un and fn. Note: since we are enforcing periodic boundary conditions on the computational domain, the Fast Fourier transform (FFT) [37, 38] is used to solve for these updated quantities at an accelerated rate.
Step 4: Update the fiber model positions, Xn+1, using the local fluid velocities, Un+1, using un+1 and equation (5). e.g. move the immersed structure at the local fluid velocities thereby enforcing no slip boundary conditions.
2.1. Fiber models
In this section, all current fiber models implemented in IB2d are described. Various fiber models give the immersed boundary certain desirable material properties relevant to many scientific applications. Currently the following types of fiber models are available:
Springs (Hookean or Non-Hookean)
Torsional Springs
Target Points
Mass Points (with or without gravity)
Porosity
Muscle-Fluid-Structure Models
Once the deformation energy has been calculated in the algorithm, e.g. in Step 3,
| (9) |
the corresponding elastic forces can be computed via derivatives of the elastic energy, where the elastic deformation force at point c of fiber model k is calculated as
| (10) |
Note that X contains the coordinates of all immersed boundary points, M is the number of fiber structures in the system, M is the number of immersed boundary points in fiber structure, and the negative sign is chosen to drive the system towards a minimal energy state. Furthermore we note that (9) is a combination of the deformation energies from all respective fiber models, which are described below.
2.1.1. Springs
Resistance to stretching between successive Lagrangian points can be achieved by modeling the connections with Hookean (or Non-Hookean) springs of resting length RL and spring stiffness kS. If the virtual spring displacement is below or beyond RL, the model will drive the system back towards a lower energy state. The elastic potential energy for a Hookean spring is given by
| (11) |
where XM and XSL are master and slave node coordinates respectively. The corresponding deformation forces is given by differentiation of the elastic energy as in equation (10)
| (12) |
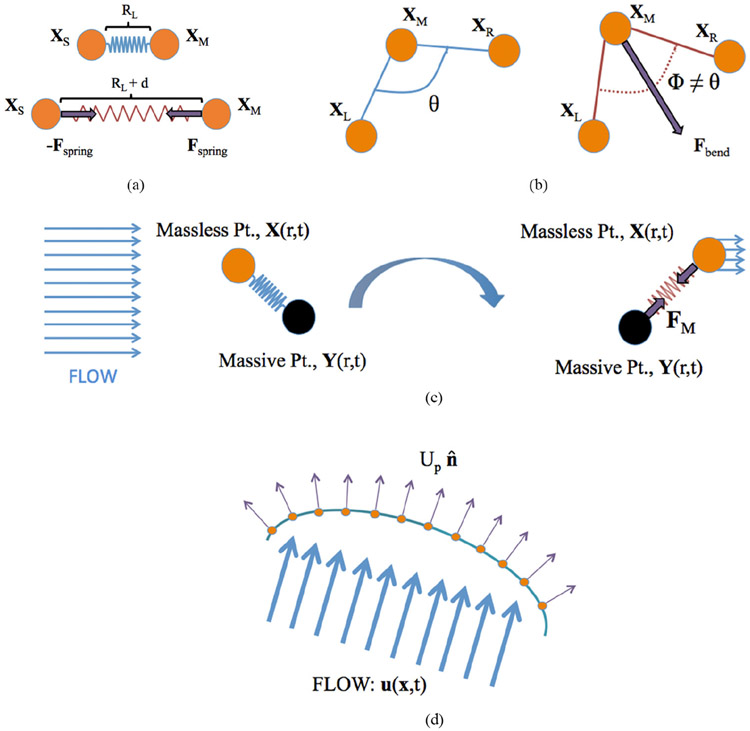
This fiber model is illustrated in figure 2(a). Note that the above calculation computes the forces acting on the master node; a change in sign gives the forces acting onto the slave node. Two nodes are connected by a virtual spring shown when the spring is at resting-length (top). A rendering of the longitudinal forces induced when the spring is stretched is also depicted (bottom).
Figure 2.
Illustrating the key points of various fiber models implemented in IB2D. (a) Two nodes connected by a virtual spring held at the resting-length of the spring (top) and a rendering of the longitudinal forces induced when the spring is stretched (bottom). (b) A torsional spring connecting three adjacent Lagrangian nodes at its equilibrium configuration, e.g. angle θ (left) and an illustration of the force experienced by the middle node, XM, when the system is not at its lowest energy state (right). (c) A massless and massive point, X and Y respectively, connected by a stiff virtual spring. Incoming flow moves the massless point to a new position, which exerts a pulling-like effect on the massive point. The massive point will move depending on a coupled constitutive equation. (d) Incoming flow permeates a porous boundary. The amount of flow that moves through the body depends on the permeability of the membrane; all flow through the boundary is normal to the body itself.
Furthermore, IB2d also implements nonlinear springs that assume the nonlinear extension of equation (11), i.e.
| (13) |
where . The corresponding force onto the master node is then given by
| (14) |
2.1.2. Torsional springs (‘beams’)
Resistance to bending between three successive Lagrangian points is modeled using a torsional spring connecting the three nodes. The model assumes a desired angle θ, a prescribed ‘curvature’ between the three Lagrangian points, with corresponding bending stiffness kB. Hence the bending energy is given as
| (15) |
where XR, XL, and XM are right, left, and master Lagrangian nodal coordinates, and C = dLMdMR sin θ. Note that C is not the standard definition of curvature, but a curvature defined at the desired angle θ and distances between links, dLM and dMR. This is only accurate for small changes in amplitude or radii and higher order accurate curvature models will be implemented in future releases.
The penalty force is designed to drive any deviations in the angle between these links back towards a lower energy state, i.e. θ. The corresponding bending force is given by
| (16) |
An illustration of 2D torsional springs is shown in figure 2(b), where a torsional spring connects three adjacent Lagrangian nodes XL, XM, and XR at their equilibrium configuration with angle θ (left). The force is experienced by the middle node, XM, when the system is not at its lowest energy state (right), driving it back to its preferred configuration.
In this configuration, torsional deformation forces can only occur on immersed boundary points on the interior or the fiber structure, not the endpoints.
2.1.3. Target points
Target points can be used to prescribe a preferred position or motion of the Lagrangian points. In this formulation, each Lagrangian point is associated with a virtual or target point. The boundary point is connected to its virtual target point via a stiff spring, i.e. a spring with zero resting length. Essentially the virtual point mandates where the target point should be. The deformation energy is given similarly to equation (11),
| (17) |
where kT is the target point stiffness and XM and are the coordinates of the physical Lagrangian point and virtual target point, respectively. Hence the corresponding deformation forces are given as
| (18) |
Note that in both cases, it is standard for kT to be very large in order to hold the Lagrangian points nearly rigid or move them in a prescribed manner based on updating the positions of the virtual nodes. Many scientists have used this formulation to prescribe motion in a variety of contexts [8, 39].
2.1.4. Massive points
Artificial mass can be modeled on the fiber structure using an approach that is similar to target points. Y(r, t) gives the Cartesian coordinates of the massive points, with associated mass density M(r). These points do not interact with the fluid directly and can be thought to be a virtual point. X(r, t) give the Cartesian coordinates of the Lagrangian boundary points which are massless and interact with the fluid. Recall that the boundary points also move at the local fluid velocity, and exert elastic deformation forces to the local fluid grid. If the massive points deviate from the Lagrangian boundary points, a restoring force will drive them back together.
The equations modeling this system are
| (19) |
| (20) |
where kM is a stiffness coefficient with kM ≫ 1, and g is the acceleration due to gravity in direction .
Note that the coupling is very similar to the target point formulation with the distinct difference that, rather than the movement of the massive points being prescribed, it is based on a constitutive equation, equation (20). Furthermore, gravity does not have to be applied in equation (20); rather, the system can be modeled by purely artificial mass alone without the influence of gravity.
A simple rendering of the massive point fiber model is depicted in figure 2(c). The Lagrangian boundary point and massive point, with Cartesian coordinates X and Y, are shown respectively, connected by a stiff virtual spring. Background fluid flow potential moves the massless point to a new position which exerts a pulling-like effect on the massive point. The massive point will move depending on the coupled constitutive equation given in equation (20).
2.1.5. Porosity
An interpretation of Darcy’s Law is used to make the immersed structure permeable to fluid. In other words, the porous structure allows fluid to flow through it. Darcy’s Law is a phenomenologically derived constitutive equation, which states the velocity of the fluid flowing through a porous medium is proportional to a pressure gradient of the two sides of the medium. This relation can be written as
| (21) |
where is the porous slip velocity and κp is the membrane permeability, μ is the fluid’s dynamic viscosity, σ is the structure’s thickness, [ p ] is the pressure gradient across the boundary, and is a unit vector normal to the structure. However, the pressure jump may be simplified by first integrating across equation (2) to eliminate the singular forcing term and obtain jump conditions for the normal and tangential fluid stresses across the boundary, which can be simplified to reduce the pressure jump to
| (22) |
as in [40, 41]. Hence the porous slip velocity is found to be
| (23) |
where is the porous slip parameter and Xr is the position of the porous Lagrangian structure. As stated in [40], since κp can be easily obtained from experiments, α can be easily found as well.
Once the Darcy porous slip velocity, e.g. equation (23), is found, equation (5) must be adjusted to account for the porosity
| (24) |
This formulation was first described in [42] and the discretization used to find the normal vectors in IB2d can be found in appendix. An illustration of porosity is shown in figure 2(d), where incoming fluid flow permeates a porous boundary. The amount of flow that moves through the body depends on the permeability parameter, α, associated with the membrane. All flow through the boundary is normal to the body itself.
2.1.6. Muscle-fluid-structure models: FV-LT model
The simple muscle model described in [11] has been incorporated into IB2d. This muscle model attempts to model both a force-velocity (FV) and length-tension (LT) relationship in muscle without coupling in the underlying cellular processes like calcium signaling, myosin cross-bridge attachment and detachment, or filament compliance.
The force a muscle can generate depends on the speed of muscle contraction; e.g. the faster a muscle shortens, the less force it generates. Traditionally a Hill model is used to describe this relationship and takes the following form [43, 44],
| (25) |
where VF is the muscle fiber’s shortening velocity, F is the force generated by the fiber, and Fmax is the maximum load at zero contractile velocity. Parameters a and b can be determined experimentally and are are related to the internal thermodynamics of the muscle. An example force-velocity curve is shown in figure 3(a).
Figure 3.
Example force-velocity and length-tension curves illustrating the respective relationships that the FV-LT model is trying to capture.
The force a muscle fiber can generate is also known to be a function of its length. Initially when the thick filaments begin to bind to the thin filaments, the resulting force increases as the muscle shortens. However, if the muscle is contracted too far, there are fewer myosin heads to attach to the actin filaments, and the resulting force exerted is smaller. Hence the maximal muscle tension is generated between the two extremes, i.e. when the myosin heads are within reach of the thin filaments. An example length-tension curve is shown in figure 3(b) where actin and myosin binding is depicted at varying muscle lengths. A simple model of a length-tension relationship is described in [45],
| (26) |
where is the ratio of the length of the muscle fibers to their length when they generate their maximum tension, FI is the maximum isometric tension at a given fiber length LF, FIO is the maximum isometric force exerted at the optimum length of the muscle fibers, and SK is a parameter specific for each muscle. Note that these parameters can be determined experimentally.
An easy way to combine equations (25) and (26) is to take the product of their normalized versions, as in [11, 46]. The resulting model is given by
| (27) |
where af is the activation strength of the muscle and is the normalized maximum isometric force generated at the full activation of the muscle fibers at their optimum lengths, and F1(LF) and F2(VF) are normalized versions of equations (25) and (26), given by
| (28) |
| (29) |
2.1.7. Muscle-fluid-structure models: 3-element Hill model
The 3-Element Hill model of muscle activation describes sustained muscle contraction by modeling the actin and myosin cross-bridges, muscle tendon, and connective tissues for a muscle. The model has a contractile element which models the force generated by the actin and myosin cross-bridges at the sarcomere level, and two non-linear spring elements, one in parallel and one in series with the contractile element. The series element models the muscle tendon, i.e. the intrinsic elasticity of the myofilaments, and has a soft tissue response and provides energy storing mechanism. The parallel element takes care of the passive behavior when the muscle is stretched, representing connective tissues with a soft tissue-like behavior. Furthermore, the contractile element is fully extensible when inactive but capable of shortening when activated [43, 44]. The 3-elements are depicted in figure 4.
Figure 4.
Schematic diagram of the 3-Element Hill model of muscle contraction, containing a contractile element, series element, and parallel element modeling actin and myosin cross-bridges, tendons, and connective tissues, respectively.
The net force-length properties of a muscle are a result of both the active (contractile element and series element) and passive (parallel element) components’ force-length characteristics. If FCE, FSE, and FPE represent the force produced by the contractile, series, and parallel elements respectively, their relations satisfy
| (30) |
| (31) |
where Ftot is the total force produced by muscle contraction. Furthermore the relations for muscle shortening are
| (32) |
where Ltot is the total length of the muscle. Since the overall muscle length is conserved, if the series element is stretched, the contractile element must contract an equal amount.
As mentioned previously, to model the force produced from the series and parallel elements, we use non-linear springs, e.g.
| (33) |
| (34) |
where kSE and kPE are the spring stiffnesses for the series and parallel elements respectively, and LPER is the resting-length of parallel element’s non-linear spring. Note that the series element’s spring has zero resting-length as it’s length depends solely on the length of the contractile element. n is an integer assumed to be greater than or equal to 2. There are many ways to represent these elements; these are only one possible choice.
The contractile element assumes the length-tension and force-velocity relationship of muscle. For this reason, equation (27) is one possible choice for modeling its force generation, e.g.
| (35) |
where LCE is the length of the muscle fibers and VCE is the contraction speed of the muscle fibers being represented in the contractile element. Another possible choice is described in [12].
2.2. Incorporated models
In this section, we will describe inclusions within the current IB2d software that are in addition to the fiber and material property models. Currently the following capabilities have been added to the framework:
Tracer particles
Concentration gradients of a chemical (advection-diffusion)
Background flow profiles (artificial forcing)
Basic electrophysiology frameworks
These models are incorporated either by additional forcing terms in equation (2) (background flow profiles), a constitutive equation that depends on u(x, t) without affecting the fluid momentum itself (tracers and concentration gradients), or by coupling into a specific fiber model (electrophysiology).
2.2.1. Tracers
Tracers are neutrally buoyant particles that move at the local fluid velocity. They have no impact on the fluid motion themselves, but rather ‘go with the flow’. If a tracer’s position is given by Xtr, their equation of motion is solely given by
| (36) |
where utr(x, t) is the background fluid velocity interpolated to the tracer particle. Tracers are useful to observe the fluid motion during a simulation. The tracers move in the simulation by harnessing the discrete delta functions to interpolate the velocity of the exact position of the tracer.
2.2.2. Concentration gradients
Similar to tracers, concentration gradients can be used to observe the motion of the underlying fluid; however, this model also incorporates diffusion. Rather than observing individual particles advect and diffuse, a concentration gradient is given as a continuum, c, which then gets spread out by an advection-diffusion constitutive equation,
| (37) |
where D is the diffusivity coefficient. We note that D is a constant in this formulation, there are no sources or sinks, and that u is, of course, assumed to be incompressible. The details of the numerical solver are found in appendix.
Future implementations will incorporate a Boussinesq approximation as to couple the advection-diffusion equation to forces [47].
2.2.3. Background flow profiles (artificial forcing)
Although the computational domain is assumed to have periodic boundaries, one can induce a desired background flow profile by artificially adding a force onto the fluid, realized as an additional forcing term on equation (2).
Essentially, the additional force will be a penalty-type term, which exerts a force onto a desired subset of the fluid grid, if the fluid velocity does not match the desired flow profile. Such a forcing term can take the form
| (38) |
where karb is the penalty-strength coefficient, and uflow(x, t) is the desired background flow profile as in [39, 48], where it was used to create parabolic inflow into a channel along the x-direction, i.e.
| (39) |
We note this idea has also been used when a preferred mode of active force is desired [49-51].
This idea is illustrated in figure 5, where the fluid grid is given by a rectangular grid with the selected grid points to enforce the penalty-force highlighted and circled in green and orange, respectively. The penalty force is applied to those green fluid lattice points if the flow profiles do not match at those selected nodes. A example rending of the resulting flow is illustrated as the blue arrows, if the desired flow profile is parabolic. Note that this addition of momentum (energy) into the system is not an issue, because of the assumed periodic boundary conditions.
Figure 5.
A depiction of exerting an arbitrary force onto the background fluid grid to obtain the desirable flow profile. The fluid grid is given by the rectangular grid with the selected grid points to enforce the penalty-force highlighted and circled in green and orange. The penalty force is applied to the fluid lattice points in green if the flow profiles do not match at those selected nodes. A cartoon rendering of the resulting flow is illustrated as the blue arrows.
2.2.4. Electrophysiology
A basic model of action potential propagation is incorporated using the FitzHugh–Nagumo equations (FHN) to model the system. FHN is a reduced order model of the Hodgkin–Huxley equations, which were the first equations to describe the propagation of an electrical signal along excitable cells. FHN has been incorporated into fluid-structure interaction models before [19]. The governing equations are given as
| (40) |
| (41) |
where v(x, t) is the membrane potential, w(x, t) is the blocking mechanism, is the diffusion rate of the membrane potential, va is the threshold potential, γ is the resetting rate, ϵ is the blocking strength parameter, and is an applied current, e.g. an initial stimulus potentially from pacemaker signal activation. Note that v is the action potential and that w can be thought to model a sodium blocking channel.
Once the membrane potential is found, it must be interpolated to the Lagrangian grid. Action potential propagation can only then can be used activate pumping or initiate motion to which induces deformations of the structure to model desired biological or physical phenomena. Coupling the action potential to the generation of force can be done in many different ways for various applications, such as for cardiac contraction [19, 20, 52] or locomotion [10, 53, 54].
3. Work flow
We will now briefly describe the typical work flow for using the IB2d software. Both MATLAB and Python have their own respective directories which in turn contain two folders: ‘Examples’ and ‘IBM_Blackbox’. The Examples folder contains all currently implemented simulation examples including the necessary input files to run each simulation, with each example organized in its own folder. The IBM_Blackbox folder contains all methods for solving the fluid-structure interaction problems. The software is set up such that the user will not have to change the underlying mechanics of the immersed boundary method unless they wish to make additions to the algorithm, e.g. implementing more fiber models, etc.
Vectorized functions were used in solving the Navier–Stokes equations, i.e. updating the fluid velocities, and throughout IB2d when appropriate. At this time IB2d uses only built-in MATLAB functions for the MATLAB implementation and the Python 3 implementation uses the standard python library, as well as, packages numpy, matplotlib, numba, and pandas in its implementation.
Inside an example sub-directory, there are multiple files. Two files that must be in every example are input2d and main2d.input2d is the file where the user chooses all parameters required for a simulation, i.e. the fluid parameters, temporal information, grid parameters, fiber model construction, how to save the data, etc main2d will read in this file and then read in the corresponding input files associated with the choices selected in input2d. A graphical description of input2d is given in figure 6.
Figure 6.
Descriptions of selections in input2d. This file controls what inputs get passed to the main IB driver method.
After setting desired parameters and selecting the necessary flags in input2d, assuming the user has the appropriate associated input files corresponding to those selections the simulation is started by calling the main2d script. This script reads in all the information from input2d and passes it to the IBM_Driver script. Once the simulation finishes, a visualization folder, viz_IB2d, will have all the Lagrangian structure and dynamical data from the simulation in .vtk format [55]. .vtk files can be visualized using Paraview [56] or VisIt [57].
Each fiber model has an associated input file type, with the first line being the number of total fiber points associated with that type. If the immersed structure is called ‘struct’, the possible file types are as follows
struct .vertex: A list of all the (X, Y) initial coordinates of the Lagrangian points. The .vertex input file format is shown in figure 7.
struct .spring: A list of the master and slave nodes for each linear spring along with their associated spring stiffness, resting-length, and degree of non-linearity. Note that if using only Hookean springs, the degree of non-linearity can be omitted and IB2d will automatically assume linear springs. The .spring input file format is shown in figure 8.
struct .beam: A list of the left, middle, and right Lagrangian indices associated with each torsional spring (beam) and their associated beam stiffness and curvature. The .beam input file format is shown in figure 9.
struct .target: A list of all target point indices with their associated target point stiffness. Figure 10 gives the .target point input file format.
struct .mass: A list of all Lagrangian mass point indices along with their associated mass-spring stiffness and mass. The .mass input file format is shown in figure 11.
-
struct .porous: A list of all porous Lagrangian points, along with their associated porosity coefficient, α, and their Stencil ID. Figure 12 illustrates the .porous input file format.
Note: the stencil ID is an integer between {−2, −1, 0, 1, 2}, which declares which points around the node of interest will be used in the derivative calculations. For porosity, you need a minimum of 4 nodes surrounding the porous node. This idea is illustrated in figure 13, which shows how a group of 5 porous stencil IDs would be labeled and an example of how they would be labeled in practice for a toy example.
struct .muscle: A list of all FV-LT muscle master and slave node Lagrangian indices, along with their associated muscle length in which the fibers generate their maximum tension (LFO), SK-parameter, thermodynamic parameters, a and b, respectively, and the muscle’s maximum load at zero contractile velocity (Fmax). The .muscle input file format is shown in figure 14.
struct .tracer: A list of all tracer particles’ initial coordinates, (X, Y). Figure 15 gives the .tracer input file format.
Figure 7.
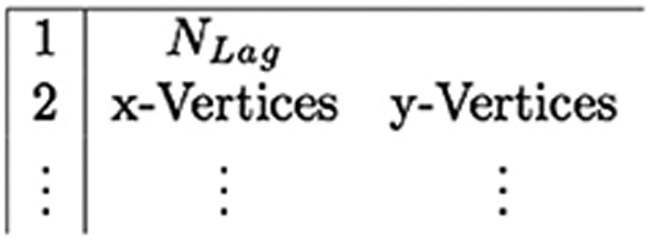
Input format for the .vertex file.
Figure 8.
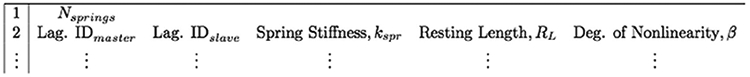
Input format for a .spring file.
Figure 9.

Input format for a .beam (torsional spring) file.
Figure 10.

Input format for a .target file.
Figure 11.

Input format for a .mass file.
Figure 12.

Input format for a .porous file.
Figure 13.
(a) Order of porous stencil IDs. (b) An example of how the stencil IDs are defined using the porous structure from figure 2(d).
Figure 14.

Input format for a .muscle (FV-LT muscle) file.
Figure 15.

Input format for a .tracer file.
These file formats are consistent with those necessary to run simulations in IBAMR, making this software an appropriate learning and analysis tool before scaling up to larger and more highly resolved simulations.
4. Examples
In this section we will present some examples which show some of the software’s functionality. The software currently contains over 30 examples built-in; we will choose some that highlight specific features of the software.
The Rubber-band
The Flexible Beam
The ‘Date’
Falling Spheres under Gravity versus Pulsatile Flow
Idealized Swimmer
HeartTube with Electrophysiology and Calcium Dynamics
4.1. The rubber-band
The rubber-band is one of the quintessential problems in FSI. The band is composed of springs between adjacent nodes, all with a preferred resting length of zero and constant spring stiffness. We will model two such rubber-bands with equivalently perturbed initial states, but the rubber-band on the left will be porous at each Lagrangian node to show how fluctuations cause it to lose volume over time. In summary, the fiber models used are:
Linear Springs
Porosity (non-traditional rubber-band)
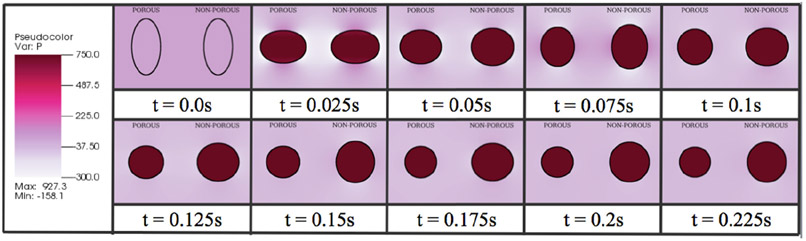
The simulation starts with the rubber band stretched into an elliptical shape with a fixed volume of fluid trapped within the elastic band. The resting lengths were chosen to be zero, as to drive the rubber bands toward their lowest energy state, which minimizes length for a given internal area, i.e. a circle. As the band moves toward this equilibrium position, it will contract and expand periodically across the semi-major and semi-minor directions of the axis. In the case of the porous rubber-band, it will also shrink in size. Simulation images are shown in figure 16.
Figure 16.
A comparison of a porous rubberband (left) and a non-porous rubberband (right) done in a single simulation. The colormap is of the fluid pressure. It is clear that both rubberbands start stretched from their equilibrium position, but end at a circle; however, the porous rubberband does not conserve the same volume, as fluid flows through it as the simulation progresses.
4.2. The flexible beam
The flexible beam is another standard problem in FSI. It includes a ‘beam’ composed of adjacent torsional springs between three successive nodes and tethered to two fixed points at the ends of the beam, modeled using target points. The torsional springs all have a preferred ‘curvature’ of zero, making any perturbation in the geometry move towards a straight line. The fiber models implemented are:
Torsional Springs
Target Points (fixed)
The simulation starts with the beam having been perturbed from its equilibrium position by an ellipsoidal arc. Since the preferred torsional spring ‘curvature’ is zero, the torsional springs will move the system towards an equilibrium where they all line up. Since the ends of the beam are fixed horizontally from each other, the lowest energy state of the system will be when the beam forms a horizontal line between the two end points. Time-slices from the simulation are illustrated in figure 17.
Figure 17.
The flexible beam shown at various times during the simulation. The colormap is of the magnitude of velocity and is depicted along with the background fluid velocity vectors.
4.3. The ‘date’
The ‘Date’ illustrates the software’s ability to update target point positions. Every Lagrangian point in this simulation is modeled as a target point and is given a specific location. As the simulation progresses, Lagrangian point positions are moved to new prescribed positions via an interpolation function, implemented within update_target_point_positions. The fiber models used are:
Target Points (with dynamically updating positions)
The simulation starts in a configuration that spells out ‘Hi KC!!’ enclosed within a square of Lagrangian points with a few other lines of Lagrangian points in decor. As the simulation progresses, those Lagrangian points are interpolated to their next prescribed configuration, spelling ‘Would you like to…’. Finally, they move to their final configuration, spelling ‘… go on a date with me?’ Snapshots of the simulation are illustrated in figure 18.
Figure 18.
‘The date’ example shows target points moving around the computational domain by interpolating positions between three states which spell out certain phrases. The background color map is vorticity.
As stated before, the script update_target_point_positions was used to dynamically update the position of the target points. Furthermore, within this script, one could also change any of the target point parameters, i.e. target point tethering stiffnesses or position.
Similarly, other scripts can be used to dynamically update parameters of springs and/or torsional springs as a simulation progresses, e.g. ‘update_springs and ‘update_beams’. In the case of springs, one can update the spring stiffnesses, resting-lengths, or even non-linearity properties ( see Example_HeartTube), and in the case of torsional springs one can update their torsional spring stiffness or preferred ‘curvature’ ( See Example_Jellyfish). The stiffnesses, resting-lengths, curvatures, etc, can be spatially or time-dependent and appropriately set in the ‘update_springs or ‘update_beams’ scripts.
4.4. Falling spheres under gravity versus pulsatile flow
This example simulates a competition between spheres falling under gravity and upward flow, which acts to help the spheres resist gravity. There are three vertical channels composed of fixed target points. In each channel there is also a sphere, composed of stiff springs and stiff torsional beams between each adjacent Lagrangian node. Each point on the sphere has an associated mass with gravity pointed in the downward vertical direction. There is also a net prescribed flow upwards, arising from an artificial force directly applied onto the Eulerian (fluid) grid. The fiber models and functionality used are:
Linear Springs
Torsional Springs
Target Points (fixed)
Massive Points
Artificial Forcing on the Fluid Grid
The simulation begins with three spheres of different masses. Each sphere is itself composed of individual uniform mass points; however, the individual mass points differ from sphere to sphere. Gravity is acting on the masses to pull them downward while upward flow is providing a force in the opposite direction. In one case, the flow dominates, in another gravity is balanced by the imposed flow, and in the other case, gravity is dominant. This is illustrated in figure 19.
Figure 19.
3 spheres of different masses, with each sphere composed of uniform mass points, under the influence of gravity with a pulsatile flow competing against gravity upwards. The sphere on the left is the lightest and sphere on the right is the heaviest. In the left case, the pulsatile flow dominates, while on the right gravity dominates, and in the middle, the pulsatile flow and gravitational forces are approximately equivalent. The colormap depicts magnitude of velocity.
4.5. Idealized swimmer
This example uses the 3-element Hill muscle model to cause an idealized swimmer, shaped like a V, to move forward and turn. There are stiff linear springs and stiff torsional springs connecting all adjacent Lagrangian points. Only 3 muscles connect one leg of the V to the other, and are equally spaced at intervals 3L/10,2L/5, and 9L/10 down the leg of the swimmer, where L is the length of each leg. The fiber models used are:
Linear and Non-Linear Springs
Torsional Springs
3-Element Hill Model
The simulation begins with the swimmer in a V-shaped starting position at rest. Throughout the simulation the muscles fire out of phase, causing the swimmer to move forward and turn. The swimming behavior is shown in figure 20.
Figure 20.
An idealized swimmer moving forward and turning due to the asynchronous muscle activation. The colormap illustrates vorticity.
4.6. HeartTube with electrophysiology and calcium dynamics
This example models a linear heart tube, in which pumps via a traveling action potential that induces muscle contraction to occlude the flexible tube. The propagation of the action potential is governed by the FitzHugh–Nagumo equations, as in equations (40) and (FHN:eq1). This model also accounts for free calcium ions binding and release to induce the action potential signal.
The rate of calcium binding to, and release from, the actin filaments and the sarcoplasmic reticulum is modeled using the law of mass action, such as in [53, 54],
| (42) |
| (43) |
where Caf is a the ratio of calcium-bound filament sites to total number of filament sites, Ca is the ratio of free calcium ions to total number of filament sites, C is the ratio of total number of calcium ions to total number of filament sites, S is the ratio of total number of sarcoplasmic reticulum binding sites to total number of filament sites, and {k1, k2, k3, k4} are rate constants for binding and release of Ca2+.
Force generation is modeled using the following non-linear spring-like formulation,
| (44) |
where kHT is a stiffness parameter and v(x, t) is the magnitude of the action potential.
The heart tube itself is composed of linear springs and torsional springs between adjacent Lagrangian points along the top and the bottom of the tube and the ends of the tube are held nearly fixed using target points.
The fiber models and functionality used are:
Linear Springs
Torsional Springs
Target Points (fixed)
Background Concentration (advection-diffusion)
Electrophysiology (via FitzHugh–Nagumo)
Movement in the simulation begins when the threshold of free Ca2+ ions have binded to the actin filaments has been exceeding, giving rise to an activation signal that propagates an action potential down the hearttube. As the action potential propagates, it induces muscle contraction to contract the flexible tube. The tube then relaxes as the action potential passes. Snapshots of the simulation are shown in figure 21. Note that this example was modeled after the computational model in [19], with the addition of the calcium dynamics.
Figure 21.
A linear heart tube, which pumps when an action potential travels down the tube, once enough free calcium binds to muscle filaments, to induce muscle contraction. The colormap illustrates a background concentration gradient.
5. Code validation
In this section we present a validation of the code, both in the form of a convergence study for a particular example, as well as in the form of a comparison to experimental data.
Consider the example of a cross-sectional piece of an insect wing moving laterally across the domain at a 45 degree angle of attack at Re = 128. The insect wing’s motion is governed by updating the target point positions, as in the example in section 4.3. Snapshots from the simulation are shown in figure 22.
Figure 22.
A cross-section of an insect wing moving laterally from left to right in a prescribed manner for Re = 128. The background colormap depicts vorticity and the vector field is the fluid velocity.
5.1. Convergence study
In this section, we perform a convergence study focusing on the forces in the x- and y-directions, respectively referred to as drag and lift, which act on the immersed structure (wing). We ran the simulations for different grid resolutions of the fluid domain (and complementary Lagrangian spacing in the immersed structure) with Re = 128 at equivalent time-step, dt, and uniform material properties of the wing. The fluid grid resolutions studied were {32 × 32, 64 × 64, 96 × 96, 128 × 128, 256 × 256, 512 × 512, 768 × 768, 1024 × 1024}. The forces over time are plotted below in figure 23.
Figure 23.
Non-dimensional lift (23(a)) and drag (23(b)) forces versus non-dimensional time for a cross-section of an insect wing moving laterally at Re = 128.
The mean lift and drag forces were calculated over the wing at t = 0.025 s for each simulation, and then the relative error was computed between each simulation and a highly resolved case using IBAMR with 1024 × 1024 fluid grid resolution. The corresponding convergence plot is shown in figure 24.
Figure 24.
A convergence study of the relative error of the lift and drag force, between each simulation and the highly resolved simulation using IBAMR with 1024 × 1024 resolution on the fluid grid. We note that the horizontal axis is the spatial step size, dx, where dx = 1/N, and N = {32, 64, 96, 128, 256, 512, 768, 1024}.
Applying a best fit line to the data produces the relative error convergence rates
| (45) |
| (46) |
For Re ≪ 1 or Re ≫ 1, e.g. Re ≲ 0.01 or Re ≳ 1000, we expect less accuracy from our software in its current implementation. More sophisticated fluid solvers could be implemented to help remedy this issues in these fluid regimes. Moreover, enforcing no-slip boundary conditions on the Lagrangian structure to higher-order, i.e. 2nd order or higher, as in [58, 59], will further increase the accuracy. Currently, IB2d only enforces the no-slip condition to 1st order.
5.2. Experimental validation
In this section we compare simulation results from IB2d to experimental data for a cross-section of an insect wing moving laterally across the domain for three orders of magnitude of Re. The experimental data was obtained using particle image velocimetry (PIV) [60], using a dynamically-scaled flapping robot, e.g. Robofly. [61, 62]. The simulations were run on a 1024 × 1024 grid.
Figure 25 shows a comparison of snapshots taken from IB2d and the PIV physical model over a range of Re. The basic flow structures are reproduced in all cases.
Figure 25.
Comparison of IB2d simulation snapshots and PIV experimental data for a wing moving laterally across the domain for Re = {1, 10, 100}. The figures show the magnitude of velocity, background velocity field, and streamlines.
6. Discussion and conclusion
IB2d is immersed boundary software with full implementations in both MATLAB and Python 3.5. It offers a vast array of fiber model options for constructing the immersed structure and has functionality for advection-diffusion, artificial forcing, muscle mechanics, and electrophysiology. Furthermore, having been written in high-level programming languages, it allows one to implement new fiber models and functionality easily and at an accelerated rate.
High-level programming languages also come with a few drawbacks. Grid sizes should not be implemented beyond a 512 × 512 resolution due to computational costs. If higher resolution is required, we suggest moving to IBAMR. Additionally unlike IBAMR, IB2d was strictly designed for 2D applications. While full 3D simulations are often desired, some applications may only require fluids with two-dimensions [10, 20, 63-65]. IB2d was written in 2D to make it more readable and to lend itself for easier modification, particularly as a first step in trying to implement a new model.
The format of IB2d was designed to mirror the input file formats used in IBAMR, and as such can used as a stepping stone to using IBAMR. Neither IB2d nor IBAMR include functionality for compressible fluids, non-Newtonian fluids, or variable density fluid applications at this time, but there are plans to incorporate them in the future.
At this time neither IB2d nor IBAMR include a turbulence model for large Re simulations. For these applications, one is directed to use other software packages such as OpenFOAM by OpenCFD LTD [66], which is capable of FSI applications and is open source. Commercial software, such as COMSOL [67] and ANSYS Fluent [68] can model FSI as well. OpenFOAM, COMSOL, and Fluent allow easier entry into FSI through well developed GUIs and manuals. However, licenses for COMSOL and Fluent are both expensive when not being used for academic teaching purposes. It is also difficult to implement or modify numerical approaches in COMSOL or Fluent, and there would be a steep learning curve for OpenFOAM.
Note that there are other methods for simulating fluid-structure interactions in addition to Peskin’s immersed boundary method. Some examples include immersed interface methods [69, 70], sharp interface methods [71, 72], the blob projection method [73], and level set methods [74, 75]. These methods have the benefit that they can capture high resolution of flow near interface when desired. For further information and broader perspective on immersed boundary methods see [76]. However, the authors are not aware of any open source implementations at this time, and thus they require a large entry time for research and development—especially in the case for 3D, adaptive, or parallelized applications. The mathematical work for compressible, non-Newtonian, and variable density fluids applications may be limited at this time as well. Furthermore, most sharp interface approaches have been limited to thin structures (e.g. elastic membranes) or rigid bodies.
For teaching FSI applications, or fast implementations of new fiber models, numerical models and approaches, or varying fluid solvers, IB2d is an ideal environment. This open source software is available from https://github.com/nickabattista/IB2d.
Acknowledgments
The authors would like to thank Charles Peskin for the development of immersed boundary method and Boyce Griffith for IBAMR, to which many of the input files structures of IB2d are based. We would also like to thank Austin Baird, Christina Battista, Robert Booth, Namdi Brandon, Kathleen Carroll, Christina Hamlet, Alexander Hoover, Shannon Jones, Andrea Lane, Julia Samson, Arvind Santhanakrishnan, Michael Senter, Anne Talkington, and Lindsay Waldrop for comments on the design of the software and suggestions for examples. This project was funded by NSF DMS CAREER #1151478, NSF CBET #1511427 NSF DMS #1151478, NSF POLS #1505061 awarded to LAM Funding for NAB was provided from an National Institutes of Health T32 grant (HL069768-14; PI, Christopher Mack) and UNC Dissertation Completion Fellowship.
Appendix.
Discretization
The discretizations used in IB2d for solving The Navier–Stokes equations, e.g. (2) and (3), for computing normal derivatives for porous elements, and for advection-diffusion will be described below.
A.1. Discretizing the Navier–Stokes equations
IB2d uses finite difference approximations to discretize the Navier–Stokes equations on a fixed lattice, e.g. the Eulerian (fluid) grid. It follows the discretization described in [31, 77], and are implicitly defined as follows
| (A.1) |
| (A.2) |
where Δt and Δx are the time-step and Eulerian meshwidth, respectively, and ρ and μ are the density of the and kinematic viscosity of the fluid, respectively. D0 is the central differencing operator, defined as
| (A.3) |
with
| (A.4) |
where (e1, e2) is the standard basis in . The viscous term, given by , is a difference approximation to the Laplacian, where the operators are the forward and backward approximations to . They are defined as
| (A.5) |
| (A.6) |
The skew-symmetric difference operator, SΔx, serves as an approximation to the non-linear advection term, u · ∇u, and is defined as follows
| (A.7) |
Using the discretizations (A.4)-(A.7), the equations (A.1) and (A.2) are linear in uk+1 and pk+1. To solve for uk+1 and pk+1 from uk, pk+1, and Fk, the Fast Fourier transform (FFT) was implemented [37, 38]. Note that this assumes a periodic domain. Future implementations will include non-square domains and projection methods to incorporate Dirichlet or Neumann Boundary conditions [34, 35].
The Navier–Stokes equations need not be discretized in this manner, and this is where one could implement a fluid solver and discretization of their choice, e.g. finite element or Lattice Boltzmann [13]. However, further consideration must be taken into account on how to spread the Lagrangian forces to the Eulerian grid and move the Lagrangian structure at the local fluid velocity, i.e. equations (4) and (5), respectively, if implementing in IB2d.
A.2. Discretizing the normal derivatives on the boundary
The normal vector to the Lagrangian structure is given by [40, 42],
| (A.8) |
where
| (A.9) |
Hence we have that
| (A.10) |
Unlike [42], who used a 3-pt central differencing operator to compute , we compute the partial derivatives using a 5-pt differentiation stencil. We do this to both minimize error near end-points of a porous structure and allow functionality for non-closed porous structures. Hence we implement the following five different differentiation operators,
A.3. Discretizing the advection-diffusion equation
The concentration is discretized on the same resolution as the Eulerian grid. Each nodal point has a scalar concentration value. The advection-diffusion equation (37) are discretized as follows,
| (A.11) |
where D is the diffusion coefficient, D2,0 is the central differencing operator for second derivatives, and is the upwind differencing operator which depends on the sign of c at that particular point in time. We explicitly define D2,0, as follows,
| (A.12) |
with
| (A.13) |
The upwind operator is defined as
| (A.14) |
with
| (A.15) |
References
- [1].Bathe KJ 2008. Fluid-structure interactions ASME Mech. Eng. Mag (April) 66–8 [Google Scholar]
- [2].Peskin C 1972. Flow patterns around heart valves: a numerical method J. Comput. Phys 10 252–71 [Google Scholar]
- [3].Peskin C 1977. Numerical analysis of blood flow in the heart J. Comput. Phys 25 220–52 [Google Scholar]
- [4].Griffith BE 2005. Simulating the blood-muscle-vale mechanics of the heart by an adaptive and parallel version of the immsersed boundary method PhD Thesis Courant Institute of Mathematics, New York University; (www.cims.nyu.edu/~griffith/docs/thesis.pdf) [Google Scholar]
- [5].Hieber S and Koumoutsakos P 2008. An immersed boundary method for smoothed particle hydrodynamics of self-propelled swimmers J. Comput. Phys 227 8636–54 [Google Scholar]
- [6].Hoover AP and Miller LA 2015. A numerical study of the benefits of driving jellyfish bells at their natural frequency J. Theor. Biol 374 13–25 [DOI] [PubMed] [Google Scholar]
- [7].Miller LA and Peskin CS 2004. When vortices stick: an aerodynamic transition in tiny insect flight J. Exp. Biol 207 3073–88 [DOI] [PubMed] [Google Scholar]
- [8].Miller LA and Peskin CS 2009. A computational fluid dynamics of clap and fling in the smallest insects J. Exp. Biol 208 3076–90 [DOI] [PubMed] [Google Scholar]
- [9].Jones SK, Laurenza R, Hedrick TL, Griffith BE and Miller LA 2015. Lift- versus drag-based for vertical force production in the smallest flying insects J. Theor. Biol 384 105–20 [DOI] [PubMed] [Google Scholar]
- [10].Tytell E, Hsu C, Williams T, Cohen A and Fauci L 2010. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming Proc. Natl Acad. Sci 107 19832–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Battista NA, Baird AJ and Miller LA 2015. A mathematical model and MATLAB code for muscle-fluid-structure simulations Integr. Comput. Biol 55 901–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Hamlet C, Fauci LJ and Tytell ED 2015. The effect of intrinsic muscular nonlinearities on the energetics of locomotion in a computational model of an anguilliform swimmer J. Theor. Biol 385 119–29 [DOI] [PubMed] [Google Scholar]
- [13].Zhu L, He G, Wang S, Miller LA, Zhang X, You Q and Fang S 2011. An immersed boundary method by the lattice boltzmann app roach in three dimensions Comput. Math. Appl 61 3506–18 [Google Scholar]
- [14].Kramer PR, Peskin CS and Atzberger PJ 2008. On the foundations of the stochastic immersed boundary method Comput. Meth. Appl. Mech. Eng 197 2232–49 [Google Scholar]
- [15].Fogelson AL and Guy RD 2008. Immersed-boundary-type models of intravascular platelet aggregation Comput. Methods Appl. Mech. Eng 197 2087–104 [Google Scholar]
- [16].Lee P, Griffith BE and Peskin CS 2010. The immersed boundary method for advection-electrodiffusion with implicit timestepping and local mesh refinement J. Comput. Phys 229 5208–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Strychalski W and Guy RD 2012. Viscoelastic immersed boundary methods for zero reynolds number flow Commun. Comput. Phys 12 462–78 [Google Scholar]
- [18].Du J, Guy RD and Fogelson AL 2014. An immersed boundary method for two-fluid mixtures J. Comput. Phys 262 231–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Baird AJ, Waldrop LD and Miller LA 2015. Neuromechanical pumping: boundary flexibility and traveling depolarization waves drive flow within valveless, tubular hearts Japan. J. Indust. Appl. Math 32 829–46 [Google Scholar]
- [20].Waldrop LD and Miller LA 2015. The role of the pericardium in the valveless, tubular heart of the tunicate Ciona savignyi J. Exp. Biol 218 2753–63 [DOI] [PubMed] [Google Scholar]
- [21].Eyre DJ and Fogelson AL 1997. Ibis: a software system for immersed boundary and interface simulations www.math.utah.edu/IBIS/
- [22].Griffith BE. An adaptive and distributed-memory parallel implementation of the immersed boundary (ib) method. 2014 https://github.com/IBAMR/IBAMR.
- [23].Griffith BE and Luo X 2016. Hybrid finite difference/finite element immersed boundary method arXiv:1612.05916 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Balay S. et al. PETSc Web Page. 2009 www.msc.anl.gov/petsc.
- [25].Lawrence Livermore National Laboratory. SAMRAI: structured adaptive mesh refinement application infrastructure. 2007 www.llnl.gov/CASC/SAMRAI.
- [26].Kirk BS, Peterson JW, Stogner RH and Carey GF 2006. libMesh: a C++ library for parallel adaptive mesh refinement/coarsening simulations Eng. Comput 22 237–54 [Google Scholar]
- [27].Gabriel E et al. 2004. Open MPI: goals, concept, design of a next generation MPI implementation Proc. 11th European PVM/MPI Users, Group Meeting (Budapest, Hungary) pp 97–104 [Google Scholar]
- [28].Froese BD and Wiens J 2013. Matib: a simple immersed boundary method solver in matlab https://github.com/eldila/MatIB [Google Scholar]
- [29].Mesnard O. Pyibm: an immersed boundary method python code. 2014 https://github.com/mesnardo/pyIBM. [Google Scholar]
- [30].Peskin CS. The immersed boundary method. 2008 www.math.nyu.edu/faculty/peskin/ib_lecture_notes/index.html. [Google Scholar]
- [31].Peskin CS 2002. The immersed boundary method Acta Numer. 11 479–517 [Google Scholar]
- [32].MATLAB version 8.5.0 (R2015a) The MathWorks Inc. Natick, Massachusetts, USA: 2015. www.mathworks.com/products.html [Google Scholar]
- [33].Van Rossum G. Python version 3.5. 2015 www.python.org. [Google Scholar]
- [34].Chorin AJ 1967. The numerical solution of the navier-stokes equations for an incompressible fluid Bull. Am. Math. Soc 73 928–31 [Google Scholar]
- [35].Brown DL, Cortez R and Minion ML 2001. Accurate projection methods for the incompressible Navier–Stokes equations J. Comput. Phys 168 464–99 [Google Scholar]
- [36].Liu Y and Mori Y 2012. Properties of discrete delta functions and local convergence of the immersed boundary method SIAM J. Numer. Anal 50 2986–3015 [Google Scholar]
- [37].Cooley JW and Tukey JW 1965. An algorithm for the machine calculation of complex fourier series Math. Comput 19 297–301 [Google Scholar]
- [38].Press WH, Flannery BP, Teukolsky SA and Vetterling WT 1992. Fast fourier transform Numerical Recipes in FORTRAN: the Art of Scientific Computing vol 2 (Cambridge: Cambridge University Press; ) ch 12, pp 490–529 [Google Scholar]
- [39].Hamlet C and Miller LA 2012. Feeding currents of the upside-down jellyfish in the presence of background flow Bull. Math. Biol 74 2547–69 [DOI] [PubMed] [Google Scholar]
- [40].Stockie JM 2009. Modelling and simulation of porous immersed boundaries Comput. Struct 87 701–9 [Google Scholar]
- [41].Peskin CS and Printz BF 1993. Improved volume conservation in the computation of flows with immersed elastic boundaries J. Comput. Phys 105 33–46 [Google Scholar]
- [42].Kim Y and Peskin CS 2006. 2d parachute simulation by the immersed boundary method SIAM J. Sci. Comput 28 2294–312 [Google Scholar]
- [43].Hill AV 1938. The heat of shortening and the dynamic constants of muscle Proc. R. Soc 126 136–95 [Google Scholar]
- [44].Fung YC 1993. Biomechanics: Mechanical Properties of Living Tissues (New York: Springer; ) [Google Scholar]
- [45].Hatze H 1981. A comprehensive model for human motion simulation and its application to the take-off phase of the long jump J. Biomech 14 135–42 [DOI] [PubMed] [Google Scholar]
- [46].Challis JH and Kerwin DG 1994. Determining individual muscle forces during maximal activity: model development, parameter determination, and validation Hum. Movement Sci 13 29–61 [Google Scholar]
- [47].Tritton DJ 1977. Physical Fluid Dynamics (New York: Van Nostrand Reinhold; ) [Google Scholar]
- [48].Santhanakrishnan A, Nguyen N, Cox J and Miller LA 2009. Flow within models of the vertebrate embryonic heart J. Theor. Biol 259 449–61 [DOI] [PubMed] [Google Scholar]
- [49].Newren EP, Fogelson AL, Guy RD and Kirby RM 2007. Unconditionally stable discretizations of the immersed boundary equations J. Comput. Phys 222 702–19 [Google Scholar]
- [50].Teran JM and Peskin CS 2009. Tether force constraints in stokes flow by the immersed boundary method on a periodic domain SIAM J. Sci. Comput 31 3404–16 [Google Scholar]
- [51].Teran JM, Fauci L and Shelley M 2010. Viscoelastic fluid response can increase the speed and efficiency of a free swimmer Phys. Rev. Lett 104 038101. [DOI] [PubMed] [Google Scholar]
- [52].Griffith BE and Peskin CS 2013. Electrophysiology Commun. Pure Appl. Math 66 1837–913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Williams TL, Bowtell G and Curtin NA 1998. Predicting force generation by lamprey muscle during app lied sinusoidal movement using a simple dynamic model J. Exp. Biol 201 869–75 [DOI] [PubMed] [Google Scholar]
- [54].McMillen T, Williams T and Holmes P 2008. Nonlinear muscles, passive viscoelasticity and body taper conspire to create neuromechanical phase lags in anguilliform swimmers PLoS Comput. Biol 4 e1000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Schroeder W, Martin K and Lorensen B 1993. The Visualization Toolkit 4th edn (Carrboro: Kitware; ) [Google Scholar]
- [56].Ahrens J, Gerveci B and Law C 2005. ParaView: an End-User Tool for Large Data Visualizations (Amsterdam: Elsevier; ) [Google Scholar]
- [57].Childs H et al. 2012. VisIt: an end-user tool for visualizing and analyzing very large data High Performance Visualization-Enabling Extreme-Scale Scientific Insight (Philadelphia, PA: CRC Press; ) pp 357–72 [Google Scholar]
- [58].Griffith BE and Peskin CS 2005. On the order of accuracy of the immersed boundary method: higher order convergence rates for sufficiently smooth problems J. Comput. Phys 208 75–105 [Google Scholar]
- [59].Griffith BE, Hornung R, McQueen D and Peskin CS 2007. An adaptive, formally second order accurate version of the immersed boundary method J. Comput. Phys 223 10–49 [Google Scholar]
- [60].Kiger K, Westerweel J and Poelma C 2016. Introduction to particle image velocimetry www2.cscamm.umd.edu/programs/trb10/presentations/PIV.pdf [Google Scholar]
- [61].Gotz MHDK 1993. Unsteady aerodynamic performance of model wings at low reynolds numbers J. Exp. Biol 174 45–64 [DOI] [PubMed] [Google Scholar]
- [62].Birch J, Dickson W and Dickinson MH 2004. Force production and flow structure of the leading edge vortex at high and low reynolds numbers J. Exp. Biol 207 1063–72 [DOI] [PubMed] [Google Scholar]
- [63].Crowl LM and Fogelson AL 2011. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions J. Fluid Mech 676 348–75 [Google Scholar]
- [64].Zhang C, Guy RD, Mulloney B, Zhang Q and Lewis TJ 2014. The neural mechanism of optimal limb coordination in crustacean swimming PNAS 111 13840–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Lewis OL, Zhang S, Guy RD and del Alamo JC 2015. Coordination of contractility, adhesion and flow in migrating physarum amoebae J. R. Soc. Interface 12 20141359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Foundation O. Official openfoam repository. 2014 https://github.com/OpenFOAM.
- [67].Multiphysics C version 4.2 (R2015a) COMSOL Inc. Burlington, MA, USA: 2015. www.comsol.com/products [Google Scholar]
- [68].ANSYS Fluent C, CFD, version 17.0 ANSYS Inc. Cecil Township, Pennslyvania, USA: 2016. www.ansys.com/products/ [Google Scholar]
- [69].Lee L and Leveque RJ 2003. An immersed interface method for incompressible navier-stokes equations SIAM J. Sci. Comput 25 832–56 [Google Scholar]
- [70].Li Z 2003. An overview of the immersed interface method and its applications Taiwanese J. Math 7 1–49 [Google Scholar]
- [71].Ubbink O and Issa RI 1999. Method for capturing sharp fluid interfaces on arbitrary meshes J. Comput. Phys 153 26–50 [Google Scholar]
- [72].Udaykumar H, Mittal R, Rampunggoon P and Khanna A 2001. A sharp interface cartesian grid method for simulating flows with complex moving boundaries J. Comput. Phys 20 345–80 [Google Scholar]
- [73].Cortez R and Minion M 2000. The blob projection method for immersed boundary problems J. Comput. Phys 161 428–53 [Google Scholar]
- [74].Sethian JA 1999. Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science (Cambridge: Cambridge University Press; ) [Google Scholar]
- [75].Osher SJ and Fedkiw R 2002. Level Set Methods, Dynamic Implicit Surfaces (New York: Springer; ) [Google Scholar]
- [76].Mittal R and Iaccarino C 2005. Immersed boundary methods Annu. Rev. Fluid Mech 37 239–61 [Google Scholar]
- [77].Peskin CS and McQueen DM 1996. Fluid dynamics of the heart and its valves Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology ed Adler FR et al. (Englewood Cliffs, NJ: Prentice-Hall; ) ch 14, pp 309–38 [Google Scholar]