Abstract
Numerous fluid-structure interaction problems in biology have been investigated using the immersed boundary method. The advantage of this method is that complex geometries, e.g., internal or external morphology, can easily be handled without the need to generate matching grids for both the fluid and the structure. Consequently, the difficulty of modeling the structure lies often in discretizing the boundary of the complex geometry (morphology). Both commercial and open source mesh generators for finite element methods have long been established; however, the traditional immersed boundary method is based on a finite difference discretization of the structure. Here we present a software library for obtaining finite difference discretizations of boundaries for direct use in the 2D immersed boundary method. This library provides tools for extracting such boundaries as discrete mesh points from digital images. We give several examples of how the method can be applied that include passing flow through the veins of insect wings, within lymphatic capillaries, and around starfish using open-source immersed boundary software.
Keywords: immersed boundary method, fluid-structure interaction, mathematical biology, biomechanics, biofluids
1. Introduction
The immersed boundary method (IBM) is a mathematical formulation and numerical method for fully-coupled fluid-structure interaction (FSI) problems that dates back to Peskin in 1972 [1]. Since its creation, the IBM has been used to study a wide variety of problems in biological fluid dynamics and fundamental fluid dynamics at low to intermediate Reynolds numbers (Re < 10 000). Diverse examples include the aerodynamics of insect flight [2-4], lamprey swimming [5, 6], jellyfish swimming [7, 8], and fluid flows through organs such as the heart and esophagus [9-11]. The relative ease of implementation and the availability of open source codes has made it particularly useful in research and education [12-14].
The original IBM formulation discretizes immersed, elastic boundaries on a curvilinear finite difference mesh. Many immersed boundary (IB) studies are performed in 2D and use simple geometries with easy mathematical descriptions such as plates [2, 15], strings [16, 17], tubes [10, 18, 19], ellipses [20, 21], hemiellipses [8, 22], and circles [23-25], or in 3D with spheres [26] or cylinders [27]. In other cases, more complicated geometries are manually constructed by the user via explicit mathematical functions or sets of functions that describe the elastic boundary [9, 28, 29]; this endeavor is, however, non-trivial. David Baraff, a Senior Research Scientist at Pixar Animation Studios has publicly said, ‘I hate meshes. I cannot believe how hard this is. Geometry is hard’ [30].
This immediately highlights a challenge in performing IB simulations for many biological applications that have complicated geometries. Most meshing tools are finite element based, such as MeshLab [31], Gmsh [32], or TetGen [33], all of which are open source. As far as we are aware, there is not an openly available and easy to use tool for generating curvilinear finite difference meshes. A few finite difference meshing tools that are available constrain the mesh to a Cartesian grid using cuboids, such as the open source AEG Mesher [34], which was designed for electromagnetic simulations, and the propriety software Argus ONE [35], which was designed to help incorporate geographic information system into numerical models [36].
What’s more, many applications, especially those in biology and medicine, usually have some imaging data from which a mesh is estimated. For example, imagine generating a numerical model of blood flow through an arterial network. There are highly resolved images that clearly illustrate arterial branching patterns from which desirable geometric data, e.g., artery diameters, lengths, branching locations, etc, can be obtained. To perform numerical simulations that reveal the spatial variations in the flow due to small scale geometric effects, one must reconstruct this arterial network in detail. Even for 2D simulations this process is non-trivial, as one would first need to recreate the structure using parametric functions and then select particular parameter values that sample the structure’s geometry to obtain a computational mesh with equally-spaced points. While this laborious approach may work for some simplified arterial geometries, if the actual arterial network contains walls that are not perfectly smooth or flat, simple tubular models may be insufficiently detailed and hence give rise to non-realistic results. Our software aims to fill this gap using edge detection on the original image, thereby preserving the original pattern and information from the images. Bézier curves are then used to mathematically describe the images, after which they are appropriately sampled to obtain a curvilinear mesh.
The challenge here is two-fold: first a continuous, parameterized description of the boundary of interest must be found, potentially through image segmentation, and then this boundary must be represented as a finite difference mesh with sampling to give the desired geometric spacing between adjacent geometric nodes. Given the widespread use of the IBM approach in both research and education [12-14, 37, 38], we found it useful to create the open source software package MeshmerizeMe, a tool that both detects boundaries in image data and creates finite difference meshes where the nodes are nearly uniformly spaced. The output files are designed to be coupled with IB2d [12, 13, 39], IBAMR [40], and other IB 2D software.
We provide an overview of the software MeshmerizeMe in section 2. In particular, we detail MeshmerizeMe’s implementation, workflow (section 2.1), and how the software computes a discretized mesh from parametric curves (section 2.2). We then present a variety of examples using the software in section 3; including two internal flow examples and one external flow example. The examples include hemolymph flow through dragonfly wing veins (section 3.1), flow through a lymphatic capillary (section 3.2), and oscillatory flow past a starfish (section 3.3).
The most straightforward IB simulations using this software would be developed to simulate the flow past or through nearly rigid, complex, biological boundaries, as demonstrated in these examples. We do not currently have a method for using multiple images to simulate moving boundaries. There are, however, a few ways that one can model moving and deformable boundaries. To begin, each of the Lagrangian points can be translated or rotated using a prescribed mathematical function rather than moving the boundary based on image tracking. This approach has been used for a variety of biological applications, including flapping insect wings [2], swimming jellyfish [8, 41], flapping swimmerets [42] and heart pumping [19]. If, in addition to vertex points, springs and beams are added to pairs or triads of vertex points, elastic deformations due to the FSI can also be simulated. This type of approach has been used for leaves in flow [43], flapping filaments [16], the deformation of prey prior to puncture [44], and the movement of red blood cells [45, 46].
2. MeshmerizeMe implementation
MeshmerizeMe is a software package for the creation of 2D geometry files for use with open source IB software such as IB2d and IBAMR. The software comes with two main scripts: 1) ContourizeMe, which reads in an image file and uses automatic edge detection to extract contours of interest into an ‘scalable vector graphics’ (SVG) file, and 2) MeshmerizeMe, which processes SVG files and IB2d- or IBAMR-style input2d files to create * .vertex files describing the geometry of the SVG file at the appropriate resolution. Both SVG and vertex files are UTF encoded text files. SVG is a widely supported vector graphics format, while the vertex-format is used by IB2d and IBAMR to describe Lagrangian mesh points in an IB simulation. The MeshmerizeMe script also includes a tool that uses Matplotlib to allow the user to plot the geometry created by MeshmerizeMe for visual verification. These scripts are written to run in Python 3.x, and upon installation both scripts are added to the path on a Linux and Mac environment. This dual-script setup allows the end-user two distinct entry points into the workflow; see figure 1 for an illustration.
Figure 1.
Flow chart illustrating the MeshmerizeMe workflow. Blue rounded boxes represent files, while square orange boxes represent user actions. The flow chart illustrates the two main entry points into the work flow from the source image: automatic edge extraction using the ContourizeMe script as well as manually creating the SVG by drawing ‘over’ the image using software like Inkscape.
To provide a concrete example of the workflow, suppose an image is available either from the field or an experiment. To detect the edges and generate an SVG file, the user would run the ContourizeMe script on the desired image file (e.g., by typing ContourizeMe image.jpg in the commandline). This opens a GUI with several features that may be used to modify and enhance the image (see figure 2). Note that common image formats such as jpg, png, and tiff are supported. For best performance, the image should provide a good contrast between the object boundary and background, while also having little noise. If this is not the case, ContourizeMe allows the user to adjust the image contrast and saturation7 using simple sliders to better highlight the boundary of interest. Using a slider for the pixel cutoff, the smoothness of the matched curve can be adjusted to account for noise. All of these sliders update in real time. If this proves insufficient, unwanted edges that were detected can easily be deleted at a later step. Once the user is satisfied with the result, the curve is exported to an SVG file to be used as input for the MeshmerizeMe script.
Figure 2.
The ContourizeMe GUI in action on Manjaro Linux 18.0.4 with Gnome DE emulated in VirtualBox. The main window to the left allows the user to select the desired type of parameterization of the source image. The user can chose grayscale, RGB, or HSV. The sliders allow the user to set the desired threshholding in that parameterization. The detected edges are displayed in the live image (upper right) in green. The user may optionally display the result of the paramterization and filtering (lower right). Starfish image reproduced from [47].
In some cases, the original image quality may be high enough to proceed directly to the discretization phase. In most cases, however, the user will want to make minor edits to the SVG file to remove any potential artifacts, such as curves corresponding to background noise in addition to the boundaries of interest. These edits can be done using common vector graphics software such as Inkscape (open-source) or Adobe Illustrator (commercial). Note that this also provides an alternate entry-step in the MeshmerizeMe workflow: curves can be freely drawn using such software if image data is either not available, the boundary structure is purely hypothetical, or in cases when the original image is too poor in quality for reliable edge detection. In the latter case, image layers may be used in software such as Inkscape that allows the user to trace over the desired edges to create the SVG file with the necessary boundaries. Once the SVG file has been cleaned in this manner, it is advised to collapse underlying groups and simplify contiguous paths, which in some vector graphics software can be done from the ‘save’ menu. In other cases, software to do this is freely available online, such as SVGO and SVGOMG [48, 49].
With the desired geometry extracted into an SVG image, the next step consists of making a folder in which the SVG file itself can be found, as well as an IB2d-style file called input2d. This latter file includes information such as the spatial discretization step size (more details on this can be found below). Our script reads this file to calculate and sample the appropriate mesh. MeshmerizeMe is run by pointing it to the appropriate SVG file (e.g., typing MeshmerizeMe image.svg from the command line). It will then create the .vertex file containing the mesh. Note that the filename of the vertex file will be taken straight from the input2d file, regardless of the SVG filename. If multiple meshes are to be created, MeshmerizeMe can be run in batch mode by providing it with a list of file names. We also support piping from STDIN. This allows the user to easily pass a list of file names, such as one created by the find command, to MeshmerizeMe for batch processing.
The resulting
.vertex
file can then be used as input for IB simulations using IB2d and IBAMR. Note that the user will need to supply some additional information as to the relationship between the boundary points, for example whether or not they are connected with springs, beams, masses, and so forth. Currently, files that store this information must be manually created, although a few of these relations are implemented as classes in the MeshmerizeMe library to help with writing such scripts. Once this stage is completed, the IB simulation is ready to run.
2.1. Overview of contour extraction
In this section, we provide an overview of how ContourizeMe extracts contours from images. This is motivated by the need to accurately estimate the shapes of objects from planar images or within some cross-section. Many techniques, ranging from edgefinding using image gradients to image segmentation accomplished through supervised training of deep neural nets, have been proposed as generalized methods to extract such edges [50, 51]. The niche filled by MeshmerizeMe is to easily obtain 2d meshes from image data that can be directly used in IB2d and IBAMR. In essence, it allows for the semi-automated generation of meshes from image data using simple contour estimation from hand chosen thresholds of pixel values [52] as a first step in the IBM workflow. This replaces the need to completely create the structure mesh manually by finding idealized functions approximating the shape of interest. This method was chosen for its simplicity and fast estimation in obtaining user-verified 2d shapes of arbitrary smoothness and precision.
The ContourizeMe GUI was developed with the Python package Tkinter. Contour estimation from image thresholding works by first applying noise reduction to a given image if needed. The contour is assumed to be represented in the image by a gradient or steep change in the pixel values that separates the foreground, or object of interest (OOI), from the background. For many images this means the existence of one or three inequalities or pixel-value bounds (3 for the case of RGB and HSV values) that quantify this separation. Image noise from one or multiple sources can make these inequalities ill-defined. Possible sources of image noise are numerous and include sensor and electronic-circuit noise, analog-to-digital conversion errors, and even statistical quantum fluctuations [53, 54]. ContourizeMe provides implementations of various common noise reduction techniques that the user may choose from depending on the source and strength of the noise present in their own images.
In the next step after determining an appropriate noise reduction technique, the user manually determines one or more pixel value bounds depending on a given parameterization (RGB, grayscale, HSV, etc) that forms the lowest-area hull that corresponds to the OOI. This closed region is used to produce a binary image with pixel values of 1 corresponding to those contained in the provided region and 0 corresponding to those not in this region. A topological algorithm in OpenCV [52] is applied to this binary image to give contours that fully describe ‘separate’ clusters of homogeneous pixels (in this case pixels that all equal 1). This algorithm yields integer pixel estimates of the boundaries, which are then refined to sub-pixel estimates with user specified smoothness via the Chan–Vese algorithm. More details are provided in the following subsections.
These contours themselves are estimations of the shapes of interest that are then used to yield precise descriptions of the shapes as a set of continuous Bézier curves (see appendix B). Bézier curves are constructed using evenly spaced points from the sub-pixel boundary estimates and exported in the SVG format.
2.1.1. Noise reduction
Filtering algorithms, the topological contour estimation algorithm, and most of the image manipulations (such as RGB to HSV conversion, thresholding, etc) are accomplished in ContourizeMe via Python bindings of the OpenCV package [52]. OpenCV is a computer vision suite developed in C++ built to tackle various problems including segmentation, 3D reconstruction, edge-finding, and other related tasks.
ContourizeMe’s main GUI includes:
An average filter which essentially is a type of down sampling that assumes the true value of any pixel can be estimated by the average pixel value of a K by K window surrounding that pixel. This is equivalent to convolving the image with a low-pass filter kernel.
A Gaussian filter which convolves the image with a Gaussian kernel of a specified size and standard deviation in both the x and y directions. This is similar to the average filter, but pixels are weighted via the 2D Gaussian function specified before they are averaged.
A median filter which instead of the average over a window, takes the median pixel value. This kind of filter is typically used for ‘salt and pepper’ type image noise, and has the advantage of leaving only pixel values that would have been observed in the original image.
A bilateral filter which is the recommended choice. The bilateral filter behaves similarly to the Gaussian filter, but in addition to weighting pixels by their spatial distance it also weights them by their difference in intensity in an attempt to preserve edges or gradient information.
While the bilateral filter is recommended because of its intended edge-preservation [55], one may want to employ one of the other convolution filters as they can smooth boundaries produced by the thresholding and topological algorithms. We must also stress that this selection is highly limited in scope and much more sophisticated and robust techniques for the denoising of images exist depending on the image acquisition method and content. It may be that making a model of the noise via a deep neural net such as UNet [56], CAIR [57], Noise2Noise or Noise2Void [58] may be required or produce better results. Any method may of course be employed before using this segmentation GUI.
2.1.2. Smoothing the results from OpenCV’s algorithm
In order to give the user control over the smoothness of the resulting curve they obtain, we use a Python implementation of the Chan–Vese level set algorithm [59]. This method of smoothing the curve ensures that reductions in the curvature are chosen such that they have minimal costs to accuracy and that the contour remains true to the original image. We allow users to specify both the error tolerance in pixels, as estimated from each iteration of the Chan–Vese algorithm, and the parameter α which controls the contribution of the total curvature of the boundary to the energy functional and thus the smoothness of the obtained contour.
2.2. Going from curves to mesh
The second part of our software package consists of a script that takes vector based graphics, specifically the SVG standard, to obtain a discretized curvilinear mesh that describes the boundary of the OOI. The idea behind vector graphics is to represent shapes in terms of control points of non-uniform rational basis splines. Only control points of the parameterized curves are stored while the standard defines the basis polynomials themselves. The resulting curves can be represented smoothly at any scaling or resolution of interest and can easily be mapped to the simulation space using an affine transformation.
A variety of vector graphics file formats are available, several of which are proprietary. We have chosen to implement our software using the SVG standard because it is a popular, open-source standard and for its ease of use. SVG files are UTF encoded text files following an XML schema, making them amenable to XML parsing methods. A particular benefit of the SVG standard is that it is widely supported; if edge detection fails or gives insufficient resolution, multiple vector graphics programs such as Inkscape or Adobe Illustrator may be used to clean up or directly hand-draw the boundaries of interest from an image. The standard has support both for Bézier curves as well as geometric primitives (rectangles, triangles, etc), and the current version of MeshmerizeMe utilizes the free path element, which encodes curves as Bézier curves.
To reduce the need for additional configuration files, MeshmerizeMe has been built to utilize the ‘input2d’ file format that is utilized by IB2d and IBAMR. This file is required, and the MeshmerizeMe code expects the following variables to be defined in the input2d file8:
Lx, Ly: the length of the computational domain in the x and y direction, respectively.
Nx: number of points in the x direction.
Even if the user chooses to use a different CFD software for the simulation, MeshmerizeMe can still be used to create the requisite mesh points. Strict adherence to the IB2d format is not required. A minimal working example of the input2d file required for MeshmerizeMe requires only four lines. The example below will create a mesh appropriate for a [0, 0.5] × [0, 0.5] domain with a 64 × 64 mesh.
NX=64 LX=0.5 LY=0.5 String_name=test
Please note that this minimal example is only sufficient for MeshmerizeMe. A simulation for IB2d or IBAMR will require additional settings in the
input2d
file, such as the fluid parameters
mu
and
rho
and temporal information such as the desired time step dt and time the simulation is to run. Any such additional settings may be present in the
input2d
file, but will be ignored by MeshmerizeMe.
MeshmerizeMe will automatically compute the appropriate boundary point spacing of , where . We note that it is standard in the IB literature to set the spacing between the IB points to half that of the spatial step for the Navier–Stokes solver, [14]. This choice of spacing allows the boundary points to move independently while also restricting most of the flow between the points. Using these parameters, the software will parse the supplied SVG file itself and extract the path objects, splitting them up into individual Bézier curve objects. The control points are then converted to the experimental coordinate system defined by Lx and Ly.
Let represent a particular Bézier curve. To create the mesh, we seek n parameters {ti} with 0 ⩽ t1 < t2 < ⋯ < tn ⩽ 1 such that the distance between points on the curve with these parameters is fixed:
| (1) |
We utilize a gradient descent method to find these parameters. Specifically, we define our cost function J(t) using the mean squared relative error of all d(ti) values (scaled by to cancel the power of 2 coming from the partial derivatives in (4))
| (2) |
and minimize J(t) by iteratively updating t with a variable learning rate α:
| (3) |
where
| (4) |
Here, we use the notation ⟨a, b⟩ to denote the inner product between a and b.
The number of points n to be found per path are estimated by dividing the arc-length by the desired length Δs. This may result in more dense than optimal spacing of points, but in practice achieves sufficient accuracy. The error will depend on the curvature of γ.
We then evaluate our curve at the points ti obtained from this technique to determine the discretized boundaries of interest. The produced Lagrangian mesh is output to a file called
fname.vertex
where ‘fname’ is based on the value of
string_name
taken from the ‘input2d’ file. The vertex file itself is a simple text file. The first line consists of an integer giving the total number of mesh points and the following lines contain one mesh point each, given as a space delimited pair of floats representing the x and y direction coordinates.
2.2.1. Distribution of errors in approximation
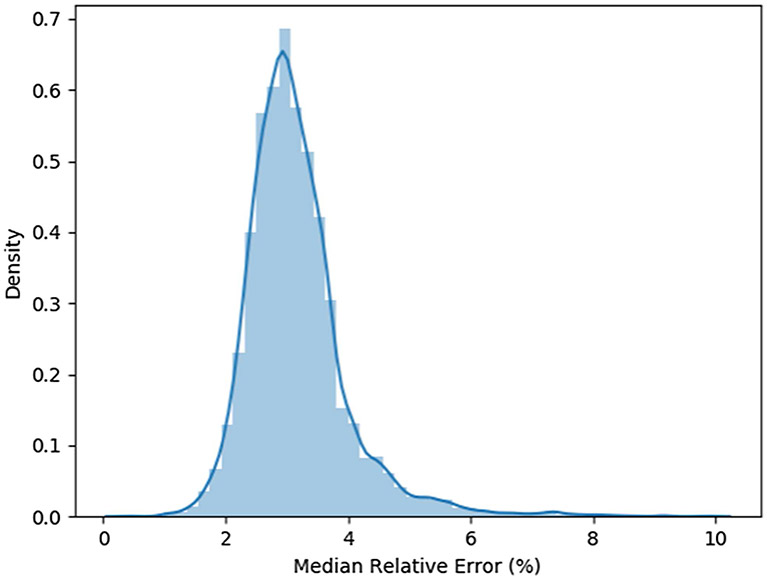
To test the relative accuracy of our script, we created 5000 SVG files each containing a randomly generated cubic Bézier curve. For purposes of uniformity during testing, each curve was generated on a 1000 × 1000 pixel domain to be mapped onto a 1 × 1 mesh domain using a 256 × 256 grid. All parameters were set to default values. A script was then run to calculate the minimum, maximum, mean, and median relative errors for each curve. The mean of the median relative error of curves in the script is 3.2%. The middle 50% of median relative errors is in the 2.6–3.5% range. See figure 3 for the distribution of the median relative errors.
Figure 3.
A distribution plot of median errors calculated from the meshes created for the error experiments in section 2.2.1.
Note that if a higher degree of accuracy is desired, the user is able to experiment with different parameters that can influence the average error. MeshmerizeMe allows the user to set both the learning rate as well as the convergence threshold of the mean squared error as command-line options when creating the mesh.
One potential limitation on the error is the method we have chosen to seed the curves. Specifically, after reading the SVG our script merges all individual SVG path objects into a single path object. This path object is then split into several sub-paths of equal arc-length. Each of these sub-paths are seeded with n = Lsp/Δs points, where Lsp is the length of the sub-path and Δs is the desired Euclidean distance between mesh-points. For sub-paths with very large curvature, this seeding method may overestimate the number of points necessary for ideal discretization. In such cases, the user may re-run the MeshmerizeMe script with the
num-points
flag to manually specify a lower number of points per sub-path. In our experience, this is an unusual occurrence that can usually be solved by experimenting with the
num-points
flag.
It should also be noted that our current algorithm assumes the OOI is a contiguous path, that is we assume the object can be represented by a single poly-Bézier curve with at least geometric continuity. In the SVG file, this representation is not limited to representation by a single path element. When the SVG file is parsed, all path elements are merged into a single poly-Bézier path object. This object is then divided into several sub-paths of approximately equal length which are then processed in parallel. If the OOI consists of two non-contiguous paths or multiple objects are represented in the source SVG, the MeshmerizeMe script will report a large error resulting from the distance between two sequential points on non-contiguous paths. In the presence of several non-contiguous paths, the minimization algorithm will lead to a slight skewing of points toward path boundaries.
3. Examples: bringing everything together
We present several examples that illustrate the software’s ability to recreate complex geometries. In each example, ContourizeMe is used to extract contours from images, MeshermizeMe is then used to compute the model’s discretized geometry. The flow within or around the geometries is solved using an open-source implementation of IBM, either IB2d or IBAMR. The following examples are illustrated:
Hemolymph flow through dragonfly wing veins (section 3.1)
Lymph flow through a branching lymphatic capillary (section 3.2)
Oscillatory flow past a starfish or array of starfish (section 3.3)
In every example, we present the original image on which the computational geometry is based, followed by images that illustrate how MeshmerizeMe computed its associated discretized mesh. Finally, we present computational results to illustrate successful integration of the geometry into the IBM software.
3.1. IB2d: dragonfly wing veins example
For our first example, we chose a public domain image of a dragonfly wing shot with a Canon EOS 5D Mark with a 100 mm lens [60]. For the purpose of running a tractable FSI simulation, we cropped this image to a section of the wing and manually occluded parts of the veins using the open source image manipulation software GIMP [61]. Figure 4 shows the original image of the dragonfly wing and the region that was chosen for numerical simulation.
Figure 4.
(a) The original public domain image of a dragonfly wing [60]. (b) The partial region of the dragonfly wing that was chosen for numerical simulation in IB2d. Some vessels were opened so that flow would have obvious entry and exit paths.
As shown in figure 2, we used the ContourizeMe GUI to create boundaries describing the subsection of the wing vasculature. Briefly, the image was cropped so that only a couple dozen vessel segments would be considered. The image was then loaded into the ContourizeMe GUI. Noise reduction was then applied to the image, and a pixel bound was selected such that the lowest-area hull sufficiently matches the edge of the vessel network. The edges were then smoothed using the Chan–Vese algorithm, and the result was exported to SVG.
The MeshmerizeMe script was then used to obtain a curvilinear mesh from the SVG file. The x, y coordinates of this mesh were written to the
. vertex
file. The file contained the coordinates for approximately equally-spaced Lagrangian points that were then used as an input into IB2d. For the purpose of running an IB2d simulation where the complex geometry remains relatively fixed while the fluid is driven through it, we only require the vertex point of each Lagrangian Point, i.e. the (x, y) values of each point along the insect wing. Since the wing veins should be relatively rigid and not move, each Lagrangian vertex point was tethered to a target point (see A.1). This has the effect of applying a force proportional to the distance between the location of the actual boundary and the desired position. In other words, the boundary is pushed back into place as fluid moves through the network. The necessary input information for IB2d is written in the
wing_veins.vertex
and
wing_veins.target
files.
This example can be found in the open source IB2d software available at github.com/nickabattista/IB2d and this example can be found in the following subdirectory,
IB2d/matIB2d/Examples/Example_MeshmerizeMe/Dragonfly_Wing/.
More details on IB2d and the IBM in general can be found in appendix A.
To drive flow through the wing, a penalty force is applied to the fluid that is proportional to the difference between the local fluid speed and the local target velocity (see A.1). For our example, a parabolic flow profile is enforced at the inlet of the insect wing, and all subsequent flows through the veins result from that inflow and are not themselves prescribed (see figure A.11). The full implementation of this simulation can be found in the
please_Compute_External_Forcing.m
script.
To illustrate flow through the wing vein geometry, we ran multiple simulations corresponding to various Reynolds numbers (Re), given by
| (5) |
where ρ is the density of the fluid (kg m−2), μ is the dynamic viscosity (N s m−1), and L and U are characteristic length and velocity scales respectively. We note that in these simulations, we varied μ while holding ρ = 1000 kg m−2, L = w (width of the vein where the inflow is produced), and U = 5 m s−1 (the maximum speed of the parabolic inflow). Simulations were run over a couple orders of magnitude of Re ranging through Re ∈ [0.1, 100] on a [0, 0.5] × [0, 0.25] grid with resolution of dx = 0.5/1024 = 0.25/512 = dy.
The result illustrates the flowthrough the complex geometry as shown in figures 5 and 6. We note that the example of flow through a subset of the veins in a dragonfly wing was chosen to showcase the functionality of the software to capture and digitize intricate complex structures.
Figure 5.
Snapshots comparing the magnitude of velocity for different Re, Re = 0.6, 6, 60.
Figure 6.
Snapshots comparing the pressure for different Re, Re = 0.6, 6, 60.
Figures 5 and 6 compare the flow profiles and pressures generated for three simulations when inflow reaches its steady state through the dragonfly’s complex wing vein geometry at Re = 0.6, 6, 60. It is clear there is more flow through the complex morphology with higher pressures for higher Re. Note that when using the IBM, the entire structure is fully immersed within a fluid, so there is fluid in the region enclosed between veins. Hence the pressure fields in such regions are not physical but instead are artifacts of these regions being within a fluid environment and being enclosed.
3.2. IBAMR: lymphatic capillary example
As another example of how our software can be used, we present a case in which the vessel walls of a junction from a dermal lymphatic capillary are reconstructed from an image. This image is courtesy of Dr Wenjing Xu from the Kathleen Caron lab (UNC-CH) and was taken from the back region of a wild type mouse embryo. The image was generated with fluorescence microscopy to highlight the lymphatic vessel boundaries as shown in figure 7(a). The simulations described below were performed using the IBM with adaptive mesh refinement (IBAMR) (see appendix A).
Figure 7.
(a) Source image for modeling flow through a junction in a lymphatic capillary, courtesy of Dr Wenjing Xu from the Kathleen Caron lab. (b) SVG rendering of bifurcating vascular structure. (c) Vertex points discretized from SVG file. (d) Colormap of the magnitude of velocity of flow through a bifurcating dermal lymphatic capillary. Note that the vessel ends were artificially extended to allow for fully developed flow within the vessels.
After the contours were extracted using ContourizeMe, the ends of the vessels were extended using image software to allow the flow within the vessels to fully develop before reaching the actual vessel geometry. Parabolic outflow was prescribed as a boundary condition to effectively ‘pull’ the fluid into the vessel ends with a maximum velocity of 10−5 m s−1. This velocity is consistent with the reported range of observed lymphatic flow velocities, which are as low as 10−7 and as high as 10−3 m s−1 [62, 63]. Note that the vessel ends were placed at the left domain edge for this purpose. Neumann boundary conditions were used at the right edge of the domain to allow volume conservation (fluid escapes on this side), and periodic boundary conditions were used at the top and bottom of the domain. The vessel was assumed to be nearly rigid over the time scale of a simulation. The Navier–Stokes equations were discretized on a 512 × 512 grid with 3 levels of mesh refinement and a refinement ratio of 4. The fluid domain size was set to L = 1.2 × 10−3 m, where the spatial step size was set to Δx = L/512. The vessel walls were described using a curvilinear mesh where the distance between IB points was set to Δs = Δx/2. The time step size was taken as dt = 5.0 × 10−6 s. The lymph was parameterized with mass density ρ = 1000 kg m−3 and dynamic viscosity μ = 10−3 N s m−2.
3.3. IB2d: starfish example
The last example we present is that of flow around a starfish using IB2d. The original JPG image of the starfish was taken from WikiMedia Commons, courtesy of NOAA Sea Grant Program in the Coral Kingdom Collection [47]. The SVG file was produced by ContourizeMe, and the boundaries were discretized using MeshmerizeMe as shown in figure 8. Figures 8(c), (d) and (f) give the discretized geometries for the starfish at resolutions appropriate for an IB simulation in a square fluid domain with Lx = Ly = 1 where the spatial step size within such domain was set to Δx = Lx/128 (128 × 1238) and Δx = Lx/256 (256 × 256), and Δx = Lx/1024 (1024 × 1024) respectively. Note that in figure 8(f) that the starfish’s outline is still composed of discretized points. Recall that the average spacing between boundary points is set to one half of the spatial step size, e.g., Δs = 0.5Δx. Once the boundary describing the starfish is discretized at the desired resolution, it is placed inside of a rigid channel, where oscillatory flow will be prescribed to rush past the starfish as shown in figure 8(e).
Figure 8.
(a) Original starfish image courtesy of NOAA Sea Grant Program [47] (b) SVG image of the starfish generated by ContourizeMe script (c), (d), (f). The discretized geometry at grid resolutions of 128 × 128, 256 × 256, and 1024 × 1024 respectively. (e) Computational geometry containing a starfish in a channel with prescribed oscillatory parabolic inflow (see A.1).
We acknowledge that the starfish geometry is rather complex, and our simulation is relatively coarse. As such, we are likely not resolving the details of the flow very close to the starfish body. We would like to point out, however, that the purpose of this example is to further illustrate MeshmerizeMe’s ability to resolve and capture the fine structure detail of an SVG image. Thus, our goal in this example is not necessarily to resolve these fine scale flow structures. This example also highlights that once the geometry has been created for a single starfish, it can be easily altered. For example, this geometry can be copied, translated to different regions of the domain, or rotated since the software provides a parameterized set of points.
We ran a single starfish simulation at Re = 800 (see equation (5)), where L = 0.08 m, the height of the starfish, V = 1.0 m s−1, half the maximum oscillatory inflow speed, and ρ and μ are 1000 kg m−2 and 0.1 N s m−1, respectively. An oscillatory flow condition was used to produce flow past the starfish with frequency of f = 2 Hz, see A.1. The numerical simulation was performed for a fluid domain with lengths [0, 1] × [0, 0.25] and a consistent spatial step size in each direction, e.g., dx = 1.0/1024 = 0.25/256 = dy. Snapshots from the numerical simulation that illustrate a colormap of vorticity are found in figure 9.
Figure 9.
Snapshots showing oscillatory flow past a rigid starfish at Re = 800 during the first 6 pulsation periods. The background colormap illustrates vorticity.
Previously, one of the main difficulties in performing this IB simulation would be the finite difference discretization of the starfish. MeshmerizeMe provides a convenient way to do this, without having to manually piece together the geometry either by point-by-point construction or combining user-defined piecewise functions or splines. To demonstrate the versatility of this method, we insert multiple starfish into the channel. Figure 10 provides snapshots showing the vorticity during the first pulsation period of oscillatory flow around one, three, or five starfish within a channel. The example for flow around a single starfish can be found in the open source IB2d software’s sub-directory,
IB2d/matIB2d/Examples/Example_MeshmerizeMe/Starfish/
.
Figure 10.
Snapshots showing oscillatory flow past 1, 3, or 5 rigid starfish at Re = 800 during the first pulsation period. The background colormap illustrates vorticity.
4. Discussion
In this paper, we introduce a software library that will extract edges from images, fit these images with Bézier curves, and discretize the curves into a curvilinear finite difference mesh with nearly constant spacing between points. Such meshes are useful in a variety of mathematical applications, including 2D numerical simulations of FSI problems using the IBM. We present three such applications of the tool used in conjunction with the IBM including 1) flow of hemolymph in the veins of an insect wing (internal flow), 2) flow of lymph in a mouse lymphatic capillary (internal flow), and 3) flow of water around starfish (external flow). These images were taken with either high resolution digital cameras or fluorescence microscopy. Prior to this software release paper, the software was successfully applied in another internal flow application of blood flows over the tra-beculae in zebrafish embryonic hearts [64]. Here the meshes were created from images taken from an inverted (light) microscope [65]. This illustrates the software’s robustness in its ability to construct discretized meshes from various imaging methods. Note that all of the above examples were performed using open-source implementations of the IBM, either IB2d [12, 13] or IBAMR [66].
While MeshmerizeMe merely provides 2D geometries, its output format can serve as a starting point in the development of 3D models. Commercial CAD software such as Fusion360 allow the import of SVG images, such as those produced by the ContourizeMe script, as sketches. Fusion360’s built-in scripts allow the import of a CSV file describing a spline using XYZ coordinates. The latter is easily produced via commandline tools like tail and sed from the vertex files produced by the MeshmerizeMe script. This likewise imports the curves as a sketch. These imported sketches can then be turned into 3D objects using extrude and rotate commands. From here on, existing 3D meshing tools may be used to produce a mesh suitable for a 3D simulation.
To create simple 3D geometries, the 2D mesh could be extruded manually by adding a third coordinate, and this coordinate could be varied by Δs to obtain a finite difference mesh that describes an outer wall. Similarly, the 2D mesh could be rotated about a central axis to obtain another simple 3D geometry. Sample applications of these simple geometries could include wings or fins with constant cross sections and axisymmetric structures such as tubular hearts, jellyfish, and some worms. The meshes could also be used in other finite difference approaches to FSI problems, including the method of regularized Stokeslets [67], the immersed interface method [68], sharp interface methods [69, 70], or the blob projection method [71]. The software library could also be applied in the numerical simulation of other physics problems, including the uptake of particles [72] and electrodiffusion [73]. In future releases of the software library, we plan to add additional functionality that includes the automation for material property model input files, e.g., springs, beams, etc, for the geometry’s discretized points.
In addition to use in research, this library may serve as a powerful tool for student research and education, particularly in mathematical modeling at the undergraduate and graduate levels. MeshmerizeMe provides students with open source tools that can easily be used to build relatively complicated 2D meshes from images. These boundary meshes are easily imported and used in IB2d and IBAMR, both of which are also open source libraries. One of the coauthors has developed a series of online videos to make the use of this software even easier for students [74]. Both IB2d and MeshmerizeMe have been used in the authors’ undergraduate and graduate courses, including mathematical modeling, mathematical biology, numerical analysis, and a first year seminar on biological fluid dynamics. Furthermore, the libraries have been successfully used in numerous undergraduate research projects [75, 76] and contemporary locomotion research endeavors [77].
Acknowledgments
The authors would like to thank Charles Peskin for the development of immersed boundary method and Boyce Griffith for IBAMR, to which many of the input files structures of IB2d are based. We would also like to thank Christina Battista, Robert Booth, Christina Hamlet, Alexander Hoover, Shannon Jones, Julia Samson, Arvind Santhanakrishnan, and Lindsay Waldrop for comments on the design of the software and suggestions for examples. This project was funded by NSF DMS CAREER #1151478, NSF CBET #1511427, NSF DMS #1151478, NSF POLS #1505061 awarded to LAM and NSF IOS #1558052 awarded to Jake Socha. Computational resources for NAB were provided by the NSF OAC #1826915 and the NSF OAC #1828163. Funding for NAB was provided by the TCNJ Support of Scholarly Activity (SOSA) Grant, the TCNJ Department of Mathematics and Statistics, and the TCNJ School of Science.
WCS gratefully acknowledges the support of Simons Foundation Grant # 585322, which helped to fund travel during this project. Certain images in this publication have been obtained by the author(s) from the Wikipedia/Wikimedia website, where they were made available under a Creative Commons licence or stated to be in the public domain. Please see individual figure captions in this publication for details. To the extent that the law allows, IOP Publishing disclaim any liability that any person may suffer as a result of accessing, using or forwarding the image(s). Any reuse rights should be checked and permission should be sought if necessary from Wikipedia/Wikimedia and/or the copyright owner (as appropriate) before using or forwarding the image(s).
Appendix
Appendix A. Details on the immersed boundary method
The two-dimensional formulation of the IB method used in this paper to study flow through dragonfly wing veins, lymphatic capillaries, and around starfish is provided below. IB2d [12, 13, 39] and IBAMR [40] are the two open source implementations that were used for these studies. For a full review of the IBM, please see Peskin [14].
A.1. Governing equations of IB
The conservation of momentum equations that govern an incompressible and viscous fluid are listed below:
| (A.1) |
| (A.2) |
where u(x, t) is the fluid velocity, p(x, t) is the pressure, f(x, t) is the force per unit area applied to the fluid by the IB, ρ and μ are the fluid’s density and dynamic viscosity, respectively. The independent variables are the time t and the position x. The variables u, p, and f are all written in an Eulerian frame on the fixed Cartesian mesh, x.
The interaction equations, which handle all communication between the fluid (Eulerian) grid and curvilinear mesh describing the IB (Lagrangian grid) are given by the following two integral equations:
| (A.3) |
| (A.4) |
where F(s, t) is the force per unit length applied by the boundary to the fluid as a function of Lagrangian position, s, and time, t, δ(x) is a three-dimensional delta function, and X(s, t) gives the Cartesian coordinates at time t of the material point labeled by the Lagrangian parameter, s. The Lagrangian forcing term, F(s, t), gives the deformation forces along the boundary at the Lagrangian parameter, 5. Equation (A.3) applies this force from the IB to the fluid through the external forcing term in equation (A.1). Equation (A.4) moves the boundary at the local fluid velocity. This enforces the no-slip condition. Each integral transformation uses a twodimensional Dirac delta function kernel, δ, to convert Lagrangian variables to Eulerian variables and vice versa.
Figure A.11.
Illustrating the subset of the insect vein geometry where the prescribed inflow condition is enforced.
The way deformation forces are computed, e.g., the forcing term, F(s, t), in the integrand of equation (A.3), is specific to the application. To hold the geometry nearly rigid, all of the Lagrangian points along the IB were tethered to target points. This has the effect of holding the boundary in place through a penalty forcing term where the force applied to the fluid is proportional to the difference between the actual location of the boundary and the desired location. In this model, the target force penalty term took the following form,
| (A.5) |
where ktarg is a stiffness coefficient and Y(s, t) is the prescribed position of the target boundary. Note that Y(s, t) is a function of both the Lagrangian parameter, s, and time, t; however, in this model ktarg was chosen to be very large to minimize movement of the boundary.
For the case of the dragonfly wings, another penalty forcing term was used to prescribe the inflow conditions into the wing veins. This penalty force was applied directly onto the Eulerian (fluid) grid. The penalty force was proportional to the difference between the local fluid velocity and the desired fluid velocity and is given as
| (A.6) |
where kflow is the penalty-strength coefficient, and uflow(x, t) is the desired background flow profile as in [78]. For the simulations involving hemolymph flow through wing veins, we enforce the following parabolic inflow into the wing vein along the x-direction,
| (A.7) |
where Umax is the desired max peak velocity in the parabolic inflow, MP is the midpoint of the vein and w is the width of the vein. Note that a hyperbolic tangent is used to ramp up the inflow during the course of the simulation.
Similarly, for the simulations of oscillatory flow past one or more starfish, we enforce the following oscillatory parabolic inflow into the starfish channel in the x-direction,
| (A.8) |
where f is the frequency of pulsation (set to 2 Hz) and the other parameters are analogous to before except with w and MP being the width and midpoint of the channel, respectively.
Using a regularized delta function as the kernel in the interaction equations given by equations (A.3) and (A.4) makes the IBM relatively easy to implement and flexible. To approximate these integrals, a discretized (and regularized) delta function was used. In this paper, we use one described in [14], e.g., δh(x),
| (A.9) |
where ϕ(r) is defined as
| (A.10) |
A.2. Numerical algorithm
For the wing vein and starfish examples that use IB2d, we impose periodic and no slip boundary conditions on a rectangular domain. To solve equations (A.1)-(A.4) we need to update the velocity, pressure, position of the boundary, and force acting on the boundary at time n + 1 using data from time n. The IB does this in the following steps [14], with an additional step (4b) for IBAMR [40, 79]:
Step 1: find the force density, Fn on the IB, from the current boundary configuration, Xn.
Step 2: use equation (A.3) to spread this boundary force from the Lagrangian boundary mesh to the Eulerian fluid lattice points.
Step 3: solve the Navier–Stokes equations, equations (A.1) and (A.2), on the Eulerian grid. Upon doing so, we are updating un+1 and pn+1 from un, pn, and fn. Note that a staggered grid projection scheme is used to perform this update.
Step 4: 4a. Update the material positions, Xn+1, using the local fluid velocities, Un+1, using un+1 and equation (A.4).
4b. (IBAMR only) refine Eulerian grid in areas of the domain that contain an immersed structure or where the vorticity exceeds a predetermined threshold, if on a selected time-step for adaptive mesh refinement.
Appendix B. Background on Bézier curves
Bézier curves are a type of interpolating polynomial known as a spline. An nth degree Bézier polynomial may conveniently be written as a sum of n + 1 weighted control points Pi. The weights are known as Bernstein basis polynomials and take the form
A curve γ(t) may then be written as
The parameter t is defined to be on the closed interval [0, 1]. The derivative of a Bézier curve is itself a Bézier curve. Specifically, the first derivative is given by
Paths are modeled as a curve Γ(s) that is at least a C0 sequence of curves, where s = [0, 1] is a parameter used to map to the individual Bézier curves that make up the path. If Pj is the ith control point of the jth curve in Γ, then C0 continuity translates into the requirement that
To achieve C1 continuity, we additionally require that
Perhaps the most common Bézier curve in applications is the cubic Bézier which takes the explicit form
The explicit derivative of the cubic Bézier is given by
To rescale a curve from one domain V to another domain U, an affine transform of the control points is sufficient. In the particular case U, this transform may be represented as a simple matrix operator by representing a point , in the form (x, y, 1)T. Scaling and translating of control points may be achieved by the function
| (B.1) |
For our particular use case we want to map a point Pi from the SVG coordinate system [xmin, xmax] × [ymin, ymax] to the coordinate system [0, Lx] × [0, Ly] used in the simulations. Note that the origin of the SVG coordinates is in the upper left-hand corner of the image, while the coordinate system used in IB2d and IBAMR has its origin in the lower left hand corner. Accounting for this and letting w = xmax – xmin and h = ymax – ymin our operator will be defined as
| (B.2) |
Footnotes
Those changes are temporary and do not affect the original image data.
MeshmerizeMe expects a square discretization, that is Δx = Δy, but does not require a square computational domain.
References
- [1].Peskin CS 1972. Flow patterns around heart valves: a numerical method J. Comput. Phys 10 252–71 [Google Scholar]
- [2].Miller LA and Peskin CS 2004. When vortices stick: an aerodynamic transition in tiny insect flight J. Exp. Biol 207 3073–88 [DOI] [PubMed] [Google Scholar]
- [3].Miller LA and Peskin CS 2009. Flexible clap and fling in tiny insect flight J. Exp. Biol 212 3076–90 [DOI] [PubMed] [Google Scholar]
- [4].Jones SK, Laurenza R, Hedrick TL, Griffith BE and Miller LA 2015. Lift vs drag based mechanisms for vertical force production in the smallest flying insects J. Theor. Biol 384 105–20 [DOI] [PubMed] [Google Scholar]
- [5].Tytell ED, Hsu C-Y, Williams TL, Cohen AH and Fauci LJ 2010. Interactions between internal forces, body stiffness, and fluid environment in a neuromechanical model of lamprey swimming Proc. Natl Acad. Sci 107 19832–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Tytell ED, Hsu C-Y and Fauci LJ 2014. The role of mechanical resonance in the neural control of swimming in fishes Zoology 117 48–56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Hoover A and Miller L 2015. A numerical study of the benefits of driving jellyfish bells at their natural frequency J. Theor. Biol 374 13–25 [DOI] [PubMed] [Google Scholar]
- [8].Hershlag G and Miller LA 2011. Reynolds number limits for jet propulsion: a numerical study of simplified jellyfish J. Theor. Biol 285 84–95 [DOI] [PubMed] [Google Scholar]
- [9].Griffith BE, Luo X, McQueen DM and Peskin CS 2009. Simulating the fluid dynamics of natural and prosthetic heart valves using the immersed boundary method Int. J. Appl. Mech 01 137–77 [Google Scholar]
- [10].Jung E and Peskin CS 2001. Two-dimensional simulations of valveless pumping using the immersed boundary method SIAM J. Sci. Comput 23 19–45 [Google Scholar]
- [11].McQueen D and Peskin C 1997. Shared-memory parallel vector implementation of the immersed boundary method for the computation of blood flow in the beating mammalian heart J. Supercomput 11 213–36 [Google Scholar]
- [12].Battista NA, Strickland WC and Miller LA 2017. IB2d: a Python and MATLAB implementation of the immersed boundary method Bioinspiration Biomimetics 12 036003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Battista NA, Strickland WC, Barrett A and Miller LA 2018. IB2dReloaded: a more powerful Python and MATLAB implementation of the immersed boundary method Math. Methods Appl. Sci 41 8455–80 [Google Scholar]
- [14].Peskin CS 2002. The immersed boundary method Acta Numer. 11 479–517 [Google Scholar]
- [15].Zhu L, He G, Wang S, Miller L, Zhang X, You Q and Fang S 2011. An immersed boundary method based on the lattice Boltzmann approach in three dimensions, with application Comput. Math. Appl 61 3506–18 [Google Scholar]
- [16].Zhu L and Peskin CS 2002. Simulation of a flapping flexible filament in a flowing soap film by the immersed boundary method J. Comput. Phys 179 452–68 [Google Scholar]
- [17].Ryu J, Park SG, Kim B and Sung HJ 2015. Flapping dynamics of an inverted flag in a uniform flow J. Fluid Struct 57 159–69 [Google Scholar]
- [18].Baird A, King T and Miller L 2014. Numerical study of scaling effects in peristalsis and dynamic suction pumping Biol. Fluid Dyn. Modeling, Comput. Appl 628 129–48 [Google Scholar]
- [19].Waldrop LD and Miller LA 2015. Large-amplitude, short-wave peristalsis and its implications for transport Biomech. Model. Mechanobiol 15 629–42 [DOI] [PubMed] [Google Scholar]
- [20].Kim Y and Peskin CS 2007. Penalty immersed boundary method for an elastic boundary with mass Phys. Fluids 19 053103 [Google Scholar]
- [21].Stockie JM 2009. Modelling and simulation of porous immersed boundaries Comput. Struct 87 701–9 [Google Scholar]
- [22].Kim Y and Peskin CS 2006. 2D parachute simulation by the immersed boundary method SIAM J. Sci. Comput 28 2294–312 [Google Scholar]
- [23].Lee DS, Ha MY, Kim SJ and Yoon HS 2006. Application of immersed boundary method for flow over stationary and oscillating cylinders J. Mech. Sci. Technol 20 849–63 [Google Scholar]
- [24].Pinelli A, Naqavi IZ, Piomelli U and Favier J 2010. Immersed-boundary methods for general finite-difference and finite-volume Navier–Stokes solvers J. Comput. Phys 229 9073–91 [Google Scholar]
- [25].Lo DC, Lee C-P and Lin I-F 2018. An efficient immersed boundary method for fluid flow simulations with moving boundaries Appl. Math. Comput 328 312–37 [Google Scholar]
- [26].Campregher R, Militzer J, Mansur SS, Silveira N and da Silveira Neto A 2009. Computations of the flow past a still sphere at moderate Reynolds numbers using an immersed boundary method J. Braz. Soc. Mech. Sci. Eng 31 333–52 [Google Scholar]
- [27].Strickland C, Miller L, Santhanakrishnan A, Hamlet C, Battista N and Pasour V 2017. Three-dimensional low Reynolds number flows near biological filtering and protective layers Fluids 2 62 [Google Scholar]
- [28].Peskin CS and McQueen DM 1996. Fluid dynamics of the heart and its valves Case Studies in Mathematical Modeling: Ecology, Physiology, and Cell Biology ed Adler FR, Lewis MA and Dalton JC (Englewood Cliffs, NJ: Prentice-Hall; ) ch14 pp 309–38 [Google Scholar]
- [29].Battista NA, Lane AN, Liu J and Miller LA 2018. Fluid dynamics in heart development: effects of hematocrit and trabeculation Math. Med. Biol 35 493–516 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Wilson TJ. Masters Thesis. Universitat Politecǹica de Catalunya; Simultaneous untangling and smoothing of hexahedral meshes. [Google Scholar]
- [31].Cignoni P, Callieri M, Corsini M, Dellepiane M, Ganovelli F and Ranzuglia G 2008. MeshLab: an open-source mesh processing tool Eurographics Italian Chapter Conf. ed Scarano V, Chiara RD and Erra U (The Eurographics Association; ) pp 129–136 doi: 10.2312/LocalChapterEvents/ItalChap/ItalianChapConf2008/129-136 [DOI] [Google Scholar]
- [32].Geuzaine C and Remacle J-F 2009. Gmsh: a 3D finite element mesh generator with built-in pre- and post-processing facilities Int. J. Numer. Methods Eng 79 1309–31 [Google Scholar]
- [33].Hang S 2015. Tetgen, a delaunay-based quality tetrahedral mesh generator ACM Trans. Math. Softw 41 1–36 [Google Scholar]
- [34].Berens MK, Flintoft ID and Dawson JF 2016. Structured mesh generation: open-source automatic nonuniform mesh generation for fdtd simulation IEEE Antennas Propag. Mag 58 45–55 [Google Scholar]
- [35].Argus Holdings, LTD 2015. Argus one: open numerical environments URL: http://www.argusone.com/index.html
- [36].Voss CI, Boldt D and Shapiro AM 1997. A graphical-user interface for the US geological survey’s sutra code using argus one (for simulation of variable-density saturated-unsaturated ground-water flow with solute or energy transport) US Geological Survey Open-File Report 1 97–421 [Google Scholar]
- [37].Battista NA 2020. Fluid-structure interaction for the classroom: interpolation, hearts, and swimming! (arXiv:1808.08122) [Google Scholar]
- [38].Battista NA and Mizuhara MS 2019. Fluid-structure interaction for the classroom: speed, accuracy, convergence, and jellyfish! (arXiv:1902.07615) [Google Scholar]
- [39].Battista NA, Baird AJ and Miller LA 2015. A mathematical model and matlab code for muscle-fluid-structure simulations Integr. Comp. Biol 55 901–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Griffith BE 2014. An adaptive and distributed-memory parallel implementation of the immersed boundary (ib) method URL: https://github.com/IBAMR/IBAMR (accessed 21 October 2014) [Google Scholar]
- [41].Hamlet C and Miller LA 2012. Feeding currents of the upside-down jellyfish in the presence of background flow Bull. Math. Biol 74 2547–69 [DOI] [PubMed] [Google Scholar]
- [42].Zhang C, Guy RD, Mulloney B, Zhang Q and Lewis TJ 2014. Neural mechanism of optimal limb coordination in crustacean swimming Proc. Natl Acad. Sci 111 13840–5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Miller LA, Santhanakrishnan A, Jones S, Hamlet C, Mertens K and Zhu L 2012. Reconfiguration and the reduction of vortex-induced vibrations in broad leaves J. Exp. Biol 215 2716–27 [DOI] [PubMed] [Google Scholar]
- [44].Hamlet C, Strychalski W and Miller L 2020. Dynamics of ballistic strategies in nematocyst firing Fluids 5 20 [Google Scholar]
- [45].Crowl LM and Fogelson AL 2009. Computational model of whole blood exhibiting lateral platelet motion induced by red blood cells Int. J. Numer. Methods Biomed. Eng 26 471–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Crowl L and Fogelson AL 2011. Analysis of mechanisms for platelet near-wall excess under arterial blood flow conditions J. Fluid Mech 676 348–75 [Google Scholar]
- [47].McVey JP 2007. Reef0297.jpg https://commons.wikimedia.org/wiki/File:Reef0297.jpg, NOAA Sea Grant Program: The Coral Kingdom Collection; (accessed 25 June 2019) [Google Scholar]
- [48].Archibald J 2019. Svg optimizer is a nodejs-based tool for optimizing svg vector graphics files https://github.com/svg/svgo (accessed 25 June 2019) [Google Scholar]
- [49].Archibald J 2019. Svgomg is svgo’s missing gui, aiming to expose the majority, if not all the configuration options of svgo https://jakearchibald.github.io/svgomg/ (accessed 25 June 2019) [Google Scholar]
- [50].Long J, Shelhamer E and Darrell T 2015. Fully convolutional networks for semantic segmentation IEEE Conf. on Computer Vision and Pattern Recognition (CVPR) pp 3431–40 [DOI] [PubMed] [Google Scholar]
- [51].Garcia-Garcia A, Orts-Escolano S, Oprea S, Villena-Martinez V, Martinez-Gonzalez P and Garcia-Rodriguez J 2018. A survey on deep learning techniques for image and video semantic segmentation Appl. Soft Comput 70 41–65 [Google Scholar]
- [52].Bradski G. The OpenCV Library. Dr. Dobb’s J. Softw. Tools [Google Scholar]
- [53].Gonzalez RC and Woods RE 2002. Digital Image Processing 2nd edn (Englewood Cliffs, NJ: Prentice-Hall; ) pp 122–25 [Google Scholar]
- [54].Bovil K 2005. Handbook of Image and Video Processing 2nd edn (New York: Academic; ) [Google Scholar]
- [55].Tomasi C and Manduchi R 1998. Bilateral filtering for gray and color images Proc. of the 6th Int. Conf. on Computer Vision, ICCV ’98 (Washington, DC, USA: IEEE Computer Society; ) p 839 URL: http://dl.acm.org/citation.cfm?id&tnqx3d;938978.939190 [Google Scholar]
- [56].Ronneberger O, Fischer P and Brox T 2015. U-net: convolutional networks for biomedical image segmentation (arXiv:1505.04597) [Google Scholar]
- [57].Berge GT, Granmo O, Tveit TO, Goodwin M, Jiao L and Matheussen BV 2018. Using the tsetlin machine to learn human-interpretable rules for high-accuracy text categorization with medical applications (arXiv:1809.04547) [Google Scholar]
- [58].Lehtinen J, Munkberg J, Hasselgren J, Laine S, Karras T, Aittala M and Aila T 2018. Noise2noise: learning image restoration without clean data (arXiv:1803.04189) [Google Scholar]
- [59].Wang X-F, Huang D-S and Xu H 2010. An efficient local Chan–Vese model for image segmentation Pattern Recognit. 43 603–18 [Google Scholar]
- [60].Kratochvil P 2013. Insect wing structure: macro photo of a dragonfly wing structure [Camera: Canon EOS 5D Mark II 1/160 s, f 16.0, ISO 100, 100 mm; uploaded September 26, 2013] URL: http://www.publicdomainpictures.net/view-image.php?image=25113&large=1&picture=insect-wing-structure (accessed 22 February 2018) [Google Scholar]
- [61].Kimball S, Mattis P and GIMP Development Team 2019. Gnu image manipulation program https://www.gimp.org/ (accessed 21 August 2019) [Google Scholar]
- [62].Bertram CD, Macaskill C, Davis MJ and Moore JE Jr. 2014. Development of a model of a multi-lymphangion lymphatic vessel incorporating realistic and measured parameter values Biomech Model Mechanobiol 13 401–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Dixon JB, Greiner ST, Gashev AA, Cote GL, Moore JE Jr and Zawieja D C 2006. Lymph flow, shear stress, and lymphocyte velocity in rat mesenteric prenodal lymphatics Microcirculation 13 597–610 [DOI] [PubMed] [Google Scholar]
- [64].Battista N, Douglas D, Lane A, Samsa L, Liu J and Miller L 2019. Vortex dynamics in trabeculated embryonic ventricles Jcdd 6 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Liu J, Bressan M, Hassel D, Huisken J, Staudt D, Kikuchi K, Poss KD, Mikawa T and Stainier DYR 2010. A dual role for erbb2 signaling in cardiac trabeculation Development 137 3867–75 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Griffith B 2019. An adaptive and distributed-memory parallel implementation of the immersed boundary (ib) method https://github.com/IBAMR/IBAMR (accessed 18 June 2019) [Google Scholar]
- [67].Cortez R 2001. The method of regularized Stokeslets SIAM J. Sci. Comput 23 1204–25 [Google Scholar]
- [68].Li Z 2003. An overview of the immersed interface method and its applications Taiwanese J. Math 7 1–49 [Google Scholar]
- [69].Ubbink O and Issa RI 1999. A method for capturing sharp fluid interfaces on arbitrary meshes J. Comput. Phys 153 26–50 [Google Scholar]
- [70].Udaykumar HS, Mittal R, Rampunggoon P and Khanna A 2001. A sharp interface Cartesian grid method for simulating flows with complex moving boundaries J. Comput. Phys 174 345–80 [Google Scholar]
- [71].Cortez R and Minion M 2000. The blob projection method for immersed boundary problems J. Comput. Phys 161 428–53 [Google Scholar]
- [72].Waldrop LD, Miller LA and Khatri S 2016. A tale of two antennules: the performance of crab odour-capture organs in air and water J. R. Soc. Interface 13 20160615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Lee P, Griffith BE and Peskin CS 2010. The immersed boundary method for advection-electrodiffusion with implicit timestepping and local mesh refinement J. Comput. Phys 229 52085227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Battista NA 2019. Ib2d video tutorials! https://github.com/nickabattista/IB2d/ (accessed 18 June 2019) [Google Scholar]
- [75].Miles JG and Battista NA 2019. Don’t be jelly: exploring effective jellyfish locomotion (arXiv:1904.09340) [Google Scholar]
- [76].Miles JG and Battista NA 2019. Naut your everyday jellyfish model: exploring how tentacles and oral arms impact locomotion Fluids 4 169 [Google Scholar]
- [77].Pallasdies F, Goedeke S, Braun W and Memmesheimer R 2019. From single neurons to behavior in the jellyfish Aurelia aurita (biorxiv10.1101/698548v1) [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Santhanakrishnan A, Nguyen N, Cox JG and Miller LA 2009. Flow within models of the vertebrate embryonic heart J. Theor. Biol 259 449–61 [DOI] [PubMed] [Google Scholar]
- [79].Griffith BE 2005. Simulating the blood-muscle-vale mechanics of the heart by an adaptive and parallel version of the immsersed boundary method PhD Thesis Courant Institute of Mathematics, New York: University [Google Scholar]