Structural Control over Bimetallic Core–Shell Nanorods for Surface-Enhanced Raman Spectroscopy

Abstract

Bimetallic nanorods are important colloidal nanoparticles for optical applications, sensing, and light-enhanced catalysis due to their versatile plasmonic properties. However, tuning the plasmonic resonances is challenging as it requires a simultaneous control over the particle shape, shell thickness, and morphology. Here, we show that we have full control over these parameters by performing metal overgrowth on gold nanorods within a mesoporous silica shell, resulting in Au–Ag, Au–Pd, and Au–Pt core–shell nanorods with precisely tunable plasmonic properties. The metal shell thickness was regulated via the precursor concentration and reaction time in the metal overgrowth. Control over the shell morphology was achieved via a thermal annealing, enabling a transition from rough nonepitaxial to smooth epitaxial Pd shells while retaining the anisotropic rod shape. The core–shell synthesis was successfully scaled up from micro- to milligrams, by controlling the kinetics of the metal overgrowth via the pH. By carefully tuning the structure, we optimized the plasmonic properties of the bimetallic core–shell nanorods for surface-enhanced Raman spectroscopy. The Raman signal was the most strongly enhanced by the Au core–Ag shell nanorods, which we explain using finite-difference time-domain calculations.

Introduction

Gold nanorods (AuNRs) exhibit enhanced plasmonic properties with large local field enhancements compared to, e.g., spherical particles.¹ Nanorods have both a transverse localized surface plasmon resonance (LSPR), perpendicular to the length of the rods, and a shape-induced longitudinal LSPR in the direction of the length of the rods at lower energies. The longitudinal LSPR can easily be tuned by changing the aspect ratio (AR) of the rods and extended from visible wavelengths into the near-infrared region of the electromagnetic spectrum.^2,3 This makes AuNRs valuable plasmonic nanoparticles for, e.g., biological applications,^1,4 as biological cells and tissues show significantly less absorption in this region of the spectrum. Compared to single-component Au nanorods, bimetallic nanorods offer enhanced physiochemical properties.^5,6 For example, Ag has superior plasmonic properties with respect to Au due to less damping of the plasmonic resonances.⁶⁻⁸ Coating AuNRs with a Ag layer therefore significantly improves their plasmonic properties and can improve their performance in surface-enhanced Raman spectroscopy (SERS).⁹ For catalytic applications, the addition of Pd or Pt can be beneficial, since these metals are highly active in catalysis.^10,11 Coating a Au core with a thin Pd (or Pt) layer can therefore lead to strongly enhanced catalytic properties while maintaining most of the plasmonic properties.¹² Such bimetallic rods are for example useful for in situ monitoring of chemical reactions by SERS,^13,14 for hydrogen sensing,^14,15 or for plasmon-enhanced catalysis.^12,16−20

The exact composition and morphology of the surface and subsurface layers strongly influence the optical and catalytic properties of bimetallic nanorods.^{5,8,17,18,21−24} However, precise tuning of the number of atomic shell layers and the shell morphology is challenging. So far, the overgrowth of a second metal is typically performed on bare AuNRs^9,14,24−28 and is often performed on a relatively small scale (milliliters), which yields an insufficient amount of particles for, e.g., self-assembly and/or catalysis applications. The final shell thickness and shape of the bimetallic rods are difficult to tune, and the particle shape can easily transform from a spherocylinder to a bricklike particle,^26,29,30 which can only be prevented by the addition of shape-directing additives.^14,31 Uncoated AuNRs are also prone to aggregation during metal overgrowth, and secondary nucleation can occur in the presence of surfactants needed for the stabilization of AuNRs. The control over the stability and shape of bimetallic core–shell NRs can significantly be enhanced by performing metal overgrowth within a larger porous scaffold, such as a mesoporous silica shell. Herein, the porosity, shape, and thickness of the outer silica shell can be used to control the morphology of the inner second metal shell.³²⁻³⁵

Metal deposition is not straightforward for all metals. The morphology and crystal structure of the metal shell largely depend on the interaction between the core and shell metal, their surface energies, and their structural characteristics, such as the lattice spacings.^22,25,36,37 Additionally, the reduction potentials of the metals are important for successful core–shell growth, as galvanic replacement can occur when the core material is oxidized upon reduction of the shell metal, resulting in hollow and partially alloyed metal structures.^22,38−40 Metal overgrowth with a metal that has a similar crystal structure and lattice constant, and a lower surface energy, which is the case for Ag overgrowth on Au, typically results in smooth, epitaxially grown metal shells. On the other hand, the smaller lattice parameter and high surface energy of Pd and Pt compared to Au can lead to dendritic, nonepitaxial Pd/Pt shell growth onto Au.^{20,21,25,34,41} The formation of small Pt/Pd nanoparticles on the surface of AuNRs results in ill-defined surface structures and inhomogeneous shell thicknesses. This is particularly problematic when using such particles as catalysts, where the exact surface morphology and composition are crucial.

Here, we present a systematic study on the synthesis, plasmonic properties, and SERS performance of mesoporous silica-coated, bimetallic Au core Ag/Pt/Pd shell nanorods with a tunable metal composition and surface morphology. The bimetallic core–shell nanorods were synthesized using mesoporous silica-shell-coated AuNRs as starting materials.³⁴ We controlled the size and shape of the Au cores via either anisotropic or more isotropic etching using H₂O₂ as an oxidant. The subsequent metal overgrowth occurred within the mesoporous silica shell, onto the Au cores. The metal composition of the bimetallic nanorods was tuned precisely by varying the metal-precursor concentration and/or reaction time. The reaction rate was controlled via the pH, allowing scaling up from microgram to milligram. Furthermore, the morphology and crystallographic orientation of the metal shells were tuned via thermal annealing. Herein, the mesoporous silica coating was crucial in preventing aggregation and functioned as a shape-preserving template to retain the spherocylindrical shape of the nanorods at elevated temperatures. In the subsequent SERS measurements, the mesoporous silica shell around the bimetallic nanorods also prevented strong plasmonic coupling between NRs while still allowing access to the NR surface, enabling a fair comparison between the different bimetallic core–shell NRs. Finally, we discuss the key parameters governing the metal shell growth mechanism and therefore the shell morphology and crystal structure of the resulting core–shell nanoparticles. Such knowledge is important in predicting the metal overgrowth behavior of different combinations of metals and in extending the synthesis method described in this paper to different particle shapes and metal compositions.

Results and Discussion

Modifying the Etching Behavior of Au Nanorods within Mesoporous Silica Shells

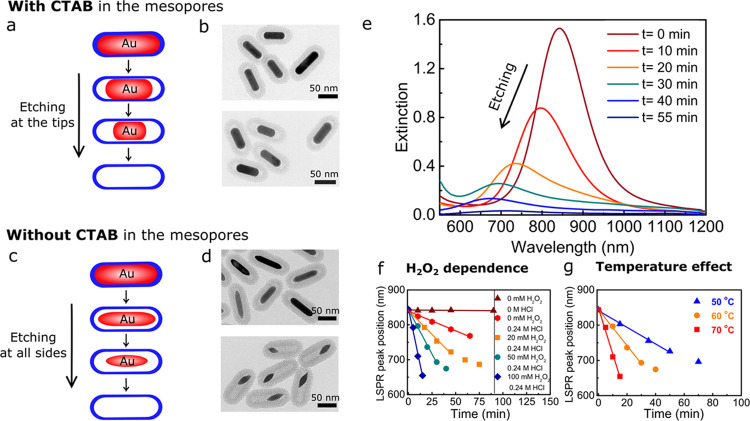
Tuning of the AuNR size within the mesoporous silica shells was performed by oxidative etching in methanol (MeOH). Employing H₂O₂ as an oxidant, instead of O₂ from the air as used previously,³⁴ allows etching in a more reproducible and controlled way. Moreover, the etching behavior of the silica-coated gold nanorods (Au@SiO₂ NRs) could be tuned from anisotropic etching taking place predominantly at the tips of NRs to etching with roughly equal rates from all sides of the rods, by either leaving the cetyltrimethylammonium bromide (CTAB) template or removing it from the mesopores in the surrounding silica shells and from the AuNR surface. We schematically illustrate the two distinct etching modes in Figure 1a,c and the corresponding transmission electron microscopy (TEM) images in Figure 1b,d. Here, CTAB removal was achieved by washing the Au@SiO₂ NRs with an acidified ethanol solution (0.1 M HCl in EtOH). Thermogravimetric analysis (TGA) confirmed that most (≥70 wt %) of the CTAB was removed after the washing procedure (Figure S1), and nitrogen physisorption showed that the mesopore diameter was 2.5 nm (Figure S2). The difference in etching behavior and etching rate before and after CTAB removal is most likely explained by the difference in accessibility of the AuNRs through the pores of the silica shell, where a larger accessibility leads to a higher etching rate.

Figure 1.

Etching of Au@SiO₂ NRs with and without CTAB in the mesopores (a–d) Schematic representation and corresponding TEM images of the etching process of the Au@SiO₂ NRs with CTAB (a, b) and without CTAB (c, d) in the mesopores after 10 and 25 min of etching in methanol containing 0.24 M HCl and 50 mM H₂O₂. (e) Extinction spectra of the Au@SiO₂ NRs in MeOH during etching with 50 mM H₂O₂ and 0.24 M HCl. (f) LSPR peak position during etching with 0 mM HCl and 0 mM H₂O₂ (brown) and 0, 20, 50, and 100 mM H₂O₂ with 0.24 M HCl in MeOH at 60 °C. (g) LSPR peak position during etching at 50, 60, and 70 °C with [H₂O₂] = 50 mM. The data in (b, e–g) were acquired for the etching process of the Au@SiO₂ NRs with CTAB in the mesopores.

During etching, we monitored the LSPR peak shift of the Au@SiO₂ NRs in methanol. In Figure 1e, the extinction spectra of Au@SiO₂ NRs (L = 72 nm; D = 19 nm; aspect ratio (AR) = 3.8; λ_LSPR = 844 nm) with CTAB in the mesopores during etching at 60 °C with 50 mM H₂O₂ are shown. Upon etching, the LSPR peak position shifted to shorter wavelengths, indicating that the aspect ratio of the NRs was lowered and that etching predominantly took place at the tips of the nanorods. The lowering of the LSPR peak intensity is explained by the decrease in AR combined with a loss in particle volume upon etching. A similar blue shift of the LSPR peak was observed when etching Au@SiO₂ NRs without CTAB in the mesopores (Figure S3) but now in a shorter time period due to the more facile mass transport of the oxidants to the AuNR surface.

In Figure 1f,g, we show that the etching rate for Au@SiO₂ NR with CTAB in the mesopores can be controlled and varied from minutes to hours by varying the H₂O₂ concentration and temperature. By increasing the H₂O₂ concentration, the etching was also found to take place at room temperature (RT). However, this makes the etching reaction more difficult to stop at a specific Au core size. It is therefore desirable to make the etching process sufficiently slow at elevated temperatures such that the reaction can easily be quenched at any desired LSPR peak position and Au core dimension. The quenching was typically done by diluting the reaction mixture by a factor 2 with cold (∼4 °C) methanol. The etching process could be carried out on a milliliter scale, but also on a liter scale.

For the metal overgrowth presented in the rest of this paper, we quenched the etching at λ_LSPR = 748 nm, which corresponded to Au@SiO₂ NRs with L = 62 nm, D = 18 nm, and AR = 3.4. Compared to the initial Au@SiO₂ NRs, 20% of the particle volume had been removed.

Ag Overgrowth: Controlling the Plasmonic Properties of Au Core–Ag Shell Nanorods

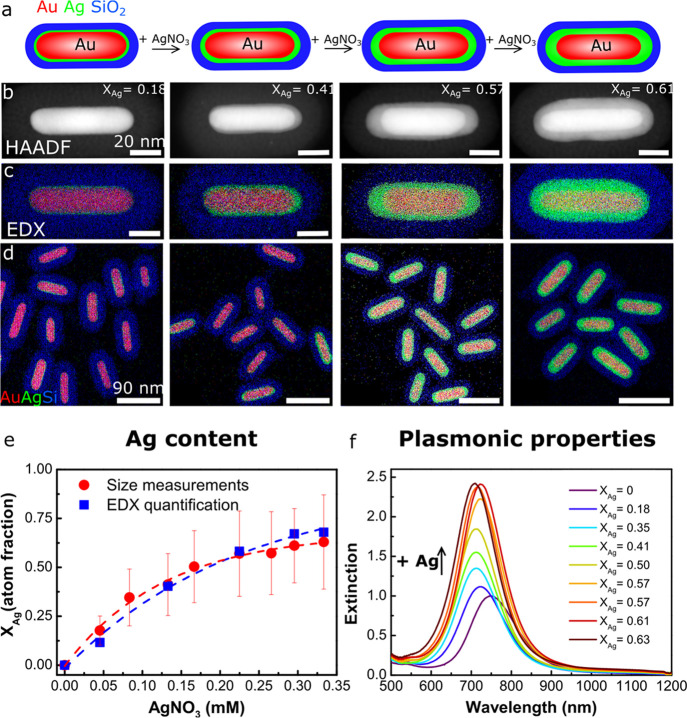
The Au cores were overgrown with a Ag shell in water using AgNO₃ as a silver precursor and ascorbic acid as a reducing agent (see the Experimental Section and Table S2 for details). The use of this relatively mild reducing agent ensured that the silver ions were selectively reduced on the Au cores and prevented the formation of new, individual Ag nanoparticles in solution and in the mesopores of the silica shell. Figure 2 shows the resulting Au core–Ag shell nanorods (Au@Ag@SiO₂ NRs) grown with 0.045–0.33 mM AgNO₃ and 0.18–1.3 mM ascorbic acid in water. Due to the difference in Z-contrast, the Ag shell appeared as a light shell around a bright Au core in the high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) images. The energy-dispersive X-ray spectroscopy (EDX) maps show the Au core, Ag shell, and SiO₂ shell in red, green, and blue, respectively. Both the HAADF-STEM images in Figure 2b and the EDX maps in Figure 2c,d clearly show that the Ag shell thickness increased with increasing AgNO₃ concentration.

Figure 2.

Controlled growth of Ag on Au@SiO₂ cores in water. (a) Schematic representation of the Ag overgrowth with increasing AgNO₃ concentration, leading to an increased Ag shell thickness. From left to right: (b) HAADF-STEM and (c) EDX intensity maps of single and (d) multiple Au@Ag@SiO₂ core–shell nanorods grown with 0.05, 0.13, 0.22, and 0.30 mM AgNO₃. (e) Atomic Ag fraction (X_Ag) of the core–shell nanorods synthesized with 0–0.33 mM AgNO₃ as determined from TEM size measurements (red) and EDX quantification (blue). (f) Extinction spectra of the Au@Ag@SiO₂ NRs grown with various 0–0.33 mM AgNO₃. See Table S2 for the full set of experimental details.

Using the electron microscopy images, we analyzed the dimensions of the Au@Ag@SiO₂ NRs before and after Ag deposition and list them in Table S1. For the Au@Ag@SiO₂ NRs grown with 0–0.33 mM AgNO₃, the particle volume increased from 1.4 to 4.0 × 10³ nm³ (based on the two-dimensional, 2D projection TEM images), which is a factor 2.2 larger than the initial volume of the nonetched Au@SiO₂ NRs. This shows that the silica shell is rather flexible⁴² and can accommodate a larger particle volume than that of the initial, unetched AuNR. This is further supported by the fact that the silica shell thickness decreased from 18.8 to 16.7 nm when increasing X_Ag from 0.18 to 0.63 (Figure S4). The flexibility of the SiO₂ shell therefore also allows direct growth of Ag on unetched AuNRs. In Figure S5, an EDX map of Au@Ag@SiO₂ NRs is shown after direct metal overgrowth on Au@SiO₂ NRs without performing an etching step beforehand. Only when growing very thick Ag shells with a volume 5 times larger than the Au core and 3.5 times larger than the original Au rod before etching, the flexibility of the silica shell is no longer sufficient and the mesoporous shell cracks open (Figure S6).

The size parameters from Table S1 and EDX maps from Figure 2d were used to quantify the metal composition of the Au@Ag@SiO₂ NRs. The plot in Figure 2e shows the atomic Ag fraction, X_Ag, versus the AgNO₃ concentration. X_Ag values determined from the TEM-based size measurements (100 particle average) and EDX quantification (10 particle average) are displayed in red and blue, respectively. X_Ag increased with [AgNO₃] from 0 to 0.62. Based on the AuNR and Ag concentrations used in the metal overgrowth, the percentage of Ag depositing on the AuNRs was calculated to be ≥90% (Table S5), confirming that the Ag selectively grew on the Au cores and no secondary nucleation occurred.

The increase in X_Ag strongly affected the optical properties of the Au@Ag@SiO₂ NRs. In Figure 2f, we show the extinction spectra corresponding to the Au@Ag@SiO₂ NRs grown with 0–0.33 mM AgNO₃ and X_Ag = 0–0.62. The intensity of the LSPR peak increased by a factor 2.4 for the NRs with the largest Ag shell thickness. The enhanced plasmonic properties are due to an increase in Ag content and particle volume. The LSPR peak also blue-shifted from 748 to 710 nm, which is due to a decrease in AR from 3.4 to 2.8 and an increase in X_Ag.

To investigate the orientation of the lattice planes in the Ag shell with respect to the Au core, high-resolution transmission electron microscopy (HRTEM) measurements were performed. The resulting bright-field images are shown in Figure S7. The HRTEM images show that the Ag shell grew on the AuNR surface with its (200) lattice planes oriented in the same direction as the (200) lattice planes of the Au core, indicating epitaxial growth.

Pd Overgrowth: Controlling the Shell Thickness and Morphology

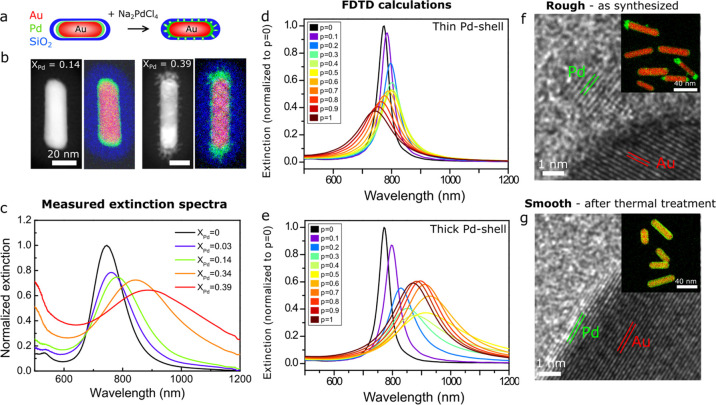
The Au@Pd@SiO₂ NRs were grown with 0.083–0.83 mM Na₂PdCl₄ and 0.33–3.3 mM ascorbic acid in water (see the Experimental Section and Table S3 for details). In Figure 3a–c, a schematic representation, HAADF-STEM images, EDX maps, and extinction spectra of the resulting Au@Pd@SiO₂ NRs are shown. In the EDX maps, Au, Pd, and Si are depicted in red, green, and blue, respectively. From the EDX map in Figure 3b, it can be seen that at low Na₂PdCl₄ concentrations, a thin Pd shell was formed on the Au rod surface. On increasing the Pd concentration, the shell became more irregular and dendritic, which is most clearly visible in the HAADF-STEM images. The atomic Pd fraction (X_Pd) was quantified for the different Au@Pd NRs with EDX, averaged over at least 10 particles. In Figure S8, lower-magnification TEM images and a plot of X_Pd as a function of the Na₂PdCl₄ concentration are shown. The Pd fraction increased with increasing Na₂PdCl₄ concentration, from 0.03 to 0.39. The plots in Figures 2e and S8 show a similar trend, where X_Ag and X_Pd increase as a function of the AgNO₃ and Na₂PdCl₄ concentrations. Yet, the yield during Pd overgrowth is lower than during Ag overgrowth: ∼40% (Table S6) versus ≥90%. This difference could be related to the lower standard reduction potential of PdCl₄^2– compared to Ag⁺ ions: +0.591 versus +0.800 V (25 °C, 1 atm), respectively.⁴³

Figure 3.

Control over the Pd shell morphology: switching between smooth and rough Pd layers to alter the plasmonic properties. (a) Schematic representation of the Pd overgrowth with increasing Na₂PdCl₄ concentration, leading to an increase in roughness of the Pd shell. (b) HAADF-SEM images and corresponding EDX intensity maps of Au@Pd@SiO₂ NRs grown with 0.18 mM (X_Pd = 0.14) and 0.83 mM (X_Pd = 0.39). (c) Measured extinction spectra of the Au@Pd@SiO₂ NRs in water, grown with 0–0.83 mM Na₂PdCl₄ and X_Pd = 0–0.39. (d, e) Finite-difference time-domain (FDTD)-calculated extinction spectra of Au@Pd@SiO₂ NRs with a thin (d) and a thick (e) Pd shell as a function of the Pd packing fraction p of the shell, where p < 1 and p = 1 correspond to a discontinuous and continuous Pd shell, respectively (see the Experimental Section for details). The Au@Pd@SiO₂ NRs with a thin and a thick Pd shell correspond to experimental results with 0.083 mM Na₂PdCl₄ (Au core: 58.5 × 17.7 nm; Au@Pd NR: 60.5 × 19.7 nm) and 0.83 mM Na₂PdCl₄ (Au@Pd NR: 78.6 × 19.4 nm), respectively. (f, g) HRTEM image and EDX intensity map of Au@Pd@SiO₂ NRs with a rough shell morphology before (f) and after (g) thermal treatment for 1 h at 300 °C in H₂. See Table S3 for the full set of experimental details.

For the thinner Pd shells (e.g., X_Pd = 0.03–0.14), it is difficult to discern whether the Pd shell is continuous, as the STEM images and EDX maps are 2D projections of a three-dimensional (3D) particle. We therefore investigated the continuity of the Pd shells by studying the optical properties of the core–shell NRs. In Figure 3c, the extinction spectra of the Au@Pd@SiO₂ NRs are plotted, showing the change in plasmonic properties upon Pd shell growth. The LSPR peak red-shifted, decreased in intensity, and broadened upon Pd shell growth. Using finite-difference time-domain (FDTD) calculations, the extinction spectra of Au@Pd@SiO₂ NRs with a thin Pd shell and a thick Pd shell were computed, corresponding to the experimental results for 0.083 and 0.83 mM Na₂PdCl₄, respectively. Using an effective-medium approach for the composite dielectric function consisting of Pd and the surrounding solvent, we varied the Pd packing fraction p of a Pd dielectric shell from 0 to 1, where p < 1 and p = 1 correspond to a discontinuous and continuous Pd shell, respectively (see the Experimental Section for details). For a thin Pd shell, the plasmon peak red-shifts when the shell is discontinuous (p ∼ 0–0.6) but blue-shifts with respect to the Au cores for more continuous shells (p ∼ 0.7–1). The best match between the experimentally measured spectrum and the calculated spectra is found for p = 0.1, showing that the thin Pd shells were most likely discontinuous (Figure S9). For the thicker Pd shell (Figure 3e), the LSPR peak red-shifts and broadens, which is similar to the trend observed experimentally (Figure 3b), where p = 0.4 gives the best match between the experimental and calculated spectra (Figure S9).

In Figure 3f,g, we show that the shell morphology of the Au@Pd@SiO₂ NRs was controlled to obtain smooth, epitaxial Pd shells around the AuNRs via thermal annealing. Herein, we first synthesized rough Pd shells at room temperature. Next, the Au@Pd@SiO₂ NRs were heated in H₂ for 1 h at 300 °C, which is below the alloying temperature of Au–Pd.⁸ During the heating, the protective mesoporous silica shell was crucial in preventing the NRs from aggregating and in retaining the spherocylindrical shape. Additionally, the silica shell also enabled redispersion of the Au@Pd@SiO₂ NRs in polar solvents after thermal treatment. In Figure 3f,g, the Au@Pd@SiO₂, as-synthesized and after heating to 300 °C, are shown. For clarity, we specifically used Au@Pd@SiO₂ NRs, which had a very inhomogeneous Pd shell prior to the thermal annealing (Figure 3f). After heating them to 300 °C for 1 h, the Pd coating was successfully transformed to a smooth, epitaxial shell (Figure 3g). HRTEM revealed that the as-synthesized, polycrystalline Au@Pd@SiO₂ NRs transformed into single-crystalline particles during thermal treatment (Figure 3f,g). Furthermore, the blue shift of the LSPR peak after heating confirmed a transition from a discontinuous to a continuous, smooth Pd shell (Figure S10).

Pt Growth: Dendritic Pt Shells with Variable Spike Lengths

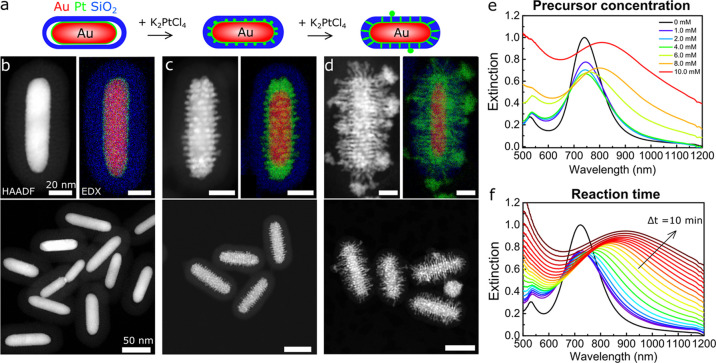
Au@Pt@SiO₂ NRs were prepared using K₂PtCl₄ as a metal precursor. The K₂PtCl₄ concentration of the aqueous solution was varied from 0.083 to 3.3 mM. In Figure 4, the HAADF-STEM images, corresponding EDX maps, and extinction spectra of the Au@Pt@SiO₂ NRs with increasing Pt shell thickness are shown. The EDX maps in Figure 4b–d display Au, Pt, and Si in red, green, and blue, respectively. At low Pt concentrations, a thin Pt shell grew around the Au core (Figure 4b). At higher Pt concentrations, additional Pt spikes started to extend into the pores of the silica coating and revealed the ordered nature of the local pore structure around the AuNRs (Figures 4c and S11). Once the spikes extended outside the silica shell, the metal structure became more disordered (Figure 4d). In Figure 4e, the extinction spectra of the Au@Pt@SiO₂ NRs grown with different Pt precursor concentrations are shown. Similar to the Au@Pd@SiO₂ NRs, the LSPR peak of the Au@SiO₂ NRs broadened and dampened upon Pt shell growth, which is likely a combination of roughness of the Pt shell and the more lossy plasmonic properties of Pt compared to Au.

Figure 4.

Dendritic Pt shell growth with tunable spike lengths. (a) Schematic representation of the Pt overgrowth with increasing K₂PtCl₄ concentration, leading to filling of the mesopores of the silica shell. (b–g) HAADF-STEM images and corresponding EDX intensity maps of Au@Pt@SiO₂ NRs synthesized with 0.33 (b), 3.3 (c), and 17 mM (d) K₂PtCl₄. (e) Extinction spectra of Au@Pt@SiO₂ NRs grown with 0–3.3 mM K₂PtCl₄; reaction time is 20 min. (f) Extinction spectra of Au@Pt@SiO₂ NRs grown with 6.6 mM K₂PtCl₄ with increasing reaction time. Every 10 min, a spectrum was recorded for 3 h. See Table S4 for the full set of experimental details.

Additionally, we observed that the growth rate of Pt was much lower than for Ag or Pd. The Pt content could therefore also be controlled by varying the reaction time, as we show in Figure 4f, where the extinction spectra of Au@Pt@SiO₂ NRs are shown during the metal overgrowth. The broadening of the spectra with increasing reaction time shows that the Pt overgrowth occurred in a similar manner compared to the Pt overgrowth using different Pt concentrations and a fixed reaction time.

We also studied the orientation of the lattice planes in the Pt shell with respect to the Au core. In Figure S12, an HRTEM image of Au@Pt@SiO₂ NRs recorded in the bright-field mode is shown. The HRTEM image shows that a thin crystalline Pt layer had grown on the AuNR surface, but that the (111) lattice planes of the Pt layer were oriented in a different direction compared to the underlying Au(111) lattice planes.

Furthermore, we would like to note that the Pt spikes filled the pores of the surrounding silica shell without destroying it. However, we observed that when thicker Pd or Ag shells were grown, the silica shell would crack. The Pt spike diameter was 2.5 nm (Figure S11), which is in good correspondence with the pore diameter of the mesopores in the silica shell (Figure S2) and of MCM-41-like materials in general,^44,45 while it became significantly thicker when the Pt growth reached the outside of the mesoporous silica shell. Thus, Pt overgrowth can be used to visualize the 3D, local pore structure in direct contact with the AuNR using HAADF-STEM tomography.

Upscaling the Core–Shell Synthesis by Slowing Down the Growth Kinetics

In the small-scale reactions, carried out in ultrapure water (Milli-Q), the Ag and Pd metal overgrowth generally took place in less than 10 s. Due to these short reaction times, only small-scale syntheses with growth solutions below 1 mL resulted in homogeneously coated Au@Ag@SiO₂ NRs and Au@Pd@SiO₂ NRs without secondary nucleation. To prevent inhomogeneous shell growth and secondary nucleation, the reaction time should be longer than the time needed to fully mix all reagents. To slow down the reaction kinetics, we lowered the pH of the reaction mixture by adding HCl. Below a pH of 4.1, part of the ascorbic acid is transformed into its fully protonated, nonreactive form, which cannot be oxidized under the used synthesis conditions (Figure 5a).⁴⁶ Via the equilibrium between the deprotonated and protonated ascorbic acid, new deprotonated ascorbic acid is formed as metal overgrowth takes place and the reactive, deprotonated ascorbic acid is consumed. Therefore, the kinetics of metal growth can be tuned via the pH and the reaction time can be varied from seconds to minutes. In Figure 5b–d, we show the influence of pH on reaction time, where the latter is defined as the time needed for completion of Ag overgrowth. By varying the HCl concentration from 0 to 8 mM, the reaction time was tuned from a few seconds to 25 min. TEM analysis of the resulting samples did not show any difference in the structure and composition of the Au@Ag@SiO₂ NRs grown at different pH. Regardless of the reaction kinetics, identical Au@Ag@SiO₂ NRs were obtained.

Figure 5.

Tuning the reaction rate of the Ag metal overgrowth and scaling up of the core–shell synthesis. (a) Structural formulas of the nonreactive, fully protonated (top) and reactive, deprotonated forms of ascorbic acid (bottom). The pK_a is 4.1. (b) Extinction spectra taken during Ag overgrowth on Au@SiO₂ NRs, which was performed in an acidified solution with 6 mM HCl. The spectra were recorded over 15 min with an interval between the spectra of 1 min. (c) LSPR peak intensity vs the reaction time when 2–8 mM HCl was present. (d) Plot of the reaction time versus the HCl concentration (mM). (e) Extinction spectra of the Au@Ag@SiO₂ NRs synthesized at a 1 mL (blue) and a 400 mL (red) scale.

The slow reaction rate at low pH enabled us to scale up the Ag and Pd overgrowth drastically. In Figure 5e, the extinction spectra of Au@Ag@SiO₂ NRs synthesized at a 1 mL and a 400 mL scale are shown. The spectra match closely: λ_LSPR^smallscale = 783 nm and λ_LSPR = 794 nm. The EDX map in Figure S5 shows that also at a large (400 mL) scale, uniform Au@Ag@SiO₂ NRs were synthesized. The yield of Au@Ag@SiO₂ NRs was 26 mg with a metal loading of 85 wt %. Such relatively large quantities allow studies of these well-defined colloidal particles in, e.g., in situ X-ray absorption spectroscopy,⁴⁷ self-assembly,^48,49 and catalysis. Moreover, the slow growth dynamics allow scaling up to even larger quantities.

Bimetallic Core–Shell Nanorods for Surface-Enhanced Raman Spectroscopy

Our ability to control the structural properties of the bimetallic core–shell nanorods allowed optimization of their plasmonic properties for surface-enhanced Raman spectroscopy (SERS). In this paper, our aim is to illustrate the enhancements caused by the properties of the individual NRs. Future work will involve self-assembly of these bimetallic nanorods to create arrangements where we have control over interparticle hotspots as well.^49,50 Here, we studied the SERS performance of Au@Ag@SiO₂ with X_Ag = 0.20, 0.42; Au@Pd@SiO₂ NRs with X_Pd = 0.21, 0.32; and Au@SiO₂ NRs with X_Au = 1.0 (see Table S5 for particle dimensions). In all cases, the CTAB template was removed from the mesoporous silica shells using mild acid washing as confirmed by TGA (Figure S1) and pyridine-based SERS (Figure S13). To study the SERS signal of the different nanorods in a quantitative and reproducible way, all SERS measurements were performed in solution. This has three important advantages compared to SERS on dried particle ensembles and probe molecules. First, by measuring in a dilute particle dispersion, interparticle plasmonic hotspots, which strongly enhance the SERS signal but usually in a highly uncontrolled way, can be prevented. Such interparticle hotspots were further prevented by the 18 nm thick mesoporous silica shell surrounding the NRs. Second, in solution, the particle concentration can be controlled precisely, which enables a direct comparison between different NR systems. Here, the metal concentration was fixed at 0.5 mM Au, as determined via inductively coupled plasma atomic emission spectroscopy (ICP-AES) analysis, in each measurement. Third, the probe concentration is homogeneous throughout the sample when measuring in solution, whereas inhomogeneities in the probe concentration upon drying would complicate a direct comparison between the different bimetallic NR samples. As a probe molecule, we chose crystal violet (CV) as it does not chemically bind to the surfaces,³³ which prevents changes in the polarizability of the molecule when binding to different metal surfaces.⁵¹ The CV concentration was fixed at 1.0 μM in a 3:1 (by volume) ethanol/water solution.

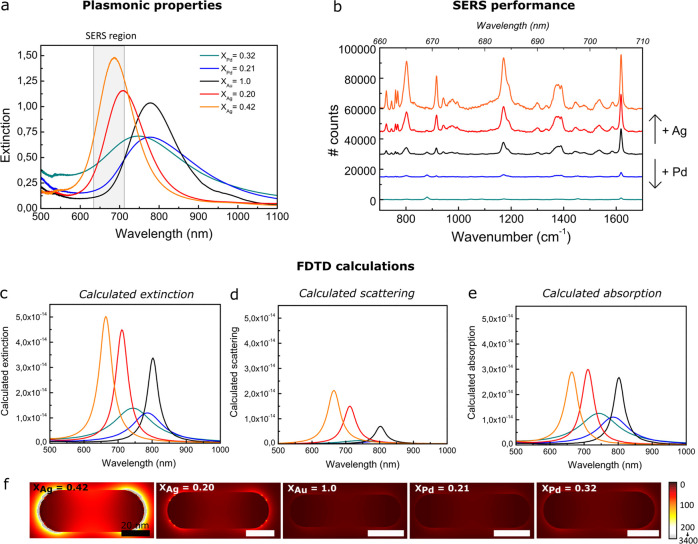
In Figure 6a, the optical spectra of the bimetallic nanorods as measured experimentally are shown. By growing a Ag shell, the LSPR peak increased in intensity, blue-shifted, and matched the spectral region relevant in the subsequent SERS measurements, indicated by the gray area in Figure 6a. Pd growth, on the other hand, led to broadening and damping of the LSPR peak. In the latter case, etched Au cores with a shorter aspect ratio than the Au@SiO₂ NRs from Figure 6a were used, which is why the LSPR peak of the Au@Pd@SiO₂ NRs lies at slightly shorter wavelengths.

Figure 6.

Tuning the plasmonic properties of bimetallic core–shell rods for surface-enhanced Raman spectroscopy. (a) Experimentally measured extinction spectra of Au@Ag@SiO₂, Au@SiO₂ NRs, and Au@Pd@SiO₂ NRs with X_Ag = 0.42 (orange), X_Ag = 0.20 (red), X_Au = 1.0 (black), X_Pd = 0.21 (blue), and X_Pd = 0.32 (turquoise) in a 3:1 (by volume) EtOH/H₂O mixture. For the experimental spectra, an equal Au concentration of [Au] = 0.1 mM was used. (b) Raman spectra of crystal violet measured in the presence of Au@Ag@SiO₂, Au@Pd@SiO₂ NRs, and Au@SiO₂ NRs. The SERS measurements were performed in a 3:1 (by volume) EtOH/H₂O mixture containing a constant metal concentration of [Au] = 0.5 mM and 1 μM crystal violet (CV). FDTD-calculated extinction (c), scattering (d), and absorption (e) spectra of the Au@X@SiO₂ NRs. (f) FDTD-calculated local field around the Au@Ag@SiO₂ (left), Au@SiO₂ (middle), and Au@Pd@SiO₂ NRs (right) when using a 633 nm light source. In Table S6, the maximum local field enhancements are listed.

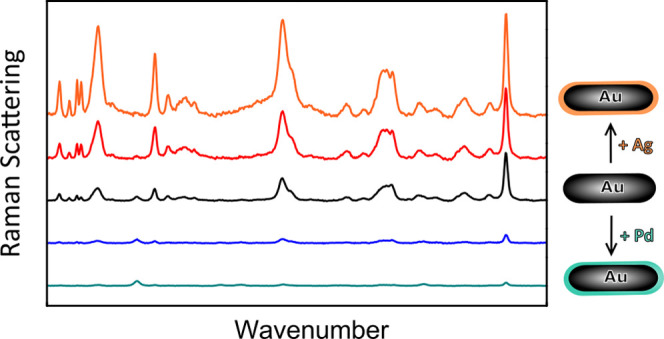
In Figure 6b, the SERS spectra of 1.0 μM CV in ethanol/water in the presence of different core–shell NRs are shown. All NRs enhanced the Raman signal of crystal violet, showing that CTAB removal from the mesopores was successful and the metal particle surface was accessible for the crystal violet molecules. The spectra shown in Figure 6b are an average of 800 spectra recorded at different positions in the sample. By measuring in a dilute, homogeneously mixed dispersion and averaging over 100 spectra per spot, we successfully obtained reproducible SERS spectra throughout the sample. The excellent reproducibility of our SERS measurements is demonstrated in Figure S14. The intensity of the SERS signal of crystal violet was the highest for Au@Ag@SiO₂ NRs with the largest Ag content (X_Ag = 0.42) and decreased with decreasing Ag and increasing Pd contents. These observations are in line with observations described in the literature on uncoated Au core–Ag shell nanostructures^27,28 and uncoated Pd-coated Ag nanocubes⁵² in the presence of strongly binding thiol-functionalized probe molecules.

To better understand the observed dependence of the SERS performance on the metal shell type and thickness, we performed FDTD calculations. The calculated extinction, scattering, and absorption spectra are shown in Figure 6c,d,e, respectively. The local field enhancements around the Au@Ag@SiO₂, Au@Pd@SiO₂ NRs, and Au@SiO₂ NRs are shown in Figure 6f, and the maximum local field enhancements are listed in Table S6. The enhancement of the Raman signal is proportional to |E_loc(ω_exc)E_loc(ω_RS)|²,⁵¹⁵¹ where E_loc(ω_exc) and E_loc(ω_RS) are the local field intensities at the wavelength of the incident light (ω_exc = 633 nm) and at the wavelengths of the inelastically scattered light of the probe molecules (ω_RS = 660–710 nm, 700–1700 cm^–1), respectively. We find that the local field enhancement at 633 nm is the highest for the Au@Ag NRs, especially for the Au@Ag@SiO₂ NRs with X_Ag = 0.42 (Figure 6f, Table S6). Furthermore, the scattering cross section of the Au@Ag@SiO₂ NRs is the largest at ω_RS, meaning that the inelastically scattered light from the CV molecules is scattered most efficiently by the Au@Ag@SiO₂ NRs. We therefore ascribe the enhanced SERS performance upon Ag shell growth to the increased spectral overlap of the LSPR peak of the Ag@Au@SiO₂ NRs, the 633 nm laser light, and the inelastically scattered light of the CV probe molecules and to the stronger, less damped, plasmonic fields themselves.

Predicting the Growth Behavior of Core–Shell Nanoparticles

Depending on the type of metal, we observed different shell morphologies and crystal lattice orientations in the metal overgrowth of Ag, Pd, and Pt onto Au cores. We will now identify the physiochemical properties known for bulk metals that play an important role in the shell growth behavior, when assuming thermodynamic equilibrium conditions. Such knowledge is useful in predicting the metal structures that would form when extending our synthesis method to different metals than Au, Ag, Pd, and Pt.

For the Au@Ag@SiO₂ and Au@Pd@SiO₂/Au@Pt@SiO₂ NRs, smooth and continuous shell growth and rough and discontinuous shell growth were observed, respectively. The morphology of the metal shell depends on the dominating growth mechanism during metal deposition. According to the crystal growth theory for gas-phase deposition, three growth modes can be distinguished: (1) a layered growth mode (Frank van der Merwe, FM), (2) an intermediate growth mode (Stranski Krastanov, SK), and (3) an island growth mode (Volmer Weber, VW).^36,37 Herein, FM growth leads to smooth continuous shells, whereas rough, discontinuous shells are formed in VW growth. In SK growth, a smooth shell is formed initially, followed by discontinuous growth. This can happen when the strain energy increases with an increasing number of atomic shell layers, for example, due to a lattice mismatch between the core and the shell crystal structure. Which of the growth modes occurs depends on the surface tensions of, and interactions between, the core and the shell metal.

In Table 1, the solid–vapor surface free energy (E_S) values for Au, Ag, Pd, and Pt (determined at 0 K) are listed. When E_S(shell) is smaller than E_S(core), wetting of the core by the shell metal is favorable and continuous growth can occur, given that the interfacial energy is small. As the interfacial surface tensions and energies between the metals are not known, we listed the bond dissociation energies between two atoms of the same metal E_D(M–M) and the bond dissociation energies between a metal atom with a Au atom E_D(Au–M) in Table 1 as well. These bond dissociation energies indicate whether the interaction between the shell and core materials is favorable compared to the shell–shell interaction. Continuous shell growth is likely when E_D(Au–M) > E_D(M–M).

Table 1. Summary of Key Parameters of Bulk Au, Ag, Pd, and Pt^a.

	Au	Ag	Pd	Pt
FCC lattice constant (Å)53	4.08	4.09	3.89	3.92
surface energy, ES (J/m2)53,54	1.50	1.24	2.00	2.49
bond dissociation energy M–M, ED(M–M) (kJ/mol)56	226	160	100	307
bond dissociation energy, ED(Au–M) (kJ/mol)56	226	203	155

^aThe face centered cubic (FCC) lattice constant, solid–vapor surface free energy at 0 K, and the bond dissociation energy of two equal metal atoms (M–M) and between Au and a different metal atom (Au–M).⁵³⁻⁵⁶

From the E_S and E_D values in Table 1, it follows that E_S(Ag) < E_S(Au) and E_D(Ag–Au) > E_D(Ag–Ag), meaning that continuous growth of a smooth Ag shell around a gold core is thermodynamically favorable. This is in good agreement with our experimental results presented in Figure 2, showing smooth, continuous, epitaxial Ag shell growth. Smooth Ag growth on differently shaped AuNPs has also been observed in the literature, both for uncoated and for partially coated NPs.^{6,7,26,32−34,36,40,57,58} To the best of our knowledge, there are no reports of rough, discontinuous Ag shell growth on Au.

The growth behavior of Pt shells on Au cores, presented in Figure 4, can be explained in a similar way. E_S(Pt) > E_S(Au) and E_D(Pt–Pt) > E_D(Au–Au), meaning that discontinuous, rough, nonepitaxial shell growth is indeed expected. Note that E_D(Au–Pt) is not known since Au and Pt do not form an alloy for bulk metals. Our experimental findings are in line with previous reports of metal overgrowth on uncoated and partially coated Au NPs, where always rough shell growth was observed regardless of the presence of a (porous) surface coating.^32,34,36,41

Predicting the type of metal growth for Pd on Au is more complex than for Ag or Pt shell growth. The surface energy of Pd is higher than that of Au, whereas the bond dissociation energy E_D(Au–Pd) is larger than E_D(Pd–Pd). The latter indicates that continuous Pd shell growth is in principle favorable. However, when overgrowing Au with Pd, we observed that Pd, like Pt, tended to grow a rough shell extending into the mesopores of the silica shell. For uncoated Au–Pd NRs, both continuous and discontinuous shell growth have been observed.^21,36 In the case of uncoated AuNRs, the growth behavior could be tuned from continuous to discrete when growing the Pd shell in the presence of Br^– and Cl^– ions, respectively.²¹ This difference in growth behavior is probably due to a variation in the reduction potential and thus in the reduction rate of Pd ions when adding Br^– and Cl^–, which are known to strongly coordinate with Pd ions.^22,59 In our case, the growth occurred in the presence of Cl^– ions coming from the Na₂PdCl₄ precursor, resulting in discontinuous shell growth. By thermally annealing the Au@Pd@SO₂ NRs, the rough Pd shells turned into smooth, continuous, epitaxial Pd shells (Figure 3), while the anisotropic out-of-equilibrium particle shape still remained. The latter result shows that continuous Pd shell Au core NRs are thermodynamically the more favorable local structures.

Whether epitaxial growth occurs (partially) depends on the lattice parameters of the core and shell metal and on the thickness of the shell. In Table 1, the lattice constants for FCC Au, Ag, Pd, and Pt crystals are given. Ag and Au have similar lattice constants, differing by only 0.2%, explaining why we observed epitaxial growth of Ag on Au. The HRTEM images in Figure S7 show a crystalline Ag shell, with the lattice planes running in the same crystallographic orientation as the underlying Au core. For Pd and Pt, the lattice mismatch with Au is significantly larger, about 4%. Typically within 5% mismatch, epitaxial growth is still possible.^36,60 For Pd, the shell growth was nonepitaxial as separate Pd nanocrystals were grown with their crystals in random orientations with respect to the underlying AuNR crystal (Figure 3f). However, via thermal annealing, these nonepitaxial shells were successfully transformed into epitaxial Pd shells (Figure 3g), showing that a 4% lattice mismatch still allows for epitaxial growth of Pd on Au,^36,61 most likely because the shells were relatively thin.

Conclusions

We have shown that careful tuning of the composition and morphology of mesoporous silica-coated, bimetallic core–shell nanorods is essential in controlling their plasmonic properties. Both in experiments and with FDTD calculations, we demonstrated that the intensity of the longitudinal surface plasmon peak increased with its peak position blue-shifting upon Ag shell growth, whereas the intensity decreased and the peak broadened upon Pd/Pt shell growth. Our ability to precisely tune the structure allowed optimization of the plasmonic properties for surface-enhanced Raman spectroscopy. We showed that the Au@Ag@SiO₂ NRs outperformed Au@Pd@SiO₂ and Au@SiO₂ NRs due to the increased strength and spectral overlap of the LSPR peak with the 633 nm laser light and the inelastically scattered light of the probe molecules. The metal overgrowth approach described in this paper is not limited to small-scale, rod-shaped particles or to Ag, Pd, and Pt only, but can be extended to different, nonprecious metals and other particle shapes as well.²² Herein, the growth behavior of the resulting metal shells depends on physiochemical bulk parameters such as the binding energy between the shell and core atoms, the surface tensions, and the lattice parameters of the metals used. We therefore expect that our work will open the way to the large-scale synthesis of well-defined, multimetallic nanostructures of key importance for self-assembly, plasmonics, catalysis, and sensing.

Experimental Section

Chemicals

All chemicals were used as received without further purification. Hexadecyltrimethylammonium bromide (CTAB, >98.0%) and sodium oleate (NaOL, >97.0%) were purchased from TCI America. Hydrogen tetrachloroaurate trihydrate (HAuCl₄·3H₂O) and sodium hydroxide (NaOH, 98%) were purchased from Acros Organics. l-Ascorbic acid (BioXtra, ≥99%), hydrogen peroxide (H₂O₂, 30 wt % in H₂O), hydrochloric acid (HCl, 37 wt % in water), silver nitrate (AgNO₃, ≥99%), sodium borohydride (NaBH₄, 99%), sodium tetrachloropalladate-(II) (Na₂PdCl₄, 98%), potassium tetrachloroplatinate-(II) (K₂PtCl₄, 98%), and tetraethyl orthosilicate (TEOS, 98%) were purchased from Sigma-Aldrich. Ultrapure water (Millipore Milli-Q grade) with a resistivity of 18.2 MΩ was used in all of the experiments. Methanol was purchased from Interchema (≥99.85%.) All glassware for the AuNR synthesis was cleaned with fresh aqua regia (HCl/HNO₃ in a 3:1 volume ratio), rinsed with large amounts of water, and dried at 100 °C before usage.

Synthesis of the Core–Shell Nanorods

Step 1: Gold Nanorod Synthesis

Monodisperse AuNRs were synthesized according to the protocol of Ye et al.² The synthesis was performed on a 500 mL scale with a growth solution containing 7.0 g of CTAB, 1.24 g of NaOL, 250 mL of MQ H₂O, 250 mL of 1.0 mM HAuCl₄, 7.2 mL of AgNO₃, 2.10 mL of concentrated HCl (37 wt %, 12.1 M), 64 mM ascorbic acid, and 1.0 mL of seed solution. The seeds were prepared from a solution containing 10 mL of 0.10 M CTAB, 51 μL of 50 mM HAuCl₄, and 1.0 mL of 6.0 mM NaBH₄. The subsequent rod growth was performed under static conditions in a 30 °C water bath overnight. The resulting AuNR suspensions had a longitudinal LSPR (λ_LSPR) of 892 nm and a maximum extinction (Ext) of 1.0 when diluted 4× in H₂O. The rods were centrifuged at 8000 rcf (relative centrifugal force) for 30 min (Rotina 380R Hettich centrifuge), washed once with H₂O, and redispersed in about 40 mL of 5.0 mM CTAB H₂O.

Step 2: Mesoporous Silica Coating

The CTAB-stabilized AuNRs were coated with an 18 nm mesoporous silica shell via the method of Gorelikov et al.⁶² The coating was performed in 170 mL of 1.5 mM CTAB aqueous solution containing 1.0 mM NaOH and an AuNR concentration corresponding to an extinction maximum of 1.0 when diluted 10× in H₂O. While magnetically stirring at 300 rpm in a 30 °C water bath, 3 times 0.510 mL of 0.90 M TEOS in EtOH was added with a 30 min time interval. The silica-coated gold nanorods (Au@SiO₂ NRs) were centrifuged at 8000 rcf for 30 min and washed once with water and once with ethanol.

Step 3: Oxidative Etching

First, 200 μL of HCl (37 wt %, 12.1 M) and 200 μL of 50 mM H₂O₂ in MeOH (containing 0.19 M H₂O) were added to 10 mL of silica-coated AuNRs (λ_LSPR = 838 nm, Ext = 1.6 when 2× diluted in MeOH) in MeOH, resulting in final HCl and H₂O₂ concentrations of 0.24 M and 1.0 mM, respectively. Thereafter, the reaction was immediately heated in a 60 °C oil bath while magnetically stirring at 400 rpm. After 12 min, the reaction was quenched with 10 mL of fresh MeOH. The longitudinal LSPR peak position of the etched AuNRs in MeOH had shifted to 748 nm. An additional 20 mL of fresh MeOH was added, and the particles were centrifuged at 8000 rcf for 25 min. Next, the particles were washed with 9 mL of MeOH and 9 mL of H₂O and redispersed in ∼7 mL of H₂O (λ_LSPR = 748 nm, Ext = 2.2).

To remove the CTAB and open the mesopores of the silica-coated AuNRs, we washed the NRs with 0.10 M HCl in EtOH. To a 31 mL dispersion of Au@SiO₂ NRs in EtOH, 260 μL of concentrated HCl (12.1 M) was added such that the HCl concentration in EtOH was 0.10 M. The acidified dispersion was sonicated for 30 min at room temperature (RT). Next, the Au@SiO₂ NRs were centrifuged at 8000 rcf for 35 min and washed with 20 mL of EtOH and twice with 10 mL of EtOH to remove the HCl. Thereafter, the rods were redispersed in 10 mL of EtOH.

Step 4: Metal Overgrowth

For metal overgrowth, 0.300 mL of etched AuNRs@meso-SiO₂ (λ_LSPR = 746–748 nm, Ext = 2.2) in H₂O was used, to which AgNO₃, Na₂PdCl₄, or K₂PtCl₄ (1–100 mM, 0.030 mL) was added. Next, ascorbic acid (4× [metal precursor] mM, 0.030 mL) was added and the mixture was gently shaken for 20 min at room temperature (for Ag and Pd) or overnight (for Pt). The complete set of experimental parameters for Ag, Pd, and Pt overgrowth is listed in Tables S3–S5, respectively. In the tables, the concentration and volume of the added metal precursor and ascorbic acid solutions are given and the final metal precursor and ascorbic acid concentration in the reaction mixture. Next, the reaction mixtures were diluted to 1.0 mL H₂O to study their plasmonic properties by recording the vis–IR spectra. Afterward, the core–shell nanorods were washed with 4 mL of H₂O and 2 mL of EtOH and redispersed in 1.0 mL of absolute EtOH (centrifugation at 7000–9000 rcf for 10–15 min). TEM analysis was used to determine the size of the Ag@Au@SiO₂ NRs. Due to the dendritic nature of the Pd and Pt shell, this could not reliably be done for the Au@Pd@SiO₂ and Au@Pt@SiO₂ NRs.

Thermal Treatment

Thermal treatment was performed in a tubular oven (Thermolyne 79300 tube furnace) under a constant H₂ flow (∼50 mL/min). The core–shell NRs were first dried in a glass vial and then heated in a quartz tube oven. The heating rate was 2 °C/min, and the particles were heated to 300 °C for 1 h and cooled down under H₂ to RT before taking them out of the oven. After heating, the NRs were redispersed in 1 mL of EtOH. The shell morphology of the rods was analyzed in a transmission electron microscope (TEM), and the optical properties were analyzed by recording extinction spectra (see the Characterization Section for details).

Controlling the Growth Kinetics

To follow the growth kinetics, in situ Fourier transform visible–infrared spectroscopy (vis–IR) measurements were performed (see details below). The Au@SiO₂ cores were dispersed in 1.0 mL of H₂O such that λ_LSPR = 744 nm and Ext = 1.0. To this solution, 20–80 μL of 0.10 M HCl was added. The 0.10 M HCl solution was prepared by mixing 83 μL of concentrated HCl (37 wt %, 12.1 M) with 9.92 mL of H₂O. Next, 10 μL of 15 mM AgNO₃ was added and an extinction spectrum was recorded before addition of 10 μL of 60 mM ascorbic acid. The final HCl, AgNO₃, and ascorbic acid concentrations in the growth solution were 2–8 mM, 0.15 mM, and 0.60 mM, respectively. Every minute for 25 min, a spectrum was recorded between 400 and 1200 nm with a step size of 1 nm.

Upscaling

For the small- and large-scale Au@Ag@SiO₂ NR syntheses, unetched Au@SiO₂ NRs with L_Au = 107 and D_Au = 35 nm were used. Prior to metal overgrowth, the Au@SiO₂ NRs were washed with 0.10 M HCl in EtOH solution (30 mL of absolute EtOH with 246 μL of concentrated HCl (37 wt %, HCl)), followed by 3× washing with EtOH and redispersion in H₂O (λ_LSPR = 819 nm and Ext = 2.8). The HCl washing was performed to remove most of the remaining CTAB molecules from the pores of the mesoporous silica shell.³³ It is necessary to carry out this step when performing metal overgrowth directly on unetched Au@SiO₂ NRs. For the etched Au@SiO₂ NRs, this step is not required, since (part of) the CTAB is removed during the etching process. The small-scale metal overgrowth was carried out in a disposable cuvette containing 1.0 mL of Au@SiO₂ NRs in H₂O (λ_LSPR = 744 nm and Ext = 1.0), 20 μL of 0.10 M HCl, 20 μL of 5.0 mM AgNO₃, and 20 μL of 20 mM ascorbic acid. The large-scale metal overgrowth was performed in a 500 mL Erlenmeyer flask with 400 mL of Au@SiO₂ NRs in H₂O, 8.0 mL of 0.10 M HCl, 8.0 mL of 5.0 mM AgNO₃, and 8.0 mL of 20 mM ascorbic acid. The reaction time for both experiments was 30 min, during which the large-scale reaction mixture was magnetically stirred at 400 rpm. Afterward, the rods were washed with ethanol twice and redispersed in 2 mL (small-scale) and 25 mL (large-scale) of EtOH for storage. The λ_LSPR values for the Au@Ag@SiO₂ NRs synthesized at small and large scales were 783 and 794 nm, respectively.

Long-Term Storage of Core–Shell NRs

The storage of Au@Ag@SiO₂ NRs in EtOH should always be done in the dark and at low temperature to prevent oxidation and subsequent dissolution of the Ag shell. In the fridge (4 °C), the rods can be stored >1 year. We advise also storing the Au@Pd@SiO₂ NRs in the fridge. Storage at RT does not lead to dissolution of the Pd shell, but due to partial oxidation of the Pd shell, the plasmonic properties of the Au@Pd@SiO₂ NRs will be lost in time. We observed that the Au@Pt@SiO₂ NRs can be stored well at RT.

Characterization

Extinction spectra were measured using a vertex 70 FTIR spectrometer (BRUKER) and 1.0 cm cuvettes. The optical spectra were recorded over a spectral range from 400 to 1200 nm with a step size of 1 nm and averaged over 60 spectra. Bright-field transmission electron microscopy images, HAADF-STEM images, and EDX maps were recorded with a FEI Talos F200X operated at 200 kV, which is part of the Electron Microscopy facility EM Square at Utrecht University. The particle sizes were measured from TEM images. Per sample, the size of 100 particles was determined. The obtained EDX intensity maps were quantified using the Cliff–Lorimer method. The metal compositions determined via EDX are an average of 10 particles. The CTAB content of the unwashed and washed Au@SiO₂ NR samples was determined with TGA analysis. The TGA measurements were performed on a PerkinElmer balance (Pyris 1). The samples (typically 10 mg) were heated in 20 mL/min O₂ to 100 °C with 5 °C and kept at 100 °C for 30 min. Thereafter, the sample was heated with 5–600 °C. Inductively coupled plasma atomic emission spectroscopy (ICP-AES) analysis was carried out to determine the metal concentration and composition of the Au@Pd@SiO₂ NR dispersions. The ICP-AES experiments were carried out on a PerkinElmer optical emission spectrometer Optima 8300 equipped with a PerkinElmer S10 autosampler. Prior to the ICP analysis, 10 μL of NRs in EtOH was centrifuged at 8000 rcf for 5 min, dissolved in 500 μL of aqua regia (HNO₃, Sigma-Aldrich, ≥99.999 trace metal basis and HCl, Fluka, for trace analysis), and diluted with 4.50 mL of MQ H₂O to 10 vol % aqua regia in H₂O. Thereafter, the solution was centrifuged for 5 min at 15 000 rcf (to remove remainders of the silica shell). The top 4.50 mL was then used for the ICP analysis.

Raman Measurements

The Raman measurements were carried out on a Renishaw Raman microscope equipped with an RL633nm HeNe laser giving 633 nm light with a maximum power of ∼12.5 mW. A 50× air objective with NA = 0.75 and a laser spot size of about 1 μm was used. Typically, a laser power of 1% (∼0.14 mW), exposure time of 1 s, and 100 accumulations were used. A 3:1 ethanol/water dispersion containing the NRs with a fixed metal concentration of 0.5 mM Au and crystal violet concentration of 1.0 × 10^–6 M was loaded onto a glass capillary, sealed, and mounted on a glass slide with UV glue. During the SERS measurements, 10 different spots in each sample were probed, where an average of 100 spectra was taken at each spot. In this way, we ensured that on average an equal amount of particles contributed to the SERS signal in all measurements.

FDTD Calculations

The FDTD simulations were carried out with the commercial software package Lumerical FDTD Solutions 8.11. A total field scattered field source was used to simulate a propagating plane wave interacting with the nanostructures, with a wavelength range of 500–1200 nm. Only the longitudinal surface plasmon resonance was calculated by setting the polarization parallel to the long axis of the AuNRs. A three-dimensional nonuniform mesh was used with a grid size of 0.3 nm for the Au metal nanorods and the immediate vicinity of the structures. The sizes used in the simulations were determined from TEM images and are summarized in Table S2 for the Au–Ag, Au–Pd, and AuNRs. The shape of the Au core was modeled as a cylinder capped with a hemisphere at each end. For the core–shell nanorods, the shell was modeled by wrapping the Au core with a shell layer of the same shape. The dielectric functions of the metals were obtained by fitting the data of Olmon et al. (Au),⁶³ Yang et al. (Ag),⁶⁴ and Rakić et al. (Pd, Pt).⁶⁵ To calculate the effective dielectric function of the composite shell consisting of Pd with varying volume fractions and the dielectric shell, we used Bruggeman’s effective-medium theory for spherical inclusions⁶⁶

1

where ϵ_m, ϵ_d, and ϵ_e are the dielectric functions of the shell metal (Pd), the dielectric environment (silica-solvent), and the composite system, respectively. p is the volume fraction of the Pd in the composite shell. d is the dimensionality of the system and is equal to 3. Once the effective dielectric function of the medium was calculated by solving eq 2, it was inserted into FDTD software. In the FDTD calculations, we assumed a porosity of 63% (f) for the mesoporous layer of silica⁶⁷ to which we assigned a refractive index of 1.45 (n_SiO2) and assumed that the pores were filled with a solvent (3:1 ethanol/water) having a refractive index of 1.34 and used a volume-weighted average of the pores and silica

2

The obtained effective index of refraction is 1.38, which we assumed to be valid for all wavelengths.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c06321.

• Figures on template removal, metal overgrowth, FDTD calculations, and SERS measurements; and tables summarizing the synthesis details (PDF)

Author Present Address

^§ School of Electronics and Information Engineering, Hangzhou Dianzi University, Hangzhou 310018, China.

Author Contributions

^∥ JvdH and TSD contributed equally to this work. AvB initiated the project. JvdH and LO were supervised by PdJ and AvB. TSD and WA were supervised by AvB. JvdH, TSD, and LO synthesized the particles. WA performed the FDTD calculations. JvdH preformed the HAADF-STEM EDX measurements and SERS measurements. JvdH wrote the manuscript. All authors analysed and discussed the results.

The authors declare no competing financial interest.