Identifying the predictors of Covid-19 infection outcomes and development of prediction models

Abstract

Background

The infection of Corona Virus Disease (Covid-19) is challenging health problems worldwide. COVID-19 pandemic is spreading all over the world with the number of infected cases increased to 54.4 million with 1.32 million deaths. Different types of statistical models have been developed to predict viral infection and multiple studies have compared the performance of these predictive models, but results were not consistent. This study aimed to develop and provide easy to use model to predict the Covid-19 infection severity in the patients and to help understanding the patient’s condition.

Methods

This study analyzed simulated data obtained from the large database for 340 patients with an active Covid-19 infection. The study identified predictors of Covid-19 outcomes that may be measured in two different ways: the total T-cell levels in the blood with T-cell subsets and number of cells in the blood infected with virus. All measures are relatively unobtrusive as they only require a blood sample, however there is a significant laboratory cost implications for measuring the number of cells infected with virus. This study used methodological approach using two different methods showing how multiple regression and logistic regression can be used in the context of Covid-19 longitudinal data to develop the prediction models.

Results

This study has identified the predictors of Covid-19 infection outcomes and developed prediction models. In the regression model of Total_T Cell, the predictors BMI, comorbidity and Total_Tcell were all associated with increased levels of infection severity (p < 0.001). For BMI, the mean % of unhealthy cells increased by 0.42 (95% CI 0.24 to 0.60) and comorbidity predictor has on average 8.3% more unhealthy liver cells than without comorbidity (95% CI — 2.9%–1.29%). The results of multivariate logistic regression model predicting the Covid-19 Infection severity were promising. The significant predictors were observed such as Age (OR 0.95, p = 0.02, 95% CI: 0.91–0.99), Helper T_cells (OR O.93, p = 0.03, 95% CI: 0.87–0.99), Basic_Tcell (OR 1.11, p = 0.001, 95% CI: 1.06–1.71) and Comorbidity (OR 0.41, p = 0.05, 95% CI: 0.16–1.07).

Conclusions

In this study recommendation has been provided to clinical researchers on the best way to use the various Covid-19 infections measures along with identifying other possible predictors of Covid-19 infection. It is imperative to monitor closely the T-cell subsets using prediction models that might provide valuable information about the patient’s condition during the treatment process.

Introduction

The coronavirus disease (COVID-19) was first reported in Wuhan, China, in December 2019 [1]. Later on, it was declared a “public health emergency of international concern” in January 2020, by the World Health Organization. It was reported in June 2020 that the virus was spread all over the world covering 213 countries and territories with almost 7 million cases of COVID-19, with over 400,000 deaths [2]. The latest statistics of Covid-19 infections reported in November 2020 are 54.4 million infected cases in the world with 1.32 million deaths [3].

There was an immediate concern to identify the factors associated with adverse outcomes for people with COVID-19. The two main factors or predictors were considered that may contribute to the severity of this infection such as age and comorbidities (diabetes and cardiovascular disease). The survey of literature revealed that older age is the most consistent risk factor for severity of COVID-19 infection [4,5]. We found in literature some evidence to suggest that comorbidities might be an important predictors associated with increased Covid-19 severity and mortality [5,6].

McKeigue et al. [7] have reported that the most common comorbidities in the UK population were cardiac disease, diabetes, chronic pulmonary disease. It has been difficult to quantify the risk associated with comorbidities due to lack of comparisons with a specified population [5,8].

Two recent studies in the UK have included population comparators and have reported associations of hospitalization with COVID-19 or death from COVID-19 with comorbidities including diabetes, and heart disease [9,10]. However, the impact of comorbidities on Covid-19 patients is not clearly illustrated and reported, therefore more studies are required to be conducted to find out the evidence of strong correlation between comorbidity and COVID-19 infection [7]. In addition, these studies should also explore the association between cardiovascular and kidney diseases and the severity of the infection with COVID-19 in patients suffering with these diseases [11].

The association between obesity and mortality has been explored in this current study by investigating the association of body mass index with the outcome variable (Covid-19Inf) and the results are in agreement with the UK-based study [12].

The body mass index as a predictor contributed to the model significantly (p = 0.03). However, we did not carry out the regression analysis based on BMI classification in this study. It has been reported by Ortiz et al. [13] that BMI 25 kg/m² was associated with progression of fibrosis. In addition, obesity was associated with a poor response to combination therapy and increased fibrosis [14].

In the process of predictive model development, multiple items might be of prognostic value. These multiple items are mostly correlated, therefore, the predictive model should take this dependency into account. For example, if clinicians are capable of predicting those patients who are at high risk of disease progression, then expensive and time consuming therapies may be directed to the patients requiring urgent treatment [15]. Therefore, these risk predictive models will be useful to provide clinicians vital information to guide them to perform clinical monitoring of the patients [16].

The aim of this study is to identify the predictors of Covid-19 virus infection and to develop prediction models by evaluating the various predictive modelling approach. In this study, the associations between the predictors and outcome variable were modelled and causality was not implied.

The predictors such as T-Cells, Subset of T-cells, Infected cells are viral-related as well as patient-related and have been evaluated to predict the outcome of the model that is predicting the Covid-19 infection in patients.

Therefore, various models which have been developed in this study are based on these predictors. Among these, we found that T_ Cell is the most important predictor to predict Covid-19 infection severity in patients [17]. These Covid-19 prediction models were refined so that these can be used by clinicians to predict the T_cells in patients and use that valuable information to perform clinical monitoring and timely treatment to these patients.

Methods

Data source

The simulated data for 340 patients with an active Covid-19 infections was obtained from the large data base of Wuhan Pulmonary Hospital, China [17] and the data obtained represent closely the original database. Out of this data set, there were 310 patients who were discharged after the recovery from Covid-19 episode and 30 patients died of the infection. Using simulation to create data that serves as a foundation for research of diagnostic tools for regression analysis is a powerful tool [18]. The “simstudy" package was used to generate the simulated data for modelling purposes. The means and covariances were calculated within the data set and samples data were obtained from the multiple normal distribution from those means and covariances. Also, any categorical variable such as comorbidity (diabetes) in the dataset was declared as ordered factors [18]. Therefore, the simulated data have maintained the same, variable names, level names (for ordered factors), pattern of missing data and frequency counts for each observed category for ordered factors.

Statistical analysis

The statistical analysis was performed using STATA 15 software (StataCorp. 2015. Stata Statistical Software: Release 15. College Station, TX: StataCorp LP). A p-value < 0.05 was considered as criterion of statistical significance. In order to assess the demographic characteristics and clinical measurements between Covid-19 positive cases, a Student t-test was performed and multiple and logistic regression models were developed and used to evaluate the predictors and their association with Covid-19 infections. Quantitative univariate analysis was carried out and identified any obvious issues with the dataset.

Logistic regression model was used to assess the association between Total T-cells, Infected cells and the subset of T-cells predictors. Also performed likelihood ratio test to assess the statistical significance of adding these predictors in the model. The Hosmer & Lemeshow test was used to evaluate how the model fits the data.

Ethics approval

The study does not require any ethical approval as the simulated data was used in this study from a large database which was already approved by the Ethics committee of Wuhan Pulmonary Hospital (WPE 2020–8), China [17].

Results

Descriptive statistics for predictors and outcome variables in the data set of 340 patients is shown in Table 1 . The dependent or outcome variable (Covid19Cells) had an average percentage of unhealthy liver cell estimated from the biopsy was 47.49% with the standard deviation of 12.60 with minimum and maximum values of 19.28%–78.7%.

Table 1.

Descriptive statistics of predictors and outcome variables (n = 340).

Variables	Observation	Mean	SD	Min	Max
Age (in years)	340	59.32	13.79	21	86
<60 years	155	46.82	8.85	21	59
≥60 years	185	69.79	6.55	60	86
Comorbidity Patients	140
Non-comorbidity	200	0.41	0.49	0	1
Body mass index [kg/m2]	340	27.72	5.80	17.07	45.15
Alcohol consumption	340	7.11	5.52	0	33
Covid19Cells (outcome)	340	47.49	12.60	19.28	78.7
Basic_TCell	340	64.42	13.39	3.23	88.95
Helper_TCell	340	37.95	11.16	1.86	70.04
Supp_T cell	340	24.93	9.04	1.46	57.44
Total_T cell	340	2024.20	397.21	533	3142
Infect_Cell	340	101	18.86	35	162

Note: n = number of patients; SD = standard deviation; the outcome variable “Covid19Cells” levels.

given in %. Comorbidity is a binary variable (0 = absent; 1 = present).

From Table 1, it can be seen that the average alcohol consumption per week is highly variable with a mean of around 7 standard drinks and minimum of 0 and maximum of 33. Ages ranged from 21 to 86 years.

The results from the Basic_Tcell (baseline T-cells) show that the average level of Covid-19 specific T-cells in the blood is 64.42; whereas the minimum value is 3.23 and maximum value is 88.95. In addition, the data set contains only 140 patients with comorbidity and remaining 200 patients are without comorbidity.

The univariate regression analysis of each predictor in data set of 340 patients was carried out to see their association with the outcome variable (Covid19Cells) and we have found that all the predictors were associated with the Covid19Cells variable (p < 0.01).

Multivariable regression models

The multiple linear regression equation used for regression modelling is expressed as:

$$Y_i={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2\mathrm{..........}+{\beta }_n{x}_n+{\epsilon }_i$$ (1)

where, i = 1, 2, ……., n and Yi is the observed value of the random variable and x₁, ….., x_n are the various predictors. β₀ is an intercept and β₁ is a slope of the regression line and ${\epsilon }_i$ is a random error. All assumptions of linear regression models such as normality of residuals, linearity and homoscedasticity have been addressed and satisfied in the analysis.

We developed two multivariable regression models called Total_Tcell and Infect_Cells. These models were fitted with only Total_Tcell or Infect_Cells in the model, the other covariates remained the same in the modelling phase. From a clinical point of view, we have decided not to consider Infect_Cells model and preferred Total_Tcell model as there is a significant cost implications associated with measuring the number of infected cells.

The Total_T-cell model is appropriate as this model is capable of capturing the information on Covid-19 infection severity, it is a simple model with less variables and all contribute significantly (p < 0.001) towards the overall model’s performance. Most importantly, the model is cost effective and easy to use to predict the Covid-19 infections among the patients.

In the final Total_T Cell Model, the predictors BMI, Alcohol, comorbidity and Total_Tcell were all associated with increased levels of unhealthy cells (p < 0.001). After adjusting for other factors, for every 1 kg/m² increase in BMI, the mean % of UnHlthCells is expected to increase by 0.42 (95% CI 0.24–0.60). Those with Comorbidity have on average 8.3% more unhealthy liver cells than those without Comorbidity (95% CI — 2.9%–1.29%). For every 10 copies per ml increase in Total-Tcells levels in the blood, the percentage of unhealthy liver cells is expected to increase by 0.07% (95% CI 0.05% to 0.09%).

Tcell model for Covid-19 infected patients

Liu et al. [17] observed in their study that T cells were correlated with the viral infection. The authors mentioned that as the baseline T_cells tests were conducted at the time of the patient’s admission in the hospital, there was some evidence of T_cells decreasing in the sample of blood of 340 patients. The patient’s condition further improved with the increase in T_cells levels and deteriorated with the decline in T_cells [17].

We considered T-cell application to Covid-19 infection with only a few strong predictors in the model. Logistic regression was used to assess whether there was an association between the predictors and the outcome variable in the data set of 340 patients infected with Covid-19. The data set of 340 patients with infection consists of 310 patients who were discharged after the recovery from Covid-19 episode and 30 patients in this data set died of Covid-19 infection.

The multiple logistic regression model used in this study is represented as follows:

$$log\left(\pi /\left(1-\pi \right)\right)=\text{α}+{\beta }_1{x}_1+{\beta }_2{x}_2\mathrm{........}+{\beta }_k{x}_k$$ (2)

Where

• •π = probability of infection = response
• •β₁ = log risk of infection without exposure
• •X = exposure level as a numerical variable (x_1,……..,x_k, are different predictors)
• •β₂ = change in log risk for each unit increase in exposure level
• •α = The intercept alpha, is the log (probability of infection)
• •Log is a link function

The logistic regression models included binary and predictors and the models were fitted with all predictors as independent variables. In order to dichotomise the outcome variable, a cutoff value was selected for this variable to convert the outcome variable to a binary variable to be used in logistic regression analysis. The cutoff probability value, say C was selected as a minimum value to distinguish high risk from low risk patients. If Prob < C, the patient is low risk and if Prob ≥ C, the patient is at high risk. Therefore, all patients with this cutoff score C were classified as potential candidates for high or low risk. The probability for high risk and low risk patients were calculated: Prob (high risk) │Covid-19) = sensitivity; Prob (high risk) │no Covid-19) = 1-specificity.

We fitted a logistic regression model to assess the association between age and Covid-19 infection in this sample of 340 patients and found strong evidence of an association between age and Covid-19 infected patients (p < 0.001). For every 1-year increase in age, the odds of Covid-19 infection increase by 9.3% (odds ratio 0.93, 95% confidence interval 0.9–0.96, p < 0.001).

The other logistic regression models were developed based on all the individual predictors with the outcome variable “Covid-19Inf.” The adjusted odds ratios, log likelihood, p-values and confidence intervals for all predictors from the logistic regression model are shown in Table 2 .

Table 2.

Logistic regression models parameters of individual predictors vs outcome.

Predictors	Odds ratios	95% CI	Log likelihood	p-Values
Age (years)	0.93	0.89–0.96	−91.21	<0.001
Alcohol	0.87	0.82−0.92	−90.02	<0.001
BMI (kg/m2)	1.09	1.01–1.18	−98.61	0.026
Comorbidity	0.22	0.09−0.52	−94.48	<0.001
Basic_Tcell	1.07	1.04−1.10	−88.40	<0.001
Helper_Tcell	1.04	1.00–1.07	−99.14	0.031
Supp_Tcell	1.17	1.10–1.24	−84.26	<0.001
Total_Tcell	1.00	0.99–1.00	−99.65	0.050

The Table 2 shows that individually all predictors are associated with the outcome variable (Covid-19 infection) and contribute to the model (p < 0.001, for most of the predictors). The other predictors such as BMI with p = 0.026 and Helper_Tcell with p = 0.031 are also statistically significant and provide evidence of association with Covid-19 infection (outcome variable).

Multivariable logistic regression model 1

The logistic regression models included binary and predictors and the models were fitted with all predictors as independent variables. In order to dichotomise outcome variable, a cutoff value was selected for this variable to convert the outcome variable to a binary variable to be used in logistic regression analysis.

For the likelihood function of logistic regression, the probability function for the binomial distribution was selected and represented as follows:

$$\begin{array}{cc}\hfill p\left(y\right)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill y\hfill \end{array}\right){\pi }^y{\left(1-\pi \right)}^{n-y},\hfill & \hfill y=0,1,2,\dots ,n,\hfill \end{array}$$ (3)

and the binomial log likelihood function is given by:

$$L\left(\pi \right)=\log \left[{\pi }^y{\left(1-\pi \right)}^{n-y}\right]=y\log \left(\pi \right)+\left(n-y\right)\log \left(1-\pi \right)$$ (4)

Logistic regression was used to assess whether there was an association between the predictors and the outcome variable in this data set of 340 patients infected with Covid-19. The estimated coefficients, odds ratios and confidence intervals were interpreted for all the predictors.

The multivariable logistic regression analysis was performed using generalized liner modelling method to develop model using predictors such as Age, Comorbidity (underlying disease status), the baseline T_cell, Helper_Tcell and Total_Tcell to predict the patient outcome (Covid-19Inf).

The significant predictors were observed such as Age (OR 0.95, p = 0.02, 95% CI: 0.91–0.99), Helper T_cells (OR O.93, p = 0.03, 95% CI: 0.87–0.99), Basic_Tcell (OR 1.11, p = 0.001, 95% CI: 1.06–1.71) and Comorbidity (OR 0.41, p = 0.05, 95% CI: 0.16–1.07). However, Total T_cells (p = 0.148) was not significant predictors in the multivariable logistic regression model.

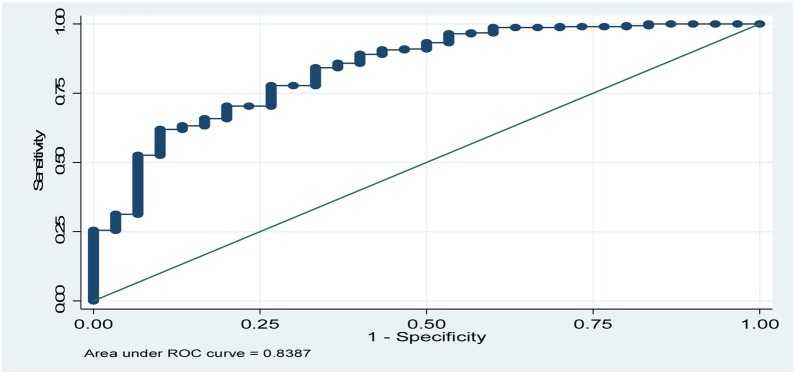
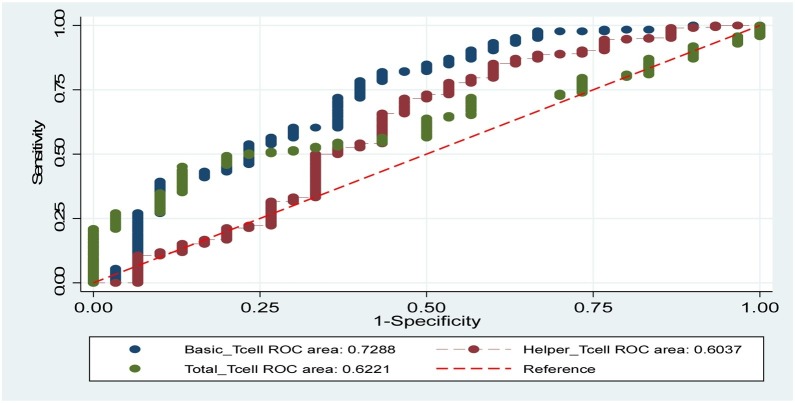
The Receiver Operating Curve (ROC) of the logistic regression model was constructed to evaluate the predictions of COVID-19 virus severity. ROC showed that the area under the curve equal to 0.84 (Fig. 1 ), indicating the good predictive power of the logistic model [19]. Fig. 2 shows the areas under ROC curves for other predictors. The ROC curves for other two models were constructed and the area under the curve was 0.80 for Model 2, and for Model 3 the area under the curve was 0.77.

Fig. 1.

ROC curves showing the area under the curve for Model 1 (0.84).

Fig. 2.

ROC curves showing the areas under the curves for other predictors (Basic_Tcell = 0.72; Helpe_Tcell = 0.60; Total_Tcell = 0.62).

It was also important to assess how this multivariable logistic regression model fits the data of 340 covid-19 infected patients. For this purpose, Hosmer-Lemeshow test with 10 groups was carried out. The results of Hosmer-Lemeshow test indicated a good fit of the data (X² = 7.47, df = 8, p = 0.49).

We have considered another two cases to develop multivariable logistic regression models called “Model 2” and “Model 3” for these cases. For “Model 2”, we have included all the predictors related to Total_Tcell and its subsets and for “Model 3”, we considered the two most important predictors “Age” and “Comorbidity” which are significantly associated with the Covid-19 infected patients. The outcome variables used in these cases were “Discharge” (patients recovered from Covid-19 infection) and “Death” (patient died in the hospital).

The Table 3 provides a comparison between the deviance, Pearson X², AIC, BIC and R² for all three models: Model 1 (Age, Comorbidity, T_cell, Helper_Tcell, Total_Tcell); Model 2 (Total_Tcell and all its subsets) and Model 3 (Age and Comorbidity).

Table 3.

Multivariable logistic regression statistics for Covid-19 infection models.

Logistic models	AIC	BIC	X2	Deviance	R2
Model 1	0.48	−1797.00	53.09	149.85	0.26
Model 2	0.51	−1790.78	41.02	161.91	0.20
Model 3	0.54	−1786	24.60	178.34	0.12

The quality of the three models was compared by using the comparison criteria of AIC and BIC. The best model is the one which has the lowest values of AIC and BIC. Therefore, model 1 is preferred over model 2 and Model 3 based on the selection criteria. The other selection criteria is based on the goodness of fit measures such as X² and Deviance (lower the statistics, the more preferred is the model). In this case, model 1 is preferred as Pseudo R² values of model 1 (R² = 0.26) explains slightly better variability of the data as compared to other two models.

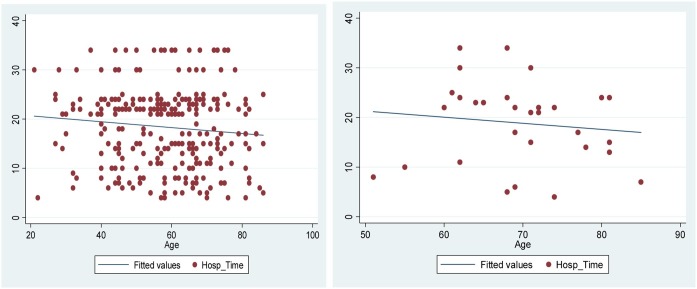
We have also examined the scatter plots between Hosp_Time (Duration of stay in hospital) and Age for the outcome variables “Discharge’ and Death” (Covid-19Inf) in Fig. 3 . It may be observed from these plots that older patients have more comorbidities problem as compared to younger patients. Also, the Hospital Time is longer among the older infected patients. The straight lines passing through the data points in the plots show the regression line. In “Death” group, older patients died more quickly than the younger ones.

Fig. 3.

Scatter plots between Hosp_Time and Age for “Discharge’ and Death” variables.

Prediction capability (Logistic regression model)

The prediction capability is based on the multivariable logistic regression Model 1 (Age, Comorbidity, T_cell, Helper_Tcell, Total_Tcell). The model equation can be used to predict the probability of Covid-19 infection for a patient of any age group. For a logistic regression model, the predicted probability can be calculated using the formula:

$${\pi }_i=\frac{\text{exp}\left({\beta }_1+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3}+\dots \right)}{1+\text{exp}\left({\beta }_1+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3}+\dots \right)}$$ (5)

by using the coefficients from the model and inserting in the formula.

$$constant={\beta }_1=0.979,coefficientforAge{\beta }_2=-0.053$$

$$coefficientforComorbidity{\beta }_3=-0.893,coefficientforBasic\_Tcell{\beta }_4=0.107$$

$$coefficientforHelper\_Tcell{\beta }_5=-0.071,coefficientforTotal\_Tcell{\beta }_6=0.001$$

Discussions

In this study we have used methodological approach by using two different modelling approach to develop the prediction models such as multivariable regression and logistic regression models.

The predictive models used frequently are the logistic regression models when the outcome is a binary variable [20]. These models predict the infected patient’s health condition based on the level of Tcells in the blood. However, there are many other modelling approach in literature such as classification and regression trees (CART) and the Spiegel halter-Knill-Jones (SKJ) approach [21,22]. There are many other studies which have compared the performance of different predictive models, but results were not consistent [23,24].

In this study, a wide range of predictors have been discussed that are used to develop the prediction models. Of particular mention are the predictors such as Age, Gender, BMI (Body Mass Index), Alcohol, Comorbidity (diabetes, CVD), Infected cells (number of infected cells), T-cell (level of specific T-Cells), and the subsets of T-cells. Initial descriptive and regression analysis were carried out on the most important predictors “Age” and “Comorbidity”.

We have found a very strong evidence of an association between age and Covid-19 infected patients (p < 0.001). Liu et al. [17] also reported that the duration of hospitalization was increased with elderly patients infected with Covid-19. The older patients had a higher probability to have comorbidities (underlying diseases) and the death event occurred more quickly among elderly patients [17]. Co-morbidities such as cardiovascular disease, diabetes and obesity are some of the most common underlying conditions associated with worse clinical outcome for severe infection of COVID-19 [25,26].

Moreover, older patients experience greater clinical severity of COVID-19 [17], males may experience more severe disease than females and genetic variations have been reported to affect the clinical outcomes for patients with COVID-19 [27]. However, how these co-morbidities are associated with T-cell responses during COVID-19 remains largely unknown.

We have performed multivariable logistic regression analysis to develop various models using predictors in different combinations and found the best logistic regression model using different comparison criteria. The best model was based on the predictors such as Age, Comorbidity (underlying disease status), the baseline T_cell, Helper_Tcell and Total_Tcell to predict the patient outcome (Covid-19Inf). The significant predictors were observed such as Age (OR 0.95, p = 0.02, 95% CI: 0.91–0.99), Helper T_cells (OR O.93, p = 0.03, 95% CI: 0.87–0.99), Basic_Tcell (OR 1.11, p = 0.001, 95% CI: 1.06–1.71) and Comorbidity (OR 0.41, p = 0.05, 95% CI: 0.16–1.07)

Study limitation

The main limitation of our study is the small sample size (n = 340) with only one clinical site of data collection, used to carry out the analysis of Covid-19 infected patients. The results of this study are applicable to specific group of 340 patients from a Wuhan Pulmonary Hospital. While these results may not be widely generalizable, we would expect these results to apply to patients with similar characteristics to those described here. In its present form, the predictive models developed may be used successfully as clinical decision tool for certain population and its application should be considered with a limited scope.

However, developing these models as universally accessible web-based tool would further increase their accessibility and usefulness in clinical practice. The other limitation, as an epidemiological study is the lack of specifying the entry criteria of the study population and the need to provide causal relationship analysis.

Recommendations

It is recommended for future research to use longitudinal data for the development of prediction model as these models are more practical in clinical settings as they can incorporate nonlinear disease progression in Covid-19 infection and therefore outperform basic prediction models. In addition, artificial intelligence approach for developing the models is very useful as it captures complex relationships between predictors and outcomes, yielding more accurate predictions as the models can help to guide the intensity of clinical monitoring required, and provide prognostic information to patients.

Conclusions

The study has identified the predictors of Covid-19 virus infection outcomes and developed logistic regression models which can be used by clinicians to predict T_cells in patients infected with Covid-19 and use that valuable information to perform clinical monitoring and timely treatment to these patients. The study has demonstrated that the predictors age and comorbidity played an important and significant role in Covid-19 infected patients. The older patients had more comorbidities problem as compared to younger patients and therefore, spent more time in the hospital to recover than the younger patients. In addition, the death rates of older patients with Covid-19 infection was higher than the younger patients.

Funding

No funding sources.

Competing interests

None declared.

Ethical approval

Not required.

Authors' contributions

RM used the simulated data and analyzed and interpreted the patient’s data related to Hepatitis C and Covid-19 infections and performed all the statistical analysis. PB reviewed the manuscript and provided written comments to enhance the overall presentation of the results, read and approved the final manuscript.