Abstract
Contrast enhanced cardiac computed tomography angiography (CTA) is a prominent imaging modality for diagnosing cardiovascular diseases non-invasively. It assists the evaluation of the coronary artery patency and provides a comprehensive assessment of structural features of the heart and great vessels. However, physicians are often required to evaluate different cardiac structures and measure their size manually. Such task is very time-consuming and tedious due to the large number of image slices in 3D data. We present a fully automatic method based on a combined multi-atlas and corrective segmentation approach to label the heart and its associated cardiovascular structures. This method also automatically separates other surrounding intrathoracic structures from CTA images. Quantitative assessment of the proposed method is performed on 36 studies with a reference standard obtained from expert manual segmentation of various cardiac structures. Qualitative evaluation is also performed by expert readers to score 120 studies of the automatic segmentation. The quantitative results showed an overall Dice of 0.93, Hausdorff distance of 7.94 mm, and mean surface distance of 1.03 mm between automatically and manually segmented cardiac structures. The visual assessment also attained an excellent score for the automatic segmentation. The average processing time was 2.79 minutes. Our results indicate the proposed automatic framework significantly improves accuracy and computational speed in conventional multi-atlas based approach, and it provides comprehensive and reliable multi-structural segmentation of CTA images that is valuable for clinical application.
Keywords: Computed tomography, heart segmentation, multi-atlas segmentation, random walk
I. INTRODUCTION
Contrast enhanced cardiac computed tomography angiography (CTA) is an advanced imaging modality for evaluating the coronary arteries and the morphology of the heart non-invasively. It allows the physician to examine the patency of the coronary arteries for atherosclerotic disease. It also provides a comprehensive evaluation of the anatomical features of the heart and its surrounding vessels for structural heart diseases. Quantitative assessment of various anatomical structures of the heart such as its four chambers, myocardium, and great vessels on the CTA images can help to detect potential cardiac anomalies or to evaluate disease progression and treatment effects. However, this process can be laborious, time-consuming, and may be prone to user variations since measurements of these cardiac structures is often performed manually.
Computer-based automatic segmentation is desirable but can be challenging due to anatomical variations of the heart among different individuals, indistinct boundaries between substructures of the heart (e.g. right ventricle and right atrium), or between the heart and surrounding tissues (e.g. liver, ribs, sternum). Moreover, technical complexities such as the differences in field-of-view reconstruction, scanning parameters, imaging protocols, and the presence of imaging or motion artifacts, suboptimal contrast-to-noise ratio or signal-to-noise ratio can all affect the image quality and result in imperfect image segmentation. Thus, it is essential to develop automatic and reliable computerized methods that can accurately segment the heart and its anatomical structures and evaluate the methods on a large dataset.
In this paper, we present a fully automatic pipeline for comprehensive multi-structure CTA image segmentation that can achieve high accuracy with efficient processing time for practical clinical applications. The proposed method extends our previous work [1] by incorporating an improved combined multi-atlas approach with corrective segmentation to label the whole heart (WH), left ventricular cavity (LV), left atrial cavity (LA), left ventricular myocardium (LVM), left atrial appendage (LAA), right ventricular cavity (RV), right atrial cavity (RA), ascending aorta (AA), superior vena cava (SVC), inferior vena cava (IVC), pulmonary artery (PA), and pulmonary vein (PV) in the CTA images. The method also separates other intrathoracic non-cardiac structures such as lung, chest wall (CW), spine, descending aorta (DA), and liver from the CTA images.
Our framework is aimed at addressing the high computational cost in the multi-atlas based approach while improving its robustness and accuracy for large scale contrast enhanced cardiac CTA imaging applications. The main contributions of this work are as follows:
We present a comprehensive strategy to simultaneously segment 17 independent cardiovascular and intrathoracic structures at once.
We propose a robust and rapid atlas selection scheme and an enhanced label fusion scheme to improve the speed and accuracy of multi-atlas registration.
We incorporate a corrective segmentation process to further increase the final segmentation accuracy.
Our methods are implemented in a multi-threading architecture to increase computational efficiency. We evaluate the proposed method on a large clinical dataset and compare the results with a manual reference standard as well as conventional multi-atlas segmentation.
II. PREVIOUS WORK
Several papers have summarized various automatic 3D cardiac segmentation methods across multimodality medical imaging. Kang et al. [2] and Zhuang [3] reviewed some early works on the whole heart segmentation. A recent comparison of 10 methods participated in MICCAI-STACOM challenge 2017 was summarized by Zhuang et al.[4]. Among these techniques, atlas-based approaches have been widely used to segment numerous cardiac structures [5]–[19]. More recent works also incorporate deep learning-based approaches for automatic cardiac segmentation [20]–[24].
In a literature survey, most of the previous works only segmented a limited number of cardiac structures. Table I summaries various cardiovascular and intrathoracic structures explored by these prior developments. For the WH segmentation, Funka-Lea et al. [25] proposed a graph-cuts method, Zheng et al. [26] presented a marginal space learning method, and van Rikxoort et al. [5] proposed a multi-atlas based segmentation technique. Likewise, Jolly [27] proposed a graph-cuts and EM-based method to segment the LV, Karim et al. [17] segmented the LA, Yang et al. [8] segmented the LV and LVM, and Tobon et al. [9] segmented the LA and PA only.
TABLE I.
Summary of automatic cardiac CTA image segmentation of various structures from previously published literatures.
| LV | LA | LVM | LAA | RV | RA | AA | WH | SVC | IVC | PA | PV | DA | Spine | Liver | CW | Lung | N | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Proposed method | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • | • | 36 (120*) |
| Baskaran 2019 [24] | • | • | • | • | • | 17 | ||||||||||||
| Liu 2019 [23] | • | • | • | • | • | • | • | 4 | ||||||||||
| Ye 2019 [22] | • | • | • | • | • | • | • | 10 | ||||||||||
| Wang 2018 [18] | • | • | • | • | • | • | • | • | • | • | • | 48 | ||||||
| Karim 2018 [17] | • | 20 | ||||||||||||||||
| Katouzian 2018 [16] | • | • | • | • | • | • | • | • | • | • | • | 43 | ||||||
| Payer 2017 [21] | • | • | • | • | • | • | • | 40 | ||||||||||
| Yang 2017 [20] | • | • | • | • | • | • | • | 40 | ||||||||||
| Yang 2017 [15] | • | • | • | • | • | • | • | 20 | ||||||||||
| Lu 2017 [14] | • | • | • | • | • | • | 15 | |||||||||||
| Zhou 2017 [12] | • | • | • | • | • | • | • | • | • | • | • | • | 19 | |||||
| Cai 2017 [29] | • | • | • | • | • | • | 14 | |||||||||||
| Zhuang 2016 [11] | • | • | • | • | • | • | • | • | 30 | |||||||||
| Tobon 2015 [9] | • | • | • | 30 | ||||||||||||||
| Yang 2014 [8] | • | • | • | 8 | ||||||||||||||
| Zuluaga 2013 [7] | • | • | • | • | • | • | 8 | |||||||||||
| Kirişli 2010 [6] | • | • | • | • | • | • | • | 8 (1300*) | ||||||||||
| van Rikxoort 2010 [5] | • | 29 | ||||||||||||||||
| Zheng 2010 [26] | • | 589 | ||||||||||||||||
| Zheng 2008 [28] | • | • | • | • | • | 323 | ||||||||||||
| Ecabert 2008 [30] | • | • | • | • | • | • | • | 28 | ||||||||||
| Jolly 2006 [27] | • | 18 | ||||||||||||||||
| Funka-Lea 2006 [25] | • | 70 |
LV: left ventricular cavity, LA: left atrial cavity, LVM: left ventricular myocardium, LAA; left atrial appendage, RV: right ventricular cavity, RA: right atrial cavity, AA: ascending aorta: WH: whole heart, SVC: superior vena cava, IVC: inferior vena cava, PA: pulmonary artery, PV: pulmonary vein, DA: descending aorta, CW: chest wall. N: the number of studies included for quantitative (and qualitative*) evaluations.
Several other works have attempted to segment more cardiovascular structures. Zheng et al. [28] and Baskaran et al. [24] segmented the four chambers and the LVM. In Zuluaga et al. [7] and Lu et al.’s [14] works, the four chambers, LVM, and AA were segmented. Cai et al. [29] also segmented above six cardiac structures using a Gaussian filter-based method. Kirişli et al. [6] segmented those six cardiac structures plus the WH region. In the works by Yang et al.[15], Yang et al.[20], and Payer et al.[21], the four chambers, LVM, AA and PA were segmented. Ecabert et al. [30] presented an active shape model to extract above seven cardiac structures. Zhuang et al. [10] segmented those seven cardiac structures plus the DA. A more comprehensive coverage was shown in Zhou et al.’s [12] work for segmenting 15 structures, and in Katouzian et al. [16] and Wang et al. [18] for 16 structures. However, these works split the PA into left and right trunks, and the AA into aortic arch and root as separate structures.
Some works have focused on segmenting different cardiac structures from non-contrast enhanced CT images. They aimed to assist thoracic radiation treatment planning [12], [19] and coronary calcium scoring [13]. As cardiac structures are not clearly distinguishable in these non-contrast CT applications, Zhou et al. [12] and Shahzad et al. [13] used the atlas based approach by registering the non-contrast enhanced CT with contrast enhanced CT images of the same patients, and then transformed the cardiac structure labels from the contrast enhanced images to the non-contrast enhanced dataset for cardiac segmentation. Morris et al.’s [19] work was also based on the multi-atlas approach, but it registered non-contrast enhanced CT and magnetic resonance (MR) images of the same patient, with various cardiac structures manually labelled on the MR dataset. Heinrich et al. [31] applied a random walk algorithm to the results produced by the multi-atlas segmentation. However, their work was applied to cardiac MR images to segment seven cardiac structures.
III. METHODOLOGY
Multi-atlas segmentation is one of the most widely used image segmentation techniques in biomedical imaging applications [32]. It is an extension of the atlas-based segmentation approach that leverages the spatial information between a given target image and an atlas image via a deformable registration strategy. An atlas consists of a pair of data, an image and an associated label, in which the label contains pre-delineated regions of interest of the image which can be propagated to the target image space through a nonlinear transformation as obtained from a pairwise non-rigid registration of the target and atlas images. Compared to a single-atlas segmentation, multi-atlas segmentation maintains a higher flexibility by retaining anatomical variations among a library of atlas datasets to improve the segmentation quality.
Our automatic CTA image segmentation method is based on the multi-atlas approach and aimed to improve such method. Fig. 1 shows the flow diagram of our fully automatic processing pipeline: a combined multi-atlas and corrective segmentation (CMACS) framework. There are two core blocks in the processing framework (1) multi-atlas segmentation and (2) corrective segmentation, that will be described in the following sections.
Fig. 1.
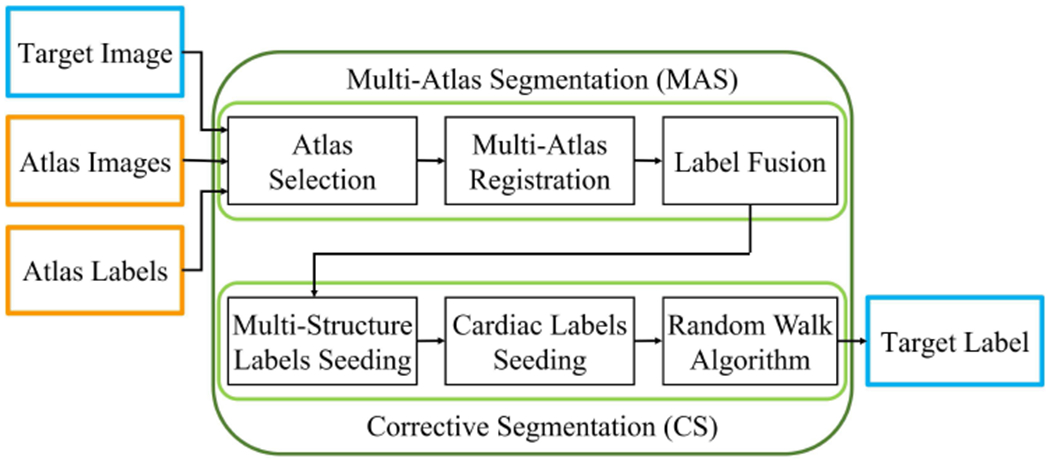
Flow diagram of the proposed combined multi-atlas and corrective segmentation (CMACS) framework for fully automatic multi-structure cardiac CTA image segmentation.
A. MULTI-ATLAS SEGMENTATION
The multi-atlas segmentation (MAS) block includes a sequence of steps to improve the common multi-atlas based methods. First, we establish an atlas library consisting of a collection of pre-labeled CTA dataset that covers a wide range of heart sizes. Each atlas contains 12 annotated labels representing different cardiovascular structures of interest that are to be transformed to the target image space after the image registration. These labels include seven cardiac structures: LV, LA, RV, RA, LVM, LAA, AA; as well as four associated vascular structures including SVC, IVC, PA, and PV all of which carry blood to or from the heart. Additionally, a WH label is delineated to encompass the entire heart volume including the four chambers, LVM, LAA, AA, and the surrounding pericardium.
Next, we propose a strategy to rapidly select an optimal set of atlases from the library by matching structural similarities between the target and each atlas images. This step effectively reduces the overall computational time by registering only the selected atlases instead of the entire atlas dataset with the target image. To further improve the computational speed, the image registration was implemented in a multi-threading scheme to register all selected atlases simultaneously. After the multi-atlas registration, an enhanced label fusion scheme is proposed to merge these transformed atlas labels into a target label. The following subsections will describe each step in more details.
1). ATLAS SELECTION:
The first step in the MAS block is to find a subset of atlas images that are best matched in anatomical or structural similarity with the target image. This step is aimed to 1) reduce the computational time and 2) improve registration performance by registering only those best matching atlas images to the target image.
We use a structural similarity index (SSI) calculated between each atlas and the target images to find the best matched atlases. This index was originally proposed to evaluate the perceptual quality of image compression schemes with an application to natural images [33]. It is highly indicative for summarizing the conformity between a target image and a reference image by taking luminance, contrast, and structure similarity into account. We use a cubical patch size of 7 × 7 × 7 voxels to compute the SSI for each voxel between the target image X and the atlas image Y to generate an SSI map. Each pair of the target and atlas images are aligned to their volume center before computing the SSI map.
Equation (1) shows the function of SSI computed in each patch. Here μx, μy, σx, σy, σxy are the local mean, variance, and covariance within the local 3D patch x of image X and y of image Y. A symmetric Gaussian weighting function w = {ωi |i = 1, 2, … , N} with standard deviation of 1.5, normalized to unit sum , is used to obtain the local statistics.
| (1) |
| (2) |
| (3) |
| (4) |
c1 and c2 equal (0.01 × c)2, (0.03 × c)2, respectively. They are constant terms used to avoid instability from dividing by zero. Note that SSI equals 1 for a perfect match and equals −1 for a complete divergency between two regions. Finally, a mean SSI, as described in (5), is calculated to represent the overall similarity between two image volumes X and Y. Here, xj, yj are local patches and M is the total number of patches.
| (5) |
In our framework, the five atlas images with the highest mean SSI scores are selected for the multi-atlas registration during the next step. A multi-threading scheme is used to compute the SSI from all 36 atlases concurrently.
In a previous work [34], the luminance and contrast terms in the SSI was exploited to reduce the label fusion computing time in brain segmentation, but the SSI was not used for optimal atlas selection. In contrast, Yang et al. [15] used mutual information for atlas selection in their cardiac MAS method.
2). ATLAS REGISTRATION:
Image registration is an essential step to determine the spatial correspondence between the target and the atlas images. A pairwise atlas-to-target deformable image registration is performed to obtain a nonlinear transformation to warp the atlas label into the target image space. A multi-threading scheme is implemented to register the five selected atlas images to the target image concurrently.
Deformable image registration poses a highly non-convex optimization problem which is prone to local minima. Discrete optimization overcomes these limitations as it does not require a derivative of the cost function as used in continuous optimization. We apply an efficient 3D discrete deformable registration developed by Heinrich et al. [35]–[37] that uses a Markov Random Field (MRF) objective function C:
| (6) |
is a set of nodes that constitute a graph. Each node √ corresponds to a control point in a uniform B-spline grid with a spatial location xp and a set of 3D displacements fp = up = {up, vp, wp} between the target X and the atlas Y images. The objective function has two terms: a unary cost D (fp) and a pair-wise regularization cost R (fp, fq).
The unary cost D (fp) measures the similarity of the voxels around a control point p in the image X and the voxels around that control point , displaced by up, in the image Y based on the sum of absolute differences [35]. The similarity is estimated based on patch-based self-similarity context (SSC) [36], [37]. SSC is described by a sum of squared differences between image patches within an image with a noise estimate σ2. For a patch x in image X, the SSC is given by:
| (7) |
where y defines the corresponding patch within a neighborhood in image Y, and contains six connected voxels around x. Thus, the unary cost is given by:
| (8) |
The pair-wise cost R (fp, fq) regularized the displacement of the neighboring control points q that are directly connected to p with p, q ∈ ε where ε is a set of neighboring node pairs. It is given by squared differences:
| (9) |
This MRF-based optimization problem is solved using message passing on a minimum spanning tree for computational efficiency [35]. For each node p, the cost Cp of the best displacement fq of its parent q is given by:
| (10) |
α is weighting parameter that equals 1.6 in our framework. c are the children nodes of p. For leaf nodes, only the first two terms in (10) is calculated as it has no children nodes [35].
3). LABEL FUSION:
After the multi-atlas registration, the label in each selected atlas is warped to the target image space using the corresponding transformation matrix. The next step is to fuse these transformed atlas labels into a consensus target label. This process improves the segmentation accuracy by eliminating false positive voxel from individually transformed atlas label. A common approach for label fusion is based on majority voting [38] that ranks each voxel by the frequency it appears in all transformed labels and then produces the final target label from the voxels that retain the most counts.
However, this approach does not consider the underlying voxel-to-voxel similarity of the target and the transformed atlas images which may possess large discrepancies due to mis-registration. Several studies exploited the voxel-to-voxel relationship between the warped atlas and the target images to boost the performance [5], [10], [39], [40], [41].
Here we propose a simple technique based on structural similarity of each image pair to improve this step. First, an SSI map as described in (1) is computed between the target and each warped atlas images. Voxels within the transformed atlas labels will be re-indexed as the background if they have negative SSI values. This process effectively removes the voxels with low similarity between the target and the warped atlas images. Next, the voxels in the transformed atlas label that have an intensity value less than −400 Hounsfield Unit (HU) in the target image are also re-indexed as the background, as they represent the air spaces in the lung. Lastly, the majority voting is used to combine the transformed and processed atlas labels into a single target label.
B. CORRECTIVE SEGMENTATION
The corrective segmentation (CS) block is designed to 1) refine the cardiovascular labels generated from the MAS processing block, and 2) separate the intrathoracic structures surrounding the heart. The first step is to identify non-cardiac structures in the CTA image and classify them into different regions including lung, CW, liver, spine, and DA. This is based on our previous work [1] to automatically extract seed voxels representing these five structures. The additional segmentation of the non-cardiac structures in this processing block is aimed at improving the segmentation of the cardiac structures. The next step is to combine these five non-cardiac structures with those 12 cardiovascular structures from the previous MAS processing block for a joint 17-structure labels. The voxels in these labels then serve as the seeds to run through a random walk algorithm to improve the segmentation for each structure. The final segmentation is obtained by additional post-processing refinement steps. The following subsections provide more details for each step in the CS block.
1). MULTI-STRUCTURE SEEDING:
A modified version of our previous work [1] is used to extract the best representative seed voxels (seeding) for these intrathoracic structures. The first step is to detect potential lung regions based on an intensity window between −1000 and −400 HU as the lung contains air and some soft tissues. For each binarized region, its major-axis length is measured. The regions with the maximum length are selected as the lung seed voxels. Next is to find the chest wall region by locating the top-most boundary points from the previously detected lung and the whole heart regions. A surface fit is performed on these points using a linear radial basis function to separate the lower (mediastinum) and the upper (chest wall) regions. The upper region is further processed to retain voxels with greater than zero HU as the chest wall seed voxels.
The next step is to define the whole heart region based on the cardiac labels obtained from the previous MAS block. Here the bright voxels in LV and LA labels and intermediate enhanced RV, RA, and LVM voxels are merged with the AA and LAA labels into one region to represent the whole heart seed voxels. Next is to detect descending aorta and spine tissues by locating the region outside the lower part of the whole heart and the lung regions. Voxels with intensity values lower than zero HU are removed, and then a morphological erosion is used to process the region. The largest connected region is selected as the seed voxels for the descending aorta and spine joined region.
The last step is to detect the liver tissues by merging all regions detected from the previous stages and then analyzing the remaining regions in the image. A series of intensity thresholding and morphological operations are used to estimate potential liver regions.
2). CARDIAC STRUCTURE SEEDING:
This processing stage is aimed at extracting representative seed voxels from the 12 cardiovascular regions obtained from the previous MAS processing block. Before the seed selection, the following preprocessing steps are applied to each region except for the LVM region. An intensity window between one standard deviation above and below the median HU is used to extract intermediate intensity voxels, followed by a morphological closing at each region.
In the subsequent steps, six cardiac regions are sequentially processed in the order of LV, AA, RV, LVM, LA, and RA to extract corresponding seed voxels. These processes are based on domain knowledge of cardiac anatomy, analyses of voxel intensity, distance, connected region size, and mathematical morphology operations.
For example, HU values in AA, LV, LA are typically higher than RV, RA, LVM in contrast enhanced CTA study and can thus be used to remove misclassified voxels. Distance analysis is also useful to rule out misclassified voxels among different structures. For instance, a 3D convex hull analysis is used to include papillary muscle in the initial LV region; candidate voxels that are within 10 mm distance to the RV are removed. Such distance threshold is derived from the thickness of ventricular septum that separates the LV and RV.
Similarly, for the RV seeding, a distance measure is calculated for each voxel in the initial RV region. Voxels less than 10 mm to the LV, or 2 mm to the AA, or 4 mm to the CW are removed. For the LVM seeding, voxels that are 2 mm adjacent to RV, or 4 mm adjacent to the LA, or 4 mm to the CW are removed. For the LA seeding, voxels that are 4 mm and 2 mm adjacent to the DA or AA are removed. For the RA seeding, voxels that are 2 mm adjacent to the AA, or 4 mm adjacent to the LA are also removed.
The largest connected region is used at each step as these structures contain one whole component. The other regions including PA, PV, SVC, IVC, and LAA are used as their corresponding seeds without further processing.
3). RANDOM WALK SEGMENTATION:
Random walk algorithm [42] requires a set of initial seed voxels to proceed. It is formulated on a weighted graph, where each node represents a voxel. A graph G = (V, E) has the vertices v ∈ V and edges e ∈ E. An edge, e, of two vertices, vi, vj, is denoted by eij. The weight of edge eij is denoted wij. The degree of a vertex is di = ∑ w (eij). Given a weighted graph, VM is a set of labeled vertices and VU is a set of unlabeled vertices. The random walk algorithm labels each unknown vertex vi ∈ VU with a label yi ∈ Y by measuring the probability, xi, that this vertex is first reach the marked vertex vj ∈ VM, i.e., a set of seeds, which has been assigned to label yi. The segmentation is completed when each unknown vi is assigned to the label for which it has the highest probability, i.e., with s is the total number of labels in Y. The algorithm solves the Laplace equation by minimizing the cost function C:
| (11) |
T is the transpose operator. Lvivj is the combinatorial Laplacian matrix defined as dvi if i = j. It equals to −wij if vi and vj are adjacent vertices, and zero otherwise.
A slightly modified 3D version of random walk algorithm [43] is used to regularize the segmentation based on the seed voxels in different tissue structures as described in sections III.B.1. and III.B.2. This process is performed on each seed region in a single-label and multiple-pass fashion. Each label is processed by indexing seeds in the corresponding structure as foreground while seeds from all other structures are marked as background. In addition, a contour of 4 mm around each target seed region are marked as background to avoid over segmentation and improve boundary smoothness. To speed up the process, a multi-threading scheme is implemented to execute multiple random walk processes simultaneously.
After the random walk segmentation, a few post-processing steps are performed to separate descending aorta and spine regions. A threshold at 200 HU is used to remove darker pixels and then following by morphology erosion and connected region analysis. The region with a higher HU standard deviation is labelled as the spine since it contains mixed tissues structure such as bone and fluid. The region with a lower intensity standard deviation is labelled as the DA due to its more homogeneous HU distribution. Finally, the 3D surface of each label is processed by a mean filter in the polar space to smooth the distance of adjacent neighbors to the volume center and to improve the visualization quality.
IV. EXPERIMENTS
A. CLINICAL DATA AND ATLAS ANALYSIS
One hundred twenty clinical CTA scans of patients with suspected coronary artery disease referred to the National Heart, Lung and Blood Institute between April 2017 and September 2017 were retrospectively collected for this study. Patients with congenital heart defects, cardiac structural abnormalities, or serious arrhythmias were excluded. All CTA exams were performed under procedures and protocols approved by the Institutional Review Board of the National Institutes of Health. Written informed consent was obtained from all subjects prior to participating in the study. There were 73 males and the average age was 57 ± 12 years. A subset of 36 CTA studies from the 120 studies were selected as the atlas library. The selection was based on the heart size to assemble a similar size distribution of the entire dataset (Fig. 2). For each of these 36 cases, as defined previously in section III.A, 12 cardiovascular structures were manually delineated by 2 trained observers using a custom developed interactive image analysis software and reviewed by experienced cardiologists to assemble the reference atlas label dataset.
Fig. 2.
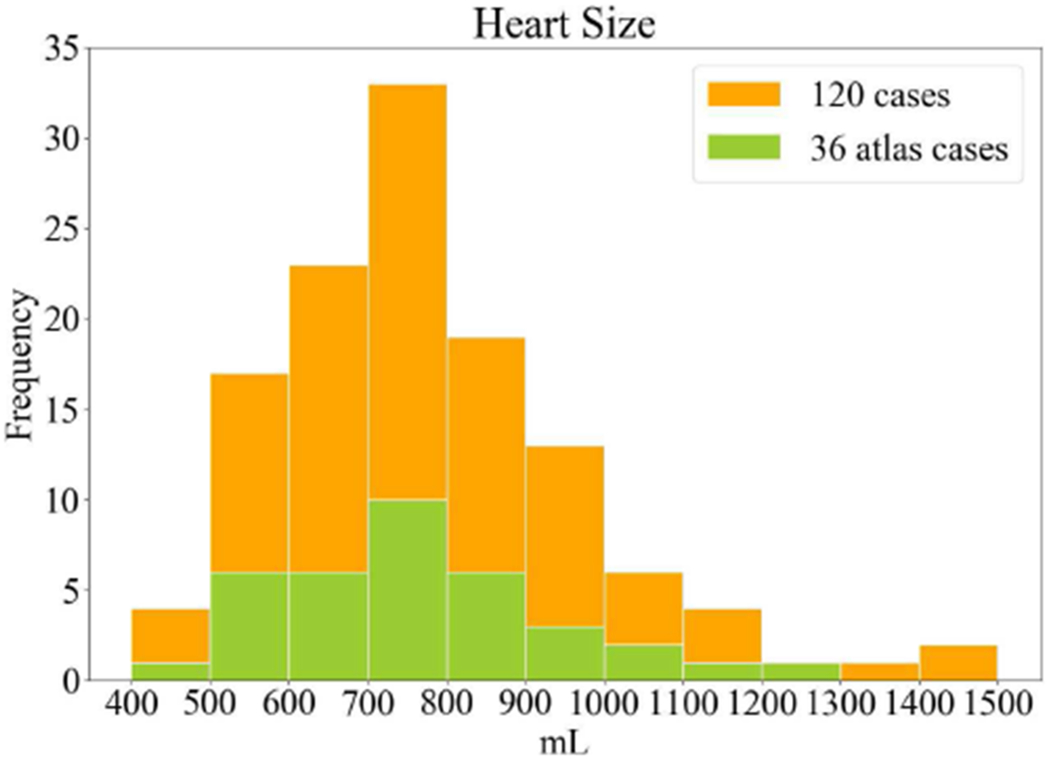
Histogram of the heart volume size measured in the entire 120 cases and the selected 36 cases of the atlas library.
B. CTA IMAGE ACQUISITION AND PROCESSING
All CTA studies were performed on a 320-detector row scanner (Aquilion One Genesis, Canon Medical Systems) with 0.5 mm detector collimation, 275 msec gantry rotation time, 100–120 kVp tube voltage, 200–850 mAs tube current according to patient’s attenuation profile determined by the scout image. Contrast material dose was 50–70 mL administered at a flow rate of 5.0–5.5 mL/sec and adjusted for patient weight. Prospective ECG-triggered image acquisition was initiated by a target threshold of 300 HU in the descending aorta. Images were reconstructed with a matrix size of 512 × 512 and a field-of-view of 148 to 220 mm, resulting to a pixel size of 0.29×0.29 mm2 to 0.43×0.43 mm2. For each dataset, images were reconstructed at a 5% phase window around the diastasis in the cardiac cycle. Each study contains 240 to 520 images with a slice thickness of 0.5 mm and a slice spacing of 0.25 to 0.5 mm. All CTA images were subsampled to an isotropic voxel size of 1.0 × 1.0 × 1.0 mm3 to improve the symmetrical property of the voxel for 3D image processing.
All algorithms were implemented in Python (www.python.org) and Interactive Data Language (Harris Geospatial Solutions). The registration method was developed in C++ by Heinrich et al. [35] and compiled to dynamic link library under Microsoft Visual Studio in our framework. All studies were processed with the same parameter settings on a computer with an Intel Core i9-7980XE 2.6GHz CPU and 128GB RAM.
C. EVALUATION METHODS
The automatic segmentation results were quantitatively evaluated and compared with expert manual segmentation on the 36 atlases reference dataset. Here we assessed eight of the 12 cardiovascular structures including LV, LA, LVM, LAA, RV, RA, AA, and WH. The other four structures including PA, PV, SVC, IVC were not assessed quantitatively as they are connecting vessels to the heart and do not possess a complete structure form in the CTA images.
The performance was evaluated using leave-one-out cross validation in which each study was withheld in turn for validation while the remaining 35 studies were used as the atlas library for the automatic segmentation. Segmentation quality was evaluated using a Dice coefficient, 3D Hausdorff distance (HD) and mean surface distance (MSD). Summary statistics are expressed as the median and 95% confidence interval due to non-normally distributed data. The volume size (mL) of each cardiac structure obtained from the two segmentations was compared using Spearman rank-order correlation coefficient and nonparametric Mann-Whitney rank test. A p-value > 0.05 indicated a statistically non-significant (NS) difference.
To compare the performance of our proposed framework against conventional multi-atlas segmentation, we implemented a baseline multi-atlas segmentation (bMAS) which consisted of the same optimal atlas selection and multi-atlas registration steps, but with a conventional label fusion based on majority voting and without the CS processing block. The results of bMAS were also compared against the reference manual segmentation using the same leave-one-out cross validation from those 36 reference datasets.
For the entire 120 studies, evaluation of the automatic segmentation was performed qualitatively by three cardiologists visually inspecting each automatically segmented cardiac structure in the images. The criterion of qualitative evaluation was based on a five-point rating score, as described in Table II.
TABLE II.
Segmentation quality score classification.
| Score | Automatic Segmentation Result |
|---|---|
| 1 | Excellent |
| 2 | Good |
| 3 | Acceptable |
| 4 | Needs improvement |
| 5 | Segmentation failed |
On the assessment of multi-structure segmentation for all 17 cardiovascular and intrathoracic structures, the HU distributions for each structure was computed to quantify the range (variability) of HU values for specific tissues and the extent of their HU value overlap with spatially adjacent tissues. The HU values at the 25th, 50th, and 75th percentiles for each structure’s distribution were calculated. Furthermore, the percentile difference which describes the width of the HU distribution, and the interpatient HU variability which is expressed as the standard deviation of median HU values, were computed to characterize different tissue types.
V. RESULTS
The proposed automatic multi-structure cardiac CTA image segmentation framework successfully processed the entire dataset without exclusion. The data in our study cover a wide range of heart size. The average whole heart volume size was 826 ± 184 mL, with a minimum size of 471 mL and a maximum size of 1524 mL. The computational time to process a CTA image volume averaged 2.79 ± 0.59 minutes.
A. CARDIAC STRUCTURE SEGMENTATION
1). SEGMENTATION COMPARISONS:
In Fig. 3, the results of our CMACS framework versus conventional atlas based segmentation are compared for qualitative assessment. To demonstrate the effectiveness of atlas selection using the proposed SSI, results of single-atlas segmentation based on the atlas images with the minimum vs. maximum mean SSI scores of the 36 matchings were displayed. The segmentation quality is considerably better by using the atlas with the maximum SSI score than the one with the minimum SSI score in this single-atlas based comparison.
Fig. 3.
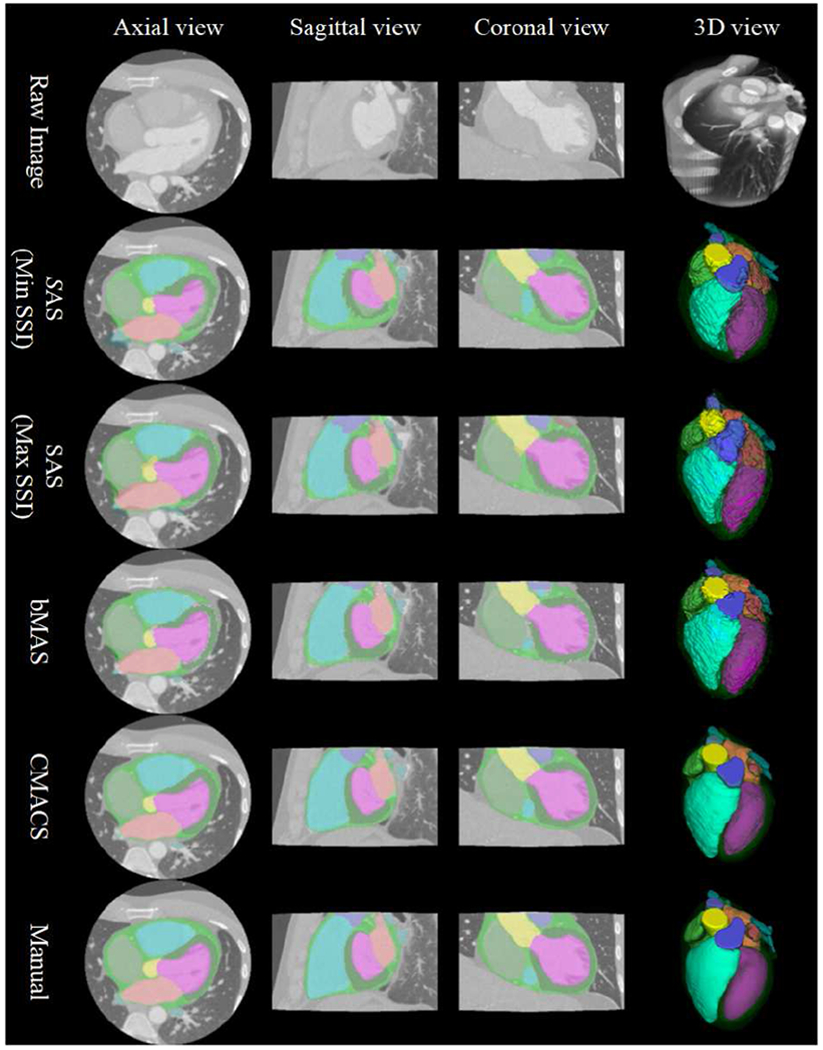
Comparison of different segmentation: single-atlas segmentation (SAS) based on the minimum and maximum structure similarity index (SSI) matched atlases; baseline multi-atlas segmentation (bMAS) and the proposed combined multi-atlas and corrective segmentation (CMACS) based on the five highest SSI matched atlases; and the reference manual segmentation for the 12 cardiac structures. Color labels: LV, LA, LVM, LAA, RV, RA, AA,, WH, SVC, IVC, PA, PV.
For multi-atlas based comparison, we performed baseline multi-atlas segmentation (bMAS) as mentioned in the section IV.C. It is evident that bMAS based on the best matched five atlas images with majority voting label fusion further improves the results compared to the single-atlas based approaches. Finally, the results of the proposed CMACS framework produced considerably better labels than the bMAS and single-atlas methods. They appear to be closest to the reference manual segmentation as shown in Fig. 3.
2). QUANTITATIVE EVALUATIONS:
For the results of leave-one-out validation based on the 36 atlases dataset, Fig. 4 shows three cases with the maximum, median, and minimum averaged Dice indices between the proposed CMACS and manual segmentations. The results of our automatic segmentation can also be viewed in the supplementary video files for volumetric evaluation. Overall, our automatic segmentation shows well-maintained results on all cases and even on the one with the lowest Dice index.
Fig. 4.
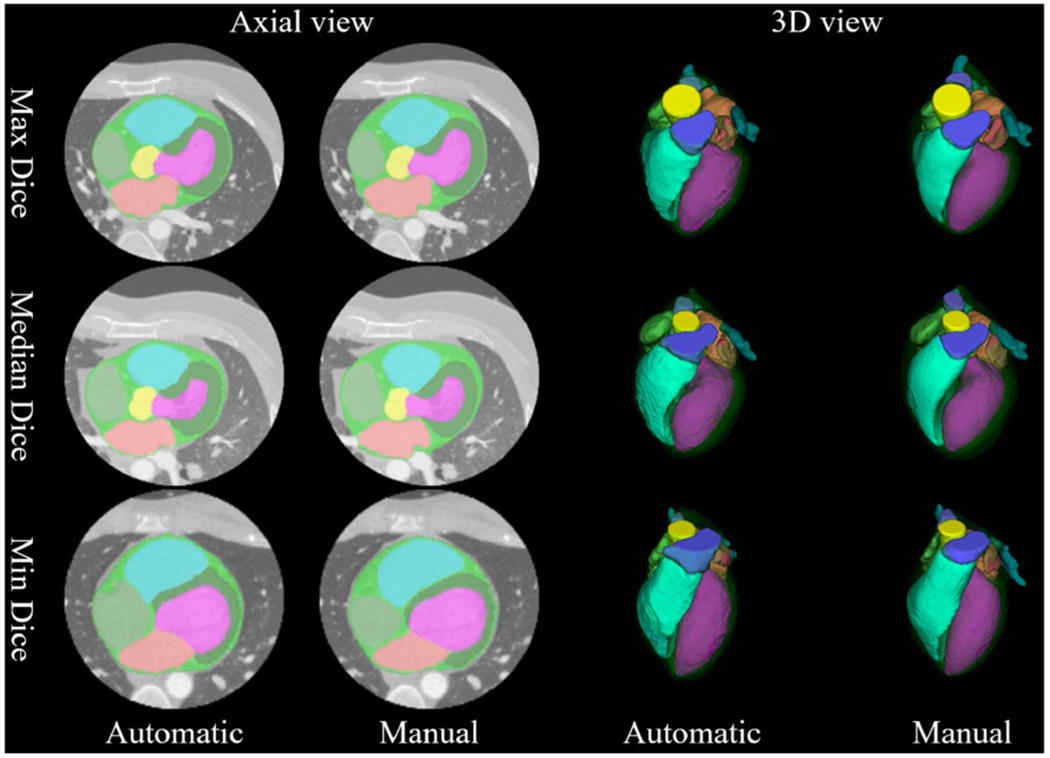
Comparison of automatic versus manual segmentation on three cases with the minimum, median, and maximum averaged Dice indices. Detailed color overlay comparisons for each structure and animated cross-sectional results of the automatic segmentation can also be viewed in the supplementary files.
Table III summarizes the quantitative comparisons of eight cardiac structures segmented by the bMAS method and the CMACS framework against the manual reference standard. Our framework achieved better results than the bMAS for each of the eight structures in all Dice, HD, and MSD indices compared. The Dice results of CMACS are significantly better than bMAS with p<0.001 for all structures compared. For the HD index, the CMACS results also are significantly better than the bMAS results with p<0.05 for LVM, LAA, AA, and WH structures, but are not significantly different for LV, LA, RV, and RA structures. Lastly, the MSD results of CMACS are significantly better than the bMAS results with p<0.05 for all structures except RA. Overall, these results indicate that the enhanced label fusion and corrective segmentation block included in our pipeline processing method consistently improves the performance of conventional multi-atlas segmentation method.
TABLE III.
Performance evaluation of the baseline MAS (bMAS) method vs. the proposed CMACS framework.
| Metrics | Methods | LV | LA | LVM | LAA | RA | RV | AA | WH |
|---|---|---|---|---|---|---|---|---|---|
| Dice | bMAS | 0.93 [0.81,0.92] | 0.90 [0.86,0.93] | 0.80 [0.66,0.85] | 0.63 [0.48,0.74] | 0.89 [0.83,0.92] | 0.89 [0.81,0.92] | 0.88 [0.81,0.92] | 0.93 [0.91,94] |
| CMACS | 0.95† [0.94,0.96] | 0.95† [0.93,0.97] | 0.88† [0.84,0.91] | 0.79† [0.67,0.85] | 0.92† [0.85,0.94] | 0.91† [0.87,0.94] | 0.94† [0.92,0.96] | 0.96† [0.94,0.97] | |
| HD (mm) | bMAS | 6.56 [4.50,9.26] | 8.31 [5.72,11.6] | 7.84 [5.68,13.0] | 11.1 [6.75,16.8] | 9.08 [6.46,15.7] | 12.2 [7.40,19.3] | 5.83 [4.18,9.94] | 37.6 [33.1,44.0] |
| CMACS | 5.56 [3.61,9.63] | 7.18 [4.82,13.5] | 6.44† [3.94,10.1] | 8.28† [5.28,14.8] | 8.54 [4.84,13.2] | 12.1 [6.26,19.5] | 4.58† [2.81,8.05] | 13.0† [11.5,18.6] | |
| MSD (mm) | bMAS | 1.07 [0.82,1.72] | 1.30 [1.02,1.74] | 1.21 [0.95,1.71] | 2.09 [1.41,3.11] | 1.46 [1.12,2.24] | 1.75 [1.25,2.89] | 1.18 [0.82,1.80] | 2.92 [2.53,3.79] |
| CMACS | 0.86† [0.70,1.12] | 0.76† [0.52,1.09] | 0.85† [0.71,1.03] | 1.31† [0.93,2.09] | 1.32 [0.99,2.16] | 1.55† [1.11,2.16] | 0.71† [0.48,0.91] | 1.46† [1.11,1.84] | |
Quantitative Dice index, 3D Hausdorff distance (HD) and mean surface distance (MSD) are calculated between the automatic and manual segmentation. Results are expressed as the median and 95 % confidence interval.
indicates significantly better performance in a higher Dice, a lower HD, or a lower MSD (p<0.05).
Fig. 5 illustrates 3D volume size comparisons, showing the correlation plots between our automatic results against the manual segmentation among the eight cardiac structures. There was excellent relationship between automatic and manual segmentations in all cardiac structures, with correlation coefficients of 0.99 for LV, 0.97 for LA, 0.97 for LVM, 0.82 for LAA, 0.94 for RV, 0.92 for RA, 0.97 for AA, and 0.98 for WH. Table IV summaries the size of various cardiac structures measured by the automatic versus the manual segmentations. The Mann-Whitney test indicates there was no significant difference in size between the automatic and expert segmentations for all structure compared (all p = NS).
Fig. 5.
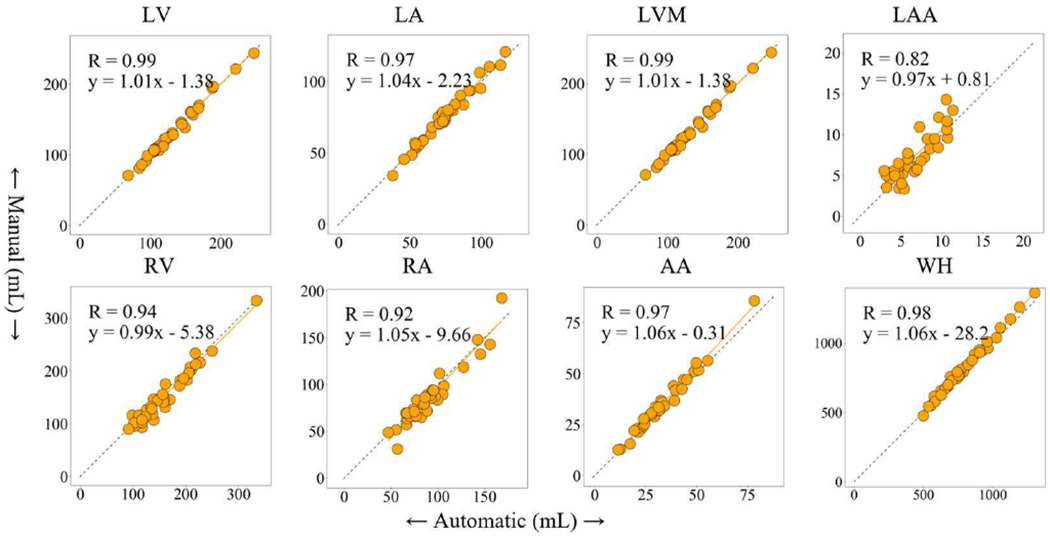
The correlation analyses of cardiac structures between the proposed automatic and manual segmentation. (R: Spearman correlation value)
TABLE IV.
Comparison of the proposed segmentation versus the manual segmentation for measuring different cardiac structure sizes.
| Size (mL) | LV | LA | LVM | LAA | RV | RA | AA | WH |
|---|---|---|---|---|---|---|---|---|
| Automatic | 120 [87,197] | 73 [50,107] | 108 [76,167] | 6 [3, 11] | 157 [101, 233] | 84 [56, 148] | 31 [16,52] | 756 [551,1143] |
| Manual | 123 [85,203] | 74 [48,110] | 105 [72,166] | 6 [3, 12] | 146 [95, 235] | 79 [51, 144] | 33 [15,56] | 811 [562,1207] |
Results are expressed as the median and 95 % confidence interval. All results are non-significantly different (p=NS).
3). QUALITATIVE EVALUATIONS:
In addition to the quantitative evaluation, our automatic segmentation results were also qualitatively assessed by expert cardiologists for the entire 120 CTA studies. All automatic segmentation results were compiled into animated cross-sectional images in the same format as the included supplementary video files for visual inspections. Based on the quality scores as classified in Table II for visual assessment, our automatic segmentation results obtained an excellent overall score of 1 for all cardiac structures evaluated.
For individual cardiac structure visual assessment, less than 3% of the cases included one or more of the following conditions: the RA segmentation slightly extended into the RV or included the right coronary artery, the RV segmentation slightly extended into the PA, the LA segmentation slightly extended into the PV, the LV segmentation slightly extended into the LA, the LAA segmentation included small portions of the left circumflex coronary artery or the LA, the AA segmentation slightly extended into the left or right coronary artery. Additionally, less than 10% of the cases had slight contamination in the WH region that included minor amounts of liver tissues. However, these segmentation flaws were generally limited within small areas and did not yield large percentage errors.
B. MULTI-STRUCTURE SEGMENTATION
In addition to cardiac structures, our CMACS framework also performs automatic segmentation of intrathoracic non-cardiac structures in the CTA images. Fig. 6 shows an example of our automatic pipeline segmenting all 17 cardiovascular and intrathoracic structures. Detailed animated cross-sectional images can also be viewed in the supplementary video files for volumetric evaluation of our multi-structure segmentation.
Fig. 6.
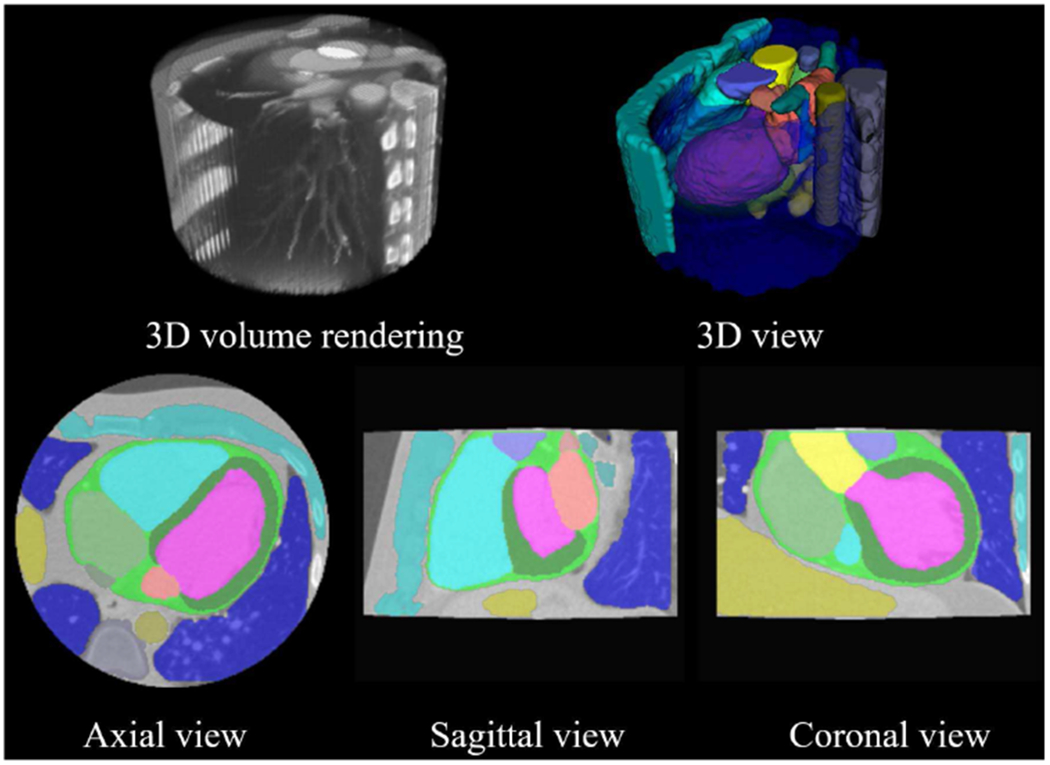
Example of the proposed CMACS framework of all 17 cardiovascular and intrathoracic structures. Top row shows the 3D rendered display of the raw CTA image and the segmented structures. Bottom row shows 2D cross-sectional images and labels. Detailed animated cross-sectional results of the automatic segmentation can also be viewed in the supplementary video files. Color labels: LV, LA, LVM, LAA, RV, RA, AA, WH, SVC, IVC, PA, PV, DA, Spine, Liver, CW, Lung.
To assess our multi-structure segmentation for characterizing different tissues, Table V and Fig. 7 summarize the ranges of the HU values among all 17 structures from our automatic segmentation across the entire 120 cases. In the group comparisons, there were several blood containing structures such as the LV, LA, LAA, AA, PV, and DA that had significantly higher HU values (all median HU > 500) than other blood containing structures such as the LVM, RV, RA, SVC, IVC, and PA (all median HU < 200) that were less-enhanced (all p<0.05). However, all of the 12 blood containing structures had significantly higher HU values than the liver that showed a typical HU range for non-contrast enhanced soft tissues (all p<0.05). Among those six high-contrast enhanced structures, there was a large degree of overlap in the HU ranges as shown in Fig. 7. A similar extent of overlap was also observed among the six less-enhanced structures. This overlap of HU distributions among spatially adjacent cardiac structures makes the segmentation of different structures surrounding and within the heart based on the HU values alone a challenging task.
TABLE V.
Statistics of the hounsfield unit (HU) distributions for 17 structures across 120 CTA scans from the proposed method.
| (HU) | Empirical percentiles | Percentile difference | Interpatient variability | ||
|---|---|---|---|---|---|
| Structure type | 25% | Median | 75% | |25%-75%| | SD of medians |
| LV | 349 | 503 | 561 | 212 | 138 |
| LA | 503 | 543 | 577 | 73 | 163 |
| LVM | 47 | 74 | 101 | 54 | 14 |
| LAA | 372 | 507 | 576 | 204 | 128 |
| RV | 85 | 120 | 154 | 69 | 48 |
| RA | 65 | 96 | 125 | 61 | 42 |
| AA | 528 | 568 | 599 | 71 | 140 |
| WH | 44 | 115 | 380 | 336 | 40 |
| SVC | 81 | 114 | 145 | 65 | 97 |
| IVC | 43 | 68 | 93 | 50 | 27 |
| PA | 125 | 155 | 180 | 56 | 62 |
| PV | 461 | 507 | 547 | 86 | 161 |
| DA | 453 | 503 | 546 | 93 | 134 |
| Spine | 49 | 169 | 295 | 246 | 49 |
| Liver | 19 | 46 | 73 | 54 | 15 |
| CW | 31 | 71 | 132 | 101 | 20 |
| Lung | −840 | −791 | −721 | 119 | 79 |
Fig. 7.
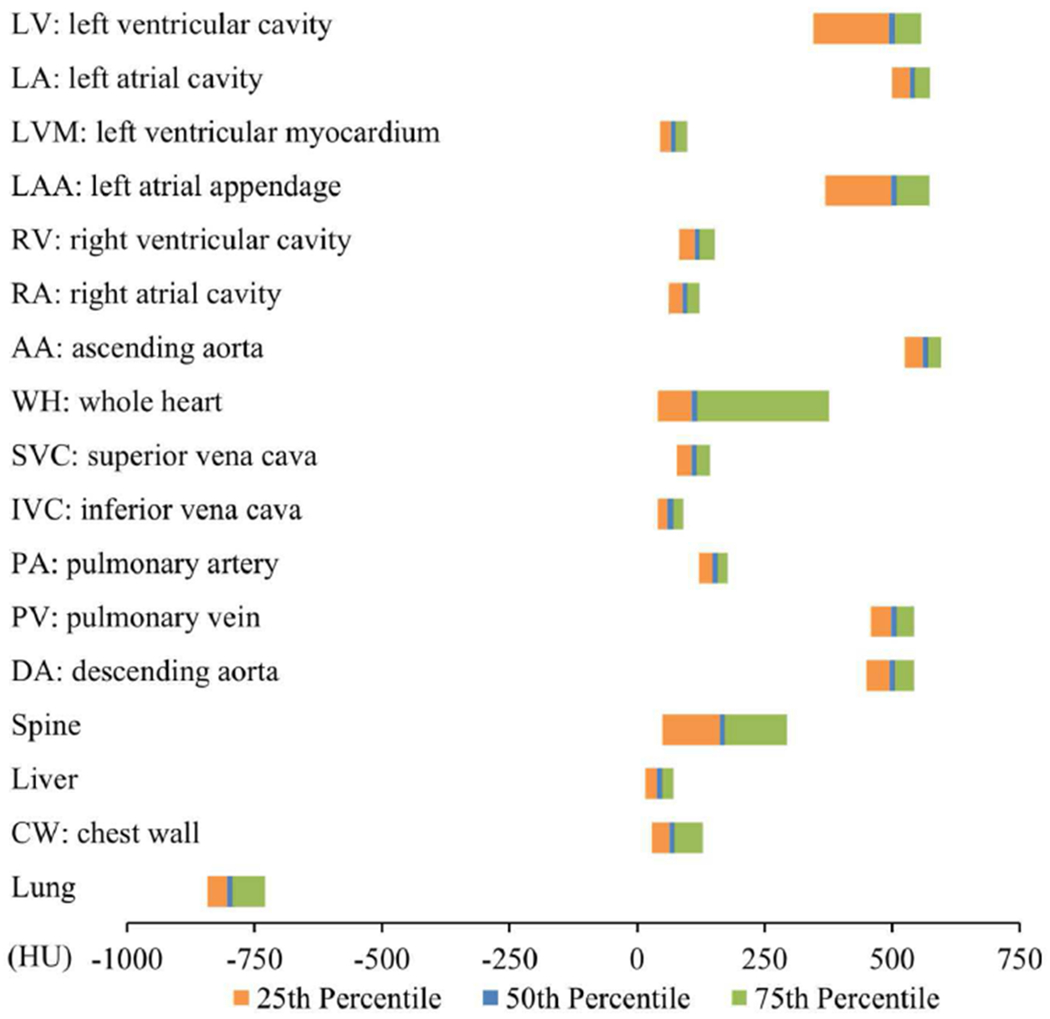
Summary of the Hounsfield unit (HU) ranges for all 17 cardiovascular and intrathoracic structures labelled from the proposed automatic segmentation of 120 CTA studies.
For the interpatient variability comparison of different tissue structures, Table V shows the high-contrast enhanced blood containing tissues of the LV, LA, LAA, AA, PV, and DA also had a higher interpatient variability (all > 100 HU) than other structures that were less enhanced. For the comparison of percentile differences between 25% and 75% of the HU distributions, the largest difference was observed in the WH region as it combined both high-contrast and less-contrast enhanced tissues. The spine region also had a high percentile difference as this structure is comprised of bone, soft tissue, and cerebrospinal fluid.
VI. DISCUSSIONS
We present a fully automatic image processing system to segment the heart and its peripheral structures in contrast enhanced cardiac CTA images. The proposed framework facilitates a combined multi-atlas and corrective segmentation approach that outperforms conventional atlas-based segmentation in our quantitative comparisons. The qualitative assessment performed by expert cardiologists also showed our automatic segmentation attained an excellent quality score for all cardiac structures evaluated in this study.
In the literature, most studies performed quantitative evaluation based on Dice, HD, and MSD indices for various cardiac structure segmentation; Kirişli and colleagues also included qualitative assessment [6]. To compare the methods that required less than five minutes processing time, an MSD of 1.57 mm [28], 0.98 mm [30], and 2.2 to 8.6 mm [20] were reported. A Dice index from 0.77 to 0.90 [16], from 0.78 to 0.94 [20], from 0.84 to 0.93 [21], and from 0.67 to 0.96 [23] were also described. In a recent MICCAI-STACOM challenge [4], a Dice range from 0.81 to 0.91, an HD range from 25.2 to 55.4 mm, and an MSD range from 1.11 to 4.20 mm were summarized from the comparison of ten cardiac CTA segmentation algorithms. Comparatively, our method showed an excellent Dice score from 0.91 to 0.96 on most cardiac structures, except for the LVM and LAA. Our distance indices were also comparable with other groups, with an MSD from 0.71 to 1.46 mm and an HD from 4.58 to 13.0 mm. The HD in our results is noticeably better than those reported in [4].
On comparing the computational speed for different multi-atlas methods for automatic CTA segmentation, whereas some groups [8], [9], [14], [17], [29] did not report the computational time, those groups that did [5]–[7], [10], [12], [15], [18] required a much longer processing time (greater than five minutes) than our method (less than three minutes). The processing voxel size is unsurprisingly one of the key factors influencing the overall segmentation time. A recent study [18] reported a computational time of greater than three hours using an isotropic 1.5 mm3 voxel size, or greater than one hour using an isotropic 2.0 mm3 voxel size for processing. Their segmentation time can be reduced to less than 30 minutes if performed under a larger voxel size, e.g. 3 mm3 or greater. Advantageously, our proposed CMACS pipeline framework requires less than three minutes using a 2 mm3 voxel size in the MAS processing block and 1 mm3 voxel size in the CS processing block. In contrast, deep neural network methods were considerably faster than the existing multi atlas-based methods and generally require less than two minutes for the inference processing time [20], [21].
In a recent work [4], the advantages and potential limitations of multi-atlas and deep-learning based approaches for cardiac CTA segmentation were compared and discussed. Eight out of the ten methods benchmarked in the study were based on deep neural networks whereas the other two were multi-atlas based. One possible reason that the multi-atlas approach is less prevalent is due to its longer processing time of greater than 20 minutes. However, deep-learning approaches showed large interquartile ranges and outliers in Dice compared to the multi-atlas methods, and they require large amounts of annotated training data in order to produce good results.
Furthermore, unlike some poor quality examples in [4] that displayed an incomplete heart shape, our segmentation produced a realistic heart shape in all 120 cases that were tested. The Fig. 4 example demonstrates that our segmentation looks well-maintained even for the case with the minimum overall Dice score.
Overall, our proposed method could generate more stable segmentation results compared to deep-learning based approaches. Our results were also competitive in terms of mean accuracies and computation efficiency compared to conventional multi-atlas based approaches.
In our summary assessment of multi-structure segmentation for different tissue characterization, we observed two groups of HU distributions that categorize 12 blood containing cardiovascular structures into high-contrast (LV, LA, LAA, AA, PV, and DA) versus less-contrast (LVM, RV, RA, SVC, IVC, and PA) enhanced tissues. Such a large discrepancy in HU values among anatomically adjacent structures is primarily due to our contrast administration and scan timing protocol that uses a bolus tracking technique to trigger the scan when the contrast bolus arrives in the descending aorta. Our automatic framework can thus be a useful quality assurance tool to measure optimal contrast enhancement in routine CTA scans. This multi-structure segmentation feature may also be useful to differentiate HU characteristics in muscle, liver, and cancer tissues, or to assess interpatient HU discrepancies [44]. Moreover, this automatic segmentation feature can also be used for computer-based image context-driven annotation of cardiac CTA image dataset, such as a similar work performed on abdominal CT for multi-label image annotation [45].
The HU ranges for different structures measured in our study may be compared to a contrast enhanced thoracic CT study that characterized the HU distribution of various intrathoracic structures through manual planimetry [44]. For the common structures that were labelled in both studies, their results showed lower HU values for those high-contrast enhanced structures than ours. Their median HU values for the AA and DA regions were only 246 and 236, versus 568 and 503 in ours. On the other hand, our study had lower HU values for the structures that are less-enhanced. Our median HU values for the PA, IVC, and liver regions were 155, 68, and 46, versus 218, 129, and 92 in theirs. For the whole heart region, their median HU was 169; whereas ours was 115. These differences in HU ranges can likely be explained by different imaging protocols, contrast timing and doses administered, e.g. continuous slow infusion versus first-pass bolus injection, between their thoracic CT and our cardiac CTA studies.
Our study has some limitations: It used retrospectively collected data from a single center and single vendor. The dataset represents only a single-phase (75% time point) of the cardiac cycle. No inter- or intra-operator analysis was evaluated on the atlas dataset. The segmentation results for intrathoracic structures were not evaluated against a reference standard as they were not the primary aim of this study. Our work did not evaluate patients with congenital heart defects such as single ventricle, atrial and ventricle septal defects, or other abnormal cardiac structures. A future study including different scanner vendors and imaging protocols, or a direct comparison with various techniques such as in MICCAI challenge [4], is needed to fully evaluate the proposed method under different clinical settings.
VII. CONCLUSION
In this paper, a novel automatic segmentation framework for contrast enhanced cardiac CTA images has been introduced. It incorporates a combined multi-atlas and corrective segmentation approach to improve conventional atlas-based segmentation. Our results have shown the proposed framework produced significant improvement over conventional multi-atlas segmentation, a strong agreement with expert manual labeling, and a high segmentation quality score in all cardiac structures assessed. We demonstrated the proposed framework can reliably segment 17 cardiovascular and intrathoracic structures from cardiac CTA images and provide high-quality results that are more consistent and faster than manual labeling. This automatic system may assist clinicians by more easily and rapidly integrating quantitative size and morphology evaluation into routine clinical practices.
Supplementary Material
Acknowledgments
This work was supported by the intramural research program of the National Heart, Lung and Blood Institute (ZIA HL006220-02).
Biographies

VY BUI received the B.S. degree and M.S. degree in electrical engineering from The Catholic University of America, Washington DC, USA, in 2012 and 2014. She is currently pursuing a Ph.D. degree in electrical engineering at The Catholic University of America, Washington DC, USA. She is working on medical image computing research within the Cardiovascular CT laboratory at the National Heart, Lung, and Blood Institute since 2016. Her research interests include image processing, computer vision and deep learning for medical and biomedical image analysis.

SUJATA SHANBHAG received her M.D. degree from St. Louis University School of Medicine in 2000 and completed a M.P.H degree at the Harvard T.H. Chan School of Public Health in 2013. She is a Staff Cardiologist at the National Heart, Lung, and Blood Institute of the National Institutes of Health, Bethesda, Maryland. In her clinical practice, she balances her research interests in translating newer cardiovascular MR and CT imaging methods into patient studies and outcomes research. She has a specific interest in the diagnosis, management of non-ischemic cardiomyopathies, myocardial ischemia and infarction, and evaluating rare disease phenotypes using combined advanced imaging techniques.

OSCAR LEVINE is a B.A. candidate in a Philosophy-Neuroscience-Psychology program at Washington University in St. Louis, St. Louis, MO, USA. He has worked as a Summer Intern in the National Heart, Lung, and Blood Institute from 2015-2017 and in 2019, focusing on clinical research projects within the Cardiovascular CT laboratory of Dr. Marcus Chen. He plans to attend medical school following graduation in May 2020.

MATTHEW JACOBS received the B.S., M.S., and Ph.D. degrees in computer science from The Catholic University of America (CUA) in 2010, 2012, and 2018, respectively. From 2018-2019, he completed a post-doctoral position at the Advanced Cardiovascular Imaging Laboratory within National Heart, Lung, and Blood Institute and the CUA. He is currently a visiting Assistant Professor of Computer Science at the School of Engineering at CUA. His research interests include scientific image processing, both medical and astronomical, pattern recognition, and machine learning.

W. PATRICIA BANDETTINI received her B.A. and M.D. degrees in a combined program at the University of Missouri-Kansas City in 1995. She then completed an Internal Medicine residency and General Cardiology fellowship at Lutheran General Hospital in Park Ridge, Illinois, and an advanced cardiovascular imaging fellowship at the National Institutes of Health in Bethesda, Maryland. Currently, Dr. Bandettini is a Senior Research Physician within the Cardiology Branch of the National Heart, Lung, and Blood Institute at NIH. She has clinical and research interests in teaching and promoting cardiovascular MR and CT imaging for various clinical applications.

LIN-CHING CHANG received her M.Sc. and D.Sc. degrees in computer science from the George Washington University, Washington DC, USA in 1993 and 1998. She is an Associate Professor in the Department of Electrical Engineering and Computer Science and the Director of Data Analytics Program at the Catholic University of America. Prior to that, she was a postdoctoral fellow within the Intramural Research and Training Award program at the National Institutes of Health working on computational neuroscience projects with a focus on quantitative image analysis of diffusion tensor MRI. Her main research interests include machine learning, data analytics, computer vision and medical informatics.

MARCUS CHEN is the Director of Cardiovascular CT at the National Heart, Lung, and Blood Institute of the National Institutes of Health in Bethesda, MD, USA. He received his B.S. degree in biology from the California Institute of Technology in 1994 and M.D. degree from the University of Wisconsin in Madison in 1998. As a multi-modality imager in computed tomography, magnetic resonance imaging and nuclear techniques, he has clinical and research interests in technical development of new imaging methods and applications.

LI-YUEH HSU (SM’06) received his M.Sc. and D.Sc. degrees in electrical and biomedical engineering from the George Washington University, Washington DC, USA in 1993 and 1999. He has been a Staff Scientist with the National Heart, Lung, and Blood Institute, National Institutes of Health at Bethesda, Maryland since 2002. His main research interests include multi-dimensional medical imaging, image computing, machine learning, computer vision, pattern recognition, computer-aided detection and diagnosis, computational modeling in biology and physiology.
References
- [1].Bui V, Hsu LY, Chang LC and Chen MY, “An automatic random walk-based method for 3D segmentation of the heart in cardiac computed tomography images,” in: IEEE Int. Sym. on Biomed. Img, 2018, pp.1352. [Google Scholar]
- [2].Kang D, Woo J, Kuo C, Slomka P, Dey D and Germano G, “Heart chambers and whole heart segmentation techniques,” J. of Elec. Img, vol.21, no.1, pp.0901, Apr. 2012. [Google Scholar]
- [3].Zhuang X, “Challenges and methodologies of fully automatic whole heart segmentation: a review,” J. of Healthcare Eng, vol.4, no.3, pp.371, Mar. 2013. [DOI] [PubMed] [Google Scholar]
- [4].Zhuang X, Li L, Payer C, Stern D, Urschler M, Heinrich MP et al. , “Evaluation of Algorithms for Multi-Modality Whole Heart Segmentation: An Open-Access Grand Challenge,” Med. Image Anal, vol.58, pp.101537, Aug. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].van Rikxoort EM, Isgum I, Arzhaeva Y, Staring M, Klein S, Viergever M, et al. , “Adaptive local multi-atlas segmentation: Application to the heart and the caudate nucleus,” Med. Image Anal, vol.14, no.1, pp.39, February 2010. [DOI] [PubMed] [Google Scholar]
- [6].Kirişli HA, Schaap M, Klein S, Papadopoulou S, Bonardi M, Chen C, et al. , “Evaluation of a multi-atlas-based method for segmentation of CCTA data: a large-scale, multicenter, and multivendor study,” Med. Phys, vol.37, no.12, pp.6279, Dec. 2010. [DOI] [PubMed] [Google Scholar]
- [7].Zuluaga M, Cardoso M, Modat M and Ourselin S, “Multi-atlas propagation whole heart segmentation from MRI and CTA using a local normalised correlation coefficient criterion,” in: Int. Conf. on Funct. Imaging Model Heart, 2013, pp.174. [Google Scholar]
- [8].Yang G, Chen Y, Tang L, Shu H & Toumoulin C, “Automatic left ventricle segmentation based on multi-atlas registration in 4D CT images,” in: IEEE Int. Sym. on Biomed. Img., 2014, pp.413. [DOI] [PubMed] [Google Scholar]
- [9].Tobon-Gomez C, Geers A, Peters J, Weese J, Pinto K, Karim R, et al. , “Benchmark for algorithms segmenting the left atrium from 3D CT and MRI datasets.” IEEE Trans. Med. Imaging, vol.34, no.7, pp.1460, Feb. 2015. [DOI] [PubMed] [Google Scholar]
- [10].Zhuang X, Bai W, Song J, Zhan S, Qian X, Shi W, et al. , “Multiatlas whole heart segmentation of CT data using conditional entropy for atlas ranking and selection,” Med. Phys, vol.42, no.7, pp.3822, Jul. 2015. [DOI] [PubMed] [Google Scholar]
- [11].Zhuang X, Shen J, “Multi-scale patch and multi-modality atlases for whole heart segmentation of MRI,” Med. Image Anal, vol.31, pp.77, Jul. 2016. [DOI] [PubMed] [Google Scholar]
- [12].Zhou R, Liao Z, Pan T, Milgrom S, Pinnix C, Shi A, et al. , “Cardiac atlas development and validation for automatic segmentation of cardiac substructures,” Radiother. Oncol, vol.122, no.1, pp.66, Jan. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Shahzad R, Bos D, Budde R, Pellikaan K, Niessen W, van der Lugt A, et al. , “Automatic segmentation and quantification of the cardiac structures from non-contrast-enhanced CCT scans,” Phys. Med. Biol, vol.62, no.9, pp.3798, Apr. 2017. [DOI] [PubMed] [Google Scholar]
- [14].Lu X, Yang R, Xie Q, Ou S, Zha Y and Wang D, “Nonrigid registration with corresponding points constraint for automatic segmentation of cardiac DSCT images,” Biomed. Eng. Online, vol.16, no.1, pp.39, Dec. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Yang G, Sun C, Chen Y, Tang L, Shu H and Dillenseger J, “Automatic whole heart segmentation in CT images based on multi-atlas image registration,” in: Int. Workshop on Stat. Atlases Comput. Models Heart, 2017, pp.250. [Google Scholar]
- [16].Katouzian A et al. , “Hashing-Based Atlas Ranking and Selection for Multiple-Atlas Segmentation,” in: Int. Conf. on Med. Image Comput. Comput. Assist. Interv., 2018, pp.543. [Google Scholar]
- [17].Karim R, Wang H, Conjeti S, Tang H, Dehghan E, Karargyris A, et al. , “Algorithms for left atrial wall segmentation and thickness–Evaluation on an open-source CT and MRI image database,” Med. Image Anal, vol.50, pp.36, Dec. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wang H et al. , “Fast Anatomy Segmentation by Combining Coarse Scale Multi-Atlas Label Fusion with Fine Scale Corrective Learning,” Comput. Med. Imaging Graph, vol.68, pp.16, Sep. 2018. [DOI] [PubMed] [Google Scholar]
- [19].Morris ED, Kakrania D, Tang H, Prasanna P and Syeda-Mahmood T, “Cardiac Substructure Segmentation and Dosimetry Using a Novel Hybrid Magnetic Resonance and Computed Tomography Cardiac Atlas,” Int. J. Radiat. Oncol. Biol. Phys, vol.103, no.4, pp.985, Mar. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Yang X, Bian C, Yu L, Ni D and Heng PA, “Hybrid Loss Guided Convolutional Networks for Whole Heart Parsing,” in: Int. Workshop on Stat. Atlases Comput. Models Heart, 2017, pp.215. [Google Scholar]
- [21].Payer C, Štern D, Bischof H and Urschler M, “Multi-label whole heart segmentation using CNNs and anatomical label configurations,” in: Int. Workshop on Stat. Atlases Comput. Models Heart, 2017, pp.190. [Google Scholar]
- [22].Ye C, Wang W, Zhang S, and Wang K, “Multi-depth fusion network for whole-heart CT image segmentation,” IEEE Access, 2019. [Google Scholar]
- [23].Liu T, Tian Y, Zhao S, Huang X, and Wang Q, “Automatic Whole Heart Segmentation Using a Two-Stage U-Net Framework and an Adaptive Threshold Window,” IEEE Access, 2019. [Google Scholar]
- [24].Baskaran L, Maliakal G, Al’Aref SJ, Singh G, Xu Z et al. , “Identification and Quantification of Cardiovascular Structures From CCTA: An End-to-End, Rapid, Pixel-Wise, Deep-Learning Method,” JACC Cardiovasc. Imaging, 2019. [DOI] [PubMed] [Google Scholar]
- [25].Funka-Lea G, Boykov Y, Florin C, Jolly M, Gobard R, Ramaraj R, et al. , “Automatic heart isolation for CT coronary visualization using graph-cuts,” in: IEEE Int. Sym. on Biomed. Img., 2006, pp.614. [Google Scholar]
- [26].Zheng Y, Vega-Higuera F, Zhou S and Comaniciu D, “Fast and automatic heart isolation in 3D CT volumes: Optimal shape initialization,” In: Int. Workshop on Machine Learning on Med. Imaging, 2010, pp.84. [Google Scholar]
- [27].Jolly M, “Automatic segmentation of the left ventricle in cardiac MR and CT images,” Int. J. Comput. Vis, vol.70, no.2, pp.151, Nov. 2006. [Google Scholar]
- [28].Zheng Y, Barbu A, Georgescu B, Scheuering M and Comaniciu D, “Four-chamber heart modeling and automatic segmentation for 3D CCT volumes using marginal space learning and steerable features,” IEEE Trans. on Med. Imaging, vol.27, no.11, pp.1668, Aug. 2008. [DOI] [PubMed] [Google Scholar]
- [29].Cai K, Yang R, Chen H, Li L, Zhou J, Ou S, et al. , “A framework combining window width-level adjustment and Gaussian filter-based multi-resolution for automatic whole heart segmentation,” Neurocomputing, vol.220, pp.138, Jan. 2017. [Google Scholar]
- [30].Ecabert O, Peters J, Schramm H, Lorenz C, von Berg J, Walker M, et al. , “Automatic model-based segmentation of the heart in CT images,” IEEE Trans. on Med. Imaging, vol.27, no.9, pp.1189, Apr. 2008. [DOI] [PubMed] [Google Scholar]
- [31].Heinrich M, Oster J, “MRI whole heart segmentation using discrete nonlinear registration and fast non-local fusion,” in: Int. Workshop on Stat. Atlases Comput. Models Heart, 2017, pp.233. [Google Scholar]
- [32].Iglesias J and Sabuncu M, “Multi-atlas segmentation of biomedical images: a survey,” Med. Image Anal, vol.24, no.1, pp.205, Aug. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Wang Z, Bovik AC, Sheikh H and Simoncelli E, “Image quality assessment: from error visibility to structural similarity,” IEEE Trans. on Med. Imaging, vol.13, no.4, pp.600, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [34].Coupé P, Manjón JV, Fonov V, Pruessner J, Robles M and Collins DL, “Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation,” Neuroimage, vol.54, no.2, pp.940, Jan. 2011. [DOI] [PubMed] [Google Scholar]
- [35].Heinrich M, Jenkinson M, Brady M and Schnabel J, “MRF-based deformable registration and ventilation estimation of lung CT,” IEEE Trans. on Med. Imaging, vol.32, no.7, pp.1239, Feb. 2013. [DOI] [PubMed] [Google Scholar]
- [36].Heinrich M, Jenkinson M, Papież B, Brady M and Schnabel JA, “Towards real-time multimodal fusion for image-guided interventions using self-similarities,” in: Int. Conf. on Med. Image Comput. Comput. Assist. Interv., 2013, pp.187. [DOI] [PubMed] [Google Scholar]
- [37].Heinrich M, Maier O and Handels H, “Multi-modal Multi-Atlas Segmentation using Discrete Optimization and Self-Similarities,” in: IEEE Int. Sym. on Biomed. Img., 2015, pp.27. [Google Scholar]
- [38].Kittler J, “Combining classifiers: A theoretical framework,” Pattern Anal. Appl, vol.1, no.1, pp.18, Mar. 1998. [Google Scholar]
- [39].Rohlfing T, Brandt R, Menzel R and Maurer CR Jr, “Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains,” NeuroImage, vol.21, no.4, pp.1428, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [40].Aljabar P, Heckemann R, Hammers A, Hajnal J and Rueckert D, “Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy,” Neuroimage, vol.46, no.3, pp.7268, Jul. 2009. [DOI] [PubMed] [Google Scholar]
- [41].Wang H, Suh J, Das S, Pluta J, Craige C, et al. , “Multi-atlas segmentation with joint label fusion,” IEEE Trans. Pattern Anal. Mach. Intell, vol.35(3), pp.611–623, Jun. 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Grady L, “Random walks for image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell, vol.11, pp.1768, Nov. 2006. [DOI] [PubMed] [Google Scholar]
- [43].Van der Walt S, Schönberger J, Nunez-Iglesias J, Boulogne F, Warner J, Yager N, et al. , “Scikit-image: Image processing in Python,” PeerJ, vol.2, pp.453, June 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Corson N, Sensakovic W, Straus C, Starkey A and, Armato S, “Characterization of mesothelioma and tissues present in contrast-enhanced thoracic CT scans,” Med. Phys, vol.38, no.2, pp.942, Feb. 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Xue Z, Antani S, Long L and Thoma G, “Automatic multi-label annotation of abdominal CT images using CBIR,” In: Proc. SPIE, Med. Imaging, pp.1013807, 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


