Modal and non-modal voice quality classification using acoustic and electroglottographic features

Abstract

The goal of this study was to investigate the performance of different feature types for voice quality classification using multiple classifiers. The study compared the COVAREP feature set; which included glottal source features, frequency warped cepstrum and harmonic model features; against the mel-frequency cepstral coefficients (MFCCs) computed from the acoustic voice signal, acoustic-based glottal inverse filtered (GIF) waveform, and electroglottographic (EGG) waveform. Our hypothesis was that MFCCs can capture the perceived voice quality from either of these three voice signals. Experiments were carried out on recordings from 28 participants with normal vocal status who were prompted to sustain vowels with modal and non-modal voice qualities. Recordings were rated by an expert listener using the Consensus Auditory-Perceptual Evaluation of Voice (CAPE-V), and the ratings were transformed into a dichotomous label (presence or absence) for the prompted voice qualities of modal voice, breathiness, strain, and roughness. The classification was done using support vector machines, random forests, deep neural networks and Gaussian mixture model classifiers, which were built as speaker independent using a leave-one-speaker-out strategy. The best classification accuracy of 79.97% was achieved for the full COVAREP set. The harmonic model features were the best performing subset, with 78.47% accuracy, and the static+dynamic MFCCs scored at 74.52%. A closer analysis showed that MFCC and dynamic MFCC features were able to classify modal, breathy, and strained voice quality dimensions from the acoustic and GIF waveforms. Reduced classification performance was exhibited by the EGG waveform.

I. Introduction

The classification of voice quality plays an important role in the clinical assessment of voice disorders [1]. Voice quality assessment is typically performed using auditory-perceptual judgments using protocols that define perceptual dimensions assumed to be related to physiological deficits of the voice production system. For example, the Consensus Auditory-Perceptual Evaluation of Voice (CAPE-V) protocol [2] defines six primary auditory-perceptual dimensions of voice: overall severity, roughness, breathiness, strain, pitch, and loudness. Using the CAPE-V form, the listener’s task is to grade the degree and consistency of each dimension on a visual analog scale that is then translated to a value between 0 and 100, inclusive. Although some CAPE-V studies report sufficiently high intra-rater and inter-rater reliability [3], especially for trained raters [4], subjective ratings of voice quality are known to exhibit a high degree of variability due to multiple factors such as the instability of internal representations of perception, the difficulty of isolating individual dimensions, and the resolution and anchoring of measurement scales [5]. To aid in complementing subjective methods, researchers have also studied objective correlates of voice quality dimensions.

The automatic classification of voice quality has the potential to be a reliable, objective method that can be used to produce clinical outcome measures, e.g., to objectively document voice improvements due to laryngeal surgery or voice therapy [6]. Commonly employed signals to assess voice quality include the acoustic voice signal, estimates of glottal flow from the glottal inverse filtered (GIF) signal, aerodynamic measures of subglottal air pressure, neck-surface acceleration, and electroglottography (EGG). The majority of research has focused on detecting the presence or absence of a certain type of voice disorder using features extracted from the acoustic waveform [7]–[10]. Some efforts have taken advantage of voice-related features of the GIF signal [11]–[13], which assumes a linear source-filter model of voice production. The presence of a structural or functional laryngeal pathology, however, often introduces non-linear subglottal-supraglottal acoustic coupling due to incomplete glottal closure patterns [14], which has the potential to make GIF challenging for non-modal voice analysis.

The electroglottograph (EGG), also known as a laryngograph, is a device which measures the change in conductance between two electrodes placed on either side of the thyroid cartilage. The output waveform is thought to be proportional to glottal contact area [15]; thus, with positive polarity indicating increasing conductance (reduced impedance), the waveform is at its maximum during the closed phase of a phonatory cycle and at its minimum during the open phase. Specialized equipment is required in order to obtain adequate EGG waveforms and is thus not ubiquitous for speech and voice assessment, especially for real-life applications. However, our recent work showed that voice modes produce distinct EGG waveform characteristics that may be exploited for voice quality classification [16].

A. Voice Quality Dimensions

Modal phonation is defined as phonation in which a mostly full glottal closure occurs during the closed phase of a phonatory cycle [17]. The glottal flow derivative contains a discontinuity at the moment of glottal closure and its spectrum is rich in harmonics. On the other hand, non-modal phonation is a very broad term for any phonation style that deviates from modal. Since the long-term goal of this investigation is to provide an objective classification of voice quality for the clinical assessment and treatment of voice disorders, three non-modal voice qualities—breathy, strained, and rough—from the CAPE-V protocol were used for the classification problem.

Breathy phonation is a common linguistic feature occurring due to insufficient glottal closure; which results in excessive air leakage through the glottis and a formation of turbulent airflow in the larynx and supraglottic tube. The vocal folds may exhibit periodic vibration, but the glottal flow derivative does not contain a discontinuity at the moment of glottal closure. The energy of low- and mid-frequencies associated with F0 and higher harmonics is lowered, while there is an increase in high frequency noise [18]. The general trend is a decrease in the spectral slope.

Strained phonation commonly occurs in participants who attempt to compensate for incomplete vocal fold adduction or glottal closures due to certain physiological and neurological disorders [19]. The increased phonation effort is caused by increased muscular tension in pulmonary, laryngeal, and pharyngeal muscles. The strained voice quality is thus described as an impression of excessive vocal effort, as if a person were talking while lifting a heavy object. The result is an increased subglottal pressure, decreased glottal flow and increased duration of glottal closure [20], [21]. Its effects on the spectrum are not yet fully understood but certain studies associate strain with increased high-frequency energy [22] and changes in energy distribution in general [23].

Rough phonation is described as a perceived irregularity in voice source signal due to differences in laryngeal muscle tension or their pliability. It either means a complete lack of regularity in vibratory patterns or, more often, a simultaneous occurrence of double or triple fundamental frequencies, also called diplophonia or triplophonia. These stochastic and deterministic variations can also occur at the same time. The glottal flow derivative contains multiple discontinuities in a single phonatory cycle. An analysis of irregular glottal pulses in [24] showed that deterministic variations give rise to multiple pitches in spectrum, main harmonics shift in frequency and multiple subharmonics arise. The stochastic variations introduce high-pass noise and a low-pass line spectrum.

B. Related Work on Voice Quality Classification

The tasks of objective voice pathology diagnosis or voice quality detection represent well developed fields, both in terms of features and machine learning schemes. Features usually fall into one of the following categories: periodicity and voice stability measures, spectral/cepstral measures, noise-related measures or non-linear modeling [25], [26]. The task of creaky voice detection in particular has been well researched. The work of [8] introduced power-peak, intra-frame periodicity and inter-pulse similarity measures; [27] used F0, spectral amplitude at the first two harmonics, the spectral slope and the first three formants for creaky voice detection; [28] employed the aperiodicity, periodicity and pitch detector [29]; or [30] which employed secondary and tertiary peaks in the residual signal [31]. A summary of the performance of different kinds of features for detecting laryngeal pathologies can be found in [32], which concluded that periodicity and stability measures in particular, and then spectral/cepstral and non-linear measures, provide good performance.

Voice quality assessment is a generalization of the previous problems as it requires classifying among several voice pathology parameters (also called dimensions) and/or predicting their severity. [33] analyzed the GIF waveform for modal, vocal fry, falsetto, and breathy voice types and concluded that the most important parameters for voice quality assessment were glottal pulse width, pulse skewness, abruptness of glottal closure, and turbulent noise. They also found that creaky voice had the highest harmonic richness factor and lowest spectral slope out of all studied voice types. This work was expanded upon in [34], where linear predictive coding (LPC)–based GIF was used to determine the Liljencrants-Fant (LF) model [35] parameters for modal, breathy, and vocal fry voice qualities. Their analysis showed a statistically significant deviation for glottal pulse width, pulse skewness, abruptness of closure, and spectral tilt. A similar approach of using LF model was presented in [36], which examined the significance of open quotient, speed quotient, and return quotient using self-organizing clustering. This work was notably different as the authors did not specify the voice styles beforehand, but rather let the system come up with its own categories. After classification, listeners were asked to evaluate the resultant clustering in terms of acoustic similarity, achieving 81.4% performance.

Later work focused on using wavelet transform parameters (Peak Slope) for detecting modal, breathy and tense (strained) segments of speech [37]. The authors reported 75% accuracy on a data set of Finnish vowels. The same experimental protocol was later used for automatic clustering of breathy and tense voice regions [38]. The authors also used the set of features introduced in [39] to detect creaky segments and achieved 87% match with the results from A/B listening tests.

A very similar approach to the one investigated in this article was presented in [40], where the authors employed a hidden Markov Model (HMM) with K-means classifiers to categorize modal, breathy, creaky, and rough voice types. Their feature vector consisted of spectral gradient measures [41] extracted from the acoustic GIF signal. The HMM classifier reached 38.9%, 56.9%, 77,1% and 61.3% accuracy for detecting modal, breathy, creaky, and rough voice qualities, respectively. It is noted, however, that the system employed a speaker-dependent classifier built from a large number of data.

Multiple studies have shown that the cepstral-based measure termed cepstral peak prominence (CPP) correlates very well with perceived breathiness [42]–[44] and strain [23], although weakly with roughness [45]. Recent works of [46]–[48] have employed mel-frequency cepstral coefficients (MFCCs), as they are cepstral-derived features well suited for machine learning. The logarithm of the mel-frequency spectrum serves the purpose of Gaussianization, and the discrete cosine transform outputs decorrelated features to further improve feature space separability. The combination of these factors made MFCCs widely popular for a range of audio-related tasks, such as speaker identification, music retrieval, and detection of neurological disorders [49]–[51].

All of the previously cited works relied on hard labeling which is usually annotated by expert listeners or hard classification without any overlap between the classes. The authors of [52] employed the fuzzy-input fuzzy-output SVM classifiers in conjunction with a large set of features (LF model parameters, Peak Slope, F0, normalized amplitude quotient and spectral gradients) for detecting modal, breathy, and tense voice qualities. The performance of the system was then evaluated in both hard and soft labeling tasks. The hard labeling task achieved 86.1% overall accuracy, but interestingly the most difficult voice quality to classify was modal voice. This observation was consistent with findings in [40].

C. Goals of Current Study

The goal of this study was to analyze the performance of acoustic, GIF, and EGG signals for the task of voice quality classification with multiple feature types. Conventional features were extracted using the COVAREP [53] feature extraction toolbox, which extracts a set of glottal source, spectral envelope modeling, and phase distortion measures. We also analyzed the performance of several classifiers: Gaussian mixture model (GMM), support vector machine (SVM), random forests (RF) and deep-neural network (DNN). The article then focuses on MFCC features as a way to model the spectral envelope of a signal in a compact way, which allowed us to extract them from acoustic, GIF, and EGG signals. Also, two other reasons supported the decision to focus on MFCCs. First, the mel-filter bank has higher resolution at lower frequencies, which is where most of the information is contained. Second, first- and second-order dynamic MFCCs were investigated for voice modality classification since they capture the temporal evolution of the spectral envelope.

II. Methods

A. Speaker Database

The experiments presented in this article were performed on a database consisting of sound booth recordings from 28 adult participants (21 female, 7 male) with normal voices. The average (mean±SD) age for the female participants was 35±12 years and 26±12 years for the male participants. Normal vocal status was confirmed via laryngeal videostroboscopy. Each speaker was asked to sustain vowels (/a/, /e/, /i/, /o/, /u/), each for 2–5 seconds, in their typical speaking voice at a comfortable pitch and loudness. Subsequently, participants were asked to produce the same vowel set while mimicking three non-modal voice qualities: breathy, strained, and rough. Speakers were enrolled in a larger study on smartphone-based ambulatory voice monitoring, in which microphone and EGG signals were simultaneously recorded in a laboratory protocol. Both signals were time-synchronized and sampled at 20 kHz.

B. Auditory-Perceptual Screening

Mimicking non-modal voice qualities was often a difficult task. Certain vowels were not necessarily perceived to be pure productions of the prompted voice quality dimension, and other vowels were perceived to be a pure production of a different dimension. An expert listener—licensed speech-language pathologist who specializes in the assessment and treatment of voice disorders—rated each sustained vowel using the CAPE-V protocol with no knowledge of the prompted voice quality dimension. This step helped screen out utterances produced with obviously inconsistent or mixed voice quality. The listener also re-rated a random sample of 200 sustained vowels to derive intra-rater reliability statistics. From this sample, utterances determined by the listener to be purely modal (n = 86), rough (n = 14), breathy (n = 31), or strained (n = 32) were selected for intra-rater analysis. Cohen’s κ was used to evaluate intra-rater reliability within each pure voice quality using the re-rated samples. Congruence between prompted labels and a speaker’s “success” at reproducing the prompted voice quality throughout the entire data set (n = 937) was also evaluated using κ. To compare the entire data set with the prompted labels, a perception label was derived for each utterance, which represented the highest CAPE-V score (e.g., if roughness, breathiness, and strain were rated as present, the highest scored dimension served as the perception label). This process effectively created a completely new set of labels which were then taken as ground truth.

Table I presents the confusion table between the prompt and perception labels, and the number of utterances within each voice quality dimension exhibiting a pure auditory-perceptual label (with zero CAPE-V scores for the other dimensions). The labels matched for 71.2% of utterances. The mean (standard deviation) of CAPE-V scores for the re-rated data were 53.8 (8.0) for roughness, 37.9 (16.8) for breathiness, and 26.7 (12.7) for strain. κ for intra-rater reliability was 0.82 for modal, 0.82 for roughness, 0.88 for breathiness, and 0.68 for strain. Speakers were consistent in producing breathy and modal voice qualities (95.3% and 88.9%, respectively), but much less consistent in producing strained and rough voice qualities (47.9% and 42.9%, respectively). Interestingly, when people were asked to mimic strained phonation, they most often produced modal (louder) voicing according to the perception labels. In about an equal percentage of cases, the subjects produced breathy or strained voicing when attempting to mimic roughness. Despite this variability, agreement between prompt and perception labels was good-to-strong (i.e., κ ≥ 0.6). Since intra-rater reliability was higher than this agreement, automatic classification was carried out on the subset of utterances that were labeled as exhibiting “pure” voice quality (i.e., only one voice quality dimension labeled by the listener).

TABLE I.

Confusion matrix between prompt and perception labels for breathy (B), modal (M), strained (S) and rough (R) qualities. Overall agreement was 71.2% (κ = 0.6). Utterances with “pure” voice quality are in bold.

		Perception
		B	M	S	R
Prompt	B	164	8	0	0
	M	21	311	11	7
	S	7	86	93	8
	R	43	5	69	88
	Pure	178	410	108	38

C. Pre-Processing

The GIF signal was derived from the acoustic signal using the iterative adaptive inverse filtering (IAIF) algorithm [54], which estimates the glottal flow derivative in two iterative steps. Figure 1 illustrates several periods of the acoustic, GIF, and EGG signals from a female speaker producing the vowel /a/ in a modal voice quality. Figure 2 illustrates the log-magnitude spectra Y(ω) of these signals. The major portion of information is contained by frequencies up to 4000 Hz while the spectrum flattens afterwards. Thus only only spectral components up to 4 kHz were employed.

Fig. 1.

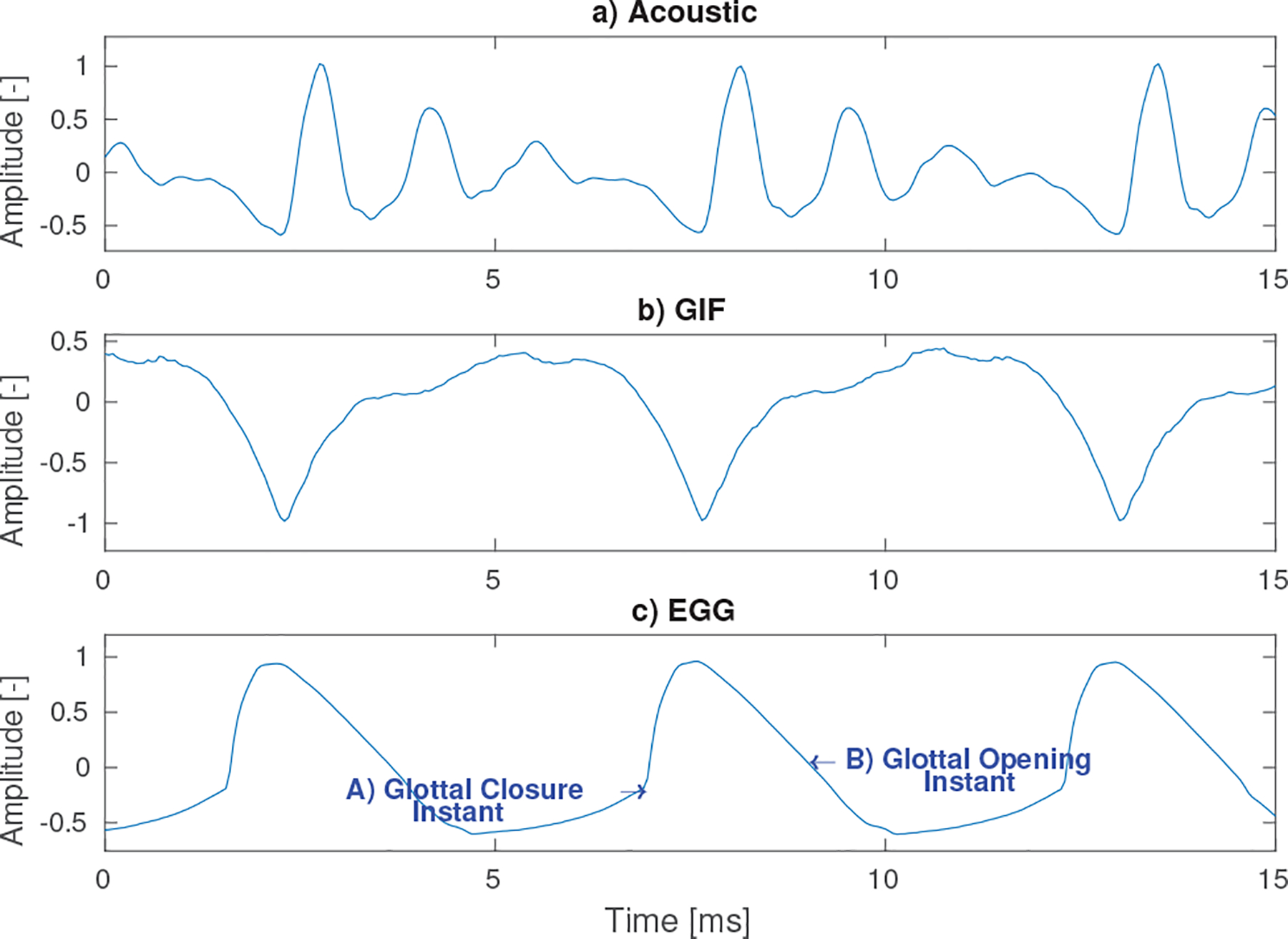
A 15 ms segment of time-synchronized a) acoustic, b) glottal inverse filtered (GIF), and d) electroglottography (EGG) signals of the vowel /a/ in modal voice quality for a female speaker.

Fig. 2.

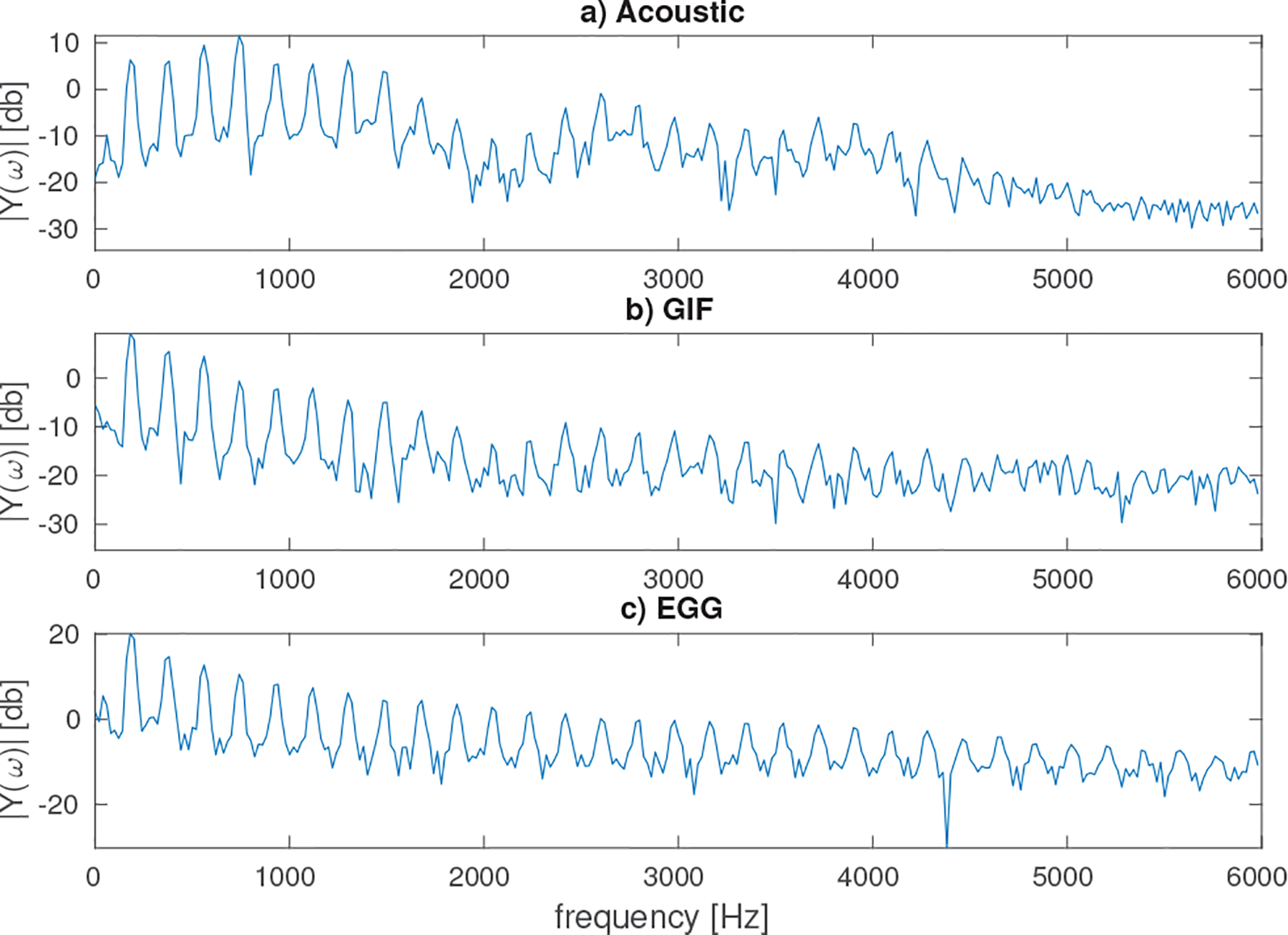
Magnitude spectra of a) acoustic, b) glottal inverse filtered (GIF), and d) electroglottography (EGG) signals.

Each glottal cycle can be described by two instants. The A) Glottal Closure Instant (GCI) marks the moment of time when the vocal folds come into contact. This moment is commonly associated with a sharp rise of the EGG signal, a notable peak in its time derivative. The GCI is followed by a closed phase during which the subglottal pressure builds up. When the pressure reaches a critical threshold, the folds start to open again at a moment called the B) Glottal Opening Instant and stays open until the next GCI. In a healthy participant producing a modal voice quality, this characteristic movement is regular in time, approximately periodic, and displays a low variability in waveform shape.

1). Voice Activity Detection:

Voice activity detection (VAD) is defined as a problem of distinguishing voiced segments from unvoiced segments in a signal. However, the majority of published algorithms are designed for modal speech and do not take into account the effects of non-modal voice characteristics. Our goal was to develop a reliable VAD algorithm that would perform well on both modal and non-modal voice qualities using the framework already developed for classification. The implemented solution was a modified version of the unsupervised VAD proposed in [55].

The principal idea was to initialize Gaussian mixture models (GMMs) using a fraction of highest and lowest energy frames (5% for voiced and unvoiced frames equally), evaluate the data to obtain the labels, and retrain once more. For illustration, the final GMMs were trained on 80.6% and 18.2% of voiced and unvoiced frames, respectively. The system was not designed to achieve an optimal performance point with regard to sensitivity versus specificity. Maximum specificity was preferred even at the expense of lower sensitivity, as the goal was to remove any ambiguity from the classification due to the presence of noise artifacts.

Table II summarizes VAD performance evaluated on a set of randomly selected 150 utterances that were manually annotated. Results differed greatly among voice quality categories. Modal and breathy utterances achieved the best overall results, whereas the strained and rough utterances exhibited lower VAD performance. Specificity did not drop below 0.99 for any voice quality dimension, which was the primary goal. The bootstrapping process could have been repeated several times over but we decided to stop after just a single pass as the VAD performed at a satisfactory level, and no significant improvement was observed by repeating the process.

TABLE II.

Performance of the GMM-based VAD with MFCCs in terms of equal error rate (EER), sensitivity and specificity.

	Breathy	Modal	Strained	Rough
EER [%]	3.3	2.8	4.1	10.3
sensitivity	0.96	0.97	0.95	0.89
specificity	0.99	1.00	1.00	1.00

D. Feature Extraction

COVAREP features were extracted only from the acoustic voice signal using default settings and consisted of 73 distinct features [53]. We included F0 from our analysis and worked with the remaining 72 COVAREP features. The COVAREP features were split into three subsets: 1) glottal source (GlotS) features, 2) spectral envelope modeling features - frequency warped cepstrum (FWCEP), and 3) harmonic model phase distortion (HMPD) measures - phase distortion mean and deviation (PDM, PDD). Their performance was analyzed separately to asses their partial contributions and suitability. The full COVAREP feature list is summarized in [53].

The MFCC feature extraction setup was identical to what is generally used for automatic speech recognition. Fixed-length framing was performed with a 25 ms window and 10 ms overlap. A Hamming window was applied. The number of filters in the mel-filter bank was set to 22, in the frequency range from 50 Hz to 4000 Hz, and 13 MFCCs were computed. The additional first and second order dynamic coefficients were computed over a context of two neighboring frames. The MFCC features were normalized to have zero mean and unit variance on per-speaker basis. The list of feature subsets is summarized in Table III.

TABLE III.

The list of analyzed features

Glottal Source fea.	Spectral env. fea.	HMPD fea.
NAQ, QOQ, H1H2, HRF, PSP, MDQ, PeakSlope R_d, creak	FWCEP, MFCC	PDM, PDD

Table IV summarizes the total number of utterances and extracted frames for each voice quality. An approximate balance across voice qualities was achieved except for less tokens for the rough voice quality.

TABLE IV.

Number of utterances (utt.) and frames for each voice quality.

	Breathy	Modal	Strained	Rough
utt.	178	410	108	38
frames	22 632	65 215	13 792	3 158

E. Machine Learning Classification

Classification was done using GMM, SVM, RF, and DNN classifiers. The GMM parameters Θ_GMM = {φ, μ, Σ} were initialized for each class separately using K-means clustering and then re-estimated using the expectation-maximization algorithm. This approach was more robust and produced more consistent results than random or global initialization. The GMMs employed full covariance matrices Σ. All mixtures were added right at the start, and their number was set to 12 for modal and breathy, 6 for strained, and 4 for rough quality to reflect the different amount of data for each dimension. The utterance-level results were obtained by accumulating the posteriors over the whole utterance and applying a maximum a posteriori criteria (MAP) to yield an utterance-level label.

The SVM classifier was built using the radial basis function kernel as it showed the best overall results in our preliminary analysis. Since SVM natively supports only a binary classification task, six separate SVMs were built for each modality pair. The utterance-level prediction labels were derived from the frame-level labels by the majority rule.

The RF classifier used 48 trees for all data stream. Although the out-of-bag errors for GIF and EGG signals were higher than those for the acoustic signal, their trends converged for about 44 grown trees. For this reason, the RF classifier used a common setup of 48 trees. The utterance level prediction labels were derived from the frame-level labels by a majority rule.

The DNN classifier was built using a feed-forward architecture, one hidden layer with 100 neurons, and sigmoid activation function. The net was initialized with random weights and trained using cross-entropy error function. The utterance level prediction labels were derived from the frame-level labels by the majority rule.

Speaker-independent classification was carried out with a leave-one-speaker-out strategy. One speaker was set aside for testing, the classifier was trained on data from remaining speakers and its performance was evaluated for the test speaker. The process was then repeated for all speakers selected for this study. The reported results were an aggregation from all individual classification runs. The results were evaluated in terms of classification accuracy [%] against the obtained perception labels.

All classification systems were built in the MATLAB environment. The SVM, RF and DNN systems were based on native MATLAB implementations and the GMM system was constructed using our own implementation.

III. Results

The initial analysis assessed the performance of the full COVAREP feature vector, its subsets, and MFCCs using all classifiers. The GIF and EGG signals were excluded from this analysis as the GlotS features, for example, were not primarily defined for these signals. The strong and weak points of each feature sets are summarized. The subsequent analysis focused on MFCC features.

A. Performance of COVAREP features

The results using full COVAREP feature set and its subsets for the acoustic signal are summarized in Tab. V. The overall best results of 79.97% were achieved by the SVM, followed closely by 79.79% using the RF classifier, which was well within the margin of error. The DNN achieved 76.98% and GMM only 68.12%. Let us now discount the GMM from the subsequent discussion as it achieved significantly worse results. The differences between particular classifiers were within 3 percentage points (pp), which showed that the used machine learning scheme was not nearly as significant. Also, the RF showed the best average results across the subsets, followed by the DNN and SVM. This observation was slightly surprising if we consider that DNN are notoriously data hungry and our database contained a limited amount of data. It shows their potential for the future when more data are available.

The analysis of confusion matrices for full feature set revealed that modal and breathy modes were the easiest to classify, as the average accuracy reached 89.8% and 79% respectively. The accuracy for strained and rough modes reached 50.9% and 39.5%. The breathy voice was most often confused with the modal one, for 19.7% of utterances, whereas the modal voice was equally often confused with breathy and strained, for 4.8% of utterances. The strained and rough modes were mostly confused with modal, in 43.8% and 41.2% of cases respectively. It might be argued that this trend reflected an unbalanced data distribution and biased the classifiers towards modal class. This trend was most notable for GMM and least prominent for DNN classifier.

The comparison of standalone feature subsets revealed mixed results, but the overall trend was as follows. The results for the full feature set were better than for any other feature subset. The FWCEP features achieved the average results across classifiers of 72.8%, followed by 73.6% for glottal source and 76.4% for HMPD measures. A closer look at the confusion matrices revealed that HMPD measure outperformed the other two feature subsets due to a comparatively better performance for modal, strained and breathy modes. The FWCEP features were accurate for classifying modal and breathy modes but underperformed for strained mode. The results for rough mode were at the level of random guessing. The glottal source features performed well also for rough mode. It might be argued that their performance would have been better, in comparison to other feature subsets, had our database been more balanced. Figure 3 illustrates the percentage of correctly classified utterances for each voice mode and all feature sets.

Fig. 3.

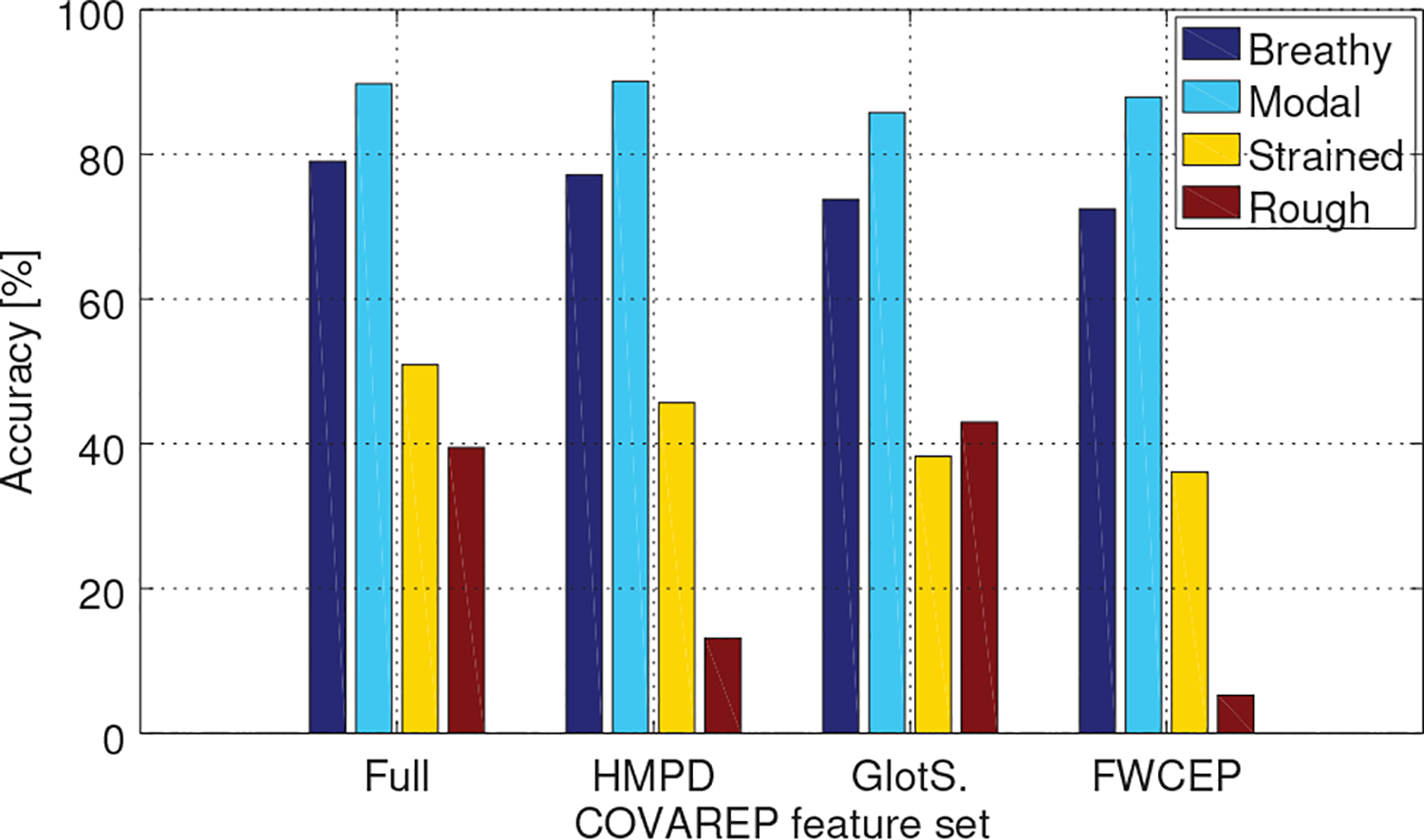
Average accuracy for breathy, modal, strained and rough modes for DNN, RF and SVM classifiers using the full COVAREP feature set.

B. Performance of MFCC features

The following section summarizes results for the RF classifier as it achieved the best overall performance in our previous analysis with COVAREP features and also because our prior analysis for MFCCs proved its superior performance over other classifiers. For comparison, the accuracy with DNN was lower by about 2 pp on average for all signals. The overall best result of 74.52% was achieved for the acoustic signal using static+Δ feature vector. However, this improvement was still not sufficient to outperform the GlotS or HMPD features if we compare the results for RF classifier. The results for GIF stream were worse by about 5 pp, whereas the results for EGG were worse by about 18 pp.

The addition of first-order dynamic MFCC features improved the performance for all signals. The accuracy reached 74.52%, 69.17%, and 56% for acoustic, GIF and, EGG signals, respectively. The improvement was statistically significant for GIF only, as the improvement for acoustic and EGG signals was within the margin of error. The addition of ΔΔ features had only marginal effect for GIF and EGG signal classification and a negative improvement for acoustic signal classification.

The feature level combination of data streams has improved the recognition results. This trend was most prominent for streams which included the acoustic signal. For example, the acoustic+GIF stream performed at 75.2%, which meant about 1.5 pp improvement over a standalone acoustic stream. The addition of ΔΔ features increased the accuracy to 75.61%, which was even marginally better than results for GlotS features. The main advantage was that combining acoustic and GIF streams was just a matter of additional computational cost. On the other hand, adding EGG signal required collecting the additional signal, and no improvements were observed when it was combined with other signals. The misclassification rates for dynamic and combined MFCCs displayed the same trends as the ones reported for full COVAREP set. In short, breathy was mostly confused with modal, modal with breathy and strained, strained and rough with modal. Finally, it can be concluded that combining the feature streams brought larger improvement than extending the static MFCC feature vector with dynamic or ΔΔ MFCC coefficients.

The last experiment examined the possibility of extending the standard COVAREP vector with static MFCCs computed for ACO+GIF signals. We did not include the dynamic coefficients as the improvement over just the static ones was marginal but its addition inflated the vector size considerably. The same was true about the combination of all data streams and was most apparent for the ACO+GIF+EGG vector with ΔΔ coefficients. The performance was again tested with all machine learning schemes. The accuracy reached 78.38%, 79.53%, 56.26%, and 76.7% for SVM, RF, GMM, and DNN respectively. These values were marginally worse, but within the margin of error, than the results for just the COVAREP features. Thus, we could not confirm the contribution of combining the original COVAREP feature vector with the MFCCs computed from acoustic and GIF signals.

IV. Discussion

Misclassification rate trends between particular modes provided an insight into the distribution of modes in the MFCC space. The largest portion of misclassified breathy frames (across all signal types) were in the modal category, which indicates that breathy voicing was much closer to modal than strained or rough. Strained utterances were also most often confused with modal voicing. The described behavior may likely be explained by a common conceptual model of voice quality, where there is a continuum from lack of glottal closure (i.e., breathy) to tight glottal closure at the extremes and modal voicing in the middle [14].

A. Interpretation of MFCC hyper-space and its correlation with CAPE-V scores

The overall performance of static MFCCs was worse than for the COVAREP feature set. This drop was mostly caused by worse recognition results for strained quality. Results for roughness were at the level of random guessing, but the amount of data for rough quality was also significantly lower than for other qualities which might have played a role in its poor performance. The addition of first order dynamics improved performance by about 1.5 pp in general. The combination of acoustic and GIF streams has proved to yield the best overall results, of 75.2% for static features only and of 75.61% for static + ΔΔ features. These results were even slightly better than results for the glottal source features, but still worse than HMPD features. The analysis of MFCC feature space hinted that vowels uttered in different modalities form separate clusters. This hypothesis was later put to test by computing the Bhattacharyya distance between selected voice mode pairs.

Results presented in the previous section demonstrated that breathy, modal, and strained qualities occupy distinct places in the MFCC hyper-space. This was, however, not the case of rough quality as it heavily overlapped with strained and modal feature spaces. This fact can also be easily shown by estimating an average class probability for a frame belonging the correct class. The average output probability reached 0.63, 0.72, 0.61 and 0.16 for breathy, modal, breathy, and rough qualities, respectively. In another words, rough frames had a significantly lower probability of being classified correctly than all other voice qualities.

Our hypothesis was that the distribution of frames in the MFCC space was not random but rather content and voice mode specific. To prove this, the frames for each voice mode were clustered together, split randomly into a train and test set with 9:1 ratio, and the Bhattacharyya distance D_B(p, q) for all possible voice mode pairs was computed under the assumption of their normal distribution. In addition, each vowel was analyzed separately. The process was repeated 10 times, and the values reported as the cross-mode distance were the minimum while the same-mode distance values were the maximum from all runs. This approach let us prove that, even in the worst case scenario, the MFCCs created mode- and content-specific clusters. Rough voice quality is not presented since results from previous analyses were not statistically significant.

The Bhattacharyya distances are summarized in Table VII. The distance values for vowel /a/ showed that modal quality creates the most tight cluster, followed by strained and breathy. Several conclusions can be taken from the cross-mode distance values. First, breathy quality was more similar to modal than to strained; in fact, breathy and strained modes formed the most distinct distributions. Second, the distribution of modal quality was only slightly closer to strained than to breathy quality. The distances for vowel /e/ followed the trends described for vowel /a/. On the other hand, M-S distance for vowel /i/ higher than B-M distance. This would indicate that modal /i/ was more similar to breathy /i/ than to strained /i/. This was also the case for vowel /o/ and /u/.

TABLE VII.

Bhattacharyya distance D_B(p, q) for each pair of breathy (B), modal (M), and strained (S) voice modes and each vowel.

	B-B	M-M	S-S	B-M	B-S	M-S
/a/	0.15	0.006	0.05	1.95	3.75	1.91
/e/	0.14	0.006	0.04	2.09	4.08	1.90
/i/	0.15	0.006	0.03	1.76	3.35	2.11
/o/	0.15	0.006	0.04	1.77	3.24	2.11
/u/	0.18	0.006	0.11	2.86	6.99	5.31

There were multiple general conclusions which are shared for all vowels. First, the same-mode distance was always lower than cross-mode distance. In fact, the it was always lower by an order of magnitude at least. Second, M-M distance was the lowest observed distance from all pairs, by far. Third, the vowels behaved in two distinct ways when in breathy, modal, and strained mode. The first group consists of /a/ and /e/ for which the modal quality appeared to be more similar to strained than to breathy. The second group consists of /i/, /o/, /u/, where the trend was the other way around.

Based on this observation, we concluded that the constructed system similarly to a speech recognizer that differentiated between modal, breathy, and strained versions of vowels. The constructed system pooled all vowels into a single model and created what is referred to as a universal background model in speech recognition. In our case, we had successfully trained breathy, modal, and strained voice quality vowel models.

The obtained classification provided an insight into the distribution of modes in the feature space, but did not explain the correlation between hard automatic and soft perception scores. Our initial assumption was that the utterances with higher CAPE-V scores would cluster more tightly around the mixture centers, and thus have higher probability, but the analysis found no correlation between classification soft scores and CAPE-V scores. Pearson’s correlation coefficient was zero for strained and rough scores and 0.31 for breathy. This observation would indicate that utterances perceived as more breathy, rough, or strained did not cluster more tightly around mixture centers. More work is warranted to tie MFCC features to CAPE-V ratings.

B. Prototype Waveforms

Although the results demonstrated that MFCCs can be used to accurately classify different voice quality dimensions, the analysis thus far has not provided insights into which aspects of the waveform were considered important for the classifier; i.e., what do prototype waveforms for modal, breathy, strained, and rough dimensions look like? To answer the question, class conditional probabilities of each MFCC vector were tied to the corresponding frame and the prototype waveforms were estimated using the weighted average computed as:

$$O_{\mathit{\text{proto}}(j)}=\frac{1}{N}\sum _{i=1}^N\frac{p\left(O_i|j\right)}{\sum _{j}p\left(O_i|j\right)}{O}_i,$$ (1)

where Oproto(j) was the prototype observation vector for class j and p(O_i|j) was the probability of vector O_i being generated by class j. In order to avoid using frames from utterances with different content or from different speakers, prototype waveforms were estimated from a single utterance which achieved the highest average class probability for given voice quality. The primary problem was a random time delay between frames since the feature extraction used a fixed window-shift without any pitch synchronization. This problem disallowed a simple averaging as each frame was effectively time-shifted in respect to other frames. The solution employed in this study made use of auto-correlation function to detect the time-shifts between the current frame and the reference frame. The reference frame was selected at random.

The second problem was the deviation in F0 within an utterance. The within utterance difference reached 2.23%, 1.13%, 2.02% and 17.5% for breathy, modal, strained and rough quality respectively. These values were computed as a relative difference in percent with respect to the mean value. The choice to report relative values instead of absolute values (in Hz) was to penalize participants with low F0, for which a small absolute deviation causes a significant error in the number of samples during F0 normalization. The differences were minimal, which leads to conclusion that participants were very consistent in producing vowels with a stable F0. The only notable difference was the rough quality. This observation was not surprising as rough quality is known to lack a periodic structure, which makes application of any F0 detection algorithm challenging. However, in order to produce as truthful waveforms as possible, the subharmonic-to-harmonic ratio [56] pitch detection algorithm was used to estimate F0 in each frame, and that frame was then either stretched or compressed with respect to the reference frame.

Figures 4, 5, and 6 illustrate the prototype waveforms for the acoustic, GIF, and EGG signals. The actual averaging was done by selecting a reference frame at random and then stretching or compressing the time axis to accommodate for the F0 difference for all consecutive frames. The phase synchronization was performed afterward as the auto-correlation function gives more accurate results in cases that the signals have the same F0. The frames were also averaged in relation to their number so that the resulting waveforms could be compared in terms of their amplitudes among each other.

Fig. 4.

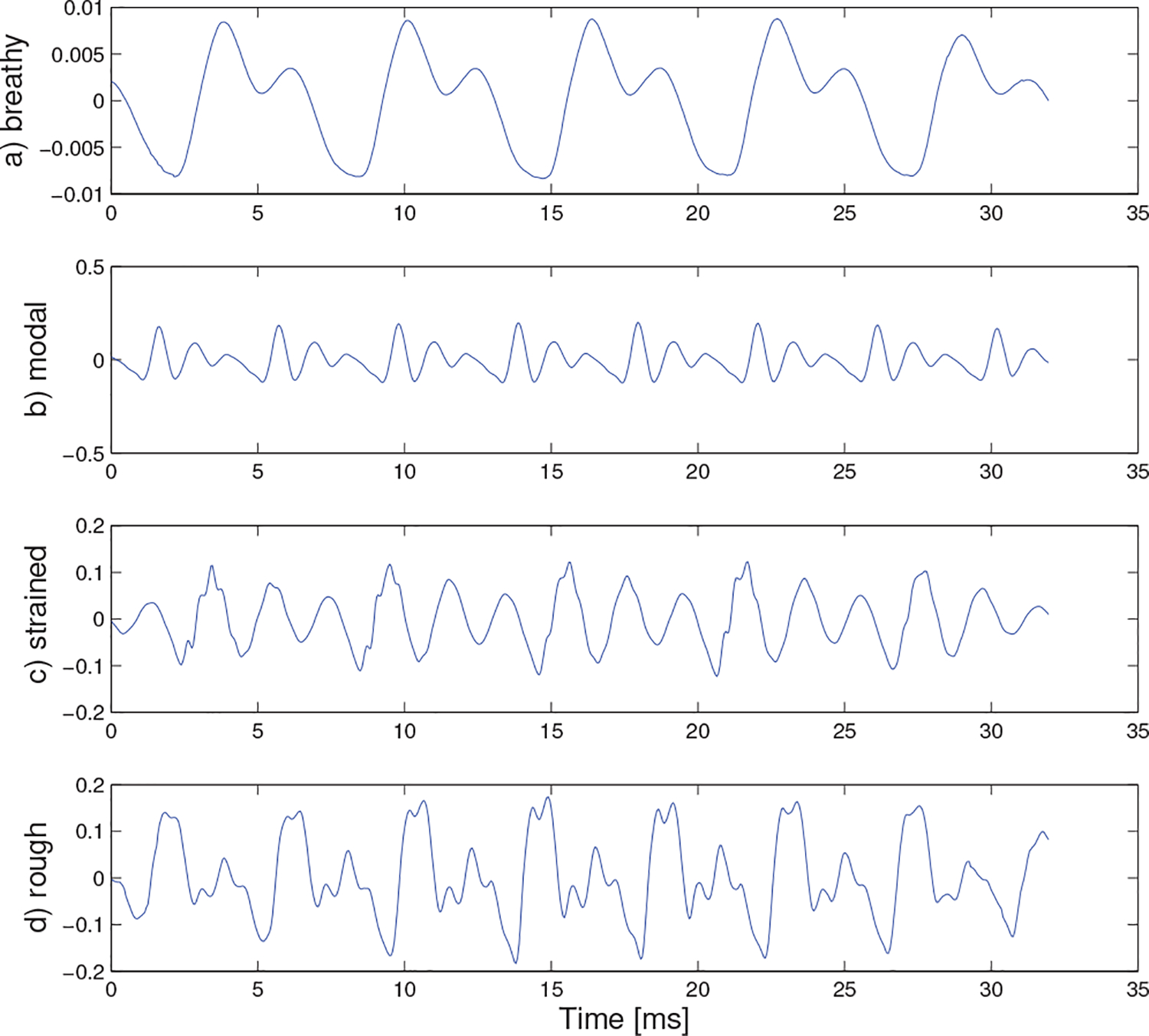
Prototype acoustic signal for a) breathy, b) modal, c) strained, and d) rough quality.

Fig. 5.

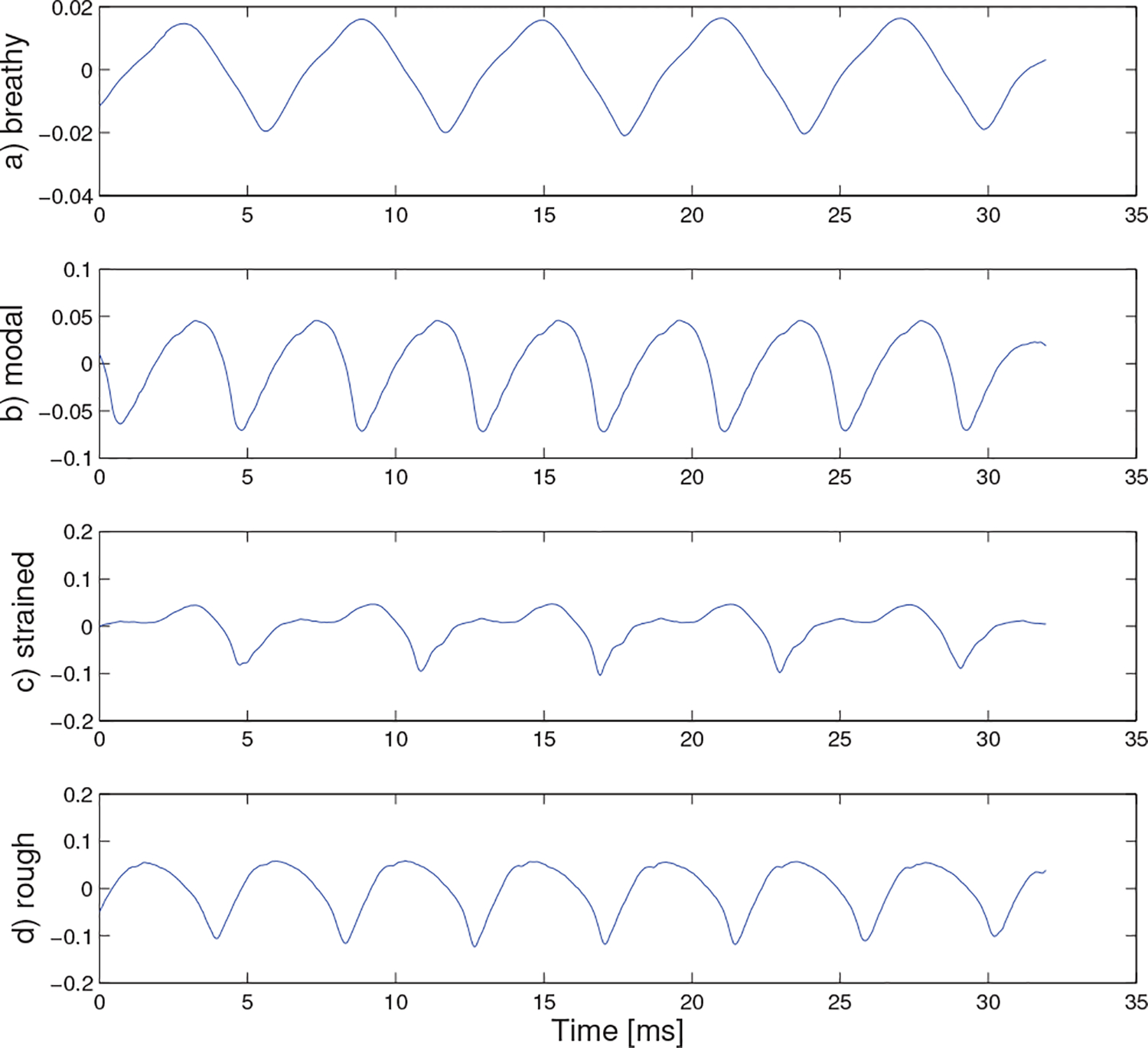
Prototype glottal inverse filtered signal for a) breathy, b) modal, c) strained, and d) rough quality.

Fig. 6.

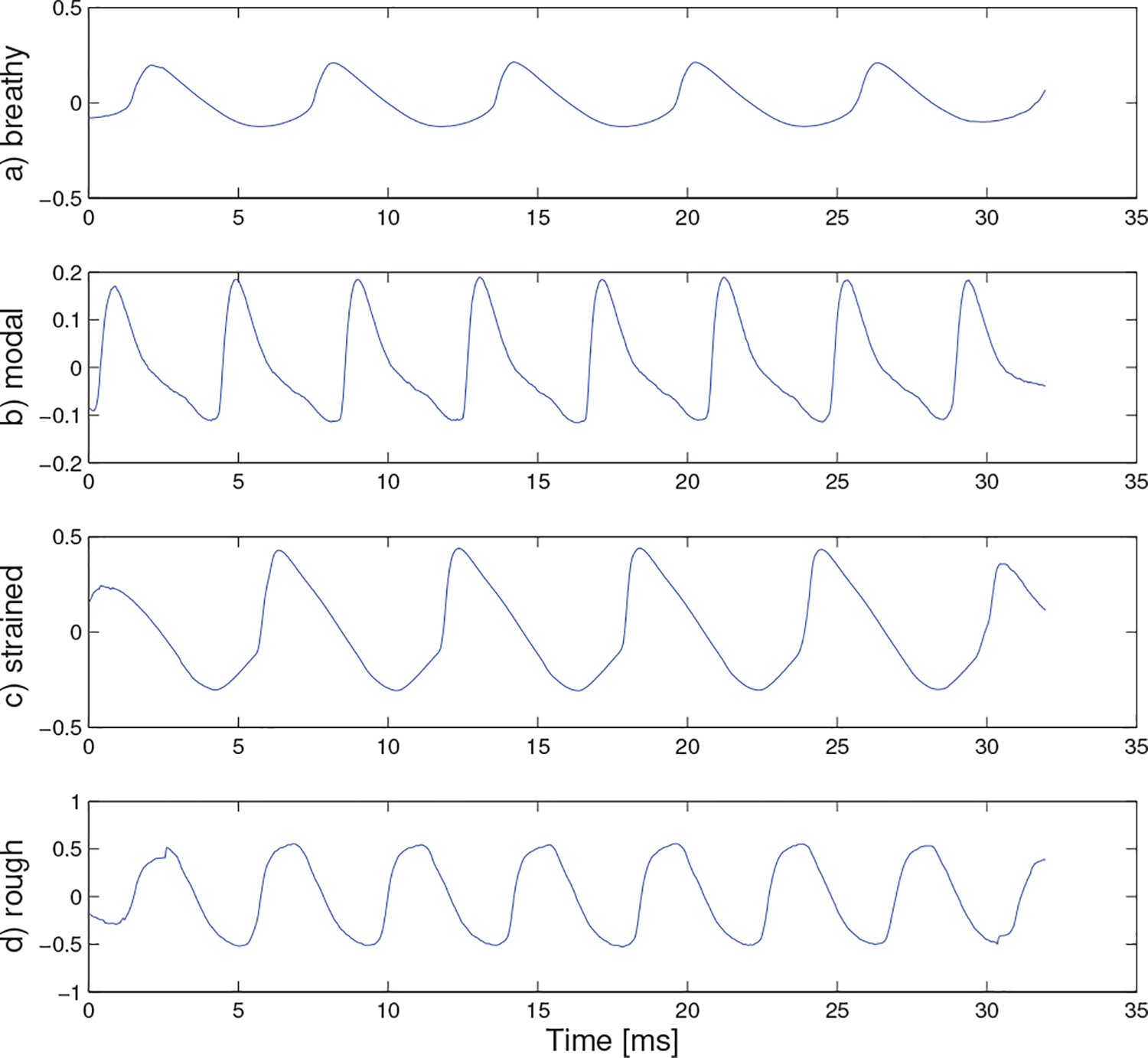
Prototype electroglottograph speech signal for a) breathy, b) modal, c) strained, and d) rough quality.

The prototype waveforms can provide an intuitive method for interpreting why certain signals were classified into specific classes. For example, breathy voicing is often defined by both turbulent airflow and the absence of a discontinuity at the moment of glottal closure. However, the reconstructed prototype waveforms from the acoustic and GIF signal appear to capture the absence of a discontinuity at the moment of glottal closure, but it seems as though the model did not use any information from high-frequency noise content. In other words, the classifier relied primarily on pulse characteristics that did not involve noise/turbulence. The prototype signal for strained voice quality shows increased high-frequency harmonic content in the acoustics, increased glottal waveform skewing and increased maximum flow declination rate in the GIF, and the highest peak (i.e., highest degree of tissue contact) in the EGG (all expected effects of strained voice quality). The rough prototype waveform is difficult to interpret since high probability utterances were scattered throughout the MFCC hyper-space, meaning that the prototype waveform could look dramatically different despite minimal decreases in the cumulative probability metric.

C. Prototype MFCC vectors

The MFCCs are high-level features that were designed to emulate the human auditory system. Despite their great success in speech recognition, speaker identification or music retrieval, a clear interpretation exits only for the first two coefficients. The zeroth coefficient corresponds to the energy across all frequencies and the first is the ratio between the low- and high-frequency components. These two characteristics were evident by looking at averaged MFCC vectors extracted from the prototype waveforms illustrated in Figure 7. The breathy quality displayed the lowest MFCC[0], which indicated that its waveforms had the lowest overall energy. Strained quality displayed the lowest MFCC[1], which corresponded with hypothesis of increased high-frequency energy described in Section I-A.

Fig. 7.

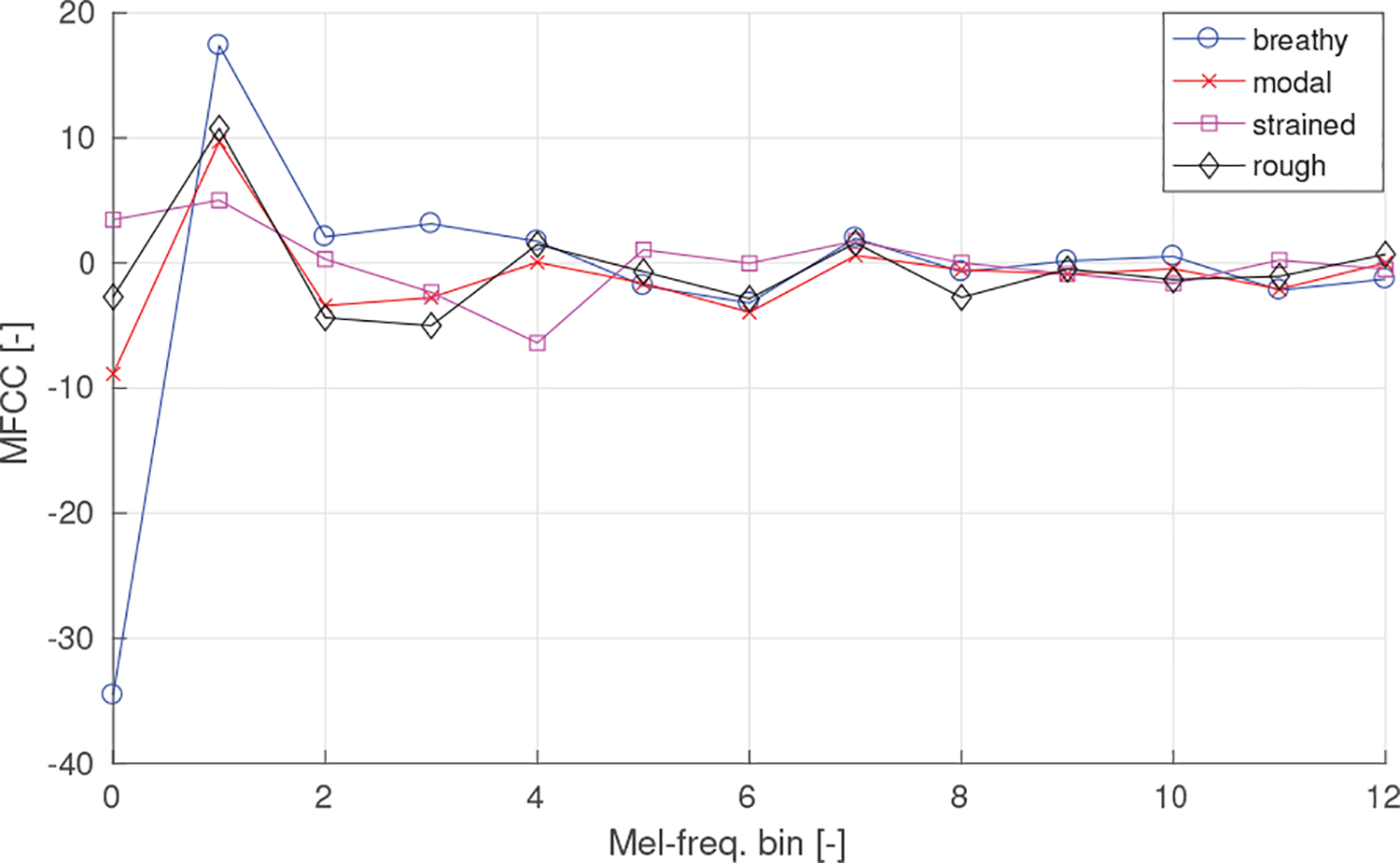
Prototype MFCC vectors for prototype waveforms for breathy, modal, strained, and rough quality.

D. Study Limitations

There are several limitations to the methods presented in this article. First, is the uneven distribution of data in terms of voice qualities. The participants were instructed how to utter the vowels in all qualities, but our subsequent auditory-perceptual screening revealed that people sometimes did not produce the desired or pure quality, which resulted in an uneven spread of data. This problem naturally complicated the process of training the classifiers and lowered the statistical significance for rough quality in particular. Second, the auditory-perceptual screening was performed by a single expert listener. The listener achieved good-to-high intra-rater reliability, but this fact is to be expected, as multiple studies showed higher intra-rater than inter-rater reliability scores. Third, the analysis does not provide an interpretation of the results achieved with MFCCs as only first two coefficients were successfully tied to known voice mode characteristics. Finally, the study is done using data from participants mimicking prompted voice qualities. Even though the extracted prototype waveforms correlated well with known voice characteristics, further research is needed to successfully transfer the conclusions reached in the article to objective voice quality assessment of pathological voice.

V. Conclusion

This article analyzed the suitability of different features sets combined in the COVAREP features set for the purpose of voice quality classification. The article later focused on the analysis of MFCCs using the acoustic voice signal, acoustic-based GIF signal, and EGG waveform and compared them to COVAREP features. All three signals were derived from vocally healthy speakers who produced breathy, modal, strained, and rough voice. Utterances were perceptually evaluated using the CAPE-V protocol, and dichotomous labels were acquired for subsequent classification. The experimental framework used the setup commonly used for speech recognition. The experiments proved that COVAREP features can successfully distinguish between breathy, modal, and strained voice quality dimensions. The best overall results were achieved for the full COVAREP set. Out of three analyzed COVAREP subset, the HMPD measures performed the best, followed by the glottal source features and then by the FWCEP features. Future work calls for voice quality analysis of connected speech data and the fusion of the MFCC feature space with other voice quality measures in the time, spectral, and cepstral domains.

TABLE V.

Classification accuracy [%] for full COVAREP feature set and its subsets for acoustic voice quality classification.

	SVM	RF	GMM	DNN
Full	79.97±1.4	79.79±1.4	68.12±1.7	76.98±1.5
GlotS	70.98± 1.6	75.2±1.5	66.49±1.7	74.76±1.6
FWCEP	71.25± 1.6	73.71±1.5	64.44±1.8	71.6±1.6
HMPD	74.11± 1.6	78.47±1.5	49.86±1.8	76.7±1.5

TABLE VI.

Classification accuracy [%] with MFCCs for acoustic (ACO), glottal inverse-filtered (GIF) and electroglottogram (EGG) signals with RF classifier.

	Static	Static+Δ	Static+ΔΔ
Acoustic	73.4±1.6	74.52±1.6	74.15±1.6
GIF	66.49±1.7	69.17±1.6	69.71±1.6
EGG	55.85±1.8	56.25±1.8	56.79±1.7
ACO+GIF	75.2±1.5	75.06±1.5	75.61±1.5
ACO+EGG	72.01±1.6	71.93±1.7	72.88±1.6
GIF+EGG	68.52±1.7	69.34±1.7	69.34±1.7
ACO+GIF+EGG	75.34±1.6	73.56±1.6	73.29±1.6