Static and Time-dependent Mechanical Response of Organic Matrix of Bone

Abstract

Bone derives its mechanical strength from the complex arrangement of collagen fibrils (type-I primarily) reinforced with hydroxy-apatite (HAp) mineral crystals in extra- and intra-fibrillar compartments. This study demonstrates a novel approach to obtain organic matrix of bone through its demineralization as well as mechanically characterize it at small length scales using static and dynamic indentation techniques. Sample surface preparation protocol used in the present work maintained the surface integrity of demineralized bone samples which resulted sample surface of roughness (RMS) magnitude of approximately 14 nm (averaged over 1×1 µm² area duly verified by atomic force microscope (AFM)). Elemental composition analysis via energy dispersive X-ray spectroscopy (EDX) (for probed depth upto 2 µm) confirmed the complete removal of HAp mineral from bone samples during their demineralization using EDTA leaving collagen molecule assemblies unaffected as represented by Second Harmonic Generation (SHG) imaging. The modulus magnitudes of organic matrix obtained using from quasistatic as well as dynamic indentations (at constant frequency of 30 Hz) as ∼2.6 GPa and 4.5 GPa respectively, demonstrated the influence of loading rate on the estimated mechanical properties. For indentation depth to surface roughness ratio greater than ∼5:1, interestingly, measured material properties of organic matrix were found to depend on increasing magnitude of indentation depth of up to ∼500 nm value which probed from few collagen fibrils to next level of hierarchy i.e. collagen fibers. These findings are very useful to accurately determine the elastic and visco-elastic response of organic matrices of mineralized tissues for various applications including tissue engineering, bio-mimetics, etc.

1. Introduction

Mineralized tissues are composed of organic matrix of collagen protein which is reinforced by hydroxy-apatite (HAp) mineral. The organic matrix carries HAp mineral in two distinguished spaces: a) intra-fibrillar i.e. within the collagen fibrils, preferentially in the gap zone between collagen molecules and, b) extra-fibrillar i.e. on the surface of the collagen fibril [1]. The mineral is associated with collagen either directly or through non-collagenous proteins like proteoglycans (PG). The partitioning of HAp mineral i.e. the relative proportion of mineral associated with each compartment is uncertain, and it varies with the total level of mineral present in the tissues. Sub-micron size collagen fibrils display a characteristic 67 nm banded structure of gap and overlap zones [2–11]. The HAp crystals are believed to nucleate initially in the gap zone between the molecules, followed by secondary mineralization of the interstitial positions between the fibrils [12]. In bone, ∼75% of the mineral is extra-fibrillar [13, 14].

For microscopic mechanical properties [15–17] of the bone, mineral content is a critical parameter that vary with disease (e.g. Osteoporosis, changes in subchondral trabecular bone with osteoarthritis), prosthetic implantation, weightlessness, ethnicity, age [18], and diabetes [19]. Macroscopic tensile experiments performed on the cortical bone have shown that the increase in calcium content results in an approximately linear increase in stiffness as well as yield stress, a linear decrease in post-yield stress, work, ultimate strain and strain-to-failure, and has a minimal effect on ultimate stress [15]. The origin of (in)elasticity dependence on mineral content is intuitive from the consideration of the standard rule of mixtures^′ approximation for a composite material [20]. The mineral present in the calcified tissues represents elasticity individually [21, 22] while the combination mineral and organic matrix is expected to contribute towards visco-elastic response of the tissues. The nanoscale mechanisms by which mineral content control visco-elastic as well as plastic behavior of bone, are expected to be more complex and are not completely known to date.

The mechanical behavior of bone tissue has also been reported to depend on the rate of its deformation [23–26]. The deformation or strain rate dependence of mechanical behavior of tissue has been known to be influenced by its hydration state [23, 27] which affects the collagen-HAp interaction at small length scales [28–30]. Bone volume has almost 80% contribution of mineralized collagen fibrils and rest as water [31, 32]. The amount of collagen in bone remains almost constant while water is replaced by the mineral content during the mineralization process [31]. Therefore, the understanding of mechanical response of the organic matrix obtained by removing mineral content as well as exploring its time dependent mechanical properties can help to explain the mechanical behavior of bone tissues which can be extended to understand the structure-property relationship of these hierarchical structures, influence of mineralization on mechanical properties of bone for tissue engineering applications and designing as well as developing better bio-materials for future. [33–38].

Nowadays, nanoindentation technique is increasingly used to assess the mechanical properties of the hard and soft tissues at small length scales [39–41]. However, the material property data obtained from nanoindentation studies has been often characterized by considerable variability, with maximum standard deviations ranging from 40% to 60% for measurements made within a single specimen [42, 43]. The large magnitudes of standard deviations reflect the natural material inhomogeneity as well as the contribution of experimental artifacts to the observed variabilities. Most nanomechanical property studies of bone did not report the contribution of surface roughness on calculated mechanical properties and have used deep indentations [44–46]. Shallow indentations correspond to small sampled volumes, but the indentations must be adequately deep to avoid the substantial influence of surface roughness on the measured material properties. The surface roughness effects are of particular concern with a surface-sensitive technique such as nanoindentation. For high finish surfaces (with RMS roughness values of few angstroms), modulus, hardness measurements have been reported to be almost independent of indentor tip-radius [47], and surface roughness have been found to influence measurements upto indentation depths not more than 2–3 times of surface roughness RMS values in nanoindentation experiments [21, 47, 48]. Therefore, the minimization of sample surface roughness is crucial for making measurements of the material properties of organic matrix through nanoindentation while probing small volumes formed by few collagen fibrils to larger volumes formed by much number of collagen fibrils assembling to form collagen fibers. Hence, an appropriate sample surface preparation technique for producing smooth surface of bone samples as well as careful selection of indentation depth are prerequisites for making accurate nanomechanical property measurements through nanoindentation technique. Atomic force microscope (AFM) allows imaging of sample surface in near-physiological conditions with nanometer resolution [49–53]. For partially demineralized bone tissues, AFM has revealed collagen fibrils of varying topographical profile [5, 8–11, 53] and best suites for relative measurements and thus usually employed for estimation of surface roughness magnitudes because of compliant cantilever and ultra sharp tips. In general, instrumented nanoindentation is preferred over AFM for quantitative material property measurements. Additionally, dynamic indentation technique has been reported for estimating time dependent mechanical response of soft as well as hard tissues [54–60].

Demineralization (or decalcification) of hard tissues is done via dissolving the calcium present in the bone using strong acids, weak acids or chelating agents. Strong acids such as hydrochloric or nitric acid at concentrations up to 10% are the most rapid in action but may cause a loss of nuclear staining and can macerate tissues. Weak acids such as formic acid can be used as a simple 10 % aqueous solution or combined with formalin or with a buffer. Although these are slower than the strong acid agents but are much gentler in action and less likely to interfere with nuclear staining [61, 62]. Picric acid, as a component of some fixatives has weak decalcifying properties. Chelating agents such as ethylenediaminetetracetic acid (EDTA), work by capturing the calcium ions from the surface of the apatite crystal, slowly reducing its size. Because the process is very slow but very gentle, this reagent is more appropriate for research applications where very high quality morphology is required or particular molecular elements are to be preserved for further study [63]. The rate at which EDTA demineralizes, is pH dependent (kept as 7.0) which works more rapidly at pH 10 but some tissue elements can be damged at alkaline pH.

Hence, in order to understand physical behavior of complex material like bone which is primarily dictated by interaction of collagen protein with HAp crystals, it would be very useful to know the mechanical response organic matrix of bone which is obtained by gently dissolving its mineral content. As mentioned in previous para, organic matrix obtained through EDTA treatment of bone is expected to result its undamaged native structure, thus making it best candidate for studying organic content’s contribution on mechanical behavior of bone. Limited by sample surface roughness, using ultra sharp-tip in indentation experiments with increasing indentation depths may facilitate probing across hierarchy levels which would start with very small probed volumes at low indentation depths while reaching comparatively larger volumes for deeper indentations. Thus, probing hierarchy materials at smaller indentation depths reflects mechanical properties of collagen fibrils (which has diameters upto 400 nm) whereas upto 2 µm deep indentations may elucidate their assembled form making collagen fibers (next hierarchy level of bone). With no such report in available literature on the physical behavior of organic matrix of demineralized bone, keeping in mind the importance of mechanical behavior of organic matrix of bone along with the contribution of surface roughness towards precise measurements particularly through instrumented nanoindentation, the following objectives have been fulfilled in our study

• To prepare the surface of demineralized samples with high finish, suitable for making shallow as well as deep indentations and quantify roughness

• To understand the influence of demineralization protocol on collagen assemblies and elastic behavior of organic matrix

• To estimate the static and time dependent properties mechanical properties of organic matrix of bone obtained via its demineralization

We hypothesize that (a) the demineralization protocol dissolves HAp crystals in calcified tissues without significantly affecting the sub-micron structure of organic matrix (b) as the maximum indentation load magnitude increases in nanoindentation method, the values of obtained mechanical properties of organic matrix of bone would depend on indentation depth because of piercing across structural hierarchy levels and would finally converge to a single composite value because of decrease in the influence of surface roughness, and (c) as dynamic indentation involves higher loading rates as compared to quasistatic indentation method, the higher average modulus values of bone obtained from dynamic indentations is not solely result of HAP-collagen interactions but also contributed by strain rate dependent of mechanical properties of organic matrix of bone.

2. Materials and Methods

For making a systematic study, we followed certain steps including sample preparation, composition measurement, quantifying effect of EDTA treatment on collagen packing and nanomechanical characterization which are discussed in the subsections below.

2.1. Bone sample preparation

Bovine bone samples obtained from the metacarpal of approximately nine years have been investigated in the present study. As shown in figure 1, the longitudinal sections of bone were cut parallel to its long axis. The samples were cut down to 3∼4 mm thickness specimens by using a low-speed bone saw (Buehler, Isomet) running at 50−70 RPM with constant deionized (DI) water irrigation. All grinding and polishing of samples was performed with a semi-automatic polisher (Buehler Automet) at 30 RPM with 10 N sample load and were grounded on silicon carbide paper (320, 400 and 600 grit). In order to obtain high surface finish of samples, the samples were polished with full series of diamond slurries (9, 3, 1, 0.25 and 0.05 µm particle size). At each polishing step, the samples were ultrasonically cleaned in deionized (DI) water for 10 minutes to remove debris from the sample surface. Demineralization etches on the sample surface were performed using 0.5 M ethylenediaminetetraacetic acid (EDTA) followed by vigorous rinsing with DI water. We used EDTA at a concentration of approximately 14% as a neutralized solution [62, 64]. The samples were then immediately stored in the solution of normal saline and ethanol (in 50:50 proportion) at room temperature for at least 16 hours of rehydration time [65–67]. AFM (Multimode-8, Bruker) was used in the tapping mode to measure the surface roughness at various locations of the polished undemineralized as well as demineralized bone samples [5].

Figure 1:

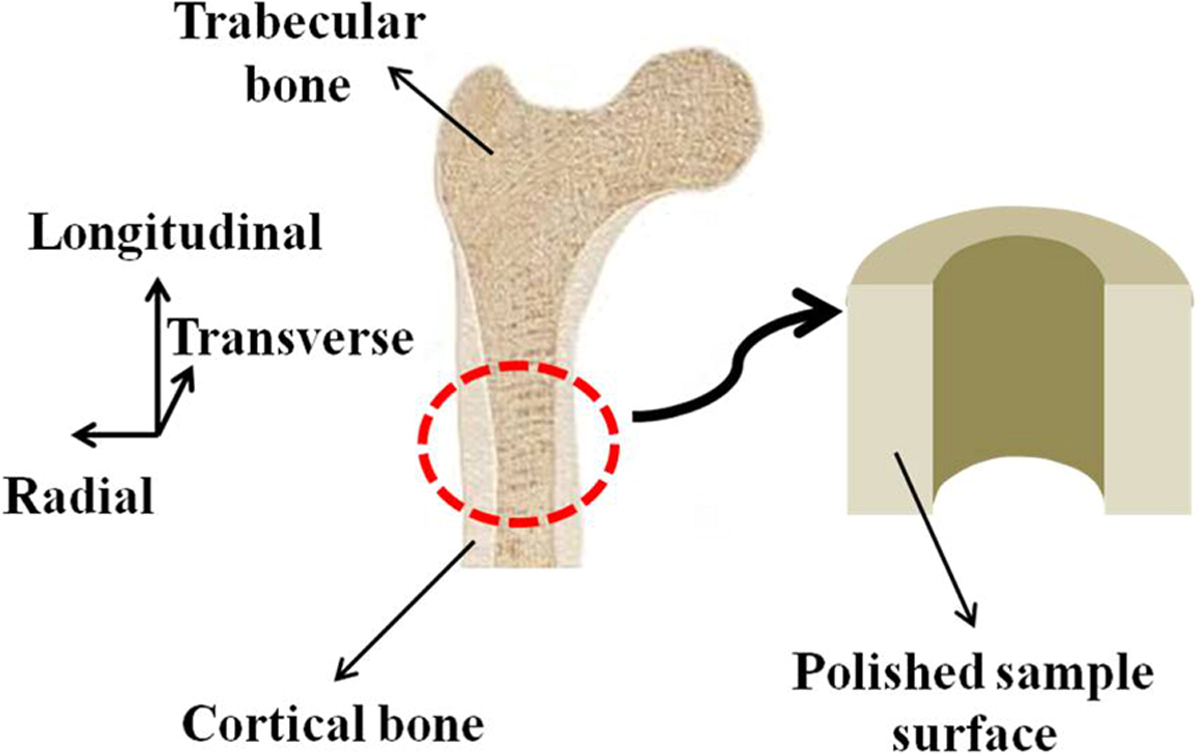
The orientation of the sample surface used for nanomechanical testing.

2.2. Composition measurements

For composition analysis through scanning electron microscope (SEM) (JEOL JSM-6610LV), samples were coated with a few nm thick Pt for imaging samples surface in order to identify different locations for investigation. The working distance was kept as 20 mm, the sample plane was oriented perpendicular to electron beam incidence, and a 15 kV accelerating voltage was employed with a 64 µA operating current. Contrast and brightness levels were adjusted and held so that electron image would appear optimally for the sample using Backscattered Electron (BSE) detection. To determine that whether the mineral phase was removed during demineralization of bone samples or not, energy dispersive X-ray spectroscopy (EDX) was used to assess the presence of mineral elements (up to a few microns depth) on the undemineralized as well as demineralized bone sample surface [68–70].

2.3. Effect of EDTA treatment on collagen assemblies

Leica SP8 multi-photon microscope (upright) was used to see whether EDTA treatment has considerable influence on the assemblies of collagen molecules resulting higher order structures like collagen fibrils or collagen fibers. We employed non-invasive method of Second Harmonic Generation (SHG) imaging using multi-photon microscope which is highly sensitive to packing of collagen fibrils with larger diameter collagen fibrils scattering more forward (transmitted) signal whereas smaller diameter fibrils providing mostly backward (reflected) signal [71]. Qualitatively, increasing in F-B (Forward/Backward) signal ratio reflects assembling of smaller fibrils to make larger fibrils while decreasing F-B ratios representing disassembling of fibrils. No change in F-B ratio value indicates nearly unchanged packing through almost no change in collagen fibril diameter. Because SHG image intensity is proportional to thickness of samples as well as orientation of fibrils with respect of polarization direction of incident light, therefore EDTA treated polished bone samples cannot be considered right candidates to quantify packing of collagen structures because of random orientation of collagen fibrils in bone in addition to possibility of structural damage during very thin sample preparation particularly for SHG imaging. As mice tail tendon have 70−80% dry weight as collagen, and function as dynamic structures, responding to the magnitude, direction, frequency, and duration of physiologic as well as pathologic mechanical loads in the tissues, thus, we used fascicles (of 150 µm diameter approx.) extracted from NSG mice (kept for another study) tail tendon for studying effect of EDTA treatment on collagen assemblies which are sufficiently thin to produce forward scattering as well as are highly oriented in longitudinal direction instead of bone samples for quantification of collagen packing through SHG imaging.

2.4. Nanomechanical characterization

Instrumented Nanoindenter (Hysitron TI-950) system [72] was employed in the indentation mode to estimate the nanomechanical properties of the bone samples. Before indenting into the sample surface, indentor tip shape was calibrated by using the method proposed by Oliver and Pharr [73] through a series of indentations on standard quartz calibration specimen (E ≈ 69.6 GPa). The measured contact stiffness as well as known specimen modulus magnitude were used to establish the relationship between tip contact depth and contact area. The indentations on bone samples were made using a sharp cube corner diamond tip having tip-radius of ∼ 40 nm. The indentation experiments were performed by keeping the bone samples in the air instead of dipping in solution, to keep the sample surface free from small droplets of solution, and testing was completed within one hour to maintain the hydration state of samples [23, 74, 75]. Prior to each indentation experiment, the indentation site on the sample surface was selected randomly using an optical microscope. In a particular indentation experiment, tests at six different locations were performed on the sample surface by following a defined pattern. The data obtained from last five tests were used for calculation of final average material property as well as standard deviation values. The averaging over five tests was done to minimize error incurred in the measurements due to the drift of transducer during the time of approach and making first indent on the sample surface. The smallest possible contact load value was selected to minimize the deformation of sample surface during initial contact.

Two types of indentation experiments i.e. quasistatic and dynamic, have been performed in the present study which are discussed in the following subsections.

2.4.1. Quasistatic indentation

In a quasistatic indentation test, the reduced modulus (E_r) is calculated from the unloading portion of the Load-Displacement (L-D) curve by using the Oliver-Pharr method [73].

The reduced modulus (E_r) is calculated from the slope of unloading segment of the L-D curve by using following equation (relation 1) [76, 77]:

$$E_r=\frac{S\sqrt{\pi }}{2\sqrt{A_c}};$$ (1)

where S is the measured contact stiffness and A_c is the projected contact area obtained from tip shape calibration. Stiffness calculations are usually made from the linear portion of initial unloading slope by using a power-law fit [76].

The contact hardness (H) is calculated as the average pressure under maximum load by using the following equation (relation 2)

$$H=\frac{P_{max}}{A_c}$$ (2)

where P_max is the maximum indentation load, and A_c is the projected contact area.

In the quasistatic indentation, multiple load as well as single load indentation experiments were performed on five demineralized bone samples. In each multiple load indentation experiment, a total of six tests was performed at different locations on the sample surface. Each of these indentation tests comprised of sequential load/unload cycles at increasing maximum loads, with a final maximum load of 1000 µN which was selected to keep indentation depth below 2 µm thus ensuring probing of completely demineralized material duly verified through EDX investigation. The variation of indentation load with time for each single test in a multiple load indentation experiment is shown in figure 2(a). The actual L-D curve for a particular multiple load indentation test is shown in figure 3(a). Each test comprised of twenty load/unload cycles resulting in twenty modulus measurements. Therefore, total one hundred twenty elastic modulus as well as contact hardness measurements were made for a complete multiple load indentation experiment on each sample. Because of drift of transducer as in previous section, only last hundred out of total one hundred twenty measurements were used for the average magnitude calculation of the modulus as well as contact hardness values for each sample.

Figure 2:

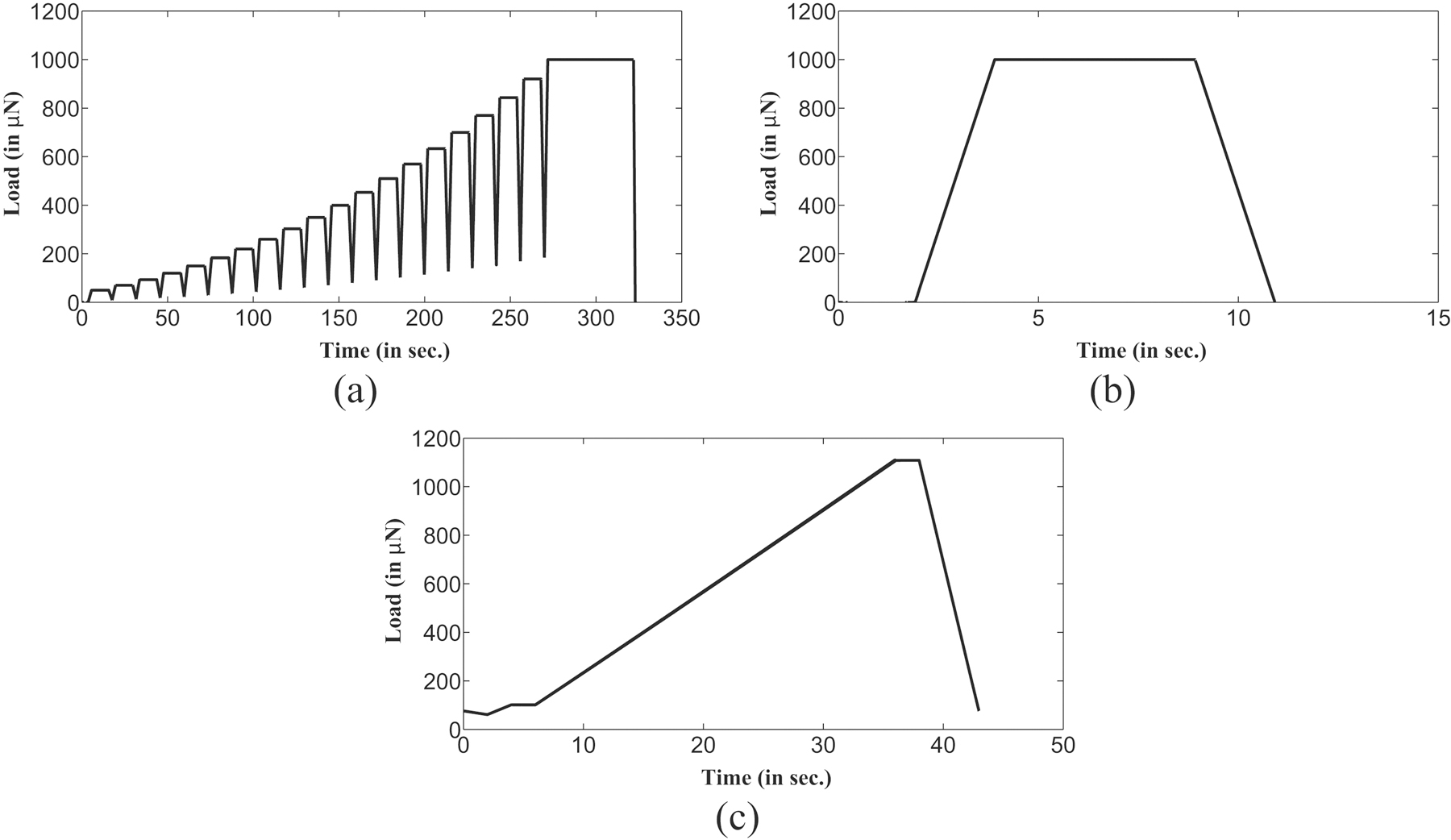
Time dependence of load for different indentation experiments (a) Quasistatic multiple load indentation experiment (b) Quasistatic single load indentation experiment (c) Dynamic indentation experiment with constant frequency of 30 Hz.

Figure 3:

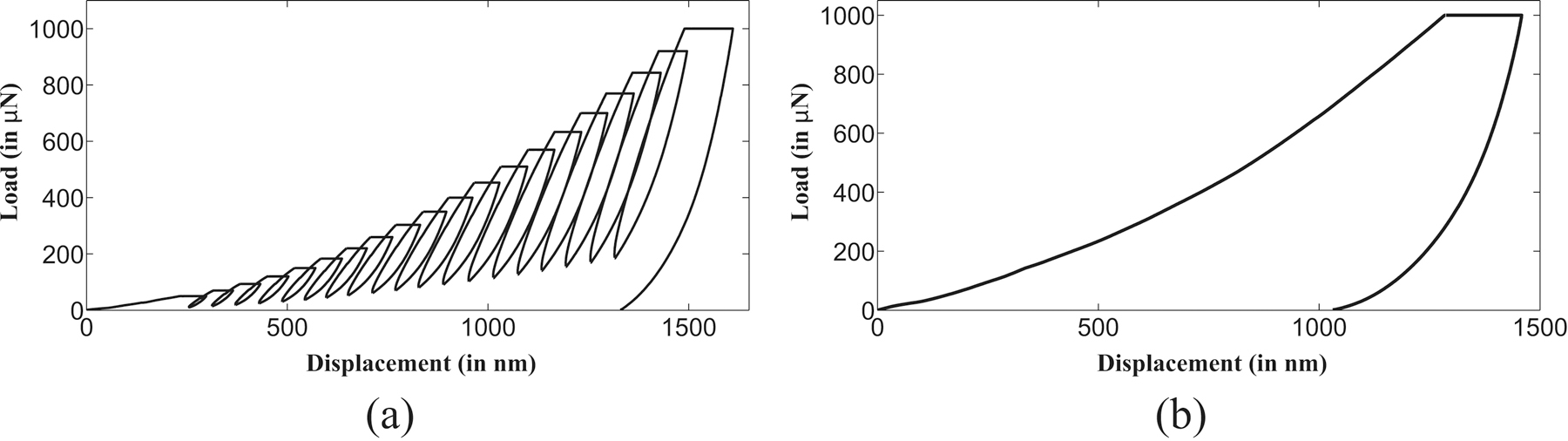
Load-displacement (L-D) curves for quasistatic indentation experiments maintaining indentation depth under 2 microns in a (a) Multiple load test (b) Single load test.

To compare the results obtained from multiple load indentation experiments, single load indentation experiments were also performed on each sample with constant maximum load of 1000 µN. Similar to the tests performed in each multiple load indentation experiment, single load indentation tests were executed at six different locations on the sample surface. The variation of indentation load magnitude with time in a single load indentation test is shown in figure 2(b). For single load indentation tests, the loading as well as unloading rates (50 µN/s) were maintained almost equal to multiple load indentation test. L-D curve obtained in a single load indentation test on the de-mineralized sample surface is shown in figure 3(b) which comprises of single load/unload cycle. All L-D curves begin with almost same preload and, the effects of larger preload were not believed to be considerable as the load was distributed over the size of the tip thus yielding low stresses [78]. The quasistatic indentation experiments were intended to characterize the timeindependent mechanical response of the bone sample, therefore a five second hold segment was used to minimize the influence of time-dependent deformation on the unloading segment as well as its possible effects on determined reduced modulus value [76, 77, 79].

2.4.2. Dynamic indentation

Dynamic indentation involves ramp load profile which superimposes increasing amplitude of the oscillatory load of constant frequency on the linearly increasing static indentation load value. Thus, ramp load profile in dynamic indentation experiments allows the testing of samples at various indentation depths. Dynamic indentation experiments characterize the mechanical behavior of material in terms of its storage modulus (E_storage) and loss modulus (E_loss). The modulus magnitudes are derived from the Sneddon’s equations, and are represented in the Kelvin−Voigt material model for time-dependent strain-related elastic and visco-elastic behavior. Both storage and loss modulus are used together to model time dependent viscoelastic behavior [78, 80] in form of complex modulus (E_complex), as shown in the following equation (relation 3):

$$E_{complex}=E_{storage}+i{E}_{loss};$$ (3)

The storage modulus (E_storage) describes the elastic in-phase response of material which is represented as the following equation (relation 4):

$$E_{storage}=\frac{S\sqrt{\pi }}{2\sqrt{A_c}};$$ (4)

where S is the measured contact stiffness, A_c is the projected contact area. Correspondingly, loss modulus (E_loss) measures the phase delay between the applied load and the material’s response, and it is calculated by the following equation (relation 5):

$$E_{loss}=\frac{\omega D_c\sqrt{\pi }}{2\sqrt{A_c}};$$ (5)

where D_c is the measured contact damping, A_c is the projected contact area and ω is the frequency of oscillatory load. The ratio of the phase-delayed loss modulus to the in-phase storage modulus reflects the overall damping response of the material in the form of dissipation factor [78].

Single frequency ramp load indentation tests known as ”ramp load” indentation tests, were performed in the dynamic indentation experiment to investigate the influence of strain rate on the mechanical properties of bone sample. For a particular test in a dynamic indentation experiment, the variation of static indentation load magnitude with time is shown in figure 2(c) where the static indentation load value has been increased up to 1000 µN. In dynamic indentation experiments, values of static indentation loading rates are similar to that of used in quasistatic indentation experiments. On each sample, the dynamic indentation tests were performed at a constant frequency of 30 Hz (which is lower frequency bound for the instrument although is quite higher than physiological range) with small oscillatory load magnitude having linear variation from 0.5 to 3.16 µN. Similar to quasistatic indentation experiments, the maximum static indentation load magnitude of 1000 µN for the dynamic indentation experiments was selected for the present investigation.

3. Results

The results obtained from experiments in the present study are classified into following subsections.

3.1. Surface roughness and composition analysis

The surface roughness (RMS) of magnitude ∼8 nm (averaged over 1 × 1 µm² area) at various locations of each undemineralized bone sample surface was estimated using AFM. The typical topography of a well polished undemineralized bone sample is shown in figure 4(a). After demineralization of polished bone sample surface, the surface roughness (RMS) magnitude increased to ∼14 nm. For comparison of respective compositions, well polished samples of undemineralized as well as demineralized bone were selected for analysis. It must be noted that samples used for composition analysis were kept separate from the samples used for nanoindentation testing because composition analysis involves coating of bone samples with Pt. The uniform composition of a demineralized sample surface through Backscattered Electron Composition (BEC) is shown in figure 4(b). EDX measurements for composition analysis of bone (undemineralized as well as demineralized) samples were done on the four random locations on the samples surface. The elemental distribution at particular location on undemineralized and demineralized bone samples is shown in figure 5(a) and figure 5(b) respectively. The composition analysis of undemineralized bone sample surface (shown in figure 5(a)) confirmed the presence of mineral elements like Calcium (Ca), Phosphorus (P) whereas no trace of these mineral elements on the demineralized bone sample surface (as shown in figure 5(b)) was identified for a probe depth of ∼2 µm. The details of EDX results obtained for the elemental distribution on demineralized bone sample surface are shown in table 1.

Figure 4:

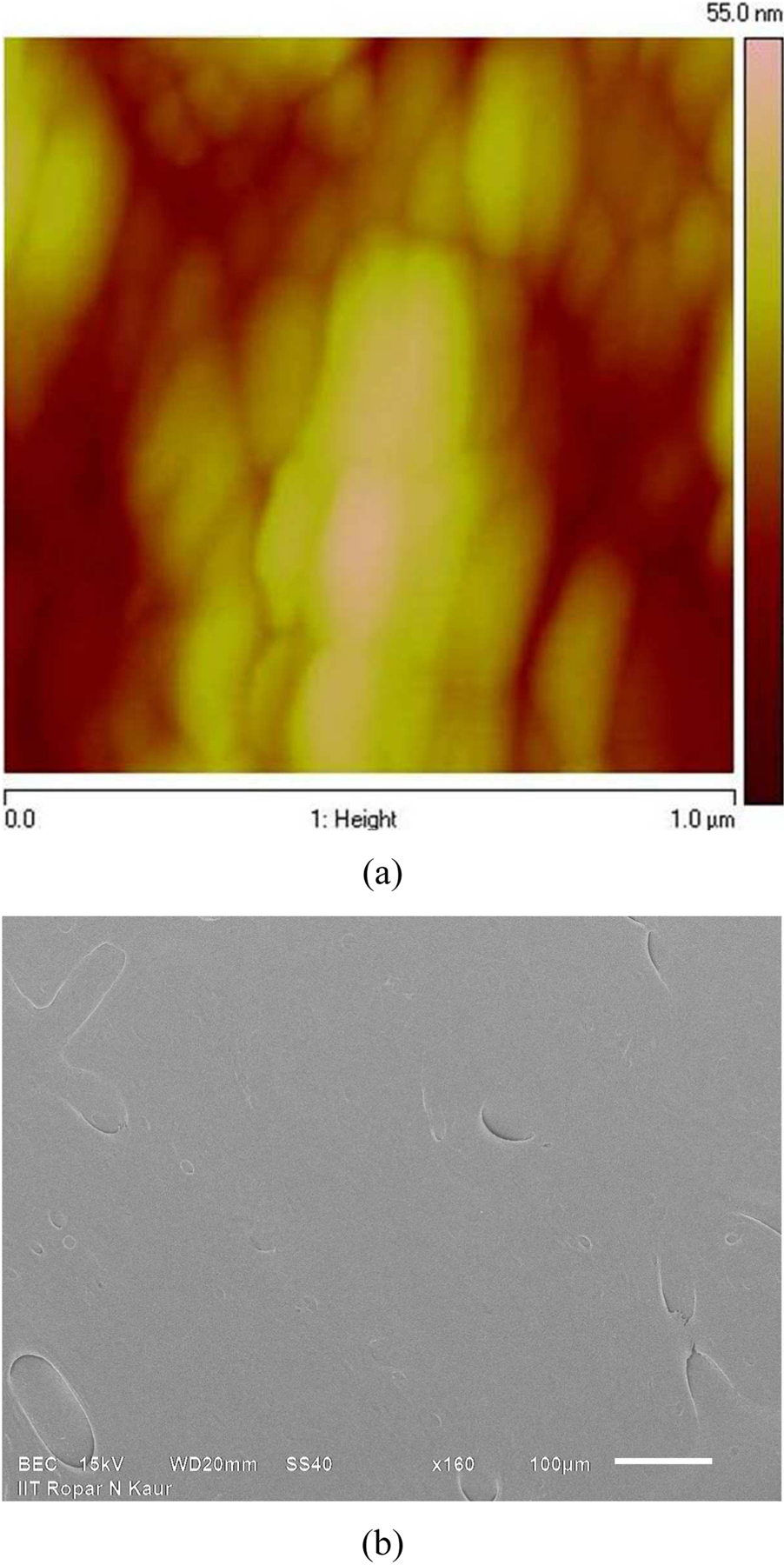
Surface of EDTA treated bone sample through (a) Atomic Force Microscopy for topography (b) Backscattered Electron Composition (BEC) for composition.

Figure 5:

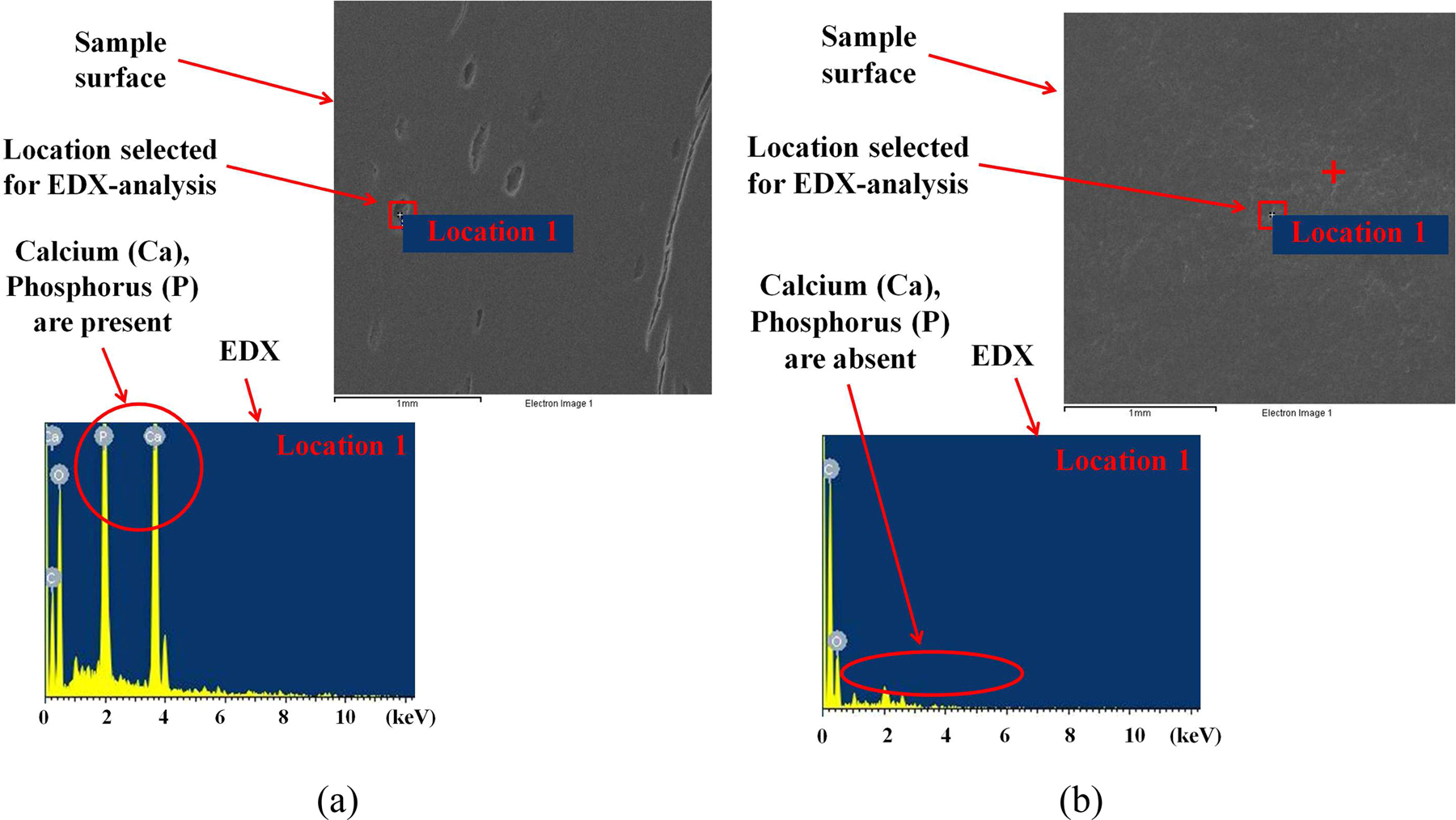
Composition analysis of bone sample surface indicating removal of mineral elements during demineralization of bone samples (a) before demineralization (b) after demineralization, through elemental distribution by EDX at particular locations on each sample.

Table 1:

EDX results of demineralized bone

Element	Weight(%)
C	63.14−67.37
Ca	0
Cl	0−1.82
O	27.77−36.86
P	0
Zr	0−3.74

3.2. Effect of EDTA treatment

In order to predict the response of EDTA treatment on the collagen molecular assemblies, SHG intensity measurements were made in the forward and backward directions in the present work. A comparison of total SHG intensity magnitude of fascicles at different time points during EDTA treatment, in the forward as well as backward directions is shown in the figure 6. We estimated total SHG intensity magnitudes on sample before EDTA treatment, after EDTA treatment, after keeping sample for 30 minutes in DI water and after continuously keeping for 24 hours in DI water. At these four timepoints, normalized values with respect to intensity magnitudes before EDTA treatment are respectively 1, 1.11±0.12, 1.18±0.01 and 0.81±0.01 in forward direction (shown in figure 6(a)), and 1, 0.76±0.09, 1.23±0.01 and 0.88±0.06 in backward direction (shown in figure 6(b)).

Figure 6:

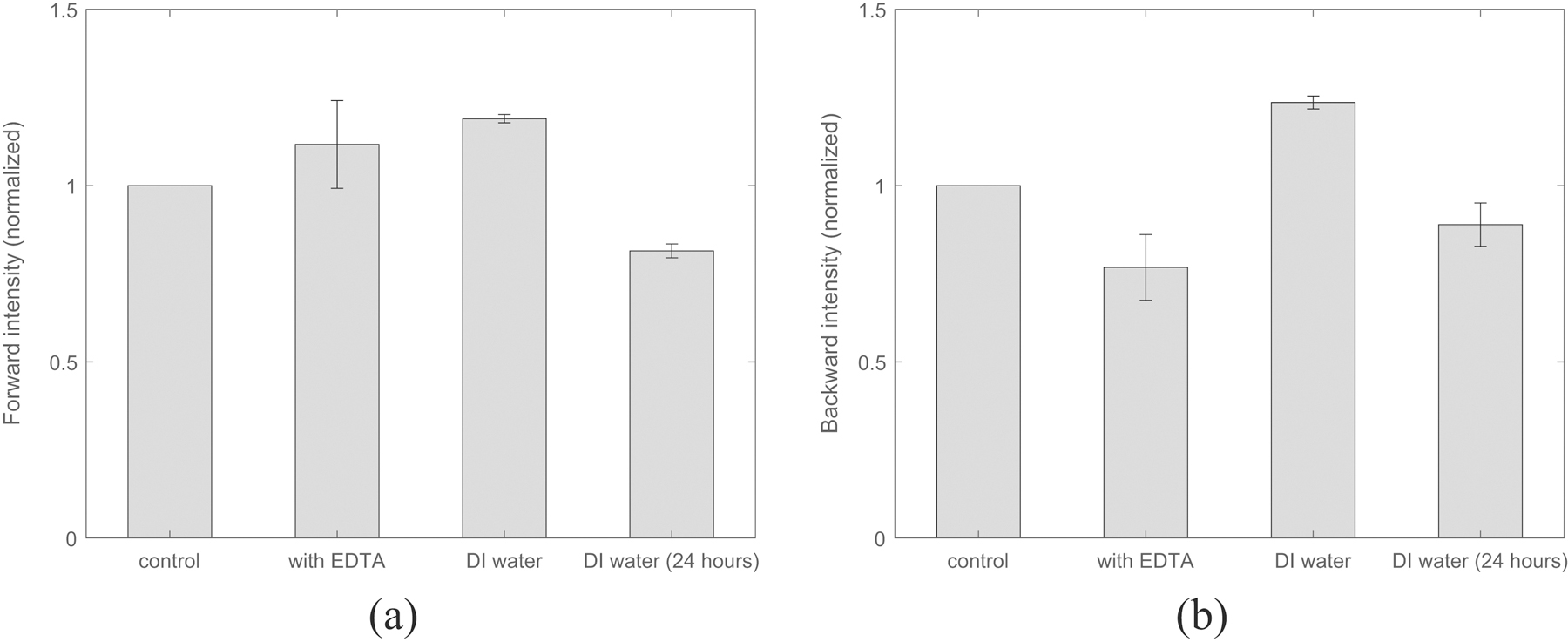
Collagen fibril size (represented by F-B ratio) is found affected immediately after EDTA treatment but keeping in DI for longer reverses the influence of EDTA treatment as shown via SHG (a) Forward intensity (b) Backward intensity.

For nanomechanical characterization during EDTA treatment, single load indentation experiments were performed on five samples to determine their mechanical properties like elastic modulus and contact hardness. The effect of EDTA treatment for different durations on elastic modulus and contact hardness is shown in figure 7. Elastic modulus magnitude has been found to decrease from 15.02±1.08 GPa to 2.74±0.35 GPa as the duration of EDTA treatment on bone samples is increased to 60 minutes. For ramp load indentation experiments on five undemineralized samples, the average values of storage and loss modulus were obtained as 18.21±1.87 GPa and 1.87±1.33 GPa respectively which were found to decrease much lower values (shown in figure 7(a) and figure 7(b) respectively) after demineralization. For undemineralized bone samples, the estimated values of quasistatic and dynamic mechanical properties are in complete agreement with the values reported in literature [55, 56, 60].

Figure 7:

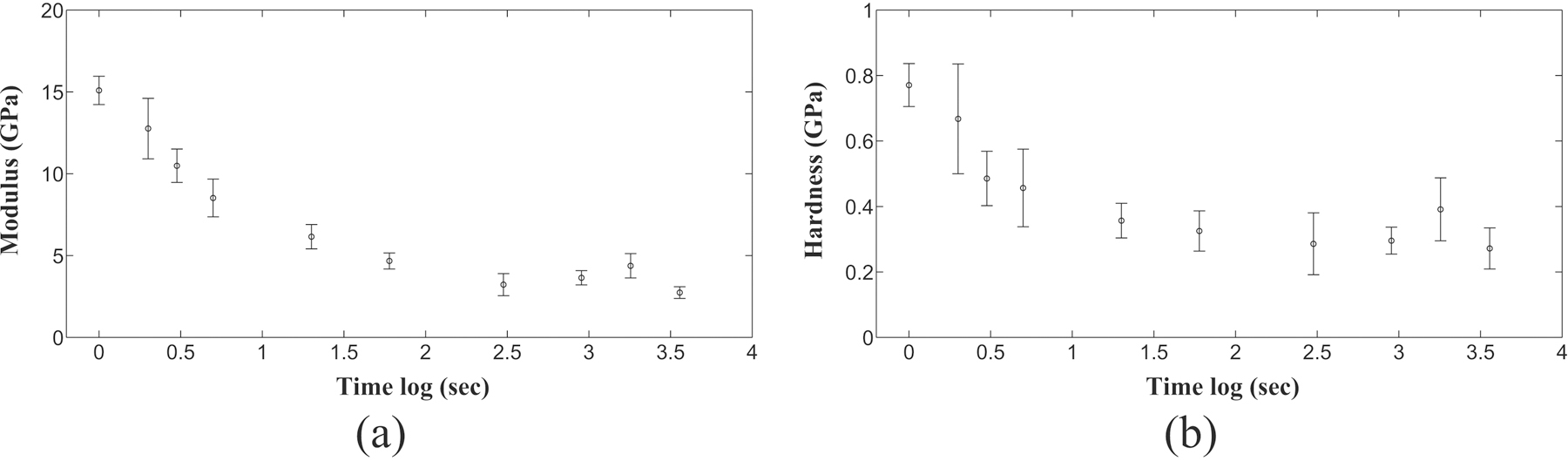
EDTA treatment of bone samples beyond 60 minutes does not produce further change nanomechanical properties of bone as reflected by (a) Reduced modulus with treatment duration (b) Contact hardness with treatment duration.

3.3. Quasistatic indentation experiment

For maximum indentation load of magnitude 1000 µN in single load indentation experiments as well as multiple load indentation experiments, L-D curves for single test in a multiple load and single load indentation experiment on the demineralized bone sample are shown in figure 3(a) and figure 3(b) respectively. The reduced modulus and contact hardness values as a function of indentation load magnitude in multiple load indentation experiment on demineralized bone sample are shown in figure 8(a) and figure 8(b) respectively. The average values of reduced modulus and contact hardness for the whole indentation load range in multiple load indentation experiments on five samples were obtained as 2.74±0.35 GPa and 0.27±0.06 GPa respectively. Modulus and hardness magnitudes vary from ∼4 GPa to 2.58±0.21 GPa and ∼0.47 GPa to 0.23±0.01 GPa respectively when indentation load is increased from 25 µN (representing ∼75 nm indentation depth) to 250 µN (representing ∼500 nm indentation depth) and remains almost constant thereafter when indentation load is further increased in the experiments. For single load indentation experiments on five samples, the average magnitudes of reduced modulus and contact hardness were observed as 2.61±0.08 GPa and 0.24±0.01 GPa respectively.

Figure 8:

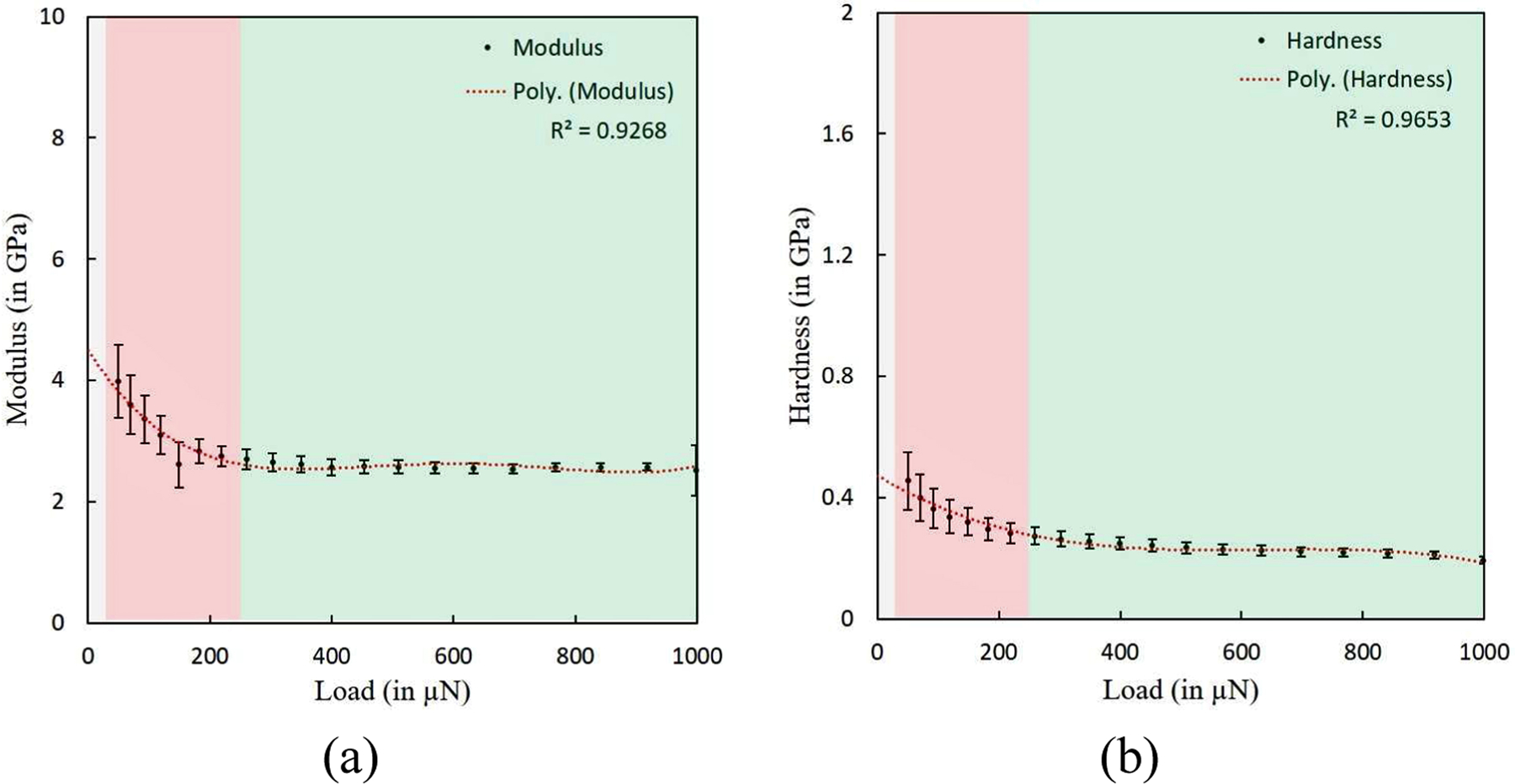
Material properties of demineralized bone as a function of indentation load (or indentation depth) in a quasistatic multiple load indentation experiment show three different regions with primary contribution towards material property from i.e. surface roughness (with indentation depth varying from 0 to ∼75 nm shown by grey color), collagen fibrils (with indentation depth varying from ∼75 nm to ∼500 nm represented by red) and collagen fibers (with indentation depth varying from larger than ∼500 nm represented by green) (a) Reduced modulus with indentation load (b) Contact hardness with indentation load.

3.4. Dynamic indentation experiment

The dynamic mechanical properties of demineralized bone samples were measured by using ramp load indentation experiments at 30 Hz frequency. For a particular ramp load indentation experiment consisting of five tests on each sample, the storage and loss modulus magnitudes as a function of indentation load magnitude are shown in figure 9(a) and figure 9(b) respectively. For ramp load indentation experiments on five demineralized samples, the average values of storage modulus and loss modulus at various indentation loads were observed as 4.48±0.46 GPa and 0.57±0.03 GPa respectively. Storage and loss modulus magnitudes vary from ∼11 GPa to 4.27±0.42 GPa and ∼1.75 GPa to 0.52±0.05 GPa respectively when indentation load is increased from 25 µN to 250 µN, and does not change significantly when indentation load is further increased in the experiments.

Figure 9:

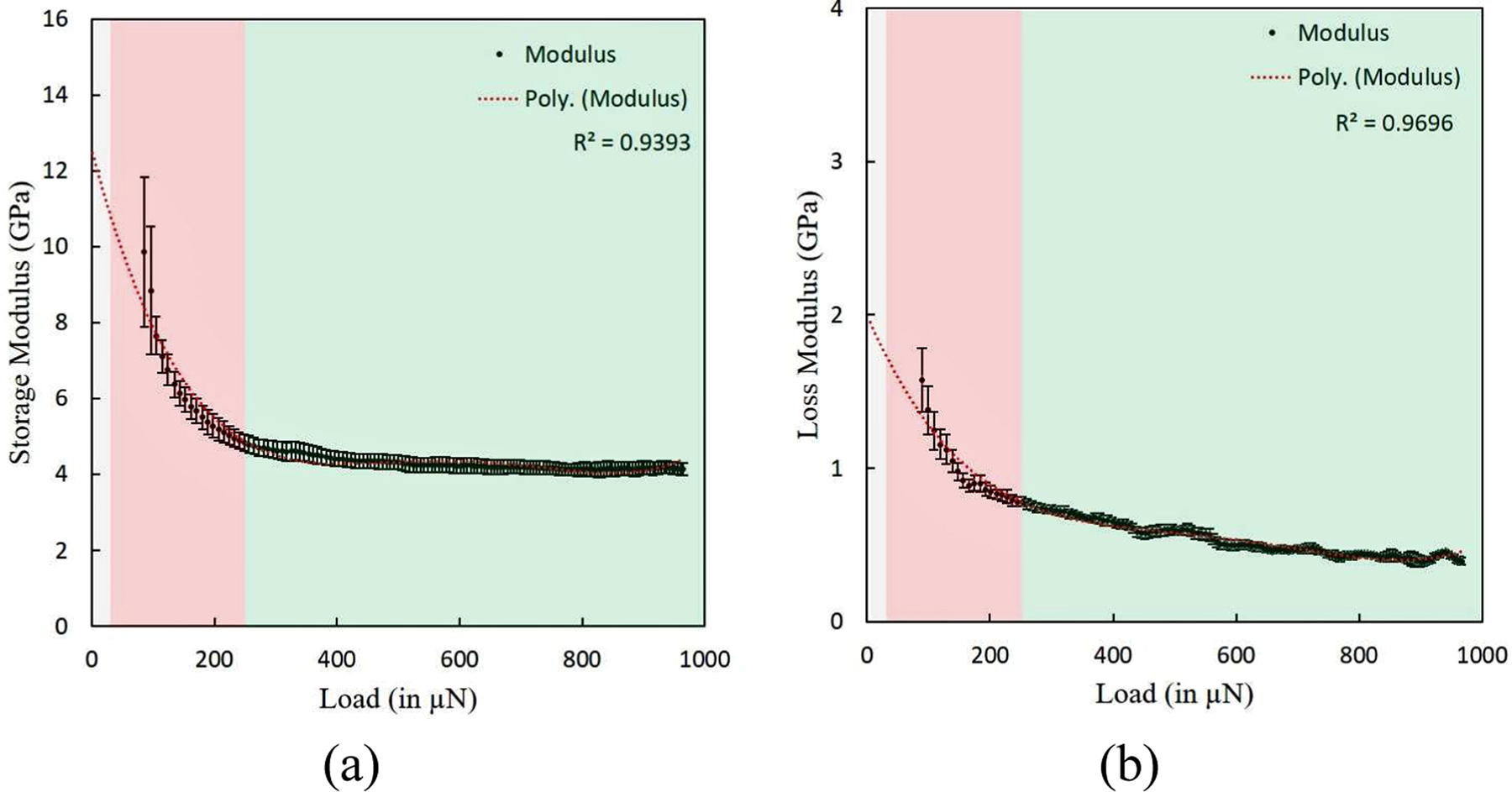
Complex modulus components of demineralized bone as a function of indentation load (or indentation depth) in a dynamic indentation experiment at 30 Hz frequency show three different regions with primary contribution towards material property from i.e. surface roughness (with indentation depth varying from 0 to ∼75 nm shown by grey color), collagen fibrils (with indentation depth varying from ∼75 nm to ∼500 nm represented by red) and collagen fibers (with indentation depth varying from larger than ∼500 nm represented by green) (a) Storage modulus with indentation load (b) Loss modulus with indentation load.

4. Discussion

As shown in the figure 6(a), SHG intensity magnitude in forward increase by ∼11% after 30 minutes of EDTA treatment whereas values in figure 6(b) show a intensity decrease of ∼24% in backward direction. This is result of increase in number of collagen fibrils having comparatively larger diameters and decrease in number of collagen fibrils having smaller diameters due to EDTA treatment because forward signal is sensitive to large diameter fibrils and backward signal is sensitive to smaller diameter fibrils of ∼40 nm in diameter. Thus, small diameter fibrils are assembling to form larger diameter fibrils after EDTA treatment. After removing EDTA solution, when samples are kept in DI water for 30 minutes before imaging, a intensity gain of ∼7% and ∼23% respectively in both forward and backward directions has been observed with respect to control values whereas after keeping samples for 24 hours in DI water, decrease of ∼19% in forward intensity and ∼12% in backward intensity with respect to control values was observed. Thus keeping samples in DI water for 24 hours results in reversing the effects caused by EDTA treatment on collagen fibril assemblies. F-B ratio consistently remaining closer to 1 when samples are washed with DI water after EDTA treatment while kept in DI water, qualitatively indicates non-detrimental effect of EDTA treatment on samples. Based on these findings, nanomechanical testing of samples after EDTA treatment and consecutively keeping them for nearly 12 hours in DI water would be ideal to maintain native packing of collagen molecules in organic matrix through demineralization protocol used in the present work.

It has been observed that there is considerable influence of EDTA treatment exposure time on nanomechanical properties of bone samples (as shown in figure 7). Hence, we found 60 minutes duration of EDTA treatment to be sufficient for complete demineralization of bone samples to obtain its organic matrix for detailed investigation. HAp crystals are known to have high elastic modulus value than undemineralized bone whereas modulus values of collagen molecules or assemblies are found to be quite lower than that of undemineralized bone. Hence for quasistatic and dynamic indentation experiments, the decrease in elastic modulus magnitude with demineralization is consequence of absence of contribution of HAp crystals towards the resulting mechanical response. It further shows that mechanical response of organic matrix obtained through complete demineralization via EDTA treatment of bone, is reflecting the properties of collagen fibrils only. The higher value of elastic modulus in dynamic indentation experiments than quasistatic indentation experiments show strain rate dependent mechanical response of organic matrix of bone. The strain dependent observations of our experiments are in complete agreement with the strain dependent response of biological materials reported in literature [55, 56, 60].

Taking into consideration in-homogeneities in the samples arising from ‘size dependent hierarchy’, we assumed much higher indentation depth to surface roughness ratios of ∼5:1 for our analysis as compared to ∼3:1 reported in the literature [21, 47, 48] and, based on RMS values of roughness of our samples, we assumed that measured properties at indentation depth more than ∼75 nm (representing 25 µN of indentation load) would not be influenced by sample surface roughness. Therefore, values of material properties at indentation depths closer to ∼75 nm and more, with tip of ∼40 nm radius can assumed to be representative properties of small sub-volume formed by few collagen fibrils whose diameters ranges up to ∼400 nm. With further increase in indentation depth (much larger than ∼75 nm), indentation material properties can assumed to be reflective of much larger domain of collagen fibrils representing collagen fibers. The values of reduced modulus and contact hardness at various indentation load magnitudes in a particular multiple load indentation experiment are shown in figure 8(a) and figure 8(b) respectively which show considerable variation in reduced modulus, contact hardness magnitudes when loads are increased from ∼25 µN to ∼250 µN (indentation depth increasing from ∼75 nm to ∼500 nm) and reaching a plateau for all values obtained at indentation loads larger than ∼250 µN. Near the surface, indentation depth ranging from 0 nm to ∼75 nm (as shown in figure 8(a) and figure 8(b) by extrapolating the values obtained through polynomial fit), values are much larger as reported in available literature [75].

On the basis of quasistatic indentation experiments conducted in the present work, it can be concluded that the average magnitude of reduced modulus for the multiple load indentation experiments is approximately 5% greater than the average reduced modulus magnitude estimated from the single load indentation experiments when contributions from individual collagen fibrils closer to surface are excluded towards material property calculations whereas are almost equal to each other with reduced modulus observed as ∼ 2.6 GPa when values at higher indentation loads are considered towards averaging of modulus values. Similarly, the magnitude of average contact hardness in the multiple load indentation experiments for whole indentation load range is approximately 10% larger than its magnitude in single load indentation experiments, and similar to reduced modulus values, hardness values converge to 0.24 GPa for both multiple load and single load experiments when values at higher indention load in multiple load experiments are considered towards calculations. Critical observation of data shown in figure 8(a) and figure 8(b) suggests that reduced modulus and contact hardness magnitudes decrease by ∼40–50% (i.e. from ∼4 GPa to 2.58±0.21 GPa and from ∼0.47 GPa to 0.23±0.01 GPa for reduced modulus and contact hardness respectively) when indentation depth is increased from ∼75 nm to ∼500 nm and remains constant thereafter with further increase in indentation depth. In nanoindentation measurements on a functionally graded material like bone, material property value at particular indentation depth should be considered as resultant of individual contribution from collagen fibrils (with modulus as 4 GPa in present work and other studies [75]) and their assemblies into collagen fibers (with a modulus magnitude of upto 0.5 GPa [81]) without ignoring the molecular interactions between tip and sample surface which are not negligible [82, 83]

Similar to that of observed in quasistatic indentation experiments, in each dynamic indentation experiment beyond 250 µN of indentation load, storage and loss modulus magnitudes converge to a single value, as shown in figure 9(a) and figure 9(b) respectively; and further increase in indentation load magnitude does not have considerable influence on the estimated storage and loss modulus values. The average storage modulus magnitudes obtained through dynamic indentation experiments at 30 Hz is approximately 4.5 GPa (for whole range of indentation loads considered in the present study), which is larger in magnitude than average modulus magnitude obtained in quasistatic indentation experiments (approximately 2.6 GPa). As discussed in previous para on transition of probed volume from incorporating individual collagen fibrils to volume consisting of much larger assemblies of collagen fibrils by increase in indentation depth, storage and loss modulus magnitudes vary from ∼11 GPa to 4.27±0.42 GPa and ∼1.75 GPa to 0.52±0.05 GPa respectively when indentation load is increased from 25 µN to 250 µN, and does not change significantly when indentation load is further increased in the experiments. The comparatively higher storage modulus in dynamic indentation experiments than static indention experiments at larger indentation depth is reflective of strain rate dependent material properties of organic matrix of bone formed by collagen fibrils as higher strain rate results from the higher loading rate involved in the dynamic indentation experiments due to imposition of oscillatory load on static indentation load. The variation in material properties (storage and loss moduli) with the indentation load magnitude in the dynamic indentation experiment is much higher than that of observed in the quasistatic indentation experiments when observed for indentation loads up to 250 µN. In the ramp load indentation experiment, the variation in oscillatory load amplitude slightly changes the loading rate experienced by the sample at various indentation depths. In a dynamic indentation experiments of varying oscillatory load amplitudes (at higher indentation loads in particular), the change in the modulus magnitudes (remains within same order of magnitude) with change in indentation load magnitude is very small which predicts that the loading rate variation resulting from variation in oscillatory load amplitude have a little effect on the storage and loss modulus magnitudes. Insubstantial variation in modulus magnitudes with change in oscillatory load amplitude confirms the observations of reduced strain-rate sensitivity seen in visco-elastic biological tissues and solids [78, 84].

The average storage and loss modulus magnitudes for demineralized bone samples (for whole range of indention loads) were used to estimate tanδ i.e. dissipation factor (tanδ = 0.127 i.e. delta = 7.23 ^◦) during dynamic indentation experiments. Similarly, on the basis of average modulus magnitudes for unmineralized bone samples, the dissipation factor (tanδ = 0.102 i.e. delta = 5.82 ^◦) was estimated for untreated bone at 30 Hz frequency. As observed in the dynamic indentation experiments on both undemineralized and demineralized bone samples, the loss modulus magnitude was observed to be uniformly low and much smaller than the storage modulus magnitude, further indicating that the most of the energy is recovered upon unloading rather than dissipated instantaneously [85]. It must be noted that tanδ value increases from 0.102 to 0.127 when HAp is removed via demineralization of bone, indicating that organic matrix in itself contributes towards visco-elastic behavior of bone. For indentation depth dependent storage and loss moduli, delta values decreased from 9.09 ^◦ and 6.95 ^◦ when indentation load is increased from 25 µN to 250 µN indicating higher dissipation effects occurring at collagen fibril (tanδ equal to 0.16) level as compared to collagen fiber (tanδ equal to 0.12) hierarchy level of organic matrix of bone. Prior dynamic studies on the modulus magnitudes of biological materials and polymers show a similar and considerable difference in magnitude between storage and loss modulus values across different frequencies [78, 86]. For the dynamic indentation experiments at 30 Hz, higher magnitudes of dissipation factor for demineralized bone than undemineralized bone represent large energy dissipation for the organic matrix of bone. Future studies are required to explore the frequency dependence of mechanical response of organic matrix of bone as well as the effect of demineralization to various extents on the visco-elastic response of bone to further explain the mechanisms controlling its mechanical response.

5. Conclusion

The protocol adopted for preparation of organic matrix samples via demineralization of bone produced very low surface roughness samples suitable for probing few collagen fibrils to larger assemblies of collagen fibrils forming collagen fibers. Demineralization of bone samples done via EDTA treatment for 60 minutes has been found to remove completely the mineral content present in bone sample surface to expose its organic matrix without affecting collagen assemblies forming the matrix at least up to 2 µm. Keeping in mind the influence of the surface roughness, reduced modulus and contact hardness of organic matrix were found to lie between 2.6−4 GPa and 0.23−0.47 GPa respectively for indentation depths between 75 nm and 500 nm whereas for depths beyond 500 nm, average values of reduced modulus, hardness converged for single load multiple load experiments. Due to higher loading rates (i.e. higher strain rates) involved in the dynamic indentation experiments performed at 30 Hz frequency as compared to quasistatic indentation experiments, the modulus magnitudes obtained in dynamic indentation experiments are uniformly larger (depending upon indentation depth) than that of obtained in quasistatic indentation experiments (∼2.6 GPa approximately) concluding loading rate dependent mechanical response of the organic matrix of bone. With demineralization of bone samples, the increase in dissipation factor value from 0.102 to 0.127 shows that organic matrix of bone has more dissipate effects than undemineralized bone, and these dissipation are more at collagen fibril level with disssipation factor as 0.16 when compared to collagen fibers which has respective value of 0.12.