Pairwise Versus Multiple Global Network Alignment

Abstract

Biological network alignment (NA) aims to identify similar regions between molecular networks of different species. NA can be local or global. Just as the recent trend in the NA field, we also focus on global NA, which can be pairwise (PNA) and multiple (MNA). PNA produces aligned node pairs between two networks. MNA produces aligned node clusters between more than two networks. Recently, the focus has shifted from PNA to MNA, because MNA captures conserved regions between more networks than PNA (and MNA is thus hypothesized to yield higher-quality alignments), though at higher computational complexity. The issue is that, due to the different outputs of PNA and MNA, a PNA method is only compared to other PNA methods, and an MNA method is only compared to other MNA methods. Comparison of PNA against MNA must be done to evaluate whether MNA indeed yields higher-quality alignments, as only this would justify MNA’s higher computational complexity. We introduce a framework that allows for this. We evaluate eight prominent PNA and MNA methods, on synthetic and real-world biological networks, using topological and functional alignment quality measures. We compare PNA against MNA in both a pairwise (native to PNA) and multiple (native to MNA) manner. PNA is expected to perform better under the pairwise evaluation framework. Indeed this is what we find. MNA is expected to perform better under the multiple evaluation framework. Shockingly, we find this not always to hold; PNA is often better than MNA in this framework, depending on the choice of evaluation test.

I. INTRODUCTION

A. MOTIVATION AND BACKGROUND

Networks can be used to model complex real-world systems in many domains, including computational biology. A popular type of biological networks are protein interaction networks (PINs). While PIN data are available for multiple species [1], the functions of many proteins in many species remain unknown [2], [3]. Network alignment (NA) compares networks to find a node mapping that conserves similar regions between the networks. Then, analogous to genomic sequence alignment, NA can be used to predict protein functions by transferring functional knowledge from a well-studied species to a poorly-studied one between the species’ conserved (aligned) PIN regions [4]-[8]. While we focus on the biological NA of PINs, NA can be used for many applications [9], including computer vision [10], online social networks [11], and ontology matching [12].

NA is related to the subgraph isomorphism, or subgraph matching, problem. This problem asks to find a node mapping such that one network is an exact subgraph of another network. NA is a more general problem in that it asks to find a node mapping that best “fits” one network into another network, even if the first network is not an exact subgraph of the second. A widely used measure that quantifies this “fit” is the amount of conserved (aligned) edges, i.e., the size of the common conserved subgraph between the aligned networks. Since maximizing edge conservation is NP-hard [13], heuristic methods are needed for NA.

Like genomic sequence alignment, NA can be local or global [7], [8]. Initial research was on local NA, which searches for small highly conserved regions across the compared networks, irrespective of the overall similarity between the networks; the conserved network regions can, but are not required to, overlap. More recent efforts have focused on global NA, which searches for a node mapping that maximizes overall similarity of the compared networks and thus results in large but suboptimally conserved network regions. Each of local NA and global NA has its (dis)advantages [7], [8], [14]. Because in the recent years global NA has received more attention than local NA, in this paper we also focus on global NA, and henceforth, we refer to global NA as NA.

Also, and importantly for our study, NA methods can be pairwise or multiple [5], [8]. While pairwise NA (PNA) aligns two networks at once, multiple NA (MNA) can align more than two networks at once. Since MNA can capture conserved network regions between multiple networks, it is hypothesized that MNA may lead to deeper biological insights (i.e., higher-quality alignments) compared to PNA. However, this hypothesis has not been tested yet (for reasons described in the following paragraphs). Because of this, and because both PNA and MNA have the same ultimate goal, which is to transfer knowledge from well- to poorly-studied species, we argue that they need to be compared in order to determine which category of methods produce higher-quality alignments. Note that MNA is computationally harder than PNA, because the complexity of the NA problem can increase exponentially with the number of considered networks. So, a comparison of PNA and MNA in terms of their alignment quality can also answer whether the additional computational complexity of MNA is worth it.

Since typical PNA and MNA methods produce alignments of different types (Fig. 1), it has been difficult to compare them. Namely, when aligning two networks, PNA typically produces a one-to-one node mapping between the two networks, which results in aligned node pairs (Fig. 1(a)). When aligning more than two networks, MNA produces a node mapping across the multiple networks, which results in aligned node clusters. If an aligned cluster contains more than one node from a single network, then it is a many-to-many alignment (Fig. 1(d)). If each of the aligned clusters contains at most one node per network, then it is a one-to-one alignment (Fig. 1(b)). Typical MNA methods produce many-to-many alignments (Fig. 1(d)), and they are called many-to-many MNA methods. MNA methods that produce one-to-one alignments (Fig. 1(b)) are called one-to-one MNA methods. MNA methods can also be trivially used to align pairs of networks, which results in aligned node clusters for many-to-many MNA methods (Fig. 1(c)) and in aligned node pairs for one-to-one MNA methods (Fig. 1(a)).

FIGURE 1.

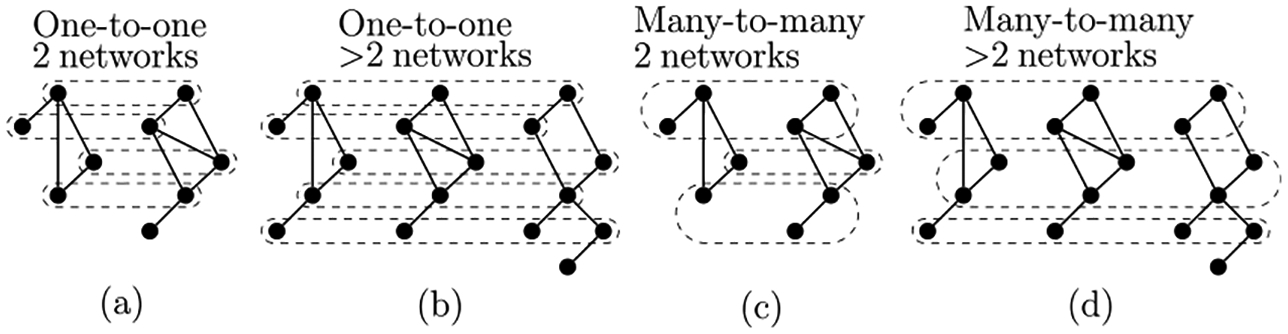
Illustration of different alignment types.

There is sometimes confusion in the literature that one-to-one alignments are automatically global (i.e., outputted by global NA methods), and that many-to-many alignments are automatically local (outputted by local NA methods). However, this is not necessarily the case. First, one-to-one alignments can result in only small regions aligned to each other (clearly without any nodes overlapping), meaning that they are local one-to-one alignments. Second, many-to-many alignments can result in aligned node clusters covering nodes from all analyzed networks, meaning that they are global, many-to-many alignments. In other words, in our opinion, “local” and “global” describe how much of the networks’ nodes are covered by (i.e., are a part of) the given alignment, and not on whether the nodes are aligned in one-to-one or many-to-many fashion. It is important to note that most of the recent one-to-one methods will not actually produce local alignments, because they require all nodes of the smaller networks to be mapped to nodes of the larger networks, automatically leading to global (one-to-one, or even more formally, injective) alignments. However, this is an algorithmic design choice of many existing methods rather than a requirement of any and every one-to-one method. As discussed above, we focus on global NA, considering both one-to-one and many-to-many methods.

Again, because PNA and MNA generally produce alignments of different types (aligned node pairs versus aligned node clusters, respectively), alignment quality measures designed for alignments of one type do not necessarily work for alignments of the other type. Also, alignment quality measures designed for alignments of two networks do not necessarily work for alignments of more than two networks. Due to this difficulty, when a new PNA or MNA method is proposed, it is only compared against other NA methods from the same category. However, since both PNA and MNA have the same goal of across-species knowledge transfer, we argue that there is a need to compare them. This is especially true because early evidence suggests that aligning each pair of considered networks via PNA and then combining the pairwise alignments into a multiple alignment spanning all of the networks can be superior to directly aligning all networks via MNA [15].

B. OUR CONTRIBUTIONS

Thus, we propose an evaluation framework for a fair comparison of PNA and MNA (Fig. 2).

FIGURE 2.

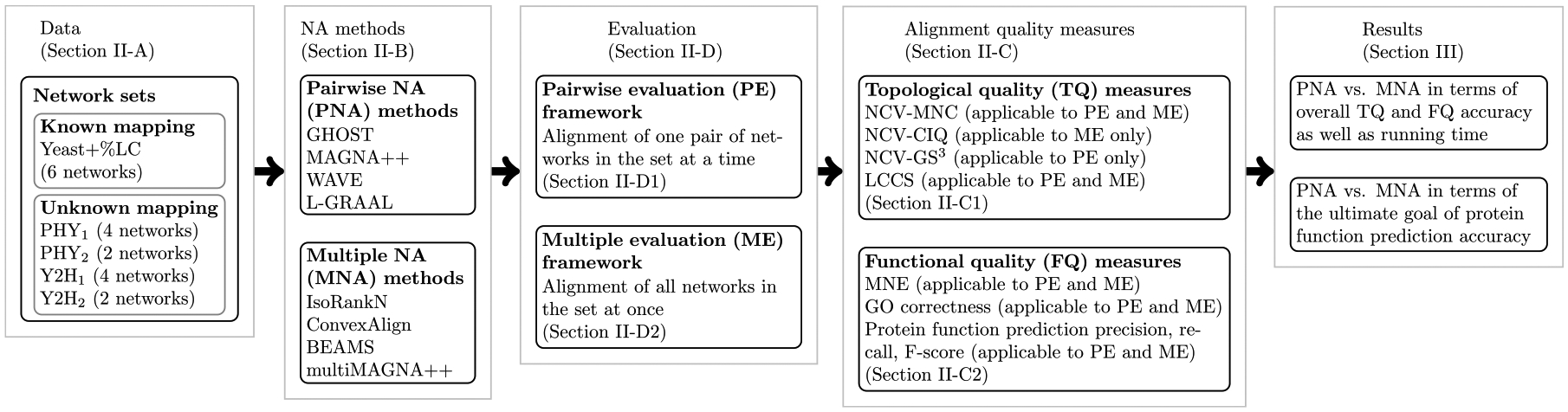
Overview of our PNA versus MNA evaluation framework.

We evaluate PNA and MNA on synthetic networks with known true node mapping (we know the underlying alignment that a perfect method should output) and real-world PINs of different species with unknown node mapping (we do not know which protein in one species corresponds to which protein in the other species). The network data are discussed in Section II-A.

We evaluate prominent PNA and MNA methods that were published by the beginning of our study, were publicly available, and had user-friendly implementations. This includes four PNA methods (GHOST [16], MAGNA++ [37], WAVE [18], and L-GRAAL [19]), and four MNA methods (Iso-RankN [20], BEAMS [21], multiMAGNA++ [22], and ConvexAlign [23]), which are discussed in Section II-B. Most of these methods are recent and were thus already shown to be superior to many past methods, e.g., IsoRank [24], MI-GRAAL [13], GEDEVO [25], and NETAL [26] PNA methods, plus GEDEVO-M [27], FUSE [28], and SMETANA [29] MNA methods. Note that newer NA methods have appeared since, such as SANA [30], ModuleAlign [31], SUMONA [32], and PrimAlign [33], which is why they were not included here. Importantly, we believe that their inclusion is not required. This is because our goal is not to determine the best existing (PNA or MNA) method. Instead, it is to properly evaluate the whole category of prominent recent PNA methods against the whole category of equally prominent recent and thus fairly comparable MNA methods. While the best existing NA method would likely change with introduction of each new method (or possibly even a new measure for evaluating alignment quality), the best category of NA approaches is less likely to change, unless there is a drastic shift in how the NA problem is approached and solved (or possibly even just how alignment quality is evaluated). And one of the purposes of our study is to determine if such a shift is needed.

We evaluate the PNA and MNA methods in terms of their alignment quality (i.e., accuracy) as well as running time. We evaluate alignment quality using topological and functional alignment quality measures. An alignment is of good topological quality if it reconstructs well the underlying true node mapping (when known) and if it has many conserved edges (i.e., if it conserves a large common subgraph between the networks). An alignment is of good functional quality if its aligned node pairs/clusters contain nodes with similar biological functions. The alignment quality measures are described in Section II-C.

We evaluate the PNA and MNA methods in both a pairwise (native to PNA) and multiple (native to MNA) manner, as described in Section II-D.

Section II describes the data, alignment quality measures, and evaluation framework. Section III describes our findings.

II. METHODS

A. DATA

We use five network sets: one synthetic network set with known true node mapping, and four real-world network sets with unknown true node mapping. For each network, we use only its largest connected component.

1). NETWORK SET WITH KNOWN TRUE NODE MAPPING

This synthetic network set, named Yeast+%LC, contains a high-confidence S. cerevisiae (yeast) PIN with 1, 004 proteins and 8, 323 interactions [34], along with five lower-confidence yeast PINs constructed by adding 5%, 10%, 15%, 20%, or 25% of lower-confidence interactions to the high-confidence PIN (Supplementary Table S1). This network set has been used in many existing studies [7], [13], [16], [22], [35]-[37]. Since all networks have the same node set, we know the true node mapping. Hence, for this set, we can evaluate node correctness, i.e., how well the given NA method reconstructs the true node mapping (Section II-C.1).

2). NETWORK SETS WITH UNKNOWN TRUE NODE MAPPING

The four real-world network sets with unknown node mapping are named PHY₁, PHY₂, Y2H₁, and Y2H₂. Each contains PINs of four species, S. cerevisiae (yeast), D. melanogaster (fly), C. elegans (worm), and H. sapiens (human). The PIN data, obtained from BioGRID [1], have been used in recent studies [7], [22]. For each species, four PINs are created that contain the following protein interaction types and confidence levels: all physical interactions supported by at least one publication (PHY₁) or at least two publications (PHY₂), as well as only yeast two-hybrid physical interactions supported by at least one publication (Y2H₁) or at least two publications (Y2H₂) (Supplementary Table S1). Just as was done in the existing studies, we also remove the fly and worm networks from the PHY₂ and Y2H₂ network sets, because these networks are too small and sparse (53–331 nodes and 33–260 edges), resulting in the PHY₂ and Y2H₂ network sets containing only two networks each. The four network sets have unknown true node mapping, and thus we cannot evaluate node correctness. However, we use alternative measures of alignment quality that are based on Gene Ontology annotations (Section II-C.2).

3). GENE ONTOLOGY (GO) ANNOTATIONS

For alignment quality measures (Section II-C) that rely on GO annotations of proteins [38], we use experimentally obtained GO annotations from the GO database from January 2016.

4). PROTEIN SEQUENCES

When NA methods use protein sequence information to produce an alignment (Section II-B), we use BLAST protein sequence similarities as captured by E-values [39]. The sequence data were acquired from the NCBI website (https://www.ncbi.nlm.nih.gov/).

B. NA METHODS THAT WE EVALUATE

We study GHOST, MAGNA++, WAVE, and L-GRAAL PNA methods, and IsoRankN, BEAMS, multiMAGNA++, and ConvexAlign MNA methods.

1). PNA METHODS

Most NA methods are two-stage aligners: first, they calculate the similarities (based on network topology and, optionally, protein sequences) between nodes of the compared networks, and second, they use an alignment strategy to find high scoring alignments with respect to the total similarity over all aligned nodes. GHOST is a two-stage PNA method (Supplementary Section S1.1). An issue with two-stage methods is that while they find high scoring alignments with respect to total node similarity (a.k.a. node conservation), they do not account for the amount of conserved edges during the alignment construction process. But the quality of an alignment is often measured in terms of edge conservation. To address this, MAGNA++ directly optimizes both edge and node conservation while the alignment is constructed (Supplementary Section S1.1). MAGNA++ is a search-based (rather than a two-stage) PNA method. Search-based aligners can directly optimize edge conservation or any other alignment quality measure. WAVE and L-GRAAL were proposed as two-stage (rather than search-based) PNA methods that, just as MAGNA++, optimize both node and (weighted) edge conservation (Supplementary Section S1.1).

2). MNA METHODS

IsoRankN, BEAMS, and ConvexAlign are two-stage MNA methods. IsoRankN optimizes node conservation. BEAMS and ConvexAlign optimize both node and edge conservation (Supplementary Section S1.1). On the other hand, like MAGNA++, multiMAGNA++ is a search-based method that optimizes both edge and node conservation. IsoRankN and BEAMS produce many-to-many alignments. ConvexAlign and multiMAGNA++ produce one-to-one alignments.

3). ALIGNING USING NETWORK TOPOLOGY ONLY VERSUS USING BOTH TOPOLOGY AND PROTEIN SEQUENCES

In our analysis, for each method, we study the effect on output quality when (i) using only network topology while constructing alignments (T alignments) versus (ii) using both network topology and protein sequence information while constructing alignments (T+S alignments). For T alignments, we set method parameters to ignore any sequence information. All methods except BEAMS can produce T alignments and all methods can produce T+S alignments. For T+S alignments, we set method parameters to include sequence information. Supplementary Table S2 shows the specific parameters that we use, and Supplementary Section S1.1 justifies our parameter choices.

C. ALIGNMENT QUALITY MEASURES

Typical PNA methods produce alignments comprising node pairs and typical MNA methods produce alignments comprising node clusters. We introduce the term aligned node group to describe either an aligned node pair or an aligned node cluster. With this, we can represent a pairwise or multiple alignment as a set of aligned node groups. For formal definitions, see Supplementary Section S1.2.

1). TOPOLOGICAL QUALITY (TQ) MEASURES

A good NA method should produce aligned node groups that have internal consistency with respect to protein labels. If we know the true node mapping between the networks, we can let the labels be node names. We consider measures that rely on node names to be capturing topological quality (TQ) of an alignment. If we do not know the true node mapping, we let the labels be nodes’ (i.e., proteins’) GO terms. We consider measures that rely on GO terms to be capturing functional quality (FQ) of an alignment; we discuss such measures in Section II-C.2. We measure internal consistency of aligned protein groups in a pairwise alignment via precision, recall, and F-score of node correctness (P-NC, R-NC, and F-NC, respectively); these measures, introduced by [7], work for both one-to-one and many-to-many pairwise alignments (Supplementary Section S1.2.1). We do this in a multiple alignment via adjusted multiple node correctness (NCV-MNC); this measure, introduced by [22], works for both one-to-one and many-to-many multiple alignments (Supplementary Section S1.2.1).

Also, a good NA method should find a large amount of common network structure, i.e., produce high edge conservation. We measure edge conservation in a pairwise alignment via adjusted generalized S³ (NCV-GS³); this measure, introduced by [7], works for both one-to-one and many-to-many pairwise alignments (Supplementary Section S1.2.1). We do this in a multiple alignment via adjusted cluster interaction quality (NCV-CIQ); this measure, introduced by [22], works for both one-to-one and many-to-many multiple alignments (Supplementary Section S1.2.1).

Finally, for a good NA method, conserved edges should form large and dense (as opposed to small or isolated) conserved regions. We capture the notion of large and connected conserved network regions (for both pairwise and multiple alignments) via largest common connected subgraph (LCCS). This measure, recently extended from PNA [37] to MNA [22], works for both one-to-one and many-to-many alignments, and for both pairwise and multiple alignments (Supplementary Section S1.2.1).

2). FUNCTIONAL QUALITY (FQ) MEASURES

Per Section II-C.1, a good alignment should have internally consistent aligned node groups. Instead of protein names as in Section II-C.1, in this section we use GO terms as protein labels to measure internal consistency. Having aligned node groups that are internally consistent with respect to GO terms is important for protein function prediction.

We measure internal node group consistency with respect to GO terms in two ways. First, we do so via mean normalized entropy (MNE); this measure, introduced by [20] (also, see [22] for formal definition), works for both one-to-one and many-to-many alignments, and for both pairwise and multiple alignments (Supplementary Section S1.2.2). Second, we do so via an alternative popular measure, GO correctness (GC); this measure, recently extended from PNA [35] to MNA [22], works for both one-to-one and many-to-many alignments, and for both pairwise and multiple alignments (Supplementary Section S1.2.2).

In addition to measuring internal node group consistency, we directly measure the accuracy of protein function prediction. That is, we first use a protein function prediction approach (Section II-C.3) to predict protein-GO term associations, and then we compare the predicted associations to known protein-GO term associations to see how accurate the predicted associations are. We do so via precision, recall, and F-score measures (P-PF, R-PF, and F-PF, respectively); these measures work for both one-to-one and many-to-many alignments, and for both pairwise and multiple alignments (Supplementary Section S1.2.2).

3). PROTEIN FUNCTION PREDICTION APPROACHES

Here, we discuss how we predict protein-GO term associations from the given alignment. We use a different protein function prediction approach for each alignment type. Therefore, below, first, we discuss an existing approach that we use to predict protein GO-term associations from pairwise alignments (approach 1). Second, we discuss an existing approach that we use to predict these associations from multiple alignments (approach 2). Third, since the existing approach for multiple alignments (approach 2) is very different from the existing approach for pairwise alignments (approach 1), to make comparison between pairwise and multiple alignments (i.e., between PNA and MNA) more fair, we extend approach 1 for pairwise alignments into a new approach for multiple alignments (approach 3). As we show in Section III-E.1, our new approach 3 in general improves upon the existing approach 2. So, we propose approach 3 as a new superior strategy for predicting protein-GO term associations from multiple alignments, which is another contribution of our study.

a: APPROACH 1. EXISTING PROTEIN FUNCTION PREDICTION FOR PAIRWISE ALIGNMENTS

Here, we predict protein GO-terms associations using a multi-step process proposed by [7]. For each protein v in the alignment that has at least one annotated GO term, and for each GO term g, first, we hide v’s true GO term(s). Second, we determine if the alignment is statistically significant with respect to g, i.e., if the number of aligned node pairs in which the aligned proteins share GO term g is significantly high (p-value below 0.05 according to the hypergeometric test;see [7] for details). Repeating this process for all nodes and GO terms results in set X of predicted protein-GO term associations.

b: APPROACH 2. EXISTING PROTEIN FUNCTION PREDICTION FOR MULTIPLE ALIGNMENTS

Here, we predict protein GO-term associations using the approach of [4], as follows. For each protein v in the alignment that has at least one annotated GO term, and for each GO term g, first, we hide the protein’s true GO term(s). Second, given that v belongs to aligned node group C, we measure the enrichment of C in g using the hypergeometric test. If C is significantly enriched in g (p-value below 0.05; see [22] for details), then we predict v to be associated with g. Repeating this process for all nodes and GO terms results in set X of predicted protein-GO term associations.

c: APPROACH 3. NEW PROTEIN FUNCTION PREDICTION FOR MULTIPLE ALIGNMENTS

Here, we introduce a new approach to predict protein GO-term associations from a multiple alignment. First, for each node group C_i in the alignment, C_i is converted into a set of all possible $\left(\underset{2}{\left|C_i\right|}\right)$ node pairs in the group. The union of all resulting node pairs over all groups C_i forms the set F of all aligned node pairs. Second, for each protein v in the alignment that has at least one annotated GO term, and for each GO term g, we hide v’s true GO term(s). Third, we determine if the alignment is statistically significant with respect to g, i.e., if the number of aligned node pairs F in which the aligned proteins share GO term g is significantly high (p-value below 0.05 according to the hypergeometric test; see Supplementary Section S1.2.3 for details). Repeating this process for all nodes and GO terms results in a set of predicted protein-GO term associations. Our proposed approach 3 is identical to approach 1 except for its first step of converting a multiple alignment into a set of aligned node pairs.

4). STATISTICAL SIGNIFICANCE OF ALIGNMENT QUALITY SCORES

Since PNA and MNA methods result in different output types (as they produce alignments that differ in the number and sizes of aligned node groups for the same networks), to allow for as fair as possible comparison of the different NA methods, we do the following. For each NA method, each pair/set of aligned networks, and each alignment quality measure, we compute the statistical significance (i.e., p-value) of the given alignment quality score. Then, we take the significance of each alignment quality score into consideration when comparing the NA methods (as explained in Section II-D.3). We compute the p-value of a quality score of an alignment as described in Supplementary Section S1.2.4.

D. EVALUATION FRAMEWORK

Given a network set, to fairly compare PNA and MNA, we compare the NA methods when aligning all possible pairs of networks in the set (pairwise evaluation framework, Section II-D.1), as well as when aligning all networks in the set at once (multiple evaluation framework, Section II-D.2). PNA is expected to perform better under the pairwise evaluation framework (which is native to PNA), and MNA is expected to perform better under the multiple evaluation framework (which it is native to MNA).

1). PAIRWISE EVALUATION (PE) FRAMEWORK

In the PE framework, given a network set, we compare NA methods using pairwise alignments of all possible pairs of networks in the set. Due to the various ways that a pairwise alignment of two networks can be created using PNA or MNA methods, we categorize the pairwise alignments into the following three categories. Specifically:

• We apply PNA to all possible network pairs, denoting the resulting alignments as the PE-P-P alignment category. Here, since all PNA methods are one-to-one, their pairwise alignments will be one-to-one.

• We apply MNA to all possible network pairs, denoting the resulting alignments as the PE-M-P alignment category. Here, if an MNA method is many-to-many, then its pairwise alignments will also be many-to-many. Otherwise, they will be one-to-one.

• We apply MNA to the whole network set and break the resulting multiple alignment into all possible pairwise alignments, as illustrated in Fig. 3(a). Specifically, given a multiple alignment spanning all of the networks (in our Fig. 3(a) illustration, three), we create a pairwise alignment for every pair of networks (i.e., three pairs) as follows: for the two networks in a given pair, we remove every node from the multiple alignment that is not a part of the two networks, which results in a pairwise alignment of the two networks. We denote the resulting pairwise alignments as the PE-M-M alignment category. Again, for a one-to-one or many-to-many MNA method, its pairwise alignments will also be one-to-one or many-to-many, respectively.

In the PE framework, we align all pairs of networks within each of the five analyzed network sets (Yeast+%LC, PHY₁, PHY₂, Y2H₁, and Y2H₂; Section II-A). We evaluate using all alignment quality measures for pairwise alignments, namely F-NC, NCV-GS³, and LCCSTQ measures as well as MNE, GC, and F-PF FQ measures (Section II-C).

FIGURE 3.

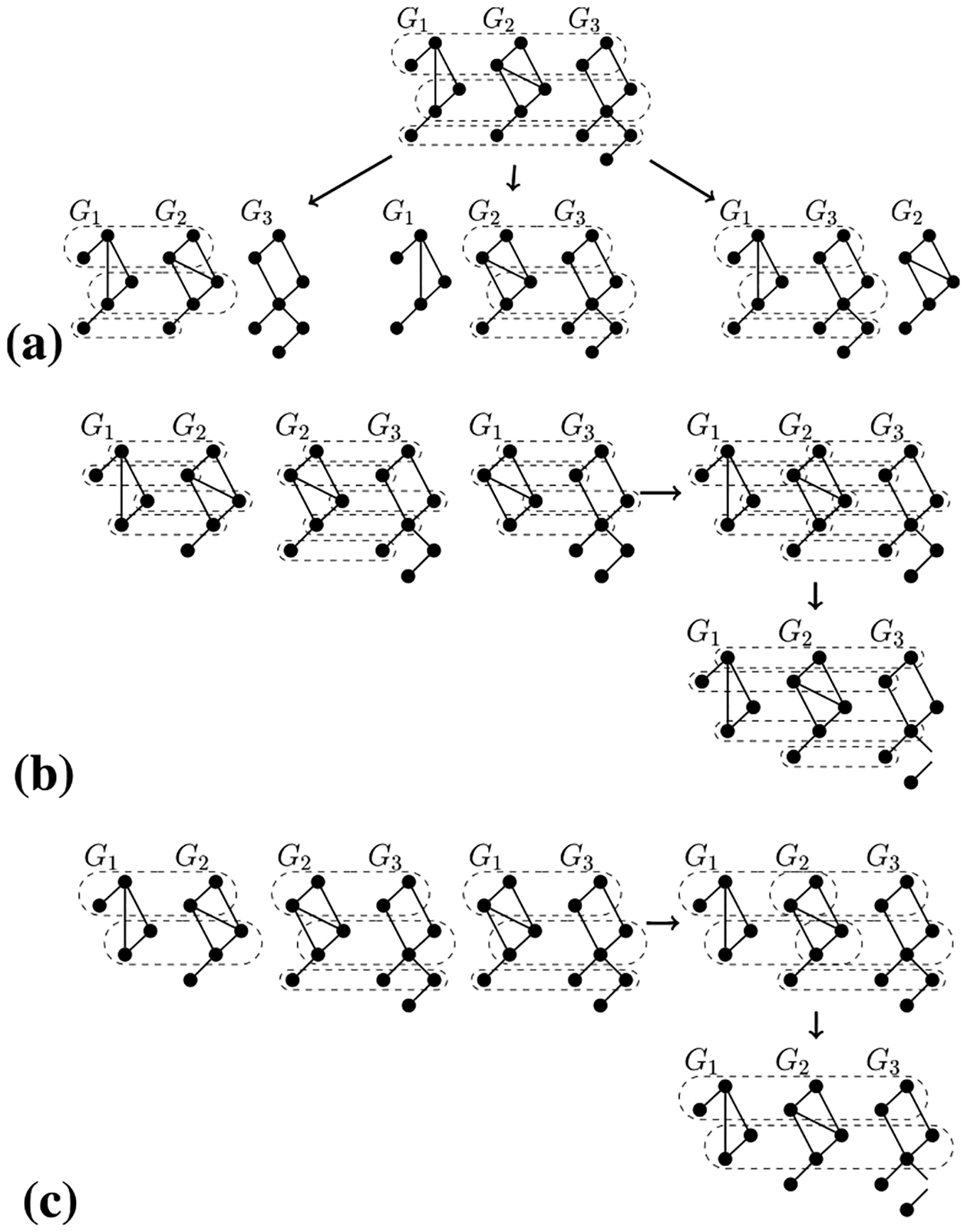
Illustration on a set of three networks (G₁, G₂, and G₃) of how we convert: (a) a multiple alignment to pairwise alignments, (b) one-to-one pairwise alignments to a multiple alignment, and (c) many-to-many pairwise alignments to a multiple alignment.

2). MULTIPLE EVALUATION (ME) FRAMEWORK

In the ME framework, given a network set, we compare NA methods using the resulting multiple alignments of the set. Due to the various ways that a multiple alignment of a network set can be created, we categorize the multiple alignments in the following three categories. Specifically:

• We apply PNA to all possible network pairs and combine the resulting pairwise alignments into a multiple alignment that spans all networks in the set using a variation of a method introduced by [15], as illustrated in Figs. 3(b)–(c) and Supplementary Section S1.3. In more detail, given pairwise alignments of all networks pairs in the set (in our Fig. 3(b)–(c) illustrations, three pairs of networks, (G₁, G₂), (G₂, G₃), and (G₁, G₃)), produced by PNA, we combine the pairwise alignments into a multiple alignment as follows. First, we select a “scaffold” network (in our illustration, G₂). Second, we create a set of node groups consisting of the pairwise alignments between the scaffold network and the other networks (in our illustration, (G₁, G₂) and (G₂, G₃)). Third, we merge node groups that have at least one node in common. This procedure yields a multiple alignment of all networks in the set. We denote the resulting alignment as the ME-P-P alignment category. Here, even though all PNA methods are one-to-one, their pairwise-combined-to-multiple alignments will be many-to-many.

• We apply MNA to all possible network pairs and combine the resulting pairwise alignments into a multiple alignment that spans all networks in the set using the same variation of the method introduced by [15] as above (Fig. 3(b)–(c) and Supplementary Section S1.3), denoting the resulting alignment as the ME-M-P alignment category. Here, independent of whether an MNA method is one-to-one or many-to-many, its pairwise-combined-to-multiple alignments will be many-to-many.

• We apply MNA to the whole network set to align all networks at once, denoting the resulting alignment as the ME-M-M category. Here, if an MNA method is one-to-one, its direct multiple alignments will also be one-to-one. Otherwise, they will be many-to-many.

In the ME framework, we align each of the analyzed network sets that has more than two networks (Yeast%+LC, PHY₁, and Y2H₁; Section II-A). We evaluate using all alignment quality measures for multiple alignments, namely NCV-MNC, NCV-CIQ, and LCCS TQ measures as well as MNE, GC, and F-PF FQ measures (Section II-C).

3). COMPARING THE PERFORMANCE OF NA METHODS

We compare two NA methods in terms of their alignment quality (i.e., accuracy) and running time.

In terms of alignment quality, given a network pair/set and an alignment quality measure (i.e., in a given evaluation test), we compare two NA methods as follows. Let x and y be the methods’ respective alignment quality scores. If both x and y are significant (p-values below 0.001; Section II-C.4) and are within 1% of each other $\left(\frac{\left|x-y\right|}{\left(x+y\right)/2}<0.01\right)$, then the two methods are tied. They are also tied if both x and y are nonsignificant. If both x and y are significant and not tied, then the method with the best score is superior. If x is significant and y is not, then the method with score x is superior, and vice versa.

Given k network pairs/sets and l alignment quality measures, i.e., given k × l evaluation tests, for each evaluation test, we rank all methods from the best one to the worst one, as follows. Given the methods’ alignment quality scores, for methods with non-significant scores, we rank the methods last. For methods with significant scores, we perform the following procedure. If a given method has the best alignment quality score, then we give it rank 1 (as the 1^st best method). We give the next best performing method rank 2, and so on. If a given method is tied with the next best performing method, then we rank both methods with the superior (i.e., lower) rank. The subsequent methods are ranked as if the previous methods were not tied. For example, if methods a and b are tied, they are both given rank 1, and if method c is not tied with method a or method b, then method c is given rank 3). We call this resulting rank for a given evaluation test an evaluation test rank. We calculate the overall ranking of an NA method by taking the mean of its ranks over all k×l evaluation tests. To evaluate whether the overall rankings of two methods are significantly different from each other, we apply the one-tailed Wilcoxon signed-rank test on the k×l evaluation test ranks of the two methods.

We also compare the NA methods with respect to their running times. Specifically, for each network pair/set, for each alignment category in the PE and ME frameworks, we give the fastest method rank 1, the second fastest method rank 2, and so on. Each method is restricted to use a maximum of 64 cores.

III. RESULTS AND DISCUSSION

In Section III-A, we compare the quality of T alignments and T+S alignments. In Sections III-C and III-D, we compare PNA against MNA in the PE and ME framework, respectively, in terms of TQ and FQ accuracy as well as running time. In Section III-E, we compare PNA against MNA exclusively in terms protein function prediction accuracy, as the main goal of biological NA is to predict protein functions in one species from protein functions in another species, based on the species’ network alignment.

A. T VERSUS T+S ALIGNMENTS

Network topology alone can be used to find good alignments of PINs [35]. But protein sequence information can be used to complement network topology in order to produce superior alignments [40]. Due to the complementarity of network topology and protein sequence information, we expect T+S alignments to have higher alignment quality than T alignments. In fact, we verify this. Namely, for each NA method, we compare the given method’s T alignments to their corresponding T+S alignments, in terms of TQ and FQ measures, under the PE and ME frameworks (Fig. 4). We find the following.

FIGURE 4.

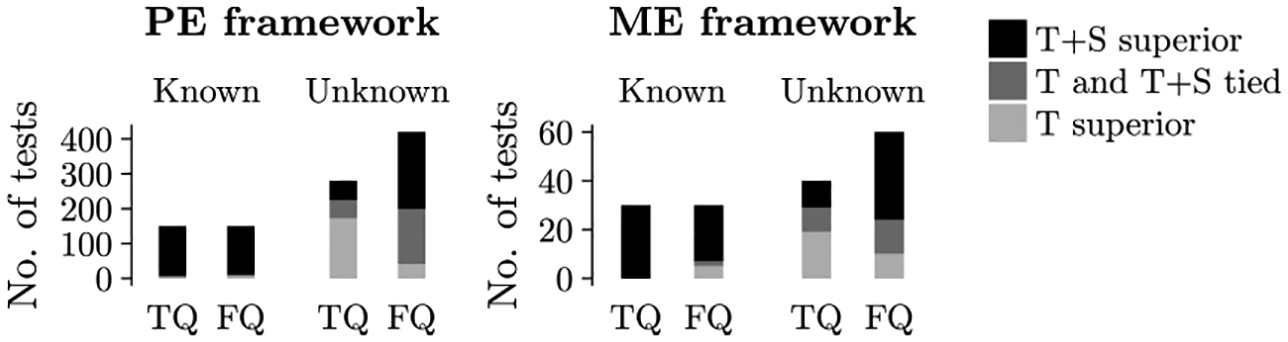
Comparison of the quality of T alignments versus the corresponding T+S alignments, under each of the PE and ME frameworks. Each bar shows the number of cases (here, a case refers to a combination of NA method, a network pair/set, and an alignment quality measure) in which the T alignment is superior, the T+S alignment is superior, or the two alignments are tied (i.e., within 1% of each other’s accuracy). The cases are separated into network pairs/sets with known true node mapping and network pairs/sets with unknown true node mapping.

For networks with known true node mapping, T+S alignments are superior to the corresponding T alignments in almost all cases. Note that as already recognized by [22], for these networks, i.e., for the Yeast+%LC network set, the superiority of T+S alignments over T alignments is not a surprising result. This is because this dataset contains networks that all have the same set of nodes. Consequently, it contains many inter-network pairs of nodes that are the same proteins. Sequence similarities of such matching node pairs are higher than those of other non-matching node pairs. These matching inter-network node pairs can likely form aligned node groups that have very high intra-group sequence similarity due to the node pairs containing identical proteins. This could explain the superiority of T+S alignments over T alignments for the set of networks with known node mapping.

Even for the sets of networks with unknown node mapping (PHY1, PHY2, Y2H1, Y2H2), whose networks contain different node sets, we still see that T+S alignments are overall superior to T alignments. Namely, only in terms of TQ, T alignments are somewhat superior to T S alignments, but T+S alignments are still superior to or tied with the corresponding T alignments in just under a half of all cases. In terms of FQ, T+S alignments are superior to or tied with the T alignments in almost all evaluation tests.

So, we conclude that T+S alignments are overall superior to T alignments. Because of this, because T+S alignments are more relevant in the computational biology domain, and because of space constraints, henceforth, we mainly analyze T+S alignments. Importantly, our findings for T+S alignments also hold for T alignments (Supplementary Fig S6).

Due to space constraints, for additional results on the similarity (overlap) of the alignments produced the different NA methods, which demonstrate that using protein sequence information overall yields alignment consistency between the different NA methods, see Supplementary Section S1.4 and Supplementary Figs. S1–S3.

B. METHOD COMPARISON: EVALUATION DETAILS

In Fig. 5, we compare PNA and MNA over all evaluation tests (where a test is a combination of a network pair/set and an alignment quality measure) for T+S alignments; analogous comparison for T alignments is shown in Supplementary Fig. S6. In this section, we discuss how we evaluate and compare PNA and MNA. We show the results of the comparison in Section III-C for the PE evaluation framework and in Section III-D for the ME evaluation framework.

FIGURE 5.

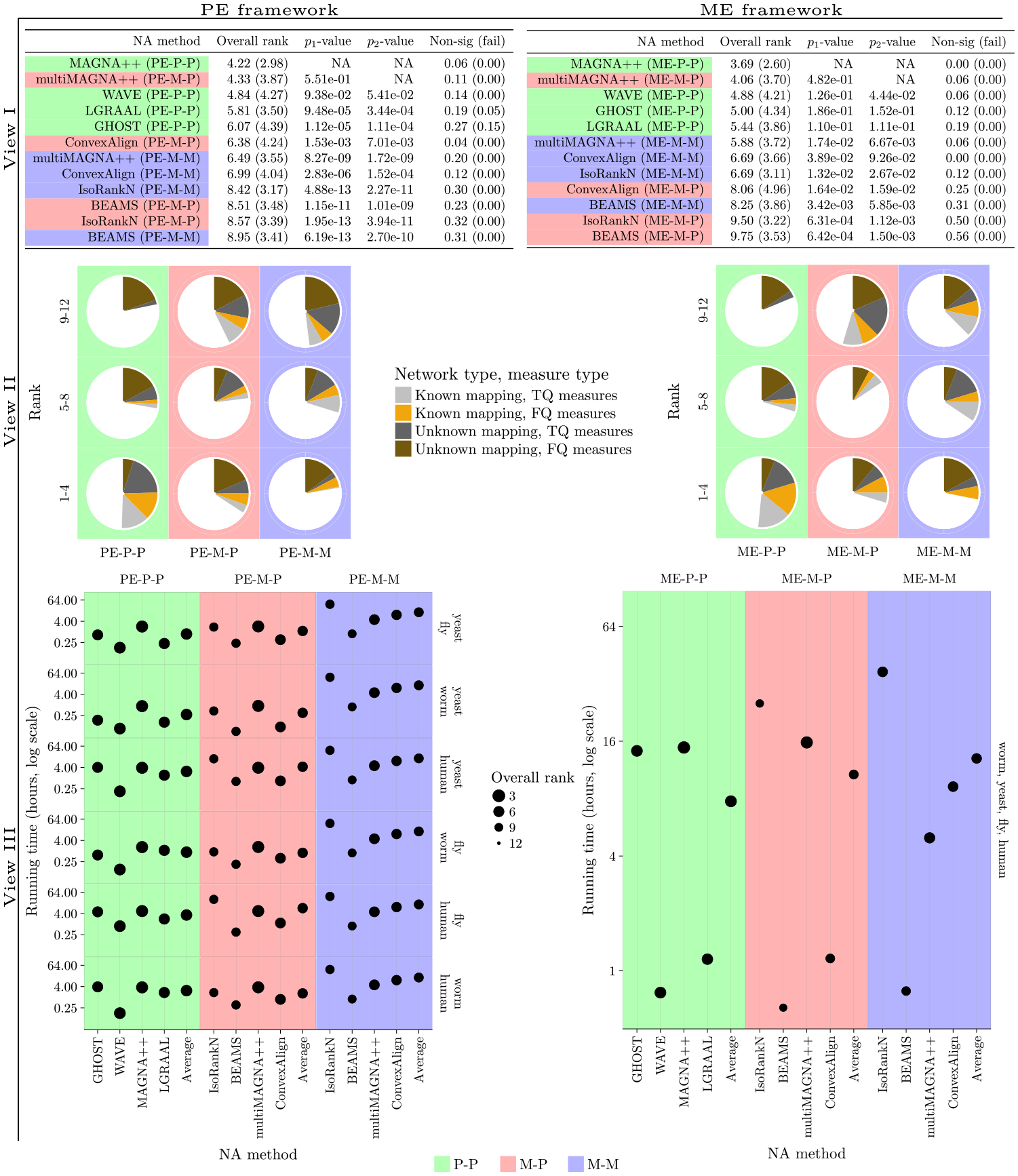
Alignment category comparison results for each of the PE and ME frameworks over all evaluation tests for T+S alignments. The alignment categories (i.e., PE-P-P, etc.) are color-coded. View I. Overall ranking of the NA methods. The “Overall rank” column shows the rank of each method averaged over all evaluation tests, along with the corresponding standard deviation (in brackets). View II. Alternative view of ranking of the NA methods. Each pie chart shows the fraction of evaluation test ranks that fall into the 1–4, 5–8, and 9–12 rank bins out of all evaluation test ranks in the given alignment category. The pie charts are color-coded with respect to alignments of network pairs/sets with known and unknown node mapping, and TQ and FQ measures. View III. Overall ranking of an NA method versus its running time for the Y2H_n1 network set. The size of each point visualizes the overall ranking of the corresponding method over all evaluation tests, corresponding to the “Overall rank” column in View I; the larger the point size, the better the method.

In all of Sections III-B, III-C, and III-D, when we refer to an “NA method”, we mean the combination of a PNA or MNA method and an alignment category (Section II-D). Namely, there are 12 NA methods in the PE framework (four PNA methods associated with the PE-P-P category and four MNA methods associated with each of the PE-M-M and PE-M-P categories) and 12 NA methods in the ME framework (four PNA methods associated with the ME-P-P category and four MNA methods associated with each of the ME-M-M and ME-M-P categories). We analyze the NA methods via three views, described below and visualized in Fig. 5:

• View I: Overall ranking of the NA methods, as described in Section II-D.3. Since there are 12 methods in a given (PE or ME) framework, the possible ranks range from 1 to 12. The lower the rank, the better the given method. The “p₁-value” column shows the statistical significance of the difference between the ranking of the 1^st best ranked method and each other method. The “p₂-value” column shows the statistical significance of the difference between the ranking of the 2^nd best ranked method and each other method. The “Non. sig. (fail)” column shows the fraction of all evaluation tests in which the alignment quality score is not statistically significant, and, in brackets, the fraction of evaluation tests in which the given NA method failed to produce an alignment.

• View II: Pie charts showing the fraction of evaluation test ranks that fall into the 1–4, 5–8, and 9–12 rank bins out of all evaluation test ranks in the given alignment category. For example, for the PE framework, in the PE-P-P alignment category, 56%, 26%, and 18% of the evaluation test ranks fall into ranks 1–4, 5–8, and 9–12, respectively, totaling to 100% of the evaluation test ranks in the PE-P-P alignment category. The pie charts allow us to compare the three alignment categories rather than individual NA methods in each category. The larger the pie chart for the better (lower) ranks, and the smaller the pie chart for the worse (higher) ranks, the better the alignment category. For example, in the PE framework, PE-P-P has the most evaluation tests ranked 1–4 and the fewest evaluation tests ranked 9–12, followed by PE-M-P, followed by PE-M-M. This implies that PE-P-P is superior to PE-M-P and PE-M-M.

• View III: Overall ranking of an NA method versus its running time, as described in Section II-D.3. In order to allow for easier comparison between the different alignment categories, “Average” shows the average running times and average rankings of the methods in each alignment category.

C. METHOD COMPARISON: RESULTS IN THE PE FRAMEWORK

We expect that under the PE framework, PNA will perform better than MNA. This is exactly what we observe. So, the most interesting and shocking results of our study do not originate from this section. Instead, they originate from Section III-D below, when comparing PNA and MNA in the ME framework.

Namely, in the PE framework, the overall ranking of the PNA methods (T+S alignments from the PE-P-P category) is generally better (lower) than the overall ranking of the MNA methods (T+S alignments from the PE-M-P and PE-M-M categories) (View I of Fig. 5). An exception is multiMAGNA++’s alignments from the PE-M-P category (multiMAGNA++ directly applied to network pairs), whose overall ranking is also very good (low). This could be due to multiMAGNA++ being a one-to-one MNA method, which might have caused it to behave similarly as PNA methods (all of which are also one-to-one) when it is used to align only two networks. This is further supported by the fact that the only other considered one-to-one MNA method, ConvexAlign, and specifically its PE-M-P version, is also ranked better (lower) than the remaining two many-to-many MNA methods, IsoRankN and BEAMS. Nonetheless, ConvexAlign still has worse (higher) ranking than any PNA method (View I of Fig. 5).

Next, we break down the results into those for networks with known versus unknown node mapping, and also, into those for TQ versus FQ measures (View II of Fig. 5); additional, even more detailed results for the PE framework are shown in Supplementary Table S14. For networks with known mapping, we find that PNA performs better than MNA in terms of both TQ and FQ. For networks with unknown mapping, PNA performs better than MNA in terms of TQ, while in terms of FQ, the situation is not as clear.

Namely, for networks with unknown mapping and FQ, as can be seen in View II of Fig. 5, MNA falls into the best (lowest) ranks 1–4 in more of the evaluation tests than PNA This implies that MNA is better than PNA. However, at the same time, MNA also falls into the worst (highest) ranks 9–12 in more of the evaluation tests than PNA. This implies that MNA is worse than PNA. Because we are interested in comparing the whole category of the considered PNA approaches against the whole category of the considered MNA approaches (per our discussion in Section I-B), the above two results combined could be interpreted as MNA and PNA being comparable for networks with unknown mapping and FQ. On the other hand, for the same networks (with unknown mapping) and TQ, as well as for networks with known mapping and both TQ and FQ, PNA falls into the best ranks 1–4 in more of the evaluation tests than MNA, and at the same time, PNA falls into the worst ranks 9–12 in fewer of the evaluation tests than MNA, which means that PNA is superior to MNA.

Another observation is as follows (Supplementary Tables S4–S7). For evaluation tests in which PNA is clearly superior in terms of method rankings to MNA (again, with the exception of multiMAGNA++’s PE-M-P version), which are tests excluding networks with unknown mapping and FQ, the best-ranked PNA method (MAGNA++ or WAVE) is significantly superior to the best-ranked MNA method (multiMAGNA++’s PE-M-M version, followed by all other MNA methods that are all similarly ranked), with p-values below 1.8 × 10⁻⁶. On the other hand, for tests where it is unclear which of PNA and MNA is better, which are tests involving networks with unknown mapping or FQ, the best-ranked MNA method (ConvexAlign’s PE-M-P version) is only marginally better than the best-ranked PNA method (MAGNA++), with p-values between 0.048 and 0.332. This justifies referring to PNA and MNA as comparable for networks with unknown mapping and FQ, and to PNA as being superior in all other cases.

Next, we want to comment on the two MNA methods that perform well in at least some evaluation tests in the PE (pairwise) framework: multiMAGNA++ and ConvexAlign. Both of these methods produce one-to-one mappings, unlike the other two MNA methods, BEAMS and IsoRankN, which produce many-to-many mappings. Given that all PNA (pairwise) methods are also one-to-one, it might not be surprising that the two one-to-one MNA methods also perform well in the PE framework. This could be because the existing measures for pairwise alignment accuracy favor one-to-one mappings. However, we believe that it is not just the one-to-one aspect of multiMAGNA++ and ConvexAlign that is relevant. First, while multiMAGNA++ performs reasonably well in all tests (networks with both known and unknown node mappings, and both TQ and FQ), ConvexAlign performs poorly for networks with known mapping or TQ but exceptionally well (marginally better than multiMAGNA++) for networks with unknown mapping and FQ. So, even though both methods are one-to-one, each has its unique (dis)advantages. Second, in Section III-D, which evaluates the methods in the ME (multiple) framework, of the four MNA methods, it is again multiMAGNA++ and ConvexAlign that perform the best.This is despite the fact that the existing measures for multiple alignment accuracy do not necessarily favor one-to-one mappings, and some (especially FQ) actually favor many-to-many mappings.

A likely reason why ConvexAlign performs well only for networks with unknown node mapping and FQ is because its parameter values that were recommended and pre-set by its authors and that we use (Supplementary Section S1.1) were determined via cross-validation, by optimizing FQ (GO term similarity of mapped nodes) in alignments of networks with unknown node mapping (PPI networks of mouse and human) [23]. Hence, ConvexAlign is semi-supervised, i.e., pre-trained to achieve high FQ scores, which makes it biased compared to the other considered NA methods, all of which are unsupervised.

1). ACCURACY VERSUS RUNNING TIME

The PNA methods are not only more accurate in general (as demonstrated above), but on average they are also at least somewhat if not much faster (View III of Fig. 5). In fact, no MNA method has both better running time and better ranking than any PNA method, while many PNA methods have both better running time and better ranking than every MNA method. Additional results where each method is restricted to use a single core are shown in Supplementary Fig. S4.

D. METHOD COMPARISON: RESULTS IN THE ME FRAMEWORK

We expect that under the ME framework, MNA will perform better than PNA. Shockingly, we do not find this. Instead, our results reveal the opposite trends, which match those observed under the PE framework. So, the most interesting results of our study originate from this section.

Namely, in the ME framework, the overall ranking of the PNA methods (T+S alignments from the ME-P-P category) is generally better (lower) than the overall ranking of the MNA methods’ T+S alignments from the ME-M-M category, which in turn is generally better than the overall ranking of the MNA methods’ T+S alignments from the ME-M-P category (View I of Fig. 5). Again, multiMAGNA++ is an exception: its alignments from the ME-M-P category (multiMAGNA++ first being applied to network pairs and then its pairwise alignments being combined into a multiple alignment) are ranked very good (low).

When we inspect the ranking of the methods in more detail (View II of Fig. 5), again, we find similar trends as in the PE framework. Namely, for networks with known mapping, we find that PNA performs better than MNA in terms of both TQ and FQ. For networks with unknown mapping, PNA performs better than MNA in terms of TQ. In terms of FQ, just as under the PE framework, MNA falls into the best (lowest) ranks in more of the evaluation tests than PNA, but at the same time, MNA also falls into the worst (highest) ranks in more of the evaluation tests than PNA. Additional, even more detailed results for the ME framework are shown in Supplementary Table S15.

Another result also applies to the ME framework: of the MNA methods, multiMAGNA++ and ConvexAlign perform better than BEAMS and IsoRankN, where multiMAGNA++ performs consistently well across all tests, and ConvexAlign performs extremely well only for networks with unknown node mapping and FQ (Supplementary Tables S8–S11).

Notice that under the ME framework, the best (PNA or MNA) methods are all one-to-one. Because all considered PNA methods are one-to-one, one might suspect that PNA may be overall better than MNA in the ME framework not because of the “pairwise” part but simply because of the “one-to-one” part, possibly because one might suspect our evaluation measures in the ME framework to favor one-to-one methods. However, we argue that this is not the case, as follows.

First, if we could show that any existing one-to-one method performed worse than any existing many-to-many method in our ME framework, this would suffice to show that our ME framework does not favor one-to-one-methods. While for our considered methods it is the case that one-to-one (PNA or MNA) methods are superior to many-to-many (MNA) methods, this could be simply because the considered one-to-one methods are more recent and thus more powerful than the considered many-to-many methods. Indeed, when we add to our ME evaluation an older (and thus inferior) one-to-one MNA method, GEDEVO-M [27], we find that this one-to-one method is outperformed by the considered many-to-many MNA methods (Supplementary Tables S16–S20). If one-to-one methods had some advantage over many-to-many methods in our ME framework, this would not have happened. So, a method’s performance in our ME framework does not seem to be directly related to it being one-to-one or many-to-many.

Second, by design, our evaluation measures do not favor one-to-one methods. Namely, recall that many of our evaluation measures were proposed by studies that introduced or analyzed many-to-many NA methods (Section II-C). An example is one of our considered FQ measures, mean normalized entropy (MNE), which originates from the IsoRankN study [20], where IsoRankN is one of the considered many-to-many MNA methods. So, MNE is unlikely to favor one-to-one methods, as it was proposed in the many-to-many context. Actually, when we mirror the exact same MNE evaluation as in the IsoRankN study (see [20] for details) on the methods we consider here (rather than combine MNE with our other FQ measures as done so far in the paper), the considered one-to-one methods still perform well (i.e., the best of all considered one-to-one methods is still better than the best of all considered many-to-many methods) (Supplementary Tables S12–S13). That is, even a measure designed explicitly for many-to-many alignments still ranks one-to-one-alignments better than many-to-many alignments. This additionally confirms that the overall superiority of the considered one-to-one (PNA or MNA) methods over the considered many-to-many (MNA) methods in the ME framework is likely because the one-to-one methods actually yield higher-quality alignments.

In summary, with these two findings in mind, it is more likely that the considered one-to-one methods perform better than the considered many-to-many methods in the ME framework because recent studies have focused on one-to-one alignments. Consequently, increased research in this area has likely led to better methodological advancements of one-to-one methods compared to many-to-many methods, explaining the one-to-one methods’ superior performance.

1). ACCURACY VERSUS RUNNING TIME

When we compare the overall rankings of the NA methods to their running times (View III of Fig. 5), again, we find similar trends as in the PE framework: the PNA methods are not only more accurate (as demonstrated above), but on average they are also faster.

Since the PNA methods must align every pair of networks in order to produce a multiple alignment, and since this results in a quadratically increasing running time with respect to the number of networks k, we ask whether there is some value of k at which PNA might become less efficient (i.e., slower) than MNA. Due to space constraints, we present this discussion in Supplementary Section S1.5 and Supplementary Table S3. Additional results where each method is restricted to use a single core are shown in Supplementary Fig. S5.

E. METHOD COMPARISON FOCUSING ON ACCURACY OF PROTEIN FUNCTION PREDICTION

1). NEW FUNCTION PREDICTION APPROACH UNDER THE ME FRAMEWORK

Here, we focus on addressing a potential issue with the existing approach for protein function prediction for multiple alignments, which we have used up to this point. As discussed in Section II-C.3, since the existing approach for multiple alignments (approach 2) is very different than the existing approach for pairwise alignments (approach 1), to make comparison between pairwise and multiple alignments (i.e., between PNA and MNA) more fair, we extend approach 1 for pairwise alignments into a new approach for multiple alignments (approach 3).

Then, we compare the new approach 3 against the existing approach 2, in hope that approach 3 will outperform approach 2. If so, in our subsequent analyses, we will use approach 3 for protein function prediction for multiple alignments. This way, comparing results of approaches 1 and 3 will be much more fair than comparing results of approaches 1 and 2. Consequently, we will be able to more fairly compare PNA against MNA.

Indeed, we find that our new approach 3 overall outperforms the existing approach 2 (Fig. 6 and Supplementary Fig. S7). Specifically, approach 3 is overall comparable to approach 2 for networks with known node mapping (marginally inferior in terms of precision, marginally superior in terms of recall) and it is superior to approach 2 for networks with unknown node mapping (in terms of both precision and recall).

FIGURE 6.

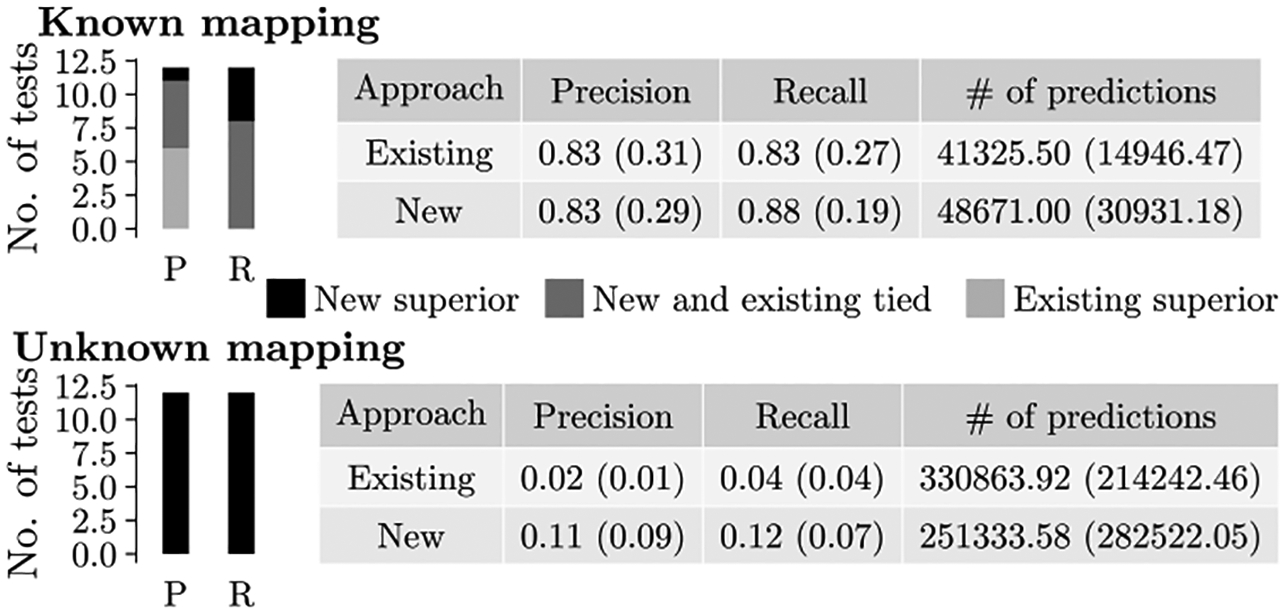
Comparison of protein function prediction accuracy between the new (approach 3) versus existing (approach 2) prediction approach for multiple alignments. Each bar on the left of the figure shows the number of cases (i.e., alignments) in which the new approach is superior, the existing approach is superior, or the two approaches are tied. Each table shows the precision, recall, and number of predictions averaged over all tests. In parentheses, we show standard deviations. The results are separated into network sets with known and unknown node mapping.

For networks with known node mapping, the number of predictions made by approach 3 is just 0.5%−5.8% larger than that made by approach 2, depending on the NA method, as shown in Supplementary Fig. S7 (with the exception of ConvexAlign, which produces up to 54% more predictions under approach 3 than under approach 2). The slightly more predictions by approach 3 could explain its slightly lower precision and slightly higher recall. But the differences in the number of predictions as well as accuracy of these two approaches on networks with known mapping are so minor (within 2%−5%) that we consider them as comparable.

For networks with unknown node mapping, the number of predictions made by approach 3 is 2%−72% smaller than the number of predictions made by approach 2, depending on the NA method (with exception of ConvexAlign and BEAMS, which in one instance produce 6% and 158% more predictions, respectively, under approach 3). While the fewer predictions under approach 3 could explain higher precision of approach 3 compared to approach 2, interestingly, approach 3 also results in higher recall than approach 2, despite the latter making more predictions (Fig. 6).

2). PROTEIN FUNCTION PREDICTION UNDER PE VERSUS ME FRAMEWORKS

Next, we compare protein function prediction accuracy between the PE and ME frameworks, relying on approach 1 for pairwise alignments and on the fairly comparable approach 3 for multiple alignments. For analogous results where we use the existing approach 2 for the ME framework, see Supplementary Fig. S10.

For both the network sets with known and unknown node mapping, the predictions under the PE framework have higher precision while the predictions under the ME framework have higher recall (Fig. 7 and Supplementary Fig. S8. Note that here, higher precision and lower recall for the PE framework compared to the ME framework could be due to somewhat fewer predictions under the PE framework than under the ME framework. Also, note that for networks with known node mapping, both sets of predictions have impressively high precision and recall scores, so any difference in their scores (1%−6%) can be considered marginal. This is not the case for networks with unknown node mapping, where the scores are lower. In this case, the superiority of the PE framework’s precision over the ME framework’s precision (17%) is more pronounced than the superiority of the ME framework’s recall over the PE framework’s recall (8%). Additionally, achieving higher precision might be more preferred than achieving higher recall in the task of protein function prediction by experimental scientists who would potentially validate the predictions. Thus, we can argue that overall the PE framework (i.e., pairwise alignments) results in more accurate predictions than the ME framework (i.e., multiple alignments).

FIGURE 7.

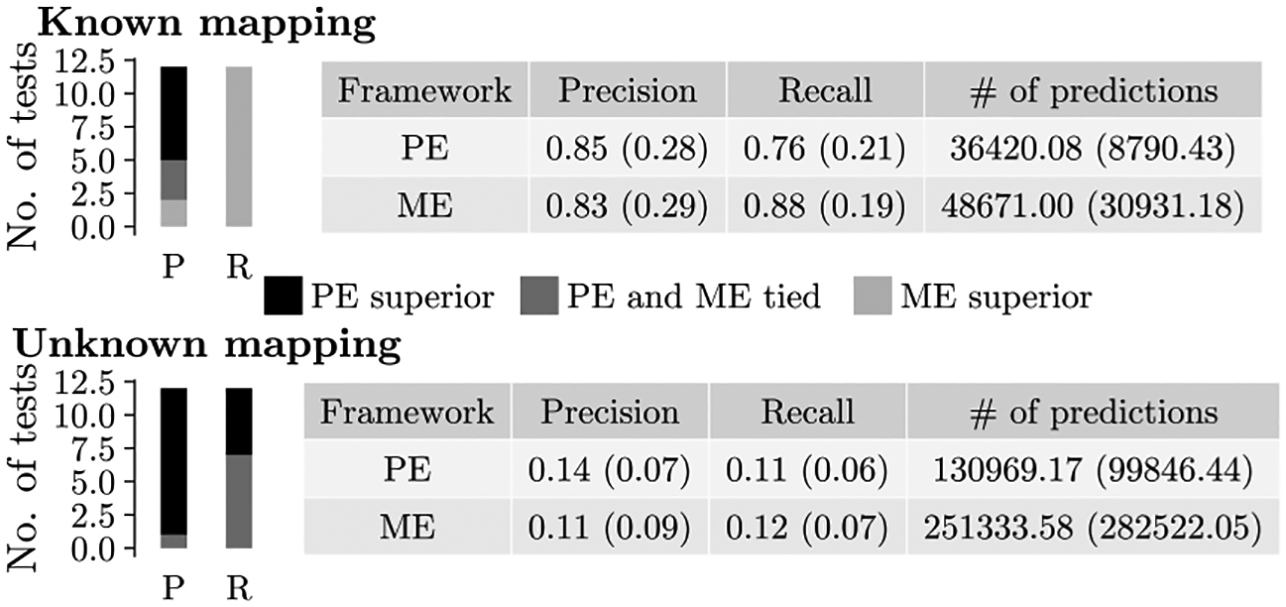
Comparison of protein function prediction accuracy under the the PE and ME frameworks. The figure can be interpreted the same way as Fig. 6. Here, we use new approach 3 for the ME framework.

IV. CONCLUSION

We introduce an evaluation framework for a fair comparison of PNA against MNA, in order to test the hypothesis that MNA can capture deeper biological insights, i.e., produce higher-quality alignments, compared to PNA. We find that (i) the considered PNA methods produce pairwise alignments that are of higher quality than the corresponding pairwise alignments produced by the considered MNA methods, and (ii) the PNA methods produce multiple alignments that are of higher quality than the corresponding multiple alignments produced by the MNA methods. Also, using the pairwise alignments leads to higher protein function prediction accuracy than using the multiple alignments. Importantly, in addition to PNA being overall more accurate, it is also overall faster than MNA. This holds both both of T+S alignments and T alignments.

In our evaluation, i.e., thus far in the paper, we have aimed to compare the two categories of approaches, PNA and MNA, rather than to identify which specific NA method (whether of the PNA or MNA type) is the best, for reasons discussed in Section I-B. Only here, we briefly comment on the performance of the best approach(es) in each category.

In the PNA category, most of the considered approaches, and especially MAGNA++, perform well consistently across the different scenarios (in both PE and ME framework, for both networks with known and unknown node mapping, and for both TQ and FQ), with some exceptions (Supplementary Tables S4–S11). In the MNA category, only multiMAGNA++ works well consistently across all scenarios. Additionally, ConvexAlign works well for FQ and networks with unknown node mapping.

However, no method is always the best (i.e., has an overall rank of 1 over all evaluation tests). Namely, while in both PE and ME frameworks several PNA methods and the multiMAGNA++ MNA method achieve very good (low) overall ranks in the 1–2 range for networks with known node mapping or TQ, for networks with unknown node mapping and FQ, overall ranks start at about 4 (Supplementary Tables S4–S11). That is, for networks with unknown mapping and FQ, even the best methods (ConvexAlign and multiMAGNA++) work well for some but not all networks or alignment quality measures. So, there seems to be a lot more room for improvement on how to better perform PNA or MNA to improve FQ (the quality of functional predictions) from networks with unknown mapping (PPI networks of different species). Fig. 7 further signals this, given low prediction accuracy under both the PE and ME frameworks.

Importantly, the best approaches in our study in terms of FQ are of the one-to-one type, which we hypothesize is because of heavier recent focus on and thus methodological advancements of such methods compared to those of the many-to-many type, per our discussion in Section III-D. But one-to-one alignments cannot capture gene duplication events that exist in biological networks [41], which require existence of paralogs, i.e., a gene in one network being mapped to multiple genes in the same or another network. While many-to-many alignments can in theory capture these events, the considered many-to-many methods do not perform well in terms of FQ. So, developing better many-to-many methods might be a crucial future step in NA research.

Since we demonstrate in the ME framework that PNA can (by integrating pairwise alignments) produce multiple alignments that are superior to multiple alignments produced by MNA, we believe that any new MNA methods should be compared not just to existing MNA methods but also to existing PNA methods using our evaluation framework, to properly judge the quality of alignments that they produce. Our suggestion is similar to that of [7], who evaluated local versus global NA (rather than PNA versus MNA) and concluded that any new NA method should be compared against existing local as well as global NA methods.

Moreover, in the ME framework, PNA can produce multiple alignments that are superior to multiple alignments produced by MNA even with the simple variation of the pairwise alignment integration strategy (i.e., scaffolding procedure) introduced by [15]. Any more sophisticated scaffolding procedure that might be developed in the future will yield even more superior PNA-based multiple alignments and consequently even further emphasize the superiority of PNA over MNA. In other words, for MNA to gain advantage over PNA, a drastic redesign of the current MNA algorithmic principles might be needed.

In summary, our current results suggest that perhaps it might be sufficient to focus on the faster PNA and integration of pairwise alignments into multiple ones rather than on the slower MNA. Of course, with development of newer approaches, the conclusions from our study might change. It is crucial that we (the NA community) gain in-depth understanding of practical implications of one-to-one versus many-to-many, pairwise versus multiple, local versus global, and other types of NA. This understanding is even more crucial given recent shift from traditional NA of static and homogeneous (single node type and single edge type) networks towards dynamic [42]-[44] or heterogeneous [45], [46] NA, as well as from data-uninformed (i.e., unsupervised) to data-driven (i.e., supervised) NA [47].

Biographies

VIPIN VIJAYAN was born in Kollam, Kerala, India, in 1986. He received the B.S. degree in physics and mathematics from Virginia Polytechnic Institute and State University, in 2009, and the M.S. and Ph.D. degrees in computer science and engineering from the University of Notre Dame, in 2012 and 2017, respectively.

From 2010 to 2017, he was a Research Assistant with the Computer Vision Research Laboratory and the Complex Networks Laboratory in the University of Notre Dame. He is currently a Machine Learning Engineer with the Research and Development organization, Radiance Technologies. He has authored multiple articles in the fields of computer science and network science. His research interests include network science, computer vision, and machine learning, with a focus on satellite imagery and activity analysis.

SHAWN GU received the B.S. degree in mathematics and the B.A. degree in computer science from Duke University, Durham, NC, in 2016. Since 2016, he has been a Research Assistant with the Complex Networks Laboratory, University of Notre Dame. His research interests include network science, computational biology, and machine learning.

ERIC T. KREBS was born in Indianapolis, IN, USA, in 1996. He received the B.S. degree in computer engineering from the University of Notre Dame, Notre Dame, IN, in 2018.

From 2016 to 2017, he was an Undergraduate Researcher with the Dr. Tijana Milenkovic’s Complex Networks Lab. In 2017, he worked as a Software Engineering Intern at Garmin. After his graduation, he lived as Novice with the friars of the Dominican Eastern Province. Since 2019, he has been a Software Engineer with Zenuity, Novi, MI. He has interests in graph theory and autonomous driving software.

Mr. Krebs is a member of Tau Beta Pi. He was a recipient of the Ford College Network Scholarship, in 2017, and the Steiner Award for all-around excellence in the Notre Dame College of Engineering, in 2018.

LEI MENG received the B.Sc. degree in software engineering from the Harbin Institute of Technology, Harbin, China, the M.Sc. degree in computer science from Baylor University, and the Ph.D. degree in computer science from the University of Notre Dame, under the supervision of Dr. A. Striegel and Dr. T. Milenković. During her Ph.D., she primarily focused on networks and graph analysis. She is currently working on deep learning and natural language processing with Google Research, Mountain View.

TIJANA MILENKOVIĆ received the B.Sc. degree in electrical engineering and computer science from the University of Sarajevo, in 2005, and the M.Sc. and Ph.D. degrees in computer science from the University of California Irvine (UCI), in 2008 and 2010, respectively. She has been a Notre Dame faculty, since 2010. She is currently an Associate Professor of computer science and engineering with the University of Notre Dame. The Milenković lab solves challenging problems in the fields of network science, graph algorithms, computational biology, scientific wellness, and social networks. She received the prestigious 2015 National Science Foundation (NSF) CAREER and 2016 Air Force Office of Scientific Research (AFOSR) Young Investigator Program (YIP) awards, among others. She will serve on the Board of Directors of the International Society for Computational Biology (ISCB), from 2020–2023, representing the Society’s Communities of Special Interest (COSIs). She has been an Associate Editor of the IEEE/ACM TCBB, since 2014, and Scientific Reports (Nature), since 2018. She is committed to increasing participation of women and diversity in computer science.