Stochastic Simulation of Cellular Metabolism

Abstract

Increased technological methods have enabled the investigation of biology at nanoscale levels. Such systems require the use of computational methods to comprehend the complex interactions that occur. The dynamics of metabolic systems have been traditionally described utilizing differential equations without fully capturing the heterogeneity of biological systems. Stochastic modeling approaches have recently emerged with the capacity to incorporate the statistical properties of such systems. However, the processing of stochastic algorithms is a computationally intensive task with intrinsic limitations. Alternatively, the queueing theory approach, historically used in the evaluation of telecommunication networks, can significantly reduce the computational power required to generate simulated results while simultaneously reducing the expansion of errors. We present here the application of queueing theory to simulate stochastic metabolic networks with high efficiency. With the use of glycolysis as a well understood biological model, we demonstrate the power of the proposed modeling methods discussed herein. Furthermore, we describe the simulation and pharmacological inhibition of glycolysis to provide an example of modeling capabilities.

I. INTRODUCTION

Cellular metabolism is a complex network of enzymes, metabolites, and biomolecules that are required to both maintain homeostasis and appropriately react to stimuli. Biochemists began examining cell metabolism in the mid-19th century, and with the advancements in both experimental techniques and computational capacities, increasing comprehension of metabolic intricacies has been realized. Metabolomic studies, as a relatively new field, are concerned with the detection and quantification of metabolites. The analytical side of metabolomics and metabolism can quickly become daunting when considering the complexity of the metabolome. The KEGG Compound database currently contains more than 18,000 metabolites and other small molecules, presenting scientists with a nearly impossible task to understand the complexities of metabolite dynamics [1]. Thus, the computational modeling and simulation of metabolic systems have become essential for their investigation.

Within the last decade, the pursuit of mathematical models for biological systems that can accurately predict cellular- and systems-level behaviors, in addition to providing quantitative data, is an essential area in metabolomics requiring further investigation. Furthermore, a quantitative model with the ability to predict phenotypic changes reliably with perturbation or challenges in silico could lead to scientific breakthroughs not available with traditional means of inquiry. Models as a whole strive to provide a better representation of reality, aiming to represent the system of inquiry accurately. Inclusion of all cellular components directly or indirectly involved are considered too complex to model with current technology. Consequently, assumptions and simplifications are frequently applied in place of “unknowns”, where details are perceived as non-pivotal and with elements such as stochastics omitted for simplicity. Despite these adjustments, the accuracy and competence of the model are still dependent on these assumptions and simplifications.

A variety of approaches are available to model the dynamics of metabolic systems; importantly, these include deterministic and stochastic modeling approaches. Frequently, kinetic models of metabolism were formed using Ordinary Differential Equations (ODE), providing a deterministic modeling approach that provides quantitative information on interactions, underlying dynamics, and system regulation components [2]. ODE models operate with the assumption that all reactions occur under evenly mixed homogenous populations with plentiful molecules available in the environment. Previously, ODEs have been used to simulate biochemical kinetics and biochemical networks. With historically limited computational power, this approach was sufficient to represent the interactions and dynamics occurring within basic biochemical networks. Rapoport et al. described the ability to determine metabolite concentrations of glycolytic intermediates in erythrocytes using a desktop calculator [3]. As computational power has improved over time, metabolite concentrations within a limited chain of reactions can now be determined in a matter of seconds. While ODE modeling reduces computational efforts, the assumptions and simplifications come at the cost of omitting noise and stochastic elements that are inherent in biological systems. Thus, stochastic modeling approaches could be more appropriate representations of in vitro and in vivo systems and provide the capacity to incorporate their statistical properties [2].

While ODE methods are well defined in the biological context, more recently, systems biology has extended the limits of what was previously computationally feasible: modeling the complexities of biological variation that includes the stochastic nature inherent in biology. There are different approaches to modeling stochastics in biological systems, with disparities between those often used at molecular and system levels [4]. Notably, the model proposed here is flexible in its source of stochasticity, which currently employs computed Gaussian randomness; however, an alternative probability distribution could be easily substituted if desired.

Stochastic models are typically formulated by the Chemical Master Equation (CME), with the ability to capture simple stochastic occurrences in biological systems [5,6]. However, the drawback comes with the increased mathematical and computational complexity, considerably limiting the size of the network [7]. The Gillespie algorithm, introduced in 1977, provides exact simulation methods to simulate the CME and can be optimized with the addition of Tau leaps [8,9,10]. Recent studies have also implemented the Gillespie algorithm with additional functions (Hill) to experiment with stochastic gene expression modeling in cases where expression can operate with “switch-like” behavior [11]. Still, attempts are being made to further improve stochastic simulation and overcome the computational intensity required [2,5,12–17]. In addition to the traditional ODE approaches, some larger gene regulatory networks have been assembled with the use of Bayesian model averaging [18,19]. A relatively recent approach to complex biological modeling is the application of queueing theory and networks/models. Similar to the Gillespie algorithm, queueing networks can be considered as a hidden Markov chain, and are more convenient than directly implementing the Gillespie algorithm [20].

Queueing networks have been used broadly to describe data communication networks [21], patient triage at hospitals [22], the HIV infection process [23], pharmacokinetic modeling [24], and non-viral gene delivery [25]. Moreover, the implementation as described by Martin et al. [25], has incorporated other cell processes, such as mitosis or cell necrosis, which are challenging to implement with an ODE approach. Queuing networks have additionally been used to develop a simple working model of metabolism [26] and enzyme-substrate interactions [27]. Briefly, queueing theory is a method of approaching stochastic simulations, doing so in a computationally less intensive process by grouping similar types of molecules and reactions [28]. Queueing theory possesses the ability to potentially describe more complex networks that would not be practical by alternative stochastic methods due to extended time to execute. Advantageously, queueing networks are capable of 1:1 mapping of biochemical pathways creating an intuitive structure that is simple to understand [29]. Since the advent of queueing models, some more specialized adaptations have been developed such as atomic routing models which have sought to optimize how objects (i.e. substrates) might flow through networks demonstrating implementation versatility [30].

We have recently developed a tool to recapitulate observed insulin responses in vitro and to measure the effects of Wortmannin-like inhibition on glucose uptake [31]. This system has provided insight into transient changes in molecule concentrations within the insulin signaling pathway and laid the groundwork to identify critical drug-targetable components, including those associated with insulin resistance. The application of queueing theory has provided the means to incorporate natural variation of kinetic constants and initial molecular concentrations, that are inherent in cells and tissues [32]. Herein, we present our current queueing model to simulate the stochastic effects of glucose metabolism as a demonstration to model more complex metabolic networks. We then provide qualitative comparisons of pharmacological inhibition in both simulated conditions and metabolic data from a cancer cell dataset to validate the model.

II. METHODS

Investigators frequently utilize glycolysis for model development as this pathway is well characterized biochemically. With known experimental endpoints, one can compare results and validate the computational methods in development. Consequently, we have used glycolysis here to present the modeling of metabolic networks by queuing theory. A brief overview of glycolysis and glucose metabolism can be found in Berg et al. [33].

We made use of previously derived mechanistic equations employing Michaelis-Menten kinetics to develop this model initially. The mathematical analyses of the rate equations and parameters used are described in Mulukutla et al. [34]. We aimed to build upon a previously defined model to implement our proposed queueing approach. Thus, the parameters and kinetic constants for the current model were chosen to reflect the model investigated in Mulukutla et al. Notably, the current model applies experimental and observed initial metabolite molar concentrations reported by Mulquiney et al. [33]. When considering metabolic flux, it is essential to evaluate changes in molar concentrations instead of mass, to account for chemical modifications to metabolic products. Furthermore, our model accounts for reactions that utilize and/or produce more than one reactant or product. Concentration and parameter values that were either absent or substantially different between sources were obtained from previously published literature. Energy nucleotides and metal ions were fixed in our model for simplification and to centralize our model around the intermediate metabolites of glycolysis. Table 1 lists the initial concentrations of the metabolites measured in the simulation output, and Table 2 provides concentrations of additional substrates required for calculations, but not directly measured from the simulation.

TABLE I.

Initial Concentrations of Glycolytic Metabolites

Metabolite	Concentration(mM)	Reference
GLC	5.0	[35]
G6P	0.039	[35]
F6P	0.013	[36]
F1,6BP	0.00231	[35]
F2,6BP	0.004	[36]
DHAP	0.02	[35]
GAP	0.00194	[36]
1,3BPG	0.000369	[36]
3PG	0.069	[35]
2PG	0.01	[36]
PEP	0.017	[35]
PYR	0.0586	[36]

Table 1 shows the intracellular concentrations for each metabolic intermediate. Metabolite concentrations (mM) are used in each simulation to initiate the model and are dynamic throughout the simulations.

TABLE II.

Additional Metabolites and Energy Nucleotides

Metabolite	Concentration(mM)	Reference
MgATP	1.52	[35]
MgADP	0.11	[35]
NAD	0.0599	[35]
NADH	0.000245	[35]
Pi	1.0	[35]
Mg	0.4	[35]
ATP	0.159	[35]
ADP	0.0937	[35]
AMP	0.03	[35]
H+	0.0000721	[37]
2,3BPG	3.1	[35]
GSH	3.2	[35]
ALA	0.2	[36]
G16BP	0.106	[35]

Intracellular concentrations required for rate equation calculations. The listed metabolites influence the kinetics of the reactions but were held constant for simulations to highlight concentration changes observed in glycolytic intermediates directly.

To demonstrate the mechanics of applying queueing networks to the modeling of metabolic pathways, one can consider a pathway of N interacting metabolites M₁, …, M_N having initial concentrations at time instant t₀ of C₁(t₀), …, C_N(t₀). Within the considered metabolic pathway, each metabolite M₁, …, M_N is involved in K_i reactions, i = 1, …, N. The corresponding reaction rates υ_{i, j} (C₁(t), …, C_N(t), t); i = 1, …, N; j = 1, …, K_i, are dependent on the instantaneous concentrations of the interacting metabolites at time t, as well as other metabolites and enzymes, and the associated time variabilities of rates are denoted as additional time dependency of t. The reaction rates can be positive or negative. A positive sign represents the production of metabolites, while a negative sign represents the consumption of metabolites. To find the concentration of a specific metabolite, C_i(t), at given time instant t, one traditionally would solve set(s) of ODEs in the form of:

$$\begin{gathered} \frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{C}}_{\mathbf{1}}(\mathit{t})={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{K}}_{\mathbf{1}}}{\mathit{v}}_{\mathbf{1},\mathit{j}}\left({\mathit{C}}_{\mathbf{1}}(\mathit{t}),\dots ,{\mathit{C}}_{\mathit{N}}(\mathit{t}),\mathit{t}\right) \\ \frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{C}}_{\mathbf{1}}(\mathit{t})={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{K}}_{\mathbf{1}}}{\mathit{v}}_{\mathbf{1},\mathit{j}}\left({\mathit{C}}_{\mathbf{1}}(\mathit{t}),\dots ,{\mathit{C}}_{\mathit{N}}(\mathit{t}),\mathit{t}\right) \\ \frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{C}}_{\mathbf{2}}(\mathit{t})={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{K}}_{\mathbf{2}}}{\mathit{v}}_{\mathbf{2},\mathit{j}}\left({\mathit{C}}_{\mathbf{1}}(\mathit{t}),\dots ,{\mathit{C}}_{\mathit{N}}(\mathit{t}),\mathit{t}\right) \\ \dots \\ \frac{\mathit{d}}{\mathit{d}\mathit{t}}{\mathit{C}}_{\mathit{N}}(\mathit{t})={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{K}}_{\mathit{N}}}{\mathit{v}}_{\mathit{N},\mathit{j}}\left({\mathit{C}}_{\mathbf{1}}(\mathit{t}),\dots ,{\mathit{C}}_{\mathit{N}}(\mathit{t}),\mathit{t}\right) \end{gathered}$$ (1)

with the initial condition C₁(t₀), …, C_N(t₀).

Given the interdependency of concentrations C₁(t₀), …, C_N(t₀), which are frequently (and highly) non-linear, and further dependency of other time-varying circumstances, random factors, or both, achieving the solution of such sets of equations is not only computationally intensive, but also not guaranteed to produce a numerically stable result. The problem is further complicated by the fact that concentrations C₁(t), …, C_N(t) are always non-negative, and as reported by Infante et al. [38], and Erbe et al. [39], this is a non-trivial task and a solution may not exist presently. Unfortunately, there is no guarantee that ODE modeling a biological process is suited to satisfy conditions for the existence of a non-negative solution. This is due in part to the fact that biological processes will slow/halt once the variables involved drop below a certain threshold. One can force the numerical solver to produce a non-negative solution, for example, by using MATLAB®’s ‘NonNegative’ option in the ‘odeset’ solver [39]. However, this significantly increases computation time, and the solution may not be accurate or numerically stable. This can be more problematic for those metabolites that are not expressed in high concentrations and/or very rapidly consumed in other reactions. For example, the metabolite glucose-6-phosphate (G6P) is also an intermediate in the Pentose Phosphate Pathway (PPP) and glycogen metabolism [40]. This presents an advantage with queuing theory for simulating systems where sections of metabolic pathways can be segmented and computationally halted instead of producing negative values, which better represents the nature of biological systems.

To find a method to simulate processes described by the set of ODEs (1), one can notice that each of the ODEs in (1) is of the form describing an average behavior of an M(t)/M(t)/c non-depleting queue [20]. In general, the M(t)/M(t)/c queue is such a system where arrivals form a single queue and are governed by a time-varying Poisson process. There are c servers and job service times are exponentially distributed with time-varying rates. The M(t)/M(t)/c non-depleting queues are exceptional cases of queues [22] where, for each time interval, the difference between corresponding arrival rate and service rate is non-negative. Massey et al. [20] also analyzed a general case of M(t)/M(t)/c queues, for which there is no simple method to describe them utilizing ODEs, but which can be depleted to zero elements in the queue or in other words for queues that can be emptied entirely.

Hence, the M(t)/M(t)/c queues can be used to model metabolic pathways for simulation purposes, and instead of solving sets of ODEs (1), one can simulate a network of interconnected M(t)/M(t)/c queues, provided that the concentrations C₁(t), …, C_N(t) are digitized. The arrival rates within this system are used as queues, and the service rates are used as reaction rates υ_{i, j} (C₁(t), …, C_N(t), t) normalized to the duration of a single simulation time step, Δt_iΔt_i, and the concentration increment, Δ(C_i(t)), which denotes a finite change of C_i(t) in a finite time increment of Δt_i. It should be noted here that instead of using the infinitely small time increment dt, as in formula (1), we use a finite time increment, Δt_i, that leads to finite concentration increment, Δ(C_i(t)). Of course, the introduced discretization of concentrations introduces some quantization error, which could be minimized by choosing a smaller value of Δ(C_i(t)). However, by selecting a smaller value of Δ(C_i(t)), it could potentially lead to increased computation time because it may require a reduction in the time step, Δt_i, resulting in more simulation steps to achieve the desired simulation time duration. Therefore, a balance is required, and normalization of the reaction rates to achieve arrival and service rates for the queues is calculated according to the formula:

$${\mathit{\mu }}_{\mathit{i},\mathit{j}}=\frac{|\mathit{v}\mathit{i},\mathit{j}(\mathit{C}\mathbf{1}(\mathit{t}),\dots ,\mathit{C}\mathit{N}(\mathit{t}),\mathit{t})|\mathbf{\Delta }{\mathit{t}}_{\mathit{i}}}{\mathbf{\Delta }\left({\mathit{C}}_{\mathit{i}}(\mathit{t})\right)}$$ (2)

If the reaction rate υ_{i, j} (C₁(t), …, C_N(t), t) is positive then the corresponding normalized rate μ_{i, j}, is an arrival rate while if υ_{i, j} (C₁(t), …, C_N(t), t) is negative the corresponding normalized rate, μ_{i, j}, is a service rate. The instantaneous length of each queue provides a possible realization of a stochastic Markovian process representing variations in the concentration for a given metabolite. Certainly, the average changes in concentration can be achieved by averaging the simulation results for several simulation runs. To ensure the correctness of simulation, the simulation time step, Δt_i, and the concentration increment, Δ(C_i(t)), have to be selected where all μ_{i, j} are less than one, as the arrival and service rates are representative of probabilities for arrival and service of Δ(C_i(t)) in the given time interval. To ensure that a single Δ(C_i(t)) is processed in each time interval, the necessary condition is as follows:

$${\mu }_{i,j}\ll 1,$$ (3)

for j = 1, …, K_i and i = 1, …, N

However, neither the simulation time step, Δt_i, nor the concentration increment, Δ(C_i(t)), need be the same for all i = 1, …,N, but can be chosen in a way that minimizes simulation time while ensuring the condition (3) is satisfied. Although the time increments can be calculated dynamically within each step, for the current model, we have chosen constant time increments for every reaction. As some reaction rates are orders of magnitude different, there would be a misuse of simulation time if we use the shortest time increment where condition (3) is satisfied for every reaction. The cumulative reaction time is equal for all reactions, thus ensuring the conservation of molar masses. Given the stochastic nature of chemical reactions, where reaction rates can vary depending on environmental conditions, the reaction rates can be randomized by adding Gaussian (or other) noise to the kinetic constants used to calculate values of υ_{i, j} (C₁(t), …, C_N(t), t). The same can be performed at time instant, t₀, for the initial concentrations, C₁(t₀), …, C_N(t₀).

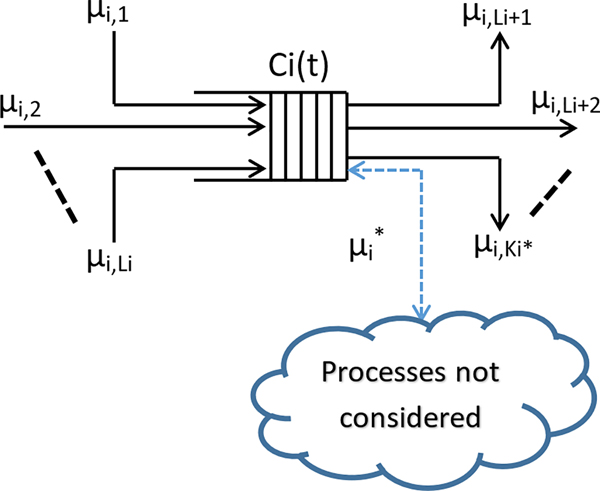
A queue representing the concentration of a single metabolite is shown in Fig. 1. The inputs to the queue represent reactions leading to the production of the metabolite, and outputs represent reactions that consume the metabolite. The cloud, connected to the queue via a bidirectional arrow, represents processes not considered (or currently unknown) that result in an imbalance between both aggregated inputs and outputs, to and from the queue, respectively. The arrivals to the queue, representing discrete increments in the concentration of the metabolite, are modeled by Poisson processes, while an exponential distribution models the service time (time intervals between two consecutive output events). These assumptions are consistent with classical queueing theory approaches [22]. Therefore, the number of arrivals in any given time interval (t, t + τ] follows a Poisson distribution with a parameter (μτ), such that :

$$\mathit{P}[(\mathit{N}(\mathit{t}+\mathit{\tau })-\mathit{N}(\mathit{t}))=\mathit{k}]=\frac{{\mathit{e}}^{-\mathit{\mu }\mathit{\tau }}{(\mathit{\mu }\mathit{\tau })}^{\mathit{k}}}{\mathit{k}!}$$ (4)

Fig. 1.

Example Queue. Queue representing concentration C_i(t) of the metabolite M_i; μ_{i, j}, j = 1, …, L_i, are arrival rates as corresponding to processes resulting in production of metabolite M_i; μ_{i, j}, j = L_i + 1, L_i + 2, …, $K_i^{*}$, are service rates corresponding to processes using metabolite M_i. $K_i^{*}$ = number of reactions that involve metabolite M_i within the model. Additional input/output pathways are included as dashed lines to account for unknown or missing reactions. Queue adapted from Wysocki et al. 2017, Simulation of Central Glucose Metabolism Using Queueing Network, IEEE International Conference on Electro Information Technology (EIT), Lincoln, NE, 2017, pp. 217–222.

Where N(t + τ) − N(t) = k is the number of arrivals in the interval (t, t + τ]. The time required for the server to process the packet is described by the exponential distribution using the probability distribution of a random variable X in terms of the rate parameter μ as follows:

$$\mathit{f}(\mathit{x};\mathit{\mu })=\{\begin{array}{cc}\mathit{\mu }{\mathit{e}}^{-\mathit{\mu }\mathit{x}}& \mathit{x}\ge \mathbf{0},\\ \mathbf{0}& \mathit{x}<\mathbf{0}.\end{array}$$ (5)

Therefore, the resulting arrival process at the input of a subsequent queue to which that output of the considered server is connected, again, follows a Poisson distribution. Assuming that in total, there are c-outputs from the queue, the queue can be considered as a standard M(t)/M(t)/c queue, as previously described.

For the description to be valid, both the sums of all arrival rates, μ_{i, j}, j = 1, …, L_i, and the sum of all service rates μ_{i, j}, j = L_i + 1, L_i + 2, …, $K_i^{*}$ must be less than one. This condition can be satisfied by either reducing the duration of time increment or increasing the concentration. Of course, reducing the time increment increases the simulation time, as more simulation steps must be considered for the duration of an experiment, while increasing the concentration unit may reduce the accuracy of the simulation results. Therefore, a balance is ideal while choosing parameters. From the perspective of implementing a simulation of the metabolic process, it is convenient to ensure that in a given simulation step, only one concentration unit of a given metabolite M_i will be processed. Assuming that there are $J_i=K_i^{*}-L_i$ possible reactions that can utilize metabolite M_i, the probability P_i1 that this occurs is given by the formula:

$${\mathit{P}}_{\mathit{i}\mathbf{1}}={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{j}}{\prod }_{\begin{array}{c}\mathit{k}=\mathbf{1}\\ \mathit{k}\ne \mathit{j}\end{array}}^{{\mathit{J}}_{\mathit{i}}}\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{k}}\right)$$ (6)

Assuming condition (3) is satisfied, (6) can be simplified to:

$${\mathit{P}}_{\mathit{i}\mathbf{1}}={\sum }_{\mathit{j}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{j}}$$ (7)

The conditional probability, P_i{j|1}, states if one concentration unit is processed in a simulation step, it is processed in the reaction associated with the reaction rate μ_{i, j}, which is given from the definition as:

$$\begin{gathered} {\mathit{P}}_{\mathit{i}}\{\mathit{j}\mid \mathbf{1}\}=\frac{{\mathit{P}}_{\mathit{i}}\{\mathit{j}\cap \mathbf{1}\}}{{\mathit{P}}_{\mathit{i}\mathbf{1}}}=\frac{{\mathit{\mu }}_{\mathit{i},\mathit{j}}{\prod }_{\begin{array}{c}\mathit{k}=\mathbf{1}\\ \mathit{k}\ne \mathit{j}\end{array}}^{{\mathit{J}}_{\mathit{i}}}\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{k}}\right)}{{\sum }_{\mathit{l}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{l}}{\prod }_{\begin{array}{c}\mathit{k}=\mathbf{1}\\ \mathit{k}\ne \mathit{j}\end{array}}^{{\mathit{J}}_{\mathit{i}}}\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{k}}\right)} \\ =\frac{{\mathit{\mu }}_{\mathit{i},\mathit{j}}}{\sum _{\mathit{l}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{l}}\frac{{\prod }_{\begin{array}{c}\mathit{k}=\mathbf{1}\\ \mathit{k}\ne \mathit{j}\end{array}}^{{\mathit{J}}_{\mathit{i}}}\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{k}}\right)}{{\prod }_{\begin{array}{c}\mathit{k}=\mathbf{1}\\ \mathit{k}\ne \mathit{j}\end{array}}^{{\mathit{J}}_{\mathit{i}}}\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{k}}\right)}}=\frac{{\mathit{\mu }}_{\mathit{i},\mathit{j}}}{\sum _{\mathit{l}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{l}}\frac{\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{j}}\right)}{\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{l}}\right)}} \\ =\frac{{\mathit{\mu }}_{\mathit{i},\mathit{j}}}{\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{j}}\right)\sum _{\mathit{l}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}\frac{{\mathit{\mu }}_{\mathit{i},\mathit{l}}}{\left(\mathbf{1}-{\mathit{\mu }}_{\mathit{i},\mathit{l}}\right)}} \end{gathered}$$ (8)

Where P_i {j∩1} denotes the probability where in this specific simulation step only one concentration unit is processed and only in the reaction associated with the reaction rate μ_{i, j}.

Again, if (3) is satisfied, (8) simplifies to:

$${\mathit{P}}_{\mathit{i}}\{\mathit{j}\mid \mathbf{1}\}=\frac{{\mathit{\mu }}_{\mathit{i},\mathit{j}}}{\sum _{\mathit{l}=\mathbf{1}}^{{\mathit{J}}_{\mathit{i}}}{\mathit{\mu }}_{\mathit{i},\mathit{l}}}$$ (9)

Notably, current metabolomics datasets are often incomplete or semiquantitative data, and some connections between metabolites remain undefined. To account for unknown or missing reactions, an additional input/output pathway is included in our model for every metabolite considered, as illustrated in Fig. 1 as a dashed line connection which can be bidirectional. The rate ${\mu }_i^{*}$ is determined as the rate which balances the steady-state value of the concentration C_i(t). If in steady-state, there is an outflow of metabolite M_i, with a resulting metabolite concentration unequal to the steady-state value that will require scaling by a factor equal to the ratio of the actual concentration and the steady-state concentration. Conversely, during inflow the scaling is inversely proportional. As previously mentioned, we have used queues to describe additional biological pathways and have provided detailed explanations of the proposed queueing theory methods [41,42]. Additionally, the pseudocode of the queueing theory application is provided as a supplementary file.

Simulations were performed on an Intel® Core ™i7–2600 CPU @ 3.40 GHz, RAM 32 GB running MATLAB® R2017b.

III. RESULTS

For the current study, our interest was in exploring the feasibility of modeling enzymatic reactions to simulate the dynamics of glycolysis utilizing queues with the addition of stochastics. Briefly, queueing theory is a mathematical tool used to describe, model, and analyze waiting lines (i.e. queues) [43]. At the molecular level, metabolites are produced and consumed through enzymatic reactions forming queues of metabolites. Production or absorption of the metabolite adds to the appropriate queue length, whereas consumption reduces metabolites and the queue length. Discrete random processes describe both production and consumption of a given metabolite, referred to as “arrival” and “service” processes, respectively [44]. Queues can be easily interconnected, have been successfully used to model internet function, and are well suited to metabolic networks as they are quite similar [21]. Our previous work demonstrates the ability to accurately simulate conditions seen in vivo using a fraction of the computing power of classical quantitative approaches [31]. We have adjusted our approach with queues to model metabolic pathways given mechanistic rate equations of all glycolytic reactions and validated experimental metabolite data.

As a core metabolic pathway common to all lifeforms, glycolysis is the enzymatic breakdown of glucose into a usable form of energy, additionally supplying intermediate metabolites as “building blocks” for connecting pathways that further support life. Naturally, glycolysis provides a scaffold to begin extending our model to incorporate additional sections of the metabolome.

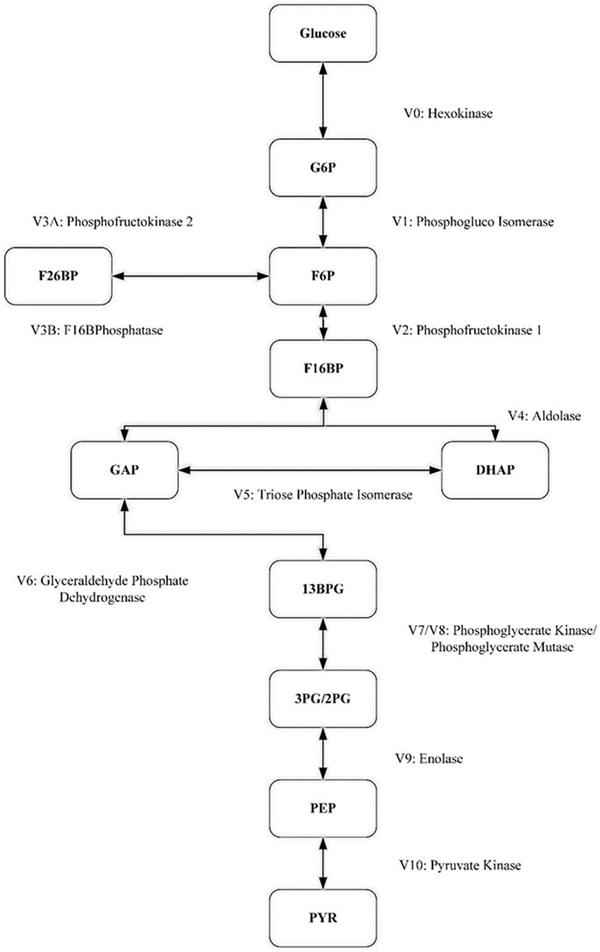
For the initial development of our model, we made use of previously derived mechanistic equations employing Michaelis-Menten kinetics. For model simulations, all intermediate metabolites were represented by different queues, as described in the methods section. The queues representing metabolites are connected if there is a reaction converting one metabolite into another. Fig. 2 illustrates the assembled queueing network representing glycolysis from glucose to pyruvate.

Fig. 2.

Simulated metabolic pathway from glucose to pyruvate. Arrows denote the modeled reactions. Vi, i = 0, …, 10, and V3A, V3B, are the reaction rates; for bidirectional arrows, the direction is determined by the sign of the corresponding reaction rate with the positive direction being from the top down. GLC, glucose; G6P, glucose 6-phosphate; F6P, fructose 6-phosphate; F16BP, fructose 1,6-bisphosphate; F26BP, fructose 2,6-bisphosphate; GAP glyceraldehyde 3-phosphate; DHAP, dihydroxyacetone phosphate; 13BPG, 1,3-bisphosphoglycerate; 3PG, 3-phosphoglycerate; 2PG, 2-phosphoglycerate; PEP, phosphoenolpyruvate; PYR, pyruvate.

For the stochastic simulations presented, the rate equations and model parameters were used as they are indicated in the literature (Table 1 and Table 2). Notably, the illustrated simulation pathways mimic a diagrammatic representation of metabolic flow similar to traditional biochemical illustrations. Thus, it can be more readily comprehended than sets of complex ODE equations which can quickly become daunting. Highlighting the significance of the approach, the current methods enabled rapid alteration of parameters and additional simulations under a variety of selected in silico conditions. For example, due to the rapid catalytic conversion of 3-PG and 2-PG in combination with the low metabolic concentrations as separate queues, the metabolites 3-PG and 2-PG were readily depleted given the 1 microsecond time scale used for the metabolite calculations. As the conversion from 3-PG to 2-PG is not a rate-limiting reaction, 3-PG and 2-PG were grouped into a single queue, avoiding the need to decrease simulation time step and unnecessary increases to simulation time.

Biological systems and reactions are inherently stochastic processes. Consequently, stochastic elements such as randomness and variation were incorporated into the model simulations. Reaction rates were randomized during simulation by adding an arbitrarily defined 10% Gaussian noise to the kinetic constants used to calculate values of υ_{i, j} (·). The same adjustment was included for the initial concentrations at time instant t₀ for all glycolytic intermediates. During simulations, each cell is calculated independently; that is, concentrations of each molecule in the metabolic network are stochastic and bound by error values listed in the literature. The queueing theory approach causes the actual concentrations of given molecule types to be simulated as separate queues within each cell. The probability of a movement happening at any time slice from one queue to the next is determined by the relevant normalized reaction speed. Movements between storages occur at a particular time instant if a randomly drawn number from the interval [0,1] at that time instant is smaller than the normalized reaction speed governing the movement.

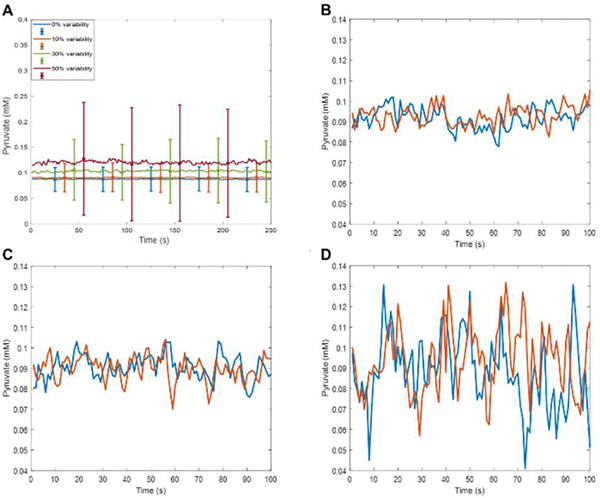
After simulations have been performed for every considered cell, the results are averaged over the cell population. In the current model, variations of 10% glucose levels are randomly computed for every simulated second. The simulations were run using a 1 microsecond time step, and random variations in the values of kinetic constants used in calculating reaction rates were introduced every second to simulate intrinsic biochemical noise. Initial concentrations were randomized by including an arbitrarily defined 10% Gaussian noise to reflect variability among cells in the population. The effect of such randomization on the simulated level of pyruvate is shown in Fig. 3. In Fig. 3A, it is evident that increased variability leads to greater dynamic range of pyruvate among cells. Additionally, increased variability resulted in an increased simulated average for pyruvate: a result of metabolite amounts bound at or above 0 with no set upper limits.

Fig. 3.

Effect of random variability of initial concentrations of all glycolytic intermediates and kinetic constants on the simulated concentration of pyruvate. A) Means and standard deviations calculated over populations of 100 independent cells with variability applied to the concentrations of the metabolites of interest and the enzymes involved in all of the glycolysis reactions. The percent variability is derived from a zero mean Gaussian with a standard deviation of x/3 and is multiplied by the nominal concentration value. The initial concentrations of the metabolites of interest are chosen that way, and for the concentration of other enzymes involved, the operation is repeated every second, while the simulation step is 0.1 millisecond. Computation time for simulating 100 cells for 300 seconds with 0.1 millisecond time step was 36,767.18 seconds. B) Two individual cells, 10% variability of initial concentrations and 10% Gaussian noise. C) Two individual cells, 20% variability of initial concentrations and 20% Gaussian noise. D) Two individual cells, 50% variability of initial concentrations and 50% Gaussian noise.

A. Glycolytic Flux

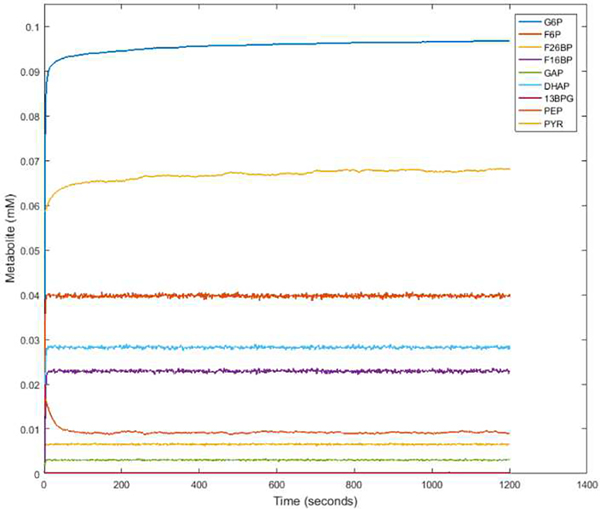
Previously, Mulukutla et al. aimed to assess the regulation of different isoforms of three rate-limiting glycolytic enzymes on overall pathway flux and behavior. The rate-limiting enzymes of glycolysis, hexokinase (HK), phosphofructokinase (PFK), the bifunctional enzyme phosphofructokinase-2/ fructose 2,6-bisphosphatase (PFKFB), and pyruvate kinase (PK), each have multiple isoforms and may be expressed in combination within a single cell in a cell-type dependent manner. We considered regulatory mechanisms of PFK, PFKFB, and PK by including parameters and terms in the rate equations to consider the feedback inhibition and activation, keeping both upper and lower glycolytic regulatory loops active in our simulations. The feedback considered consists of F26BP (an important activator of glycolytic flux) and F16BP activation of PFK, F16BP activation of PK, and PEP inhibition of PFKFB activity. The parameters set to simulate the feedback loops are as follows: K_PFKf16bp=0.65 mM and K_PKf16bp=0.04 mM. The PFKFB kinase/phosphatase (K/P) ratio, the ratio between the kinase and phosphatase activity, was set to 0.1 by adjusting the value of the PFKFBPase Vmax leaving the kinase Vmax at its original value. Different K/P ratios are given in the literature based on specific tissue and cell type. The range varies from less than 1 to 710 depending on the isoform of PFKFB expressed and the tissue type in which it is found. Notably, PFKFB is highly dependent on signaling and hormonal regulation, which can transiently change the K/P ratio given the stimulus. Signaling regulation was not considered in this model, though this component is of interest for further study. Thus, we aimed to keep F26BP relatively constant throughout the initial steady-state testing to keep the flux toward a stable level. We found that the K/P ratio of 0.1 kept F26BP and all other metabolites constant over time with the given the parameters used. Therefore, the 0.1 K/P ratio was used to further test the ability of the model to simulate metabolite changes. Simulations were repeated for 30 cells, and once completed, the average concentrations of each metabolite per cell were graphed as a function of time (Fig. 4).

Fig. 4.

Steady-state glycolytic flux. Metabolite concentrations were simulated with an input of 5 mM glucose over a span of 1200 seconds to model an unperturbed and constant state.

B. Gapdh Inhibition

In vitro experiments and model simulations were performed to assess the performance of the proposed queueing approach. The rationale being that biologically known endpoints documented in literature can be used as benchmarks to demonstrate the model efficacy. FK866 is a noncompetitive inhibitor of nicotinamide phosphoribosyltransferase (NAMPT), the enzyme that supplies the majority of the intracellular pool of NAD+, a required substrate for the GAPDH reaction. Extensive research has characterized the effects of FK866 on high glycolytic flux in cancer cells [45–48]. Under limited NAD+ concentrations, the GAPDH reaction represents a bottleneck in glycolysis, producing a block in the glycolytic flux. Experimental results show the upper-level glycolytic metabolites, including G6P, F6P, F16BP, GAP, and DHAP accumulate while the lower-level glycolytic metabolites, 13BPG, 3PG/2PG, PEP, and PYR, decrease as substrates become unavailable. Thus, we hypothesized that with the reduction of GAPDH activity and, consequently, simulation of enzyme inhibition in silico, the model should be able to mimic the qualitative metabolic trends seen in vitro. Notably, kinetics and enzyme concentrations for the specific cancer cell lines were unknown; to account for the differences between the cancerous and non-cancerous simulations, the reaction rates were scaled. The effects of FK866 are presented in the experimental data provided by [47] in Fig. 5, and by the present model outcomes of GAPDH activity inhibition in Fig. 6.

Fig. 5.

Effects of FK866 on metabolite concentrations in vitro. A) Experimental metabolomics data measuring G6P and F6P concentrations with the inhibitor FK866 in (solid blue and dashed green lines) A2780 and (red) HCT116 cancer cells, B) effects of FK866 on FBP concentrations in vitro, C) effects of FK866 on G6P and F6P concentrations in vitro, D) effects of FK866 on PEP concentrations in vitro.

Fig. 6.

Effects of GAPDH Inhibition on metabolite concentrations in silico. A) G6P and F6P, B) FBP, C) GAP and DHAP, D) PEP. In all cases, the Vmax of GAPDH was varied between 0 and 100 percent of its initial value to simulate varying levels of enzyme inhibition.

GAPDH activity was reduced by adjusting the Vmax of the reaction catalyzed by GAPDH. Inhibition was simulated by varying GAPDH activity between 0% and 90%, with each inhibitory level run as a separate simulation for a population of 30 cells. The simulated results of GAPDH inhibition of G6P+F6P, F16BP, GAP+DHAP, and PEP, are plotted as dose-response curves in Fig. 6 to reproduce the effect of metabolite changes from experimental pharmacological inhibition of two cancerous cell lines (Fig. 5). The FK866 inhibitor concentrations, used in both A2780 ovarian and HCT116 colorectal cancer cell lines in vitro, were compared to in silico reduction of the percent GAPDH activity. Of note, we assume that at the lowest FK866 concentration (0.3 nM) used in vitro does not inhibit GAPDH activity.

F16BP and PEP were reported as individual metabolites in the two cancer cell lines, A2780 and HCT116. The comparison of the simulated and experimental data is presented in Fig. 5 and 6. Due to difficulties in distinguishing isobaric metabolites from one another, G6P+F6P and GAP+DHAP were grouped in the experimental data, and the sum of these metabolites are reported. The model was able to determine the individual metabolite concentrations; however, following each simulation, the two metabolites from the model data (G6P+F6P and GAP+DHAP) were added for a closer comparison to the experimental data. Moreover, the data was normalized so that each experiment (in vitro and in silico) began with the same metabolite concentration, again for a clearer comparison of the actual changes occurring as FK866 doses increased (experimental) and as GAPDH inhibition increased (model simulations).

In silico, we observed increases in all upper glycolytic metabolites with inhibition of GAPDH, supporting the metabolic data of NAMPT inhibition. The lower glycolytic metabolite, PEP, showed reduction following increased inhibition of GAPDH, in agreement with the results seen in the experimental data. Using a K/P ratio of 0.1, F26BP was the only metabolite that did not change mean values over time throughout the course of GAPDH inhibition at any level. Notably, the experimental data showed a wide range of metabolite concentrations with similar inhibitory doses, between and within both cell lines. For example, the G6P+F6P concentration in the HCT116 cell line increased from 0.052 mM to 0.512 mM with the highest FK866 treatment, and in the two separate experiments with the A2780 cells, the metabolite concentrations increased to only 0.18 mM and 0.13 mM (Fig. 5A).

The inhibition simulations aimed to observe the overall trend of metabolite changes, intended for a qualitative comparison. There are slight variations present between the experimental data and the model data. Still the results are similar or within range of the experimental data; in the model simulation, the F16BP concentration increased from 0.0022 mM to 0.0548 mM at the highest inhibition level, while the F16BP concentration in the HCT116 cell line rose from 0.0022 mM to 0.0496 mM at the highest FK866 treatment (Fig. 5A–6A). Specific kinetics and prior knowledge of experimental data may aid in reproducing results that are more consistent in the future.

By comparing the simulation results with the experimental one, it can be noticed that in both in vitro and in silico cases, significant changes in observed metabolite concentrations appear to occur at specific drug dosage in vitro and 90% inhibition of GAPDH activity in silico. Therefore, one can speculate that roughly 90% of GAPDH inhibition is achieved with a dose of around 5 nM of FK866. Although a further increase of GAPDH inhibition in silico simulations causes further significant changes in the metabolite concentrations, this is only partially observed in vitro with higher doses of FK866.

IV. CONCLUSION

This paper presents a computational model of glycolysis constructed as a queueing network; a modeling approach widely used in modeling telecommunication packet networks. Dynamic modeling of biological systems, while exceptionally useful, poses computational challenges and in reproducing natural stochastic variation. The application of queueing theory in dynamic modeling may provide a method to overcome such challenges. The current applications of this work hold promise for advancing computational biology and biochemical research. The queueing theory represents a mainstay modeling approach of telecommunication networks with application to simulate intracellular metabolism. By viewing enzymes as “gates” and their substrates as “packets,” we have reduced the computational complexity of the simulation to the advantage of much more rapid calculation. Previously, we have shown that we can model intracellular mechanisms and do so while capturing the random variation inherent with living cells [25, 29].

Research techniques in metabolomics have evolved rapidly since their introduction. Modeling strategies must be flexible to accommodate novel information and amend the data as needed. The modularity of queues provides a suitable approach for further model extension, whether that be additional metabolic reactions, parameter refinement, or multiscale modeling approaches. Moreover, this approach enables the ability to simulate biochemical reactions stochastically without the need to implement or solve stochastic algorithms. As seen above, GAP and DHAP were represented experimentally as a combination of metabolic intermediates, due to their chemical similarities. Although mass spectrometry has become increasingly sensitive for detecting small molecules, isobaric metabolites are often difficult to distinguish from one another. This is the case not only for several metabolic intermediates of glycolysis but also for additional metabolic pathways. An advantage to the in silico mechanistic modeling of metabolic networks is the ability to represent such metabolites as individual entities investigating distinct metabolic reactions and the dynamics of each metabolite providing a more in-depth observation of the intracellular interactions.

The need for models to be informed from and then simulate data using metabolomics sources represents a significant advance in future possibilities with this approach. Due to the ability to change variables and quickly analyze the resulting metabolic effects, investigators can simulate the effects of drugs or mutations on such processes. In all, the ability to accurately and quickly simulate intracellular and intratissue pathways represents a considerable leap forward in the ability to understand the central biochemical underpinnings of cellular life. The advancement of technology in both experimental biology and computational systems has allowed scientific discovery and investigation on the chemical level. Elucidation of intracellular metabolite and chemical dynamics can provide valuable insight into how cells utilize cellular components to grow, respond to environmental stimuli, and ultimately support life. We believe queues have potential to simulate metabolic reactions with greater efficacy by including stochastic elements to modeled pathways as described here. An additional advantage of the queueing approach is a more natural and intuitive fit for biological pathways as they are frequently represented in the field and depicted in models of metabolism [29]. In summary, the current study presents the application of queuing theory as a beneficial modeling approach for simulating metabolic pathway dynamics and predicting the effects of pharmacological inhibition.

Biography

Tadeusz A. Wysocki (M’95-SM’98) received the M. Eng.Sc. degree with the highest distinction in telecommunications from the Academy of Technology and Agriculture, Bydgoszcz, Poland, in 1981. He received the Ph.D. degree (summa cum laude), from the Warsaw University of Technology, in 1984, and the D.Sc. degree (Habilitation) in 1990 in telecommunications engineering from the Warsaw University of Technology. In January 1992, he moved to Australia, where he worked at different Universities and research centers. In 1993, he was with the University of Hagen, Germany, within the framework of Alexander von Humboldt Research Fellowship, and in December 1998, he joined the University of Wollongong as an Associate Professor. In 2003, he established the Wireless Research Group, which he directed until the end of 2007, when he moved to take up a Professorship of Computer and Electronics Engineering at Peter Kiewit Institute, University of Nebraska⣔Lincoln. In 2013, a life title of Professor was conferred on him by the President of Poland. Currently, he holds a Professorship at the Department of Electrical and Computer Engineering, University of Nebraska-Lincoln, and at the UTP University, Bydgoszcz, Poland. He is the author or coauthor of seven books, more than 250 research publications, and nine patents. His areas of research interest include: molecular communications, modeling of biological processes at nano-scale, and signal processing for communication systems.

Beata Joanna Wysocki graduated from Warsaw University of Technology, Warsaw, Poland, receiving the M.Eng. degree in electrical engineering in 1991. In 1994, she started the Ph.D. degree in the Australian Telecommunications Research Institute at Curtin University of Technology. In March 2000, she was awarded her Ph.D. for the thesis “Signal Formats for Code Division Multiple Access Wireless Networks.” From October 1999 until 2008, she was with the Telecommunications & Information Technology Research Institute at the University Wollongong as a research fellow. Currently, she is with the Department of Biology of University of Nebraska at Omaha, as a visiting scientist. Her research interests include: modeling biological processes at nanoscale, space-time signal processing, and spreading sequence design.

Paul H. Davis received the B.S. degree in microbiology from Brigham Young University, Provo, UT, in 2001 and the Ph.D. degree in molecular microbiology from Washington University in St. Louis, St. Louis, MO, in 2006. He is currently an Associate Professor of Biology at the University of Nebraska at Omaha, where he specializes in molecular biology, bioinformatics, and infectious diseases.

Thomas T. Schulze holds a B.S. degree in kinesiology from Iowa State University and a M.S. in biology from the University of Nebraska. He is currently pursuing a Ph.D. degree from the University of Nebraska Medical Center in Immunology, Pathology, and Infectious Disease, where he is also an Applied Defense and Education Pipeline Training (ADEPT) fellow.

Ghada A. Soliman received her medical degree from Cairo University, Egypt and earned her PhD in Nutritional Sciences from the University of Arizona, Tucson, with a major in Nutritional Biochemistry and minor in Immunology and Microbiology. In addition, she completed her Dietetic Internship at the University of Michigan, Ann Arbor; and earned her post-doctoral fellowships at Baylor College of Medicine, Houston, at the Children’s Nutrition Research Center, Atherosclerosis, Lipoprotein Research, and Vascular Biology as well as translational research. She is now an is Associate Professor of Nutrition in the Department of Environmental, Occupational and Geospatial Health Sciences at the City University of New York Graduate School of Public Health and Health Policy. Her transdisciplinary research portfolio spans cardiometabolic and cancer research, chronic disease prevention, population health, school nutrition, systems biology, and laboratory-based nutrient metabolism.

Emalie J. Clement completed her B.S and M.S in Biology at the University of Nebraska at Omaha. She is now a Ph.D. student at the University of Nebraska Medical Center studying Cancer Biology.