Abstract
We present the Rate from Event Durations (RED) scheme, a new scheme that more efficiently calculates rate constants using the weighted ensemble path sampling strategy. This scheme enables rate-constant estimation from shorter trajectories by incorporating the probability distribution of event durations, or barrier-crossing times, from a simulation. We have applied the RED scheme to weighted ensemble simulations of a variety of rare-event processes that range in complexity: residue-level simulations of protein conformational switching, atomistic simulations of Na+/Cl− association in explicit solvent, and atomistic simulations of protein–protein association in explicit solvent. Rate constants were estimated with up to 50% greater efficiency than the original weighted ensemble scheme. Importantly, our scheme accounts for the systematic error that results from statistical bias toward the observation of events with short durations and reweights the event duration distribution accordingly. The RED scheme is relevant to any simulation strategy that involves unbiased trajectories of similar length to the most probable event duration, including weighted ensemble, milestoning, and standard simulations as well as the construction of Markov state models.
I. INTRODUCTION
Of great interest to chemical physics and biophysics is the estimation of rate constants for long-time scale processes. These rate constants may be directly obtained from molecular simulations with enhanced sampling approaches that maintain rigorous kinetics. Among these approaches are path sampling strategies, which focus the computing power on the functional transitions between stable states rather than the stable states themselves,1 exploiting the fact that for rare events, the event duration, tb, or barrier-crossing time is much shorter than the associated waiting times between events (tb ≪ k−1, where k is the corresponding rate constant).2,3 Path sampling strategies fall broadly into two categories: (i) methods that generate continuous transition paths [e.g., weighted ensemble (WE)4,5 and other “splitting” strategies,6–8 transition interface sampling,9 and forward flux sampling10,11] and (ii) methods that generate discontinuous paths (e.g., milestoning12 and weighted ensemble milestoning13). Alternatively, Markov State models14,15—discrete state kinetic models—can be constructed at the post-simulation stage to obtain long-time scale information from either continuous trajectory (e.g., from weighted ensemble simulations)16,17 or short, discontinuous trajectories (e.g., from adaptive sampling7).
One challenge of the weighted ensemble (WE) strategy has been the estimation of rate constants from trajectory ensembles that have not yet reached a steady state. To tackle this challenge, history-augmented Markov State models that employ “micro-bins” have been applied to estimate rate constants from pre-steady state trajectories.16,17 Alternatively, the non-Poisson kinetics of the transient “ramp-up time”—or approach to steady state—of a WE simulation can be incorporated into the rate-constant estimation, improving on previous WE studies of complex biological processes such as large-scale protein conformational transitions18 and protein–ligand binding19–21 that have focused on only the latter portions of the simulations where the rate-constant estimate was no longer sensitive to the earliest (and least probable) successful pathways.
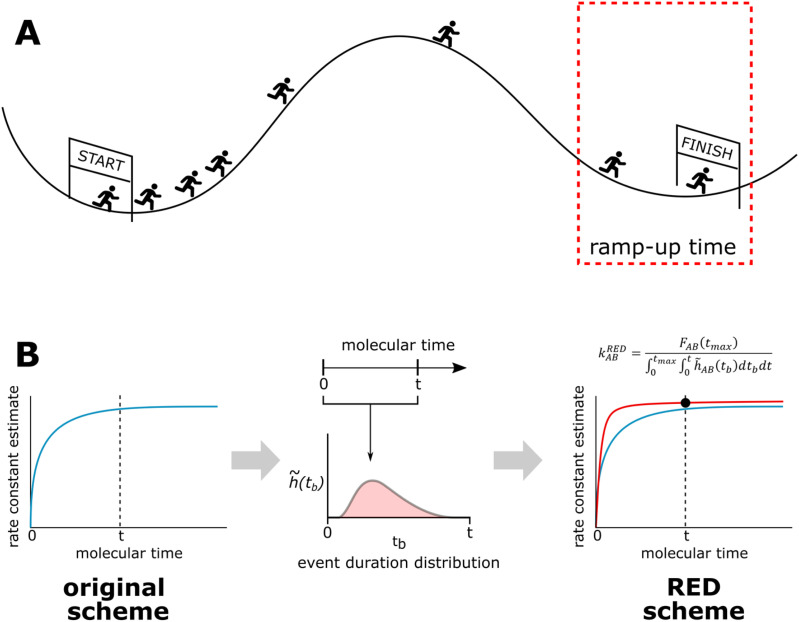
Here, we present the Rate from Event Durations (RED) scheme, a more efficient scheme for estimating rate constants that exploit the ramp-up time from the early part of a WE simulation by incorporating the distribution of event durations (barrier-crossing times) that have been sampled. To illustrate the rationale of the RED scheme, we make an analogy of rare-event sampling to a cross-country race in which officials wish to estimate the average rate for runners to surmount the first hill, or barrier [Fig. 1(a)]. Rather than waiting for all of the runners to complete the race, the officials can estimate the average rate more quickly by constructing a probability distribution of event durations that is solely based on the initial pack of runners that make it over the barrier. The effectiveness of this scheme therefore depends on the extent to which the initial distribution of event durations reflects the width and steepness of the barrier after all runners have finished the race.
FIG. 1.
Illustration of the RED Scheme for rate-constant estimation. (a) Estimating the rate constant from the ramp-up time is analogous to estimating the average rate at which all runners in a race reach the finish line from the first few finish times. (b) In the context of a WE simulation, the RED scheme enhances the efficiency of rate-constant estimation by using the “ramp-up time” for the rate constant, i.e., an initial portion of the distribution of event durations. To compare the RED scheme against previous calculation methods, we ask “for a given time t, what is the best estimate that our scheme could have produced if we stopped the simulations at time t?”
The RED scheme is relevant to any simulation strategy that relies on unbiased pathways of a similar length to the typical event duration, including weighted ensemble,4,5 milestoning,12 and standard simulations as well as the construction of Markov state models.14,15 To demonstrate the power of the RED scheme for calculating rate constants, we applied the strategy to a set of three increasingly complex rare-event processes.
First, we applied the RED scheme to residue-level simulations of a protein conformational switching process of an engineered protein-based Ca2+ sensor. These simulations have enabled the rational enhancement of the sensor’s response time by as much as 32-fold.18 This sensor was engineered using the alternate frame folding (AFF) scheme, fusing together the wild-type calbindin protein and a circular permutant of calbindin such that the two proteins partially overlap in sequence in the resulting calbindin-AFF construct and, therefore, fold in a mutually exclusive manner.22 Importantly, WE simulations of this switching process are an ideal “proof-of-principle” application of the RED scheme as the simulations each exhibit a large “ramp-up time” before steady-state convergence of the rate constant, and each simulation captures the entire distribution of event durations.18
Second, we applied the RED scheme to the molecular association of Na+ and Cl− ions in explicit solvent. This association process was one of four benchmark applications in a previous study that demonstrated the efficiency of WE relative to standard simulations in generating rate constants and pathways.23
Finally, we applied the RED scheme to atomistic simulations of a complex biological process in explicit solvent: protein–protein binding. In particular, we re-analyzed a previously completed protein–protein binding simulation that has yielded rate constants and pathways for the barnase and barstar proteins20 using <1% of the total simulation time used for a Markov state model study of the same binding process.24
II. THEORY
For a rare-event process, the majority of event durations (barrier-crossing times) will be short compared to the waiting times between events. As the system evolves in time and begins to generate event duration times that are substantially longer than the most probable event duration, the distribution of waiting times becomes near-exponential, which is consistent with a Poisson point process in which the events are stochastic and independent.25 However, when the simulations of a rare-event process are only as long as the most probable event duration—as is often the case for WE and other rare-event sampling strategies—the number of events per unit time displays transient, pre-steady state behavior, and the initial edge of the distribution of waiting times deviates from an exponential distribution. Our Rates from Event Durations (RED) scheme leverages this transient behavior to estimate rate constants from pre-steady state trajectories. Below, we briefly summarize the weighted ensemble (WE) strategy and then present details of the original WE scheme for rate-constant estimation and the RED scheme.
A. The weighted ensemble (WE) strategy
The WE strategy enhances the sampling of rare events by orchestrating the periodic resampling of parallel, weighted trajectories.4 The goal of the strategy is to provide reasonably even coverage of configurational space—typically divided into bins along a progress coordinate toward the target state—to yield an ensemble of continuous, successful pathways with rigorous kinetics. The resampling step is performed at a fixed time interval τ and involves evaluating trajectories in the same bin for either replication or combination to maintain the same number of target trajectories/bin. Rigorous management of trajectory weights ensures that no bias is introduced into the dynamics. To maintain non-equilibrium steady-state conditions, trajectories that reach the target state are “recycled,” i.e., terminated followed by initiation of a new trajectory with the same weight.
B. Original WE scheme for rate-constant estimation
In the original WE scheme, the macroscopic rate constant kAB for a rare-event process involving an initial state A and target state B is computed as follows:26
| (1) |
where is the running average of the conditional flux of probability carried by trajectories originating in state A and arriving in state B and ⟨pA⟩ is the running average of the fraction of trajectories more recently in A than in B, which is equal to one in non-equilibrium steady-state WE simulations. In practice, if a steady state has not been reached, then is approximated by the running average ⟨fAB⟩ of the conditional flux (not necessarily steady state) from state A to state B. For bimolecular processes, we divide Eq. (1) by the effective molar concentration C0 of the associating molecules to estimate a rate constant in units of M−1 s−1.
C. Rate from event durations (RED) scheme
The Rate from Event Durations (RED) scheme reduces the impact of transient effects from a WE simulation on rate-constant estimation by incorporating the distribution of sampled event durations (barrier-crossing times tb, which exclude the dwell time in state A). The motivation behind this scheme is that short WE simulations may not capture pathways with relatively long barrier-crossing times that have yet to enter state B; therefore, the original WE scheme tends to underestimate the true rate constant by a predictable quantity that depends on the probability of observing pathways with longer event durations. The RED scheme incorporates this quantity as a correction factor to the rate-constant estimate of the original scheme at a given time of the simulation.
We consider a rare-event process with the following properties:
-
1.
The system is in an initial state A at time t = 0 such that an event of duration tb is less than or equal to the longest possible trajectory length tmax of the WE simulation.
-
2.
While in the initial state A, the system has a constant probability per unit time of initiating a successful transition path to the target state B, denoted kAB.
-
3.
The event durations are assumed to be randomly distributed according to a probability density function hAB, where .
-
4.
Upon arriving in a target state B, the system is immediately “recycled” to the initial state A.
To derive an expression for estimating the rate constant, we begin by defining the flux fAB from an initial state A into a target state B as a convolution of the rate constant kAB for completing the A → B transition in a time tb distributed according to hAB (see the Appendix for additional details),
| (2) |
We then integrate and rearrange Eq. (2) to obtain an expression for kAB that depends only on the true cumulative number of events FAB(tmax) and cumulative distribution of event durations HAB(t),
| (3) |
where the numerator , the denominator is the integral of over all values of ranging from to , the cumulative distribution is the integral of , and is the true distribution of event durations. Compared with the original WE scheme, where the denominator would be the time tmax, the denominator in Eq. (3) represents a “corrected time,” which accounts for the time during which it was possible to see events. Equivalently, the denominator in Eq. (1) of the original WE scheme could be written as , which indicates that an estimate derived from Eq. (3) would be greater than that of the original WE scheme, since HAB(t) is a cumulative density function that is less than one.
Next, we use Eq. (3) to derive an estimate for the rate constant based on the “observed” distribution of event durations that are sampled by the WE simulation. While we may naively estimate hAB(tb) as the observed histogram of event durations, the observed histogram is likely skewed toward shorter event durations due to the transient phase for the time evolution of the rate constant ( indicates the observed quantity). To obtain a corrected estimate of the histogram, we divide the observed histogram by the interval of time (tmax − tb) in which it is possible to observe an event of duration tb from a simulation with a maximum trajectory length tmax,
| (4) |
where the constant of proportionality is chosen such that the corrected is normalized []. In essence, this modified histogram estimate corrects for statistical bias in the observed histogram . This bias results from the inability to observe successful pathways that have an exited state A, but not yet entered state B, which occurs more often for pathways with longer event durations. Our corrected histogram provides an asymptotically unbiased estimate of the true event duration distribution hAB(tb), assuming that hAB(tb) is continuous. For a full derivation of Eq. (4), see Subsection 2 of the Appendix.
Finally, we define the RED scheme estimate of the true rate constant kAB as follows:
| (5) |
where is the observed cumulative probability of A → B transitions up to the maximum trajectory length tmax; and the denominator is a correction factor C equal to in units of time, yielding a rate-constant estimate in units of inverse time. For bimolecular processes, we divide Eq. (5) by the effective molar concentration C0 of the associating molecules to estimate a rate constant in units of M−1 s−1 (as is also the case for the original WE scheme).
D. Error estimation for rate constants
In cases where it is not possible to sample the entire distribution of event durations, the RED scheme provides a framework for understanding the systematic error that results from not observing trajectories with longer event durations. Given a maximum trajectory length tmax, the corrected estimate of the event duration distribution hAB(tb) will be zero for tb > tmax, and since is normalized such that , will be artificially inflated for tb < tmax,
| (6) |
In other words, since we cannot observe event durations of tb > tmax, the normalization factor for the corrected histogram implicitly assumes that such events do not occur; since approximates the true event duration distribution hAB(t) up to a constant of proportionality (see Subsection 2 of the Appendix), we can then deduce that our lack of knowledge of events with durations tb > tmax tends to inflate our estimate of the distribution for tb < tmax.
If we plug the right-hand side (RHS) of Eq. (6) back into Eq. (5)—that is, by replacing in the correction factor C with the equivalent value from Eq. (6)—we find that underestimates kAB by a factor of , the observed fraction of the distribution of event durations,
| (7) |
For example, if 20% of pathways reaching the target state have longer event durations tb than the maximum trajectory length tmax and are, therefore, not captured during the simulation, then we tend to underestimate the true rate constant kAB by 20%. Despite this underestimation, the RED scheme estimate is still an improvement over the original scheme for estimating rate constants [Eq. (1)].
For multiple, independent WE simulations 1, 2, …, N, we estimated uncertainties in the rate constants by first applying the RED scheme individually to map each simulation i to a corresponding rate constant estimate kRED,i and then applying Bayesian bootstrapping27 to estimate 95% credibility regions (CRs). To prevent underestimating the uncertainty, the distributions of event durations were calculated independently for each simulation, as pooling data to make a smoother estimate of hAB would introduce correlations and, therefore, break the independence between the kRED,i. For cases where only a single WE simulation was run (i.e., for barnase–barstar association), the uncertainty in the rate constant calculated by the RED scheme is not reported as the error estimation is not straightforward in these cases see Sec. 1 of the Appendix.
III. METHODS
A. WE simulations
All WE simulations were run using the open-source, highly scalable WESTPA software package (https://westpa.github.io/westpa).28 WE parameters and details of dynamics propagation are provided below for each rare-event process.
1. Protein conformational switching
As described in DeGrave et al.,18 ten independent WE simulations were previously run to generate N′ → N switching pathways of the wild-type E65′Q calbindin-AFF construct under non-equilibrium steady-state conditions. Each WE simulation was run for 2000 WE iterations with a fixed time interval τ of 100 ps and a target number of 5 trajectories/bin, yielding an aggregate simulation time of 65 µs for each simulation. A two-dimensional progress coordinate was defined as (i) the pseudo-atom root-mean-square deviation (RMSD) of the N frame after aligning on the folded N frame structure and (ii) the pseudo-atom RMSD of the N′ frame after aligning on the folded N′ frame. Dynamics were propagated using a Brownian dynamics algorithm with hydrodynamic interactions, as implemented in the UIOWA-BD software.29,30 All analyses were performed with conformations sampled every 50 ps. A minimal residue-level protein model was employed in which each residue is represented by a single pseudo-atom at the position of its Cα atom. The conformational dynamics of the protein were governed by a Gō-type potential energy function31,32 that was parameterized to reproduce the experimental folding free energies of the isolated wild-type protein and the circular permutant of the protein.18
2. Na+/Cl − association
Five independent WE simulations were run to generate pathways of the Na+/Cl− association process under non-equilibrium steady-state conditions. Each WE simulation was run for 1000 WE iterations with a fixed time interval τ of 2 ps for each iteration and a target number of 4 trajectories/bin, yielding an aggregate simulation time of 0.2 µs for each simulation. A one-dimensional progress coordinate was defined as the distance between the Na+ and Cl− ions; bins were placed every 1 Å from a separation distance of 12 (unassociated state) to 2.6 Å (associated state). Dynamics were propagated using the AMBER18 software package33 with the TIP3P water model34 and corresponding Joung and Cheatham parameters for the Na+ and Cl− ions.35 Simulations were started from an unassociated state with a 12-Å separation between the Na+ and Cl− ions and a sufficiently large truncated octahedral box of explicit water molecules to provide a minimum 12 Å clearance between the ions and box walls, yielding an effective ion concentration C0 of 2.8 mM. Temperature and pressure were maintained at 298 K and 1 atm using the Langevin thermostat (collision frequency of 1 ps−1) and the Monte Carlo barostat (with 100 fs between attempts to adjust the system volume), respectively. Non-bonded interactions were truncated at 10 Å, and long-range electrostatics were treated using the particle mesh Ewald method.36
3. Protein–protein association
As described in Saglam and Chong,20 a single WE simulation was previously run to generate pathways of the association process of the barnase and barstar proteins under equilibrium conditions.20 The WE simulation was run for 650 WE iterations with a fixed time interval τ of 20 ps for each iteration and a fixed total number of 1600 trajectories at all times during the simulation, yielding an aggregate simulation time of 18 µs. A two-dimensional progress coordinate was defined as (i) the minimum separation distance between barnase and barstar, and (ii) a “binding” RMSD, which was determined by first aligning on barnase in the crystal structure of the barnase–barstar complex37 and then calculating the heavy-atom RMSD of barstar residues D35 and D39. Dynamics were propagated using the Gromacs 4.6.7 software package38 with the Amber ff03* force field,39 TIP3P water model,34 and corresponding Joung and Cheatham ion parameters.35 The system was immersed in a sufficiently large dodecahedron box of explicit water molecules to provide a minimum of 12 Å clearance between the solutes and box walls for the unbound states in which the binding partners were separated by 20 Å. A total of 31 Na+ and 29 Cl− ions were included to neutralize the net charge of the protein system and to yield the experimental ionic strength (50 mM).40 The entire simulation system consisted of ∼100 000 atoms with an effective protein concentration C0 of 1.7 mM. Heavy-atom coordinates for initial models of the unbound proteins were extracted from the crystal structure of the barnase–barstar complex (PDB code: 1BRS).37
B. Standard simulations
To validate the rate constants computed from the WE simulations for the protein conformational switching process and Na+/Cl− association process, an extensive set of standard simulations was run to provide “gold standard” rate constants for comparison. Given the computationally prohibitive time scales for the barnase–barstar association process, no standard simulations were run for this process; instead, the experimental association rate constant is used to validate the computed association rate constant from the WE simulation. For the protein conformational switching process, 50 2-µs standard simulations were run. For the Na+/Cl− association process, 10 1-µs standard simulations were run. Dynamics were propagated as described above for the corresponding WE simulations.
IV. RESULTS AND DISCUSSION
We have developed the Rate from Event Durations (RED) scheme, a new scheme for rate-constant estimation that reduces the impact of transient effects by using the distribution of event durations that correspond to simulated pathways of the rare event. To demonstrate the effectiveness of the RED scheme, we have applied the scheme to simulations of three rare-event processes: (i) residue-level simulations of protein conformational switching by an engineered protein-based calcium sensor, (ii) atomistic simulations of Na+/Cl− association in explicit solvent, and (iii) atomistic simulations of protein–protein association in explicit solvent. The effectiveness of the RED scheme was evaluated by monitoring the time evolution of the rate constant, incorporating the distribution of event durations up to each time point [Fig. 1(b)].
A. Application to residue-level simulations of protein switching
The switching process of the engineered calbindin-AFF system [Fig. 2(a)], as simulated using a residue-level model, is an example of a case where the RED scheme would be expected to be particularly effective in enabling the calculation of rate constants from shorter trajectories. This expectation is based on the relatively long “ramp-up time” of the flux in the steady state from a given WE simulation.
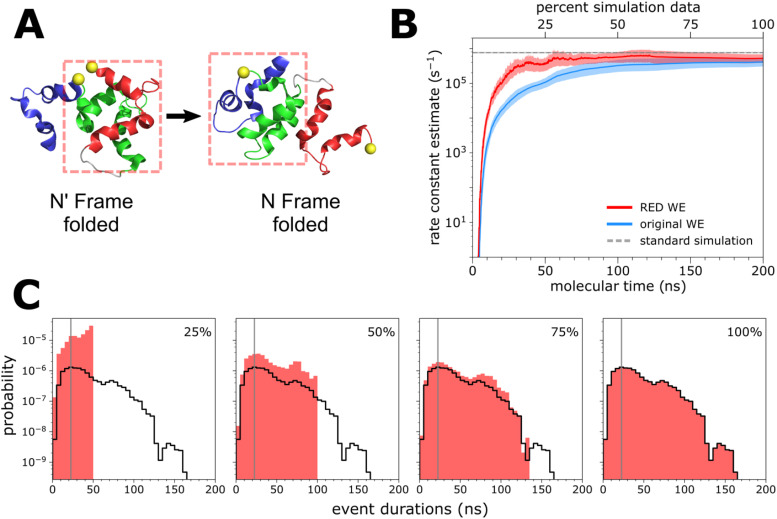
FIG. 2.
Residue-level simulations of protein conformational switching. (a) Schematic of the calbindin-AFF switch, showing the initial N′ state and target N state of the simulated switching process. (b) Comparison of the N′ → N switching rate constant (average of 10 WE simulations) using the original WE scheme () and RED scheme (), as a function of molecular time, or Nτ, where N is the number of WE iterations and τ is the fixed time interval (100 ps in this case) of each WE iteration. See also Table S1. Ten WE simulations were run for each scheme. The RED scheme was applied using the first 25%, 50%, and 75% from each WE simulation. Also shown is the rate constant calculated from 50 2-µs standard simulations (horizontal dashed line). The shaded regions show the nominal 95% credibility regions (CRs) as a function of molecular time from Bayesian bootstrapping;27 the CR from standard simulations is displayed, but too small to be visible. (c) Estimates of the probability density function hAB of event durations for the switching process, as sampled by the first 25%, 50%, and 75% of a representative WE simulation. The vertical gray line indicates the most probable event duration based on the distribution from 100% of the simulation (delineated in black).
To determine the effectiveness of the RED scheme, we examined the evolution of the rate constant as a function of molecular time, where at any given time, the estimate is based only on data from all ten independent WE simulations that were generated up to and including that time. The RED scheme yields faster convergence of the rate constant for the N′ → N switching process [Fig. 2(b)], requiring only the first 25% of the WE simulation data to reproduce the rate constant from standard simulations (50 2-µs simulations). This is almost 50% more efficient than the original scheme, which only began to converge after 75% of the simulation data had been collected and underestimated the rate constant by a factor of two (compared with that from standard simulations) due to the slow transient phase.
We determined the extent of simulation required for estimating rate constants by monitoring the position of the maximum in the distribution of event durations. If the position did not shift substantially—meaning that the most probable event duration reached a consistent value—we considered the simulation as being converged for the purpose of estimating rate constants using the RED scheme. Figures 2(b) and 2(c) show that the most probable event duration (as defined from 100% of the data collected) is captured within the initial 25% of a given WE simulation; furthermore, the cumulative probability distribution of event durations is well-resolved and not skewed toward short values, with low probability events occurring consistently throughout the course of the simulation.
We also determined the effectiveness of the RED scheme when applied to standard simulations, i.e., the first 0.5 µs of the 50 2-µs simulations of the calbindin-AFF system switching process. In this case, the RED scheme yielded the expected rate constant, but was no more efficient than the original WE scheme in doing so (Fig. S1, supplementary material). This result is not surprising since the goal of the RED scheme is to correct for rate-constant estimates that are greatly impacted by the initial transient phase, whereas the length of each standard simulation was much longer (by ∼20-fold) than the majority of the event durations and, therefore, not in the transient phase.
B. Application to atomic-level simulations of Na+/Cl− association
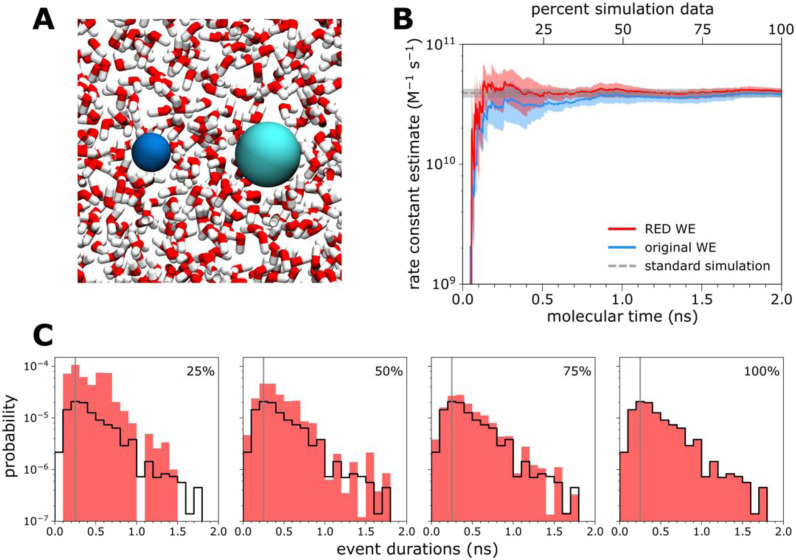
Na+/Cl− association in explicit solvent [Fig. 3(a)] occurs on the ns time scale, which is orders of magnitude faster than the calbindin-AFF switching process and the complex processes that follow. Given the fast event durations of the ion–pair association, it is not expected that the RED scheme would provide much benefit over standard WE rate constant estimation. We found that this was, indeed, the case, as the system does not exhibit a “ramp-up time” [Fig. 3(b)], and the most probable event duration is sufficiently sampled with less than 25% of the data collected [Fig. 3(c)].
FIG. 3.
Atomistic simulations of Na+/Cl− association in explicit solvent. (a) The Na+/Cl− system in explicit solvent. (b) Comparison of the Na+/Cl− association rate constant (average of five WE simulations) using the original WE and RED schemes, plotted as a function of molecular time, or Nτ, where N is the number of WE iterations and τ is the fixed time interval (2 ps) of each iteration. See also Table S1. Five WE simulations were analyzed with each scheme. The RED scheme was applied using the first 25%, 50%, and 75% from each WE simulation. Also shown is the rate constant calculated from 10 1-µs standard simulations (horizontal dashed line). The shaded regions show the nominal 95% credibility regions (CRs) as a function of molecular time from Bayesian bootstrapping.27 The y-axis shown is only a portion of the full set of values in order to more clearly show the comparison between the two schemes; see Fig. S2 for a plot using the full range of data. (c) Estimates of the probability density function hAB of event durations for the molecular association process, as sampled by the first 25%, 50%, and 75% of the 5 WE simulations. The vertical gray line indicates the most probable event duration based on the distribution from 100% of the simulation (delineated in black).
C. Application to atomistic simulations of long-time scale processes in explicit solvent
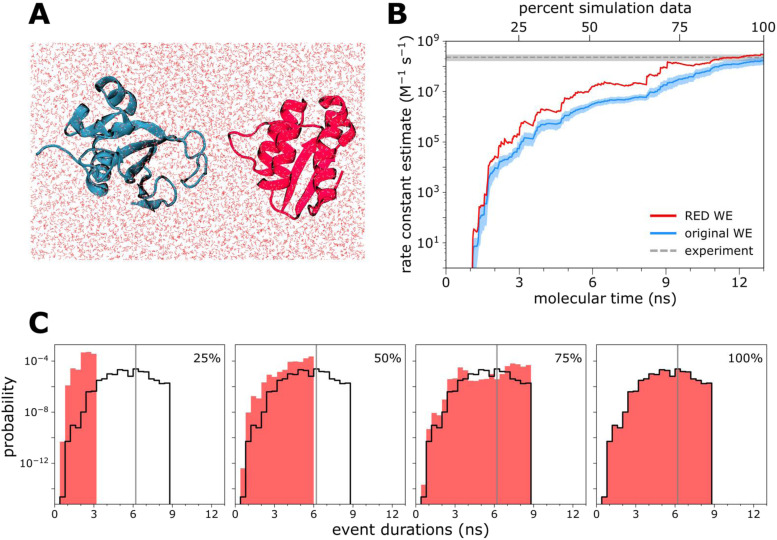
To test the effectiveness of the RED scheme in estimating rate constants from more detailed simulations of complex biological processes, we applied the scheme to a single WE simulation of a protein–protein binding process. This simulation involved the diffusion-controlled association of the barnase and barstar proteins using atomistic protein models with explicit solvent [Fig. 4(a)]. While this simulation was not performed with recycling enabled and, therefore, violates one of the RED scheme’s assumptions, based on the extremely short length of the simulation compared to the mean first passage time, the weight of the trajectories that would have been recycled is extremely low such that negligible inaccuracy is introduced. When applied to this simulation, the RED scheme is at least 25% more effective than the original scheme in estimating rate constants given that the WE simulation has just finished ramping up to a steady state. Similar to the simulation of protein conformational switching, this simulation exhibits a long “ramp-up time” [Fig. 4(b)]. In contrast, the most probable event duration is relatively long (6 ns) and just shy of being captured within the first 50% of the simulation, underestimating the rate constant compared to the eventual converged value [Fig. 4(c)]. Based on the first 75% of the simulation, the rate constant is still underestimated, but due to another reason, the most probable event duration is actually longer than that based on the entire simulation. Due to the large size of the simulation system (∼100 000 atoms) and the relatively long time scales of the protein–protein binding process, only one WE simulation was carried out; therefore, no error analysis was performed was performed for rate constants estimated by the RED scheme.
FIG. 4.
Atomistic simulations of protein–protein association in explicit solvent. (a) A representative unbound state of the barnase and barstar proteins in explicit solvent. (b) Comparison of the barnase–barstar association rate constant using the original WE and RED schemes, plotted as a function of molecular time or Nτ, where N is the number of WE iterations and τ is the fixed time interval (20 ps) of each WE iteration. See also Table S1. A single WE simulation was analyzed with each scheme. To test the length of the simulation required for a converged rate-constant estimation, the RED scheme was applied using the first 25%, 50%, and 75% from each WE simulation. Also shown is the rate constant from experiment (horizontal dashed line); the uncertainty (shaded gray) is the 95% confidence interval determined from standard errors of the mean reported for the experimental results;40 the uncertainty of the rate constant from the original WE scheme is the 95% confidence interval by Monte Carlo bootstrapping.41 (c) Estimates of the probability density function hAB of event durations for the protein–protein association process, as sampled by the first 25%, 50%, and 75% of one of the 10 WE simulations depicted in (a). The vertical gray line indicates the most probable event duration based on the distribution from 100% of the simulation (delineated in black).
D. When is the RED scheme effective and how do we monitor convergence?
Regardless of the simulation model resolution, the RED scheme is particularly efficient in rate-constant estimation for rare events that involve long “ramp ups” in the time evolution of the estimated rate constant. For atomically detailed simulations, the RED scheme works well for long-time scale processes on the μs time scale or beyond. In this study, the RED scheme is of great benefit to residue-level simulations of the protein conformational switching process involving the calbindin-AFF switch due to the large ramp-up time in the flux into the target state and to atomistic simulations of protein–protein binding on the μs time scale. On the other hand, the RED scheme has little impact on the efficiency of rate-constant estimation for the simulations of Na+/Cl− association since this process is relatively rapid and does not exhibit a large ramp-up time in the flux into the target, associated state. As recommended for the original WE scheme,23 the RED scheme is more likely to yield converged rate constants for a process if the most probable event duration has been sampled. Provided that this is the case, the RED scheme estimates rate constants more efficiently than the original WE scheme.
An effective convergence criterion for determining the amount of simulation data necessary for the RED scheme is to generate a sufficient number of successful events such that the position of the maximum in the distribution of event durations (i.e., the most probable value) does not change substantially. For both the calbindin-AFF switching process and Na+/Cl− association process, trajectories with the most probable event duration are already sampled within the first 25% of the WE simulation. On the other hand, for the barnase–barstar association process, the most probable event duration begins to stabilize only after 75% of the simulation is completed. If the most probable event duration continues to evolve after completing the simulation, the system is likely far from a steady state and will require generating a much larger number of successful pathways to yield a converged rate-constant estimate. Alternatively, if the event duration distribution involves a long tail, it may be necessary to sample more of the distribution than just the most probable value.
For challenging cases in which a large amount of computing has already been invested, we recommend applying the RED scheme to quickly gauge the extent to which the simulation has reached steady state. If the estimated rate constant is orders of magnitude from that of the expected time scales, then we recommend constructing a history-augmented Markov state model42 to adjust trajectory weights to values more representative of steady-state conditions and carrying out a separate WE simulation with the adjusted weights.
Finally, the RED scheme is general and can be applied with any simulation strategy that yields unbiased dynamics, including standard simulations. Based on our results from standard simulations of the calbindin-AFF switching process, the RED scheme yields the correct rate-constant estimate, but is no more efficient than the original WE scheme in doing so when the simulations are substantially longer than the majority of event durations. Thus, the RED scheme may be better suited to sets of short simulations (i.e., in terms of the length of each individual simulation rather than aggregate time) rather than longer simulations that are not greatly impacted by the ramp-up time associated with the rate-constant estimation.
V. CONCLUSIONS
We have developed the Rate from Event Durations (RED) scheme, a new scheme for calculating rate constants within the framework of the weighted ensemble (WE) strategy that reduces the impact of transient effects on rate-constant estimation. While the RED scheme does not eliminate the need to observe the substantial portion of the distribution of barrier-crossing times, we anticipate that this scheme—by correctly incorporating the transient phase into the rate-constant estimation rather than “throwing it away”—will enable more accurate estimation of rate constants earlier on in a simulation, using a fraction of the total simulation time required by the original WE scheme. Furthermore, as demonstrated by our results for protein–protein association, the RED scheme could be especially important for estimating the rate constants of challenging biological processes that feature long transient phases. Importantly, the scheme accounts for a systematic error that results from an artificially deflated likelihood of observing events with longer durations and reweights the distribution accordingly.
SUPPLEMENTARY MATERIAL
See the supplementary material for results from applying the RED scheme to standard simulations of the calbindin-AFF switching process, a zoomed out view of Fig. 3(b) that shows the full range of the y-axis for the time evolution of the rate-constant estimate from WE simulations of Na+/Cl− association, and a table of the computed rate constants for all processes simulated in this study using the original WE and RED schemes.
AUTHORS’ CONTRIBUTIONS
A.J.D. and A.T.B. contributed equally to this work.
DEDICATION
This paper is dedicated to Maud Menten, a Canadian woman who—together with Leonor Michaelis—developed the ground-breaking Michaelis–Menten equation for enzyme kinetics. To work with Michaelis, she crossed the Atlantic by ship in 1912—not long after the Titanic sank. Unable to find a faculty position in her native Canada, she joined the faculty in the medical school at the University of Pittsburgh in 1918.
ACKNOWLEDGMENTS
This work was supported by the NIH (Grant No. 1R01GM115805-01) and NSF (Grant No. CHE-1807301) to L.T.C. and by the University of Pittsburgh to A.J.D. (Honors College Brackenridge Undergraduate Research Fellowship) and A.T.B. (Arts & Sciences Fellowship). Computational resources were provided by NSF XSEDE allocation TG-MCB100109 to L.T.C., NSF CNS-1229064, and the University of Pittsburgh’s Center for Research Computing. We thank Daniel Zuckerman (OHSU) and Ali Saglam (U. Pittsburgh) for insightful discussions.
The authors declare the following competing financial interest: L.T.C. is an Open Science Fellow with Silicon Therapeutics.
APPENDIX: DERIVATIONS OF EQS. 3 AND 4
1. Derivation of Eq. (3)
To begin, we consider the relationship between the instantaneous flux fAB(t) at time t, the rate constant kAB, and the true probability distribution hAB of event durations. To be precise, fAB(t) is the time derivative of a cumulative flux function FAB, where FAB(t) is the total number of A → B events observed by time t.
For an A → B transition observed at time t with an event duration of tb, the event must have been initiated at time t − tb. Thus, the instantaneous flux depends on (i) the probability hAB(tb) that barrier-crossing takes time tb and (ii) the frequency at which A → B events are initiated at time t − tb, which is kAB when t − tb > 0 and zero otherwise, since the process does not start until time 0.
To derive an expression for fAB(t), we integrate over all possible event durations tb. Formally, this is a convolution of hAB with the function that is kAB for parameters greater than zero and zero otherwise,
| (A1) |
| (A2) |
Since both functions in the convolution in Eq. (S2) are non-zero only for positive values of t,
| (A3) |
Next, we integrate both sides of Eq. (S3) with respect to t,
| (A4) |
| (A5) |
| (A6) |
We define the cumulative distribution function HAB as the integral of the probability density function hAB, that is, . The left-hand side (LHS) of Eq. (A5) is given by the definition of FAB and the fundamental theorem of calculus, while the right-hand side (RHS) is given by the fact that kAB does not depend on the parameters t and tb that are being integrated. The LHS of Eq. (A6) results because the number of events FAB(0) observed by t = 0 is necessarily zero, while the RHS is given by the definition of HAB.
Finally, to obtain Eq. (3) for kAB, we divide both sides by ,
| (A7) |
where FAB(tmax) is the cumulative number of events and the integral is in units of time, yielding a rate constant kAB that has units of inverse time.
2. Derivation of Eq. (4)
As in Sec. II C, we consider a system in state A at time t = 0, which enters onto successful transition pathways into state B with a rate constant kAB and event durations tb according to the true distribution hAB. After entering the target state B, the system is reinitiated from state A. The simulation ends at time tmax.
We wish to show that a corrected estimate of event durations [Eq. (4)] is asymptotically statistically unbiased up to a constant of proportionality: as the histogram bin width approaches zero, the expected value of the corrected estimate converges to a value proportional to the true distribution hAB, i.e., , where Q is an unknown proportionality constant that does not depend on tb.
Let Ni be the number of observed events into B that occur with duration tb ∈ [ti, ti+1], where ti and ti+1 are the bounds of the ith bin of the histogram. By definition, our corrected histogram estimate evaluated at this particular t is given by
| (A8) |
To consider whether this estimate, indeed, approximates the true distribution hAB of event durations, we take the expected value of the corrected estimate as follows:
| (A9) |
Next, our derivation requires an expression for , which depends on (i) the probability of initiating a successful transition pathway, (ii) the probability that the transition path is of duration t, and (iii) the probability that the transition pathway enters state B before time tmax. For example, the system may initiate a successful transition pathway at time t ∈ [0, tmax] with rate constant kAB, then “choose” a transition pathway with an event duration tb with a probability hAB(tb), and be observed entering state B with probability obs(t) = {1 if t < tmax − tb; else 0}, since an event of duration tb that initiates after tmax − tb would not enter state B until after the end of the simulation at time tmax. Therefore, the expected number of events we will observe with duration tb ∈ [ti, ti+1] within a simulation of length tmax is
| (A10) |
| (A11) |
| (A12) |
Given this expression, the expected value from Eq. (A9) can be rewritten as follows:
| (A13) |
| (A14) |
Assuming that the true distribution hAB is continuous, the mean value theorem indicates that there exists a point ξ in the histogram bin [ti, ti+1] such that the function (tmax − ξ)kABhAB(ξ) evaluated at that point is the average value of this function over that histogram bin,
| (A15) |
For such ξ,
| (A16) |
Finally, we take the limit as ti+1 → ti. Since both tb and ξ are in the histogram bin [ti, ti+1], by the squeeze theorem, we know that if the histogram bin width approaches zero, i.e., ti+1 → ti, then tb → ti and ξ → ti. Plugging these values into Eq. (A16) gives
| (A17) |
Thus, we have the desired result that as the histogram bin width approaches zero; the constant Q depends on both kAB and the constant of proportionality in Eq. (A8). Thus, we have shown that is asymptotically unbiased up to a constant of proportionality.
Note: This paper is part of the JCP Special Collection in Honor of Women in Chemical Physics and Physical Chemistry.
DATA AVAILABILITY
The data that support the findings of this study are available within this article and its supplementary material. A Python implementation of the RED scheme for use with the WESTPA software package8 is available on GitHub (https://github.com/westpa/user_submitted_scripts/tree/main/RED_scheme).
REFERENCES
- 1.Chong L. T., Saglam A. S., and Zuckerman D. M., Curr. Opin. Struct. Biol. 43, 88 (2017). 10.1016/j.sbi.2016.11.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pratt L. R., J. Chem. Phys. 85, 5045 (1986). 10.1063/1.451695 [DOI] [Google Scholar]
- 3.Zuckerman D. M. and Woolf T. B., J. Chem. Phys. 116, 2586 (2002). 10.1063/1.1433501 [DOI] [Google Scholar]
- 4.Huber G. A. and Kim S., Biophys. J. 70, 97 (1996). 10.1016/s0006-3495(96)79552-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zuckerman D. M. and Chong L. T., Annu. Rev. Biophys. 46, 43 (2017). 10.1146/annurev-biophys-070816-033834 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Preto J. and Clementi C., Phys. Chem. Chem. Phys. 16, 19181 (2014). 10.1039/c3cp54520b [DOI] [PubMed] [Google Scholar]
- 7.Zimmerman M. I. and Bowman G. R., J. Chem. Theory Comput. 11, 5747 (2015). 10.1021/acs.jctc.5b00737 [DOI] [PubMed] [Google Scholar]
- 8.Cérou F., Guyader A., and Rousset M., Chaos 29, 043108 (2019). 10.1063/1.5082247 [DOI] [PubMed] [Google Scholar]
- 9.van Erp T. S., Moroni D., and Bolhuis P. G., J. Chem. Phys. 118, 7762 (2003). 10.1063/1.1562614 [DOI] [PubMed] [Google Scholar]
- 10.Allen R. J., Warren P. B., and Ten Wolde P. R., Phys. Rev. Lett. 94, 018104 (2005). 10.1103/physrevlett.94.018104 [DOI] [PubMed] [Google Scholar]
- 11.DeFever R. S. and Sarupria S., J. Chem. Phys. 150, 024103 (2019). 10.1063/1.5063358 [DOI] [PubMed] [Google Scholar]
- 12.Faradjian A. K. and Elber R., J. Chem. Phys. 120, 10880 (2004). 10.1063/1.1738640 [DOI] [PubMed] [Google Scholar]
- 13.Ray D. and Andricioaei I., J. Chem. Phys. 152, 234114 (2020). 10.1063/5.0008028 [DOI] [PubMed] [Google Scholar]
- 14.Chodera J. D. and Noé F., Curr. Opin. Struct. Biol. 25, 135 (2014). 10.1016/j.sbi.2014.04.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Husic B. E. and Pande V. S., J. Am. Chem. Soc. 140, 2386 (2018). 10.1021/jacs.7b12191 [DOI] [PubMed] [Google Scholar]
- 16.Adhikari U., Mostofian B., Copperman J., Subramanian S. R., Petersen A. A., and Zuckerman D. M., J. Am. Chem. Soc. 141, 6519 (2019). 10.1021/jacs.8b10735 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dixon T., Uyar A., Ferguson-Miller S., and Dickson A., Biophys. J. 120, 158 (2020). 10.1016/j.bpj.2020.11.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.DeGrave A. J., Ha J.-H., Loh S. N., and Chong L. T., Nat. Commun. 9, 1013 (2018). 10.1038/s41467-018-03228-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zwier M. C., Pratt A. J., Adelman J. L., Kaus J. W., Zuckerman D. M., and Chong L. T., J. Phys. Chem. Lett. 7, 3440 (2016). 10.1021/acs.jpclett.6b01502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Saglam A. S. and Chong L. T., Chem. Sci. 10, 2360 (2019). 10.1039/c8sc04811h [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ahn S.-H., Jagger B. R., and Amaro R. E., J. Chem. Inf. Model. 60, 5340 (2020). 10.1021/acs.jcim.9b00968 [DOI] [PubMed] [Google Scholar]
- 22.Stratton M. M., Mitrea D. M., and Loh S. N., ACS Chem. Biol. 3, 723 (2008). 10.1021/cb800177f [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zwier M. C., Kaus J. W., and Chong L. T., J. Chem. Theory Comput. 7, 1189 (2011). 10.1021/ct100626x [DOI] [PubMed] [Google Scholar]
- 24.Plattner N., Doerr S., De Fabritiis G., and Noé F., Nat. Chem. 9, 1005 (2017). 10.1038/nchem.2785 [DOI] [PubMed] [Google Scholar]
- 25.McQuarrie D. A., J. Appl. Probab. 4, 413 (1967). 10.2307/3212214 [DOI] [Google Scholar]
- 26.Suárez E., Lettieri S., Zwier M. C., Stringer C. A., Subramanian S. R., Chong L. T., and Zuckerman D. M., J. Chem. Theory Comput. 10, 2658 (2014). 10.1021/ct401065r [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mostofian B. and Zuckerman D. M., J. Chem. Theory Comput. 15, 3499 (2019). 10.1021/acs.jctc.9b00015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zwier M. C., Adelman J. L., Kaus J. W., Pratt A. J., Wong K. F., Rego N. B., Suárez E., Lettieri S., Wang D. W., Grabe M., Zuckerman D. M., and Chong L. T., J. Chem. Theory Comput. 11, 800 (2015). 10.1021/ct5010615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elcock A. H., PLoS Comput. Biol. 2, e98 (2006). 10.1371/journal.pcbi.0020098 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Frembgen-Kesner T. and Elcock A. H., J. Chem. Theory Comput. 5, 242 (2009). 10.1021/ct800499p [DOI] [PubMed] [Google Scholar]
- 31.Go N., Annu. Rev. Biophys. Bioeng. 12, 183 (1983). 10.1146/annurev.bb.12.060183.001151 [DOI] [PubMed] [Google Scholar]
- 32.Takada S., Proc. Natl. Acad. Sci. U. S. A. 96, 11698 (1999). 10.1073/pnas.96.21.11698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Case I. Y. B.-S. D. A., Brozell S. R., Cerutti D. S., Cheatham T. E. III, Cruzeiro V. W. D., Darden T. A., Duke R. E., Ghoreishi D., Gilson M. K., Gohlke H., Goetz A. W., Greene D., Harris R., Homeyer N., Huang Y., Izadi S., Kovalenko A., Kurtzman T., Lee T. S., LeGrand S., Li P., Lin C., Liu J., Luchko T., Luo R., Mermelstein D. J., Merz K. M., Miao Y., Monard G., Nguyen C., Nguyen H., Omelyan I., Onufriev A., Pan F., Qi R., Roe D. R., Roitberg A., Sagui C., Schott-Verdugo S., Shen J., Simmerling C. L., Smith J., SalomonFerrer R., Swails J., Walker R. C., Wang J., Wei H., Wolf R. M., Wu X., Xiao L., York D. M., and Kollman P. A., Amber 18, 2018.
- 34.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- 35.Joung I. S. and Cheatham T. E. III, J. Phys. Chem. B 112, 9020 (2008). 10.1021/jp8001614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Essmann U., Perera L., Berkowitz M. L., Darden T., Lee H., and Pedersen L. G., J. Chem. Phys. 103, 8577 (1995). 10.1063/1.470117 [DOI] [Google Scholar]
- 37.Buckle A. M., Schreiber G., and Fersht A. R., Biochemistry 33, 8878 (1994). 10.1021/bi00196a004 [DOI] [PubMed] [Google Scholar]
- 38.Hess B., Kutzner C., van der Spoel D., and Lindahl E., J. Chem. Theory Comput. 4, 435 (2008). 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- 39.Best R. B. and Hummer G., J. Phys. Chem. B 113, 9004 (2009). 10.1021/jp901540t [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schreiber G. and Fersht A. R., Nat. Struct. Mol. Biol. 3, 427 (1996). 10.1038/nsb0596-427 [DOI] [PubMed] [Google Scholar]
- 41.Efron B. and Tibshirani R., Stat. Sci. 1, 54 (1986). 10.1214/ss/1177013815 [DOI] [Google Scholar]
- 42.Copperman J. and Zuckerman D. M., J. Chem. Theory Comput. 16, 6763 (2020). 10.1021/acs.jctc.0c00273 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See the supplementary material for results from applying the RED scheme to standard simulations of the calbindin-AFF switching process, a zoomed out view of Fig. 3(b) that shows the full range of the y-axis for the time evolution of the rate-constant estimate from WE simulations of Na+/Cl− association, and a table of the computed rate constants for all processes simulated in this study using the original WE and RED schemes.
Data Availability Statement
The data that support the findings of this study are available within this article and its supplementary material. A Python implementation of the RED scheme for use with the WESTPA software package8 is available on GitHub (https://github.com/westpa/user_submitted_scripts/tree/main/RED_scheme).