Dynamic catch-bonding generates the large stall forces of cytoplasmic dynein

Abstract

Cytoplasmic dynein is an important molecular motor involved in the transport of vesicular and macromolecular cargo along microtubules in cells, often in conjunction with kinesin motors. Dynein is larger and more complex than kinesin and the mechanism and regulation of its movement is currently the subject of intense research. While it was believed for a long time that dynein motors are relatively weak in terms of the force they can generate, recent studies have shown that interactions with regulatory proteins confer large stall forces comparable to those of kinesin. This paper reports on a theoretical study which suggests that these large stall forces may be the result of an emergent, ATP dependent, bistability resulting in a dynamic catch-bonding behavior that can cause the motor to switch between high and low load-force states.

Introduction

Cytoplasmic dynein is a motor protein that hauls cargoes of various kinds along microtubule tracks within cells (for recent reviews, see [1,2]). These cargoes, which are vital for cellular function, include membranous organelles, cytoskeletal polymers, and other macromolecular complexes. The force generated by the motor is coupled to ATP hydrolysis, rendering cytoplasmic dynein a mechano-chemical enzyme. In comparison to kinesin, cytoplasmic dynein is a much larger and more complex motor. The dynein motor domain is made up of six AAA+ domains (AAA1-6) arranged in a ring. Domains AAA1-4 bind ATP and domains AAA1, 3 and 4 can catalyze hydrolysis of their bound ATP [2,3]. There is general consensus that AAA1 is the primary site for ATP hydrolysis and that AAA2-4, the secondary binding sites, assume a more regulatory role [4].

Using optical trapping of polystyrene beads coated with purified cytoplasmic dynein, Mallik et al. [5] reported that this motor has a variable step size that can be 8, 16, 24, or 32 nm, which represent integral multiples of the 8 nm periodicity of the tubulin dimers in the microtubule polymer. At low loads, i.e. < 0.4 pN, dynein took mostly larger steps in the range of 24 – 32 nm. At intermediate loads, i.e. 0.4 – 0.8 pN, this was reduced to 16nm steps. At high loads, i.e. > 0.8 pN, dynein took mostly 8 nm steps. At loads of about 1pN, the motor stalled. Thus, Mallik et al. concluded that dynein has the ability to change its stepping behavior in response to load, which implied that its mechano-chemical cycle possessed a molecular gear mechanism.

To gain conceptual and quantitative understanding of the observed stepping mechanism, Singh et al. [6] proposed a mathematical model that can mimic the stepping behavior reported by Mallik et al. [5]. Singh et al. hypothesized that hydrolysis occurs at the primary AAA binding site (AAA1) and that the number of ATPs bound to the secondary AAA binding sites (AAA2-AAA4) regulates the step size. ATP binding was assumed to be cooperative with a binding affinity that decreased as the occupancy of the secondary AAA binding sites increased. By further assuming that the binding affinities of the secondary sites were all load-dependent, the average step size of dynein varied under different loading constraints and was consistent with step size and stall force data available at the time in [5]. Specifically, the step size distribution reported in [5] for low ATP concentrations of 2μM was reproduced well by the model (compare Fig. 5a in [6] and Fig. 4 in [5]). Also, the transitions observed in [5] at saturating levels of ATP, from predominantly large step sizes at low load forces to predominantly 8nm step sizes at high load forces, was predicted qualitatively by the model in [6] for physiological ATP concentrations. Gao [7] also proposed a model that can explain the force dependence of dynein’s step size by decoupling the ATP hydrolysis cycle from the physical translocation of the motor.

In subsequent experimental studies, Toba et al. [8] measured the stall force of dynein to be much larger than that reported by Mallik et al. [5]. Specifically, Toba et al. reported that dynein took 8nm steps at load forces larger than 1pN and was able to generate forces up to 7pN before stalling, similar to the step size and stall force of kinesin. The authors attributed this discrepancy to improvements in their bead-coating method and the temporal resolution of their optical trap. In addition, Walter et al. [9] used a three-bead “dumbbell” optical trap configuration to show that dynein exhibited 8 nm steps under saturating ATP levels and generated forces of up to ≈ 5pN, comparable to the findings of Toba et al. [8]. Walter et al. [9] also reported that the dynein stall force decreased to about 1pN at a lower ATP concentration of 50μM (comparable to findings in [5]), but still took only 8 nm steps. More recently, broad distributions of dynein load forces ranging from approximately 1 – 5pN have been reported by Belyy et al. [10,11].

Consistently high load forces of 4.5 – 7pN have also been reported for yeast dynein [12,13]. This appears to be due to a unique structural feature of the yeast motor as it lacks the C-terminal “cap” domain that is present in mammalian dynein [14]. However, it remains unclear what accounts for the broad range of stall forces of mammalian dynein and how this is related to ATP concentration as observed in [8]. In this paper we address these questions through computational modeling. The manuscript is organized into four sections. First, in the “Model description” section we describe the model and define its kinetic parameters. Second, in the “Model calibration and testing” section we show that the predicted kinetic behavior of our dynein model is consistent with experimental data on the force-velocity relationship, run lengths, stall times, and the dependence of the step size on the load force and ATP concentration. Third, in the “Results” section we show that, at forces below the stall force, the model exhibits an emergent behavior which we term dynamic catch-bonding, and we explore the effect of this behavior on motor stepping and load-sharing. Finally, in the “Discussion” section we summarize our findings and discuss the mechanism and implications of dynamic catch-bonding in the context of other models and studies of dynein function.

Model description

Motor stepping

To develop a model for cytoplasmic dynein kinetics that accounts for the frequent backward stepping of the motor (~20% of steps for high [ATP] [15], [16]), we use a phenomenological method analogous to the kinesin-1 motor model of Kolomeisky and Fisher [17] where the motor stepping is coupled to ATP hydrolysis with appropriate matched rate constants. The model considers that the dynein motor has four conformational states (j = 1,2,3,4) associated with step sizes of Δ₁ = 32nm, Δ₂ = 24nm, Δ₃ = 16nm, and Δ₄ = 8nm, respectively. In Fig. 1, we show the kinetics of ATP hydrolysis for these conformational states. Note that the scheme depicts reversible ATP hydrolysis, which is necessary in this model in order for the motor to stall at a certain force [18, 19].

Fig. 1. Kinetic scheme for the dynein motor model.

The dynein motor is considered to exist in four conformational states j = 1,2,3,4, associated with step sizes of 32nm, 24nm, 16nm, and 8nm, respectively. Stepping of the motor in each state is coupled tightly to ATP hydrolysis. ATP binds to the dynein motor D_j with rate $a_j^{+}$. In the ATP-bound state (D_j ∷ ATP), the ATP can either be hydrolyzed with rate ${\beta }_j^{+}$ or it can dissociate with rate $a_j^{-}$. Backward stepping is modeled as reverse catalysis with the rate constant ${\beta }_j^{-}$. Note that ${\beta }_j^{+}$ technically includes both hydrolysis and release of the hydrolysis products, but for simplicity we refer to it as the hydrolysis rate constant in the present study.

Following Michaelis-Menten, ATP binds dynein with the rate [ATP]α_j⁺ where [ATP] denotes the ATP concentration (which we assume to be constant). Once ATP is bound, the dynein motor and ATP form a complex D_j ∷ ATP which can either dissociate with rates α_j⁻, or lead to catalysis and forward stepping with step size Δ_j. We model backward stepping of the motor with step size −Δ_j through a reverse catalysis rate β_j⁻. At steady-state, the forward and backward stepping rates (r_j⁺ and r_j⁻, respectively) in the four conformational states (j = 1,2,3,4) are then given by

$$\begin{array}{cc}{r_j}^{+}={\beta }_j^{+}\frac{a}{a+K_j},& {r_j}^{-}={\beta }_j^{-}\frac{K_j}{a+K_j}\end{array},$$ (1)

with K_j given by

$$K_j=\frac{{{\alpha }_j}^{-}+{{\beta }_j}^{+}}{{{\alpha }_j}^{+}+{{\beta }_j}^{-}/a},$$ (2)

where a is the ATP concentration. If we ignore the backward stepping rate β_j⁻, the quantity K_j is equivalent to the Michaelis constant in the standard Michaelis-Menten model. The maximum forward and backward stepping rates $r_j^{+}$ and $r_j^{-}$, are given by the catalysis rates ${\beta }_j^{+}$ and ${\beta }_j^{-}$, respectively. If the ATP concentration a matches K_j, i.e. $a=\left({\alpha }_j^{-}+{\beta }_j^{+}-{\beta }_j^{-}\right)/{\alpha }_j^{+}$, the forward and backward stepping rates are half their maximum stepping rates, respectively.

The average velocity of the motor is obtained by summing over all step sizes, i.e.

$$\overline{v}={\sum }_{j=1}^4{\Delta }_j\left(r_j^{+}-r_j^{-}\right).$$ (3)

Detachment kinetics

Just like kinesin motors, dynein motors can detach from their microtubule tracks resulting in finite average run lengths and run times. Dynein’s detachment kinetics were studied by Kunwar et al. [20] and Nicholas et al. [21]. Kunwar et al. [20] reported that the detachment rate increases exponentially with load force below a stall force that doesn’t exceed 1pN. For load forces above the stall force, the detachment rate decreases towards a limit value, exhibiting the characteristics of a catch-bond. We cannot adopt these experimentally determined detachment kinetics for our model, since our model predicts stall forces ranging from 1pN to several pN, as reported in the more recent literature [8,9,10,11]. Nicholas et al. [21] report anisotropic detachment forces with larger slip-bond type detachment forces of about 2pN in the direction opposing the motor movement We neglect the directionality of the detachment forces because in our study the load forces oppose the motor movement most of the time. We use a simple slip-bond type exponential detachment rate for all load forces and all four conformational states and tune this detachment rate to the experimental measurements. Detachment rates depend on the ATP concentration and the load force. The rates are dominated by the load force if ATP concentrations are in the millimolar range [22] because at these concentrations ATP is bound most of the time. During the time that ATP is attached, the rate of motor detachment is given by the Arrhenius equation, i.e.

$$r_{\mathit{det}}=r_0\exp \left(\frac{{\delta }_{d}F}{k_{B}T}\right),$$ (4)

where F is the load force, k_B is Boltzmann’s constant, and T is the temperature. The prefactor r₀ is constrained by the average run length, measured in a cargo-motor assay as described below, and the force constant δ_d is constrained by the average stall time (for a single motor) in an optical trap experiment (data taken from [23]). This approach is different from the one used in [22], where a state-independent detachment rate was calculated using a phenomenological expression for the detachment probability in conjunction with the average dwell time in the ATP-bound states.

Step size

Next, we consider the step size distribution and average step size of the motor. The rate of steps of absolute size Δ_j (forward or backward) in conformational state j is given by $r_j={r_j}^{+}+{r_j}^{-}$, resulting in the following expression for the normalized probability distribution of absolute step sizes

$$\begin{array}{cc}p\left({\Delta }_j\right)=\frac{r_j}{{\sum }_{i=1}^4{r}_i},& j=1,2,3,4\end{array}$$ (5)

with step sizes of Δ₁ = 32nm, Δ₂ = 24nm, Δ₃ = 16nm and Δ₄ = 8nm, and an average step size of

$$\overline{\Delta }={\sum }_{j=1}^4{\Delta }_{j}p\left({\Delta }_j\right).$$ (6)

In [24], dynein step size was measured based on plateau values of the displacement, but only forward steps were counted. Thus, for the specific case of comparisons with that study we analyze only forward steps in our model, resulting in the following expression for the step size distribution p⁺(Δ_j)

$$p^{+}\left({\Delta }_j\right)=\frac{{r_j}^{+}}{{\sum }_{i=1}^4{r_i}^{+}},$$ (7)

where the superscript ⁺ denotes the forward stepping direction, with an average forward step size as defined in Eq.6.

Load dependence of the kinetic rates

To account for the load dependence of the motility of the dynein motor, the kinetic rate constants of ATP binding and hydrolysis were considered to depend on the load F in accordance with

$$\begin{gathered} {{\alpha }_j}^{+}={{\alpha }_j}^{+}\left(0\right)\exp \left(-\frac{{\delta }_{\alpha ,j}F}{k_{B}T}\right) \\ {{\beta }_j}^{+}={{\beta }_j}^{+}\left(0\right)\exp \left(-\frac{{\delta }_{\beta ,j}F}{k_{B}T}\right). \end{gathered}$$ (8)

This approach utilizes an energy landscape model, where the energetic barriers of the processes depend on the load forces. For positive values of the constant δ_β,j, the ATP hydrolysis rates decrease with increasing load force, resulting in smaller velocities, while for negative values the opposite occurs. Similarly, for positive values of δ_α,j, the ATP binding rates decrease with increasing load force, also leading to smaller velocities. These individual dependencies of the ATP hydrolysis and binding rates on the load force are necessary to accommodate both the measured force dependence of the step sizes of the dynein motor and the force-velocity relation. The parameter values that we identified to reproduce most experimental data on cytoplasmic dynein (see below) are listed in Table 1.

Table 1:

Rate constants chosen for the dynein model

Parameter	Description	State 1	State 2	State 3	State 4
α+ (M−1sec−1)	ATP binding rate	8.00 · 106	1.33 · 105	2.00 · 105	4.00 · 105
δα (nm)	ATP binding force constant	2.0	6.0	4.0	2.5
α− (sec−1)	ATP dissociation rate	50	200	175	150
β+ (sec−1)	Catalysis rate	32	20	8	5
δβ+ (nm)	ATP hydrolysis force constant	12	5	1.0	−5.5
β− (sec−1)	Inverse catalysis rate	0.0	5.8	2.3	0.4
δβ− (nm)	Inverse ATP hydrolysis force constant	0.0	0	−1	−1
Δ (nm)	Step size	32	24	16	8

Motor-cargo assays

The interaction of dynein and kinesin motors with microtubules is often studied with assays consisting of beads attached to molecular motors, e.g. in an optical trap. We mimic such an arrangement with the following simple mechanical model (see Fig. 2). N dynein motors are attached to a rigid cargo (bead) through flexible elastic linkers with spring constant k_l. The cargo is either free to move or is bound to the optical trap with spring constant k_t, which pulls the cargo in the opposite direction to the dynein motors. Note that the motors on a given cargo are mechanically coupled to each other indirectly via these elastic motor-cargo linkages, and therefore can influence each other’s kinetics (e.g. [25,26]). The positive x-direction corresponds in our model to the minus-end of the microtubule (i.e. the direction of dynein movement). The movement of the cargo is assumed to be damped with a friction constant γ, which depends on the size of the cargo. Assuming that inertial forces can be neglected, the equation of motion for the cargo is given by

$$\gamma {\dot{x}}_c={\sum }_{i=1}^N{F}_i-k_t{x}_c,$$ (9)

where F_i=1…N represent the forces of the dynein motors (i = 1,2, … , N) acting on the cargo, x_c represents the location of the cargo along the microtubule, and k_tx_c represents the force of the trap on the cargo. The force F_i of each dynein motor on the cargo depends on whether that motor is leading or lagging with respect to the position of the cargo. If the motor at position x_i is ahead of the cargo at position x_c and if this distance exceeds the resting length l of the linker, then the linker is stretched and the corresponding force in the positive x-direction is given by F_i = k_l(x_i − x_c − l). If the motor at position x_i is located less than a distance l from the cargo at position x_c, it behaves more like a floppy spring with a weak entropic elasticity, e.g. F_i = 0.01 k_l(x_i − x_c). If the motor at position x_i is lagging behind the cargo at position x_c and if this distance exceeds the resting length l of the linker, the corresponding force of that motor on the cargo is similarly given by F_i = k_l(x_i − x_c + l) in the negative direction. In cases when the cargo is moving freely, i.e. without a trap, the term k_tx_c on the righthand side of Eq.9 vanishes. The above expressions refer to the forces F_i acting on the cargo; according to Newton’s third law, we consider the force acting on the motor to be equal in magnitude but opposite in direction.

Fig. 2. Model of multiple motors engaged with a cargo.

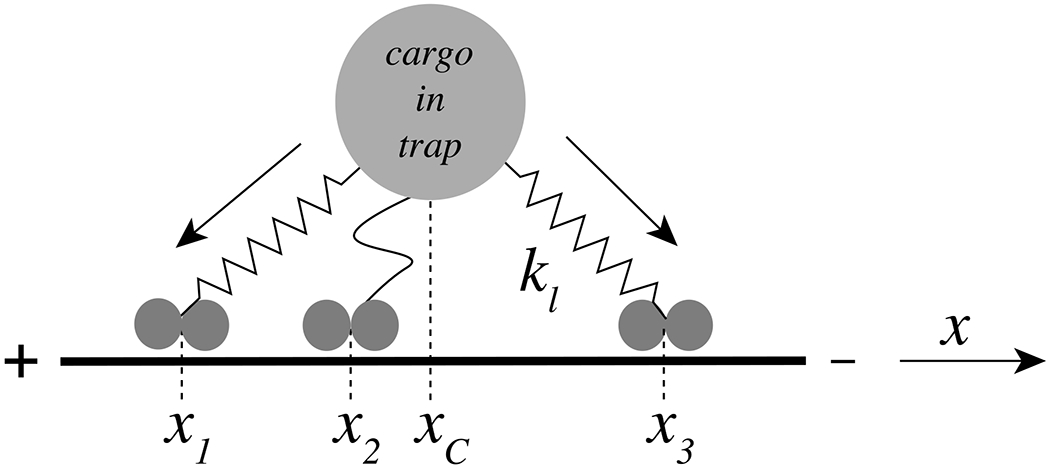
The figure shows three dynein motors at positions x₁, x₂ and x₃ attached to an optically trapped bead (cargo) at position x_c. The springs connecting the cargo with the dynein motors indicate elastic linkers that are either stretched (x₁ and x₃) or relaxed (x₂) and the arrows along the linkers indicate the direction of the force exerted by the respective motor on the cargo. The linkers are elastic (spring constant k_l) and the cargo experiences a viscous drag (friction coefficient γ). The solid bar represents a microtubule with its minus end (towards which dynein moves) to the right.

To model dynein behavior in motor-cargo assays, we must also take account of the frictional drag experienced by the cargo. According to Stokes’ law, the friction coefficient γ for a spherical cargo with radius R is given by γ = 6πμR where μ is the dynamic viscosity. To simulate cytoplasm, we assign μ the value of 5 centipoise, i.e. 0.005kg/(m s), which is 5 times the viscosity of water [27]. With a spherical cargo diameter of 1μm, this leads to a friction coefficient of γ = 0.5 · 10⁻⁷ kg/s. If we express the forces in units of pN, displacements in units of nm, time in units of s, and trap stiffness k_t in units of pN/nm, we obtain a dimensionless equation of motion with a dimensionless friction coefficient of γ = 5 · 10⁻⁵ which absorbs all conversion factors.

The Langevin equation for the motion of the cargo driven by N dynein motors in the presence of thermal noise then reads

$${\dot{x}}_c\left(t\right)=\frac{1}{\gamma }({\sum }_{i=1}^N{F}_i\left(x_1,x_2,\dots ,x_N,x_c\right)-k_t{x}_c)+\xi \left(t\right),$$ (10)

where x_i denotes the position of the motor i, x_c denotes the position of the cargo, and ξ(t) denotes zero-mean white Gaussian thermal noise acting on the cargo (see e.g. [28]), i.e.

$$<\xi \left(t\right)>=0,<\xi \left(t\right)\xi \left(t\prime \right)>=\frac{2\cdot {10}^{-3}{k}_{B}T}{\gamma }\delta \left(t-t\prime \right).$$ (11)

Here, the dimensionless thermal energy k_BT is measured in units of pN · nm and has the value of 4.14 at room temperature. This Langevin equation is solved numerically using a first order solver [28], i.e.

$$x_c\left(t+\delta t\right)=x_c\left(t\right)+\frac{\delta t}{\gamma }({\sum }_{i=1}^N{F}_i\left(x_1,x_2,\dots ,x_N,x_c\right)-k_t{x}_c)+\sqrt{\frac{2\cdot {10}^{-3}{k}_{B}T}{\gamma }\delta t}G\left(1\right),$$ (12)

where G(1) denotes a random number drawn from a Gaussian distribution with unit variance, and δt is the time interval during which we consider the change of cargo position. The prefactor of the Gaussian random variable must be small, which requires δt to be less than about 100μs at room temperature. The Langevin equation is solved in conjunction with Markov modeling of the motor kinetics, i.e. when a motor makes a step it assumes a new position independent of its previous movements. For cargo movement in vivo, the force exerted on the cargo by dynein can be opposed by motors such as kinesin. We can represent this opposing force as an additional load force F_c on the cargo, equivalent to an optical trap, and replace the force of the trap on the cargo, i.e. −k_tx_c, with the load force F_c.

Simulation of the Langevin equation above is cumbersome but can be simplified by tracking only the states where the cargo is in mechanical equilibrium. This is possible because the time that it takes for the cargo to relax to equilibrium after the stepping of the motor, i.e. τ ≈ k_l/γ ≈ 1ms, is shorter than the average time between motor steps, determined approximately by the inverse of the maximum catalysis rates (see Table 1). When one or more motors step to a new position x_i along the track, we subsequently determine the new cargo position x_c at which the total force on the cargo vanishes, i.e.

$${\sum }_{i=1}^N{F}_i\left(x_1,x_2,\dots ,x_N,x_c\right)+F_l=0,$$ (13)

and then the calculation is repeated for each subsequent step.

Model testing and calibration

In this section we show that the predicted kinetic behavior of our dynein model is consistent with observations on the force-velocity relationship, run lengths, stall times, and the dependence of the step size on the load force and ATP concentration. All the comparisons of the model with experimental data shown below were obtained using the same set of kinetic rate constants, which were selected to yield the best fit overall.

Motor stepping

In Fig. 3a, we show the load dependence of the average step size for our dynein model compared to the experimental data reported in [24] at an ATP concentration of 1mM. Experimentally, the step sizes and the corresponding forces plotted here were obtained with an in vivo optical trap setup with latex bead phagosomes, analyzing forward steps of the cargo only and measuring the step size while increasing the force on the motors until they stalled and detached. Hence, we use Eq.7 to model step sizes. Consistent with the experimental data, the model predicts that the average step size of the motor decreases with increasing applied load. In our model this reduction in average step size is determined by the differential load-dependence of the ATP binding and catalysis rates in the four conformational states associated with the four step sizes. At low load forces (0.1pN), the ATP catalysis occurs most frequently in conformational state j = 1 , resulting in predominantly 32nm step sizes, as seen in [24]. With increasing load, the larger value of the force constant δ_β⁺ results in a rapid decrease in the catalytic rate in the conformational state j = 1 , which is associated with the largest step size (see Eq.8). ATP catalysis in the other conformational states associated with smaller step sizes then carry an increasing relative weight, resulting in a reduction in the average step size. At load forces of about 1pN the motor takes predominantly 8nm steps. Note that in order to model a transition from predominantly 32nm steps at low load to predominantly 8nm steps at high load, and still comply with the observed motor speeds shown in Fig. 4, we had to choose a negative force constant ${\delta }_{\beta }^{+}\left(4\right)=-5.5nm$ for the force dependence of the catalysis rate in the conformational state associated with the 8nm step, which implies an increase in the catalysis rate with increasing load force.

Fig. 3. Dynein stepping behavior under various applied loads.

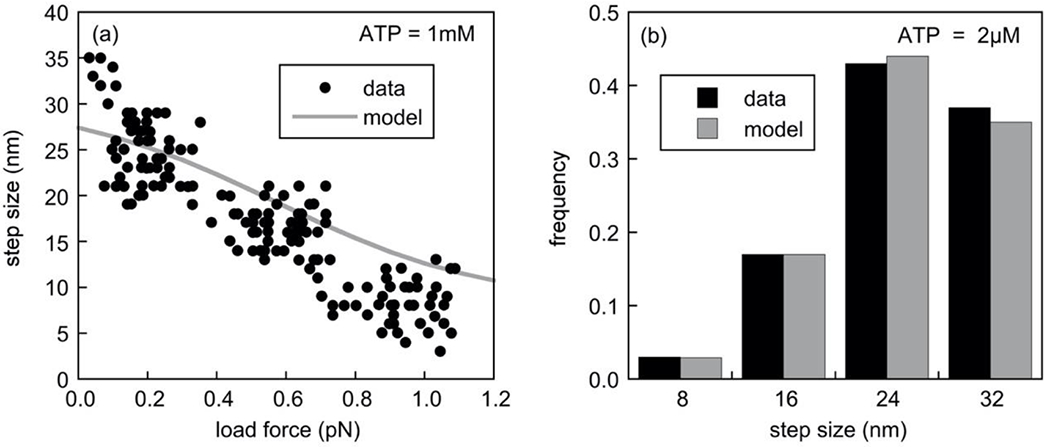
In panel (a), we compare the experimentally obtained step sizes versus load force [24] (circles) with the average step sizes obtained with our model at an ATP concentration of 1mM (solid grey line). The normalized load force in [24] is renormalized here to a stall force of 1.2pN, which is the stall force of our model at this ATP concentration. As only steps in the minus direction (the preferred direction of the dynein motor) were analyzed in the experiments, we used Eq.7 for these simulations. Data points were extracted from the published paper using the GraphClick software package [30]. As in the experimental data, the motor in the model takes predominantly large steps of 32nm and 24nm at low load and predominantly small steps of 8nm at high load, though the quantitative agreement for larger forces is not as good as for small forces. In panel (b), we compare the predicted distribution (grey bars) of the absolute step sizes (positive and negative) at a low ATP concentration (2μM) with published data for this ATP concentration [5] (black bars).

Fig. 4. Dynein velocity under various applied loads and [ATP].

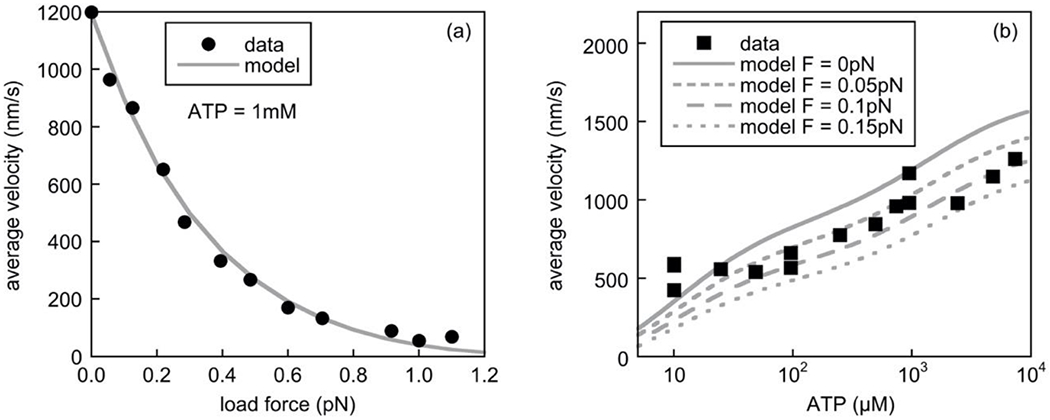
In panel (a), we compare the predicted dynein force-velocity relationship (solid grey line) with the experimental data of [24] (circles) at a 1mM ATP concentration. The force-velocity curve was scaled according to the values in table S1 in the supplementary data of [23] for a single dynein motor moving a bead along a microtubule in vitro. In panel (b), we compare the predicted average velocity of the motor as a function of the ATP concentration for load forces of 0pN, 0.05pN, 0.1pN, and 0.15pN (solid and dashed grey lines), with experimental data for minus-end directed motion from Fig. 4c in [31] (squares), reflecting retrograde movement of the dynein obtained using TIRF assays under “minimal load”. The experimental data points were extracted using the GraphClick software package [30].

In [5] a step size distribution was reported for dynein at the very low ATP concentration of 2μM. It was obtained using optical trapping interferometry in conjunction with a bead motility assay, which is the method used in [29] to determine the step sizes of kinesin motors. This method is blind to the directionality of the steps and hence, we compare the resampled distribution of observed step sizes with the step size distribution predicted by Eq.5, which considers forward and backward steps (see Fig. 3b). Note that the step sizes predicted by our model agree well with reported data for very low ATP concentrations.

One caveat of using the force-dependent step sizes of [24] is that they were obtained in vivo using optical trapping of latex bead phagosomes and the precise number of attached motors was not known. Those authors normalized the measured force on the cargo to the stall force, which was found to scale linearly with the number of motors in experiments in vitro, to calculate the force on each motor. We used this normalized data to calibrate our single-motor model. Load force step size relations for single yeast dynein motors in vitro [12] (disregarding the non-advancing stepping mode described in that study) are consistent with the estimates for mammalian dynein in vivo in [24] in that the step size for load forces larger than 1pN is approximately constant at about 8nm. Gennerich et al. [12] did not report step sizes for forces less than 1pN.

The stepping frequency is characterized by the dwell time, i.e. the time interval between two subsequent steps. We determined the dwell time in our model by simulating the motion of cargo attached to a single dynein motor using the formalism in Eq.10. With no load acting on the cargo, we obtain an exponential distribution of dwell times for an ATP concentration of 1mM, with an average dwell time of 24ms (not shown). This compares favorably with the experimental data of Toba et al. [8], who reported an exponential distribution of dwell times with an average dwell time of 27ms.

Force versus velocity

In Fig. 4a, we compare the force-velocity relationship predicted by the model with experimental data obtained from measurements in an optical trap [24] at an ATP concentration of 1mM and we find excellent agreement. As discussed in [24], the curve starts with a large negative slope associated with a rapid decline of the velocity for small changes in applied load, unlike the force-velocity relationship of kinesin which starts with a small negative slope. In our model, the cause of this rapid decline is two-fold: first, the decrease in the ATP binding rate and the hydrolysis rate with increasing load in the conformational state j = 1 associated with a step size of 32nm; and second, the increasing relative weight of ATP hydrolysis and stepping in the other conformational states, associated with smaller step sizes. In Fig. 4b, we compare the predicted dependence of the average velocity on ATP concentrations at small load forces of 0pN, 0.05pN, 0.1pN, and 0.15pN in our model with experimental data obtained for purified dynein-dynactin complexes at “minimal” load [31]. In agreement with the experimental data, the velocity of the motor increases with increasing ATP concentration in a biphasic manner and displays good overall agreement, with no saturation in velocity up to an ATP concentration of about 10mM (10⁴μM) (see [31]). This suggests, as in [10], that catalysis occurs at different rates depending on the ATP concentration, consistent with our model.

Detachment kinetics and stall forces

To determine the two parameters r₀ and δ_d in the expression Eq.4 for the detachment rate when ATP is bound, we simulated two different experiments. First, to determine r₀ = r_det(F = 0), which is the detachment rate at zero force, we simulated a cargo attached to a motor moving along a track with no force except viscous drag (i.e. Eq.12 with k_t = 0). The constant r₀ was chosen such that the average run length, i.e. the distance moved before detachment averaged over thousands of runs at an ATP concentration of 1mM, matched the 1.8μm run length for dynein-coated beads moved by one, two and three dynein motors as reported in the supplement to [23]. This resulted in the value of r₀ = 0.2/s. Second, to determine the force constant δ_d we simulated an optical trap experiment with a trap stiffness of k_t = 0.05pN/nm (see Fig. 5) using this value of r₀. For each stall event, we defined the stall time as the time interval between the time t₁, when the force on the motor prior to detachment exceeded half the stall force of f_s, and the time t₂, when the motor detached at the stall force f_s, consistent with the definition used in [24]. We sampled thousands of stall times to obtain an average stall time τ and then used Eq.12 to match the 0.2s average motor stall time reported in the supplement to [23]. This resulted in the value of δ_d = 4.5nm. We ignored premature detachments at forces less than 1pN.

Fig. 5. Measurement of dynein stall times.

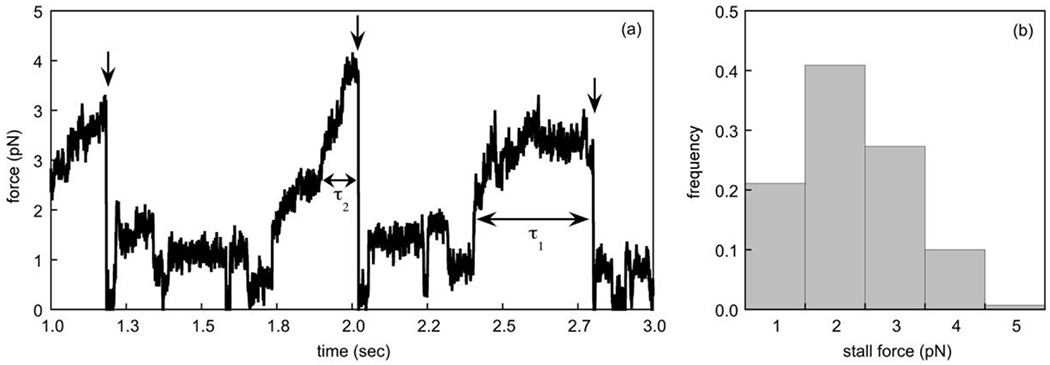
(a) We show a simulated time course of the force exerted by an optical trap on a cargo driven by a single dynein motor at 1mM ATP. Three stalling events are shown (indicated by the vertical arrows). The horizontal double-sided arrows mark the stall times for two of these events (τ₁ and τ₂). The precipitous drop in force after each stall reflects the detachment of the motor. In our simulations, the motor instantaneously re-attached to the track after detachment. (b) We show the distribution of stall forces obtained from 1000 detachment events as characterized in (a).

To test the assumption of exponential detachment kinetics governed by Eq.4 in our model, we simulated the run length and the stall times of a cargo with two or three dynein motors attached. We used the constants r₀ and δ_d calibrated to run length and stall time measurements for a single motor (see previous paragraph) and compared the results with the corresponding experimental data in [23], without any further adjustment of the model parameters. For zero load force on the cargo, our prediction for the average run length with two dynein motors was 8.3μm at an ATP concentration of 1mM, which agrees well with the experimental measurement of 8μm. For three dynein motors we obtained an average run length of about 30μm, which is consistent with the experimental measurement of > 15μm. This agreement confirms again the prefactor r₀ of the expression for the detachment rate because the exponential factor in the detachment rates vanishes in the absence of a load. In simulations of an optical trap experiment with multiple dynein motors attached, we obtained an average stall time of 0.4s for two motors, and 0.6s for three motors. This compares with experimental measurements of 0.4 ± 0.2s for two motors and 0.6 ± 0.4s for three motors, as reported in [23]. The reattachment rates of motors (on-track rates) have not been measured experimentally, so we used the value of 5/s reported in [20].

Results

Dynein exhibits dynamic catch-bonding

As described above, in order to mimic the transition from large motor steps of 16, 24, or 32nm at small load forces to small motor steps of mostly 8nm at large forces, we had to choose a negative force constant for the force dependence of the ATP catalysis rate when the motor is in the conformation associated with 8nm steps. This resulted in an increase in the catalysis rate with increasing force. We show here that this also resulted in an increase in the run length of the motor at sufficiently high ATP concentrations and larger load forces, thereby mimicking a catch-bond between the dynein motor and the microtubule track. A catch-bond is a bond that gets tighter with increasing force (for a recent review see [32]). Such bonds are normally characterized by an increase in the lifetime of the bond with increasing force. Catch-bonds were initially reported for cell adhesion molecules [33] but have also been demonstrated in the binding of dynein motors to microtubules at load forces beyond the stall force (“super-stall” forces). They have also been proposed to explain the relationship between stall force and stall time for cargoes driven by a team of dynein motors [20,24]. However, in contrast to those studies, the catch-bond behavior described here occurs at forces below the stall force and is ATP-dependent. To distinguish the catch-bond behavior described here from those studies, we refer to it as “dynamic catch-bonding”.

With our calibrated dynein motor model, we simulated the average run length of a single dynein motor (without cargo) as a function of a fixed load force. The results are shown in Fig. 6. At low ATP concentrations, i.e. below about 1mM, the run length decreased rapidly with increasing load force until a force was reached at which the run length vanished (circles in Fig. 6), i.e. the motor stalled. The dependence of the run length on the load force was not very sensitive to ATP concentration at low load forces, but this changed radically for larger load forces at ATP concentrations of 1mM or more. At these higher ATP concentrations, the force at which the motor stalled, i.e. the stall force, was 4pN or more. This can be interpreted as an increased affinity of the dynein motor for the microtubule track, i.e. a tightening of the bond to the microtubule, allowing it to withstand much larger forces before detaching. The origin of this behavior within our model is the increased ATP catalysis rate in the conformational state j = 4 associated with a step size of 8nm, which reduces the time during which detachment can occur, and thus results in a lower detachment probability.

Fig. 6. Run length of a single dynein motor driven by a constant force.

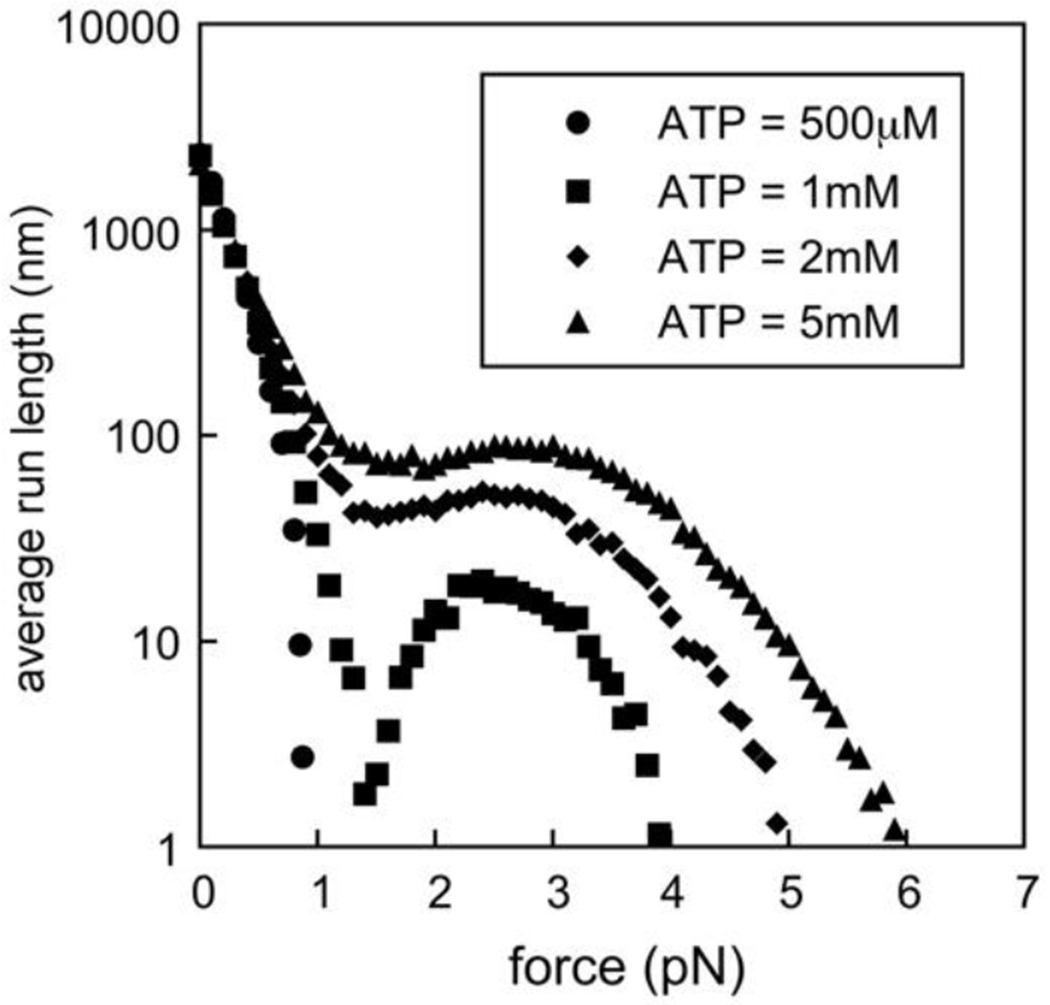
The average run length is plotted against the load force on the motor, with each data point representing a measurement of average run length at a fixed force. For an ATP concentration of 500μM (circles), the average run length dropped rapidly to zero at a load force of about 1pN. For ATP concentrations of 1mM (squares), 2mM (diamonds), and 5mM (triangles), when the dynamic catch-bond was activated, the average run length decreased initially, but then reached a minimum at a force of about 1pN before rising again to exhibit another peak and then stalling at a much larger force.

This catch-bonding behavior was also evident in the force-velocity relationship (see Fig. 7a,b). This relationship was obtained in two different ways, either by utilizing the explicit formula in Eq.3, which did not consider detachment, or by stochastic simulations of a single motor, where we recorded the duration and distance of each run (run time and run length, respectively) and then calculated the ratio of these two quantities. In both cases, the load force was held constant. The results using both approaches were identical. At ATP concentrations of about 1mM or higher, the velocity first decreased with increasing load force until it reached a minimum, and then it increased again between load forces of between about 1.5pN and 3pN to exhibit another peak before it vanished at a much larger force. As observed above for the average run length (see Fig. 6), the force at which the velocity vanished, i.e. the stall force, was dependent on the ATP concentration. Analysis of this relationship revealed an abrupt and discontinuous transition from a stall force of approximately 1pN to one of more than 4pN at an ATP concentration of about 1mM (see Fig. 7c)

Fig. 7. Force-velocity curves for dynein with a dynamic catch-bond.

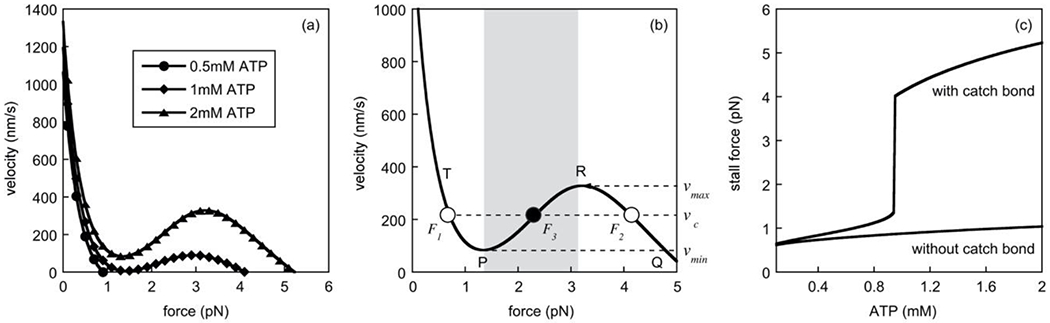
(a) The average velocity is shown as a function of a constant load force (x axis) on the motor for three different ATP concentrations, i.e. 0.5mM (circles), 1mM (diamonds), and 2mM (triangles). Dynamic catch-bonding behavior was observed at or above 1mM ATP. (b) Schematic of the force-velocity curve for 2mM ATP in (a) showing the velocity domain (see dashed lines), i.e. v_min < v_c < v_max, where three motor forces coexist for one velocity, i.e. F₁, F₂ and F₃. The grey band represents the force domain in which the motor is unstable. Points P and Q are referred to in the text. (c) The predicted dependence of the stall force on the ATP concentration in the presence (upper curve) and absence (lower curve) of dynamic catch-bonding.

Note that the velocity increase of the motor with increasing load force in Fig. 7a,b is due to the increased ATP catalysis rate in the conformational state of the motor associated with a step size of 8nm, and the fact that this step size is dominant at load forces of 1pN and above. In the next section, we show that in general, i.e. not specific to this model, such a positive slope in the force-velocity relationship has a profound consequence for the dynamics of the motor as it generates a dynamic instability.

Dynamic catch-bonding can result in mechanical instabilities

In experimental studies, the force-velocity relationship of a cargo attached to a motor is determined by optically trapping the cargo and measuring the velocity at what is effectively a fixed force (calibrated as displacement in the trap). Because of force balance the sum of the forces acting on the cargo (motors pulling forward and trap pulling back) vanishes most of the time, and thus the fixed force applied to the cargo constrains the force on the motor, i.e. the force on the motor is equal in magnitude to the force on the cargo.

We suggest here an alternate experimental paradigm in which one measures the forces that motors exert on the cargo when the cargo is moved with a fixed velocity. In this experimental regime, the force on the motor is unconstrained and adjusts itself dynamically to the controlled velocity of the cargo. Using a generic motor model (not specific for dynein) with a force-velocity relationship v(F) where the velocity increases with load in a certain force domain (indicated in gray in Fig. 7b), we show below that such an experimental paradigm can directly reveal a dynamic instability.

The motor is considered to be attached to a cargo by a linker with a resting length l and a stiffness k_l = 0.07pN/nm (adapted from [34]), and the cargo is moved by the motor towards the minus-end of the microtubule. By an external feedback mechanism, the velocity of the cargo v_c is kept constant at a value less than the velocity of the motor at zero load. Denoting load forces in the plus-end direction (i.e. opposite to the direction of motion) with a positive sign, the load force on the motor is given by F_m = k_l(x_m − x_c − l), where x_m is the position of the motor and x_c the position of the cargo. Starting the cargo at x_c(0) = 0 and the motor at x_m(0) = l , and making a change of variables, y_m(t) ≡ x_m(t) − l, the force exerted on the motor is given by F_m = k_l(y_m(t) − v_ct). Denoting the force-velocity relationship of the motor by v(F_m) = v₀g(F_m), where v₀ is the velocity of the motor at zero load and the function g(0) = 1, the equation of motion for the position of the motor y_m , is then given by

$$v_m={\dot{y}}_m\left(t\right)=v_{0}g\left(k_l\left(y_m\left(t\right)-v_{c}t\right)\right),$$ (14)

where the dot denotes a derivative with respect to time. At steady state, the motor runs at the same velocity as the cargo, i.e. v_m = v_c, but the position is shifted by a distance δ, which corresponds to the length of the stretched linker under load, i.e. $y_m^{ss}\left(t\right)=v_{c}t+\delta \mathrm{or}{x}_m^{ss}\left(t\right)=v_{c}t+l+\delta$. This gives rise to the equation for the shift δ and the force F_m on the motor, i.e.

$$v_c=v_{0}g\left(k_l\delta \right),F_m=k_l\delta .$$ (15)

For ATP concentrations lower than about 1mM, the force-velocity relationship is single-valued, i.e. for one given cargo velocity v_c, there is one value of the force F_m and hence one value for δ (see Fig. 7a). For ATP concentrations greater than about 1mM, however, the force-velocity relationship is S-shaped, i.e. for cargo velocities in the range v_min < v_c < v_max, there are three possible values of the force, i.e. F₁, F₂ and F₃ (see Fig. 7b) and correspondingly three values of the shifts, δ₁, δ₂ and δ₃. The largest value of δ, i.e. δ₂, indicates the largest force F_m = k_lδ₂ on the motor (when the linker is stretched the most) and the smallest value of δ, i.e. δ = δ₁, indicates the smallest force F_m = k_lδ₁ on the motor (when the linker is stretched the least).

We show below that in an experimental setup, only the smallest and the largest forces, F₁ and F₃, will be measured because the steady-state with the intermediate force F₂ is dynamically unstable. The stability of the three states is tested by first rewriting the equation of motion for y_m(t) (Eq.14) in terms of the force F_m(t) on the motor, i.e.

$${\dot{F}}_m\left(t\right)=k_l\left(v_{0}g\left(F_m\right)-v_c\right),$$ (16)

where the dot indicates a derivative with respect to time. The steady-state values of the force are then determined by the relation $g\left(F_m^{ss}\right)=v_c/v_0$, consistent with Eq.15. Subjecting the force to a small perturbation δF, i.e. $F_m=F_m^{ss}+\delta F$, the linearized equation of motion for the small perturbation reads

$$\dot{\delta }F=v_0{k}_{l}g\prime \left(F_m^{ss}\right)\delta F.$$ (17)

In the gray shaded domain in Fig. 7b, the slope $v\prime \left(F_m^{ss}\right)$ of the force-velocity relationship $v\left(F_m^{ss}\right),$ and therefore the slope $g\prime \left(F_m^{ss}\right)$ of $g\left(F_m^{ss}\right),$ is positive, resulting in an increase in the small perturbation δF, which renders that domain unstable. Everywhere else along the force-velocity relation, the slope $g\prime \left(F_m^{ss}\right)$ is negative-valued and the perturbations decline with time, rendering the system stable against perturbations.

At a cargo velocity of v₀, i.e. the speed of the motor at zero load, the resulting force on the motor vanishes in the average. Based on the force-velocity relationship in Fig. 7b, it can be seen that decreasing the cargo velocity is predicted to result in an increase of the load force (along the T − F₁ − P branch) until the cargo velocity reaches v_min (point P in Fig. 7b). A further decrease in the cargo velocity below v_min is then predicted to result in a discontinuous jump from point P to point Q, i.e. in a large increase of the force on the motor caused by a small change in the velocity. For further decreases in cargo velocity beyond point Q, the force on the motor is expected to increase further until the motor stalls. Assuming the motor is not detached, a subsequent increase in the cargo velocity is predicted to result in a decrease in the force on the motor, this time following the Q − F₂ − R branch of the force-velocity curve shown in Fig. 7b. A further increase in the cargo velocity beyond v_max, will result in a discontinuous transition from R to T associated with a switch back to a significantly smaller force on the motor. The difference between the cargo velocities (control parameter) at the switching points Q and R indicates dynamic hysteresis, stabilizing the low and high-load states of the motor.

Effect of dynamic catch-bonding on motor stepping

The discussion above was based on a generic force-velocity relation. We now return to our specific dynein model to explore how dynamic catch-bonding manifests itself in the stepping of the dynein motor, while still exploring the proposed experimental paradigm in which the cargo is moved at constant velocity v_c. Since stochastic stepping results in fluctuations of motor velocity and load force, the motor forces are distributed statistically. For cargo velocities in the domain v_min < v_c < v_max (see Fig. 7b), we expect to find a wider distribution of forces due to stochastic switching between the two stable forces F₁ and F₂. Where there is one force associated with one velocity, for example for v_c < v_min , we expect a narrower distribution of the load forces.

Starting with a cargo at position x_c = 0, its position at later times will be x_c(t) = v_ct . The motor steps stochastically, and the position of the motor x_m(t) and the cargo x_c(t) results in a force on the motor F_m as described above in Eq.9. In Fig. 8 we show the predicted force distributions and sample traces of the force on the motor versus time at an ATP concentration of 2mM when the cargo is moving at a fixed and controlled velocity v_c (see triangle symbols in Fig. 7a). For a larger linker stiffness, the distribution of forces in the high and low-load states was so broad as to merge together at all cargo velocities examined, hiding the instability (not shown). To demonstrate switching between the high and low-load states, we used a reduced linker stiffness of k_l = 0.02pN/nm and suppressed detachment. For a cargo velocity of v_c = 500nm/s (about half the velocity of the motor at zero load), the forces acting on the motor were distributed unimodally, ranging from 0pN to 1.5pN with an average of about 0.5pN (see Fig. 8a). This is consistent with a single-valued force-velocity relation, i.e. one in which there was only one force (approximately 0.5pN) associated with that cargo velocity. The corresponding sample force trace in Fig. 8d shows the force fluctuating around 0.5pN. For a cargo velocity of v_c = 200nm/s, which is in the domain v_min < v_c < v_max where the force-velocity relationship is multi-valued (see Fig. 7b), the force distribution exhibited two maxima at approximately 1pN and 4pN (see Fig. 8b), corresponding to the forces F_m1 and F_m2 in Fig. 7b, and a minimum between them at approximately 2.5pN, corresponding to the force F₃ where the motor is in the dynamically unstable domain shown in gray in Fig. 7b. This dynamic instability is evident in the sample force trace in Fig. 8e, in which the motor is seen to switch stochastically between a high-load state, where it maintains a force of about 4pN, and a low-load state where it maintains a force of only about 1pN. The two states are sustained by the hysteretic nature of the dynamics described above. The transitions between the two states are triggered by a large force fluctuation caused by the stochasticity of the motor stepping. For the cargo velocity of v_c = 50nm/s, which is in the domain v_c < v_min, the forces were distributed around about 5pN (see Fig. 8c) and the force traces showed a sustained large force (see Fig. 8f).

Fig. 8. Force distribution on single dynein motors constrained to move at a fixed velocity.

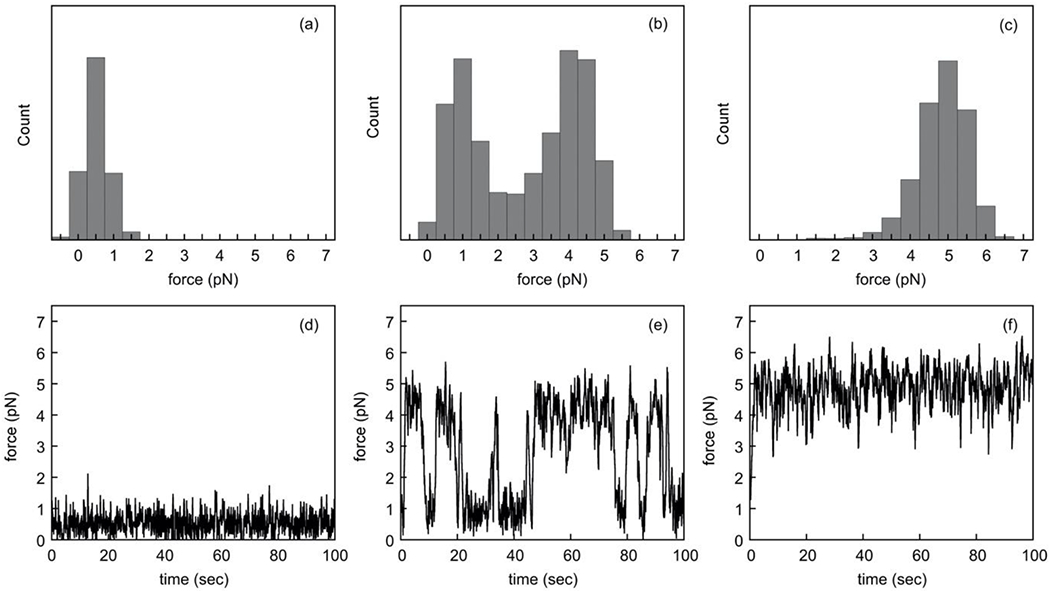
We show the frequency distributions of forces acting on a single motor in an assay where a cargo with one dynein motor attached is moved towards the minus end of the microtubule at fixed velocities of 500nm/s (a), 200nm/s (b) and 50nm/s (c), all at an ATP concentration of 2mM. Panels (d), (e) and (f) show the corresponding traces of the forces plotted versus time to show the predicted force fluctuations. To demonstrate the switching between the high and low-load states as shown in Fig. 8, we used a reduced linker stiffness of k_l = 0.02pN/nm and suppressed detachment. For higher linker stiffness k_l, the force exhibits larger and more frequent fluctuations since a single step of the motor adds a load of k_lΔx, broadening the two peaks of the bimodal force distribution in (b) such that they cannot be resolved, and eliminating the sustained intervals of high and low forces in the force traces (not shown).

Effect of dynamic catch-bonding on motor stepping and load-sharing by teams of dynein motors

Since cargoes often bind multiple dynein and kinesin motors, we now explore the consequences of dynamic catch-bonding and the resulting dynamic instabilities for cargo transported by two dynein motors pulling against a load force F_l, which could, for example, represent the force generated by opposing kinesin motors. This is a common situation in vesicular cargo transport, and the experimental paradigm developed above can probe the effectiveness with which dynein motors can overcome such opposing forces. We focus first on the motor-motor coordination in a team of two catch-bonding dynein motors while inhibiting motor detachment from the microtubule track. This initial treatment therefore applies only to the duration of time when both motors are attached to the track. We subsequently consider the case in which microtubule detachment kinetics are incorporated.

After a motor executes a step, the cargo will rapidly approach a new position at which it is in force balance, i.e. F_m1 + F_m2 = F_l, where F_m1 and F_m2 are the equilibrium forces of the two dynein motors on the cargo. Thus, most of the time the forces on these motors are constrained by this force balance. Since the two motors are identical, all combinations of forces F_m1 and F_m2 where F_m1 + F_m2 = F_l have the same probability, resulting in load forces distributed symmetrically about the average, which is half of the load force, i.e. F_l/2. In our simulations, we tracked the position x_c of the cargo and the corresponding forces F_m1 and F_m2 with time. Unlike in the case of only one motor, where the force on the motor matches the load force at equilibrium, here only the sum of the forces on the two motors must match the load force F_l, and the individual forces may not. The computed force-velocity curves of the cargo are shown in Fig. 9a for ATP concentrations of 1mM and 2mM as well as for the case of an alternate motor that doesn’t exhibit dynamic catch-bonding (implemented by using an ATP hydrolysis rate that decreases with increasing load in the conformational state associated with the step size of 8nm). We normalized the velocities (v) to the velocity under zero load (v₀) so that all force-velocity curves started at unity. In the absence of dynamic catch-bonding (slip-bond, 1mM ATP), the simulations predicted a rapid decline in the velocity with increasing force and a collective stall force for the dynein team of just above 2pN, approximately twice the stall force of a single dynein motor in our model (see Fig. 7a). In the presence of dynamic catch-bonding, we observed a biphasic decrease in the cargo velocity with substantially greater stall forces of about 8pN for the team of two motors at 1mM ATP, and of about 10pN at 2mM ATP (see Fig. 9a), again approximately twice the stall force of a single dynein motor. Remarkably, along the plateaus of the force-velocity curves for two catch-bonding dynein motors at 2mM ATP, the velocity of the cargo was not reduced as the load force increased, reflecting an increased capability of the two motors to withstand opposing forces.

Fig. 9. Cargo velocity and load-sharing for a team of two dynein motors permanently attached to their microtubule track.

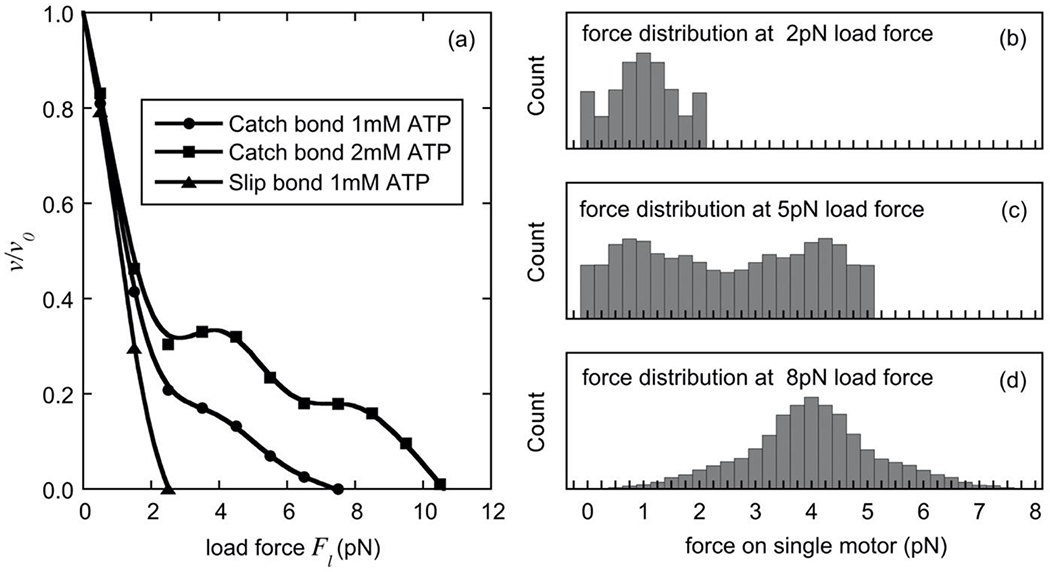
In panel (a), the average velocity of a cargo driven by a team of two catch-bonding dynein motors is shown as a function of the load force at ATP concentrations of 1mM (circles) and 2mM (squares), and in the absence of catch-bonding (“slip-bond”), i.e. for a positive value of ${\delta }_{\beta }^{+}$ in step 4 (8nm steps) (see Table 1), at 1mM ATP (triangles). To prevent motor detachment in these simulations, we set the detachment rate r_det = 0 (Eq.4). Panels (b-d) show the frequency distributions of the forces acting on the two individual catch-bonding motors for cargo forces of 2pN(b), 5pN(c), and 8pN(d) at 2mM ATP. The distributions are truncated at the load force F_l because the force on an individual motor cannot exceed the load force on the cargo.

The coordination of the motors and their load-sharing capability in our model depends on the load force. For example, at a load force of 5pN, perfect load-sharing would result in a force of 2.5pN on each motor. However, from Fig. 7 we can see that a single motor in our model is unstable at a force between about 1.5pN and 3pN at 2mM ATP, and as a consequence for a team of two dynein motors, one switches into the high-load state and the other switches into the low-load state but the sum of the two forces still equals 5pN. The frequency distribution of forces on a single motor is therefore bimodal with peaks at about 0.75pN and 4.25pN (see Fig. 9c). This means that if one of the motors holds a force of 0.75pN, the other force will be held at 4.25pN due to the force balancing. For load forces below 3pN or above 6pN, the motors with half-load forces of less than 1.5pN or more than 3pN are stable, and the force distributions peak at about the half of the load force F_l (see Fig. 9b for F_l = 2pN, and Fig. 9d for F_l = 8pN). Thus, when the average load per motor is in the range where the motors are unstable, the motors are frequently in an all-or-nothing state in which one of the motors essentially carries all the load, as long as the total load force remains below the single-motor stall force (i.e. about 5pN for an ATP concentration of 2mM). In contrast, at high load (i.e. about 8pN;see Fig. 9d), the motors share load much better, and the force distribution becomes unimodal.

Since the sum of the forces of the two motors on the cargo is balanced by the constant cargo force, perfect load-sharing occurs if both motors carry half of the load force acting on the cargo, i.e. κ₁ ≡ F_m1/(F_m1 + F_m2) = F_m2/(F_m1 + F_m2)) ≡ κ₂ = 0.5, where κ₁ and κ₂ are the fraction of the force carried by motors 1 and 2, respectively. Consequently, we characterized load-sharing as the fraction of time where 0.45 < κ < 0.55. In the above simulations, load-sharing was about 10% at small load forces (0.5pN) and then increased slowly to 16% at a load force of 2pN. For load forces between 2.5pN and 7pN, where the motors are unstable under equal load, load-sharing declined to below 10%. For high load forces (between 7pN and 10pN ) load-sharing increased substantially to up to about 40%. From this we conclude that the high load forces generated through dynamic catch-bonding appear to be crucial in overcoming opposing forces that are near the stall force.

The force-velocity relationship in Fig. 9a exhibits two plateaus, the first one starting at a force of about 2.5pN the second one starting at a force of about 6.5pN. For load forces on the cargo below 2.5pN, the load is shared relatively well between the two motors. This can be seen in the distribution of forces acting on a single motor at a 2pN total load force on the cargo in Fig. 9b, where there is a peak at 1pN, i.e. half the total load on the cargo. Starting at a total load force of 2 – 2.5pN, load-sharing declines, and most of the time a significant fraction of the total load is carried by a single motor (see Fig. 9c). Thus, when the total load just exceeds about 2.5pN, a single motor will carry a significant fraction of that force most of the time. However, the velocity of a single motor at loads between 2.5pN and 3.2pN increases (see Fig. 7b), resulting in a slight increase of the cargo velocity, i.e. the first plateau in Fig. 9a. Increasing the total load force on the cargo further, the velocity of a single motor decreases (see Fig. 7a), resulting in a decline of the cargo velocity beyond 4pN (see Fig. 9a). At 6 – 7pN, load-sharing between the two motors has improved so that each motor carries (on average) only about half the load, i.e. 3 - 3.5pN, which is near the peak of the force-velocity relationship for a single motor. Hence, further increases in the force result in only a small change in the velocity, giving rise to the second plateau.

The simulations above neglected detachment of motors in order to focus on motor-motor coordination. To explore how motor detachment and re-attachment affected our predictions of dynamic catch-bonding for a team of two dynein motors, we simulated a cargo attached to two motors that was subjected to an opposing load force F_l while also allowing each motor to detach and reattach with the kinetics described above (see Fig. 10). The velocity of the cargo was defined as the ratio of the average run length (distance traveled before both motors detached) and the average run time (time elapsed before both motors detached) and is shown in Fig. 10 as a function of the load force for ATP concentrations of 1mM (circles) and 2mM (squares). The plateau in the force-velocity curve, characteristic of the dynamic catch-bond behavior, was also present when motor detachments were allowed. However, the force distribution onto the two motors was different. If one motor detached, the entire load force F_l on the cargo was borne by a single motor. Therefore, the all-or-nothing states observed in the absence of detachment were more frequent, and we saw dominant peaks of the force distribution at zero force and full load force (not shown). Significantly, but as predicted, the stall forces were smaller in the case of detachment (for example, compare the stall force of about 8pN at 1mM ATP in Fig. 9 with about 4.5pN in Fig. 10).

Fig. 10. Force-velocity relationship for a team of two dynein motors with microtubule detachment.

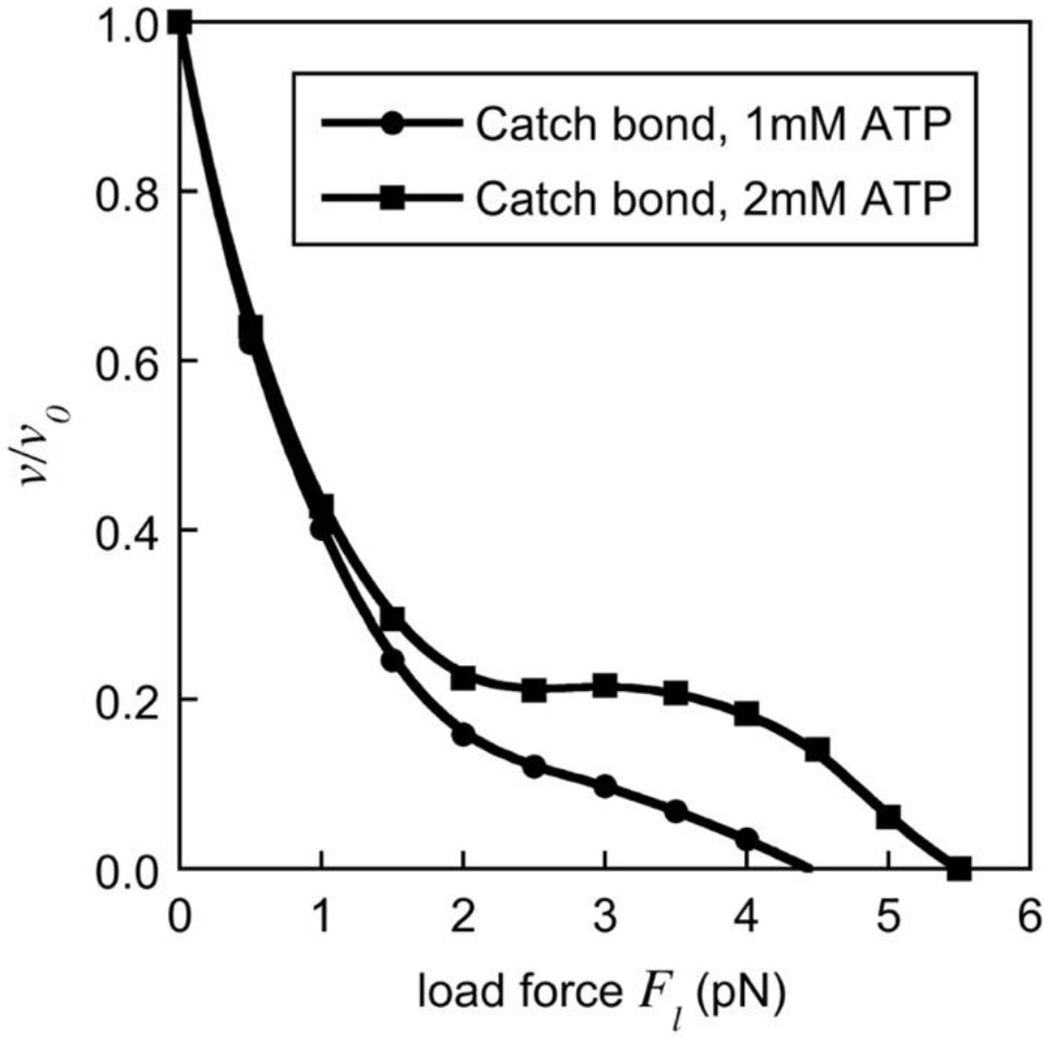
The average velocity of a cargo driven by a team of two catch-bonding dynein motors is shown as a function of the load force at ATP concentrations of 1mM (circles) and 2mM (squares) under conditions where the motors are allowed to detach and reattach to the microtubule track.

Discussion

We have proposed a mathematical model which accounts for the large range of observed stall forces of cytoplasmic dynein [10,11]. The model was constrained to published experimental data on the stepping behavior [5], the force-velocity relationship [24], and the ATP dependence of the velocity [31]. The model was scrutinized successfully by comparing predicted run lengths and stall times for cargo driven by multiple motors with published experimental data obtained using an optical trap [23]. A key assumption of the model is that differential ATP hydrolysis rates in 4 different conformational states of the motor account for the frequency and load-dependence of the observed step sizes of 32nm, 24nm, 16nm, and 8nm. In order to reproduce the transition from predominantly large step sizes of 24nm and 32nm to predominantly small step sizes of 8nm, as well as the force-velocity relationship, we proposed that the ATP hydrolysis rate in the conformational state corresponding to 8nm steps increases with increasing load force. While this is contrary to the conventional assumption that ATP hydrolysis rates decrease with increasing load force, there is no reason a priori why this could not be the case. Mechanistically, it could arise if a structural change in the motor domain induced by load were to change the conformation of the ATP binding site in such a way as to favor ATP hydrolysis.

The proposed force-dependence of the catalysis rate in our model has important consequences for dynein’s behavior. Specifically, in a simulated optical trap experiment with a cargo attached to a single dynein motor, our model predicts stall forces broadly distributed between less than 1pN and about 4pN for 1mM ATP (see Fig. 5) and larger stall forces for higher ATP concentrations, consistent with findings reported in earlier experimental studies [10,11]. In our model, these large stall forces are associated with small step sizes of predominantly 8nm, consistent with the observations in [8] (see Fig. 5c therein). This is a direct consequence of the ATP-dependent dynamic instability of the motor, which results in stochastic switching of the motor between alternating and persistent high-load and low-load states (e.g. Figs. 6c and 7).

To test directly for the predicted dynamic instability and the existence of sustained low-load and high-load states, we proposed a novel experimental paradigm in which the motor is attached to a cargo and the cargo is moved with a constant velocity along the microtubule track. In this way, the forces on the motor are not constrained through force balance and can vary widely. If the motor switches between high and low force states, this would result in a broad statistical distribution of forces on the motor, or equivalently, the forces of the motor exerted on the cargo. In contrast, if the cargo is driven by a constant load force, the force on the motor would be constrained by force balance and switching between high and low force states would not be observed, resulting in a narrow statistical distribution of forces. We propose that such an experimental paradigm would reveal features of these motors that otherwise could not be observed.

Another prediction of our model is that beyond a critical ATP concentration the run lengths of dynein motors will increase for larger load forces, although detachment rates do not, mimicking a greater affinity to the microtubule tracks (see Fig. 6). This predicted behavior is a consequence of the ATP-dependent increase of the velocity of the motor with increasing load described above (see Fig. 7), since the increased velocity results in a greater displacement and hence a greater run length. We have coined this phenomenon dynamic catch-bonding in order to contrast it with the catch-bond mechanisms in [24,35] and [20], which we shall refer to as static catch-bonding. These static catch-bonds differ from dynamic catch-bonds in that the detachment rate of the motor to the microtubule at super-stall forces decreases with increasing load force.

The effects of static dynein catch-bonds on cargo transport by teams of dynein motors has been modeled by Nair et al. [36], but the scope and focus of that work was quite different from our effort reported here. Those authors modeled the transport of cargo by teams of dynein motors governed by a phenomenological equation, in which the instantaneous velocity of the cargo declined linearly with the load force. The load force was considered to be inversely proportional to the number of engaged motors, which, in turn, depended on the rates of motor detachment and re-attachment to the microtubule tracks. The detachment rate of the motors increased with load below the stall force, which was assumed to be approximately 1pN, but then decreased with load for super-stall forces between 1pN and 10pN, describing the static catch-bond behavior observed in [24]. At load forces above 10pN, the detachment rate again decreased with increasing load. The focus of that study was how the detachment and re-attachment rates of multiple motors regulated the cargo velocity as a function of the load. While both the static and dynamic catch-bonding models generate force-velocity relations that include intervals where the cargo velocity increases with increasing load force, in the dynamic catch-bonding model this is an emergent phenomenon that results from the increase in the catalysis rate with load force at 8nm steps. Importantly, the force-dependent increase in the ATP catalysis rate in the model was chosen specifically to reproduce the correct force-dependent stepping behavior and we found that the catch-bonding mechanism arose as a consequence of that assumption.

Another modeling study, Takshak et al. [37], expanded on the model of Singh et al. [6] by incorporating the same static catch-bond detachment kinetics, mostly focused on velocity, run length, and run time of a cargo driven by multiple dynein motors. The predicted average run length decreased with increasing load at high ATP concentrations, which is different from our predictions where the run length can increase with increasing load force at high ATP concentrations. Run times, defined as the time before the cargo detached from its track, were almost constant for large load forces due to the static catch-bond of the dynein motors, which is consistent with our model. Most importantly, as in [36] the model of Takshak et al. [37] was tuned to stall forces of about 1pN for a single motor and did not address the observation of larger single-motor stall forces.

In summary, we have proposed a new model for the kinetics of dynein motors that is constrained by experimentally determined step sizes, force-velocity relations, and detachment kinetics. The dynamic catch-bond behavior of this model is emergent and ATP-dependent, and increases the stall force of a single motor significantly through a dynamic instability, explaining the broad range of stall forces reported in [10, 11]. The model generates three new testable predictions: 1) stochastic switching between high and low load-carrying states within a certain velocity domain, 2) plateaus in the force-velocity relationship of a cargo driven by more than one motor at high ATP concentrations, and 3) increases in the run-lengths of single motors with increasing force at high ATP concentrations. We have also proposed an experimental protocol that could test the predicted instability.