Skip to main content
PMC home page
AJNR: American Journal of Neuroradiology logoLink to AJNR: American Journal of Neuroradiology
. 2000 Nov;21(10):1813–1820.

Diffusion Tensor MR Imaging of the Brain: Effect of Diffusion Weighting on Trace and Anisotropy Measurements

Elias R Melhem a,b, Ryuta Itoh a, Lisa Jones a, Peter B Barker a
PMCID: PMC7974303  PMID: 11110532

Abstract

BACKGROUND AND PURPOSE: In human brain, the relationship between MR signal and b value is complicated by cerebral perfusion, restricted diffusion, anisotropy, cellular membrane permeability, and active cellular transport of water molecules. Our purpose was to evaluate the effect of the number and strength of diffusion-sensitizing gradients on measured isotropic apparent diffusion coefficients (ADCi), fractional anisotropy (FA), and their respective SD in different anatomic locations of the brain.

METHODS: Quantitative apparent diffusion coefficients and diffusion anisotropy brain maps were obtained from 10 healthy volunteers by using six different levels of diffusion weighting (b0 = 0, b1 = 160, b2 = 320, b3 = 480, b4 = 640, and b5 = 800 s/mm2), applied sequentially in six different directions (Gxx, Gyy, Gzz, Gxy, Gxz, Gyz) and coupled to a single-shot spin-echo echo-planar (2045/115 [TR/TE]) MR imaging technique. ADCi, FA, eigenvalues (λ1, λ2, λ3)1 of the principal eigenvectors, and their respective SD were measured from seven different anatomic locations in the brain. Repeated measures analysis of variance was used to evaluate for the existence of significant differences in the average and SD of the calculated ADCi and FA as a function of the number and strength of b values. When a difference existed, the Bonferroni t method was used for paired comparisons of the groups.

RESULTS: The measured ADCi was affected by the number and strength of b values (P < .05). The SD of the ADCi was affected by the strength (P < .05) but not the number of b values (P > .05). The measured FA was unaffected by the number and strength of b values (P > .05). The SD was affected by the number and strength of b values (P < .05).

CONCLUSION: The number and strength of b values do influence measures of diffusion and anisotropy. Attention to the choice of diffusion sensitization parameters is important in decisions regarding clinical feasibility (acquisition time) and normative measures.

The role of diffusion-weighted MR imaging in the early detection of hyperacute cerebral infarcts has been established in animal models and clinical practice (1–12). Recently, investigators have used the diffusion anisotropy characteristics of white matter to study normal myelination patterns and pathologic conditions that alter microstructure such as axonal integrity (13–22).

Diffusion-weighted images are influenced by T2 decay and the orientation of the diffusion-sensitizing gradients (the latter is particularly true for tissues in which the diffusivity of water is anisotropic) (23, 24). For quantification of diffusion in normal and abnormal tissues, apparent diffusion coefficient (ADC) maps become necessary. These maps are devoid of T2 contamination but remain affected by the orientation of the diffusion-sensitizing gradients (anisotropy). Additionally, the uncertainty in the ADC measurements is affected by T2 decay. The generation of the ADC maps requires at least two levels of diffusion weighting (two b values) (25).

To eliminate the effects of anisotropy, isotropic ADC (ADCi) maps are generated by taking the arithmetic mean of individual ADC values obtained during the application of the diffusion-sensitizing gradients in the three main orthogonal directions (25, 26). Diffusive transport in anisotropic media is best characterized by the diffusion tensor. From the diffusion tensor, a set of orthogonal vectors, known as eigenvectors that define the orientation of the principal axes of the diffusion ellipsoid in space are calculated. The lengths of these vectors are represented by the corresponding eigenvalues. Several indices, such as fractional anisotropy (FA), relative anisotropy, and volume ratio, are derived from these eigenvalues for quantification of anisotropy (see Appendix) (27).

With this work, we evaluated the effect of the number and strength of diffusion-sensitizing gradients on measured ADCi, FA, and their respective SD in different anatomic locations of the brain (28). Our null hypotheses were that ADCi and FA are independent of the number and strength of diffusion-sensitizing gradients.

Methods

MR Imaging

MR studies were performed on a 1.5-T superconducting MR system (ACS NT Power Trak 6000, software release 6.1.2; Philips Medical Systems, Best, The Netherlands), with a maximum gradient capability of 23 mT.m−1 and a slew rate of 103 mT.m−1.ms−1. Brain MR imaging was performed using a quadrature head coil operating in receive mode.

Assuming gaussian diffusion (matrix symmetry), diffusion tensor MR imaging of the brain was performed using six different levels of diffusion weighting (b0 = 0, b1 = 160, b2 = 320, b3 = 480, b4 = 640, and b5 = 800 s/mm2), applied sequentially in six different directions (Gxx, Gyy, Gzz, Gxy, Gxz, Gyz) and coupled to a single-shot spin-echo echo-planar readout (2045/115/8 [TR/TE/excitations]; flip angle, 90 degrees). The different b values were achieved by varying the gradient strength from 0 to a maximum of 19 mT/m while keeping the duration (δ) and the time between the diffusion gradients (Δ) fixed at 31.0 and 40.0 ms, respectively. The imaging gradients in the echo-planar readout contributed negligibly (<1%) to the b value. The field-of-view was 23 cm (80% rectangular), with a 128 × 128 matrix (1.79 × 1.79 mm in-plane resolution). A total of 10 10-mm-thick sections with an intersection gap of 1 mm were acquired in 8.5 min.

Phantom Experiment

A distilled water phantom (4093/1593 [T1/T2]) was imaged in the axial plane by using the above-described technique. This was done to assess the effects of experimental and systemic errors resulting from hardware and diffusion-sensitized pulse sequence imperfections (ie, gradient cross terms and eddy currents) on the behavior of the MR signal.

Participants

Ten consenting healthy adult volunteers (average age, 36 years; male:female ratio, 8:2) underwent imaging in the axial plane using the above-described technique. Participants with neurologic or psychiatric illnesses, claustrophobia, pacemakers, or surgical implants were excluded from the study. Internal review board approval was obtained before initiation of the study.

Data Processing and Analysis

The six independent elements of the diffusion tensor (Dxx, Dyy, Dzz, Dxy, Dxz, Dyz) were statistically estimated (multivariate linear regression) in each voxel by using on-line research software (Philips Medical Systems). From the diffusion tensor data, voxel-by-voxel water phantom and brain maps of the ADCi, FA, and eigenvalues (λ1, λ2, λ3) were calculated on-line according to equations 1 through 4 (see Appendix) and standard matrix procedures. Sorting of the eigenvalue according to size was not necessary for calculating the FA.

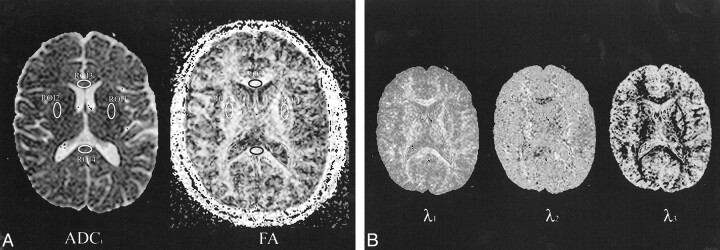
The brain maps were calculated using nine combinations of the six different b values (Table 1). All calculated brain maps (450 maps: 10 volunteers × nine b-value combinations × five different parameters) and water phantom maps (45 maps: nine b-value combinations × five different parameters) were transferred to an UltraSPARC II workstation (EasyVision, software release 4.1; Philips Medical Systems) for further analysis. Using commercially available software, measurements of ADCi, FA, λ1, λ2, and λ3 were made from variably sized oval-shaped regions of interest (ROI) placed in the water phantom, centrum semiovale (white matter), and putamina (deep gray matter) bilaterally, in the genu and splenium of the corpus callosum, and in the pons (Fig 1). In the brain, placement of the ROI in the different anatomic locations was based on the T2-weighted reference images (b value = 0). The identical placement of ROI in the various maps calculated for water phantom and for each volunteer was achieved by using a copy/paste tool and was checked visually to ascertain if they lay over the corresponding anatomic regions.

TABLE 1:

Nine combinations of the b values used to calculate the ADCi, FA, E0, E1, and E2 maps

graphic file with name ajnr-21-10-28-t01.jpg

Open in a new tab

fig 1.

fig 1.

Open in a new tab

Axial ADCi, FA, and eigenvalue maps.

A, ROI used in data analysis are superimposed on axial ADCi map and FA map calculated at the level of the basal ganglia. 1, left putamen; 2, right putamen; 3, genu of corpus callosum; 4, splenium of the corpus callosum. ROI were also placed in the pons and centrum semiovale (not shown). The location and size of the ROI varied across participants and hemispheres but was kept fixed across the different maps.

B, Axial calculated eigenvalue maps (λ1, λ2, λ3) at the level of the basal ganglia.

Statistical Analysis

The average and the SD of the measured ADCi and FA were calculated for 10 volunteers from maps generated using all six b values (b0, b1, b2, b3, b4, b5). For both the water phantom and brain, repeated measures analysis of variance (ANOVA) was used to evaluate for the existence of significant differences in the average and SD of the calculated ADCi and FA, based on the number and strength of b values. When a difference existed, the Bonferroni t method was used for paired comparisons of the groups. P values less than .05 were considered significant for the repeated measures ANOVA, and P values less than .005 were considered significant for the Bonferroni t method.

Results

Phantom Experiment

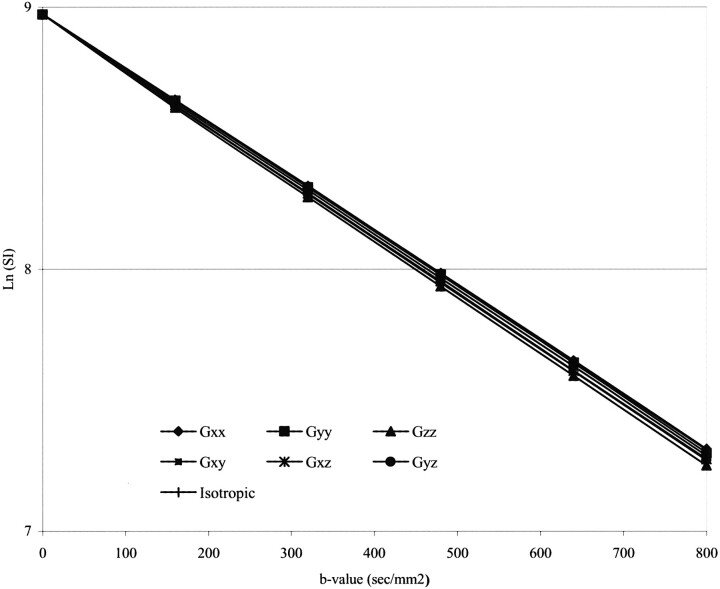
The MR signal intensity from the phantom decayed in a monoexponential manner as a function of b values (Fig 2). The measured ADCi and FA from the water phantom maps generated using all six b values (b0, b1, b2, b3, b4, b5) were 2120 × 10−6mm2/s and 0.03, respectively.

fig 2.

fig 2.

Open in a new tab

Signal decay versus b value obtained from diffusion-weighted (six directions) MR images of a water phantom. The monoexponential decay indicates minimal influence of experimental/systemic errors on measurements

There were no differences in the measured ADCi and FA with changes in the number and strength of b values (P = .94 and .88, respectively). There were no significant differences in the SD of the measured ADCi and FA with changes in the number of b values. However, the SD of the measured ADCi and FA was significantly different with changes in the strength of b values (P < .05). The largest SD in the measured ADCi and FA was for the b0b1 group (14 × 10−6mm2/s and 0.07, respectively).

Participants

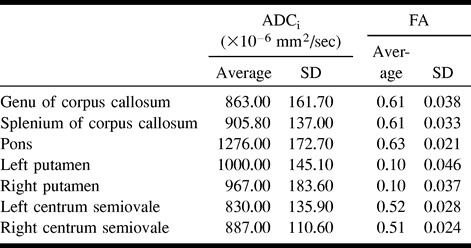
The average and SD of the measured ADCi and FA from all seven distinct anatomic locations were comparable with those of published results (21, 27, 29) (Table 2).

TABLE 2:

Measured values of average ADCi and FA obtained from maps generated using all 6 b values

graphic file with name ajnr-21-10-28-t02.jpg

Open in a new tab

ADCi versus Number of b Values

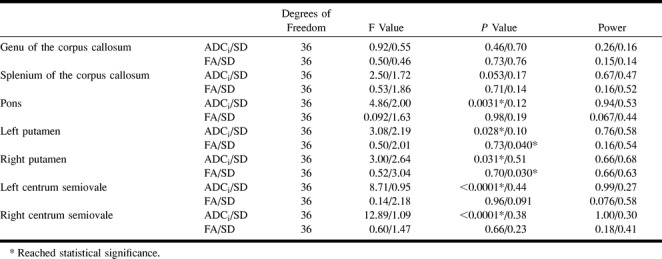
ANOVA did not reveal significant differences in the measured ADCi with changes in the number of b values from the genu and splenium of the corpus callosum (Table 3). A statistically significant difference was reached, however, for the pons, putamen, and centrum semiovale.

TABLE 3:

ANOVA for ADCi, FA, and their respective SD for the subgroups with different number of b values

graphic file with name ajnr-21-10-28-t03.jpg

Open in a new tab

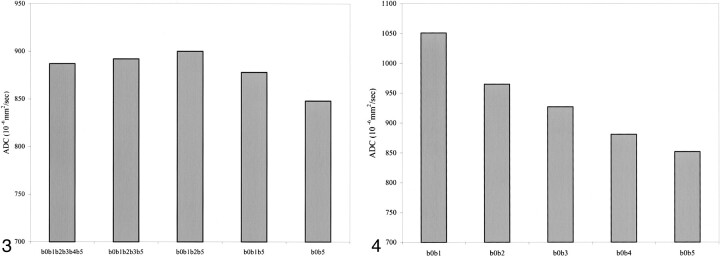
Paired comparisons of the five groups for the pons, putamen, and centrum semiovale showed a significant difference in the ADCi between the b0b5 group and the remaining four groups (b0b1b5, b0b1b2b5, b0b1b2b3b5, b0b1b2b3b4b5) (Fig 3). There were no significant differences in the SD of the measured ADCi with changes in the number of b values from all anatomic locations.

fig 3.

fig 3.

Open in a new tab

Graph of the average ADCi for the different number of b values, obtained from the right centrum semiovale, shows a significant difference between the b0b1 group and the remaining four groups.

fig 4. Graph of the average ADCi for the different strengths of b values, obtained from the right centrum semiovale, shows a significant difference between all the groups except b0b4 and b0b5.

ADCi versus b Value

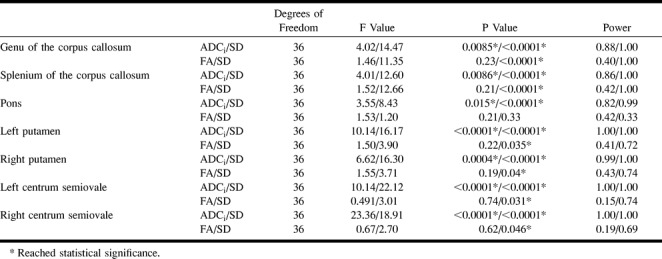
ANOVA revealed significant differences in the measured ADCi with changes in the strength of diffusion sensitization (b values) from all anatomic locations (Table 4). In the genu and splenium of the corpus callosum, there was a significant difference in the ADCi between the following groups: b0b1 and b0b2, b0b1 and b0b3, b0b1 and b0b4, and b0b1 and b0b5. In the pons, there was a significant difference in the ADCi between b0b1 and b0b4 and between b0b1 and b0b5. In the putamina, there was a significant difference in the ADCi between the b0b1 group and the remaining four groups. In the left centrum semiovale there was a significant difference in the ADCi between the b0b1 group and the remaining four groups and between the b0b2 group and the remaining four groups. Finally, in the right centrum semiovale, there was a significant difference in the ADCi between all the groups except b0b4 and b0b5 (Fig 4).

TABLE 4:

ANOVA for ADCi, FA and their respective SD for the subgroups with different strengths of b values

graphic file with name ajnr-21-10-28-t04.jpg

Open in a new tab

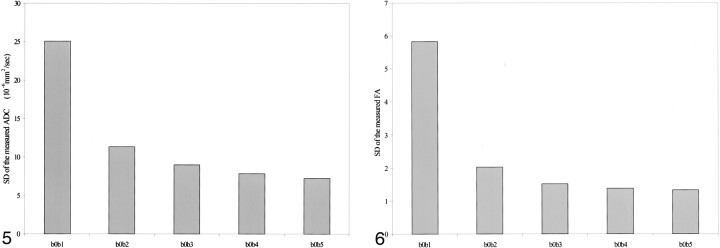
Also, there were significant differences in the SD of the measured ADCi with changes in the strength of diffusion sensitization (b values) from all anatomic locations. In all locations, there were significant differences between the following groups: b0b1 and b0b2, b0b1 and b0b3, b0b1 and b0b4, and b0b1 and b0b5. In addition, there were significant differences between b0b2 and b0b4 and between b0b2 and b0b5 in the genu of the corpus callosum and both putamina. In all locations, the SD was greatest for the weakest diffusion sensitization (b0b1), with a gradual decrease to a minimum for the strongest diffusion sensitization (b0b5) (Fig 5).

fig 5.

fig 5.

Open in a new tab

Graph of the average SD of ADCi for the different strengths of b values, obtained from the splenium of the corpus callosum, shows a significant difference between the b0b1 group and the remaining four groups.

fig 6. Graph of the average SD of FA for the different strengths of b values, obtained from the splenium of the corpus callosum, shows a significant difference between the b0b1 group and the remaining four groups.

FA versus Number of b Values

ANOVA did not reveal significant differences in the measured FA with changes in the number of b values from all anatomic locations (Table 3). On the other hand, there was a statistically significant difference in the SD of the measured FA between the b0b5 and the remaining four groups (b0b1b5, b0b1b2b5, b0b1b2b3b5, b0b1b2b3b4b5) in both putamina.

FA versus b Value

ANOVA did not reveal significant differences in the measured FA with changes in the strength of diffusion sensitization from all anatomic locations (Table 4). A significant difference did exist, however, in the SD of the measured FA with changes in the strength of diffusion sensitization from all anatomic locations except for the pons. In these locations, there were significant differences between the following groups: b0b1 and b0b2, b0b1 and b0b3, b0b1 and b0b4, and b0b1 and b0b5. The SD was greatest for the weakest diffusion sensitization (b0b1), with a gradual decrease to a minimum for the strongest diffusion sensitization (b0b5) (Fig 6). Interestingly, for the tested b values over 160 s/mm2, there was no difference in the measured FA and SD.

Discussion

The ability to determine a narrow range of normative ADCi and FA measures in different anatomic locations of the brain is critical for identifying subtle abnormalities (ie, early demyelination) in patients and defining thresholds for disease burden quantification (ie, volume of infarcts). With this goal in mind, it becomes important to study factors that may influence the normative values and their SD.

Random (Brownian) motion of water molecules along the direction of a strong magnetic field gradient results in MR signal loss from spin dephasing (22). The MR signal loss is governed by the diffusivity of water at a specific temperature and pressure and the degree of the diffusion sensitizing (b value), which is determined by the timing and strength of the diffusion gradients (23).

In the unrestricted water phantom model, the decay of the MR signal, as a function of the b value, is monoexponential. On the other hand, in biological tissue, such as the human brain, the relationship between MR signal and b value may be more complicated because of factors such as cerebral perfusion, restricted diffusion, anisotropy, cellular membrane permeability, and active cellular transport of water molecules (5, 30–32).

Departure from monoexponential decay of brain MR signal with increasing b values has been attributed to perfusion and CSF volume averaging effects at low b values (<200 s/mm2) (30, 31). Also, biexponential signal decay has been observed in rat brain over a large range of b values (10–10,000 s/mm2) (33).

Our results show the dependency of the ADCi values, in all the examined anatomic locations of the brain, on the degree of diffusion sensitizing (b value). There is a significant decrease in the ADCi values with increasing diffusion sensitization (Fig 4), which can be explained, in part, by a more pronounced direct effect of microcirculatory perfusion on measures of water diffusivity at low b values (30, 31). We also found significant differences in ADCi values, in all the examined anatomic locations of the brain except for the corpus callosum, as a function of the number of b values. These differences corroborate the multiexponential nature of diffusion-related MR signal decay, which explains the influence of the number of b values on the linear fit and should caution investigators interested in measures of diffusion quantification to consider the strength and number of b values used in the generation of normative data (5). The monoexponential decay of the MR signal from the water phantom decreases the chance that experimental or systemic errors will be responsible for multiexponential decay of brain MR signal.

Regarding the SD of the measured ADCi, we noted a dependency on the strength but not on the number of b values (Tables 3 and 4). Within the tested range of b values, we noted a decrease in the SD with the use of stronger b values (Fig 5). These findings emphasize the importance of avoiding low-b-value diffusion-weighted MR imaging when the objective is to establish a narrow range of normative ADCi values.

Diffusion anisotropy in biological media such as white matter may be characterized by a symmetrical 3 × 3 diffusion tensor (34). In the case of gaussian diffusion, the application of sensitizing gradients in at least six independent directions and measuring the resultant echo attenuation allows the determination of the diagonal and off-diagonal elements of the diffusion tensor (35).

It has been suggested by some investigators that measuring the off-diagonal elements of the diffusion tensor is important for accurate determination of white matter fiber orientation, degree of diffusion anisotropy, and the trace of the diffusion tensor (29). Using the diagonal and off-diagonal elements of the diffusion tensor, a new local orthogonal coordinate system (the principle coordinate axes: eigenvectors) is constructed and defines the orientation of the diffusion ellipsoid relative to the laboratory coordinate system. The size and shape of diffusion ellipsoid are characterized, independently of orientation, by the lengths of the eigenvectors (eigenvalues). Some measures of anisotropy (FA, relative anisotropy, volume ratio) and the trace of the diffusion tensor have been defined as functions of the eigenvalues (see Appendix). It has been shown recently, however, that these same quantities can be reliably determined without the need for the off-diagonal elements of the diffusion tensor (28).

The computed eigenvalues suffer from noise contamination, which is, in part, related to the diagonalization of the diffusion tensor, the signal-to-noise ratio of the diffusion-weighted images, and the choice of the number and strength of diffusion-sensitizing gradients (b values) (24). In addition to influencing the accuracy of the different measures of anisotropy, the off-diagonal element measurement, the number and strength of b values, and the number of signal averages all affect the imaging efficiency of these extremely motion-sensitive imaging techniques and can cause severe degrading artifacts in the clinical setting.

Recently, it has been shown, using a Monte Carlo computer simulation program, that of all the measures of anisotropy mentioned above, the FA has the highest contrast-to-noise ratio in gray and white matter (27). In this study, we have shown that the measured FA in gray and white matter is independent of the number of b values (Table 3). Within the range of b values tested, the implication is that only two b values may be necessary for determination of anisotropy. The effects of these findings on imaging efficiency are explicit.

On the other hand, the SD of the measured FA is affected by the strength of b values in all anatomic locations (Table 4). Within the tested range of b values, we noted a decrease in the SD with the use of stronger b values (Fig 6). Again, these findings serve to emphasize the importance of avoiding low b-value diffusion-weighted MR imaging when the objective is to establish a narrow range of normative FA values.

Because of very low anisotropy in gray matter structures (putamina) and in the water phantom, the SD of the measured FA is significantly affected not only by the strength of diffusion sensitization but by the number of b values as well (Table 3) (22). Similar effects are shown in the SD of the measured eigenvalues (not shown).

The measures of FA in the putamina (isotropic medium) are the lowest but are still greater than zero (Table 2). Volume averaging with adjacent white matter structures and noise contamination intrinsic to the computation of eigenvalues are probably responsible for the mild apparent anisotropy (22, 24).

Our results show a wide range of anisotropy in the different white matter structures evaluated (Table 2), with higher FA in the corpus callosum compared with the centrum semiovale. This can be explained, in part, by differences in the angular separation of the white matter tracts within the plane of a transverse image (22). For the centrum semiovale, the greater variability in the orientation of the white matter tracts within a voxel, compared with the corpus callosum, may cause an apparent reduction in anisotropy.

The assumptions and technical limitations of this study include the following: 1) gaussian diffusion of water in the brain and resultant tensor matrix symmetry (this assumption helps improve the efficiency of diffusion tensor MR imaging for clinical purposes by allowing the complete characterization of the diffusion tensor using only six of the nine scalar elements; 2) suboptimal spatial separation of the diffusion-sensitizing gradients, which can negatively influence noise levels of the calculated ADCi, eigenvalues, and FA (36); 3) inability to evaluate the effects of very high b values (>1500 s/mm2) on ADCi, eignenvalues, and FA measurements because of restrictions in peak diffusion-sensitizing gradient strength; and 4) diffusion tensor MR imaging of the entire brain with relatively thick sections (10 mm), which does increase the effects of volume averaging and phase shifts on the measurements from the different anatomic locations.

Conclusion

In the tested range, the number and strength of diffusion-sensitizing gradients does influence the measures and SD of the ADCi and FA for different anatomic locations of the brain. Attention to the choice of diffusion sensitization parameters is important in decisions regarding clinical feasibility (acquisition time) and normative measures.

Appendix

The ADC parameter for each direction is calculated according to the following equation.

graphic file with name ajnr-21-10-28-ea1.jpg

ADCi is the mean of the ADC values in the phase-encoding, read, and section directions.

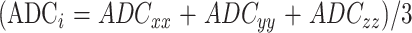graphic file with name M1.gif

Calculation of the eigenvalues is as follows:

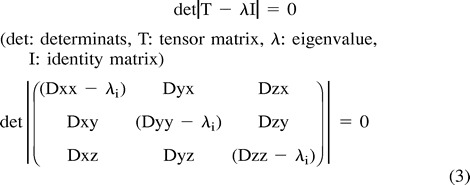graphic file with name ajnr-21-10-28-ea3.jpg

Different measures of anisotropy are shown below.

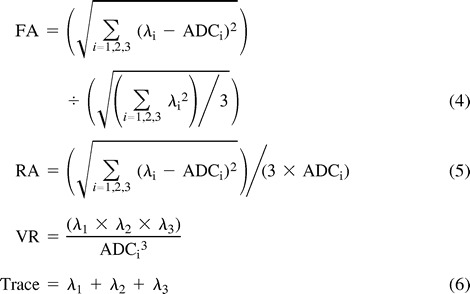graphic file with name ajnr-21-10-28-ea4.jpg

In equation 6, trace = λ1 + λ2 + λ3 and λi represents the different eigenvalues.

Footnotes

1

The work was conducted at the F.M. Kirby Functional MRI Research Center, Kennedy-Krieger Institute.

References

  • 1.Moseley ME, Kucharczyk J, Mintorovitch J, et al. Diffusion-weighted MR imaging of acute stroke: correlation with T2-weighted and magnetic susceptibility-enhanced MR imaging in cats. AJNR Am J Neuroradiol 1990;11:423-429 [PMC free article] [PubMed] [Google Scholar]
  • 2.Mintorovitch J, Moseley ME, Chileuitt L, Shimizu H, Cohen Y, Weinstein PR. Comparison of diffusion- and T2-weighted MRI for the early detection of cerebral ischemia and reperfusion in rats. Magn Reson Med 1991;18:39-50 [DOI] [PubMed] [Google Scholar]
  • 3.Minematsu K, Li L, Fisher M. Sotak CH, Davis MA, Fiandaca MS. Diffusion-weighted magnetic resonance imaging: rapid and quantitative detection of focal brain ischemia. Neurology 1992;42:235-240 [DOI] [PubMed] [Google Scholar]
  • 4.Warach S, Chien D, Li W, Ronthal M, Edelmann RR. Fast magnetic resonance diffusion-weighted imaging of acute human stroke. Neurology 1992;42:1717-1723 [DOI] [PubMed] [Google Scholar]
  • 5.van Gelderen P, de Vleeschouwer MHM, DesPres D, Pekar J, van Zijl PCM, Moonen CTW. Water diffusion and acute stroke. Magn Reson Med 1994;31:154-163 [DOI] [PubMed] [Google Scholar]
  • 6.Warach S, Gaa J, Siewert B, Wielopolski P, Edelman R. Acute human stroke studied by whole brain echo planar diffusion weighted magnetic resonance imaging. Ann Neurol 1995;37:231-241 [DOI] [PubMed] [Google Scholar]
  • 7.Sorensen AG, Buonanno FS, Gonzalez RG, et al. Hyperacute stroke: evaluation with combined multisection diffusion-weighted and hemodynamically weighted echo-planar MR imaging. Radiology 1996;199:391-401 [DOI] [PubMed] [Google Scholar]
  • 8.Lovblad KO, Baird AE, Schlaug G, et al. Ischemic lesion volumes in acute stroke by diffusion-weighted magnetic resonance imaging correlate with clinical outcome. Ann Neurol 1997;42:164-170 [DOI] [PubMed] [Google Scholar]
  • 9.Schlaug G, Siewert B, Benfield A, Edelman RR, Warach S. Time course of the apparent diffusion coefficient (ADC) abnormality in human stroke. Neurology 1997;49:113-119 [DOI] [PubMed] [Google Scholar]
  • 10.Ulug AM, Beauchamp N, Bryan RN, van Zijl PCM. Absolute quantitation of diffusion constants in human stroke. Stroke 1997;28:483-490 [DOI] [PubMed] [Google Scholar]
  • 11.Lutsep HL, Albers GW, De Crespigny A, Kamat GN, Marks MP, Moseley ME. Clinical utility of diffusion-weighted magnetic resonance imaging in the assessment of ischemic stroke. Ann Neurol 1997;41:574-580 [DOI] [PubMed] [Google Scholar]
  • 12.Singer MB, Chong J, Lu D, Schonewille WJ, Tuhrim S, Atlas SW. Diffusion-weighted MRI in acute subcortical infarction. Stroke 1998;29:133-136 [DOI] [PubMed] [Google Scholar]
  • 13.Chenevert TL, Brunberg JA, Pipe JG. Anisotropic diffusion in human white matter: demonstration with MR techniques in vivo. Radiology 1990;177:401-405 [DOI] [PubMed] [Google Scholar]
  • 14.Moseley ME, Cohen Y, Kucharczyk J, et al. Diffusion-weighted MR imaging of anisotropic water diffusion in cat central nervous system. Radiology 1990;176:439-445 [DOI] [PubMed] [Google Scholar]
  • 15.Doran M, Hajnal JV, Van Bruggen N, King MD, Youn IR, Bydder GM. Normal and abnormal white matter tracts shown by MR imaging using directional diffusion weighted sequences. J Comput Assist Tomogr 1990;14:865-873 [DOI] [PubMed] [Google Scholar]
  • 16.Douek P, Turner R, Pekar J, Patronas N, Le Bihan D. MR color mapping of myelin fiber orientation. J Comput Assist Tomogr 1991;15:923-929 [DOI] [PubMed] [Google Scholar]
  • 17.Sakuma H, Nomura Y, Takeda K, et al. Adult and neonatal human brain: diffusional anisotropy and myelination with diffusion-weighted MR imaging. Radiology 1991;180:229-233 [DOI] [PubMed] [Google Scholar]
  • 18.Coremans J, Luypaert R, Verhelle F, Stadnik T, Osteaux M. A method for myelin fiber orientation mapping using diffusion-weighted MR images. Magn Reson Imaging 1994;12:443-454 [DOI] [PubMed] [Google Scholar]
  • 19.Nomura Y, Sakuma H, Takeda K, Tagami T, Okuda Y, Nakagawa T. Diffusional anisotropy of the human brain assessed with diffusion-weighted MR: relation with normal brain development and aging. AJNR Am J Neuroradiol 1994;15:231-238 [PMC free article] [PubMed] [Google Scholar]
  • 20.Ono J, Harada K, Mano T, Sakurai K, Okada S. Differentiation of dys- and demyelination using diffusional anisotropy. Pediatr Neurol 1997;16:63-66 [DOI] [PubMed] [Google Scholar]
  • 21.Neil JJ, Shiran SI, Kinstry RC, et al. Normal brain in human newborns: apparent diffusion and diffusion anisotropy measured by using diffusion tensor MR imaging. Radiology 1998 57-66 [DOI] [PubMed]
  • 22.Shimony JS, McKinstry RC, Akbudak E, et al. Quantitative diffusion-tensor anisotropy brain MR imaging: normative human data and anatomic analysis. Radiology 1999;212:770-784 [DOI] [PubMed] [Google Scholar]
  • 23.Le Bihan D. Diffusion and Perfusion Magnetic Resonance Imaging: Applications to Functional MRI.. New York: Raven Press; 1995
  • 24.Pierpaoli C, Basser PJ. Toward a quantitative assessment of diffusion anisotropy. Magn Reson Med 1996;36:893-906 [DOI] [PubMed] [Google Scholar]
  • 25.Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time dependent field gradient. J Chem Phys 1965;42:288-292 [Google Scholar]
  • 26.Hsu EW, Mori S. Analytical expressions for the NMR apparent diffusion coefficients in an anisotropic system and a simplified method for determining fiber orientation. Magn Reson Med 1995;34:194-200 [DOI] [PubMed] [Google Scholar]
  • 27.Sorensen AG, Wu O, Copen WA, et al. Human acute cerebral ischemia: detection of changes in water diffusion anisotropy bu using MR imaging. Radiology 1999;212:785-792 [DOI] [PubMed] [Google Scholar]
  • 28.Ulug AM, van Zijl PCM. Orientation-independent diffusion imaging without tensor diagnolization: anisotropy definitions based on physical attributes of the diffusion ellipsoid. J Magn Reson Imaging 1999;9:804-813 [DOI] [PubMed] [Google Scholar]
  • 29.Pierpaoli C, Jezzard P, Basser PJ, Barnett A, DiChiro G. Diffusion tensor MR imaging of the human brain. Radiology 1996;201:637-648 [DOI] [PubMed] [Google Scholar]
  • 30.Le Bihan D, Breton E, Lallemand D, Aubin MI, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497-505 [DOI] [PubMed] [Google Scholar]
  • 31.Turner R, Le Bihan D, Maier J, Vavrek R, Hedges LK, Pekar J. Echo-planar imaging of intravoxel incoherent motion. Radiology 1990;177:407-414 [DOI] [PubMed] [Google Scholar]
  • 32.Moonen CT, Pekar J, de Vleeschouwer MH, van Gelderen P, van Zijl PC, DesPres D. Restricted and anisotropic displacement of water in healthy cat brain and in stroke studies by NMR diffusion imaging. Magn Reson Med 1991;19:327-332 [DOI] [PubMed] [Google Scholar]
  • 33.Niendorf T, Dijkhuizen RM, Norris DG, et al. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion weighted imaging. Magn Reson Med 1996;36:847-857 [DOI] [PubMed] [Google Scholar]
  • 34.Basser PJ, Mattiello J, LE Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B 1994;103:247-254 [DOI] [PubMed] [Google Scholar]
  • 35.Crank J. The Mathematics of Diffusion.. Oxford: Clarendon; 1975
  • 36.Conturo TE, McKinstry RC, Adbudak E, Robinson BH. Encoding of anisotropic diffusion with tetrahedral gradients: a general mathematical diffusion formalism and experimental results. Magn Reson Med 1996;35:399-412 [DOI] [PubMed] [Google Scholar]

Articles from AJNR: American Journal of Neuroradiology are provided here courtesy of American Society of Neuroradiology

RESOURCES