Fast Three-Point Dixon MR Imaging of the Retrobulbar Space with Low-Resolution Images for Phase Correction: Comparison with Fast Spin-Echo Inversion Recovery Imaging

Abstract

Summary: A new phase-correction algorithm for three-point Dixon (3PD) MR imaging allows on-line image reconstruction of three images per section: pure water, pure fat, and water plus fat. When combined with fast spin-echo acquisition, the sequence is suitable for routine MR imaging of the retrobulbar space. The 3PD pure water images have double the image signal-to-noise ratio of fast spin-echo inversion recovery images. The dramatic contrast-to-noise ratio of the 3PD pure fat images may offer improved lesion detection.

Imaging of the fat in the retrobulbar space necessitates an MR imaging pulse sequence with which the fat signal is suppressed, nulled, or alternatively imaged. Signal loss is inherent in techniques that either suppress or null the fat signal. Conventional chemical shift selection suppression, or CHESS, techniques reduce fat signal, but they also can reduce water signal in regions of moderate to large field inhomogeneity. Inversion recovery techniques are designed to null the fat signal, but although routinely used in orbital MR imaging, these methods have an inherent T1-related reduction in the water signal.

Dixon techniques offer a potential advantage in imaging of the retrobulbar space, because they have no inherent signal loss, and thus a theoretic improvement in the signal-to-noise ratio (SNR) occurs. Moreover, Dixon techniques have the unique ability to produce pure fat images. In the original Dixon method (1), water and fat are separated by using two image acquisitions (a two-point technique) for which the magnetization vectors for water and fat are parallel and antiparallel. The summation of the images in the complex form yields a pure water image, and the subtraction of the images yields a pure fat image. The main limitation of this two-point method is that field inhomogeneity (for example, at interfaces between air and soft tissue) yields a phase error, which leads to an incorrect solution for the water and fat images. The phase error is commonly corrected by using the information from a third data acquisition; this last method, therefore, is termed the three-point Dixon (3PD) method.

High-quality images have been achieved with the use of Dixon techniques and their variations with conventional spin-echo and gradient-echo imaging (2–8), including imaging of the retrobulbar space (9–11). However, the multiple data acquisitions required lengthening of the overall imaging time, and the Dixon techniques described to date require offline image reconstruction, limiting clinical applicability. To address the issue of acquisition time, 3PD techniques that involve a fast spin-echo (FSE) sequence have been developed (12); the current 3PD technique incorporates a FSE sequence with an echo train length of eight. The novel component of the current sequence is the ability to produce on-line images. This advance is based on the realization that the elusive phase error, in general, varies slowly in spatial terms. Therefore, the phase error can be adequately and more readily determined from a set of low-resolution images for which the SNR is substantially elevated (13).

As detailed in the Appendix, three low-resolution images are reconstructed in postprocessing, and the phase factors for all pixels with adequate water and fat signal are determined directly on a pixel-by-pixel basis. The use of this approach reduces the number of pixels requiring additional analysis—specifically, pixels with either low SNR or pixels that contain only water or fat. For these pixels, the phase factor is obtained by a region-growing process designed to ensure spatial phase continuity. The low-resolution phase factors then are used directly to correct the phase errors. The incorporation of low-resolution images and the fewer number of pixels requiring additional analysis reduce the postprocessing time of the current sequence and therefore allow on-line image reconstruction. Of note, the final output of the pure water, pure fat, and water-plus-fat images have no resolution loss, because only the phase errors are removed from the images with high resolution. The entire reconstruction is transparent to the operators and is automatically initiated after each data collection; output images are installed directly into the image database for viewing and archiving.

Analysis in Patients

Twenty pediatric patients aged 0–20 y (mean, 7.1 y) underwent imaging with the on-line 3PD sequence with T2 weighting (3000/85/8/1) (TR/TE/echo train length/excitations) and an FSE inversion-recovery (FSEIR) sequence (2500/30/8/2) oriented perpendicular to the optic nerve. For both sequences, the section thickness was 4 mm, 12 contiguous sections were used, the field of view was 24 cm, and the matrix was 256 × 192. In each patient, both sequences were performed during the same imaging session with a 1.5-T whole-body unit (Horizon LX EchoSpeed 8.2; GE Medical Systems, Milwaukee, WI). The on-line 3PD and FSEIR images were acquired within a mean of 3.6 and 2.0 min, respectively.

Signal-intensity regions of interest were used to calculate the signal intensity of brain gray matter, noise, intraconal fat, and the medial rectus muscle. The image SNR was defined as the quotient of the signal intensity of the brain gray matter divided by the signal intensity of the image noise and was computed for the 3PD pure water and FSEIR images. Region-of-interest measurements also were used to calculate orbit contrast-to-noise ratio (CNR), defined as the difference between the signal intensity of the intraconal fat and the medial rectus muscle, divided by the signal intensity of the image noise.

Three comparisons were calculated. First, the improvement in image SNR offered by the 3PD pure water images compared with FSEIR images was computed as follows:

The second and third comparisons were ratios of orbit CNR. The increase in the orbit CNR obtained from the 3PD pure fat image with respect to the FSEIR image was defined as follows:

Similarly, the change in orbit CNR between the 3PD pure water image and the FSEIR image was computed as follows:

Improvements were expressed as percentage increases, and the 95% confidence interval was computed for each.

Results

For all 20 patients, the 3PD pure water images had greater image SNR than did the FSEIR images, and the 3PD pure fat images had greater orbit CNR than did the FSEIR images (Table). With 95% confidence intervals, the mean percent increase was statistically significant. The percent increase in orbit CNR between the 3PD water and FSEIR images was not statistically significant at the 95% level, perhaps secondary to the small number of patients in the evaluation. Representative cases are illustrated in Figures 1 and 2.

Comparison of image SNR and orbit CNR for individual 3PD images and FSEIR

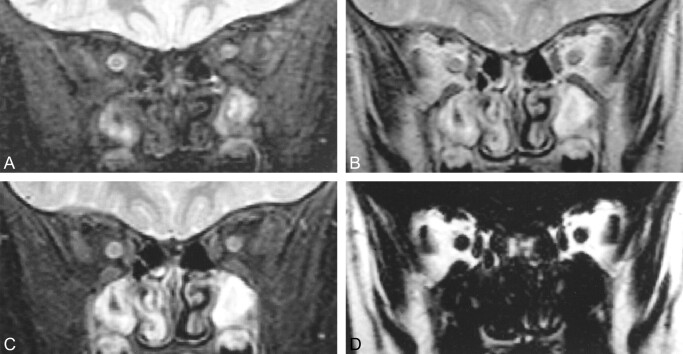
fig 1.

Coronal MR images of the retrobulbar space in a 3-year-old boy.

A, FSEIR image (2500/30/8/2) shows that nulling of fat from the inversion pulse effectively isolates the signal from the optic nerves. Structure is evident within the right optic nerve with these sequence settings.

B, 3PD water-plus-fat image (3000/85/8/1) shows both optic nerves as hypointense areas within a bright fat background. The internal structure is well depicted. Note the substantial signal from the sinuses, which is greatly nulled on the FSEIR image.

C, 3PD pure water image (3000/85/8/1) shows the optic nerves isolated from the surrounding fat. Substantial signal is present from water-containing tissue in the sinuses. Because of its relatively short T1, this signal is lost with the delay time in the FSEIR image.

D, 3PD pure fat image (3000/85/8/1) shows dramatic contrast and sharply defined margins between the water-containing structures (optic nerves and extraocular muscles) and retrobulbar fat.

Discussion

The fundamental challenge with 3PD MR imaging is robust correction for phase errors within short acquisition and reconstruction times. To minimize the acquisition time, the 3PD sequence described in this study involves a FSE sequence. The novel component of the current sequence is the shorter image processing as a result of the use of images with a reduced matrix size, increased SNR, and fewer pixels containing only water or fat. The reduction in image-processing time enables on-line reconstruction, which facilitates routine clinical use of the sequence. Using the image SNR and orbit CNR as measures of image quality, the Dixon sequence is technically superior to FSEIR, with only a small increase in imaging time. In addition, the pure fat images offered by the Dixon sequence may provide a new opportunity for retrobulbar lesion detection. Future research will focus on whether the improved SNR or added information from the pure fat images can increase lesion conspicuity or lead to more appropriate clinical management compared with conventional imaging of the retrobulbar space.

Appendix

The 3PD image reconstruction can be described mathematically from the complex MR signal (2). The following analysis is based on two assumptions. The first assumption is that the frequency spectra of water and fat in a given pixel can be described with a δ function of amplitude water (W) and fat (F). The second assumption is that the transverse relaxation (during a few ms) can be ignored.

With these assumptions, the complex MR signal S_n after Fourier transformation for the pixel from the nth sampling at time t_n can be expressed as follows:

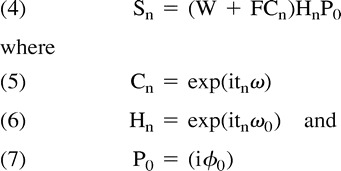The term t_n is the shift of the center of the data-acquisition window from the time when the magnetization from W and F are aligned in phase, ω is the chemical shift between water and fat, P₀ is the frequency offset associated with the field inhomogeneity, and ϕ₀ is a time-dependent phase offset. The mathematic solution for W and F over all imaging pixels corresponds to obtaining the 3PD pure water and pure fat images. Because ω is known and t_n is controlled by data-acquisition timing, C_n is known. However, the phase factors P₀ and H_n are unknown, the latter being the major challenge because it is a variable of both spatial location and data-acquisition timing.

In one approach to 3PD imaging (3), the magnetization vectors are offset by 0, π, and 2π in the three acquisitions. This is referred to as a symmetric technique. One limitation of symmetric techniques is that for each pixel, the phase error is absolutely determined over the range [−π, π] alone. Thus, potential for an incorrect assignment of the phase, so-called phase aliasing, exists. The correction of phase aliasing, called phase unwrapping, is a challenging problem, and failure in phase unwrapping reverses the water and fat signals. The 3PD sequence in this study used an alternative strategy called asymmetric data sampling (14–16). In asymmetric sampling, for at least one of the three data acquisitions, the fat and water magnetization vectors are neither parallel nor antiparallel. The main advantage of asymmetric data sampling is the ability to separate water and fat without the need for direct phase unwrapping. We used an asymmetric sampling scheme in which three data sets were collected with data-acquisition timing such that ωt₀ was equal to 0, π/2, and π. Therefore Equation 4 can be rewritten as follows:

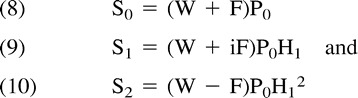The complex variables W′ and F′ are defined as follows:

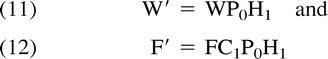Substitution into Equations 8–10 yields two sets of complex solutions for W′ and F′ in terms of the acquired data, as follows:

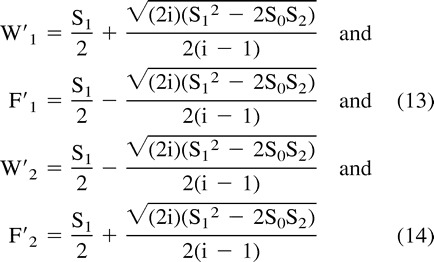Although two sets of complex solutions are possible (Equations 13 and 14), the differences in phase allow for a physical choice. Thus, water and fat vectors can be separated by pixels if the relative phase between the vectors is known. In a large proportion of image pixels, the relative phase is well defined; in a small proportion with low SNR, the relative phase is poorly defined, and when a pixel contains only a single spectral component, the relative phase is undefined. In the latter two cases, information from neighboring pixels is required. This could be obtained by determining the phase values ω₀ and t_n. However, this process would require possible phase unwrapping. A more reliable method determines H_n, which lies on a unit circle and is insensitive to phase unwrapping (17). A similar approach has been implemented in the reconstruction of phase contrast, phase array multicoil data (18).

In the reconstruction algorithm, H_n is determined by an orientation vector, as follows:

where W′_s and F′_s represent one of the two possible solutions in Equations 13 and 14. When the correct solution is chosen (as is the case for pixels that contain abundant water and fat protons), the orientation vector equals (F + W)P₀H₁ and, thus, is parallel to P₀H₁. With an incorrect choice, the orientation vector equals (FC₁ + WC₁⁻¹)P₀H₁ and thus deviates from P₀H₁ by either π/2 or −π /2. Because the separation is correct for pixels containing abundant water and fat, the binary choice for the remaining pixels can be made by comparing the angular difference of the two possible orientation vectors with that of a neighboring pixel in a region-growing process.

In the reconstruction algorithm, P₀ is determined from S₀ (Equation 8). In the first step to determine H₁, three low-resolution images (typically 64 × 64) are reconstructed from the datasets, and one of the two possible solutions for water and fat is chosen for the phase relationship in Equations 13 and 14. In the second step, a region-growing algorithm is used to correct potentially incorrect assignments. Specifically, a pixel is randomly selected as a seed, and the four neighboring pixels are sequentially checked by comparing the angular difference of the two possible orientation vectors of the pixel with that of the seed. In the binary choice, the solution with the angular difference less than a preset threshold value is chosen, because the correct assignment of water and fat in two neighboring pixels will have nearly aligned orientation vectors. The checked pixel then typically is used as a new seed for the next round of growth, on a first-in–first-out basis. To prevent growth in the noise, a threshold (±15%) is set for the relative angle of the orientation vectors between neighboring pixels. A reversal counter is used to monitor the possibility of choosing a seed with an incorrect assignment of water and fat. The counter is defined as the difference between the number of nonreversals and the number of reversals from choices made before the region-growing process; when the counter becomes negative, growth is aborted and a new seed is chosen.

After all pixels in the matrix are visited, the low-resolution orientation vector field is resized to the image field of view (typically 256 × 256) and boxcar-averaged (7 × 7 window). The possibly incorrect assignments that remain are reversed by comparing the angular difference of the orientation vector with the average orientation vector for the same pixel. The phase factor H₁ is then obtained by normalizing the new orientation vector after another boxcar averaging (7 × 7 window). Finally, P₀ and H₁ are used to correct the complex image ωt₁ = π/2. The real and imaginary parts of the regular image after phase correction then are exported as the desired water and fat images, respectively. The entire reconstruction is transparent to the operators and is automatically initiated after each data collection; output images are installed directly into the image database for viewing and archiving.

fig 2.

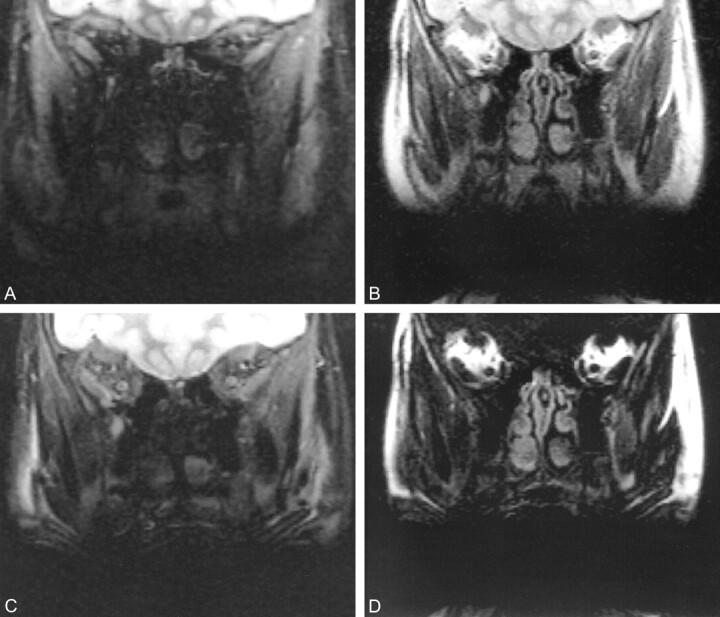
Coronal MR images of the retrobulbar space in a 12-year-old girl with dental braces.

A, FSEIR image shows that the evaluation of orbits is limited by artifact from the dental braces. Note the improved contrast between gray and white matter because of the additional T1 weighting caused by the inversion pulse.

B, 3PD water-plus-fat image (3000/85/8/1) offers dramatically improved signal; the artifact from the dental braces has a sharper margin.

C, 3PD pure water image (3000/85/8/1) shows superior anatomic detail compared with FSEIR.

D, 3PD pure fat image (3000/85/8/1) shows substantial signal from fat-containing structures outside the retrobulbar space.