Abstract
BACKGROUND AND PURPOSE: True 3D measurements of tumor volume are time-consuming and subject to errors that are particularly pronounced in cases of small tumors. These problems complicate the routine clinical assessment of tumor growth rates. We examined the accuracy of currently available methods of size and growth measurement of vestibular schwannomas compared with that of a novel fast partial volume tissue classification algorithm.
METHODS: Sixty-three patients with unilateral sporadic vestibular schwannomas underwent imaging. Thirty-eight of these patients underwent imaging two or more times at approximately 12-month intervals. Contrast-enhanced 3D T1-weighted images were used for all measurements. An experienced radiologist performed standard size estimations, including maximal diameter, elliptical area, perimeter, manually segmented area, intensity thresholded seeding volume, and manually segmented volume. A method for calculating volume was also used, incorporating Bayesian probability statistics to estimate partial volume effects. Manually segmented volume was obtained as a baseline standard measure. A computer-generated phantom exhibiting the intensity and partial volume characteristics of brain tissue, CSF, and intracanalicular vestibular schwannoma tissue was used to measure absolute accuracy of the standard technique and Bayesian partial volume segmentation.
RESULTS: The Bayesian partial volume segmentation method showed the highest correlation (R2 = 0.994) with the standard method, whereas the commonly used method of maximal diameter measurement showed poor correlation (R2 = 0.732). Accuracy of Bayesian segmentation was shown to be more than twice that of manual segmentation, with an absolute accuracy of 5% (cf, 13%) and a remeasurement accuracy of 70 mm3 (cf, 150 mm3). For the 38 patients who underwent imaging twice, definite tumor growth was shown for 12, potential growth for seven, no growth for 17, and definite shrinkage for two.
CONCLUSION: Commonly used methods such as maximal diameter measurements do not provide adequate statistical accuracy with which to monitor tumor growth in patients with small vestibular schwannomas. Bayesian partial volume segmentation provides a more accurate and rapid method of volume and growth estimation. These differences in measurement accuracy translated into a significant improvement in clinical assessment, allowing identification of tumor growth in 10 of 12 cases that appeared to be static in size when manual segmentation techniques are used. The technique is quick to perform and suitable for use in routine clinical practice.
The management of vestibular schwannoma presents the clinician with a dilemma. Screening with MR imaging now identifies many small tumors in patients with minimal symptoms. Tumor growth rate is variable, and many small vestibular schwannomas do not show evidence of growth or may even shrink (1, 2). In view of this, it may be appropriate to treat some patients conservatively while monitoring tumor growth (2–4). Conservative management of small vestibular schwannomas is now widely practiced, with serial imaging performed every 1–2 years, and a minimum follow-up time of 6 months (2, 5). Many studies have investigated the growth rates of vestibular schwannomas (2, 3, 5–19). These studies commonly span many years (2, 3, 6, 7, 20), and the use of imaging data collected over such a long time restricts tumor size analysis to simple metrics, because digital data are seldom available. The most commonly used method of estimating tumor size is measurement of the maximal anteroposterior diameter (2, 3, 7, 10–14). Estimates have also been made by using various averages between the mediolateral and the anteroposterior dimensions of the tumor in the image section exhibiting the largest tumor cross section (6, 15, 16). The American Academy of Otolaryngology-Head and Neck Surgery developed guidelines that use the square of the product of the two orthogonal diameters (10). The Academy describes a growth of 1.16 mm per year in this mean diameter as “clinically significant.” These linear metrics have also been used to produce a volumetric estimate, assuming the vestibular schwannoma is an ellipsoid (15, 17, 18), and these approximations have been used to calculate a volume doubling time (15). Few previous studies have performed true volumetric measurements, and these have used manual segmentation of the tumor (5, 18). The use of these simple measurement techniques is inappropriate in small, intracanalicular tumors, because the measurement errors due to partial volume effects will be proportionately greater. In some studies, intracanalicular vestibular schwannomas have been classified as having no volume or diameter as appropriate and, therefore, no scope for growth (3, 5, 19), whereas other studies have excluded them completely. Comparison of these studies (5) has revealed large discrepancies in the proportion of cases exhibiting “significant growth” (7). The introduction of alternatives to surgical resection, such as conservative management, stereotactic radiosurgery (9), and growth-inhibiting drug therapies, demands a more accurate technique for the estimation of tumor growth rates. These techniques must be accurate, simple to use, and, most important, have documented confidence limits.
We introduce a method for the reliable estimation of growth rates of vestibular schwannomas that can also be applied to small intracanalicular tumors. The method applies Baye’s theory to estimate the contribution of tumor, brain, and CSF or bone to the signal from a region of interest. Bayesian techniques use previous knowledge regarding the statistical distribution of values in a sample to estimate the probabilities that an individual value belongs to each of the component tissues. In the application described herein, values of mean signal intensity and distribution width for enhanced tumor, brain, and CSF or bone are measured from typical examples. This previous knowledge is used to derive a mathematical model of the signal intensity distributions that can describe all possible permutations of these three tissues in a sample. This model contains contributions for each tissue, which allow for statistical variability in the tissue intensity, and it also has a series of components that describe the behavior of partial volume effects in voxels positioned on tissue boundaries. This model is used to fit the measured voxel intensities from a 3D region of interest. Once the optimal fit has been achieved, the partial volume–corrected volume of each tissue component can be extracted from the model. This results in a simple approach that requires the user to identify only any volume of interest containing just these three tissues. The volume correction does not require the classification of individual voxels, although the fitted model can then be used to calculate the probability that any voxel belongs to a specific tissue group, so that the technique can also form the basis of a partial volume–corrected tissue segmentation technique.
Methods
Patient Recruitment
Patients were recruited from the Central Manchester Healthcare Trust vestibular schwannoma clinic. In all patients, a presumptive diagnosis of vestibular schwannoma was based on findings from the clinical history, auditory function testing, and previous MR imaging examination. Patients with neurofibromatosis were excluded from the study. A total of 63 patients were included. The median age of the participants was 62 years (age range, 36–88 years); 33 were men and 30 were women. Histologic confirmation of the diagnosis was available for 16 patients. The patients represent a contiguous sample of patients presenting at the clinic, with only one exclusion; that patient had a pacemaker and was therefore unsuitable to undergo MR imaging. The median maximal diameter, the commonly used measure of tumor size, was 0.985 cm (mean, 1.17 cm; range, 0.2–4.5 cm).
For 38 of the 63 patients, images were available from two or more occasions at approximately 12-month intervals (median, 12 months; mean, 12.1 months; range, 5–21 months). For 25 of these patients, images had been acquired at the Central Manchester Healthcare Trust as part of routine clinical management before inclusion in the study. Images obtained at other centers before inclusion were not included in the study because of difficulties in acquiring the digital image data and variations in imaging protocols among centers. For the remaining 13 patients, the study image was the first obtained at the Central Manchester Healthcare Trust and subsequent follow-up images were acquired during the course of the study.
Imaging Protocols
Imaging was performed with a 1.5-T MR imager (ACS-NT PT6000; Philips Medical Systems, Best, the Netherlands). The imaging sequence used was a 3D T1-weighted, gradient-echo fast field-echo sequence (24/11 [TR/TE]; flip angle, 30°; field of view, 230 × 230 mm; section thickness, 3 mm; matrix, 256 × 256), performed after the administration of contrast material (0.1 mM/kg gadodiamide, Omniscan; Nycomed, Oslo, Norway). The 25 images used for serial examinations that were acquired before the commencement of this study (see Patient Recruitment) were acquired on an identical MR imaging system with use of a multisection spin-echo sequence (466/20; field of view, 200 × 200 mm; section thickness, 3 mm; section gap, 0.3 mm; matrix, 256 × 256) after the administration of contrast material (0.1 mM/kg gadodiamide, Omniscan). Repeat measurements of all tumor size estimates showed no significant difference in accuracy between these two imaging protocols for any method of estimation. This is supported by the observations of Niemczyk et al (5).
Bayesian Tissue Classification Method
In MR data sets, partial volume effects occur in voxels along the borders between distinct tissues. This is because of the finite volume of tissue represented by each voxel. Assuming that there is no intensity nonuniformity across homogeneous tissue, pure tissue intensity can be reasonably modeled by a gaussian distribution. This is a common assumption that forms the basis of nearly all image segmentation techniques. Regions containing a mixture of tissue have intensities that reflect the combination of all tissues within each voxel (partial volume averaging).
The method of segmentation presented herein addresses these partial volume effects, accepting that segmentation is not binary in nature from voxel to voxel; boundaries do not normally align with the sampling grid at the resolution of the imaging sequence. Common to all approaches to statistical analysis of MR data in the literature, we started by assuming that all pure tissues can be modeled by a single distribution with fixed mean. To help ensure this, each data set was corrected for intensity nonuniformity due to radio-frequency field inhomogeneity by using a postprocessing technique (21). Finally, for the purpose of this study, all materials in the sampled region of interest were identified as brain, CSF, or tumor tissue. In some situations, such as voxels containing blood or other nonmodeled tissues, this resulted in systematic errors in the measured values. However, systematic errors can be ignored if the primary goal is case-to-case growth rate monitoring (as systematic errors cancel in a computed difference). The main requirements for such a measurement process are high repeatability and sensitivity to change. We assessed both of these issues by using a combination of patient data and statistical phantoms.
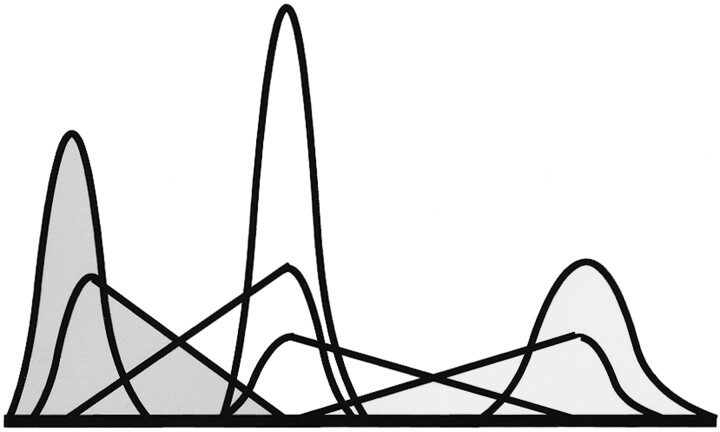
The Bayesian approach to data analysis allows us to assess the most likely distribution of tissue proportions within a voxel. The tissue volume model is composed of terms for pure tissue and partial volumes. The pure tissues follow convention and use gaussian distributions. The partial volume model is an extension of the work of Laidlaw et al (22). To make Bayesian estimation of most likely volume fraction possible, we had to model partial volumes from two tissues as two separate distributions of the expected volume fraction of each tissue within the volume. The linearity of the Bloch equations combined with our previous assumption regarding the expected gaussian distribution of the pure tissue rendered partial volume curves for each tissue, which were triangular distributions convolved with the pure tissue distribution (Fig 1). This allowed us to write down an equation for the total amount of each tissue within a particular region of the image as a sum of pure and partial volume contributions weighted with the relative proportions of each (Equation 1).
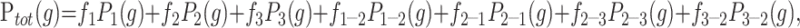 |
1) |
where fi is the weight given to each of the basis functions in the fit. Pi is the probability that a given gray level, g, has come from the basis function corresponding to tissue subclass i (1 = pure CSF, 2 = pure brain tissue, 3 = pure tumor tissue, 1–2 = CSF in partial volume voxels with brain tissue, 2–1 = brain tissue in partial volume voxels with CSF, etc).
Fig 1.
Illustration of the basis functions for each of the tissue subsets. Gaussian curves represent each of the three tissues in voxels containing a single tissue type. Reflected triangle pairs convolved with gaussian curves represent the content of voxels containing mixtures of tissues. Three levels of shading identify the contribution of each of the three tissues in both pure and partial volume voxels.
Having established the model, we must now determine the free parameters, which are the expected mean value of the pure tissues and the relative proportions of each distribution. A simplex algorithm was used to optimize the χ2 fit between an image’s intensity histogram and the regional model, Ptot(g) (23). We find that the partial volume components are essential in producing a good fit to this distribution. Given the parameters of the model that best describe the region histogram, the expected proportion of tissue (n) within a voxel of a given grey level (g) is given from Bayes theory as follows:
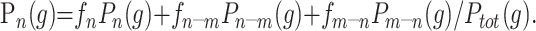 |
2) |
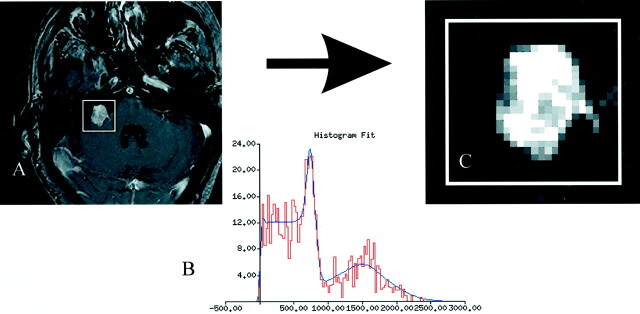
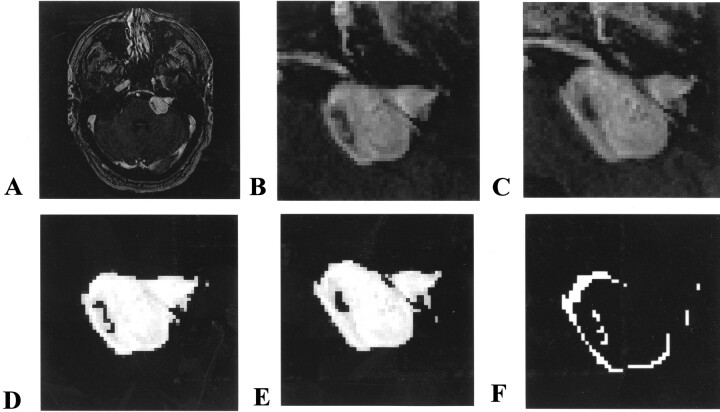
The Bayesian partial volume algorithm used, in addition to the nonuniformity correction, is available in the open source software package, TINA, which is produced in-house and is freely available on the Internet (24). An example of the algorithm at work is shown in Figure 2.
Fig 2.
Algorithm at work.
A, Contrast-enhanced T1-weighted image of a vestibular schwannoma.
B, Histogram of the region of interest fit with the theoretical basis functions.
C, Once the fit is optimized, the relative probability that vestibular schwannoma tissue could produce each voxel’s intensity is determined from the function. This should be directly related to the proportion of the tissue in that voxel.
Absolute Accuracy of Measurement Techniques
All methods, including the standard manually segmented baseline volume measurement, have measurement errors. These errors cannot be measured in vivo because the true volume of the tumor cannot be measured by any reliable criterion standard method. To estimate the statistical component of these errors, a digital phantom was generated (Fig 3). The phantom was a computer model of the general intensity and distribution characteristics for tissues, comparable with contrast-enhanced T1 volume images of vestibular schwannomas obtained in this study. Pure tissue gaussian distributions for CSF, brain tissue, and vestibular schwannoma measured from typical examples had means and errors (μ + ς) of 0 + 150, 500 ± 50, and 1600 ± 250, respectively. The phantom was generated with use of these values, with tumors of known volume. This phantom was then used to generate a phantom MR image in which partial volume effects were simulated by linear weighted addition of the required fractions in each voxel, in accordance with the Bloch equations. The four model schwannomas in the phantom had volumes of 12.54, 28.23, 50.22, and 78.48 voxels. This method of phantom construction provides a phantom in which the effects of statistical image noise and partial volume averaging are duplicated and in which the absolute true volumes of the tissues are known, providing a correct solution against which the errors of the various volume measurement techniques can be assessed. Because of the voxel-by-voxel nature of the Bayesian tissue classification, it was unnecessary to expand the model beyond a 2D section. Both the criterion standard manual segmentation and the partial volume Bayesian segmentation were performed repeatedly on the phantom to determine measurement errors of both techniques.
Fig 3.

Computer-generated phantom contains similar intensity and noise characteristics of pure and partial volume voxels of CSF, brain tissue, and tumor tissue. The artificial tumors ranged from 12 to 80 voxels in total volume. The phantom is constructed so that the absolute true volumes of the tumors are known before the effects of noise and partial volume averaging are added.
In addition, repeat maximal diameter, manually segmented volume, and Bayesian classification volume measurements were performed on a random selection of 20 vestibular schwannomas (mean diameter, 1.21 cm; range, 0.83–3.40 cm). The distribution of these measurements was used to calculate an indicator of error on repeated measurements.
Relative Accuracy of Measurement Techniques
The assessment of accuracy of volume measurements in images from patients can be performed only by comparison of different methods, because the true tumor volumes are unknown. However, because we have been able to estimate the true errors of the techniques by using the computer phantom (described earlier), we were able to identify manual segmentation as the most accurate of the conventional techniques. On the basis of the computer phantom, we have used manual segmentation to provide a criterion standard baseline volume measurement. Manual segmentation was performed on magnified images to help accurately identify the tumor boundary, manually segmenting all sections identified as containing tumor. The Spearman correlation coefficient among all methods and manual segmentation was determined to illustrate the relationship between the simple linear metrics and approximate volume estimation across a range of tumor sizes. For this, a radiologist performed six commonly used measurements on all 63 vestibular schwannomas. Four were made on the reconstructed image section identified as containing the largest apparent cross-sectional tumor area. These measurements were maximal diameter along the anteroposterior direction, diameter of the vestibular schwannomas orthogonal to the maximal diameter in the mediolateral direction, perimeter length, and manually segmented area determined by drawing around the schwannoma. A mean diameter was calculated in accordance with the American Academy of Otolaryngology-Head and Neck Surgery guidelines as the square root of the product of orthogonal diameters (10). The elliptical area was also calculated from the two diameters. In addition to the single section metrics, intensity thresholded seeding was used to calculate a volume through sections identified as containing tumor. An appropriate threshold level was chosen by using an intensity histogram of the region surrounding the vestibular schwannomas. The thresholded tumor volume was seeded by identifying a starting point within the tumor. The tumor volume was then calculated by growing the seed to contain all contiguous thresholded voxels.
Results
Accuracy of Measurement Techniques
Measurements from the four phantom tumors illustrated in Figure 3 showed that the manually segmented standard baseline volume identified the true volume of the phantoms with an error of 13% of the known true volume. Repeat measurements of the Bayesian classifier had an error of 5% of the known true volume.
Table 1 illustrates both the voxel accuracy and the accuracy relative to tumor size derived from repeat measurements in 20 randomly selected vestibular schwannomas (mean diameter, 1.21 cm; range, 0.83–3.40 cm). In addition to mean errors, the SD of the errors were calculated for confirmation of accuracy. Both methods of calculating measurement errors were statistically equivalent and provided an estimate of the reproducibility of the measurement that was related to its error. The mean error for repeat measurements of the standard manually segmented volume technique were twice as large as errors from the Bayesian volume estimations. The error of 18% for manual segmentation is comparable to that of other studies that have quoted measurement errors (5).
TABLE 1:
Repeat measurement accuracy of estimation methods in 20 randomly selected vestibular schwannomas*
| Measurement Method | Error in Units of Measurement | Average % Error Relative to Size |
|---|---|---|
| Maximal diameter | 1.8 mm (8.5–0.2) | 15 (114–0.9) |
| Manually segmented volume | 150 mm3 (430–4) | 18 (112–2.0) |
| Bayesian classification volume | 70 mm3 (342–1) | 7 (22–0.3) |
Percentages in parentheses are the ranges in measurement errors with respect to diameter or volume of each initial tumor measurement.
The mean error of 1.8 mm for maximal diameter measurements would produce a volume measurement error of 340 mm3 if the vestibular schwannomas were perfectly spherical. This implies that maximal diameter measurement was more than four times as inaccurate as the partial volume technique and more than twice as inaccurate as manual volume segmentation. A 1-cm-diameter spherical tumor could therefore grow by 65% in volume before a confident increase in size would be detected by using measurement of maximal diameter. This is in contrast to the 13% volume increase, which would provide sufficient confidence, with the Bayesian partial volume method and a 29% volume increase for the manual segmentation technique. A 0.5-cm tumor would have to grow 2.8 times its original volume for growth to be confidently detected with use of maximal diameter (cf, 1.0 times growth being statistically significant for Bayesian classification).
Relative Comparison of Measurement Techniques
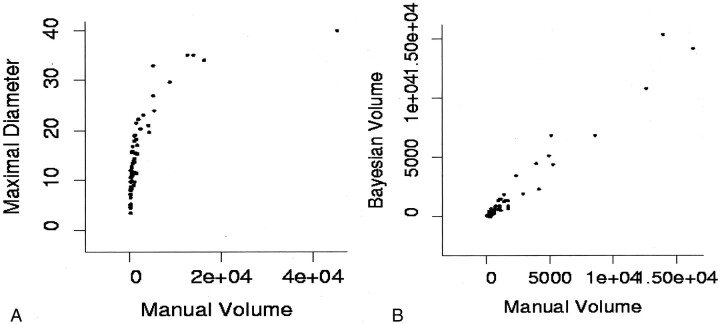
The complete battery of measurements that were performed on the original 63 contrast-enhanced vestibular schwannoma images was compared with the manually segmented criterion standard volume measurement to determine correlation. The manually segmented volume was chosen as the criterion standard because phantom studies showed it to be the most accurate of the conventional techniques. The R2 values and their 95% confidence intervals are shown in Table 2. Bayesian partial volume probabilistic tissue classification, followed closely by volume seeding, had the highest correlation with the criterion standard measurement. The perimeter measurement, although intuitively the poorest estimate of tumor size, performed better than did the mean and maximal diameter estimations. Figure 4A illustrates the poor correlation between mean diameter estimates and the criterion standard measurement . The correlation for vestibular schwannomas larger than 2.0 cm in diameter (R2 = 0.793) is higher than the correlation for smaller tumors (R2 = 0.684). Figure 4B illustrates that the correlation between manually segmented volume and Bayesian partial volume tissue classification is consistently high across all tumor sizes. This supports the use of the manual segmentation technique as a surrogate criterion standard for the comparison of conventional methods.
TABLE 2:
Correlation between measurement methods and the standard manual segmentation estimate of tumor volume
| Measurement Method | R2 Value (95% CI) |
|---|---|
| Mean diameter | 0.708(0.5572–0.814) |
| Maximal diameter | 0.732(0.592–0.830) |
| Perimeter | 0.764(0.637–0.851) |
| Elliptical area | 0.859(0.776–0.912) |
| Manually segmented area | 0.873(0.798–0.851) |
| Seeded volume | 0.949(0.917–0.970) |
| Bayesian partial volume | 0.994(0.989–0.996) |
Fig 4.
A, Illustration of the problem of taking the mean diameter as an indicator of tumor size. Although there is some correlation between volume calculations and averaged diameter measurements at large volume, this correlation breaks down at small volumes.
B, Expansion of the plot of manual volume estimation versus Bayesian partial volume segmentation for smaller tumors shows good linear correlation with manual volume estimates at all tumor sizes.
Rates of Growth
Taking into consideration the accuracy of the methods of measurement, the tumors of the 38 participants with serial images were placed into three categories with respect to Bayesian tissue classification: no growth, significant growth, and significant shrinkage. Two levels of significance were determined. Tumors with a difference in volume, from serial images, greater than the estimated error of 70 mm3 for the Bayesian tissue classification were considered possible candidates for growth. Tumors with a difference in volume greater than three times the error (210 mm3) were considered to have definite growth. The results are shown in Table 3, which uses the volume doubling time (the number of years it would take for the tumor volume to double if growth were linear) to relate the volume growth with the initial tumor volume. Taking growth significance at 1ς flags all tumors with volume doubling time <2 years as growing. Taking growth significance at 3ς misses three tumors that have volume doubling time <2 years but helps to remove tumors with volume doubling time of longer than 2 years from the significant growth group.
TABLE 3:
Growth rates determined from Bayesian measurements of tumor size in 38 patients who underwent serial MR imaging
| Rate of Growth | Significance Level 1ς |
Significance Level 3ς |
||
|---|---|---|---|---|
| No. with Growth | Volume Doubling Time <1 y/<2 y/>2 y | No. with Growth (3ς) | Volume Doubling Time(3ς) <1 y/<2 y/>2 y | |
| Significant growth | 19 | 7/7/5 | 12 | 6/5/1 |
| “No growth” | 13 | 0/0/13 | 24 | 1/2/21 |
| Significant shrinkage | 6 | 0/0/6 | 2 | 0/0/2 |
Note.—Data show the number of vestibular schwannomas demonstrating measurable growth greater than the estimated measurement error of 70 mm3 (1ς) and 3 times the measurement error (3ς). Measurements at 1ς indicate possible growth and measurements at 3ς indicate definite growth.
Tables 4 and 5 show comparisons between the two levels of growth significance between the Bayesian tissue classification method and the manual volume segmentation technique. Because of the greater error for manual segmentation, the number of tumors with definite growth decreases significantly. Most of the tumors exhibit no growth within the statistical error of manual volume segmentation.
TABLE 4:
Distribution by each growth category for both the manual segmentation and Bayesian tissue classification with a cutoff of 1ς (possible growth)
| Manual Segmentation | Bayesian Classification |
||
|---|---|---|---|
| Significant Growth | “No Growth” | Significant Shrinkage | |
| Significant growth | 9 | 2 | 0 |
| “No growth” | 10 | 8 | 3 |
| Significant shrinkage | 0 | 3 | 3 |
TABLE 5:
Distribution by growth category for both the manual segmentation and Bayesian tissue classification with cutoff of 3ς (definite growth)
| Manual | Bayesian Classification |
||
|---|---|---|---|
| Significant Growth | “No Growth” | Significant Shrinkage | |
| Significant growth | 2 | 0 | 0 |
| “No growth” | 10 | 23 | 0 |
| Significant shrinkage | 0 | 1 | 2 |
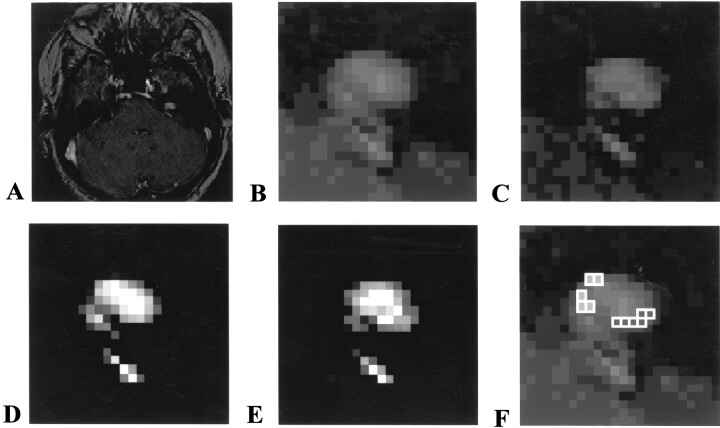
Figures 5 and 6 present two examples of follow-up studies of vestibular schwannomas, illustrating a small tumor with no evidence of growth (Fig 5) and a tumor with significant growth (Fig 6). In each case, the accuracy of the technique allows confident conclusions regarding the presence or absence of growth and comparison of the probability maps illustrates the position of growth and/or misregistration.
Fig 5.
Example of follow-up study of vestibular schwannoma, illustrating a small tumor with no evidence of growth.
A, Initial image of a 0.8-cm vestibular schwannoma.
B, Magnified view of initial image.
C, Follow-up image obtained after 11 months.
D, Probability map of initial tumor location.
E, Probability map of final tumor location.
F, Subtraction map shows differences of more than +25% (open squares) and less than −25% (shaded squares) in voxel volume change after subtraction of the two probability maps shown in D and E. This shows that the tumor has moved in the second image relative to the first, that all differences are due to partial volume changes, and that the number of voxels with apparent volume loss is matched by the number with volume gain. Overall difference in volume of the whole tumor is one voxel, well within the accuracy of the measurement.
Fig 6.
Example of follow-up study of vestibular schwannoma, illustrating a tumor with significant growth.
A, Initial image of a 2-cm vestibular schwannoma.
B, Magnified view of the initial image.
C, Follow-up image obtained after 7 months.
D, Tumor probability map of initial maximal diameter.
E, Tumor probability map of final maximal diameter.
F, Subtraction map of the two probability images shows voxels with a volume change of more than 50%. All voxels that show change show an increase in tumor volume. There is no evidence of significant misregistration between the images, and the overall volume increase is 38%.
Discussion
Several groups have studied the growth of vestibular schwannomas because of the implications of variations in growth rate on tumor prognosis and treatment (2, 3, 5–19). Although concerns have been raised previously regarding the use of mean or maximal diameter measurement to determine the size and growth rate of vestibular schwannomas, current studies continue to use these relatively crude estimations (2). Intracanalicular vestibular schwannomas are ignored in most studies.
As annual or biannual patient monitoring becomes standard practice in the treatment of vestibular schwannomas, accurate measurement of growth rate is vital. We have shown that diameter estimates are the least accurate and reproducible methods of determining tumor size.
With the availability of manual segmentation on most clinical MR imagers and workstations, tumor volume measurements could routinely be used for clinical follow-up in patients with vestibular schwannomas. The method can be time consuming, however, and manual segmentation of 1-cm-diameter acoustic neuromas typically takes between 10 and 15 minutes, in our experience. The time-intensive nature of manual segmentation techniques combined with the high dependency on user expertise and experience have prevented its routine use, and most clinical centers continue to rely on simple 2D linear measurements. In addition to the laborious nature of manual segmentation, this technique also suffers from inaccuracy when the ratio of surface area to volume is high (ie, in intracanalicular tumors). This inaccuracy results from partial volume effects on the MR images and can be compensated for by using a partial volume tissue classifier, such as the one presented herein. We have shown that this approach doubles the accuracy of volume measurements of small tumors and produces significant improvements across the entire range of tumor volumes. The outcome of hearing-preservation surgery is improved in cases of smaller vestibular schwannomas, so that accurate measurement of growth rate in these small intracanalicular tumors is increasingly important for treatment planning (3, 25). The increasing use of stereotactic radiotherapy (26) and the possible future development of novel therapeutic techniques may also demand improved prediction and monitoring of the size and growth rates of vestibular schwannomas. In the future, the development of novel antiangiogenic agents to inhibit tumor growth may also provide an alternative therapy for benign tumors of nerve sheath origin (27). The method of actions of such drugs varies; however, they are likely to be expensive and may have a toxicity profile such that long-term use must be justified on the grounds of specific clinical need. In these circumstances, accurate identification of tumors, which are progressive, together with comparative appraisal of the risks of other therapeutic approaches, is required. Similarly, accurate measurement of changes in growth rate may be the only marker of biologic efficacy during treatment (27).
The Bayesian partial volume tissue segmentation method we describe produces significant improvements in the accuracy of volume measurements and consequently of estimates of growth rate. We attribute this improvement to careful modeling of the effects of partial voluming around the edge of the tumor. These improvements are clinically relevant, particularly in cases of small tumors in which the new method identified significant growth in 10 tumors for which growth was not detected with manual segmentation.
The technique we describe has a number of potential disadvantages that should be appreciated if the technique is to be used in clinical practice. As we have implemented it, the algorithm deals with only three tissue types and is relatively sequence-specific. This could cause problems where tumor necrosis or cyst formation occur, because the algorithm will identify only areas of tumor enhancement. In practice, neither necrosis nor cyst formation occurs in intracanalicular acoustic schwannomas, with which the benefits of the Bayesian approach are greatest. In larger, extracanalicular tumors, this may be an advantage because the growth figures will relate to viable-tumor volume and will not be affected by the presence of internal necrosis. However, although the measurement of viable-tumor volume is the appropriate measurement for prediction of future growth, it is inappropriate if the clinician wants to examine the potential mass effect of these larger lesions. These shortcomings can potentially be overcome in a number of different ways. The presence of central areas of nonenhancement can be easily included in the estimate of the tumor volume by use of morphologic closing algorithms or by identification of the tumor surface combined with automated inclusion of any pixels within the surface boundary. These simplistic approaches are likely to be adequate for use in cases of vestibular schwannomas with which the tumor complexity is low. However, the use of a similar approach in other tumor types, such as glioma, with which several tissue types are seen in and around the tumor (ie, edema) will require more information to allow the accurate identification of an increased number of target tissues. Extension of this approach to correct for partial volume effects into multidimensional data sets is technically challenging but would allow automated volume measurement of a variety of relevant tissue types, such as enhancing tumor, enhancing vessels, nonenhancing tumor, cerebral edema, and so forth.
The results of this study indicate that annual follow-up of patients with vestibular schwannomas larger than 0.5 cm in diameter and biannual follow-up of patients with intracanalicular tumors will allow confident measurement of tumor growth rate and volume doubling time. The basis of our recommendation for follow-up of intracanalicular tumors is that the volume of a perfectly spherical intracanalicular 0.5-cm vestibular schwannoma that has doubled since a previous image would be equal to the method’s error. If intracanalicular vestibular schwannomas are fast growing, the chance of erroneously classifying them as static would be acceptably low. This approach requires the use of techniques for volume measurement that correct errors caused by partial volume averaging. The Bayesian tissue classification technique provides sufficient accuracy and is simple and extremely rapid to use. The method we describe makes the same assumptions in its design as are commonly found in other algorithms designed to measure change in size (eg, the edge integral technique [28]); however, our technique does not require previous coregistration of image volumes. In practice, the only user interaction is to define a rectangular region of interest on which to perform the fitting and analysis.
Conclusion
We have shown that conventional methods, which use linear or 2D markers to assess the volume of vestibular schwannoma, are subject to significant errors and show relatively poor correlation with volume measurements. Volume measurement techniques based on manual or semimanual binary classification of voxels are more accurate but produce significant errors in estimates of small tumors because of partial volume effects. Use of a volume measurement technique that corrects for partial volume errors is up to twice as accurate as other available techniques in cases of small tumors. These differences in measurement accuracy translate into a significant improvement in clinical assessment, allowing identification of tumor growth in 10 of 12 lesions that appeared to be static in size with use of manual segmentation techniques.
Footnotes
Supported by the Northwest NHS Research and Development Directorate (RD018/62), the NHS Levy, and the Cancer Research Campaign (GC838 EQB).
References
- 1.Selesnick SH, Johnson G. Radiologic surveillance of acoustic neuromas. Am J Otol 1998;19:846–849 [PubMed] [Google Scholar]
- 2.Rosenberg SI. Natural history of acoustic neuromas. Laryngoscope 2000;110:497–508 [DOI] [PubMed] [Google Scholar]
- 3.Walsh RM, Bath AP, Bance ML, Keller A, Tator CH, Rutka JA. The role of conservative management of vestibular schwannomas. Clin Otolaryngol 2000;25:28–39 [DOI] [PubMed] [Google Scholar]
- 4.Yamamoto M, Hagiwara S, Ide M, Jimbo M, Arai Y, Ono Y. Conservative management of acoustic neurinomas: prospective study of long-term changes in tumor volume and auditory function. Minim Invasive Neurosurg 1998;41:86–92 [DOI] [PubMed] [Google Scholar]
- 5.Niemczyk K, Vaneecloo FM, Lemaitre L, et al. The growth of acoustic neuromas in volumetric radiologic assessment. Am J Otol 1999;20:244–248 [PubMed] [Google Scholar]
- 6.Charabi S, Thomsen J, Tos M, Charabi B, Mantoni M, Borgesen SE. Acoustic neuroma/vestibular schwannoma growth: past, present and future. Acta Otolaryngol 1998;118:327–332 [DOI] [PubMed] [Google Scholar]
- 7.Fucci MJ, Buchman CA, Brackmann DE, Berliner KI. Acoustic tumor growth: implications for treatment choices. Am J Otol 1999;20:495–499 [PubMed] [Google Scholar]
- 8.Charabi S, Klinken L, Tos M, Thomsen J. Histopathology and growth pattern of cystic acoustic neuromas. Laryngoscope 1994;104:1348–1352 [DOI] [PubMed] [Google Scholar]
- 9.Kondziolka D, Lunsford LD, McLaughlin MR, Flickinger JC. Long-term outcomes after radiosurgery for acoustic neuromas. N Engl J Med 1998;339:1426–1433 [DOI] [PubMed] [Google Scholar]
- 10.American Academy of Otolaryngology-Head and Neck Surgery Foundation, Inc. Committee on Hearing and Equilibrium guidelines for the evaluation of hearing preservation in acoustic neuroma (vestibular schwannoma). Otolaryngol Head Neck Surg 1995;113:179–180 [DOI] [PubMed] [Google Scholar]
- 11.Amadsun J. The growth of acoustic neuromas. Arch Oto Rhino Laryngol 1977;217:99–102 [DOI] [PubMed] [Google Scholar]
- 12.Silverstein H, McDaniel A, Norrell H, Wazen J. Conservative management of acoustic neuroma in the elderly patient. Laryngoscope 1985;95:766–770 [PubMed] [Google Scholar]
- 13.Wazen J, Silverstein H, Norrell H, Besse B. Preoperative and postoperative growth rates in acoustic neuromas documented with CT scanning. Otolaryngol Head Neck Surg 1985;93:151–155 [DOI] [PubMed] [Google Scholar]
- 14.Nedzelski J, Canter RJ, Kassel EE, Rowed DW, Tator CH. Is no treatment good treatment in the management of acoustic neuromas in the elderly? Laryngoscope 1986;96:825–829 [DOI] [PubMed] [Google Scholar]
- 15.Ogawa K, Kanzaki J, Ogawa S, Yamamoto M, Ikeda S, Shiobara R. The growth rate of acoustic neuromas. Acta Otolaryngol Suppl 1991;487:157–163 [DOI] [PubMed] [Google Scholar]
- 16.Kassel EE, Nedzelski JM, Canter RJ, Rowed DW, Cooper PW. Radiologic assessment of acoustic neuroma in the elderly: is no treatment good treatment? Acta Radiol Suppl 1986;369:182–185 [PubMed] [Google Scholar]
- 17.Wennerberg J, Mercke U. Growth potential of acoustic neuromas. Am J Otol 1989;10:293–296 [DOI] [PubMed] [Google Scholar]
- 18.Laasonen E, Troupp H. Volume growth rate of acoustic neurinomas. Neuroradiology 1986. :28:203–207 [DOI] [PubMed] [Google Scholar]
- 19.Charabi S, Lassen NA, Thomsen J, Tos M, Rossen K, Jacobsen GK. Thallium chloride 201Tl combined with single photon emission computed tomography (SPECT) in the evaluation of vestibular schwannoma growth. Acta Otolaryngol 1997;117:35–40 [DOI] [PubMed] [Google Scholar]
- 20.Kovacsovics B, Davidsson L, Harder H, Magnuson B, Ledin T. MRI screening of the cerebellopontine angle and inner ear with fast spin-echo T2 technique. Arch Ital Biol 2000;138:87–92 [PubMed] [Google Scholar]
- 21.Vokurka EA, Thacker NA, Jackson A. A fast model independent method for automatic correction of intensity nonuniformity in MRI data. J Magn Reson Imaging 1999;10:550–562 [DOI] [PubMed] [Google Scholar]
- 22.Laidlaw D, Fleischer K, Barr A. Partial-volume Bayesian classification of material mixtures in MR volume data using voxel histograms. IEEE Trans Med Imag 1998;17:74–86 [DOI] [PubMed] [Google Scholar]
- 23.Press W, et al. Numerical recipes. Cambridge, England: Cambridge University Press;2000
- 24.Lacey T. Neuro-Imaging Analysis Centre. Manchester, England: University of Manchester;2000
- 25.Slattery W, Brackmann D, Hitselberger W. Hearing preservation in neurofibromatosis type 2. Am J Otol 1998;19:638–643 [PubMed] [Google Scholar]
- 26.Shirato H, Sakamoto T, Sawamura Y, et al. Comparison between observation policy and fractionated stereotactic radiotherapy (SRT) as an initial management for vestibular schwannoma. Int J Radiat Oncol Biol Phys 1999;44:545–550 [DOI] [PubMed] [Google Scholar]
- 27.Takamiya Y, Friedlander RM, Brem H, Malick A, Martuza RL. Inhibition of angiogenesis and growth of nerve-sheath tumours by AGM-1470. J Neurosurg 1993;78:470–476 [DOI] [PubMed] [Google Scholar]
- 28.Fox NC, Freeborough PA. Brain atrophy progression measured from registered serial MRI: validation and application to Alzheimer’s disease. J Magn Reson Imaging,1997;7:1069–1075 [DOI] [PubMed] [Google Scholar]