Abstract
BACKGROUND AND PURPOSE: Brain hypervascular diseases are complex and induce hemodynamic disturbances on brain parenchyma, which are difficult to accurately evaluate by using perfusion-weighted (PWI) MR imaging. Our purpose was to test and to assess the best AIF estimation method among 4 patients with brain hypervascular disease and healthy volunteers.
METHODS: Thirty-three patients and 10 healthy volunteers underwent brain perfusion studies by using a 1.5T MR imaging scanner with gadolinium-chelate bolus injection. PWI was performed with the indicator dilution method. AIF estimation methods were performed with local, regional, regional scaled, and global estimated arterial input function (AIF), and PWI measurements (cerebral blood volume [CBV] and cerebral blood flow [CBF]) were performed with regions of interest drawn on the thalami and centrum semiovale in all subjects, remote from the brain hypervascular disease nidus. Abnormal PWI results were assessed by using Z Score, and evaluation of the best AIF estimation method was performed by using a no gold standard evaluation method.
RESULTS: From 88% to 97% of patients had overall abnormal perfusion areas of hypo- (decreased CBV and CBF) and/or hyperperfusion (increased CBV and CBF) and/or venous congestion (increased CBV, normal or decreased CBF), depending on the AIF estimation method used for PWI computations. No gold standard evaluation of the 4 AIF estimates found the regional and the regional scaled methods to be the most accurate.
CONCLUSION: Brain hypervascular disease induces remote brain perfusion abnormalities that can be better detected by using PWI with regional or regional scaled AIF estimation methods.
Cerebral perfusion imaging is currently used to investigate the brain physiology in healthy patients and in those with various brain diseases. It can be used in brain hypervascular diseases (including brain arteriovenous malformations [AVMs], brain arteriovenous shunts, and capillarectasia such as proliferative angiopathies, and AVM with pseudo–Moya Moya) to observe the hemodynamic disturbances that alter the vascular regulation of the cerebral brain parenchyma1–9 and create clinical symptoms.10 To explore brain perfusion, one can use different techniques; 2 of them are well documented: positron-emission tomography (PET)11–13 and MR perfusion-weighted imaging (PWI) with gadolinium bolus injection.14, 15
The most common modeling approach used in PWI is based on the Stewart-Hamilton indicator dilution theory16 establishing the relationship between the cerebral blood volume (CBV), the cerebral blood flow (CBF), and the mean transit time (MTT). PWI quantitative measurements are performed by using an arterial input function (AIF)17 estimate. In brain hypervascular disease, hemodynamic disturbances induced by the brain arteriovenous shunt nidus can remotely stress the brain gray matter (cortex and basal ganglia), as previously reported in experimental studies.18 Unfortunately, reliable characterization of brain perfusion in brain hypervascular disease cases is difficult because of partial volume effects that potentially affect all voxels of the MR imaging acquisition,19 especially voxels including capillary signal intensity intermingled with arterial and venous signal intensity. In addition, AIF estimate may be affected by aliasing in high-flow arteries,19 especially when AIF is extracted near the shunt areas. To better study the hemodynamic disturbances induced by brain hypervascular disease remote from the nidus, we needed to improve our first-pass gadolinium-chelate bolus injection PWI results. We compared perfusion parameters (CBV and CBF computed from thalami [Th]and centrum ovales[CO]) measured by using 4 different AIF estimates on PWI data acquired in 10 healthy volunteers and 39 patients with brain hypervascular disease. The relevance of the different CBV and CBF computations by using different AIF extraction methods was assessed with an evaluation method that does not require the gold standard to be known,20, 21 and also by using Z scores.
Materials and Methods
Subjects
Before MR imaging, we obtained the approval of the ethics committee for investigating patients and healthy volunteers with perfusion MR imaging and gadolinium-chelate bolus injection. The subjects’ consents were obtained according to the Declaration of Helsinki.
Sample Size Calculation.
To estimate the sample size number (N) required for this study, we considered the analysis of each patient’s perfusion map as a simple diagnostic test that yielded either a positive (abnormal brain perfusion) or negative (normal brain perfusion) result. In a previous study,19 51% of patients with proliferative angiopathies had abnormal perfusion results remote from the nidus. We, therefore, pessimistically assumed that patients with brain hypervascular disease have a 50% chance of having abnormal brain perfusion. Considering 2 patient groups, namely those without and those with PWI abnormalities, we could derive an estimate of sample size from the estimates of the false-positive and false-negative rates of the diagnostic tests. We assumed a false-positive rate of 20% and a false-negative rate of 50% as the worst results. Considering equal numbers of patients with abnormal and normal brain perfusion, we calculated an expected χ2 = 0.098 × N. For a critical χ2 = 3.84 (degree of freedom = 1, P < .05), in a sample size N = 3.84/0.098, about 40 had a 50% chance of yielding a significant result (ie, statistical power = 0.5). Therefore, we proposed to enroll approximately 40 patients with brain hypervascular disease into the study. All patients were clinically stable and free of MR imaging or gadolinium-chelate contraindications.
Patients.
Thirty-nine patients (20 women and 19 men; aged 9–65 years; mean age, 35.45 years) were prospectively selected from 3 different neurovascular data bases in France (Bicêtre and Centre Hospitalier Sainte Anne) and Canada (Toronto Western Hospital, University Health Network). All patients matched the following inclusion criteria:
presenting with seizures, focal deficit (with or without recovery), and/or headaches;
without intracerebral bleeding (patients with a history of brain parenchyma hemorrhage were eliminated to avoid the magnetic susceptibility artifacts induced by the blood components to the MR T2* image);
MR imaging and angiographic follow-up imaging to be performed between May 2000 and March 2003;
brain AVMs (n = 25), proliferative angiopathies (n = 10), or AVM with pseudo–Moya Moya (n = 4) (Lesions were located variously in the brain. Before imaging, clinical investigations were performed to identify the patient symptoms, which were classified as follows: single focal deficit [n = 8], single headaches [n = 11], and single generalized seizures [n = 5]);
multiple symptoms (headaches and seizures, [n = 5], headaches and focal deficit [n = 7], focal deficit and seizures [n = 4], headaches and focal deficit and seizures [n = 2]), and free of symptoms [n = 3].
Patients with proliferative angiopathies who had undergone previous surgical treatment or neurovascular embolization (n = 3) were eliminated and referred for further PWI investigations.
Volunteers.
Ten fully informed healthy volunteers who were free of MR imaging or gadolinium-chelate contraindication (4 women and 6 men; mean age, 33.8 years) participated in the study and were scanned with PWI.
MR Cerebral Perfusion Imaging
PWI was performed by using the indicator dilution theory (central volume theorem of Stewart-Hamilton,16 and the relationship between endovascular gadolinium concentration and MR imaging signal intensity variation).22, 23
MR Imaging Protocol
After sagittal T1-weighted fast scout view imaging, 24 T1-weighted axial sections (5 mm; 256 × 256 matrix; 240-mm field of view; TR/TE, 450/TE ms) were positioned over the whole brain. Data were acquired by using an echo-planar T2-weighted gradient-echo MR image,22, 24 which yields a large signal intensity decrease when the gadolinium bolus arrives. The same echo-planar imaging was used on the 3 1.5T MR images (Signa EchoPlus [1 in each investigation center], General Electric Medical System, Milwaukee, Wis). The acquisition parameters were as follows: axial single-shot echo-planar T2-weighted gradient-echo sections superimposed on the T1-weighted sections partially covering the brain but registered to T1-weighted section locations; 18 interleaved sections, repeated 25 times (25 phases); 5-mm thickness; 0-mm gap; 128 × 128 matrix; 240-mm field of view; TR/TE, 2000/30 ms; flip angle, 90°. There were no macromotion artifacts (patients’ movements) during the MR imaging investigations.
Injection Protocol.
Gadolinium injections were started without delay after the beginning of the MR imaging acquisition. Fifteen milliliters of gadopentetate dimeglumine (DOTAREM, 0.1 mmol/mL) were injected with a power injector in a left antecubital vein during 2 seconds (7 mL/second flow), immediately followed by a saline serum flush (identical quantity and flow).25 The whole brain was imaged in 50 seconds every 2 seconds after the beginning of the acquisition (25 phases).
Data Analysis
PWI Analysis.
In PWI, the signal-intensity change resulting from the gadolinium bolus injection in a T2*-weighted gradient-echo MR image is based on the magnetic susceptibility T2* effect of the gadolinium bolus (with ΔR2* = 1/ΔΤ2*,22, 23,26 where ΔR2* is the relaxation rate difference). The local gadolinium concentration variation Ci(t) in voxel i at time t is related to the MR signal intensity in voxel i at time t, Si(t), by
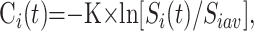 |
1) |
where K is a constant depending on the magnetic field, contrast medium type, TE and MR image; and Siavg is the averaged MR signal intensity in voxel i from t = 2 to t = 6 seconds before the gadolinium arrival and after a steady state magnetization has been achieved.16, 24, 27–29 Because the same TE was used when acquiring all sections of the bolus-tracking volumes and assuming that all tissue types (eg, large and small vessels) had similar (but not identical30) proportionality constant K (which is not true for a spin-echo echo- planar imaging26, 31), the actual value of the K-ratio can be neglected to estimate the CBV (equation 7) because it cancels out. The more the signal intensity is decreased, the more the bolus is concentrated. The second, third, and fourth images obtained before gadolinium arrival were averaged to compute the images’ Si(0). A brain mask was applied section by section to select brain parenchyma only for further analysis. For each section, the mask was generated by using a gray-level threshold applied on the image resulting from the average of the time series. Within the mask, the PWI Si(t) images were converted into gadolinium concentration images Cim(t) by using a homemade software (DPTools, http://fmritools.hd.free.fr).
AIF Estimations.
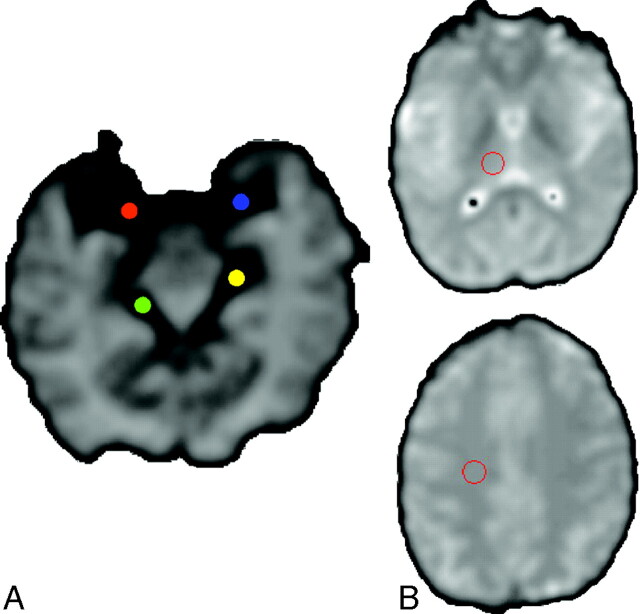
To measure cerebral perfusion, we considered 4 semiautomated methods for estimating the AIF: local, AIF was derived from only 1 middle cerebral artery [MCA]; regional, AIF was derived from arteries that vascularize specific brain location; regional scaled, same as regional but rescaled to the global maximum of AIF concentration in the whole brain; and global, average of all AIF derived from all arterial voxels in the brain. To avoid high-frequency noise, we automatically drew a 9-voxel (3 × 3) region of interest on arteries that were used in the different AIF estimation methods; locations of these AIF regions of interest were identical among the different AIF estimation methods, either right or left MCA (contralateral to the location of the lesion in the patients) in the case of local or global estimations, or left or right MCA for the CO and left or right posterior cerebral artery (PCA) for the Th in case of regional or regional scaled estimations, independent of the location of the lesion (but none of these regions of interest were set on artery branches that directly fed the brain arteriovenous shunt nidus, Fig 1).
Fig 1.
A, Arterial region of interest set on the right (red) or left (blue) MCA or right (green) or left (yellow) PCA in the regional and regional scaled estimations.
B, Tissular region of interest set on the right Th (upper) and right CO (lower).
For local AIF estimation, the AIF region of interest was used to derive arterial temporal curves, AIFAi(t), by
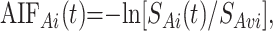 |
2) |
where AIFAi(t) is the gadopentetate dimeglumine concentration in arterial voxel Ai at time t, SAi(t) is the MR signal intensity in arterial voxel Ai at time t, and SAvi is the MR signal intensity averaged over the arterial voxel Ai from t = 2 to t = 6 seconds before the gadolinium arrival and after a steady state magnetization was achieved. All the arterial AIFAi(t) curves derived from this AIF region of interest were averaged into a single AIF(t).
For regional AIF estimation, voxels inside the selected AIF region of interest were analyzed location by location (left and right MCA for left or right CO measurements, left and right PCA for left or right Th measurements), yielding 4 AIF estimates related to the 4 location measurements of the PWI parameters (left Th, right Th, left CO, right CO). For each of these analyzed voxels, an arterial temporal curve, AIFAi(t), was generated as previously described (equation 2).
The regional scaled AIF estimation was used to try to better reflect the entire brain arterial flow in patients with brain hypervascular disease, by detecting the maximal arterial concentration of gadopentetate dimeglumine in the whole brain. This was used as a scaling factor, thus correcting for some of the arterial-flow inhomogeneities in the selected AIF region of interest. This method was similar to the regional estimation but used an arterial scaling factor CGAmax defined by
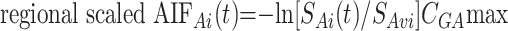 |
3) |
where regional scaled AIFAi(t) is the gadopentetate dimeglumine concentration in arterial voxel Ai at time t, SAi(t) is the MR signal intensity in arterial voxel Ai at time t, and SAvi is the MR signal intensity averaged over the arterial voxel Ai from t = 2 to t = 6 seconds before the gadolinium arrival and after a steady state magnetization was achieved. CGAmax is a scaling factor, which is calculated by detecting the arterial content of the voxels in the whole brain as follows: The drawn AIF region of interest (depending on the selected AIF location, left or right PCA or MCA) was used to derive the mean arterial peak time Tpa and the mean arterial peak height Hpa of the considered AIF region of interest by averaging all the AIFAi(t) in this region of interest. Then the arterial content of each voxel of the brain was assessed by a cost function given by
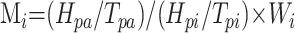 |
4) |
where Mi is the arterial weight assigned to the analyzed voxel i, Hpi and Tpi are the peak height and the peak time of the ith voxel, and Wi is a function of the distance between voxel i and the image center. Voxels with Wi smaller than 0.33 and larger than 0.66 were discarded from further analysis; only voxels with 0.33 < Mi < 0.66 were considered as arterial voxels because arterial voxels of the circle of Willis are located near the image center with Wi ∼ 0.5 (E.D. Morris et al, unpublished data, Sensor Systems, Sterling,Va). The detected arterial voxels in the whole brain had Hp and Tp identical to Hpa and Tpa, and the maximum gadolinium concentration in all these detected voxels yielded CGAmax.
For the global AIF estimate, the method was similar to the local one, with only 1 region of interest drawn over an MCA, but used the algorithm previously described (equation 4) to detect all available arterial voxels in the brain. All these selected arterial voxels were then grouped into congruent 3 × 3 voxel (32 mm2) matrix kernels, from which arterial AIFAi(t) curves were averaged to obtain a single AIF(t).
Regional scaled and global AIF estimation methods used a voxel-checking procedure by superimposing the arterial voxels on the original PWI images to visually check whether they were inside arteries: With graphic control (AIF voxels superimposed on arteries, AIF[t] time curve and its gamma fit, Fig 2), the user could check and correct AIF evaluations by drawing the original 9-voxel region of interest on another segment of the artery. If some of detected arterial voxels were inside veins, another AIF region of interest was drawn as though all the detected arterial voxels were only inside arteries.
Fig 2.
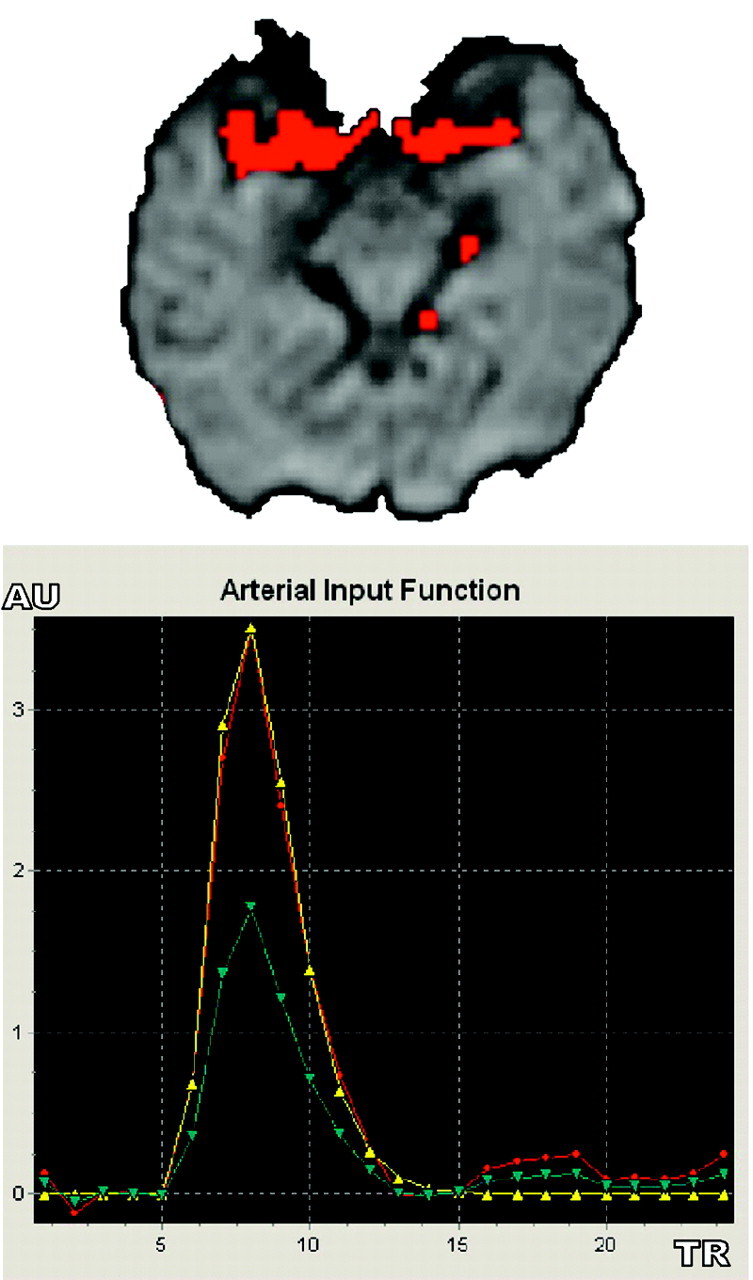
Automated AIF extraction used in regional scaled and global methods. Arterial voxels (red, upper image) are superimposed over MR PWI series to check their anatomic matching with brain arteries. Single AIF curve (red, lower image, in arbitrary unit [AU]) derived from local selected AIF curve (blue) is fitted with a gamma function to eliminate recirculation (yellow).
PWI Computations.
Using a Levenberg-Marquart32 algorithm, we fitted a gamma variate function to the resulting AIF(t) and Cim(t) curves to eliminate recirculation33–35 and to reduce noise:
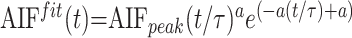 |
5) |
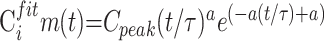 |
6) |
where AIFfit(t) and Cifitm(t) are the fitted AIF(t) and Cim(t) curves, respectively, AIFpeak or Cpeak is the maximum of the model curves, τ is the time of this maximum, a is a parameter resulting from the fit, and t represents the time.
Using AIF resulting from 1 of the 4 AIF estimation methods described previously, we calculated CBV voxel by voxel to yield a CBV parametric image, by using11, 16, 34–35
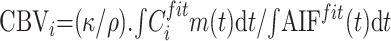 |
7) |
where κ = (1 − HCTLV)/(1 − HCTSV) accounts for the fact that hematocrit (HCT) in large vessels (HCTLV = 0.45) is superior to hematocrit in small vessels (HCTSV = 0.25), and ρ is the brain parenchyma attenuation (1.04 g/mL).34, 35
In each section, minimal, maximal, mean, and standard deviation (SD) CBV values were calculated over all voxels.
Similarly, CBF parametric images were obtained by using:
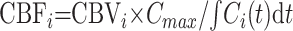 |
8 |
with
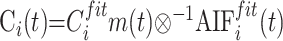 |
9) |
where Ci(t) is the tissue residual function of gadolinium concentration in brain parenchyma when arterial bolus is a unit impulse (discretely sampled from a delta function), Cmax is the maximum of the curve Ci(t), and 196−1 is the deconvolution operation.17, 27,35–39 Deconvolution was performed in the Fourier domain (Martin Sander, OptiVec, Germany), with AIFifit(t) and Cifitm(t) FFT sampling interpolated by 2 (with zero filling of the last values to obtain a multiple of 2)25 then filtered with low-pass interpolating filter: yn = xn + 1/3(xn+1 − xn).
Finally, from the central volume theorem, one derives the following:
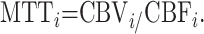 |
10) |
Parametric perfusion images of CBV and CBF were generated section by section for the whole-brain volumes. Some MTT maps were generated for illustration purposes.
PWI Measurements and Statistical Analysis.
To compare PWI results of volunteers and patients, we drew only 4 regions of interest of 49 voxels (172 mm2) in both Th and CO on the CBV and CBF parametric images of the volunteers and the patients, computed with 1 of the 4 analysis approaches. Locations of these regions of interest were identical for all AIF estimation methods. Left CBV and CBF values obtained in healthy volunteers and patients were averaged and were analyzed for each region (Th and CO) and for each estimation method. Identical processing was performed for right hemisphere PWI values. The accuracy of CBV and CBF estimates was assessed by likelihood maximization without using a gold standard (no gold standard method).20, 21
This no gold standard method is equivalent to fitting regression lines without knowing the values on the x-axis. To use this method, one needs multiple estimates of the clinical parameter of interest for each patient of a given population. No gold standard assumes that the statistical distribution for the true values of the clinical parameter of interest is a member of a given family of parameterized distributions and that the estimates of the parameters can be expressed as a linear function of the unknown true parameter values. Using these assumptions, the no gold standard method estimates the parameters characterizing the statistical distribution of the unknown true values and the parameters of the function relating the estimated parameter values to the true parameter values. This method computes the parameter “a”, which represents the slope of the linear relationship x’ = ax + b + e between the unknown true parameter (here CBF or CBV) value x and its estimate x’. The term “e” represents the random noise in the measurement, assumed to follow a normal distribution with a mean of zero and a SD of σ. The figure of merit, σ/a, characterizes the error in the estimate,20, 21 hence the smaller the better.
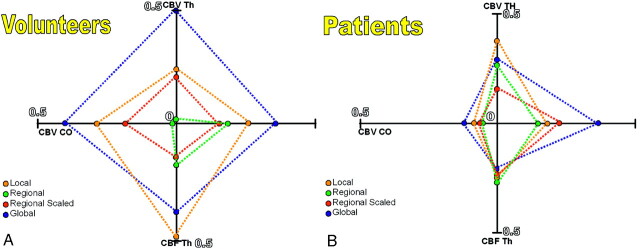
We drew a radar plot of the σ/a’ figure of merit for the 4 PWI parameters (CBV Th, CBV CO, CBF Th, and CBF CO). In this plot, because the best estimation method corresponds to the smallest σ/a values, the method yielding the most accurate AIF estimate should lead to the radar plot with the smallest area (Figs 3A, -B).
Fig 3.
Radar plots of the no gold standard σ/α results for the 4 PWI parameters (CBV Th, CBV CO, CBF Th, CBF CO) in volunteers (A) and patients (B). The plot with the smallest area corresponds to the most accurate AIF estimate.
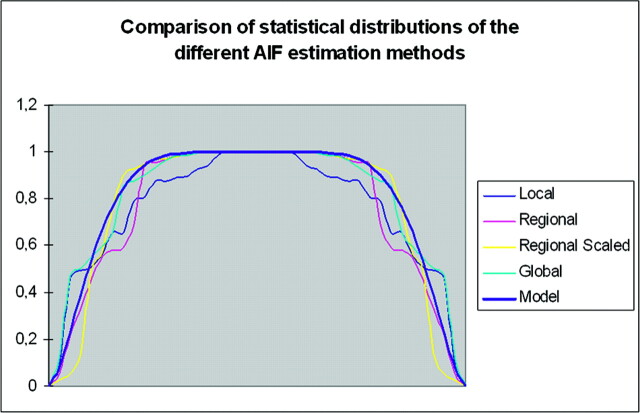
We studied the PWI measurement distributions in our patients with brain hypervascular disease and compared the results to a beta model in each of the 4 AIF estimation methods (Fig 4).
Fig 4.
Comparison of the CBF distribution measurements in Th locations of patients with brain hypervascular disease among the 4 AIF estimations methods, compared with a beta distribution. All the AIF estimation methods have a beta pattern for the CBV and CBF measurements in all locations (only CBF in Th is shown here).
We performed paired t tests among the PWI results from the different AIF estimation methods in patients and volunteers to find significant statistical differences between the AIF estimates.
For each AIF estimation method, the values of CBV and CBF obtained on volunteers were pooled to derive the mean and SD values. These were then used in Z score analysis of patients’ data to determine normal and abnormal hemodynamic regions. For this analysis, Z >1.96 (P < .05) was considered as abnormal.
Perfusion results were classified as follows: hypoperfusion corresponded to decreased CBV and CBF, hyperperfusion corresponded to increased CBV and CBF, and venous congestion corresponded to increased CBV with normal or decreased CBF.
Results
All volunteers and all patients except 3 successfully underwent MR imaging. We therefore performed PWI for 33 patients. AIF and Cmt) gamma fitting and further PWI computations were successful for all volunteers and for the 33 patients. The perfusion results for volunteers and patients are presented in Table 1, and a summarized comparison of the different AIF estimates is presented in (Table 3 and Fig 5. In both volunteers and patients, PWI CBV and CBF values had a statistical distribution close to the beta model (Fig 4), suggesting that the no gold standard method could be used to compare the AIF estimation methods.
Table 1:
Cerebral blood flow and cerebral blood volume values measured in regions of interest drawn over the thalami and centrum ovale in volunteers and patients using each of the 4 arterial input function estimates
| Local | Regional | Regional Scaled | Global | |
|---|---|---|---|---|
| Volunteers | ||||
| CBV Th | ||||
| mMean (SD) | 6.2 (1.5) | 6.0 (1.6) | 5.0 (1.2) | 5.9 (1.2) |
| Min–max | 4.2–9.6 | 3.8–8.7 | 3.4–6.9 | 4.1–8.5 |
| CBV CO | ||||
| Mean (SD) | 2.0 (0.2) | 2.0 (0.3) | 1.9 (0.3) | 2.0 (0.3) |
| Min–max | 1.6–2.5 | 1.6–2.7 | 1.4–2.4 | 1.6–2.4 |
| CBF Th | ||||
| Mean (SD) | 66.0 (13.5) | 67.5 (18.2) | 60.2 (15.3) | 63.5 (9.2) |
| Min–max | 46.1–95.3 | 36.3–94.7 | 34.2–88.4 | 47.6–80.4 |
| CBF CO | ||||
| Mean (SD) | 20.3 (4.6) | 19.9 (3.2) | 20.2 (3.6) | 21.0 (3.3) |
| Min–max | 12.8–30.4 | 12.8–25.5 | 14.8–26.9 | 15.7–25.9 |
| Patients | ||||
| CBV Th | ||||
| Mean (SD) | 6.9 (3.4) | 7.0 (3.1) | 6.0 (2.6) | 6.6 (3.0) |
| Min–max | 2.4–24.9 | 3.5–21.6 | 2.6–16.8 | 3.7–18.8 |
| CBV CO | ||||
| Mean (SD) | 2.5 (1.8) | 2.5 (1.7) | 2.3 (1.8) | 2.4 (2.6) |
| Min–max | 0.9–14.0 | 0.8–14.0 | 0.9–14.9 | 0.6–21.9 |
| CBF Th | ||||
| Mean (SD) | 72.3 (39.9 | 77.0 (43.9) | 67.3 (36.3) | 77.1 (46.6) |
| Min–max | 16.3–268.4 | 27.4–254.0 | 14.2–192.0 | 31.9–328.2 |
| CBF CO | ||||
| Mean (SD) | 20.2 (11.1) | 19.7 (10.4) | 19.7 (10.4) | 20.0 (10.5) |
| Min–max | 4.9–58.6 | 5.9–58.6 | 7.2–60.7 | 7.0–63.0 |
Note:—CBF indicates cerebral blood flow (mL/min/100 g); CBV, cerebral blood volume (mL/100 g); Th, thalami; CO, centrum ovale.
Table 3:
Results of the no gold standard method comparing the accuracy of cerebral blood volume and cerebral blood flow perfusion-weighted imaging measurements in volunteers and patients for different arterial input function estimation methods
| Local | Regional | Regional Scaled | Global | |
|---|---|---|---|---|
| Volunteers | ||||
| CBV Th | .199 | .008 | .169 | .476 |
| CBV CO | .295 | .008 | .197 | .412 |
| CBF Th | .432 | .166 | .121 | .323 |
| CBF CO | .262 | .185 | .141 | .356 |
| Patients | ||||
| CBV Th | .090 | .069 | .040 | .076 |
| CBV CO | .025 | .017 | .020 | .040 |
| CBF Th | .066 | .070 | .067 | .053 |
| CBF CO | .050 | .031 | .071 | .115 |
Note:—CBV indicates cerebral blood volume; CBF, cerebral blood flow; Th, thalami; CO, centrum ovale. Bold values indicate the best performance (ie, parameter most correlated to the unknown true values).
Fig 5.
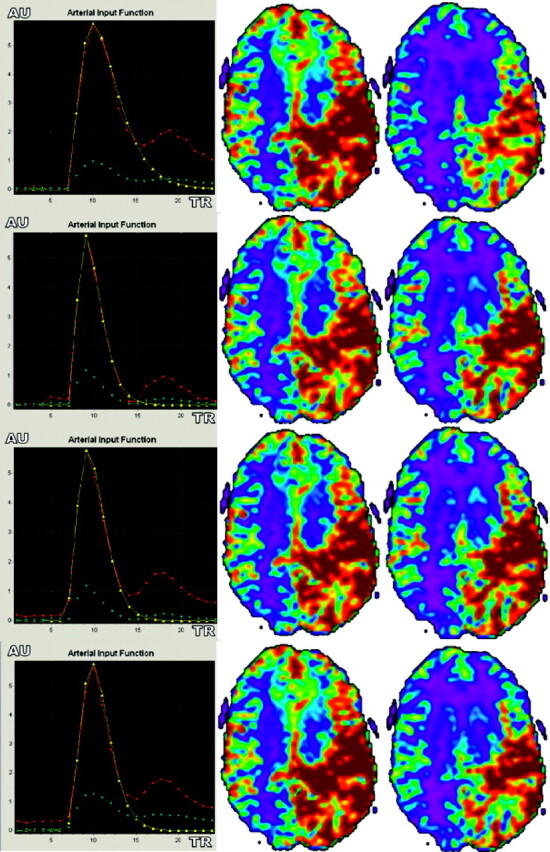
Differences between CBV and CBF parameter color-scaled maps with local (A), regional (B), regional scaled (C), and global (D) AIF estimations in a patient with brain AVM. Note that AIF curves are sharper with the regional and regional scaled methods, mainly because of AIF positioning and increased CBF values in gray matter cortices (green). Unlike the observations in volunteers, CBV and CBF images obtained with the 4 AIF estimation approaches were not that similar.
In volunteers, all PWI results by using the local or the regional AIF estimation method were close to those reported in literature (in CO, CBV = 4.7 ± 2.1 mL/100 g and CBF = 22.1 ± 1 mL/minute per 100 g; in Th, CBV = 8.8 ± 4.7 mL/100 g and CBF = 65.3 ± 3.5 mL/minute per 100 g35). PWI results by using the regional scaled or global methods were slightly inferior to those obtained with the local and regional AIF estimation methods but still ranged within the reported normal values. Paired t tests of the PWI results among the different AIF estimation methods found significant statistical differences between the 4 AIF estimates (Table 4). On the basis of the no gold standard analysis, the methods that yielded the poorest results were the local and the global methods. Evaluation of the most accurate CBV and CBF parameters performed by using the no gold standard found the regional method results to be the most accurate σ/α = 0.008, (Table 3) for CBV parameter and the regional scaled method to be the most accurate (σ/α around 0.13, Table 3) for CBF parameters in either Th or CO locations. There was not 1 method that yielded best results for all locations and for both CBF and CBV. However, overall, the regional method tended to provide the best results (Fig 3).
Table 4:
Paired t test of the pefusion-weighted imaging results from the arterial input function estimation methods in volunteers and patients
| Loc vs Rg | Loc Vs RgS | Loc vs Glb | Rg vs RgS | Rg vs Glb | RgS vs Glb | |
|---|---|---|---|---|---|---|
| Volunteers | ||||||
| CBV Th | .454 | .001 | .534 | .000 | .892 | .032 |
| CBV CO | .232 | .505 | .898 | .038 | .309 | .712 |
| CBF Th | .762 | .200 | .498 | .027 | .411 | .421 |
| CBF CO | .587 | .894 | .493 | .560 | .210 | .382 |
| Patients | ||||||
| CBV Th | .600 | .001 | .328 | .000 | .127 | .001 |
| CBV CO | .099 | .001 | .544 | .004 | .915 | .275 |
| CBF Th | .097 | .083 | .099 | .001 | .979 | .001 |
| CBF CO | .176 | .448 | .771 | .920 | .690 | .697 |
Note:—Significant statistical differences are in bold. Loc indicates local; Rg, regional; RgS, regional scaled; Glb, Global; CBV, cerebral blood volume; CBF, cerebral blood flow; Th, thalami; CO, centrum ovale.
In patients, CBV and CBF values presented a greater dispersion than the values obtained for volunteers with higher SD values. Similar to those observed in volunteers, CBF and CBV values differed slightly as a function of the estimation method with higher differences in patients than in volunteers. Paired t tests of the PWI results among the different AIF estimation methods found significant statistical differences between the 4 AIF estimates that were close to those found in volunteers (Table 4). The most accurate CBF and CBV, as identified by the no gold standard analysis, depended on the location (CO or Th) and on whether CBF or CBV was considered. However, the regional and regional scaled methods tended to yield results that were consistently the most accurate in CO locations for both CBF and CBV, similar to those observed in volunteers. Differences between regional and regional scaled methods were slight (Table 1).
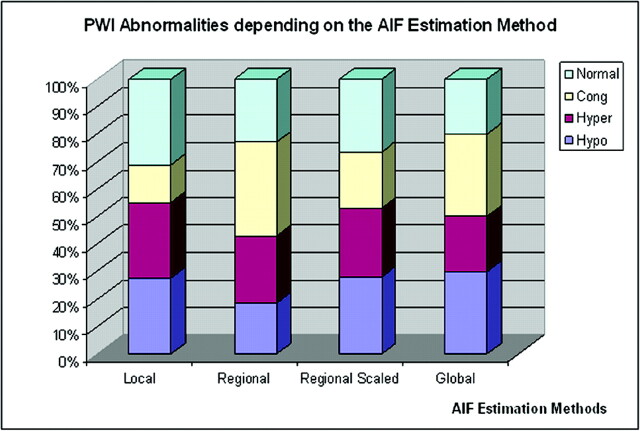
All 3 previously reported PWI abnormalities1–9, 40–43 were found (hypoperfusion, hyperperfusion, and venous congestion), but the incidence of abnormalities varied depending on the way the AIF was estimated: Abnormal PWI results ranged from 88% to 97% (Table 2 and Fig 6). Comparing results obtained with the regional and regional scaled methods, we found that the regional scaled method yielded less normal and more hypoperfusion than the regional method on the basis of the Th measurements. The results by the 2 methods were close in CO Fig 7 and (Table 2). Overall only 5 of the 33 patients had the same PWI abnormalities, regardless of the method used to derive the AIF (Table 5).
Table 2:
Patients’ perfusion-weighted imaging findings observed with the different arterial input function estimation methods
| Local | Regional | Regional Scaled | Global | |
|---|---|---|---|---|
| Th | ||||
| Hypo | 7 | 2 | 7 (1) | 8 (2) |
| Hyper | 12 (2) | 10 | 9 (1) | 15 (2) |
| Cong | 8 (2) | 10 (2) | 11 (2) | 9 (2) |
| Norm | 12 (36%) | 14 (42%) | 7 (21%) | 7 (21%) |
| CO | ||||
| Hypo | 12 (6) | 15 (9) | 16 (5) | 16 (8) |
| Hyper | 5 (3) | 10 (4) | 8 (3) | 4 (3) |
| Cong | 12 (5) | 9 (1) | 6 (2) | 9 (3) |
| Norm | 7 (21%) | 5 (15%) | 6 (18%) | 7 (21%) |
| Th & Co | ||||
| Hypo | 3 | 1 | 3 (1) | 6 |
| Hyper | 3 (1) | 3 | 2 (1) | 3 |
| Cong | 2 | 2 | 2 | 0 |
| Norm | 3 (9%) | 2 (6%) | 3 (9%) | 2 (6%) |
Note:—Hypo indicates hypoperfusion; Hyper, hyperperfusion; Cong, venous congestion; Norm, normal; Th, thalami; CO, centrum ovale. Within the Hypo, Hyper, and Cong entries, numbers in parentheses indicate perfusion-weighted imaging abnormalities that are bilateral.
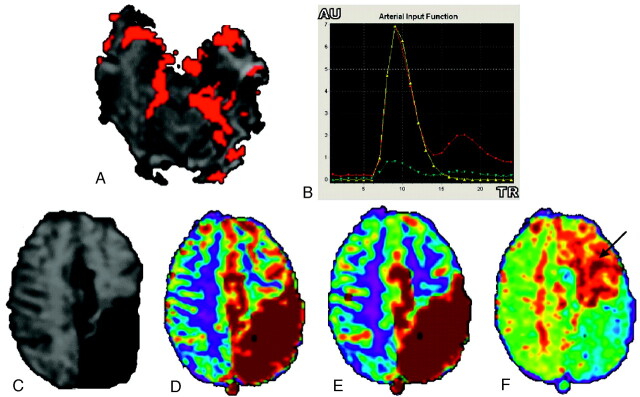
Fig 6.
AIF of a left occipital brain AVM (A, -B) with visualization of the arteriovenous shunt (red voxels inside the left occipital lobe). T2* section (C) shows T2-weighted left parietal abnormal areas related to gadolinium-chelate magnetic susceptibility effect in abnormal vessels; and color scale parametric CBV (D), CBF (E), and MTT (F) maps computed with the regional scaled method show high-flow disturbances in this area. Note that hemodynamic disturbances are seen remote from the nidus over the left CO (arrow), regardless of the AIF estimation method used.
Fig 7.
Graph shows patients’ PWI abnormalities (hypoperfusion [Hypo], hyperperfusion [Hyper], venous congestion [lswb]Cong], or Normal) found in the different AIF estimation methods. Note that PWI abnormalities may be bilateral. All PWI results varied among the different methods except for 14 patients who had the same PWI abnormalities regardless of the AIF estimation method.
Table 5:
Abnormal perfusion-weighted imaging findings in patients among the different arterial input function estimation methods
| Patient No. | Local |
Regional |
Regional Scaled |
Global |
||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hypo | Hyper | Cong | Norm | Hypo | Hyper | Cong | Norm | Hypo | Hyper | Cong | Norm | Hypo | Hyper | Cong | Norm | |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 6 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 8 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 9 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 10 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 11 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 12 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 13 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 14 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 15 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 16 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 17 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 18 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 19 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 20 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 21 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 22 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 23 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 24 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 25 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 26 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 27 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 28 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 29 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 30 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 31 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 32 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 33 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
Note:—O indicates absent; 1, present. Only 5 of 33 patients (15%) had identical perfusion-weighted imaging abnormalities among the different arterial input function methods (shaded areas). Hypo indicates hypoperfusion; Hyper, hyperperfusion; Cong, venous congestion; Norm, normal.
Discussion
Cerebral PWI is widely used in stroke disorders to locate the mismatch area (penumbra zone or hypoperfused cerebral parenchyma) on which the patient prognosis depends.14 PWI is also used in cerebral tumor screening to compute the fraction of the capillary compartment in abnormal tissue: An increased fraction is associated with a malignant transformation.15 Quantitative PWI measurements rely on compartment theories, which imply a specific input, the AIF, and an analyzed compartment, the C(t) tissue residue time curve. Extraction of the most accurate AIF is the most important step for a reliable analysis.17,44–46 Because of the Stewart-Hamilton theorem,16 AIF integral with time (area under the curve) reflects the arterial blood volume and is used to further compute other brain perfusion parameters (see Materials and Methods). When an AIF peak varies, so does the CBV estimate. When the AIF curve is sharper or wider, the resulting CBF may be under- or overestimated.17, 44, 46
Regarding the anatomic location of the AIF, previous reports suggested the importance of a correct correspondence between the location of the selected AIF and the location of the analyzed capillary voxels.17, 44, 45 Many authors estimate the AIF from a region of interest drawn over an artery such as the MCA or the basilar artery.44 This estimation method yields 2 types of AIF: local AIF, in which a single AIF derived from a single artery is used for PWI computation over the whole brain; or regional AIF, where 4 or more AIFs are derived from arteries that vascularize specific parts of the brain (eg, MCA for lentiform nuclei CO; posterior cerebral artery for Th and occipital lobe). These techniques have poor intra- and interobserver reproducibility of the region of interest selection for AIF estimate, bolus dispersion effects, arterial signal intensity saturation,47 and geometric distortions.30 Others proposed automated AIF detection by using algorithms based on the first gadolinium peak detection to automatically select the best possible AIF in the whole brain.45 This detection method is sensitive to noise or partial volume effect and can yield biased AIF,46 especially in case of arterial diseases such as brain AVMs.19
AIF location does affect the CBV and CBF results because of the different vasculatures of the analyzed capillary voxels (eg, CO voxels by the anterior part of the circle of Willis; Th voxels by the posterior part of the circle of Willis). In healthy subjects, there are minor differences in AIF estimates depending on the arterial region that is considered, but these differences may become more pronounced in high-flow diseases such as brain arteriovenous shunts (Table 4). AIF estimates from high-flow arterial regions may also sometimes be affected by aliasing (rapid MR signal-intensity variations,19), which yields incorrect AIF integral. Avoiding such aliasing is possible by using a low-pass filter to average high-flow and low-flow arterial time curves. In patients with brain arteriovenous shunts, spatial partial volume effect alters both arterial and capillary compartments, mixing arterial and capillary signals and capillary and venous signals. Venous artifacts, which are few in normal conditions, may sometimes affect quantitative measurements,19 especially in venous locations in patients with brain arteriovenous shunts (eg, insula, lateral fissure, or even cerebral cortex near cortical veins). These locations are also affected by magnetic susceptibility effects and correspond to transition areas (brain-bone-air in frontal sinuses or the petrous apex of the temporal bone).
In our study, we paid special attention to avoid PWI measurement sites aliased by magnetic susceptibility artifacts, as well as the venous partial volume effect from abnormal arteriovenous shunt veins. We tried to correct for several known pitfalls of the AIF estimation. AIF and Cm(t) gamma fittings were always successful in patients and volunteers, suggesting that brain arteriovenous shunt high-flow arteries may have a hemodynamic PWI model similar to the one used in the regular gamma fitting model (combination of power and exponential functions), even if these AIFs were sometimes slightly altered by high-frequency noise in patients, especially when the AIF location was close to the nidus. We tried to improve the aliasing correction in patients with brain arteriovenous shunts by using new AIF estimation methods we called “regional scaled” and “global” methods. The 2 other methods we investigated (local and regional) are already widely used in PWI computations.17 The regional, regional scaled, and global AIF estimation methods correspond to different trade-offs for AIF estimate: The global method corrects for arterial aliasing in patients with brain arteriovenous shunts by rescaling AIF to the maximal gadolinium concentration and by averaging all arterial voxels but does not account for the location of the region to be analyzed. The regional method estimates PWI results based on the vasculature near the region to be analyzed but is more affected by aliasing. The regional scaled method is an attempt to homogenize the arterial flow by rescaling (to better reflect the whole brain arterial flow in patients with brain hypervascular disease in decreasing aliasing), while still accounting for the regional vasculature.
The aim of our study was to assess different AIF estimation methods, each attempting to correct for 1 or several of the previously detailed pitfalls in patients with high-flow diseases. Paired t tests performed on PWI results among the different AIF estimation methods found significant differences between the AIF estimates, mostly in CBV (and few CBF) values, especially between local and regional scaled and between regional and regional scaled methods in volunteers and patients, but not between local and regional methods. Because all AIF estimations methods derive from each other, this result was expected, but determining the most accurate among these AIF estimation methods is made especially difficult because of the lack of gold standard. The no gold standard analysis method is explicitly dedicated to evaluation in the absence of a gold standard and uses multiple sets of measurements to determine which is the most accurate, assuming all measurements are linearly related with the unknown true values to be estimated. It also assumes that the unknown true values follow a beta distribution of unknown parameters. Given these 2 assumptions, the no gold standard method maximizes the likelihood of the data to determine the parameter of the linear and beta models. No gold standard has been reported to correctly classify methods with gaussian and also with nongaussian (beta) distributions.21 Because we found that the PWI measurement distributions in our patients with brain hypervascular disease had a beta pattern distribution in each of the 4 AIF estimation methods, we consequently stated that no gold standard may be used in patients with brain hypervascular disease.
No gold standard analysis demonstrated that there is no estimation method that works best on healthy and diseased subjects. This finding is expected. Indeed, the AIF estimation method that would work best for healthy patients with homogeneous CBF within the brain does not have to be the same as the one that works best for patients for whom CBF may vary greatly in different brain regions. It is perfectly conceivable to plan by using different AIF estimation methods, depending on whether the subject is suspected of having no perfusion abnormalities or is known to have such abnormalities. Difficulties arise rather from the fact that the optimal AIF estimation method may also depend on the type of brain AVMs (3 types in our study—namely AVM, proliferative angiopathies, and Moya Moya). Indeed, it is likely that the optimal AIF estimation method, which would yield the most accurate CBF and CBV values, can be different depending on the location of the abnormality and on the type of abnormal vasculature. Further investigations are needed to determine the AIF estimation method to be recommended as a function of the type of perfusion abnormality. Overall however, the regional and/or the regional scaled methods appear to be the best trade-off both in normal and diseased subjects. This conclusion is probably because this method keeps the anatomic correspondence between AIF location and analyzed capillary voxels and, in the case of the regional scaled method, decreases the AIF aliasing by minimizing the bolus dispersion and the arterial signal-intensity saturation (because of rescaling, but does not correct for geometric distortions and partial volume effect). Whether the resulting CBF and CBV are also closer to the unknown true values would have to be confirmed however, but there is no straightforward method to do so.
In volunteers, no gold standard results found the regional method to be the most accurate in CBV parameters and the regional scaled in CBF parameters. There is a slight difference between theses 2 methods (only an arterial scaling factor), which tend to decrease the aliasing of the AIF estimate. CBF computations are affected by aliasing because of our fast Fourier transformation deconvolution algorithm (equation 9). In decreasing arterial aliasing, the regional scaled method provides fewer noisy results, thus better estimates of the CBF both in Th and CO locations.
In brain arteriovenous shunts, regional vasculature may be highly affected by aliasing in high-flow arteries and shunt areas. This seems to be more critical in Th locations for both CBV and CBF estimations in patients, as suggested by the no gold standard results. There are more small arteries in Th vasculature than in CO, and these arteries are closer to the AIF reference location (region of interest drawn over the MCA or PCA). Therefore, in high-flow diseases, these arteries are more affected by high-flow aliasing than CO arteries, and the regional scaled and the global methods seem to be the most appropriate to correct for this aliasing. Unfortunately, the global method always yielded the poorest results in volunteers regardless of the estimated parameter (CBV and CBF) and the measurement location (Th or CO), probably because this method did not make use of the actual location of the region to be analyzed to derive an appropriate AIF. However, by averaging all arterial voxels detected in the brain, the AIF estimate was less affected by aliasing from the high-flow arteries and brain arteriovenous shunts, but anatomic correspondence between AIF location and analyzed capillary voxels was lost. Our results suggest that the global method also yielded the poorest results in patients (except for CBF parameter in Th locations). The global method, therefore, does not seem to be appropriate in general, unlike the regional and regional scaled methods, which account for the actual location of the region to be analyzed in the AIF estimation.
The local method, which is widely used for PWI studies in stroke, tumors, and brain AVMs,19 has been studied but does not appear to be appropriate for PWI analysis purposes in a brain arteriovenous shunt because this method does not take into account the anatomic arterial priors.
Regarding PWI abnormalities, we showed that the method used to estimate the AIF involved in CBV and CBF calculations could actually strongly affect the detection and identification of abnormalities remote from the nidus (in Th or CO). These variations were mainly due to the AIF shape and peak, both related to the AIF region of interest location. Variations were obvious in the global method, in which patients had more hypo- and fewer hyperperfused areas in CO and more hypo- and hyperperfused areas in Th. In that case, AIF estimations (from region of interest area located on the MCA) had higher peaks and wider AIF curves, contrary to the AIF estimates derived from the regional scaled method, in which the scaling factor changed the Th PWI results with increased numbers of hypoperfused and venous congestion areas. It is, therefore, not necessarily reliable to try to relate patient clinical symptoms and PWI abnormalities by using data from either local, regional, or regional scaled methods alone. The regional method yielded a number of normal PWI measurements (42% in Th, 15% in CO, overall 94% of patients had abnormal PWI measurements either in Th or in CO or both) close to those found in previous reports.1, 5, 9, 19 However, there is a discrepancy between the regional and the regional scaled method in Th locations regarding the diagnosis of hypoperfused and normal areas. This suggests that brain arteriovenous shunt PWI results must be interpreted with caution by using both methods and knowing the limitations of each of them.
Conclusion
Brain hypervascular diseases are complex high-flow diseases that induce acute and chronic hemodynamic disturbances near and remote from the nidus. We investigated various AIF estimation methods in both normal volunteers and patients with brain hypervascular disease to determine which was most appropriate for accurate characterization of brain perfusion. We found that the detection of PWI abnormality highly depends on the AIF estimation method. Regional and regional scaled AIF estimation methods appear to yield the most accurate CBV and CBF estimates in both normal volunteers and patients and in gray and white matter.
References
- 1.Fink GR. Effects of cerebral angiomas on perifocal and remote tissue: a multivariate positron emission tomography study. Stroke 1992;23:1099–105 [DOI] [PubMed] [Google Scholar]
- 2.Young WL, Pile-Spellman J, Prohovnik I, et al. Evidence for adaptive autoregulatory displacement in hypotensive cortical territories adjacent to AVMs: Columbia University AVS Study Project. Neurosurgery 1994;34:601–11 [DOI] [PubMed] [Google Scholar]
- 3.Hacein-Bey L, Nour R, Pile-Spellman J, et al. Adaptive changes of autoregulation in chronic cerebral hypotension with AVMs: an acetazolamide-enhanced single-photon emission CT study. AJNR Am J Neuroradiol 1995;16:1865–74 [PMC free article] [PubMed] [Google Scholar]
- 4.Leblanc E, Meyer E, Zatorre R, et al. Functional PET scanning in the preoperative assessment of cerebral AVMs. Stereotact Funct Neurosurg 1995;65:60–64 [DOI] [PubMed] [Google Scholar]
- 5.Kader A, Young WL. The effects of intracranial AVMs on cerebral hemodynamics. Neurosurg Clin N Am 1996;7:767–81 [PubMed] [Google Scholar]
- 6.Charbel FT, Hoffman WE, Misra M, et al. Increased brain tissue oxygenation during AVM resection. Neurol Med Chir (Tokyo) 1998;38(suppl):171–76 [DOI] [PubMed] [Google Scholar]
- 7.Meyer B, Schaller C, Frenkel C, et al. Physiological steal around AVSs of the brain is not equivalent to cortical ischemia. Neurol Res 1998;20(suppl 1):S13–17 [DOI] [PubMed] [Google Scholar]
- 8.Meyer B, Schaller C, Frenkel C, et al. Distributions of local oxygen saturation and its response to changes of mean arterial blood pressure in the cerebral cortex adjacent to AVMs. Stroke 1999;30:2623–30 [DOI] [PubMed] [Google Scholar]
- 9.Fukuda Y, Murata Y, Umehara I, et al. Perfusion and blood pool scintigraphy for diagnosing soft-tissue AVMs. Clin Nucl Med 1999;24:232–34 [DOI] [PubMed] [Google Scholar]
- 10.Lasjaunias P. Brain arteriovenous malformations. In: Lasjaunias P, Berenstein L, Ter Brugge K. Surgical Neuroangiography. Vol.1 . Heidelberg, Germany: Springer-Verlag;2002. :14–22 [Google Scholar]
- 11.Lassen NA. Cerebral transit of an intravascular tracer may allow measurement of regional blood volume but not regional blood flow. J Cereb Blood Flow Metab 1984;4:633–34 [DOI] [PubMed] [Google Scholar]
- 12.Nyberg G, Andersson J, Antoni G, et al. Activation PET scanning in pretreatment evaluation of patients with cerebral tumours or vascular lesions in or close to the sensorimotor cortex. Acta Neurochir (Wien) 1996;138:684–94 [DOI] [PubMed] [Google Scholar]
- 13.Schmidt KC, Turkheimer FE. Kinetic modeling in positron emission tomography. Q J Nucl Med 2002;46:70–85 [PubMed] [Google Scholar]
- 14.Neumann-Haefelin T, Wittsack HJ, Wenserski F, et al. Diffusion- and perfusion-weighted MRI: The DWI/PWI mismatch region in acute stroke. Stroke 1999;30:1591–97 [DOI] [PubMed] [Google Scholar]
- 15.Knopp EA, Cha S, Johnson G, et al. Glial neoplasm: dynamic contrast-enhanced T2*-weighted MR imaging. Radiology 1999;211:791–98 [DOI] [PubMed] [Google Scholar]
- 16.Meier P, Zierler LL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol 1954;6:731–44 [DOI] [PubMed] [Google Scholar]
- 17.Ostergaard L, Weisskoff RM, Chesler DA, et al. High-resolution measurement of cerebral blood flow using intravascular bolus passages. Part I. Mathematical approach and statistical analysis. Magn Res Med 1996;36:715–25 [DOI] [PubMed] [Google Scholar]
- 18.Sakaki T, Tsujimoto S, Nishitani M, et al. Perfusion pressure breakthrough threshold of cerebral autoregulation in the chronically ischemic brain: an experimental study in cats. J Neurosurg 1992;76:478—85 [DOI] [PubMed] [Google Scholar]
- 19.Ducreux D, Lasjaunias P, Meder JF, et al. MR perfusion imaging findings in proliferative angiopathies. Neuroradiology 2004;46:105–12 [DOI] [PubMed] [Google Scholar]
- 20.Hoppin JW, Kupinski MA, Kastis GA, et al. Objective comparison of quantitative imaging modalities without the use of a gold standard. IEEE Trans Med Imaging 2002;21:441–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kupinski MA, Hoppin JW, Clarkson E, et al. Estimation in medical imaging without a gold standard. Acad Radiol 2002;9:290–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Villringer A, Rosen BR, Belliveau JW, et al. Dynamic imaging with lanthanide chelates in normal brain: contrast due to magnetic susceptibility effect. Magn Res Med 1988;6:164–74 [DOI] [PubMed] [Google Scholar]
- 23.Boxerman JL, Hamberg LM, Rosen BR, et al. MR contrast due to intravascular magnetic susceptibility perturbations. Magn Res Med 1995;34:555–66 [DOI] [PubMed] [Google Scholar]
- 24.Kennan RP, Zhong J, Gore JC. Intravascular susceptibility contrast mechanism in tissues. Magn Res Med 1994;31:9–21 [DOI] [PubMed] [Google Scholar]
- 25.Smith AM, Grandin CB, Duprez T, et al. Whole-brain quantitative CBF, CBV, and MTT measurements using MRI bolus-tracking: implementation and application to data acquired from hyperacute stroke patients. J Magn Reson Imaging 2000;12:400–10 [DOI] [PubMed] [Google Scholar]
- 26.Weisskoff RM, Zuo CS, Boxerman JL, et al. Microscopic susceptibility variation and transverse relaxation: theory and experiment. Magn Res Med 1994;31:601–10 [DOI] [PubMed] [Google Scholar]
- 27.Lassen NA, Perl W. Tracer Kinetic Methods in Medical Physiology. New York: Raven;1979. :156–75
- 28.Fisel CR, Ackerman JL, Buxton RB, et al. MR contrast due to microscopically heterogeneous magnetic susceptibility: numerical simulations and applications to cerebral physiology. Magn Res Med 1991;17:336–47 [DOI] [PubMed] [Google Scholar]
- 29.Rosen BR, Belliveau JW, Buchbinder BR, et al. Contrast agent and cerebral hemodynamics. Magn Res Med 1991;19:285–92 [DOI] [PubMed] [Google Scholar]
- 30.Kiselev VG. On the theoretical basis of perfusion measurements by dynamic susceptibility contrast MRI. Magn Reson Med. 2001;46:1113–22 [DOI] [PubMed] [Google Scholar]
- 31.Grandin CB, Smith AM, Cosnard G. Quantification of brain perfusion with bolus-tracking MR imaging: comparison of gradient-echo and spin-echo sequences. ESMRMB. Sevilla 1999;MAGMA 1999;8(suppl 1) ;32 [Google Scholar]
- 32.Marquart DW. An algorithm for least squares estimation of non-linear parameters. J Soc Industr Appl Math 1963;11:431–41 [Google Scholar]
- 33.Starmer CF, Clarck DO. Computer computations of cardiac output using the gamma-function. J Appl Physiol 1970;28:219–20 [DOI] [PubMed] [Google Scholar]
- 34.Rempp KA, Brix B, Wenz F, et al. Quantification of regional cerebral blood flow and volume with dynamic susceptibility contrast-enhanced MR imaging. Radiology 1994;193:637–41 [DOI] [PubMed] [Google Scholar]
- 35.Smith AM, Grandin CB, Duprez T, et al. Whole-brain quantitative CBF and CBV measurements using MRI bolus tracking: comparison of methodologies. Magn Reson Med 2000;43:559–64 [DOI] [PubMed] [Google Scholar]
- 36.Axel L. Cerebral blood flow determination by rapid-sequence computed tomography. Radiology 1980;137:679–86 [DOI] [PubMed] [Google Scholar]
- 37.Calamante F, Thomas DL, Pell GS, et al. Measuring cerebral blood flow using magnetic resonance techniques. J Cereb Blood Flow Metab 1999;19:701–35 [DOI] [PubMed] [Google Scholar]
- 38.Wirestam R, Andersson L, Ostergaard L, et al. Measurements of rCBF using dynamic susceptibility contrast MRI: comparison of different deconvolution techniques and different locations of the arterial input function: Proceedings of the ISMRM, Philadelphia, Proliferative Angiopathies. 605, May 1999
- 39.Wirestam R, Andersson L, Ostergaard L, et al. Assessment of regional cerebral blood flow by dynamic susceptibility contrast MRI using different deconvolution techniques. Magn Reson Med 2000;43:691–700 [DOI] [PubMed] [Google Scholar]
- 40.Willinsky R, Terbrugge K, Montanera W, et al. Venous congestion: an MR finding in dural AVMs with cortical venous drainage. AJNR Am J Neuroradiol 1994;15:1501–07 [PMC free article] [PubMed] [Google Scholar]
- 41.Mast H, Mohr JP, Osipov A, et al. “Steal” is an unestablished mechanism for the clinical presentation of cerebral AVMs. Stroke 1995;26:1215–20 [DOI] [PubMed] [Google Scholar]
- 42.Gao E, Young WL, Ornstein E, et al. A theoretical model of cerebral hemodynamics: application to the study of AVMs. J Cereb Blood Flow Metab 1997;17:905–18 [DOI] [PubMed] [Google Scholar]
- 43.Hagen T, Bartylla K, Piepgras U. Correlation of regional cerebral blood flow measured by stable xenon CT and perfusion MRI. J Comp Assist Tomogr 1999;23:257–64 [DOI] [PubMed] [Google Scholar]
- 44.Rausch M, Scheffler K, Rudin M, et al. Analysis of input functions from different arterial branches with gamma variate functions and cluster analysis for quantitative blood volume measurements. Magn Reson Imaging 2000;18:1235–43 [DOI] [PubMed] [Google Scholar]
- 45.Murase K, Kikuchi K, Mike H, et al. Determination of arterial input function using fuzzy clustering for quantification of cerebral blood flow with dynamic susceptibility contrast-enhanced MR imaging. J Magn Reson Imaging 2001;13:797–806 [DOI] [PubMed] [Google Scholar]
- 46.Van Osch MJ, Vonken EP, Bakker CJ, et al. Correcting partial volume artifacts of the arterial input function in quantitative cerebral perfusion MRI. Magn Reson Med 2001;45:477–85 [DOI] [PubMed] [Google Scholar]
- 47.Ellinger R, Kremser C, Schocke MF, et al. The impact of peak saturation of the arterial input function on quantitative evaluation of dynamic susceptibility contrast-enhanced MR studies. J Comput Assist Tomogr. 2000;24:942–48 [DOI] [PubMed] [Google Scholar]