Volume Measurement of Intracranial Aneurysms from 3D Rotational Angiography: Improvement of Accuracy by Gradient Edge Detection

Abstract

Summary: Manual volume measurement of intracranial aneurysms from 3D rotational angiography varies on different threshold settings and, therefore, is operator-dependent. We developed and validated a method based on automatic gradient edge detection that is independent on threshold settings and provides an accurate and reproducible volume measurement. This method was compared with manual volume calculation in 13 aneurysm phantoms, and the results were significantly more accurate.

3D rotational angiography is increasingly used to evaluate the anatomy of cerebral aneurysms and for treatment planning. Moreover, the 3D dataset can be used to calculate aneurysm volume with machine-based software. Thresholding the 3D data generated by rotational angiography is a commonly used method to define the contours of vessels and aneurysms. A threshold value, based on visual criteria and the histogram of the dataset, is selected by the user to obtain a subjective acceptable image. Threshold setting is operator-dependent: a range of different threshold settings may provide the user a subjective acceptable image of the vessels and the aneurysm (Fig 1 and Fig 2A, -B).

Fig 1.

3D angiographic image of a posterior communicating artery aneurysm in 3 different manual threshold settings. All 3 images are visually acceptable to delineate vessel and aneurysm anatomy.

A, Low-threshold setting: not all small vessels are visible. After segmentation of the aneurysm, the calculated volume is 179 mm³ (D).

B, Intermediate-threshold setting: better visualization of small vessels. After segmentation of the aneurysm, the calculated volume is 207 mm³ (E).

C, High-threshold setting: exaggerated visibility of small vessels. After segmentation of the aneurysm, the calculated volume is 266 mm³ (F).

Fig 2.

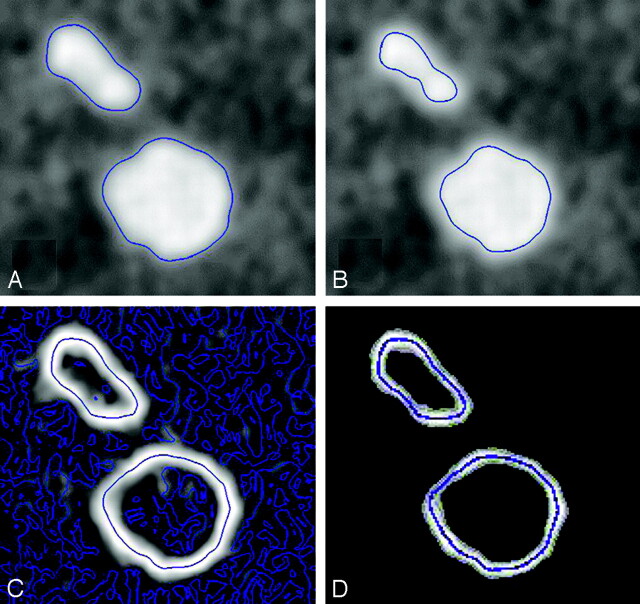
Two-dimensional illustration in a cut plane of the 3D dataset. The blue lines represent the contours in the cut plane of a blood vessel (ellipsoid) and an aneurysm (circle).

A, -B, Manual thresholding: different threshold levels change the contours of the vessel and the aneurysm.

Gradient-edge detection: voxels with high gradient values are white and voxels with low gradient values are black. In homogeneous parts of the volume, some gradient differences are present, caused by image noise (C). After the small gradient differences are filtered, the contours are unchanged (D).

The computer considers voxels with values higher than the threshold value within the vessel or aneurysm and voxels with values lower than the threshold value outside the vessel or aneurysm. The interface between voxels with values above and below the threshold value is represented by an isosurface. This isosurface defines the contour of the vessels and aneurysm. After manual segmentation of the aneurysm from the parent artery and surrounding vessels, the volume is calculated as the sum of all voxels within the segmented contour. Because the contour of the aneurysm varies with different threshold settings, the calculated volume varies accordingly. Thus, volume measurements based on manual subjective threshold settings are likely to be inaccurate. We developed and validated a method to calculate volumes of aneurysms from 3D datasets that is independent of threshold settings and provides an accurate calculation. We compared this method with the manual threshold method.

Materials and Methods

Phantoms

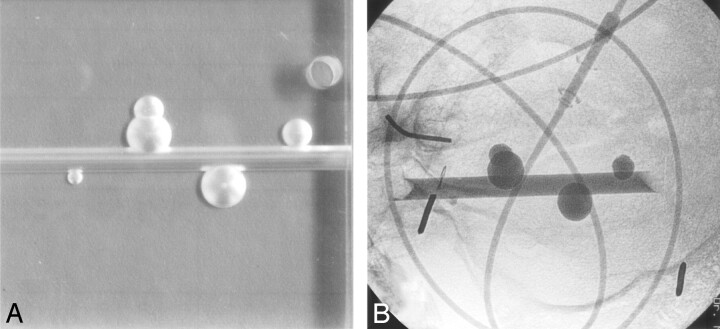
For the purpose of this study, 13 aneurysm phantoms of different shapes and sizes were made. Seven phantoms were detachable latex microballoons (Goldvalve, Nycomed, Paris, France) that were filled with a contrast agent (Omnipaque 300, Nycomed, Paris, France). The volume of the contrast agent inside the balloons was calculated by weighing the balloon before and after filling. Subtracting both magnitudes resulted in the weight of the contrast agent, and dividing this weight by the density provided the volume of the contrast agent. The other 6 phantoms were constructed as single- or double-truncated spheric aneurysms attached to a cylindric vessel in Perspex (Fig 3A). A computerized drill was used with a perfect spheric tip with known dimensions and known displacement during drilling. Volumes of the phantoms were calculated with simple geometry formulas. The effective diameters (diameter of a sphere with the same volume) of the phantoms ranged between 2.9 and 12.5 mm.

Fig 3.

A, Four aneurysm phantoms on a parent artery in different shapes and sizes in Perspex.

B, Radiograph of aneurysm phantoms filled with contrast material in a human skull placed in a water-filled bucket. Injection lines filled with contrast material simulate blood vessels.

The phantoms were placed inside a human skull in a water-filled plastic bucket. A flexible 76-cm injection line filled with contrast agent was placed inside the skull adjacent to the phantoms to mimic surrounding vessels (Fig 3B). 3D rotational imaging with a 17-cm image intensifier was performed on a biplane angiographic system (Integris V3000, Philips Medical Systems, Best, the Netherlands). A magnification of 33% of the initial 3D reconstruction volume was made in a matrix of 256³. Voxels were cubic with sizes between 0.2 and 0.5 mm.

Manual Volume Calculation

The volumes of the 13 phantoms were calculated by manual threshold setting as described in the introduction. In the magnification of the 3D reconstruction, one of us (M.J.S.) selected a threshold setting that subjectively provided the image that was thought to represent the phantom and surrounding phantom vessels best. The Perspex phantoms were subsequently segmented from the parent vessel. The volume of the phantoms was calculated by using the machine software (3DRA workstation, Philips Medical Systems, Best, the Netherlands).

Gradient Edge Detection

In the gradient edge detection method, the edge of a blood vessel or aneurysm is defined as the isosurface of voxels for which the gradient magnitude is maximal (1). The gradient of a given voxel in the volume represents the magnitude of variation of the value of this voxel and the values of its surrounding voxels. Voxels with low gradient values correspond to homogeneous locations in the volume. Voxels with high gradient values correspond to locations where the voxel values in the vicinity of this location differ largely, such as at the interfaces between contrast-filled blood vessels with high voxel values and the surrounding structures with low voxel values. The computer generates gradient values for every voxel in the 3D dataset. The isosurface of voxels with maximum gradients in the volume represents the contours of the blood vessels. In homogeneous parts of the volume, some gradient differences are present, caused by image noise. These small gradient differences are easily filtered out, leaving the voxels with the maximal gradients in the 3D dataset (Fig 2C, -D). These voxels with the maximal gradients have fixed locations in the dataset that are independent of the threshold setting. This means that with every threshold setting, the same contours of the vessels and aneurysm are delineated by the gradients and volume calculations are constant and reproducible.

Results

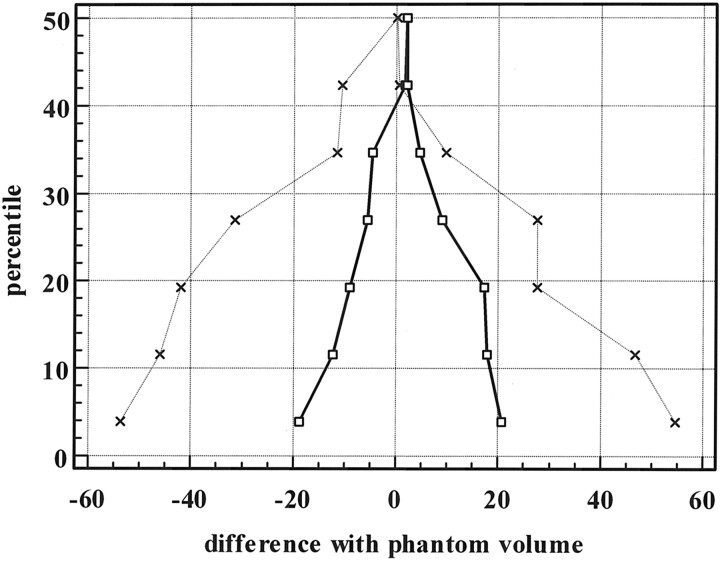
The percentage of error against the calculated phantom volumes of the 2 methods of volume measurements is displayed in Fig 4. From this figure, it is obvious that the measurement error is larger in small aneurysms for both methods and error distribution is not normal. Comparison of the 2 methods was performed by creating Bland-Altman plots (2) for both methods (MedCalc statistical software, Mariakerke, Belgium). In this graphic method, the differences (or alternatively the ratios) between the 2 methods are plotted against the averages of the 2 methods. The method with the mean difference closest to zero and the more narrow range of expected differences is the more accurate method. The mean difference and range of expected differences for the gradient edge detection method were 0.98 and 0.26 and, for the manual threshold method, 1.12 and 0.91. Differences of mean and range of expected differences as a percentage of averages were −2.7 and 27.4 for the gradient edge detection method and 9.5 and 76.7 for the manual threshold method. In Fig 5, the results are displayed in a mountain plot. These results indicate that the gradient edge detection method is more accurate than the manual threshold method.

Fig 4.

Graphic display of errors in volume measurement of 13 aneurysm phantoms with the manual threshold method and the gradient edge detection method.

Fig 5.

Mountain plot of percentile for each ranked difference from the phantom volumes for the gradient edge detection method and the manual threshold method. Dotted line indicates manual threshold method; solid line, the gradient edge detection method.

Discussion

We found that volume measurement from 3D rotational angiographic datasets based on automatic gradient edge detection is significantly more accurate than volume measurement after subjective manual thresholding. With gradient edge detection, contours of vessels and aneurysm are defined by voxels with a fixed location in the 3D dataset and, therefore, are not operator-dependent. Accurate volume measurement of cerebral aneurysms is important because aneurysm volume is increasingly used in the assessment of packing attenuation in coiled aneurysms to predict stability of the coil mesh with time (3–7). Also in the comparison of different types of coils, accurate aneurysm volume measurement is important (8). Accurate assessment of aneurysm volume may also be needed for the safe and effective use of materials that will soon be available for clinical application. These include liquid materials with physical characteristics that change once they are placed into an aneurysm and coils that combine a metal or polymer with a radioactive source or pharmaceutic agent. Volume measurements will be needed to determine the amount of liquid material needed for complete treatment.

In conclusion, volume measurement based on automatic gradient edge detection is accurate and is superior to methods that are dependent on manual subjective threshold settings.