Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 28;8(2):418–423. doi: 10.1021/acsphotonics.0c01442

Tunable s-SNOM for Nanoscale Infrared Optical Measurement of Electronic Properties of Bilayer Graphene

Konstantin G Wirth †,*, Heiko Linnenbank ‡,§, Tobias Steinle ‡,§, Luca Banszerus ∥, Eike Icking ∥, Christoph Stampfer ∥,⊥, Harald Giessen ‡,§, Thomas Taubner †,⊥
PMCID: PMC7976599  PMID: 33763503

Abstract

graphic file with name ph0c01442_0004.jpg

Here we directly probe the electronic properties of bilayer graphene using s-SNOM measurements with a broadly tunable laser source over the energy range from 0.3 to 0.54 eV. We tune an OPO/OPA system around the interband resonance of Bernal stacked bilayer graphene (BLG) and extract amplitude and phase of the scattered light. This enables us to retrieve and reconstruct the complex optical conductivity resonance in BLG around 0.39 eV with nanoscale resolution. Our technique opens the door toward nanoscopic noncontact measurements of the electronic properties in complex hybrid 2D and van der Waals material systems, where scanning tunneling spectroscopy cannot access the decisive layers.

Keywords: near-field microscopy, s-SNOM, bilayer graphene, infrared spectroscopy

The stacking and rotation of individual graphene layers leads to changes in its band structure,1−3 for example, in bi- or trilayer graphene or twisted bilayer graphene. This opens up intriguing new physical properties, including, for example, topological protected states4,5 or unconventional superconductivity, with the latter being recently reported for twisted bilayer graphene.6

Local probing of these electronic properties at the scale of individual flakes or even the moiré super lattice7−10 is usually done by scanning tunneling microscopy (STM), which requires electrical contact. Optical measurements, such as infrared absorption spectroscopy or Raman scattering, also work for noncontacted and encapsulated samples, but these techniques lack the resolution desired for the investigation of nanostructures due to the diffraction limit. Furthermore, the interpretation of Raman spectra becomes more challenging with an increasing number of layers.

The diffraction limit in resolution and the need for electrical contacts can be overcome by employing infrared scattering-type scanning near-field optical microscopy (s-SNOM). s-SNOM uses light scattering at a sharp tip to optically record samples’ properties. The lateral resolution is determined by the radius of the tip apex. Thus, a lateral resolution down to 20 nm can be achieved at infrared frequencies.11

With the help of s-SNOM, propagating surface plasmon polaritons (SPPs) and surface phonon polaritons have been imaged in 2D materials such as graphene12−16 and hexagonal boron nitride (hBN)17−19 at photon energies of below 0.2 eV. Furthermore, polariton-based contrast mechanisms are exploited to image multilayer graphene.20 The real-space imaging of polaritons allows to indirectly investigate the optical properties of graphene at submicron scale, by extracting the wave vector from the retrieved wave patterns. As polaritons only exist at frequencies below the plasma frequency, it is not possible to extract the electronic properties in the range above the plasma frequency by polariton imaging. Whereas direct probing of the conductivity resonance of multilayer graphene (MLG) over a broad spectral range has not been performed with s-SNOM so far, mainly due to the lack of tunable light sources.

Here we extend the approach of direct optical probing of the electronic properties of bilayer graphene (BLG) by deploying a commercially available tunable OPO/OPA laser source in s-SNOM, which can be continuously tuned between 0.27 and 0.9 eV. We show first results on sequential near-field spectroscopy on BLG around its interband resonance,1 paving the way for a future in-depth analysis of the electronic properties of stacked and twisted few-layer graphene and other van der Waals materials.

When going from monolayer to bilayer graphene the change of the band structure manifests itself in an absorptive resonance at 0.37 eV,1 as depicted in Figure 1b. This behavior was first observed in far-field infrared spectroscopy by Mak et al. by deploying a synchrotron as broadband infrared radiation source and an FTIR spectrometer.1 In this type of measurment (Figure 1a) the optical absorbance is directly proportional to the optical conductivity σ.21

Figure 1.

Figure 1

Open in a new tab

(a) Sketch of a far-field IR measurement at few-layer graphene (FLG) used to obtain the spectra of monolayer and bilayer graphene in (b). The plot is adapted from Mak et al.1 Insets show the bandstructure in single and BLG, which gives rise to the conductivity resonance at around 0.37 eV. (c) Schematic of the s-SNOM measurement with a tunable OPO laser used in this work. The tip oscillates at a frequency Ω. It is illuminated by the tunable laser and scatters the light. (d) Estimated s-SNOM near-field amplitude (S3/S3(SiO2)) and phase (φ3 – φ3 (SiO2)) contrasts for BLG on SiO2/Si are depicted in the plot.

The conductivity peak at 0.37 eV can be qualitatively explained by the band structure of BLG.1 Electrons in BLG can be described by a pair of hyperbolic bands. The conduction and valence bands are split in pairs of two. The upper valence and the lower conduction band touch at the K-point. The other two bands are separated by the interlayer coupling strength of γ1 ∼ 0.37 eV and can be described by the tight-binding model.1 The possible transitions from upper valence or lower conduction band to the upper conduction band (inset, Figure 1b) manifest themselves in a peak in the optical absorption.22 These transitions correspond to the peak in the absorption in Figure 1b and the calculated phase signal in s-SNOM in Figure 1d. For higher photon energies, the graphene layers become decoupled and the two layers of BLG will approach a conductivity of two times the universal conductivity/absorption of monolayer graphene.

In Figure 1c, the principle of measurement of the optical conductivity with s-SNOM is depicted. s-SNOM records the optical near-field scattering amplitude and phase at a certain laser frequency, by lock-in detection of the light scattered from an AFM tip at higher harmonics (here, third harmonic) of the tip oscillation frequency. The amplitude and phase of the scattered light can be accessed with the help of the pseudoheterodyne phase-modulation.23 Since the amplitude and the phase of the scattered light are related to the complex optical conductivity or permittivity respectively, they can in principle be reconstructed from the measurement. This method allows for the differentiation between several stacking order of graphene such as rhombohedral and Bernal stacked trilayer graphene24 and Bernal and non-Bernal stacked BLG.25 Furthermore, previous studies addressed the contrast between a monolayer and Bernal stacked BLG on top of a Si/SiO2 substrate with the point dipole model.25 At the single IR frequency of a HeNe-Laser of 0.366 eV these predictions could also be experimentally verified.

Here, we use theoretical literature data to predict the expected spectroscopic contrast in s-SNOM with an extended version of the finite dipole model26,27 and a transfer matrix model for graphene.28 With the transfer matrix model the reflection of the air/BLG/SiO2/Si layerstack is calculated, which allows us to estimate the expected scattering phase and amplitude of BLG in s-SNOM measurements (Figure 1d). Based on the literature data from Kim et al.,24 a resonance in the phase at around 0.4 eV and a derivative line shape in amplitude are obtained. Further details about the calculation and the approximations made can be found in the Supporting Information.

Set up and Sample Preparation

To survey the conductivity resonance in BLG, we use a commercially available s-SNOM (NeaSNOM, neaspec GmbH) with pseudoheterodyne detection and a LN2 cooled InSb detector (Infrared Associates) in order to record phase and amplitude data simultaneously. The previously inaccessible spectral range is accessed with a tunable short pulse OPO/OPA laser system, capable of addressing the relevant energy range from 0.27 to 0.9 eV. The laser system has a pulse duration of 0.5–1 ps and a repetition rate of 42 MHz. This provides a resolution of 6 meV and a shot noise limited performance above 300 kHz, leading to a very stable and spectrally defined excitation. Furthermore, the repetition rate is well above the tapping frequency of the AFM tip (250 kHz) and is clearly separated from the demodulation frequencies. Our sample consists of a multilayer graphene (MLG) flake deposited on top of 90 nm SiO2 on Si. On this flake single (SLG), bi- and trilayer (TLG) regions can be identified. We perform sequential spectroscopy at fixed wavelengths in the region, where SLG and BLG can be identified, by recording amplitude and phase resolved near-field images on larger areas of this flake. Also, Raman spectra have been acquired to verify the Bernal stacking of the BLG region.

Results

To show that a difference in the s-SNOM signal is observable at different photon energies beyond the surface plasmon polariton regime of multilayer graphene, we map the near-field contrast on BLG with SLG and TLG next to it (Figure 2). Figure 2a shows an optical light microcopy image of the MLG flake investigated in our experiments. In the middle of the flake there is a stripe of SLG with adjacent BLG on top and bottom. On the left and right side of the flake is the SiO2 substrate. At the left top of the flake, also a small region of TLG can be identified. The bottom panel of Figure 2a shows the integrated Raman scattered intensity around the 2D peak at 2690 cm–1, verifying the mentioned graphene stackings above. In order to confirm that the two adjacent regions to the SLG are in fact Bernal-stacked BLG, we use the distinct Raman fingerprint of BLG (spectra in SI, section B). All s-SNOM amplitude S3 and phase φ3 images in Figure 2 are normalized to the values obtained on the SiO2 substrate. The images in Figure 2b–d are recorded at three different photon energies of 0.282, 0.39, and 0.5 eV, respectively. These photon energies correspond to energies below, close to and above the expected conductivity resonance in BLG. In all three phase images a distinct contrast between the BLG and the SLG regions can be identified. Interestingly, an inversion of the phase contrast between BLG and SLG occurs between 0.282 and 0.39 eV hinting toward a large relative change of the optical conductivity of BLG with respect to SLG in this regime. In the phase contrast in Figure 2c, a distinct trend in the phase from top to bottom can be observed. This is due to a piezo drift in the pseudo heterodyne module of the s-SNOM. At these short wavelength, a piezo drift will have a larger influence compared to s-SNOM at wavelengths of the CO2 laser.

Figure 2.

Figure 2

Open in a new tab

(a) Light microscope image of the few-layer graphene flake and Raman map around the 2D-peak (details in SI). (b–d) Infrared s-SNOM amplitude s(ω) (top row) and phase φ(ω) (bottom row): images taken at three different photon energies of (b) 0.282, (c) 0.390, and (d) 0.5 eV. The images are referenced to the signal on the SiO2 substrate on the left and were recorded with a different tip than the reference spectra in Figure 3. Note that the color bars of the phase are asymmetric. The scale bars correspond to 4 μm each.

A strong amplitude contrast is observable for BLG toward SLG and the surrounding SiO2 substrate at the lower energies. This contrast vanishes toward the 0.500 eV. Meanwhile the phase contrast of BLG shows a maximum around 0.39 eV which is close to the expected conductivity resonance. At higher energies the phase contrast decreases again, but a distinct contrast between BLG and the surrounding SLG and SiO2 is still observable. This hints toward an association between the real part of the optical conductivity, which is proportional to the optical absorption21 and the s-SNOM phase.

Besides the BLG and SLG regions, a small area of TLG can be identified on the top left of the flake. This region shows a strong contrast in amplitude and phase toward the BLG at 0.282 eV. The amplitude and phase contrast almost vanishes at 0.39 eV and slightly reappears at 0.5 eV.

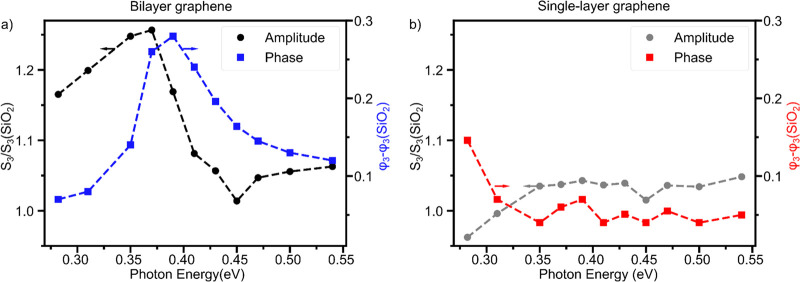
To quantitatively map the conductivity resonance, we performed s-SNOM imaging over the boundary between the substrate and the MLG, in the region where BLG and SLG are present (see SI, Figure S4). The spectra presented in Figure 3a,b are achieved by extracting the spatially averaged third demodulation order amplitude (S3) and phase (φ3) signals at BLG, SLG, and the SiO2 substrate in the respective area.

Figure 3.

Figure 3

Open in a new tab

Spatially averaged third demodulation order normalized amplitude and phase contrast of BLG/SiO2 in (a) and SLG/SiO2 in (b). The respective contrast is normalized with respect to SiO2. An inversion of the phase contrast between SLG and BLG happens around 0.31 eV. The data sets were recorded with a different tip than the images in Figure 2. The positon of the recorded images, from which the data points were extracted can be found in the SI (Figure S4).

The spectra for SLG do not show distinct features in our investigated energy range. At 0.282 eV the phase of SLG shows the largest contrast to SiO2 and the phase contrast decreases for higher energies toward a value of 0.05 rad, while the amplitude contrast increases toward 1.05. Larger amplitudes and phase contrasts at lower energies stem from Drude-like contributions of free charge carriers. As previously stated, this asymptotic behavior of amplitude and phase contrast at higher energies is due to the constant absorption of SLG at high energies, resulting in a nonvanishing, but constant, contrast.

The BLG spectra shows much richer features, in both amplitude and phase, compared to SLG. For small energies the amplitude contrast is larger compared to SLG and resembles the shape of the imaginary part of the optical conductivity of BLG. The increase in the amplitude contrast between 0.282 and 0.39 eV for BLG is approximately the same as with SLG. However, at the expected conductivity resonance of 0.39 eV, the BLG amplitude contrast shows a pronounced derivative line shape and the amplitude contrast decreases for higher energies toward that of SLG.

The phase contrast of BLG to the substrate shows a pronounced peak around 0.39 eV with a steep flank on the left and a flatter flank on the right. This behavior is very similar to the real part of the optical conductivity of BLG. For higher energies, the phase contrasts are higher than for lower energies and φ3(0.54 eV) = 0.12 rad more than twice that of SLG. The conductivity of SLG approaches largely photon energy independent values for energies above 1 eV.1,21 The conductivity is approximately σSLG ≈ πe2/2h for a single layer of graphene. For BLG this will result in an approximately constant conductivity of 2σSLG at energies well above the conductivity resonance, which explains the nonvanishing phase contrast between SLG/BLG and the SiO2 substrate. Another very interesting point is the inversion of the phase contrast between 0.282 and 0.31 eV, which was also observed in Figure 2b,c. This shows that the phase inversion is independent of the tip. However, the exact position of the inversion might vary with the tip. The observed s-SNOM contrast of BLG resembles the qualitative behavior of the calculated spectrum in Figure 1d well, where we used literature data for the complex conductivities for estimating the s-SNOM response.

The quantitative amplitude and phase contrast is highly tip dependent (see Figure S1). Deviations between measurement and calculation in amplitude and phase could stem from unintentional doping.21 The amplitude and phase contrast are sensitive to the Fermi level, while the phase contrasts shows greater variations with changes of the Fermi level.24 A further limit of state-of-the-art calculations originates in the description of the tip–sample coupling. Notably, in our calculations the finite momentum transfer of the tip is not taken into account in the optical conductivities. However, all of this will not alter the qualitative behavior of the s-SNOM contrasts around the resonance.24

Conclusion and Outlook

We have shown a direct s-SNOM measurement of the complex optical conductivity resonance in BLG around 0.39 eV with nanoscale resolution by introducing a new tunable OPO/OPA laser source. This combination allows for the spatially resolved mapping of electronic and optical properties of few-layer graphene at nanometer resolution. Our work paves the way for a detailed investigation of the IR-conductivity properties and the mapping of the specific resonance in various stacking orders. Even the local IR-conductivity properties of twisted graphene and Moiré-pattern can be investigated by extending the energy range beyond the accessible range of SPPs. By combining this technique with low-temperature s-SNOM, even superconductivity phenomena in magic-angle graphene at IR frequencies could be investigated. In contrast to STS, the optical probing does not require an electrical contact, thus, it will be applicable to stacked 2D materials with insulating or encapsulating layers on top, as required for high mobility graphene.30 This is due to the subsurface imaging capability of s-SNOM, as the probing optical fields can couple through thin dielectric layers.17,31 With improved theoretical modeling, including the tip–sample coupling, a local quantification of the complex optical conductivity will become possible.

Overall, this new imaging modality could lead to a paradigm shift in s-SNOM imaging of 2D materials: While the previously used polariton imaging relies on an indirect extraction of the electronic properties from the modeling of the plasmon polariton reflection, we can now perform a direct extraction of electronic properties. Our technique opens the door toward nanoscopic noncontact measurements of the electronic properties in complex hybrid 2D and van der Waals material systems where tunneling spectroscopy cannot access the decisive layers.

Acknowledgments

This work was supported by the Excellence Initiative of the German federal and state governments, the Ministry of Innovation of North Rhine-Westphalia, the Deutsche Forschungsgemeinschaft (SFB 917 “Nanoswitches”, SPP1839 “Tailored Disorder”, and SPP1391 “Ultrafast Nanooptics”), the European Research Council (ERC Advanced Grant Complexplas, ERC Consolidator Grant 2D4QT), Bundesministerium für Bildung und Forschung, Carl-Zeiss Stiftung, and Baden-Württemberg Stiftung.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c01442.

  • Section A: Figure S1, Comparison of the expected near field contrast for different in-plane wavevectors; Figure S2, Comparison of the expected near field contrast for real and imaginary part and amplitude and phase; Figure S3/Section B: Light microscope and Raman spectra of the MLG flake; Section C: Influence of the spectral width on pseudo heterodyne detection; Figure S4/Section D: AFM image of the MLG flake (PDF)

The authors declare the following competing financial interest(s): H. Linnenbank, T. Steinle, and H. Giessen are co-founders of SI Stuttgart Instruments GmbH, a company producing the OPO/OPA laser system such as the one used in this study. The other authors declare no conflict of interests.

Supplementary Material

ph0c01442_si_001.pdf (503.7KB, pdf)

References

  1. Mak K. F.; Sfeir M. Y.; Misewich J. A.; Heinz T. F. The Evolution of Electronic Structure in Few-Layer Graphene Revealed by Optical Spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 2010, 107 (34), 14999–15004. 10.1073/pnas.1004595107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Mak K. F.; Shan J.; Heinz T. F. Seeing Many-Body Effects in Single- and Few-Layer Graphene: Observation of Two-Dimensional Saddle-Point Excitons. Phys. Rev. Lett. 2011, 106 (4), 046401. 10.1103/PhysRevLett.106.046401. [DOI] [PubMed] [Google Scholar]
  3. Lui C. H.; Li Z.; Mak K. F.; Cappelluti E.; Heinz T. F. Observation of an Electrically Tunable Band Gap in Trilayer Graphene. Nat. Phys. 2011, 7 (12), 944–947. 10.1038/nphys2102. [DOI] [Google Scholar]
  4. Ju L.; Shi Z.; Nair N.; Lv Y.; Jin C.; Velasco J.; Ojeda-Aristizabal C.; Bechtel H. A.; Martin M. C.; Zettl A.; Analytis J.; Wang F. Topological Valley Transport at Bilayer Graphene Domain Walls. Nature 2015, 520 (7549), 650–655. 10.1038/nature14364. [DOI] [PubMed] [Google Scholar]
  5. Jiang B.-Y.; Ni G.-X.; Addison Z.; Shi J. K.; Liu X.; Zhao S. Y. F.; Kim P.; Mele E. J.; Basov D. N.; Fogler M. M. Plasmon Reflections by Topological Electronic Boundaries in Bilayer Graphene. Nano Lett. 2017, 17 (11), 7080–7085. 10.1021/acs.nanolett.7b03816. [DOI] [PubMed] [Google Scholar]
  6. Cao Y.; Fatemi V.; Fang S.; Watanabe K.; Taniguchi T.; Kaxiras E.; Jarillo-Herrero P. Unconventional Superconductivity in Magic-Angle Graphene Superlattices. Nature 2018, 556 (7699), 43–50. 10.1038/nature26160. [DOI] [PubMed] [Google Scholar]
  7. Kerelsky A.; McGilly L. J.; Kennes D. M.; Xian L.; Yankowitz M.; Chen S.; Watanabe K.; Taniguchi T.; Hone J.; Dean C.; Rubio A.; Pasupathy A. N. Maximized Electron Interactions at the Magic Angle in Twisted Bilayer Graphene. Nature 2019, 572 (7767), 95–100. 10.1038/s41586-019-1431-9. [DOI] [PubMed] [Google Scholar]
  8. Xie Y.; Lian B.; Jäck B.; Liu X.; Chiu C.-L.; Watanabe K.; Taniguchi T.; Bernevig B. A.; Yazdani A. Spectroscopic Signatures of Many-Body Correlations in Magic-Angle Twisted Bilayer Graphene. Nature 2019, 572 (7767), 101–105. 10.1038/s41586-019-1422-x. [DOI] [PubMed] [Google Scholar]
  9. Jiang Y.; Lai X.; Watanabe K.; Taniguchi T.; Haule K.; Mao J.; Andrei E. Y. Charge Order and Broken Rotational Symmetry in Magic-Angle Twisted Bilayer Graphene. Nature 2019, 573 (7772), 91–95. 10.1038/s41586-019-1460-4. [DOI] [PubMed] [Google Scholar]
  10. Choi Y.; Kemmer J.; Peng Y.; Thomson A.; Arora H.; Polski R.; Zhang Y.; Ren H.; Alicea J.; Refael G.; von Oppen F.; Watanabe K.; Taniguchi T.; Nadj-Perge S. Electronic Correlations in Twisted Bilayer Graphene near the Magic Angle. Nat. Phys. 2019, 15 (11), 1174–1180. 10.1038/s41567-019-0606-5. [DOI] [Google Scholar]
  11. Huth F.; Govyadinov A.; Amarie S.; Nuansing W.; Keilmann F.; Hillenbrand R. Nano-FTIR Absorption Spectroscopy of Molecular Fingerprints at 20 Nm Spatial Resolution. Nano Lett. 2012, 12 (8), 3973–3978. 10.1021/nl301159v. [DOI] [PubMed] [Google Scholar]
  12. Fei Z.; Rodin A. S.; Andreev G. O.; Bao W.; McLeod A. S.; Wagner M.; Zhang L. M.; Zhao Z.; Thiemens M.; Dominguez G.; Fogler M. M.; Neto A. H. C.; Lau C. N.; Keilmann F.; Basov D. N. Gate-Tuning of Graphene Plasmons Revealed by Infrared Nano-Imaging. Nature 2012, 487 (7405), 82–85. 10.1038/nature11253. [DOI] [PubMed] [Google Scholar]
  13. Chen J.; Badioli M.; Alonso-González P.; Thongrattanasiri S.; Huth F.; Osmond J.; Spasenović M.; Centeno A.; Pesquera A.; Godignon P.; Zurutuza Elorza A.; Camara N.; de Abajo F. J. G.; Hillenbrand R.; Koppens F. H. L. Optical Nano-Imaging of Gate-Tunable Graphene Plasmons. Nature 2012, 487 (7405), 77–81. 10.1038/nature11254. [DOI] [PubMed] [Google Scholar]
  14. Jiang B.-Y.; Ni G. X.; Pan C.; Fei Z.; Cheng B.; Lau C. N.; Bockrath M.; Basov D. N.; Fogler M. M. Tunable Plasmonic Reflection by Bound 1D Electron States in a 2D Dirac Metal. Phys. Rev. Lett. 2016, 117 (8), 086801. 10.1103/PhysRevLett.117.086801. [DOI] [PubMed] [Google Scholar]
  15. Jiang L.; Shi Z.; Zeng B.; Wang S.; Kang J.-H.; Joshi T.; Jin C.; Ju L.; Kim J.; Lyu T.; Shen Y.-R.; Crommie M.; Gao H.-J.; Wang F. Soliton-Dependent Plasmon Reflection at Bilayer Graphene Domain Walls. Nat. Mater. 2016, 15 (8), 840–844. 10.1038/nmat4653. [DOI] [PubMed] [Google Scholar]
  16. Sunku S. S.; Ni G. X.; Jiang B. Y.; Yoo H.; Sternbach A.; McLeod A. S.; Stauber T.; Xiong L.; Taniguchi T.; Watanabe K.; Kim P.; Fogler M. M.; Basov D. N. Photonic Crystals for Nano-Light in Moiré Graphene Superlattices. Science 2018, 362 (6419), 1153–1156. 10.1126/science.aau5144. [DOI] [PubMed] [Google Scholar]
  17. Woessner A.; Lundeberg M. B.; Gao Y.; Principi A.; Alonso-González P.; Carrega M.; Watanabe K.; Taniguchi T.; Vignale G.; Polini M.; Hone J.; Hillenbrand R.; Koppens F. H. L. Highly Confined Low-Loss Plasmons in Graphene-Boron Nitride Heterostructures. Nat. Mater. 2015, 14 (4), 421–425. 10.1038/nmat4169. [DOI] [PubMed] [Google Scholar]
  18. Dai S.; Fei Z.; Ma Q.; Rodin A. S.; Wagner M.; McLeod A. S.; Liu M. K.; Gannett W.; Regan W.; Watanabe K.; Taniguchi T.; Thiemens M.; Dominguez G.; Neto A. H. C.; Zettl A.; Keilmann F.; Jarillo-Herrero P.; Fogler M. M.; Basov D. N. Tunable Phonon Polaritons in Atomically Thin van Der Waals Crystals of Boron Nitride. Science 2014, 343 (6175), 1125–1129. 10.1126/science.1246833. [DOI] [PubMed] [Google Scholar]
  19. Li P.; Lewin M.; Kretinin A. V.; Caldwell J. D.; Novoselov K. S.; Taniguchi T.; Watanabe K.; Gaussmann F.; Taubner T. Hyperbolic Phonon-Polaritons in Boron Nitride for near-Field Optical Imaging and Focusing. Nat. Commun. 2015, 6 (1), 7507. 10.1038/ncomms8507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Geisenhof F. R.; Winterer F.; Wakolbinger S.; Gokus T. D.; Durmaz Y. C.; Priesack D.; Lenz J.; Keilmann F.; Watanabe K.; Taniguchi T.; Guerrero-Avilés R.; Pelc M.; Ayuela A.; Weitz R. T. Anisotropic Strain-Induced Soliton Movement Changes Stacking Order and Band Structure of Graphene Multilayers: Implications for Charge Transport. ACS Appl. Nano Mater. 2019, 2 (9), 6067–6075. 10.1021/acsanm.9b01603. [DOI] [Google Scholar]
  21. Mak K. F.; Sfeir M. Y.; Wu Y.; Lui C. H.; Misewich J. A.; Heinz T. F. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101 (19), 196405. 10.1103/PhysRevLett.101.196405. [DOI] [PubMed] [Google Scholar]
  22. Zhang Y.; Tang T.-T.; Girit C.; Hao Z.; Martin M. C.; Zettl A.; Crommie M. F.; Shen Y. R.; Wang F. Direct Observation of a Widely Tunable Bandgap in Bilayer Graphene. Nature 2009, 459 (7248), 820–823. 10.1038/nature08105. [DOI] [PubMed] [Google Scholar]
  23. Ocelic N.; Huber A.; Hillenbrand R. Pseudoheterodyne Detection for Background-Free near-Field Spectroscopy. Appl. Phys. Lett. 2006, 89 (10), 101124. 10.1063/1.2348781. [DOI] [Google Scholar]
  24. Kim D.-S.; Kwon H.; Nikitin A. Y.; Ahn S.; Martín-Moreno L.; García-Vidal F. J.; Ryu S.; Min H.; Kim Z. H. Stacking Structures of Few-Layer Graphene Revealed by Phase-Sensitive Infrared Nanoscopy. ACS Nano 2015, 9 (7), 6765–6773. 10.1021/acsnano.5b02813. [DOI] [PubMed] [Google Scholar]
  25. Jeong G.; Choi B.; Kim D.-S.; Ahn S.; Park B.; Kang J. H.; Min H.; Hong B. H.; Kim Z. H. Mapping of Bernal and Non-Bernal Stacking Domains in Bilayer Graphene Using Infrared Nanoscopy. Nanoscale 2017, 9 (12), 4191–4195. 10.1039/C7NR00713B. [DOI] [PubMed] [Google Scholar]
  26. Cvitkovic A.; Ocelic N.; Hillenbrand R. Analytical Model for Quantitative Prediction of Material Contrasts in Scattering-Type near-Field Optical Microscopy. Opt. Express 2007, 15 (14), 8550. 10.1364/OE.15.008550. [DOI] [PubMed] [Google Scholar]
  27. Hauer B.; Engelhardt A. P.; Taubner T. Quasi-Analytical Model for Scattering Infrared near-Field Microscopy on Layered Systems. Opt. Express 2012, 20 (12), 13173–13188. 10.1364/OE.20.013173. [DOI] [PubMed] [Google Scholar]
  28. Zhan T.; Shi X.; Dai Y.; Liu X.; Zi J. Transfer Matrix Method for Optics in Graphene Layers. J. Phys.: Condens. Matter 2013, 25 (21), 215301. 10.1088/0953-8984/25/21/215301. [DOI] [PubMed] [Google Scholar]
  29. Banszerus L.; Sohier T.; Epping A.; Winkler F.; Libisch F.; Haupt F.; Watanabe K.; Taniguchi T.; Müller-Caspary K.; Marzari N.; Mauri F.; Beschoten B.; Stampfer C. Extraordinary High Room-Temperature Carrier Mobility in Graphene-WSe2 Heterostructures. arXiv:1909.09523 [cond-mat] 2019, na. [Google Scholar]
  30. Jung L.; Pries J.; Maß T. W. W.; Lewin M.; Boyuk D. S.; Mohabir A. T.; Filler M. A.; Wuttig M.; Taubner T. Quantification of Carrier Density Gradients along Axially Doped Silicon Nanowires Using Infrared Nanoscopy. ACS Photonics 2019, 6 (7), 1744–1754. 10.1021/acsphotonics.9b00466. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ph0c01442_si_001.pdf (503.7KB, pdf)

Articles from ACS Photonics are provided here courtesy of American Chemical Society

RESOURCES