Diffusion-Tensor MR Imaging of Gray and White Matter Development during Normal Human Brain Maturation

Abstract

BACKGROUND AND PURPOSE: Conventional MR imaging findings of human brain development are thought to result from decreasing water content, increasing macromolecular concentration, and myelination. We use diffusion-tensor MR imaging to test theoretical models that incorporate hypotheses regarding how these maturational processes influence water diffusion in developing gray and white matter.

METHODS: Experimental data were derived from diffusion-tensor imaging of 167 participants, ages 31 gestational weeks to 11 postnatal years. An isotropic diffusion model was applied to the gray matter of the basal ganglia and thalamus. A model that assumes changes in the magnitude of diffusion while maintaining cylindrically symmetric anisotropy was applied to the white matter of the corpus callosum and internal capsule. Deviations of the diffusion tensor from the ideal model predictions, due to measurement noise, were estimated by using Monte Carlo simulations.

RESULTS: Developing gray matter of the basal ganglia and developing white matter of the internal capsule and corpus callosum largely conformed to theory, with only small departures from model predictions in older children. However, data from the thalamus substantially diverged from predicted values, with progressively larger deviations from the model with increasing participant age.

CONCLUSION: Changes in water diffusion during maturation of central gray and white matter structures can largely be explained by theoretical models incorporating simple assumptions regarding the influence of brain water content and myelination, although deviations from theory increase as the brain matures. Diffusion-tensor MR imaging is a powerful method for studying the process of brain development, with both scientific and clinical applications.

MR imaging has become a routine clinical tool for the assessment of brain maturation in children. The signal intensity changes on T1- and T2-weighted images during brain development have been attributed to decreases in brain water content and increases in the concentration of macromolecules such as myelin (1). These maturational processes also cause alterations in brain water diffusion that can be analyzed quantitatively with diffusion-tensor MR imaging.

Diffusion-tensor imaging characterizes the 3D spatial distribution of water diffusion in each MR imaging voxel (2–4). Geometrically, the diffusion tensor describes an ellipsoid in space, and the size, shape, and orientation of the ellipsoid are given by the eigenvalues and eigenvectors of the tensor. The eigenvalues specify the rate of diffusion along each of the three orthogonal axes of the diffusion ellipsoid. These have also been referred to as the principal diffusivities. Each eigenvalue is associated with an eigenvector that specifies its direction in space. The mean of the eigenvalues, denoted as D̄, is a measure of the spatially averaged magnitude of water diffusion (3). The coefficient of variation of the eigenvalues, denoted as Aσ, is a measure of the spatial anisotropy of water diffusion (3, 5). D̄, Aσ, and the three eigenvalues are all rotationally invariant, and hence are not affected by changes in head tilt within the magnet bore or by variation in the orientation of white matter fibers. Within the range of diffusion-weighting factors (b values) used in the experiment, the diffusion tensor and its rotationally invariant scalar metrics reflect only tissue properties and are largely independent of other MR acquisition parameters.

Diffusion-tensor imaging studies of neonates (6, 7) and children during the first decade of life (8) have shown that D̄ decreases with age in both gray and white matter, and that Aσ increases with age, especially in white matter. The presumed mechanisms of these maturational changes in water diffusivity are a decrease in brain water content; the formation of new barriers to water mobility, such as cell membranes associated with the outgrowth of axons and dendrites as well as glial processes; and white matter myelination.

In this study, we report the age-dependent magnitudes of the three diffusion tensor eigenvalues during normal human brain development, derived from previously published diffusion-tensor imaging studies of 14 preterm and term neonates (7) and 153 children ages 1 day to 11 years (8). We use these experimentally measured eigenvalues to test theoretical models of water diffusion in gray and white matter of the maturing human brain. The theoretical models incorporate simple assumptions regarding how each of the aforementioned maturational processes affects brain water motion. These models are used to predict the age-dependent magnitudes of the diffusion tensor eigenvalues in developing gray and white matter, thereby determining the 3D spatial distribution of water diffusion in these tissues. The correspondence between theory and experiment shows how well human brain maturation can be understood in terms of these underlying biologic processes.

Methods

Experimental Data Acquisition

Experimental data were obtained from previously published diffusion-tensor imaging studies of brain maturation in 14 preterm and term neonates of estimated gestational ages 31 to 41 weeks (7) and 153 children of postnatal ages 1 day to 11 years (8). All MR imaging examinations were performed on 1.5-T imagers (Magnetom Vision; Siemens, Erlangen, Germany) by using circularly polarized RF coils. The diffusion-tensor imaging protocol consisted of a single shot multisection spin-echo echo-planar pulse sequence, acquired with 3000/106 (TR/TE) in the neonate study and with 3000/97.4 in the childhood study. Four tetrahedrally oriented diffusion-weighted images, three orthogonally oriented diffusion-weighted images, and a reference T2-weighted image were obtained at each transverse section. In the tetrahedral directions, the b value was 800 s/mm² for the neonate study and 1012.4 s/mm² for the childhood study. In the orthogonal directions, b = 340 s/mm² for the neonate study and b = 337.5 s/mm² for the childhood study. Five-millimeter-thick contiguous transverse sections covering the brain were acquired with a 15 × 24 cm field of view and a 96 × 128 voxel matrix in the neonate study. Five-millimeter transverse sections, with a 1-mm gap between sections, were acquired with a 24 × 24 cm field of view and a 96 × 128 voxel matrix, interpolated to a 192 × 256 pixel matrix, in the childhood study. All images were realigned in 2D by using a combination of intra- and cross-technique affine realignment procedures to correct for image displacements and linear stretch or shear due to eddy currents (5).

Diffusion Tensor Image Analysis

For each pixel, the elements of the diffusion tensor were derived from this combination of tetrahedral and perpendicular diffusion measurements (5). In the childhood study, the reference T2-weighted image (b = 0 s/mm²), also known as the I₀ image, was not included in the diffusion tensor calculations because of the presence of artifact in some studies that arose from spurious free induction decay signal intensity (8). Further details of how the six unique elements of the diffusion tensor can be determined from the tetrahedral-orthogonal encoding technique, in the absence of an I₀ image, are presented in the Appendix. The three eigenvalues of the diffusion tensor, and their mean value D̄, were computed (3, 5). The maximum, intermediate, and minimum eigenvalues are denoted λ_max, λ_int, and λ_min, respectively. D̄ and the three diffusion tensor eigenvalues all have units of mm²/s. Illustrative images of λ_max, λ_int, and λ_min were prepared by using Photoshop 6.0 (Adobe Systems Inc., San Jose, CA) to create montages and to adjust size, brightness, contrast, and orientation.

Regions of interest were defined on Aσ images and then transferred to the anatomically co-registered λ_max, λ_int, λ_min, and D̄ images in each patient study. Regions of interest were placed bilaterally in three gray and two white matter structures on a single transverse section through the level of the basal ganglia (Fig 1). The two white matter regions were the posterior limb of the internal capsule and the splenium of the corpus callosum. These white matter structures were chosen because they exhibit visible diffusion anisotropy in neonates and are thus easily identified on Aσ images throughout the age range examined in this study. The three gray matter regions were the head of the caudate nucleus, the lentiform nucleus (comprising the putamen and the globus pallidus), and the thalamus. The selected gray matter regions are located adjacent to the white matter regions of interest and can therefore be localized by using the white matter tracts as landmarks. Data from six participants were excluded because of image artifacts.

Fig 1.

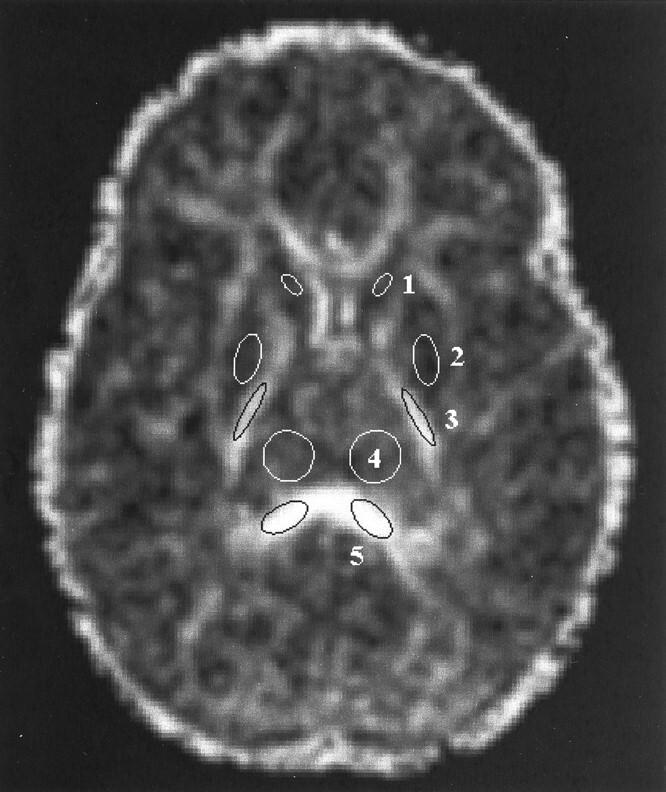
Region of interest placement is illustrated on a transverse diffusion anisotropy (Aσ) image obtained through the level of the basal ganglia in a 1-year-old child. Diffusion anisotropy is computed from a single shot echo-planar diffusion-tensor sequence: 3000/97.4/1 (TR/TE/number of excitations), using four tetrahedrally oriented diffusion gradients (b = 1012.4 s/mm²) and three orthogonally oriented diffusion gradients (b = 337.5 s/mm²). Regions of interest in gray matter are marked as white ellipses, and regions of interest in white matter are marked as black ellipses. Values from the left and right regions of interest were averaged. 1, head of the caudate nucleus; 2, lentiform nucleus; 3, posterior limb of the internal capsule; 4, thalamus; 5, splenium of the corpus callosum.

The mean pixel values of λ_max, λ_int, λ_min, and D̄ were computed in each region of interest for each participant. Values obtained from the left and right regions of interest for each structure were averaged. In the lentiform nucleus, the region of interest data from one participant was based only on the right-sided region because of the presence of image artifact in the left-sided region. For seven participants, values of λ_min for the splenium of the corpus callosum were less than zero. Although negative eigenvalues are not physically possible, these data were retained because their deviation from the true positive value could be explained by measurement noise. Results of the Monte Carlo simulations described below also produced a few negative values of λ_min for the splenium of the corpus callosum above a certain threshold of measurement noise.

Graphs of D̄ versus postconceptional age in all five regions were empirically fit with biexponential regression by using Levenberg-Marquardt least-squares minimization (8). Postconceptional age is estimated gestational age at birth plus postnatal age. Expressing participant age from the time of conception allows data from the premature neonates to be directly compared with those from the term neonates and children. Because estimated gestational ages were not available from the medical records of the participants in the childhood diffusion-tensor imaging study, their gestational ages at birth were assumed to be 40 weeks for the purpose of calculating postconceptional ages. Because most of the participants in the childhood study were many months to years of postnatal age, only small deviations from the true postconceptional age would result from pre- or post-term birth in a few participants. Because the percentage magnitude of these errors would be in most cases much less than those inherent in estimating gestational age in neonates, they are considered negligible.

Signal Intensity to Noise Ratio Measurements

Twenty of the 153 participants in the childhood study were selected for further analysis to determine the signal intensity to noise ratio (SNR) of the diffusion-tensor imaging experiments. Ten of the 20 participants were younger than 2 postnatal years, and the other 10 were older than 2 postnatal years. Participants were chosen to allow a relatively uniform sampling of the age distribution within both of the age ranges. The younger than 2 postnatal year age range was more closely sampled than the older than 2 postnatal year age range, because the largest changes in T2 relaxation times and in D̄ during postnatal life occur during the first 2 years (8, 9); therefore, the largest changes in the SNR would also be expected during that time period.

For these 20 examinations, the noise level was obtained from the SD of the pixel values in a region of interest defined in an air-filled region of the three orthogonal diffusion-weighted images obtained at b = 337.5 s/mm². The averaged noise level of the three images was used. The region of interest was placed so as to avoid any artifacts from motion or aliasing in the phase-encoding direction. The signal intensity in each of the five brain regions was calculated as the mean pixel value within that region, averaged over the three orthogonally oriented (b = 337.5 s/mm²) diffusion-weighted images. Because the I₀ images were not used to compute the diffusion tensor in the childhood study (Appendix), the orthogonal diffusion-weighted images were the highest SNR images in the examination. The SNR of each brain region was defined as the quotient of the mean signal intensity of the region of interest within the brain region and the noise in the region of interest outside the brain. Magnitude reconstruction of the original complex-valued MR image transforms gaussian noise to a Rayleigh distribution. To account for Rayleigh statistics, each SNR measurement was multiplied by 0.66. This procedure for estimating SNR has been used by other investigators (10–12).

SNR Modeling

Because both T2 relaxation times and D̄ decline during the first few years of life, the SNR of diffusion-weighted imaging can also be expected to decrease during that period. The signal intensity of diffusion-weighted imaging is given as:

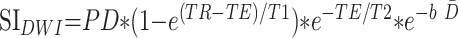1)

where PD is the proton density, b is the diffusion-weighting factor, and T1 and T2 are the longitudinal and transverse relaxation times, respectively. In a heavily T2-weighted single-shot acquisition, such as diffusion-weighted imaging, T1 effects are minimal. Age-dependent changes in proton density can also be considered negligible compared with the much larger contribution of changes in T2 and D̄. Hence, the equation for diffusion-weighted imaging signal intensity can be approximated as:

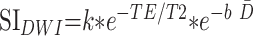2)

where k is a proportionality constant. The natural logarithm of the diffusion-weighted imaging signal intensity is then given as:

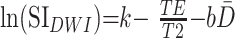3)

where k remains an arbitrary constant. The T2 relaxation times can be described as a monoexponential decay function of age (9):

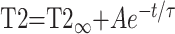4)

where t is the participant’s age, τ is the decay rate constant, A is the decay amplitude constant, and T2_∞ is the asymptotic (adult) value of T2 as t approaches infinity. D̄ can be described as a biexponential function of age (8):

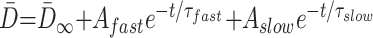5)

where D̄_∞ is a constant term that represents the asymptotic (adult) value of D̄ as t approaches infinity. τ_fast is the rapid decay constant and A_fast is the amplitude of the rapid exponential component, whereas τ_slow is the slow decay constant and A_slow is the amplitude of the slow exponential component. Substituting equations 4 and 5 into equation 3, we find that:

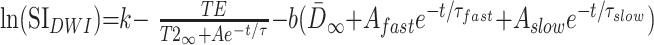6)

SNR for the diffusion-weighted image can then be expressed as:

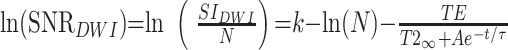7)

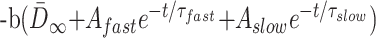where N is the experimental noise. If we assume that N is constant across all ages, then:

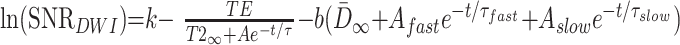8)

where k remains an arbitrary constant. This theoretical relationship between SNR and age was used to fit the experimentally derived curve with Levenberg-Marquart least squares minimization. The three free parameters of the fit were A, τ, and k. The values of D̄_∞, A_fast, A_slow, τ_fast, and τ_slow were derived from a biexponential fit of D̄ versus age in the region of interest (8). The TE of the diffusion-tensor imaging acquisition was 97.4. The value of T2_∞ was set at 65 ms (9). The value of b was 337.5 s/mm², because the orthogonal diffusion-weighted images were the highest SNR images used in the computation of the diffusion tensor in the childhood study (8). The fitted function of SNR versus postconceptional age was then provided as input to the Monte Carlo simulations described below for predicting the values of λ_max, λ_int, and λ_min at an SNR level appropriate for any given participant age. Data modeling and plots were produced with Origin 6.0 (Microcal Software, Inc., Northampton, MA).

Diffusion Models and Computer Simulations

A spherical (isotropic) diffusion model was assumed for developing gray matter. In this model, all three diffusion tensor eigenvalues are equal to each other, as well as to D̄, the mean of the three eigenvalues. In this special case, the spatial distribution of water diffusion is spherical and diffusion anisotropy is zero. Maturational changes in water diffusion are then completely accounted for by changes in D̄, the magnitude of isotropic diffusion. Monte Carlo computer simulations were performed to account for noise-induced sorting bias that causes deviations of experimentally determined diffusion tensor eigenvalues from their true values (4, 5, 10). The Monte Carlo analysis was performed by using custom software, with details provided elsewhere (5). For the spherical diffusion model of developing gray matter, the program accepts two parameters as input: the experimentally derived biexponential function describing the decay of D̄ with age in the gray matter region of interest (8) and the experimentally derived function describing the age-dependent SNR in the region of interest. The Monte Carlo simulation adds gaussian noise, produced with a random number generator, at a level prescribed by the input SNR. In the spherical diffusion model, the eigenvalues of the ideal diffusion tensor are all equal to the input D̄. The simulation then computes the signal intensities that would be observed in a tetrahedral-orthogonal diffusion-weighted acquisition given the underlying ideal diffusion tensor. Gaussian noise is then added to these signal intensities to mimic the effect of measurement noise. A new diffusion tensor accounting for the presence of measurement noise is then calculated from this combination of simulated tetrahedral and orthogonal diffusion-weighted signal intensities. This process was repeated 16,384 times for each 0.2-year interval during the entire 0- to 12-postconceptional year age range studied. This large number of repetitions is more than sufficient to give the expected statistical distribution of λ_max, λ_int, and λ_min in the region of interest at each participant age, given the SNR at that age.

A cylindrical diffusion model that allows for changes in both D̄ and cylindrically symmetric anisotropy was assumed for developing white matter. The change in D̄ accounts for the decrease in water content of white matter during maturation, whereas the change in cylindrically symmetric anisotropy accounts for the effect of progressive myelination. This formalism was tested with the diffusion tensor eigenvalues measured in the internal capsule and corpus callosum of the neonates and children. In keeping with the assumption of cylindrical symmetry, the two minor eigenvalues, λ_int and λ_min, are posited to be equal in magnitude, and both are assumed to be much less than the major eigenvalue, λ_max, which is not affected by myelination. Because D̄ is the mean of all three eigenvalues, the values of the two minor eigenvalues can be solved for by knowing the values of D̄ and λ_max:

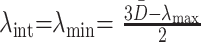9)

Monte Carlo simulations, such as those used in the gray matter spherical diffusion model, can account for departures of the two minor eigenvalues from their true values because of measurement noise. Therefore, there are three inputs to the white matter cylindrical diffusion model: the biexponential decay function describing the maturational decrease of λ_max, the biexponential decay function describing the maturational decrease in D̄ (8), and the function describing the maturational decrease in SNR (equation 8). The outputs of the model are the age-dependent values of the two minor eigenvalues. Implicit in this model is the assumption that the λ_max values are not also biased by measurement noise, because they are provided as input for the computer simulation. This is a reasonable assumption because the major eigenvalue is so much greater in magnitude than the minor eigenvalues in the white matter of the internal capsule and corpus callosum that there should be little or no overlap in their statistical distributions and therefore little or no sorting bias in the estimation of λ_max.

Results

Images of the three diffusion tensor eigenvalues, λ_max, λ_int, and λ_min, all showed decreases in magnitude with postnatal maturation throughout the brain, including both gray and white matter (Fig 2). The major eigenvalue λ_max showed less reduction with age in white matter than in gray matter. Therefore, white matter values of λ_max remained greater than gray matter values throughout the age range studied. This can be seen as white matter hyperintensity relative to gray matter in the λ_max images of Figure 2. In contradistinction, the two minor eigenvalues, λ_int and λ_min, showed greater reductions with age in white matter than in gray matter. This can be observed as reversal of gray-white matter contrast between the neonates and the older children in the λ_int and λ_min images of Figure 2. Most white matter regions in neonates are hyperintense to gray matter in the λ_int and λ_min images, but in the 6-year-old child, they have become hypointense to gray matter. The exceptions are those central white matter tracts that are already partially myelinated at birth, such as the posterior limb of the internal capsule and the splenium of the corpus callosum. These early maturing white matter regions already display hypointensity relative to gray matter in neonates, especially on the λ_min images (Fig 2).

Fig 2.

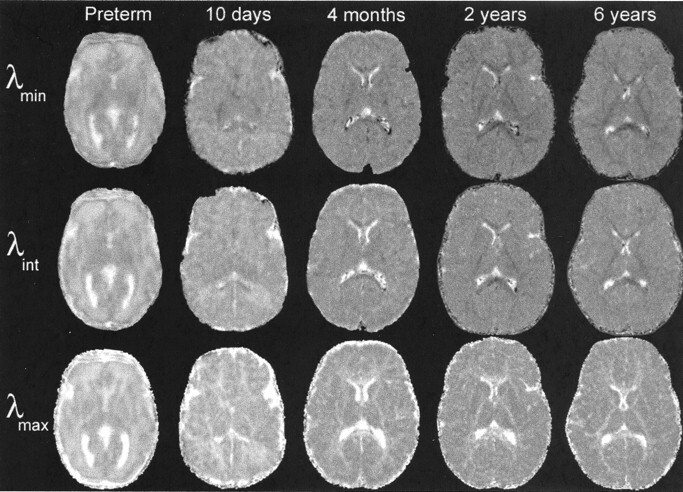
Decrease in the eigenvalues of the diffusion tensor during normal brain maturation is illustrated in five participants ranging in age from 31 gestational weeks (preterm) to 6 postnatal years. Diffusion-tensor imaging parameters are as in Figure 1, except for the preterm neonate, for whom the parameters were 3000/106/1 with four tetrahedrally oriented diffusion gradients (b = 800 s/mm²) and three orthogonally oriented diffusion gradients (b = 340 s/mm²). All images are transverse sections obtained at the level of the basal ganglia. All images are displayed with identical window and level settings to allow direct comparison of signal intensity across participants. The eigenvalues are rotationally invariant measures of the rate of water diffusion along each of the three principal axes of the diffusion tensor at each MR imaging voxel. λ_min (top row) is the eigenvalue with the smallest magnitude, λ_int (middle row) has intermediate values, and λ_max (bottom row) has the greatest magnitude.

Measurements of the noise in the diffusion-tensor imaging examinations showed no correlation with participant age (Fig. 3A), thereby confirming the assumption made in developing the mathematical relationship between the SNR of diffusion-tensor imaging and participant age. There was a steep decrease in SNR of almost 50% during the first 2 years of postnatal life in both white (Fig 3B) and gray (Fig 3C) matter. This age-dependent decrease in SNR was well described by equation 8. The proportion of the variance in SNR explained by the fit was 92% in the posterior limb of the internal capsule and 91% in the lentiform nucleus. The region with the highest SNR was the caudate nucleus, with an asymptotic value of 28.9, whereas the lowest SNR was found in the splenium of the corpus callosum, with an asymptotic SNR of 19.4. The asymptotic SNR was 24.3 in the posterior limb of the internal capsule, 26.0 in the thalamus, and 26.4 in the lentiform nucleus.

Fig 3.

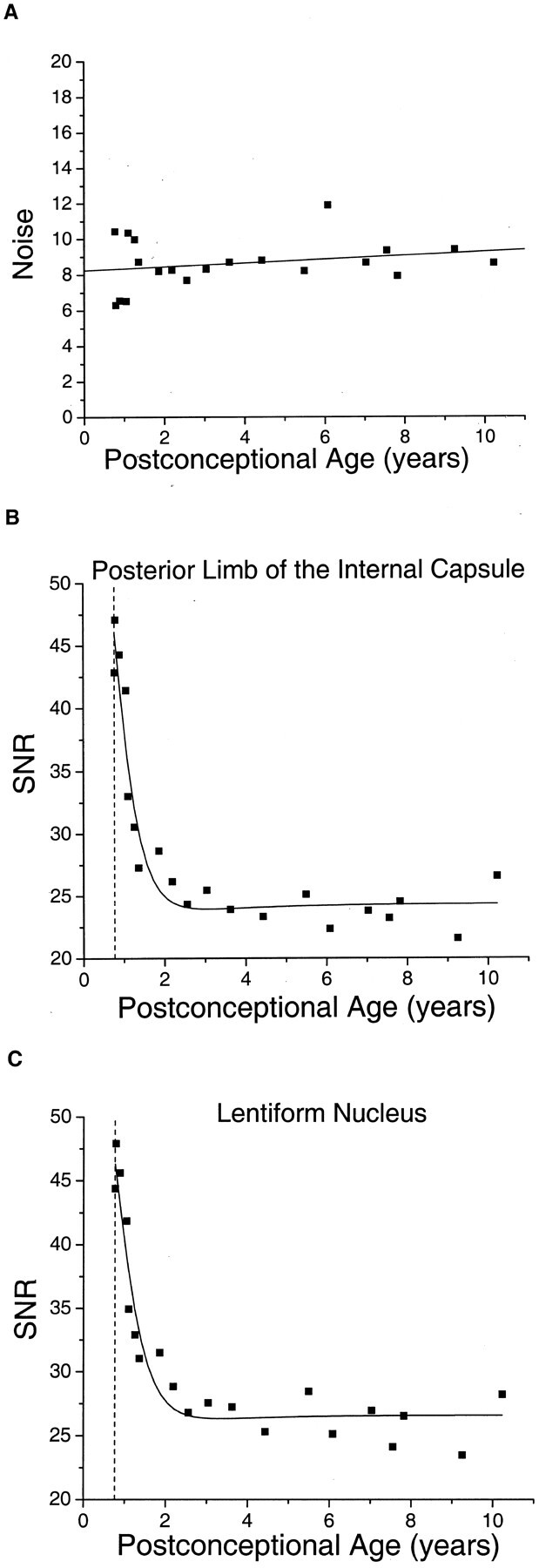
The signal-to-noise ratio of diffusion-tensor imaging decreases with brain maturation.

A, Noise in the diffusion-weighted images is age-independent. In 20 participants, the noise is calculated as the SD of pixel values in an air-filled region of interest outside the brain in the b = 337.5 s/mm² diffusion-weighted images (see Methods). The postconceptional age of each participant is the estimated gestational age added to the postnatal age. The data are fit with linear regression. The Pearson correlation coefficient of the noise with postconceptional age is 0.23, which is not statistically significant (P > .3).

B, SNR in diffusion-weighted imaging declines steeply during the first 2 years of postnatal life in the white matter of the posterior limb of the internal capsule. SNR is the quotient of signal intensity divided by noise. The signal intensity is obtained from regions of interest within the brain on b = 337.5 s/mm² diffusion-weighted images. The data are fit with a function (equation 8 in Methods) that defines the theoretical relationship between SNR and participant age. Vertical dashed line indicates the age of normal term birth: 40 gestational weeks.

C, SNR in diffusion-weighted imaging declines steeply during the first 2 years of postnatal life in the gray matter of the lentiform nucleus. Vertical dashed line indicates the age of normal term birth: 40 gestational weeks.

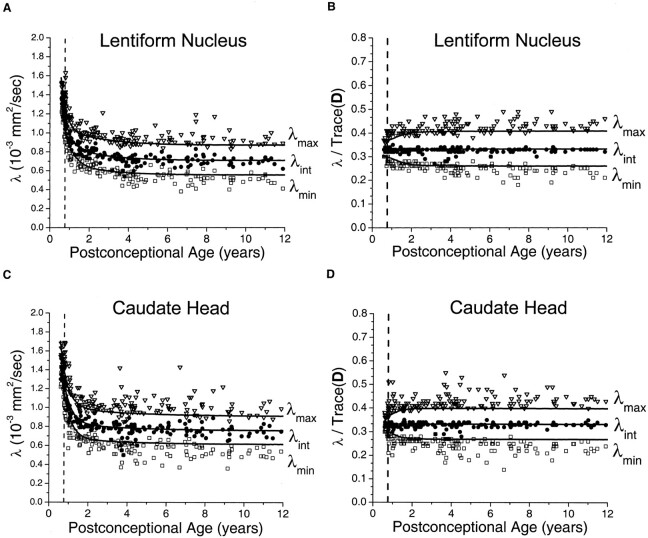
In the gray matter of the basal ganglia, large maturational decreases were observed in all three of the eigenvalues of the diffusion tensor (Fig 4). The steepest portion of the decline was seen before 2 postconceptional years, with a smaller more gradual decline after 2 years. There was very good correspondence between the age-varying magnitudes of the three diffusion tensor eigenvalues and the predictions of the spherical diffusion model. The agreement between theory and experiment was best for λ_int, which should not be affected by sorting bias in an isotropic system. In spherical (isotropic) diffusion, each of the three eigenvalues should account for one-third of the trace of the diffusion tensor, where Trace(D) is defined as the sum of the three eigenvalues. The measured values of λ_int fall very close to this ideal value in both the lentiform nucleus (Fig 4B) and the head of the caudate nucleus (Fig 4D). That there is no age dependence of λ_int after normalization by Trace(D) indicates that all of the age-dependent changes in λ_int are isotropic, with no residual anisotropy. Because of the effect of noise-induced sorting bias, measured values of λ_max are expected to be greater than this ideal proportion of one-third of the trace, and values of λ_min are expected to be smaller by the same amount. The magnitude of this overestimation of λ_max and underestimation of λ_min is inversely related to the SNR and can be predicted by Monte Carlo simulation. For λ_max and λ_min, there was excellent agreement between the experimental data and the results of Monte Carlo analysis in the neonates and younger children. Although λ_max/Trace(D) and λ_min/Trace(D) do show some age dependence in neonates and infants (Fig 4B and D), this is accounted for by changes in the SNR at these ages and does not reflect departures from isotropy. However, small departures from the simulated values of λ_max and λ_min were seen in the older children, with most values of λ_max being above the model prediction and most values of λ_min being below the model prediction.

Fig 4.

Maturational decreases of the three diffusion tensor eigenvalues (λ_max, λ_int, λ_min) in the gray matter of the lentiform nucleus and the gray matter of the head of the caudate nucleus for 161 participants of postconceptional ages 7 months to 12 years. Vertical dashed line indicates age of normal term birth: 40 gestational weeks. Solid lines through data are theoretical predictions for the age-varying values of λ_max (top line), λ_int (middle line), and λ_min (bottom line) from Monte Carlo simulation of a spherical diffusion model, to which the age-dependent parameters D̄ and SNR are given as input (see Methods for details of the theoretical model).

A, Gray matter of the lentiform nucleus. Values of λ_max (open inverted triangles), λ_int (closed circles), and λ_min (open squares) are in 10⁻³ mm²/s.

B, Gray matter of the lentiform nucleus. Each eigenvalue is expressed in terms of its fraction of the trace of the diffusion tensor Trace(D), where Trace(D) is the sum of the three eigenvalues.

C, Gray matter of the head of the caudate nucleus. Values of λ_max (open inverted triangles), λ_int (closed circles), and λ_min (open squares) are in 10⁻³ mm²/s.

D, Gray matter of the head of the caudate nucleus. Each eigenvalue is expressed in terms of its fraction of the trace of the diffusion tensor Trace(D), where Trace(D) is the sum of the three eigenvalues.

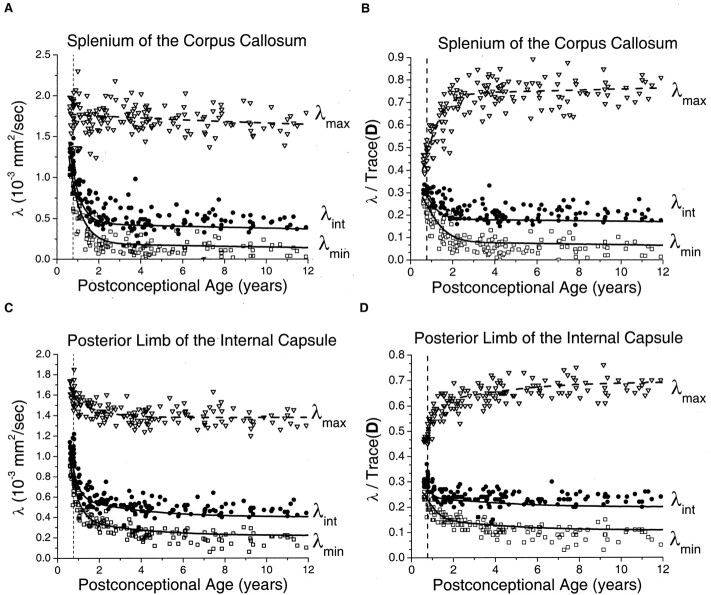
In the white matter of the internal capsule and corpus callosum, relatively small maturational decreases were seen in λ_max, with much larger declines in λ_int and λ_min (Fig 5). As in the gray matter regions, the decay was fastest during the first 2 postconceptional years and slower thereafter. Monte Carlo simulation of the effect of noise on λ_max showed virtually no difference between the simulated values and exponential regression of the experimental values. This indicated that sorting bias effects on λ_max were negligible at the SNR level of the experiment and provided justification for the use of the fitted values of λ_max as input to the cylindrical model for prediction of λ_int and λ_min. In the neonates and younger children, there was very good correspondence between the measured values of the two minor eigenvalues and the predictions of the Monte Carlo simulation based on the cylindrical diffusion model. Normalizing for isotropic effects by dividing the eigenvalues by Trace(D) did not eliminate the age dependence of the white matter eigenvalues (Fig 5B and D), as it did in the gray matter regions (Fig 4B and D). The residual age-related changes in the white matter eigenvalues after normalization reflect progressive myelination, which increases the contribution of λ_max to Trace(D) while reducing the contribution of λ_int and λ_min. The assumption of a cylindrically symmetric decrease in diffusion due to myelination means that both of the minor eigenvalues should be reduced by the same amount. Deviations of the measured values of λ_int and λ_min from the ideal of cylindrical symmetry were largely accounted for by noise bias as assessed by Monte Carlo simulation (Fig 5B and D). This noise bias causes overestimation of λ_int and underestimation of λ_min. However, divergence from the simulated values increased with increasing participant age. These deviations were somewhat more pronounced in the posterior limb of the internal capsule (Fig 5C and D) than in the splenium of the corpus callosum (Fig 5A and B) and cannot be explained by experimental noise.

Fig 5.

Maturational decreases of the three diffusion tensor eigenvalues (λ_max, λ_int, λ_min) in the white matter of the splenium of the corpus callosum and the white matter of the posterior limb of the internal capsule for 161 participants of postconceptional ages 7 months to 12 years. Vertical dashed line indicates age of normal term birth: 40 gestational weeks. Dashed line through the λ_max data represents an empirical fit to a biexponential function. Solid lines through λ_int data (top solid line) and λ_min data (bottom solid line) are theoretical predictions for their age-varying values from Monte Carlo simulation of a cylindrical diffusion model, in which the age-dependent parameters D̄, λ_max, and SNR are given as input (see Methods for details of the theoretical model).

A, White matter of the splenium of the corpus callosum. Values of λ_max (open inverted triangles), λ_int (closed circles), and λ_min (open squares) are in 10⁻³ mm²/s.

B, White matter of the splenium of the corpus callosum. Each eigenvalue is expressed in terms of its fraction of the trace of the diffusion tensor Trace(D), where Trace(D) is the sum of the three eigenvalues.

C, White matter of the posterior limb of the internal capsule. Values of λ_max (open inverted triangles), λ_int (closed circles), and λ_min (open squares) are in 10⁻³ mm²/s.

D, White matter of the posterior limb of the internal capsule. Each eigenvalue is expressed in terms of its fraction of the trace of the diffusion tensor Trace(D), where Trace(D) is the sum of the three eigenvalues.

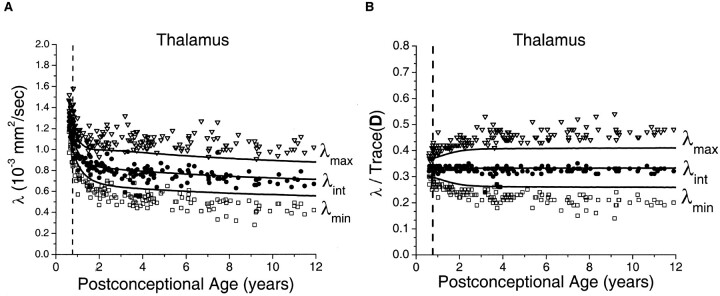
The age-dependent decrease of the three diffusion tensor eigenvalues in the thalamus (Fig 6) superficially resembled that seen in the basal ganglia (Fig 4). However, there were much larger departures of thalamic λ_max and λ_min from the Monte Carlo simulation results based on the spherical diffusion model than was found in the basal ganglia. As in the other gray and white matter regions, agreement between theory and experiment was closest in the neonates and younger children, with gradually increasing divergence from the model with increasing age.

Fig 6.

Maturational decreases of the three diffusion tensor eigenvalues (λ_max, λ_int, λ_min) in the thalamus for 161 participants of postconceptional ages 7 months to 12 years. Vertical dashed line indicates age of normal term birth: 40 gestational weeks. Solid lines through data are theoretical predictions for the age-varying values of λ_max (top line), λ_int (middle line), and λ_min (bottom line) from Monte Carlo simulation of a spherical diffusion model, to which the age-dependent parameters D̄ and SNR are given as input (see Methods for details of the theoretical model).

A, Values of λ_max (open inverted triangles), λ_int (closed circles), and λ_min (open squares) are in 10⁻³ mm²/s.

B, Each eigenvalue is expressed in terms of its fraction of the trace of the diffusion tensor Trace(D), where Trace(D) is the sum of the three eigenvalues.

Discussion

The first investigations of human brain maturation with diffusion-tensor MR imaging were performed on preterm and term neonates (6, 7) and showed that the isotropic diffusion coefficient D̄ decreases and the diffusion anisotropy rises with increasing gestational age. Mukherjee et al (8) extended these observations to normal brain development in infants and children, showing that D̄ continues to decline and anisotropy continues to increase in central gray and white matter regions during the first decade of postnatal life. In the present investigation, we combine the data presented by Neil et al (7) and Mukherjee et al (8) to examine developmental changes in brain water diffusion over the entire age range from premature neonates through children ≤12 years of age. We go beyond measurements of the isotropic diffusion coefficient and diffusion anisotropy to directly analyze the eigenvalues of the diffusion tensor. The three eigenvalues fully determine the size and shape of the diffusion ellipsoid corresponding to the diffusion tensor. In contradistinction, the isotropic diffusion coefficient D̄ and the diffusion anisotropy do not provide enough information to specify a unique tensor, so there are an infinite number of different diffusion ellipsoids that can satisfy any particular pair of nonzero D̄ and anisotropy values.

We also confirmed that, assuming constant MR acquisition parameters, the SNR of diffusion-weighted imaging decreases with brain maturation. This results from the well-known reduction of T2 relaxation time (1, 9) and of the rate of water diffusion (8, 13, 14) that occurs over this age range. We derive a mathematical relationship (equation 8), based on the theoretical contribution of T2 and diffusion changes to diffusion-weighted imaging, as well as the time course of the maturational decreases in T2 (9) and D̄ (8) that successfully explains the magnitude and time course of the age-dependent drop in SNR (Fig 3).

The maturational decreases in the three diffusion tensor eigenvalues that were found in the basal ganglia were well described by a spherical water diffusion model that simply assumes isotropic diffusion throughout the process of gray matter development (Fig 4). Several groups, all of whom used Monte Carlo simulation to adjust for the effects of measurement noise, have previously studied the issue of whether gray matter water diffusion is isotropic in the adult brain. Pierpaoli et al (4) and Shimony et al (5) independently found that adult gray matter diffusion is isotropic, whereas Sorensen et al (15) reported a small but significant deviation from perfect isotropy. Our data indicated that diffusion in the basal ganglia conforms well to isotropy in neonates and infants, but slight departures from isotropy are seen in λ_max and λ_min in the older children. Mukherjee et al (8) found a small age-dependent increase in the anisotropy measure Aσ within the basal ganglia. Our more detailed analysis of these data indicated that the early portion of the rise in anisotropy is artifactual, due to decreases in SNR that result in increases in noise bias with age. The later component of the small increase in Aσ, occurring in the older children, cannot be explained by measurement noise. However, this does not necessarily represent the development of anisotropy within the gray matter itself, considering that maturation of small white matter tracts such as the ansa lenticularis within the basal ganglia remains another possible origin.

The finding that water diffusion is predominantly isotropic in the basal ganglia throughout the course of brain maturation has important implications for the biologic processes that underlie gray matter development. The biexponential time course of the decay of D̄ in gray and white matter found by Mukherjee et al (8) closely parallels that of the maturational decrease of brain water content found in an autopsy study of 139 participants of postconceptional ages 10 weeks to 8 years (16). However, the magnitude of the decline in D̄ between its value at 40 weeks gestation and its asymptotic (adult) value is 46%, whereas the drop in brain water content over the same interval is only 12%. If decreasing brain water content causes a proportionate fall in isotropic diffusion, over the range from 90% water at birth to 79% water in adulthood (16), then the large observed age-related reduction in D̄ reflects more than just tissue water loss. The most likely additional cause of the decrease in D̄ is the increase in macromolecular concentration that occurs with brain maturation (1). The increase in macromolecules can reduce D̄ in two different ways. First, the increased binding of water to macromolecules would reduce the free water content of gray matter. Because macromolecule-bound water has very short T2 relaxation time (9, 17), this water would contribute relatively little signal intensity at the long TE of diffusion-tensor imaging but would presumably still be measured in pathologic studies of brain water content. Hence, the maturational reduction in the free water content of the brain measured by diffusion-tensor imaging may potentially be greater than 12%. Second, the incorporation of macromolecules into cell membranes and organelles as neurons and glia arborize during development would provide new barriers to water diffusion. Because these newly formed membranes create a hydrophobic environment, they tend to displace water from their volume of tissue. Hence, it is not surprising that the reduction in D̄ due to formation of new barriers to water diffusion would occur with the same time course as the decrease in tissue water content.

To maintain isotropic diffusion throughout gray matter development, there cannot be any preferred spatial orientation of the arborization of neurons and glia. Any coherent spatial organization of axons, dendrites, or glial processes would generate deviations from isotropy among the diffusion tensor eigenvalues that cannot be explained by measurement noise. This phenomenon has previously been shown in the developing human cerebral cortex from 24 to 32 weeks gestational age, when the parallel organization of radial glial fibers produces detectable anisotropy (18). It was also shown in our study by the diffusion-tensor imaging data from the thalamus (Fig 6). Although the thalamus is predominantly a gray matter structure, it has a higher fraction of internal white matter tracts than the basal ganglia, and therefore greater diffusion anisotropy (8). The large departures of the thalamic data from the spherical diffusion model indicate that anisotropy in the thalamus is not an artifact of measurement noise. The age dependence of the divergence from isotropy results from progressive myelination of the internal white matter tracts of the thalamus.

The maturational decreases in the two minor eigenvalues of the diffusion tensor in the white matter of the internal capsule and corpus callosum were well described by the cylindrical diffusion model (Fig 5), although small departures from the model predictions were seen in the older children. This discordance with the theoretical model appears more pronounced in the posterior limb of the internal capsule than it does in the splenium of the corpus callosum, despite the higher SNR attained in the former region. The lower SNR in the corpus callosum results from motion artifact due to CSF pulsations transmitted to regions bordering the ventricles (8, 19). In a diffusion-tensor imaging study of adult volunteers, Pierpaoli et al (4) found that water diffusion in the splenium of the corpus callosum is cylindrically symmetric, whereas water diffusion in the posterior limb of the internal capsule deviates from this ideal because of small differences between the two minor eigenvalues that cannot be explained by measurement noise. The data and modeling from the present investigation indicates that diffusion in the posterior limb of the internal capsule does conform to axisymmetry early in life but gradually diverges from this symmetry. The reason for this deviation is unclear, but one possible explanation is that fibers in the internal capsule are not truly parallel but instead gradually converge as they pass caudally from the centrum semiovale to the cerebral peduncles. This “fan-like” architecture of the internal capsule may cause deviations from cylindrically symmetric water diffusion that would grow more marked with myelination. Presumably, axons in the splenium of the corpus callosum are more parallel than in the posterior limb of the internal capsule.

The ability to describe white matter diffusion with a simple theoretical model such as the cylindrical model may aid the scientific study of white matter development, as the model can dissociate those changes in diffusion that are due to decreases in water content from those that are due to progressive myelination. Because diffusion along the direction parallel to the white matter axons should not be affected by myelination, the major eigenvalue, λ_max, may be a marker for changes in water content. The 7% to 13% decrease in λ_max observed in white matter between its value at term birth and its asymptotic value (Fig 5) is less than or equal to the 12% decrease in brain water content measured histologically over the same age range (16). Assuming linearity between λ_max and water content over the interval from birth to adulthood, this would imply that the increased macromolecular binding of water during myelination does not significantly influence λ_max in the central white matter pathways. Conversely, the age-dependent reduction in the minor eigenvalues, λ_int and λ_min, after normalization with λ_max may prove to be a marker for the effects of myelination. These reductions in the minor eigenvalues may not reflect changes in permeability of the axolemma due to myelination, however, because no difference in diffusion anisotropy was found between myelinated and unmyelinated axons in the excised cranial nerves of the garfish (20). Instead, it has been suggested that the increasing anisotropy of myelinating white matter is due to the increasing tortuosity of the extracellular space within fiber tracts in directions orthogonal to the long axis (21). However, other plausible hypotheses exist for the biophysical mechanisms that influence water diffusion during brain development. For example, it has been argued that the anisotropy detected in white matter tracts before the onset of myelination, known as premyelination, results from nonstructural features of axons such as the activity of sodium channels (22). Recent evidence for this hypothesis comes from a study showing that the application of tetrodotoxin, a sodium channel inhibitor, reduces anisotropy in the rat pup brain (23). Further investigation is needed to determine what role such nonstructural factors may play in governing diffusion along each of the three orthogonal axes of the diffusion ellipsoid.

The ability to separate changes in water content from changes in myelination may have clinical applications. During the acute phase of white matter diseases such as multiple sclerosis or adrenoleukodystrophy, demyelination often coexists with vasogenic edema. The finding of reduced diffusion anisotropy in acute white matter lesions would then be nonspecific, because decreased anisotropy can be caused by both demyelination (24, 25) and vasogenic edema (26). In the latter case, the drop in anisotropy is promptly reversible with resolution of the edema (26). Direct analysis of the eigenvalues may allow dissociation of these two effects, because vasogenic edema should increase the magnitude of all three eigenvalues from their normal values whereas demyelination should raise the two minor eigenvalues only.

Considering the rapid changes in brain water diffusion during childhood, the detection of altered water diffusion in clinical pediatric neuroimaging is dependent on establishing age-appropriate normal milestones. In this investigation, we provided preliminary normative values for λ_max, λ_int, and λ_min during development of the central gray and white matter structures. Because they are largely based on retrospective cross-sectional data, these values need to be confirmed by a prospective longitudinal study, as well as extended to other brain regions. Later-maturing brain regions, such as subcortical U fibers and association white matter of the cerebral hemispheres, may show continued changes in water diffusion throughout adolescence and into early adulthood. The data presented herein also emphasize the need to account for the effects of experimental noise in assessing anisotropy or the individual eigenvalues of the diffusion tensor, especially when comparing measurements from different MR imagers or different institutions, where considerable variation in SNR may exist. Theoretical modeling combined with Monte Carlo computer simulation can correct for these differences. In white matter regions that conform to the theoretical model, knowledge of the SNR can be used to eliminate noise bias and estimate the true anisotropy.

We emphasize that the models of water diffusion for gray and white matter development presented herein are parameter-free in the sense that all of the variables of the models are constrained by the experimental data. However, there are some limitations to these formalisms. The models do not explain the magnitude or time course of the changes in water diffusion during brain development: these data must be entered as input in the form of the decay curve of D̄. The models specify what the shape of the diffusion ellipsoid should be throughout maturation, without explaining its size or rate of change. Also, the cylindrical model can be applied only to large white matter tracts where the fibers are coherently organized into parallel bundles. More sophisticated models of water diffusion would be required to describe white matter regions with crossing fibers (27) or small white matter regions where there is partial volume averaging with adjacent gray matter within MR imaging voxels.

Conclusion

We report the age-dependent normal values of the three eigenvalues of the water diffusion tensor in the central gray and white matter of the human brain for 161 participants ranging in age from 31 gestational weeks to 11 postnatal years, as well as the SNR of these examinations. We find that the maturational decreases of the diffusion tensor eigenvalues can largely be described with theoretical models that incorporate simple assumptions regarding the influence of brain water content and myelination. However, small deviations from theory are seen in both gray and white matter as the brain matures. Diffusion MR imaging is a powerful tool for the scientific study of human brain development and may also play an increasingly important role in clinical pediatric neuroimaging.

Appendix

Diffusion-tensor MR imaging requires collection of a sufficient number of diffusion-weighted images to define the six unique elements of the diffusion tensor (2–4). Traditionally, six or more diffusion-weighted images are acquired with diffusion gradients applied in noncollinear directions, and an additional reference image is acquired having minimal or no diffusion weighting (an I₀ image). The I₀ image can be used to normalize the signal intensities of the six diffusion-weighted images, and multivariate regression of the natural logarithms of these signal intensity ratios yields the six unique elements of the diffusion tensor. With this approach, the log ratio provides a measure of the diffusion coefficient in the direction of the diffusion-encoding gradient, and six diffusion-weighted images and one I₀ image are sufficient to determine the tensor. Alternatively, the diffusion tensor can be fit to the log of all seven intensities (the six diffusion-weighted images and I₀) rather than fitting the log intensity ratios. In the approach of fitting the log intensities, a more general requirement for tensor measurement is that at least seven images must be acquired, with which at least six acquisitions are diffusion-weighted in noncollinear directions and the seven acquisitions contain at least two different levels of diffusion weighting (b factors).

In this framework, the tetrahedral-orthogonal encoding scheme used in this study does not require a separate I₀ image to compute the diffusion tensor, because the diffusion-weighted measurements are performed at two different b factors. The three orthogonal acquisitions have intermediate diffusion weighting (b = 337.5 s/mm²), whereas the four tetrahedral acquisitions have high diffusion weighting (b = 1012.4 s/mm²).

To see how this “no-I₀ ” tetrahedral-orthogonal method can solve for the diffusion tensor in a manner similar to the traditional approach of six high b-value images and one I₀ image, consider that the I₀ image can be reconstructed from the geometric mean of the four tetrahedral images and the geometric mean of the three orthogonal images. By assuming a linear relationship between the log of signal intensity and b value, a two-point extrapolation can be performed by using the signal intensities of the two geometric mean images (b = 1012.4 and b = 337.5 s/mm²) to compute an I₀ image at b = 0 s/mm². This reconstructed I₀ image could then be used to generate log signal intensity ratios, and the solution of the diffusion tensor could proceed in the conventional way. The assumption of linearity between log signal intensity and b value has been shown to be an excellent approximation for b values up to approximately 1000 s/mm² (28).

However, a more direct method for solving the diffusion tensor with the tetrahedral-orthogonal acquisitions, in the absence of the I₀ image, is to simply perform the multivariate regression on the log signal intensities of the diffusion-weighted images, without first calculating ratios with the I₀ image. Because the no-I₀ tetrahedral-orthogonal data set includes seven noncollinear diffusion-weighted images at two distinct b values, there is enough information to uniquely determine the values of the six independent elements of the diffusion tensor. This was the method used in the childhood diffusion-tensor imaging study presented herein.

One disadvantage of dispensing with the I₀ image is a small reduction in SNR, because the I₀ image has greater SNR than do the more highly diffusion-weighted images. There are counterbalancing advantages, however. If the I₀ image is not acquired, there will be a small reduction in imaging time. Also, because diffusion weighting suppresses signal intensity from CSF, performing diffusion-tensor imaging without an I₀ image will result in less artifact from partial volume averaging with CSF, as exists in conventional diffusion imaging (29). Moreover, traditional diffusion-tensor imaging postprocessing is sensitive to any image artifacts in the I₀ image, because this image is used as the baseline for all the signal intensity ratio calculations. By solving for the diffusion tensor from the diffusion-weighted signal intensities themselves, rather than their ratios with an I₀ image, there is reduced sensitivity to artifacts in any one type of image. Because many of the acquired b = 0 s/mm² images in the childhood diffusion-tensor imaging study did contain some artifact, we computed the diffusion tensor without using the I₀ image.