Abstract
Image reconstruction from undersampled k-space data has been playing an important role in fast MRI. Recently, deep learning has demonstrated tremendous success in various fields and has also shown potential in significantly accelerating MRI reconstruction with fewer measurements. This article provides an overview of the deep learning-based image reconstruction methods for MRI. Two types of deep learning-based approaches are reviewed: those based on unrolled algorithms and those which are not. The main structure of both approaches are explained, respectively. Several signal processing issues for maximizing the potential of deep reconstruction in fast MRI are discussed. The discussion may facilitate further development of the networks and the analysis of performance from a theoretical point of view.
Keywords: magnetic resonance imaging, deep learning, image reconstruction, neural networks, optimization algorithms
I. INTRODUCTION
Since its inception in the early 1970s, magnetic resonance imaging (MRI) has revolutionized radiology and medicine. However, MRI is known to be a slow imaging modality, and many techniques have been developed to reconstruct the desired image from undersampled measured data to improve the imaging speed [1]. In past decades, compressed sensing (CS) has become an important strategy for fast MR imaging based on the sparsity prior. However, it takes a relatively long time for the iterative solution procedure to achieve high-quality reconstruction, and the selection of the regularization parameter is empirical. Although some numerical methods, such as Stein’s Unbiased Risk Estimation (SURE) [2], have been proposed to optimize the free parameters in MR imaging, these methods are burdened with high computational complexity. Additionally, most approaches only exploit prior information, either directly from the to-be-reconstructed images or with very few reference images involved.
Recently, deep learning has demonstrated tremendous success and has become a growing trend in general data analysis [3, 4]. Inspired by such success, deep learning has been applied to computational MRI and has shown the potential to significantly accelerate MR reconstruction [5–28]. In contrast to compressed sensing and other constrained reconstruction methods, deep learning avoids complicated optimization-parameter tuning and performs superfast online reconstruction with the aid of offline training using enormous data.
Deep learning-based MRI reconstruction methods can be approximately categorized as unrolling-based approaches [5–12] and those not based on unrolling [13–28]. The unrolling-based approaches typically start from a posited optimization problem whose solution is the image to be reconstructed, and then unroll an iterative optimization algorithm to a deep network. Therefore, the network architecture of an unrolling-based method is constructed based on the steps resulting from the iterations. Parameters and functions in the reconstruction model and algorithm are learned through network training. While the methods not based on unrolling directly use the standard network architectures, which are designed for problems other than reconstruction, to learn the mapping from input to output, and may also incorporate some domain knowledge in MR imaging into the standard network.
The main purpose of this article is to give an overview of deep learning-based MR image reconstruction methods, with an effort to highlight their unique properties and similarities between them. We attempt not only to summarize the materials that are dispersed throughout the literature but also to present a discussion of the relationship among these methods. This article by no means includes a complete list of references of all contributions, as the field is fast-growing, but the methods introduced herein should serve as good examples for understanding the field.
The paper is organized as follows. Section II provides a brief introduction of deep learning and MRI reconstruction basics. The classical deep learning network architectures and the general formulation of CS-based MRI reconstruction (from undersampled measured data to image) are provided. Section III introduces unrolling-based deep networks, with a focus on how each of the popular iterative, CS-based reconstruction algorithms is unrolled to a network with its unique architecture. In particular, the regularization parameters, the regularization functions, and even the data consistency metrics are learned via training. Section IV introduces the approaches not based on unrolling. Networks with additional domain knowledge are elaborated. Section V discusses some of the signal processing issues. Section VI provides some possible future directions and the concluding remarks.
II. Basics of Deep Learning and MRI Reconstruction
A. Deep learning
Deep learning is a class of machine learning algorithms that exploits many cascaded layers of nonlinear information processing units to learn the complex relationships among data. By going deeper (i.e., more layers), the network improves its capability of learning features from higher levels of the hierarchy that were formed by the composition of lower-level features. Such capability of learning features at multiple levels of abstraction allows the deep network to learn the complex functions that directly map the input to the output from data without depending on human-crafted features.
The core of deep learning is the deep neural network, which actually is a type of artificial neural network (ANN). Although the ANN was invented in the 1950s [29], and there were several earlier ANN trends, the latest trend in ANN, which is known as deep learning, fully exhibits its power in various fields. There are three key factors that contribute to the recent success of deep learning: a) the invention of optimization strategies (e.g., layerwise pretraining, mini-batch stochastic gradient descent (SGD), batch normalization, shortcut, activation function, etc.) enables training of high-dimensional, multivariate models; b) the availability of large datasets (Big Data) overcomes the overfitting issue; c) the ever-growing computational power of hardware (e.g., GPU and parallel computing) allows the training to be performed in finite time. In addition, the availability of open-source software libraries (e.g., TensorFlow, PyTorch, Caffe, MatCovNet) makes the development of deep learning methods more efficient. These techniques make it possible to extract substantial value out of data.
Most existing deep learning algorithms use the ANN with supervised learning. In supervised learning, the weights and biases are learned from training data by minimizing a loss function (e.g., root mean square error, cross entropy, etc.). During training, a back-propagation algorithm is used to calculate the gradients of a loss function with respect to each weight/bias. Those gradients are then used in optimization algorithms (e.g., SGD) to update the weights/biases in a direction that is opposite to the gradient. Updating the weights/biases multiple times in different training samples will eventually result in a properly trained neural network.
Classic types of deep neural networks include multilayer perceptron (MLP), convolutional neural networks (CNN), recurrent neural networks (RNN), and generative adversarial networks (GAN).
1). MLP
MLP is one of the simplest neural networks. MLP consists of an input layer, an output layer, and at least one hidden layer. In a network with fully connected nodes between the adjacent layers, each node, which is known as a neuron, uses a nonlinear activation function to operate on the sum of the biases and weighted outputs of connected nodes from the previous layer, thereby allowing the representation of complex functions.
2). CNN
CNN has been mostly successful in image processing due to the capability of learning the position and scale-invariant structures of the data, which is important when working with images. This technique has achieved great success because it scales the data and model size and can be trained with back-propagation but with a fraction of the computational complexity of MLP.
An N-layer CNN with input m0 and output can be described as follows
| (1) |
where Kn eqdenotes the convolution kernel of size Kn−1 × wn × hn × kn, and bn denotes the kn dimensional bias with its element being associated with a filter. The CNN output is the output of the final layer. Here, Kn−1 is the number of the image features extracted at the layer n−1; wn × hn is the filter size, and these values could be equal; kn is the filter number at layer n; and Hn is the nonlinear mapping operator. Eq. (1) can be regarded as the forward pass of the CNN training, where the convolution kernel kn is used to extract the features, and Hn is the nonlinear activation function. For example, the widely used activation function, rectified linear units (ReLU), is given as:
| (2) |
Several advanced architectures have been integrated into CNN, such as U-net and ResNet, to aid in information preservation and network optimization.
3). RNN
RNN is a class of neural networks that makes use of the sequential information to process sequences of inputs. RNN maintains an internal state of the network by acting as a “memory,” which allows RNNs to lend themselves naturally to the processing of sequential data.
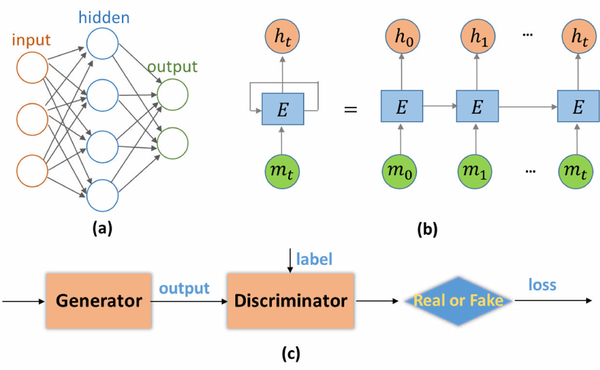
In Fig. 1(b), a portion of a neural network, E, takes some input mt and outputs the value ht. Each E loop allows information to be passed from one step of the network to the next. A recurrent neural network can be considered to be multiple copies of the same network, with each copy passing a message to a successor.
Figure 1.
(a) Architecture of multilayer perceptron (MLP) with three layers. (b) Architecture of recurrent neural networks (RNN). (c) Architecture of generative adversarial networks (GAN).
4). GAN
GAN has gained popularity due to its ability to infer photorealistic natural images. In GAN, there are two subnetworks, a generator and a discriminator The generator can generate high perceptual quality images according to the discriminator, which is a very good classifier for separating realistic and generated images.
The training objective can be formulated as the following minimax problem:
| (3) |
where is trained to maximize the probability of assigning the correct true or false label to images; is trained to minimize the difference between the generated and labeled image that the discriminator cannot distinguish. tries to produce an image that can fool , whereas avoids being fooled. Such kind of training borrows the win-loss strategy that drives both terms to improve their performance.
The loss function is defined as
| (4) |
where E[·] refers to the expectation operation; tries to generate images that look similar to images mref, which are realistic images; and aims to distinguish between
Although deep learning has gained much success in various applications, the selection of a network topology is still an engineering problem instead of scientific research. In most existing deep learning approaches, there is a lack of a theoretical explanation of the relationship between the network topology and performance. In addition, the generalizability of most networks is not understood. These are the common limitations of deep learning approaches.
B. MRI reconstruction
In MRI, spatial information of the subject, such as the spin density and relaxation parameters, is encoded in the measured data in a variety of ways [30, 31]. Typically, a forward imaging model is a mathematical description of how the measured data is related to the spatial information (i.e., image). A linear imaging model is typically used after some approximation and can be written as
| (5) |
where is the encoding matrix, is the acquired k-space data, is the image to be reconstructed, and ϵ is the measurement noise, which can be well modeled as complex additive Gaussian white noise under the assumption that the noise equally affects the entire frequency (i.e., all the samples in k-space). For example, with the Fourier imaging model, A = Fu for the case of single-channel acquisition, A = Fu S for the case of multichannel acquisition where S denotes the coil sensitivities and Fu the Fourier transform with undersampling.
During data acquisition, the measured data f and the imaging model captured in the encoding matrix A are both known. The problem of image reconstruction is to recover the desired image m from the measurements f.
There are several methods of solving for m in Eq. (5), such as obtaining the least-squares solution directly or through an iterative procedure. For example, with the single-channel acquisition, the forward MR imaging model can be formulated as a Fourier encoding. If the acquired data (so-called k-space data) is sampled on a Cartesian grid and satisfies the Nyquist sampling criterion, the image can be reconstructed directly by applying a fast Fourier transform (FFT). Multichannel acquisition entails more complicated encoding matrices but can also be reconstructed by direct matrix inversion for Cartesian sampling. On the other hand, for sub-Nyquist sampling, iterative reconstruction is typically used to solve the underdetermined inverse problem. In such scenarios, additional prior information is often incorporated into the imaging model to facilitate the reconstruction, such as the spatiotemporal correlation in dynamic imaging or the quantitative model of MR parameters.
CS is one of the revolutionary approaches to reconstruction from sub-Nyquist sampled data. The method exploits some prior models, such as sparsity and low-rankness, and solves the underlying constrained optimization problem. Details can be found in other papers in this special issue. In general, the imaging model of the sub-Nyquist data can be written as
| (6) |
where G(m) denotes a combination of sparse, low-rank, or other types of regularization functions.
In CS, the sparsity prior is usually enforced by fixed sparsifying transforms or data-driven but linear dictionaries. In contrast, deep learning goes beyond CS by extending the key component of CS- the prior becomes data-adaptive and highly nonlinear. Although deep learning requires many computations for the training step, which is sometimes several orders of magnitude higher than what is necessary for CS to converge, the training is conducted off-line, while the reconstruction (i.e., testing) step of deep learning can be computationally faster than that of CS.
III. unrolling-based Deep Learning Approaches
A. Definition
Most existing unrolling-based deep learning methods extend upon a CS reconstruction algorithm. Specifically, a CS reconstruction algorithm starts with the inverse problem based on the imaging model (e.g., Fourier transform) and prior constraints (e.g., sparsity and low rankness), and then applies an optimization algorithm to solve the inverse problem and find the desired image from the measured data. The optimization algorithm is typically iterative in nature. In unrolling-based deep learning methods, such an iterative reconstruction algorithm is unrolled to a deep network in which all free parameters and functions can be learned through training. The training of the deep network can be performed through the back-propagation of the training data. In this way, the topology of the deep network is determined by the iterations of the algorithm. As a result, the unrolling-based deep learning reconstruction methods allow understanding of the relationship between the network topology and performance.
B. Examples
The major differences among the unrolling-based methods lie in the architectures of the networks, which are derived from different optimization algorithms. In this section, we will review several key unrolling-based deep learning methods for fast MR imaging according to three different imaging models: 1) generalized CS reconstruction model; 2) denoising model; 3) general optimization model. A summary of these methods is given in Table 1.
Table 1.
Summary of some methods in the two categories.
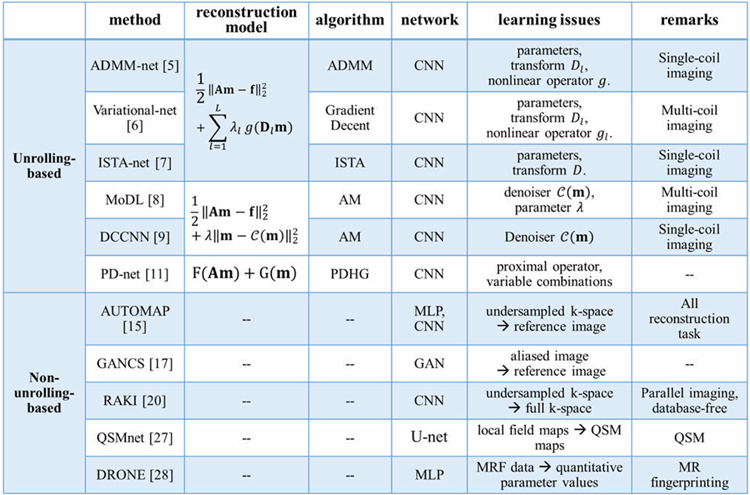 |
1). Generalized CS reconstruction model
In the context of a CS MRI reconstruction model using Eq. (6), the regularization term can be expressed as
| (7) |
where the regularization term is extended to L terms, and is a transformation matrix (e.g., discrete wavelet transform for a sparse representation); g(·) is a nonlinear operator (e.g., lq-regularizer (q ∈ [0,1]) to promote sparsity); and λl is the regularization parameter.
①. ADMM-net
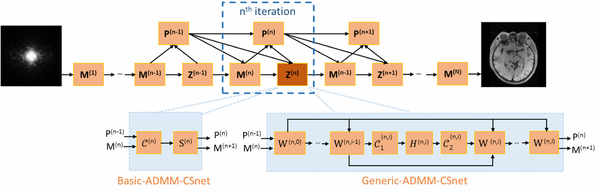
ADMM-net was designed by unrolling the alternating direction method of multipliers (ADMM) algorithm to learn the regularization parameters of CS-MRI reconstruction. The original network, denoted as the basic-ADMM-CSNet, was then generalized to Generic-ADMM-CSNet [5]. The improved network further learns the image transformations and nonlinear operators in the regularization function. operators in the regularization function.
In basic-ADMM-CSNet, a set of independent variables is introduced in the transform domain as zl = Dlm. The transform Dl aims to sparsify the image such that zl is sparse. Based on the model (6) and the regularization term (7), the ADMM iterations can thus be written as
| (8) |
The solution is
| (9) |
where is a nonlinear proximal operator of g(·) with parameters
In Generic-ADMM-CSNet, the independent auxiliary variables z = {z1, z2,...,zL} are introduced in the image domain instead. The iterations of the ADMM algorithm become
| (10) |
thereby yielding the solution:
| (11) |
Where H(·) refers to a nonlinear operation corresponding to the gradient of the regularizer g(·); i refers to the i-subiteration in each Z(n+1). In the original CS formulation, Dlz is made to be sparse. However, after the iterations are unrolled to a network, there is no explicit constraint to make Dlz sparse in the network.
In both Eqs. (9) and (11), the image m, auxiliary variables z, and multiplier β are iteratively updated. Although the computation performed in each iteration of both methods may be slightly different due to different representations of auxiliary variables, the data flow graph of the above two ADMM-nets is the same, which is illustrated in Fig. 2. As shown in Fig. 2, the n-th iteration in the data flow graph corresponds to the n-th iteration of the ADMM algorithm. Specifically, in each iteration of the graph, there are three types of nodes corresponding to three modules in ADMM: the reconstruction module (M), denoising module (Z), and multiplier update module (P). In basic-ADMM-CSNet, all parameters (ρl, λl, ηl) in the original ADMM algorithm are learnable, while Generic-ADMM-CSNet also learns the image transformation Dl, which is implemented linearly by convolving with kernels, and the nonlinear operator g(·), which is encoded by a piecewise linear function that is determined by a set of control points.
Figure 2.
The data flow graph for the ADMM-nets. convolution; H, S : nonlinear operator; W: addition.
②. Variational-net
To allow fast and high-quality reconstruction of clinical accelerated multichannel MR data, the variational network (Variational-net) [6] was developed. This network combines the mathematical structure of variational models for generalized CS reconstruction with deep networks to learn the regularization parameters, image transformations, and nonlinear operators.
In Variational-net, the solution to Eq. (6) is iteratively updated in the gradient decent direction as
| (12) |
where is the activation function corresponding to the first-order derivative of the nonlinear operator gl; transformation can be modeled as a convolution with filter kernels of Kl; and α(n) is the step size of the gradient decent. The parameter λl in (7) is implicitly contained in the activation functions. Here, the encoding matrix A consists of sub-Nyquist sampled Fourier transform and coil sensitivities.
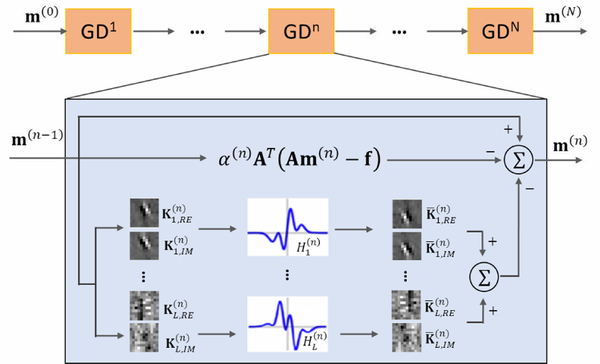
Variational-net is obtained by unfolding the iterations of Eq. (12), which is depicted in Fig. 3. As the MR data are complex, the convolution includes a real part and an imaginary part. The transpose operation in Eq. (12) can be implemented as a convolution with the filter kernels of Kl, but rotated by 180°. The parameters learned in Variational-net are the filter kernels the activation functions and the step size α(n).
Figure 3.
Structure of Variational-net. Variational-net consists of N gradient decent steps. The undersampled k-space data, coil sensitivity maps and zero-filling image are fed into the network.
It is worth noting that the coil sensitivities need to be precalculated and fed into the Variational-net.
③. ISTA-net
ISTA-net [7] aims to solve the general CS reconstruction problem with L1 regularization in (7). It is an unrolled version of the iterative shrinkage-thresholding algorithm (ISTA) to learn the image transformation and parameters that are involved in the original algorithm of ISTA. ISTA solves the optimization problem in Eq. (6) as
| (13) |
| (14) |
where ρ is the step size. It is difficult to obtain m(n + 1) if the transformation D is nonorthogonal or even nonlinear.
ISTA-net is an unrolled version of the traditional ISTA of Eq. (13) and Eq. (14) but overcomes the abovementioned drawback. With a general form of image transformation D(m), the m(n+1) module in Eq. (14) becomes
| (15) |
where θ is the merged parameter related to λ and D(·). The image can be obtained as
| (16) |
where is the left inverse of D(·) and soft(·) denotes soft thresholding.
The architecture of the ISTA-net is illustrated in Fig. 4. Each iteration of ISTA-net consists of two modules: r(n+1) module and m(n+1) module. The r(n+1) module is the same as Eq. (13), except that the step size ρ is learnable in each iteration. In the m(n+1) module, D(·) is modeled as two convolutional operators that are separated by a ReLU operator, as depicted in Fig. 4; exhibits a structure symmetric to that of D(·).
Figure 4.
Architecture of the ISTA-net. N denotes the iteration number. Each iteration has two modules that correspond to Eq. (13) and Eq. (16).
ISTA-net is designed for the general CS reconstruction problem, not for MR reconstruction only. Different from ADMM-net and Variational-net, ISTA-net adopts an l1-regularizer for the sparse prior, which is restricted by ISTA.
2). Denoising model
The denoising model enforces m to be well-approximated by the “denoised” image in which aliasing artifacts and noise are removed. The regularization term can be formulated as
| (17) |
With the alternating minimization algorithm (AM), the image can be reconstructed as
| (18) |
| (19) |
The denoising in (19) can be achieved using a CNN unit. For the single-channel acquisition, the data consistency (DC) subproblem (18) has a closed-form solution:
| (20) |
In DCCNN [9], a deep cascade of convolutional neural networks for dynamic MR reconstruction, iterations are unrolled that alternate between Eqs. (20) and (19). Another method, MoDL (model-based deep learning) [8], solves the DC subproblem (18) using the conjugate gradient (CG) algorithm to handle more complex forward models (e.g., multichannel MRI). The CG process does not need to be unrolled to a network, as there are no trainable parameters in it. In addition, DC is integrated as a layer into the network. Fig. 5 shows the architecture of the unrolled network derived from a denoising model.
Figure 5.
Network architecture with the denoising model. DC is the layer of data consistency in Eq. (18).
3). General optimization model
Noted that Eq. (6) is a special case of a more general model:
| (21) |
if Introducing an auxiliary dual variable d, the optimization problem in Eq. (21) can be solved by the primal-dual hybrid gradient algorithm (PDHG) as
| (22) |
where α, τ and θ are the algorithm parameters, and prox is the proximal operator.
PD-net, the learnable primal-dual method proposed by Adler and Öktem for tomographic reconstruction [10], is the unrolled version of the primal-dual hybrid gradient algorithm and has been applied to MRI reconstruction [11]. In PD-net, the proximal operators are replaced with parameterized operators Γ and Λ whose parameters can be learned via training. In addition, the fixed variable combinations inside the operators Γ and Λ are also relaxed. Therefore, the PD-net can be formulated as unrolled iterations alternating between primal updating (mn+1) and dual updating
| (23) |
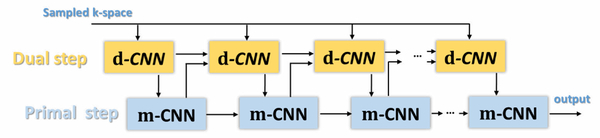
The architecture of the PD-net is shown in Fig. 6. It is worth mentioning that the data fidelity term in the PD-net is no longer the l2 norm of the estimated error at the sampled locations as in Eq. (6) but is implicitly learned from the training data instead, so is the regularization term. In particular, to ensure data fidelity, PD-net directly conveys the acquired data to the k-space-based CNN as an input rather than using the model-based minimization as in (18).
Figure 6.
Architecture of PD-net. PD-net consists of two steps: dual step and primal step mn+1 corresponding to Eq. (23).
IV. Deep Learning Approaches not Based on Unrolling
Most deep learning methods that are not based on unrolling employ certain standard neural networks to learn the mapping between input (undersampled k-space data or aliased images) and output (clean images). In this section, we start with deep learning methods that adopt standard networks only for fast MR imaging (some are summarized in Table 1) and then introduce methods that also incorporate additional MRI domain knowledge into the standard networks [13–28].
A. Standard networks for MR reconstruction
The idea of using CNN for MR imaging was first proposed by Wang et al. [13]. This method directly uses a standard CNN (1) to learn the network-based mapping between the aliased images and the clean images. In most existing works, the aliased image, which is the inverse Fourier transform from undersampled k-space data, is used as the network input, and the desired image from the fully sampled k-space data is used as output. The mapping is learned through standard networks, such as MLP, U-net, and ResNet. Due to its outstanding performance in image-to-image translation, GAN has been exploited in MRI reconstruction [16, 17] to correct the aliasing artifacts in the zero-filled reconstruction from undersampled MR data.
RAKI [20] uses a 3-layer CNN to learn the k-space interpolation for parallel imaging, and then obtains the reconstructed image from the interpolated full k-space data. AUTOMAP [15] directly takes the k-space data as the network input and provides the reconstructed image as network output, which provides an end-to-end formation for image reconstruction. It uses fully connected layers to perform the Fourier transform, a global transform, followed by convolutional layers.
The deep networks are also used in the estimation of quantitative tissue parameters from recorded complex-valued data. Such as in MR quantitative parameter mapping [25, 26], quantitative susceptibility mapping [27], and magnetic resonance fingerprinting [28]. The networks can be designed by incorporating the physical model of the quantitative parameters to be mapped [26]. QSMnet [27] constructs a 3D CNN with the architecture of U-Net to generate high-quality susceptibility source maps from single orientation data. In addition, DRONE [28] adopts a 4-layer MLP to extract tissue properties and predict quantitative parameter values (T1 and T2) from 2D MRF data.
B. Domain knowledge from MRI
Although direct adoption of standard neural networks for MRI reconstruction has been the first attempt, further development with additional domain knowledge can improve the performance of standard networks.
1). Fourier transform
In the Cartesian sampling scenario, an image can be reconstructed from fully sampled k-space data directly by an inverse Fourier transform. Most existing deep learning approaches use the aliased image, which is the inverse Fourier transform of the undersampled k-space data, as the input of the network. By doing that, the methods take advantage of the knowledge that is unique to MRI.
2). Regularization term
In [13], Wang et al. proposed two options for applying the network-based approach with the CS-based approach. One option is to use the image that is reconstructed from the learned network as the initialization for the CS reconstruction method in Eq. (6). The other option is to use the image that is generated by the network as a reference image for regularization. The formulation of the latter option can be described as
| (24) |
where α is the regularization parameter. This approach differs from the unrolling-based methods in that (24) is solved by the conventional CS algorithms with the parameters and the regularization term G(m) predefined, whereas in unrolling-based methods, (24) is solved by a deep network with the parameters and regularization term learned via training.
3). Cross-domain knowledge
In traditional image reconstruction approaches such as CS, data consistency in the k-space is one of the most critical constraints. Such cross-domain prior information can also be very useful when being incorporated into standard networks. Since most learning methods use images as the input and output of the network, the images need to be transformed into the k-space to enforce data consistency. KIKI-net [24] iteratively alternates between the image domain (I-CNN) and the k-space (K-CNN) where the data consistency constraint is enforced in an interleaving manner, as shown in Fig. 7. Each K-CNN is trained to minimize a loss, which is defined as the difference between the reconstructed and fully sampled k-space data, thereby taking full advantage of the k-space measurements. KIKI-Net addresses the issues that some structures are already lost in the network input if CNN is only trained in the image domain with the aliased image as the input.
Figure 7.

Architecture of KIKI-net.
4). Spatio-temporal correlations
In dynamic MRI, the temporal correlation has been shown to improve the reconstruction quality of the CS-based methods. To take advantage of such domain knowledge, a residual U-net structure with 3D convolution has been proposed for dynamic MRI [22]. An alternative approach is to employ a convolutional RNN to jointly exploit the dependencies of the temporal sequences and iterations [12]. Another approach of exploiting spatiotemporal correlations uses data sharing, in which the k-space data are shared among neighboring frames along the temporal direction [9].
V. SOME SIGNAL PROCESSING ISSUES
A. Theoretical analysis
Unlike constrained reconstruction with sparsity or low-rank constraints, a theoretical analysis for deep reconstruction is largely unexplored. Reference [19] provided a preliminary theoretical rationale for some existing deep learning architectures and components. That study used the concept of a convolutional framelet to explain deep CNN for inverse problems. The study showed that deep learning is closely related to annihilating filter-based approaches, by which the lifted Hankel matrix usually results in a low-rank structure that can be decomposed by using both nonlocal and local bases. Based on the framelet framework, for the deep network to satisfy the perfect reconstruction condition, the number of channels should exponentially increase with the layer, which is difficult to achieve in practice; when an insufficient number of filter channels is used instead, the network is performing a low-rank based shrinkage. Therefore, the depth of the network depends on the rank of the signal and the length of the convolution filter. On the other hand, the unrolling-based deep learning methods originate from well-accepted imaging models and therefore might provide more information on the relationship between the network topology and performance.
B. Generalizability and transfer learning
Machine learning can only capture what it has seen. If there were a significant difference between the statistical features of the training data and that of the testing data, the trained network would fail for the testing case. For example, the training stage should be performed every time the condition changes between the training and testing sets. However, it is not always possible to include all the cases in training. Knoll et al. [33] studied the generalizability of the trained Variational-net in the case of deviation between the training and testing data in terms of image contrast, SNR, and image content. In particular, when the contrast and SNR of the training data are quite different from those of the testing data, deep learning-based reconstruction has a substantial level of noise or yields slightly blurred images with some residual artifacts. In addition, a Variational-net trained from regular undersampled data is easily generalized to randomly undersampled data, although the other way would introduce residual artifacts. It is worth noting that the above conclusion is based on the empirical results from a specific variation network in [6]. In-depth studies on more generalized settings are still needed.
In the scenario of a minor mismatch occurring between the training and testing data, transfer learning can be a solution. Transfer learning is defined as adapting or transferring an existing network learned from one problem to another problem through further learning. For example, based on the similarity between projection MR and CT, Han et al. proposed to train the network by using CT data and then adapting the network parameter for MR reconstruction with fine-tuning [18]. In most cases of transfer learning, additional fine-tuning is necessary to achieve a performance that is nearly identical to the performance of the network that is trained directly in the testing condition with a large size of data.
C. Relationship with other learning-based approaches
Before deep learning became popular in MRI reconstruction, there had already been quite a few learning-based reconstruction methods, where the prior models for CS reconstruction are learned from some training data (e.g., [34–37]). These methods differ from the deep learning-based methods in that 1) there is no network structure in learning, 2) the prior comes from a specific mathematical model, and 3) few training data are needed. For example, in CS reconstruction with dictionary learning [34, 35], a linear transformation is learned using training data (simulated data from a theoretical model or low-resolution image). In CS reconstruction with manifold learning [36, 37], a highly nonlinear low-dimensional manifold is learned from training data. These methods can also be viewed as machine learning-based approaches (e.g., kernel principal component analysis and manifold learning are all well-known machine learning methods) and can also benefit from the availability of large numbers of training samples.
D. Other issues in deep learning approaches
As MR data are complex-valued, most works separate the real and imaginary parts into two channels, whereas [21] separately trains the magnitude and phase networks. Even so, the complex-valued issue is still to be addressed.
The multichannel acquisition is a standard technology in clinical scans. To handle the data from multiple channels, [6] and [8] apply the precalculated coil sensitivities as the network parameters, while [14] reconstructs the image using the multichannel data as the input of the network. Different from other studies, [20] learns the k-space interpolation from the autocalibration signal without additional training data.
Cartesian sampling is commonly used in most deep learning MR reconstruction methods, as the transform can be performed efficiently through FFT. However, the non-Cartesian acquisition is less prone to motion artifacts and the aliasing pattern shows higher incoherence than Cartesian acquisition. There are only very few works that consider the non-Cartesian scenario, due to the lack of implementation of the non-uniform FFT in any of the DL platforms (TensorFlow, PyTorch, etc.), and therefore, the training stage becomes very slow to converge. AUTOMAP [15] can reconstruct the image directly from the non-Cartesian samples, as the forward operator non-uniform FFT is learned by the network. Han et al. provide an alternative approach to image reconstruction from a radial trajectory with the help of domain adaptation from CT projection [18].
Prospective validation is very important for evaluating a deep learning method in a real application. The works in [18], [20], and [6] provide the prospective experiment results. Nevertheless, most papers on deep learning reconstruction report their validation results on private data sets. As a result, it is difficult to achieve a clear benchmark and ranking among all methods for a given scenario.
VI. Outlook
Although unrolling-based deep learning methods originate from the numerical algorithms, which have a convergence or asymptotic convergence guarantee, theoretic convergence is no longer valid for the unrolling-based methods due to naive unrolling (i.e., directly replacing functions by the network) and the dynamic nature of the network. Only a few works mention theoretic convergence and have analyzed the convergence behavior in theory [38]. Greater effort should be made to achieve rigorous mathematical derivations and analysis.
As introduced in Section III, rooted in the field of sparse coding [32], the unrolling-based deep learning methods have evolved gradually from learning the regularization parameters only to relaxing more constraints in the CS reconstruction formulation using learnable operators and functions. On the other hand, as introduced in Section IV, the deep learning reconstruction methods that are not based on unrolling has also evolved gradually from a “black box” of input to output using standard networks to well-designed networks that incorporate more domain knowledge. Relaxing more constraints in the unrolling-based approaches and incorporating more domain knowledge into standard networks are to be explored in parallel to improve the performance of MRI reconstruction.
Typically, the networks in MR reconstruction are trained in a fully supervised manner. Self-supervised learning or even unsupervised learning could be exploited in the future. As some datasets are made publicly available, such as the fast MRI data that was released by NYU Langone Health and Facebook AI Research (https://fastmri.org/dataset), it becomes possible to benchmark and compare different networks in the same settings and to evaluate the performance of each network better.
Radiomics aims to extract extensive quantitative features from medical images by using data-mining algorithms and the subsequent analysis of these features for computer-aided diagnosis (CAD). With the emergence of deep learning, deep neural networks have been successfully utilized in radiomics for disease diagnosis [39]. On the other hand, as is discussed in the article, deep learning will significantly improve the quality of the reconstructed image, which will directly benefit CAD by making the features in the training and testing images more prominent. Another way to improve image quality is to optimize the data acquisition protocol. Deep learning can also contribute to this endeavor by learning the optimal acquisition protocol through training.
Since images are not used for visual inspection in radiomics but are combined with other patient data to be analyzed by deep learning algorithms, it is conceivable that there is a synergistic opportunity to integrate deep reconstruction and radiomics for optimal diagnostic performance [40]. Deep learning can be applied to the entire end-to-end workflow from data acquisition, image reconstruction, radiomics, to the final diagnosis report. Such end-to-end workflow has significant potential to improve the diagnostic, prognostic, and predictive accuracy.
In conclusion, deep learning has demonstrated potential in MR image reconstruction. In only a few years, various networks have already been developed to take advantage of the unique properties of MRI. The overview of existing methods will inspire new developments for improved performance. Deep reconstruction will fundamentally influence the field of medical imaging.
Acknowledgment
The authors would like to thank Dr. Qiegen Liu for his helpful discussions.
This work was supported in part by the U.S. NIH grants R21EB020861 and R01EB025133, National Natural Science Foundation of China U1805261 and National Key R&D Program of China 2017YFC0108802.
Biography
Dong Liang (dong.liang@siat.ac.cn) received the B.S. degree in electrical engineering and the M.S. degree in signal and information processing from the Hefei University of Technology, China, in 1998 and 2002, respectively, and the Ph.D. degree in pattern recognition and intelligent system from Shanghai Jiaotong University, China, in 2006. From2007 to 2011, he was a Post-Doctoral Researcher and a Research Scientist with the University of Wisconsin at Milwaukee. Since 2011, he has been with the Paul C. Lauterbur Research Centre for Biomedical Imaging, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China, where he is currently a Full Professor. His current research interests include compressed sensing, image reconstruction, biomedical imaging, and machine learning.
Jing Cheng (jing.cheng@siat.ac.cn) received the Bachelor degree in school of computational and information technology from Beijing Jiaotong University, China, in 2014. She is currently working toward the Ph.D. degree in Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China. Her research interests include compressed sensing, image reconstruction and machine learning.
Ziwen Ke (zw.ke@siat.ac.cn) is a Ph.D student in SIAT, CAS, from Sep. 2016 to now. He received his Bachelor degree from Southern Medical University in 2016. Now he is a PhD student in Pattern Reorganization and Intelligent System at SIAT, and his research direction is fast MRI imaging and deep learning.
Leslie Ying (leiying@buffalo.edu) received her B.E. degree in electronics engineering from Tsinghua University, China, in 1997 and her M.S. and Ph.D. degrees in electrical engineering from the University of Illinois at Urbana-Champaign in 1999 and 2003, respectively. She is currently a Clifford C. Furnas Chair Professor of Biomedical Engineering and Electrical Engineering at University at Buffalo, the State University of New York. Her research interests include magnetic resonance imaging, image reconstruction, compressed sensing, and machine learning. She received a CAREER award from the National Science Foundation in 2009. She served as an Associate Editor of IEEE Transactions on Biomedical Engineering, Deputy Editor of Magnetic Resonance in Medicine, and Editorial Board Member of Scientific Reports. She was elected to the Administrative Committee (AdCom) of IEEE Engineering in Medicine and Biology Society 2013–2015, and served on the Steering Committee of IEEET ransactions on Medical Imaging.
Contributor Information
Dong Liang, Paul C. Lauterbur Research Center for Biomedical Imaging.; Research Center for Medical AI, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, in Shenzhen, Guangdong, China.
Jing Cheng, Paul C. Lauterbur Research Center for Biomedical Imaging..
Ziwen Ke, Research Center for Medical AI, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, in Shenzhen, Guangdong, China..
Leslie Ying, Departments of Biomedical Engineering and Electrical Engineering, University at Buffalo, The State University of New York, Buffalo, NY 14260 USA.
References
- [1].Liang Z-P, Boada FE, Constable RT, Haacke EM, Lauterbur PC, and Smith MR, “Constrained reconstruction methods in MR imaging,” Rev. Magn. Reson. Med, vol. 4, pp. 67–185, 1992. [Google Scholar]
- [2].Ramani S, Liu ZH, Rosen J, Nielsen JF, and Fessler JA, “Regularization Parameter Selection for Nonlinear Iterative Image Restoration and MRI Reconstruction Using GCV and SURE-Based Methods,” IEEE Trans Imag Process, vol. 21, pp. 3659–3672, August 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Hinton GE and Salakhutdinov RR, “Reducing the dimensionality of data with neural networks,” Science, vol. 313, pp. 504–7, July 28 2006. [DOI] [PubMed] [Google Scholar]
- [4].LeCun Y, Bengio Y, and Hinton G, “Deep learning,” Nature, vol. 521, pp. 436–444, May 28 2015. [DOI] [PubMed] [Google Scholar]
- [5].Yang Y, Sun J, Li H, and Xu Z, “ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing,” IEEE Trans Pattern Anal Mach Intell, November 28 2018. [DOI] [PubMed] [Google Scholar]
- [6].Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, et al. , “Learning a variational network for reconstruction of accelerated MRI data,” Magn Reson Med, vol. 79, pp. 3055–3071, June 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Zhang J and Ghanem B, “ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing,” IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 1828–1837, 2018. [Google Scholar]
- [8].Aggarwal HK, Mani MP, and Jacob M, “MoDL: Model-Based Deep Learning Architecture for Inverse Problems,” IEEE Trans Med Imaging, vol. 38, pp. 394–405, February 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Schlemper J, Caballero J, Hajnal JV, Price AN, and Rueckert D, “A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans Med Imaging, vol. 37, pp. 491–503, February 2018. [DOI] [PubMed] [Google Scholar]
- [10].Adler J and Oktem O, “Learned Primal-Dual Reconstruction,” IEEE Trans Med Imaging, vol. 37, pp. 1322–1332, June 2018. [DOI] [PubMed] [Google Scholar]
- [11].Cheng J, Wang H, Ying L, and Liang D, “ Model Learning: Primal Dual Networks for Fast MR Imaging,” Medical Image Computing and Computer Assisted Intervention (MICCAI), pp. 21–29, 2019. [Google Scholar]
- [12].Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, and Rueckert D, “Convolutional Recurrent Neural Networks for Dynamic MR Image Reconstruction,” IEEE Trans Med Imaging, vol. 38, pp. 280–290, January 2019. [DOI] [PubMed] [Google Scholar]
- [13].Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, et al. , “Accelerating Magnetic Resonance Imaging via Deep Learning,” IEEE Conference on International Symposium on Biomedical Imaging (ISBI), pp. 514–517, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Kwon K, Kim D, and Park H, “A parallel MR imaging method using multilayer perceptron,” Med Phys,, vol. 44, pp. 6209–6224, December 2017. [DOI] [PubMed] [Google Scholar]
- [15].Zhu B, Liu JZ, Cauley SF, Rosen BR, and Rosen MS, “Image reconstruction by domain-transform manifold learning,” Nature, vol. 555, pp. 487–492, March 21 2018. [DOI] [PubMed] [Google Scholar]
- [16].Quan TM, Nguyen-Duc T, and Jeong WK, “Compressed Sensing MRI Reconstruction Using a Generative Adversarial Network With a Cyclic Loss,” IEEE Trans Med Imaging, vol. 37, pp. 1488–1497, June 2018. [DOI] [PubMed] [Google Scholar]
- [17].Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, et al. , “Deep Generative Adversarial Neural Networks for Compressive Sensing MRI,” IEEE Trans Med Imaging, vol. 38, pp. 167–179, January 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Han Y, Yoo J, Kim HH, Shin HJ, Sung K, and Ye JC, “Deep learning with domain adaptation for accelerated projection-reconstruction MR,” Magn Reson Med, vol. 80, pp. 1189–1205, September 2018. [DOI] [PubMed] [Google Scholar]
- [19].Ye JC, Han Y, and Cha E, “Deep Convolutional Framelets: A General Deep Learning Framework for Inverse Problems,” SIAM J Imag Sci,, vol. 11, pp. 991–1048, 2018. [Google Scholar]
- [20].Akcakaya M, Moeller S, Weingartner S, and Ugurbil K, “Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging,” Magn Reson Med, vol. 81, pp. 439–453, January 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lee DW, Yoo JJ, Tak SH, and Ye JC, “Deep Residual Learning for Accelerated MRI Using Magnitude and Phase Networks,” IEEE Trans Bio-Med Eng, vol. 65, pp. 1985–1995, September 2018. [DOI] [PubMed] [Google Scholar]
- [22].Hauptmann A, Arridge S, Lucka F, Muthurangu V, and Steeden JA, “Real-time cardiovascular MR with spatio-temporal artifact suppression using deep learning-proof of concept in congenital heart disease,” Magn Reson Med, vol. 81, pp. 1143–1156, February 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Wang S, Ke Z, Cheng H, Jia S, Ying L, Zheng H, et al. , “DIMENSION: Dynamic MR Imaging with Both K-space and Spatial Prior Knowledge Obtained via Multi-Supervised Network Training,” NMR in Biomedicine, 2019. [DOI] [PubMed] [Google Scholar]
- [24].Eo T, Jun Y, Kim T, Jang J, Lee HJ, and Hwang D, “KIKI-net: cross-domain convolutional neural networks for reconstructing undersampled magnetic resonance images,” Magn Reson Med, vol. 80, pp. 2188–2201, November 2018. [DOI] [PubMed] [Google Scholar]
- [25].Cai C, Wang C, Zeng Y, Cai S, Liang D, Wu Y, et al. , “Single-shot T2 mapping using overlapping-echo detachment planar imaging and a deep convolutional neural network,” Magn Reson Med, vol. 80, pp. 2202–2214, November 2018. [DOI] [PubMed] [Google Scholar]
- [26].Liu F, Feng L, and Kijowski R, “MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping,” Magn Reson Med, March 12 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Yoon J, Gong EH, Chatnuntawech I, Bilgic B, Lee J, Jung W, et al. , “Quantitative susceptibility mapping using deep neural network: QSMnet,” Neuroimage, vol. 179, pp. 199–206, October 1 2018. [DOI] [PubMed] [Google Scholar]
- [28].Cohen O, Zhu B, and Rosen MS, “MR fingerprinting Deep RecOnstruction NEtwork (DRONE),” Magn Reson Med, vol. 80, pp. 885–894, September 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Rosenblatt F, “The perceptron: a probabilistic model for information storage and organization in the brain,” Psychol Rev, vol. 65, pp. 386–408, November 1958. [DOI] [PubMed] [Google Scholar]
- [30].Liang Z-P and Lauterbur PC, Principles of Magnetic Resonance Imaging: A Signal Processing Perspective: Wiley-IEEE Press, 1999. [Google Scholar]
- [31].Hansen MS and Kellman P, “Image Reconstruction: An Overview for Clinicians,” Journal of Magnetic Resonance Imaging, vol. 41, pp. 573–585, March 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Gregor K and LeCun Y, “Learning fast approximations of sparse coding,” Proceedings of the 27th International Conference on International Conference on Machine Learning. Omnipress, 399–406, 2010. [Google Scholar]
- [33].Knoll F, Hammernik K, Kobler E, Pock T, Recht MP, and Sodickson DK, “Assessment of the generalization of learned image reconstruction and the potential for transfer learning,” Magn Reson Med, vol. 81, pp. 116–128, January 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Ravishankar S and Bresler Y, “MR image reconstruction from highly undersampled k-space data by dictionary learning,” IEEE Trans Med Imaging, vol. 30, pp. 1028–41, May 2011. [DOI] [PubMed] [Google Scholar]
- [35].Liu Q, Wang S, Ying L, Peng X, Zhu Y, and Liang D, “Adaptive Dictionary Learning in Sparse Gradient Domain for Image Recovery,” IEEE Trans Med Imaging,, vol. 22, pp. 4652–4663, December 2013. [DOI] [PubMed] [Google Scholar]
- [36].Poddar S and Jacob M, “Dynamic MRI Using SmooThness Regularization on Manifolds (SToRM),” IEEE Trans Med Imaging, vol. 35, pp. 1106–1126, April 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Nakarmi U, Wang Y, Lyu J, Liang D, and Ying L, “A Kernel-Based Low-Rank (KLR) Model for Low-Dimensional Manifold Recovery in Highly Accelerated Dynamic MRI,” IEEE Trans Med Imaging, vol. 36, pp. 2297–2307, November 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Liu R, Cheng S, Ma L, Fan X, and Luo Z, “Deep Proximal Unrolling: Algorithmic Framework, Convergence Analysis and Applications,” IEEE Trans Image Process, May 2 2019. [DOI] [PubMed] [Google Scholar]
- [39].Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, et al. , “Dermatologist-level classification of skin cancer with deep neural networks,” Nature, vol. 542, pp. 115–118, February 2 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Kalra M, Wang G, and Orton CG, “Radiomics in lung cancer: Its time is here,” Medical Physics, vol. 45, pp. 997–1000, March 2018. [DOI] [PubMed] [Google Scholar]