Development of a Control-Oriented Model of Social Cognitive Theory for Optimized mHealth Behavioral Interventions

Abstract

Mobile health (mHealth) technologies are contributing to the increasing relevance of control engineering principles in understanding and improving health behaviors, such as physical activity. Social Cognitive Theory (SCT), one of the most influential theories of health behavior, has been used as the conceptual basis for behavioral interventions for smoking cessation, weight management, and other health-related outcomes. This paper presents a control-oriented dynamical systems model of SCT based on fluid analogies that can be used in system identification and control design problems relevant to the design and analysis of intensively adaptive interventions. Following model development, a series of simulation scenarios illustrating the basic workings of the model are presented. The model’s usefulness is demonstrated in the solution of two important practical problems: 1) semiphysical model estimation from data gathered in a physical activity intervention (the MILES study) and 2) as a means for discerning the range of “ambitious but doable” daily step goals in a closed-loop behavioral intervention aimed at sedentary adults. The model is the basis for ongoing experimental validation efforts, and should encourage additional research in applying control engineering technologies to the social and behavioral sciences.

I. Introduction

CONTROL systems engineering principles have been applied in a diverse range of fields, spanning the traditional engineering disciplines and extending into the sciences, with applications in economic, environmental, biological, and many other types of systems. Health in particular is the recipient of significant research attention because of its societal significance. In the realm of health behavior, three behavioral risk factors: tobacco use, poor diet, and inactivity, contribute to four major chronic diseases: heart disease, Type 2 diabetes, lung disease, and some cancers. Together, these behaviors account for more than 50% of preventable deaths [1]. Given these facts, the following questions are deemed pertinent: Are dynamical system models capable of describing human behavior? Can decision frameworks designed on the basis of control engineering principles be useful, and ultimately improve behavioral interventions?

Some recent efforts have been made to apply control systems principles to problems in health behavior. A presentation of how time-varying behavioral interventions can be interpreted as closed-loop dynamical systems is made in [2]. Other work develops dynamical systems models for the Theory of Planned Behavior (TPB) [3], [4], [5] with application to gestational weight gain interventions [6], [7], [8]. Additional efforts have focused on applying control principles to optimizing interventions for smoking cessation [9], [10], [11], [12] and fibromyalgia pain [13], [14].

The emerging field of mobile and wireless health services (mHealth) [1] has been a driver for the application of control engineering principles to the behavioral sciences [15]. Not only does mHealth open new avenues for gathering a much wider realm of data than traditionally possible, it enables in-context behavioral interventions via smartphones and other wearable technologies [1]. These new “intensive” data streams and intervention mechanisms present challenges to many traditional behavioral theories, particularly in the ability of these to provide insights into novel intervention frameworks such as “just-in-time” adaptive and intensively adaptive interventions (JITAI and IAI, respectively; [16], [17], [18]). Novel approaches are needed that take advantage of these new data streams to generate more effective, predictive models of behavior, and apply these to the design and analysis of subsequent behavioral interventions.

Social Cognitive Theory (SCT), used as the basis for many behavioral interventions [19], provides a conceptual framework of the theorized influences on behavior and their interdependences that is amenable to various modeling techniques, including those associated with control systems engineering. Robust computational modeling approaches can provide a flexible and rigorous test to confirm, revise, or refute SCT and other theories [20]. Furthermore, computational models can aid in better specifying contextually relevant and instantaneous interrelationships measured continuously via mobile and wireless technologies. In a recent review of mobile health interventions, SCT or one of its variants served as the basis for all smoking cessation interventions that reported a theoretical basis, and was the predominant theoretical basis for weight management interventions reviewed [16].

The purpose of this paper is to present a comprehensive, control-oriented dynamical systems model for SCT taking into account its various constructs and interrelationships [21]. To accomplish this goal, fluid analogies are used. The model features additional components to address well-theorized psychological phenomena that have a significant impact on health behavior. In the paper, this is illustrated with the use of the model in defining the right range for “ambitious but doable” daily goals in a physical activity intervention for promoting walking in sedentary adults. Ultimately the model serves a useful purpose in enabling system identification and control system design, leading to optimized behavioral interventions based on control technology such as Hybrid Model Predictive Control (HMPC) [17], [22].

This document is organized as follows. Section II presents a brief description of SCT and its core elements. Section III describes the development of the fluid analogy based on the interconnections between the constructs and components of SCT. Section IV presents how the model is built, including assumptions and mathematical details; this section further discusses simulation results for a hypothetical case study. Section V shows how the model structure and experimental data from MILES, a physical activity intervention, can be used to identify a semi-physical model for SCT. Section VI presents a case study illustrating model enhancements applied specifically to a physical activity intervention, leading to the use of the model to predict a proper range for “ambitious but doable” step goals. Section VII gives a summary of conclusions and future work.

II. Social Cognitive Theory

Social Cognitive Theory (SCT) has its foundations in early learning theory, which limited its focus to behaviors learned by prior experience and conditioning. This led to the seminal work of Bandura [23] on Social Learning Theory (SLT), which incorporated the principles of observational or vicarious learning. SLT, however, failed to incorporate the self-belief and perceptions of the individual, leading to the introduction of the concept of self-efficacy [24].

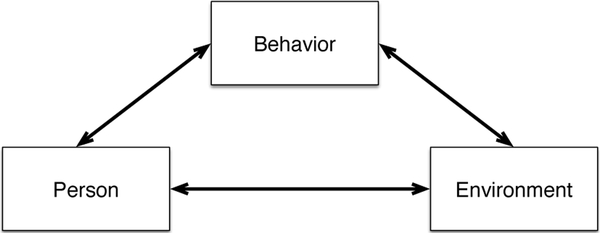
SCT describes a human agency model in which individuals proactively self-reflect, self-regulate, and self-organize [25]. Core to this perspective is the concept of reciprocal determinism or triadic reciprocity depicted in Fig. 1 in which personal influences (cognitions, affect, biology) and environment interact and mutually shape one another. Both of these factors interact and influence behavior, and that behavior, in turn, reciprocally shapes personal and environmental factors.

Fig. 1.

Triadic reciprocal determinism of Social Cognitive Theory.

In essence, SCT estimates the ability of an individual to engage in a determined behavior based on internal and external parameters and their interrelationships. Some of these are self-perceived and others can be externally measured.

The following SCT components are generated from the variation of external or internal stimuli, considered outputs from an engineering point of view. These components are:

• Self-efficacy, the perceived capability to do what is required to perform a given behavior. It plays a core role as a personal factor that influences behavior. It is influenced by behavior and other external and internal factors.

• Outcome expectancies, the perceived likelihood that performing a given behavior will result in certain outcomes. It is also a central component of the personal factors that influence behavior and are influenced by external factors and actual outcomes from previous engagements in to behavior.

• Behavioral outcomes, the outcomes (e.g., praise, criticism) added or removed as a result of engagement in the behavior of interest. These are directly related to outcome expectancies and the future behavior.

• Self-management skills, the set of skills involving a class of complex behaviors such as self-monitoring, goal setting, self-reinforcement, stimulus control, and related methods by which an individual increases the potential success for a given behavior. These contribute directly to self-efficacy and outcome expectancy.

• Behavior, the actual behavior studied, which can correspond to a particular metric of the activity (e.g., number of daily steps taken, minutes spent in daily moderate-to-vigorous physical activity) or the use of a substance (e.g., the number of cigarettes or alcoholic drinks consumed in a given day).

According to the theory, there are variables that act as stimuli to promote or discourage behavior. These are considered inputs, and can be external or internal to the individual. They are:

• Skills training. These activities help to increase (or decrease) the self-management skills of the individual. An example for physical activity is learning to use a pedometer.

• Observed behavior (vicarious learning). This influences not only self-efficacy for engaging in the behavior, but also outcome expectancies as the individual observes results of others performing the behavior.

• Perceived social support and verbal persuasion. These can help to increase self-efficacy. An example is the availability of others to engage in physical activity with the individual or to verbally support increased physical activity of the individual.

• Perceived barriers and obstacles. These are external conditions that affect self-efficacy and the resultant behavior. For example, physical activity can be reduced because of insufficient time, bad weather, and limited access to exercise facilities or safe walking paths.

• Intrapersonal states. These consist of an array of physical, mental, and emotional states of the individual, such as happiness and sadness, that either increase or decrease self-efficacy at any given time.

• Environmental context in which the behavior occurs, and which influences directly the resultant behavioral outcomes. In physical activity, this can include factors such as weather, or whether it is a weekday or weekend.

• Internal and external cues. These cues are stimuli that are antecedent to the behavior and are associated by experience over several trials with behavioral outcomes/expectancies and/or verbal rules and/or modeling. These directly influence behavior. In SCT, self-efficacy and outcome expectancies are often conceptualized as predispositions for engaging in any given behavior that is then triggered by a cue to action. In a more granular model, cue to action is likely to be treated as discrete and episodic inputs.

III. Developing a Fluid Analogy for SCT

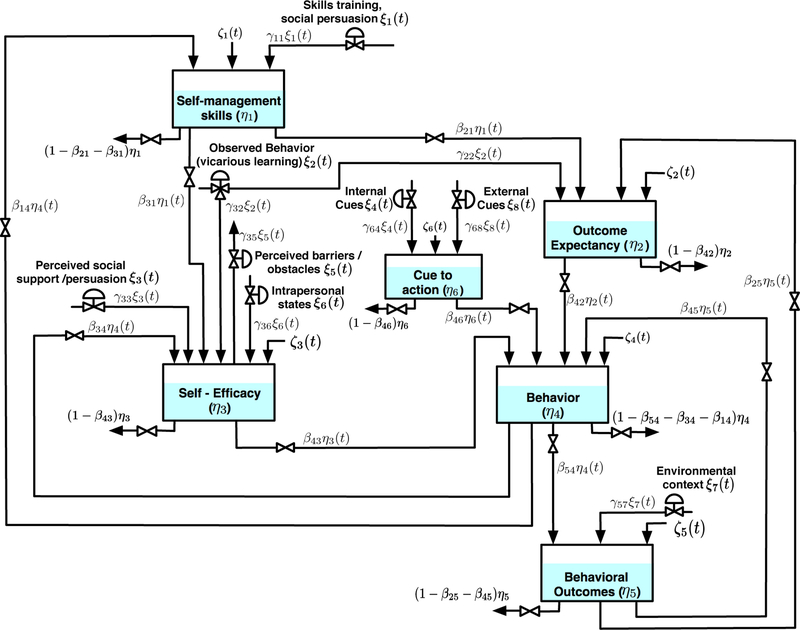
A fluid analogy of Social Cognitive Theory (SCT) is presented in Fig. 2. It depicts how the various components of SCT relate with one another over time, particularly to understand behavior. The use of a fluid analogy allows the organization of behavioral ideas into a structured framework that can be used to find a mathematical model [26], [27]. Main constructs are treated as inventories; other components and properties are depicted as inflows and/or outflows as listed in Table I.

Fig. 2.

Fluid analogy for Social Cognitive Theory.

TABLE I.

SCT signals related to variables in the fluid analogy

Inflows/Outflows (Inputs to the system)
Name	Symbol
Skills training	ξ1
Observed behavior	ξ2
Perceived social support and verbal persuasion	ξ3
Internal Cues	ξ4
Perceived barriers and obstacles	ξ5
Intrapersonal states	ξ6
Environmental context	ξ7
External Cues	ξ8
Inventory levels (Outputs from the system)
Name	Symbol
Self-management skills	η1
Outcome expectancies	η2
Self-efficacy	η3
Behavior	η4
Behavioral outcomes	η5
Cue to action	η6

In the schematic, behavior (η₄) is represented as a fluid inventory that changes its level over time. These changes can be in different factors (e.g., frequency, duration, type of activity) over time and based on various putative SCT factors. This model was developed based on a daily time frame (i.e., aggregate frequency and/or duration of behavior within any given day). Similar models with more or less granular time frames could be adapted from this daily time frame depending on the behavior of interest (e.g., smoking or cancer screening behaviors) and time frame of interest.

Self-efficacy (SE) (η₃) is a core construct of SCT and is represented as an inventory of varying levels that differs not only between individuals and specific behaviors, but also fluctuates within an individual over time. SE functions as both an independent variable influencing the likelihood of engaging in the associated behavior, and a dependent variable influenced by a number of factors that increase or decrease the inventory at any given time. The following are the SCT factors that are theorized to increase or decrease the SE inventory:

• 1)Perceived barriers and obstacles (ξ₅) to engaging in any given behavior deplete self-efficacy (SE).
• 2)Perceived social support and verbal persuasion from others increases SE (ξ₃).
• 3)Observed behavior (vicarious learning) (ξ₂). Learning from others observing their positive/negative results after their engagement in the behavior (e.g., observing others successfully performing the behavior increases SE).
• 4)Intra-personal states of the individual (ξ₆) either add to or deplete the level of SE.
• 5)Prior experience engaging in the behavior (β₃₄) is a gain parameter representing the critical learning feedback loop that adds or depletes SE to subsequently engage in the behavior. This is a feedback loop in which successfully engaging in the behavior increases SE to engage in the behavior, which subsequently increases the likelihood of engaging in the behavior.
• 6)Self-management or self-regulatory skills (η₁) influence both SE and outcome expectancies. Inputs into the self-management inventory include formal skills training, observational learning, and verbal persuasion (ξ₁).

The inventory outcome expectancies (η₂) is another important construct in SCT that contributes to the likelihood of any given behavior. These behaviors are inherently followed by positive and/or negative consequences, some proximal and some distal, or lack of consequences. For example, engaging in physical activity could result, short term, in feeling fatigued or invigorated. Social reinforcement may ensue from engaging in physical activity. Over the longer-term, physical activity may lead to improved health, or conversely in injury. These behavioral outcomes (η₅) produce a feedback loop to outcome expectancies (β₂₅). Experiencing and/or expecting positive outcomes from engaging in the behavior will lead to an increased likelihood of subsequently engaging in the behavior. As previously noted, these behavioral outcomes are greatly influenced by the environmental context in which the behavior occurs (ξ₇). Over time antecedent stimuli in the environment becomes associated with these behavioral outcomes, such that environment can cue an action given the change in the probability of the consequences.

The second input into outcome expectancies is observational learning or modeling (ξ₂). Observing the consequences of the behavior experienced by others adds or depletes the outcome expectancy inventory for that behavior. Given that observed behavior is feeding two inventories (i.e., self-efficacy and outcome expectancy), a two-way valve symbol (i.e., one input, two outputs) is used to represent this linked relationship; however, the effect of this input (ξ₂) over each inventory can be independently represented by their respective coefficient factor (i.e., γ₃₂ for self-efficacy and γ₂₂ for outcome expectancy). The third component that influences outcome expectancies is self-regulatory or self-management skills (β₂₁).

Finally, cue to action (η₆) directly influences behavior and is treated as an inventory that represents the various cues to action that occur during the day. These cues can be external (e.g., friend asks to take a walk) or internal (e.g., getting tired or stiff from sitting). They can occur naturally (e.g., good weather) or artificially (e.g., alarm reminder on phone to go for a walk) in the environment. To complete the fluid analogy, disturbances (ζ) are added. Disturbances are any exogenous factors that influence the inventories and produce unexplained variability in the model.

IV. Dynamical Model Description

To obtain a mathematical model from the fluid analogy in Fig. 2, it is necessary to describe how the inventories and their respective inflows and outflows fit within the mathematical perspective of dynamical systems. This procedure was initially illustrated in [3] in the development of a dynamic model for the Theory of Planned Behavior, and has been applied (in a less comprehensive manner than this paper) in [26], [27].

Six inventories are considered in Fig. 2, with their levels represented by the variables η₁,..,η₆. Eight exogenous inputs are shown and represented by ξ₁,..,ξ₈. From each inventory there are a number of inflow resistances represented by the coefficients γ₁₁,..,γ₆₈ and outflow resistances represented by β₂₁,..,β₅₄. One interpretation is to consider these resistances as the fraction of each inventory or input that leaves the previous instance and then feeds the next inventory.

There are other parameters that represent the physical characteristics of each inventory and flow; these have an important effect on the dynamic behavior of the system. Time constants τ₁,..,τ₆ represent the capacity and allow for exponential decay (or growth) of the inventory. Finally unmeasured disturbances (which may reflect unmodeled dynamics) are considered as ζ₁,..,ζ₆.

A. Differential Equation Representation

After the application of the fluid analogy the behavioral variables are treated as physical entities. The principle of conservation of mass is used: the sum of the inflows minus the outflows gives an accumulation term denoted by the time constant τ times the rate of change in the level of the inventory. The sum of all outflows must add up to the value of the respective inventory. For that reason, at each inventory output, an outflow of (1 − β_jk − ... − β_lm)η_i(t) is included in the model, where the β’s are the respective outflow coefficients.

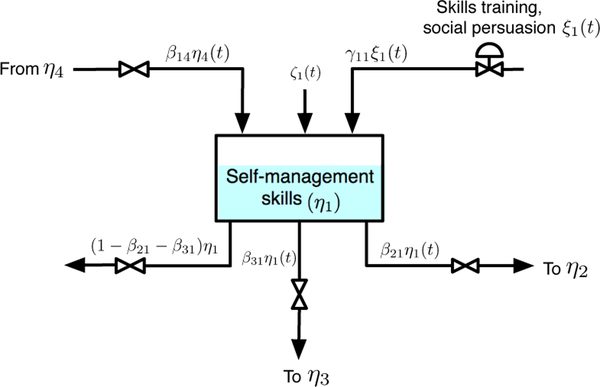
To demonstrate how the equations are derived, a subsection of the fluid analogy including only the first inventory (Self-management Skills (η₁)) with its inflows and outflows is presented in Fig. 3.

Fig. 3.

Self-management skills inventory (η₁) showing all its inflows and outflows

The principle of mass conservation applied to η₁ is:

$$\begin{gathered} {\tau }_1\frac{d{\eta }_1}{dt}={\gamma }_{11}{\xi }_1(t)+{\beta }_{14}{\eta }_4(t)+{\zeta }_1(t)-{\beta }_{31}{\eta }_1(t) \\ -{\beta }_{21}{\eta }_1(t)-(1-{\beta }_{21}-{\beta }_{31}){\eta }_1(t) \end{gathered}$$ (1)

which following simplifications yields:

$${\tau }_1\frac{d{\eta }_1}{dt}={\gamma }_{11}{\xi }_1(t)+{\beta }_{14}{\eta }_4(t)-{\eta }_1(t)+{\zeta }_1(t)$$ (2)

Applying the same procedure to all inventories, the following system of differential equations is obtained:

$$\begin{gathered} {\tau }_2\frac{d{\eta }_2}{dt}={\gamma }_{22}{\xi }_2(t)+{\beta }_{21}{\eta }_1(t)+{\beta }_{25}{\eta }_5(t)-{\eta }_2(t) \\ +{\zeta }_2(t) \end{gathered}$$ (3)

$$\begin{gathered} {\tau }_3\frac{d{\eta }_3}{dt}={\gamma }_{32}{\xi }_2(t)+{\gamma }_{33}{\xi }_3(t)-{\gamma }_{35}{\xi }_5(t)+{\gamma }_{36}{\xi }_6(t) \\ +{\beta }_{31}{\eta }_1(t)+{\beta }_{34}{\eta }_4(t)-{\eta }_3(t)+{\zeta }_3(t) \end{gathered}$$ (4)

$$\begin{gathered} {\tau }_4\frac{d{\eta }_4}{dt}={\beta }_{42}{\eta }_2(t)+{\beta }_{43}{\eta }_3(t)+{\beta }_{46}{\eta }_6(t)+{\beta }_{45}{\eta }_5(t) \\ -{\eta }_4(t)+{\zeta }_4(t) \end{gathered}$$ (5)

$${\tau }_5\frac{d{\eta }_5}{dt}={\gamma }_{57}{\xi }_7(t)+{\beta }_{54}{\eta }_4(t)-{\eta }_5(t)+{\zeta }_5(t)$$ (6)

$${\tau }_6\frac{d{\eta }_6}{dt}={\gamma }_{64}{\xi }_4(t)+{\gamma }_{68}{\xi }_8(t)-{\eta }_6(t)+{\zeta }_6(t)$$ (7)

The model per (2)–(7) consists of a system of first-order differential equations. If the dynamic response of a particular behavioral situation needs to be represented through a more elaborate transient response (such as overdamped, critically damped or underdamped responses), a second order system could be used [3]. If second order dynamics are present, these can be conceptualized as being part of an inventory system that is subject to self-regulation. This hypothetical situation is illustrated with an example considering only the effect from input external cues (ξ₈) to inventory cue to action (η₆) as a reference. To represent the correspondent transfer function as a system with one zero and two poles and assuming for simplicity that the input ξ₄ (internal cue) is equal to zero, the equation (7) can be rewritten as

$$\begin{gathered} {\tau }_6^2\frac{d^2{\eta }_6}{d{t}^2}+2\zeta {\tau }_6\frac{d{\eta }_6}{dt}={\gamma }_{68}\left({\xi }_8(t)+{\tau }_a\frac{d{\xi }_8(t)}{dt}\right) \\ -{\eta }_6(t)+{\zeta }_6(t) \end{gathered}$$ (8)

Terms τ_a and ζ are the coefficients required to extend the effect of input ξ₈ and inventory η₆ respectively to a second order representation. After neglecting perturbations, (8) yields to the transfer function:

$$\frac{{\eta }_6(s)}{{\xi }_8(s)}=\frac{{\gamma }_{68}\left({\tau }_{a}s+1\right)}{{\tau }_6^2{s}^2+2\zeta {\tau }_{6}s+1}$$ (9)

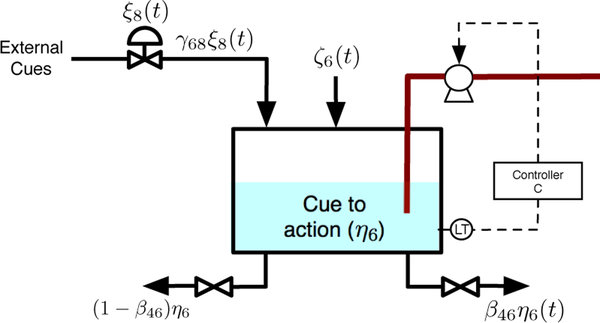
This second order system can be represented within the fluid analogy. One block that can serve for that purpose is a self-regulatory controller. To illustrate this process, in Fig. 4 the inventory cue to action (η₆) is shown with its inflows and outflows, excluding ξ₄.

Fig. 4.

Inventory Cue to Action (η₆) with the addition of a feedback controller to represent a second order system.

To obtain a more general representation, in accordance with control systems literature, the following variables are substituted:

$$d={\xi }_8;y={\eta }_6;\tau ={\tau }_6;K={\gamma }_{68}$$

yielding the following transfer function:

$$\frac{y(s)}{d(s)}=\frac{K\left({\tau }_{a}s+1\right)}{{\tau }^2{s}^2+2\zeta \tau s+1}$$ (10)

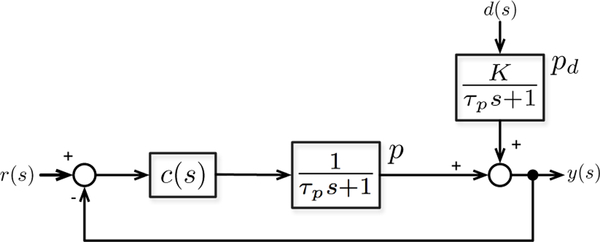
Fig. 5 represents a block diagram for a general second order inventory system with the proposed variables, where τ_p is the first order time constant for the tank.

Fig. 5.

Block diagram for a second-order inventory system.

The controller c(s) must be selected such that the transfer function from d(s) to y(s) matches the required second order system. To obtain a mathematical representation of the controller, a reverse engineering procedure is performed using the Internal Model Control (IMC) design method [28], applied to the following first order plant model:

$$\tilde{p}=\frac{1}{{\tau }_{p}s+1}$$ (11)

From here the initial Q-parametrized controller, and the obtained filter are

$$\tilde{q}={\tau }_{p}s+1,f=\frac{\text{λ}s}{({\text{λ}}_{1}s+1)({\text{λ}}_{2}s+1)}$$ (12)

resulting in

$$q=\frac{\lambda s({\tau }_{p}s+1)}{({\lambda }_{1}s+1)({\lambda }_{2}s+1)}$$ (13)

The required transfer function can be represented in terms of the IMC controller as

$$\frac{y}{d}=(1-\tilde{p}q)p_d=\left(1-\frac{\lambda s}{\left({\lambda }_{1}s+1\right)\left({\lambda }_{2}s+1\right)}\right)\frac{K}{{\tau }_{p}s+1}$$ (14)

After some mathematical simplifications the result from (14) is compared to (10), from where the following relations are obtained,

$${\text{λ}}_1{\text{λ}}_2={\tau }^2={\tau }_p{\tau }_a$$ (15)

$${\lambda }_1+{\lambda }_2=2\zeta \tau$$ (16)

$$\lambda ={\tau }_p+{\tau }_a-2\zeta \tau$$ (17)

and the values for the filter coefficients (λ_i) can be derived. To avoid a neglected controller (i.e., c(s) = 0) the following condition must be satisfied:

$${\text{λ}}_1+{\text{λ}}_2\ne {\tau }_p+{\tau }_a$$ (18)

Using these representations, the transfer function c(s) can be represented in a classical feedback controller form as

$$c(s)=\frac{(2\zeta \tau -{\tau }_a-{\tau }_p)s}{{\tau }_{a}s+1}$$ (19)

The presence of a feedback controller creates a connection to self-regulation, another behavioral theory [29].

A potential enhancement to the model per (2)–(7) is to include pure delays in the model, representing transportation lags in the inflows and outflows in the fluid diagram. This is not considered further in this paper as the experience of the authors with diverse behavioral data sets (featuring physical activity [30], [31], [32], weight and body composition change [3], [33], smoking cessation [11], and fibromyalgia [14]) has yet to show evidence of pure delays, or responses beyond second-order.

B. Model Considerations

The following model assumptions are needed to enforce the conservation of mass principle, and also to specify the simulation:

• The time unit of the model is days.

• The β coefficients must satisfy the following constraints to enforce the requirement that the sum of outflows add up to the value of the respective inventory:

  $$\begin{array}{l}{\beta }_{21}+{\beta }_{31}\le 1,{\beta }_{42}\le 1,{\beta }_{43}\le 1\\ {\beta }_{54}+{\beta }_{34}+{\beta }_{14}\le 1,{\beta }_{25}+{\beta }_{45}\le 1,{\beta }_{46}\le 1\end{array}$$
• The initial levels of the inventories are determined by solving the system of equations at steady state, obtaining the following results:

  $${\overline{\eta }}_1={\gamma }_{11}{\overline{\xi }}_1+{\beta }_{14}{\overline{\eta }}_4$$

  $${\overline{\eta }}_2=A+\left({\beta }_{21}{\beta }_{14}+{\beta }_{25}{\beta }_{54}\right){\overline{\eta }}_4$$

  $${\overline{\eta }}_3=B+\left({\beta }_{31}{\beta }_{14}+{\beta }_{34}\right){\overline{\eta }}_4$$

  $${\overline{\eta }}_4=\frac{{\beta }_{46}{\overline{\eta }}_6+{\beta }_{42}A+{\beta }_{43}B+{\beta }_{45}{\gamma }_{57}{\overline{\xi }}_7}{C}$$

  $${\overline{\eta }}_5={\gamma }_{57}{\overline{\xi }}_7+{\beta }_{54}{\overline{\eta }}_4$$

  $${\overline{\eta }}_6={\gamma }_{64}{\overline{\xi }}_4+{\gamma }_{68}{\overline{\xi }}_8$$

  where

  $$A={\gamma }_{22}{\overline{\xi }}_2+{\beta }_{21}{\gamma }_{11}{\overline{\xi }}_1+{\beta }_{25}{\gamma }_{57}{\overline{\xi }}_7$$

  $$B={\gamma }_{32}{\overline{\xi }}_2+{\gamma }_{33}{\overline{\xi }}_3-{\gamma }_{35}{\overline{\xi }}_5+{\gamma }_{36}{\overline{\xi }}_6+{\beta }_{31}{\gamma }_{11}{\overline{\xi }}_1$$

  $$\begin{gathered} C=1-{\beta }_{42}\left({\beta }_{21}{\beta }_{14}+{\beta }_{25}{\beta }_{54}\right)-{\beta }_{43}\left({\beta }_{31}{\beta }_{14}+{\beta }_{34}\right) \\ -{\beta }_{45}{\beta }_{54} \end{gathered}$$

• All inventories are restricted to have values within 0 and 100 %.

• Uncertainties are represented as zero mean stochastic signals.

• The exogenous signals: intrapersonal states (ξ₆) and environmental context (ξ₇) are considered as auto-correlated noise.

Necessary conditions for stability in the model are presented in Appendix A.

The majority of the signals considered in the model are defined as continuous (e.g, behavioral outcomes, intrapersonal states, and self-efficacy); however, some signals are considered discrete. For instance, in the physical activity problem, environmental context (where the signal can only take one of two values, meaning weekend or weekday), steps and step goals (e.g., a person can perform 100 or 101 steps, but not 100.25) are clearly discrete. From the perspective of designing optimized interventions as control systems, this dual definition of the type of signals yields to the use of techniques as Hybrid Model Predictive Control (HMPC) [22] where continuous and discrete signals are considered at the same time using the SCT model.

C. Illustrative Simulations

The simulations were designed to represent the amount of physical activity performed by an individual during a period of 20 days. The model parameters were chosen to show the model’s ability to reproduce well-known behavioral responses associated with SCT. A series of scenarios are depicted showing the dynamic response of the system to different variations on its inputs. All scenarios use the following parameter values:

• ${\tau }_1=1,{\tau }_2=1,{\tau }_3=1,{\tau }_4=2,{\tau }_5=1,{\tau }_6=3$

• $\begin{array}{l}{\gamma }_{11}=3,{\gamma }_{22}=1,{\gamma }_{32}=2,{\gamma }_{33}=1,{\gamma }_{35}=1,\\ {\gamma }_{36}=1,{\gamma }_{57}=2,{\gamma }_{64}=15,{\gamma }_{68}=15\end{array}$

• $\begin{array}{l}{\beta }_{21}=0.3,{\beta }_{31}=0.5,{\beta }_{42}=0.3,{\beta }_{43}=0.8,\\ {\beta }_{45}=0.1,{\beta }_{54}=0.3,{\beta }_{34}=0.2,{\beta }_{25}=0.3,\\ {\beta }_{14}=0.23,{\beta }_{46}=0.44\end{array}$

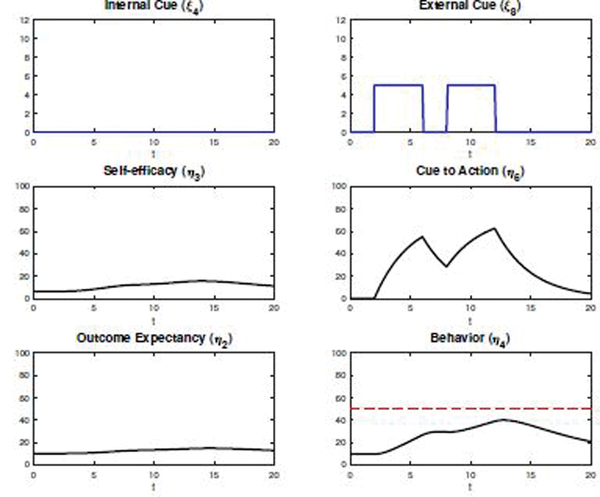
The first scenario is depicted in Fig. 6 and illustrates the effect of cue to action in the system under conditions of low self-efficacy. To produce low self-efficacy, observed behavior and perceived social support are held at constant low levels (ξ₂ = 3,ξ₃ = 3). The input perceived barriers is kept at a high value (ξ₅ = 10). In this setting, an external cue begins on day 2 (ξ₈ = 5), subsides on day 6–7, recurs on day 8 and then disappears on day 12. In the physical activity situation these cues could represent calls from friends asking the individual to go on a walk. The result of the applied signals on the inventories is a small, dampened increase on behavior that subsides when the cue to action is subsequently depleted. Because of the low self-efficacy, the engagement on the behavior is minimal.

Fig. 6.

Scenario 1: failure on the initiation of physical activity behavior under low self-efficacy and in the presence of external cues. A red dashed line at the reference level of 50% is shown for the behavior output.

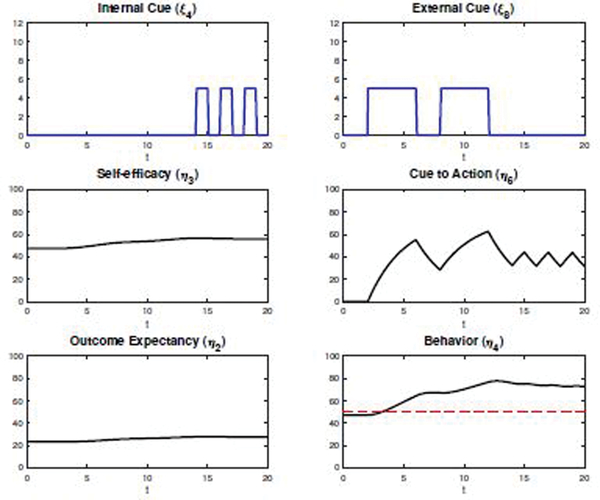
The second scenario, shown in Fig. 7, illustrates an initiation of the behavior and a further maintenance. The external cue to action (ξ₈) has similar values as the previous scenario, but within the context of high self-efficacy. Observed behavior and perceived social support are kept at high levels (ξ₂ = 10, ξ₃ = 10) and perceived barriers is decreased to a low level (ξ₅ = 2). The result is a considerable increase on the behavior inventory, and as a consequence some internal cues are now present (example: after a few days walking daily at the same time and one day resting, the individual experiences the internal desire to walk). The behavior is sustained with fewer external cues, but with an increased self-efficacy as a result of the feedback loop between SE and behavior.

Fig. 7.

Scenario 2: success of initiation and maintenance of physical activity behavior under high self-efficacy and in the presence of external and additional internal cues. A red dashed line at the reference level of 50% is shown for the behavior output.

Scenarios 1 and 2 correspond to well-known tenets from the theory that are useful from the perspective of behavioral scientists, and illustrate the performance of the model in adequately representing SCT. In the third scenario another way to represent behavior maintenance is presented. Input conditions are the same as scenario 2 with the high self-efficacy initial condition, but now the feedback loop composed by the inventories behavior (η₄), behavioral outcomes (η₅) and outcome expectancy (η₂) can be modeled with a more integrative effect so that it is capable of sustaining the magnitude of η₄. This is done with τ₄ = 15 and β₄₆ = 0.9; results are shown in Fig. 8.

Fig. 8.

Scenario 3: Maintenance of physical activity behavior under high self-efficacy, using a model possessing a higher degree of integration.

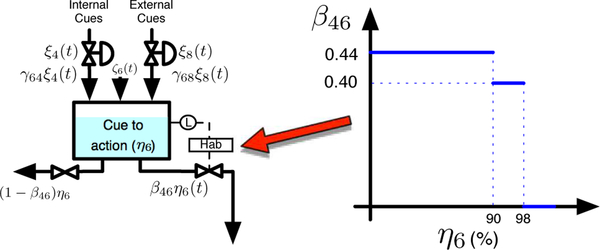
Human behavior displays many complex phenomena; for instance, in the fourth scenario, a diminished behavioral response that results from repeated stimulation can be observed. This type of response is not in accordance with the linear definition of the model; hence, a basic nonlinear strategy is implemented as follows: in the linear model if a stimulus (e.g., internal cue ξ₄) occurs continually or repeatedly, the response (behavior η₄) will grow until it reaches its maximum value, and remains there. The inventory cue to action (η₆) can be considered an accumulation of different cues such that its level is dependent on the magnitude and frequency of the received stimuli. This value is used to modify the parameter β₄₆ that represents the effect of the inventory cue to action (η₆) over behavior (η₄).

An example of a gain schedule for physical activity is shown in Fig. 9, where a reduced value of β₄₆ for higher values of (η₆) represents the reduction on the increased rate of behavior due to the effect of the repeated cues. If cue to action (η₆) is greater than 95% then β₄₆ is fixed to zero; there will be no further increases in behavior, and it will decrease to its original value. The gain schedule, shown in Table II and depicted in Fig. 9, is suitable for a physical activity example; however, a proper gain schedule should be developed individually for each particular case.

Fig. 9.

Gain schedule illustration for β₄₆

TABLE II.

Lookup table for β₄₆

Cue to action (η6)		β46
0 to 90%		0.44
91 to 95%		0.4
96 to 100%		0

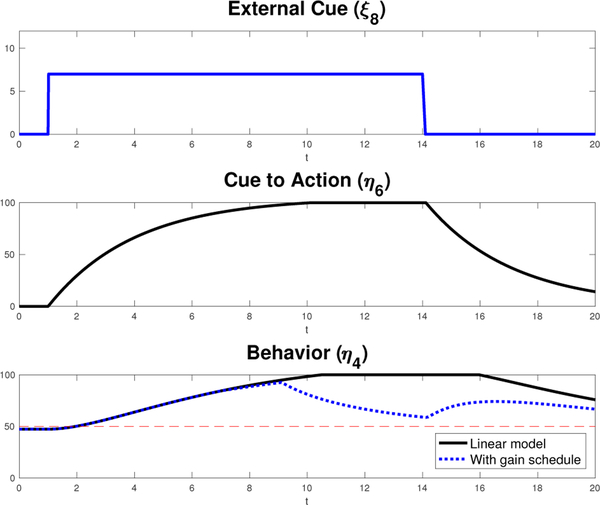
In the fourth scenario, showed in Fig. 10, external cue (ξ₈ = 7) is the only manipulated input; the other inputs have the same values defined in scenario 2. To allow the fast engagement in behavior, outputs cue to action (η₆) and behavior (η₄) are shown. Behavior (η₄) is depicted for both a linear case and the proposed model (nonlinear) with the gain schedule. An external cue (ξ₈) is applied from day 1 to day 14 (e.g., a friend calling the individual every day). Initially the individual responds with a sustained increase on the behavior, but after 7 days it starts to reduce the rate of increase (β₄₆ reduced from 0.44 to 0.4). Later, a decrease begins in behavior that ultimately results in a complete reduction of the activity (β₄₆ reduced to 0) and returns to the original value before the initial cue. At day 14, the repeated stimulus (ξ₈) is removed.

Fig. 10.

Scenario 4: Behavior under a persistent external cue that causes a reduction in reinforcer effectiveness, and later recovery after the stimulus is removed. High self-efficacy conditions are considered. Two plots for behavior are shown: one following a linear response, the other using the proposed model with a nonlinear block.

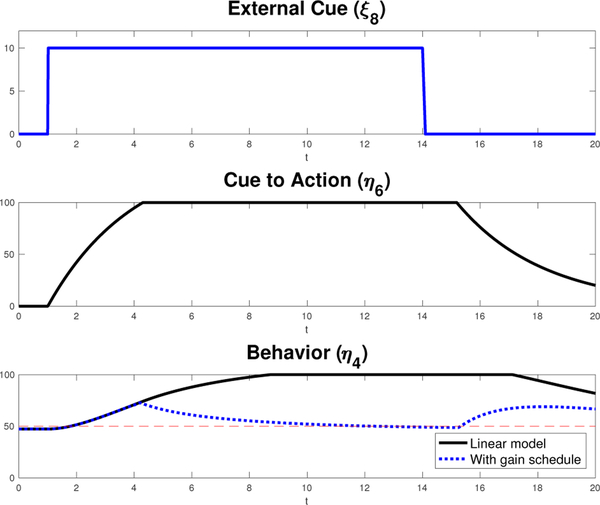
The final scenario, shown in Fig. 11, differs from the previous one only in the increased value of the external cue (ξ₈ = 10), that can be interpreted as a more frequent stimulation (e.g., a friend making more frequent calls per day). The result is an earlier engagement in the reduced response process.

Fig. 11.

Scenario 5: Behavior under a higher external cue (more frequent stimulus) that causes reduction in reinforcer effectiveness and a later recovery once the stimulus is removed. Conditions of high self-efficacy are considered.

V. Semi-physical Identification using mHEALTH Intervention Data

In this section, measured data from a physical activity intervention is used to obtain model parameters from the proposed SCT structure using semi-physical identification techniques [34]. The data is taken from a study called Mobile Interventions for Lifestyle Exercise and Eating at Stanford (MILES) [35], focused on behavioral interventions for physical activity in aging adults using mobile phones. The data is from a subset of the full sample; specifically, 68 adults ages 45 years and older agreed to participate in the experiment with the support of a smartphone for eight weeks. To measure behavioral variables, some questionnaires [35] were used and the responses were obtained via a smartphone. Physical activity (behavior) was measured by an accelerometer within the phone, which was validated relative to an ActiGraph accelerometer, which is commonly used in the physical activity literature [36].

The MILES study included multiple between-person experimental conditions (i.e., different smartphone app interventions focused on promoting behavior change using different motivational frames such as social, affective, or rational) and several variables measured on a daily basis. For comparison purposes, a smaller subset of participants with complete data was used, including interactions with the smartphone app features for the rational app [35]. The selected variables and their respective match with the SCT model are:

• Time spent (in seconds) on reading tips: skills training (ξ₁)

• Number of reminders sent to set a new goal: external cues (ξ₈)

• Self-reported physical activity self-efficacy (scale 1–11): self-efficacy (η₃)

• Average number of counts per minute: behavior (η₄).

The “counts” variable from the smartphone measures movement by the accelerometer, and is an indirect indication of the physical activity performed by the person who is carrying the phone.

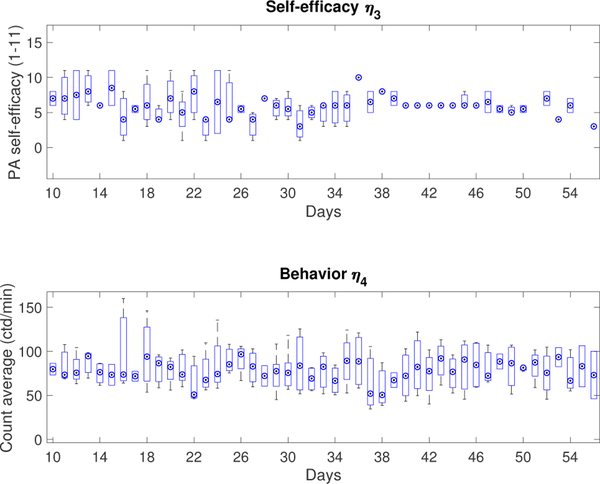
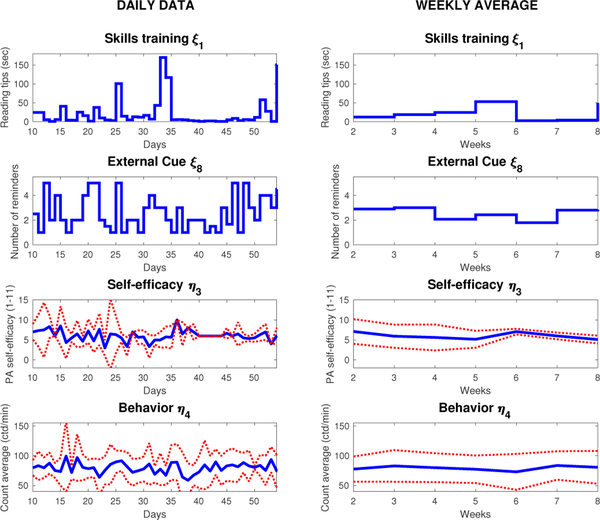
Fig. 12 presents data from six participants for the measured signals self-efficacy, and behavior. These signals are represented using box plots that illustrate the variability of the collected data by showing the 25th and 75th percentiles and the median for each sample time. Fig. 13 illustrates averaged data from the same six participants for the selected variables, and including weekly averages.

Fig. 12.

Boxplot of MILES output data averaged for a subset of six participants

Fig. 13.

MILES data averaged for a subset of six participants with the required signals for raw daily sampling and weekly average including 95 % confidence intervals represented as red dotted lines.

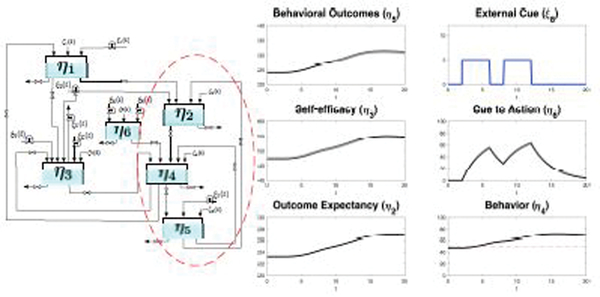
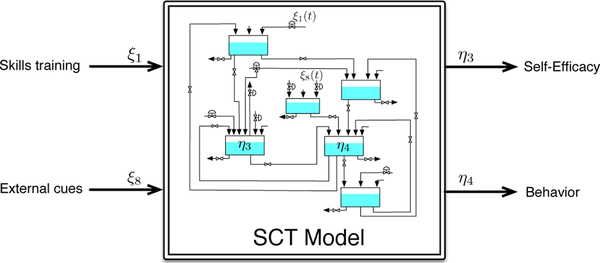
In this data based study, the purpose is to explain the effects of two inputs over two outputs in the context of the model. However, there are other signals that were still present in the experiment and in the model but were not available as measurable data. Some of these signals like environmental context and intrapersonal states could be responsible for much of the variability in the outputs. To account for variability, weekly averaged data is used instead of daily data. This consideration may be interpreted as a smoothing filtering action applied to the original data. The model parameters are estimated using the sub-system illustrated in Fig. 14, by a greybox system identification procedure [34], [37]. This allows the search of parameters to keep the defined model structure.

Fig. 14.

SCT model subsystem used for semi-physical identification with the MILES data.

Grey-box parameter estimation relies on two sources of information to estimate the required parameters: prior knowledge of the system (i.e., the SCT dynamical model) and experimental data. The state space representation of the system has the structure:

$$\begin{gathered} {\stackrel{.}{\mathit{x}}}_{\mathit{p}}(t)=\mathbf{A}({\mathit{\theta }}_{\mathit{p}}){\mathit{x}}_{\mathit{p}}(t)+\mathbf{B}({\mathit{\theta }}_{\mathit{p}}){\mathit{u}}_{\mathit{p}}(t)+\mathit{K}\mathit{e}(t) \\ {\mathit{y}}_{\mathit{p}}(t)=\mathbf{C}{\mathit{x}}_{\mathit{p}}(t)+\mathit{v}(t) \end{gathered}$$ (20)

where:

• x_p = [η₁ ...η₆] denotes a vector of n = 6 state variables,

• u_p = [ξ₁ ξ₈] denotes a vector of m = 2 input variables,

• y_p = [η₃ η₄] denotes a vector of p = 2 output variables,

• $\mathbf{A}\in {ℝ}^{n\times n},\mathbf{B}\in {ℝ}^{n\times m},\mathbf{C}\in {ℝ}^{p\times n}$ are the state matrices,

• ${\theta }_p\in {ℝ}^{np}$ denotes a vector of np = 18 unknown model parameters,

• e(t) and v(t) are uncertainties associated to each one of the states and outputs.

Based on the SCT structure the unknown model parameters are:

$$\begin{gathered} {\mathit{\theta }}_{\mathit{p}}=[\begin{array}{lllllllll}{\tau }_1\hfill & {\tau }_2\hfill & {\tau }_3\hfill & {\tau }_4\hfill & {\tau }_5\hfill & {\tau }_6\hfill & {\beta }_{14}\hfill & {\beta }_{21}\hfill & {\beta }_{25}\hfill \end{array} \\ \begin{array}{lllllll}{\beta }_{31}\hfill & {\beta }_{34}\hfill & {\beta }_{42}\hfill & {\beta }_{43}\hfill & {\beta }_{46}\hfill & {\beta }_{54}\hfill & {\beta }_{45}\hfill \end{array} \\ {{\gamma }_{11}{\gamma }_{68}]}^{\top } \end{gathered}$$ (21)

and the state matrices are:

$$\mathbf{A}({\mathit{\theta }}_{\mathit{p}})=\left(\begin{array}{cccccc}-\frac{1}{{\tau }_1}& 0& 0& \frac{{\beta }_{14}}{{\tau }_1}& 0& 0\\ \frac{{\beta }_{21}}{{\tau }_2}& -\frac{1}{{\tau }_2}& 0& 0& \frac{{\beta }_{25}}{{\tau }_2}& 0\\ \frac{{\beta }_{31}}{{\tau }_3}& 0& -\frac{1}{{\tau }_3}& \frac{{\beta }_{34}}{{\tau }_3}& 0& 0\\ 0& \frac{{\beta }_{42}}{{\tau }_4}& \frac{{\beta }_{43}}{{\tau }_4}& -\frac{1}{{\tau }_4}& \frac{{\beta }_{45}}{{\tau }_4}& \frac{{\beta }_{46}}{{\tau }_4}\\ 0& 0& 0& \frac{{\beta }_{54}}{{\tau }_5}& -\frac{1}{{\tau }_5}& 0\\ 0& 0& 0& 0& 0& -\frac{1}{{\tau }_6}\end{array}\right)$$ (22)

$$\mathbf{B}({\mathit{\theta }}_{\mathit{p}})=\left(\begin{array}{cc}\frac{{\gamma }_{11}}{{\tau }_1}& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& 0\\ 0& \frac{{\gamma }_{68}}{{\tau }_6}\end{array}\right)$$ (23)

$$\mathbf{C}=\left(\begin{array}{llllll}0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill & 0\hfill & 0\hfill \end{array}\right)$$ (24)

To estimate θ, the well-known prediction-error identification methods (PEM) [38] are used. The one-step ahead prediction error of the system is:

$$\epsilon (t,{\mathit{\theta }}_{\mathit{p}})={\mathit{y}}_{\mathit{p}}(t)-{\widehat{\mathit{y}}}_{\mathit{p}}(t|t-1,{\mathit{\theta }}_{\mathit{p}})$$ (25)

where ${\widehat{\mathit{y}}}_{\mathit{p}}\left(t|t-1,{\mathit{\theta }}_{\mathit{p}}\right)$ is the predicted output based on estimated models. Estimation is performed in MATLAB using the commands idgrey and greyest from the System Identification Toolbox. The estimated values of the model parameters are:

• $$\begin{gathered} {\tau }_1=0.66,{\tau }_2=2.25,{\tau }_3=0.55,{\tau }_4=3,{\tau }_5=0.94, \\ {\tau }_6=\mathrm{0.64.} \end{gathered}$$

• $$\begin{gathered} {\gamma }_{11}=1.32,{\gamma }_{22}=1,{\gamma }_{32}=1,{\gamma }_{33}=1,{\gamma }_{35}=1, \\ {\gamma }_{36}=1,{\gamma }_{57}=1,{\gamma }_{64}=1,{\gamma }_{68}=\mathrm{0.88.} \end{gathered}$$

• $\begin{array}{l}{\beta }_{21}=0.9,{\beta }_{31}=0.05,{\beta }_{42}=0.9,{\beta }_{43}=0.5,\\ {\beta }_{54}=0.67,{\beta }_{34}=0.18,{\beta }_{25}=0.5,{\beta }_{14}=0.65,\\ {\beta }_{46}=0.01,{\beta }_{45}=\mathrm{0.1.}\end{array}$

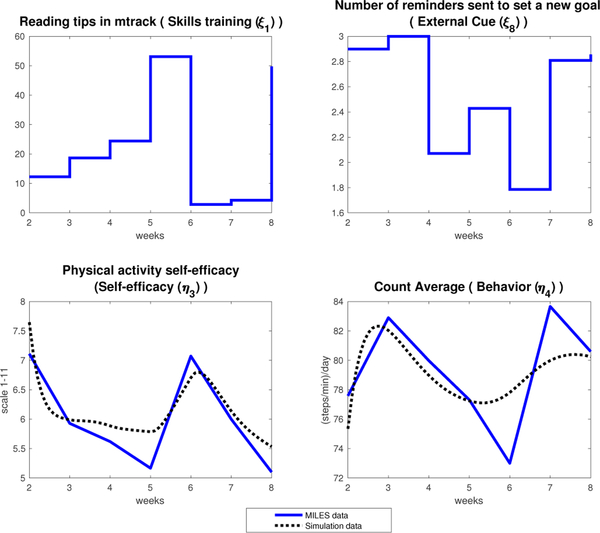
The results are shown in Fig. 15, including the MILES data and simulations based on the model, with the specified parameters.

Fig. 15.

Data from MILES study (solid line) contrasted against simulation results from the model (dotted line) considering the same input values for both scenarios.

A similar pattern between the responses from the model and the MILES data can be observed. The percentage of fit between the two signals is calculated using the formula:

$$\%fit=100\left(1-\frac{\Vert {\mathit{y}}_{\mathit{p}}-{\widehat{\mathit{y}}}_{\mathit{p}}\Vert }{\Vert {\mathit{y}}_{\mathit{p}}-\mathrm{mean}({\mathit{y}}_{\mathit{p}})\Vert }\right)$$ (26)

where $\Vert \cdot \Vert$ stands for two-norm, that for a vector r is equal to $\Vert \mathit{r}\Vert =\sqrt{{\mathit{r}}^T\mathit{r}}$. The computed fits are:

$$\mathit{\text{Self-efficacy}}({\eta }_3)=49.54\%$$

$$Behavior({\eta }_4)=34.95\%$$

The mismatch between the data and model output can be explained by unmeasured dynamics, disturbances and unknown external signals. Since the data come from human behavior and in some cases from information collected via questionnaires, this type of mismatch is expected; however, it is observable that the same shape of response could be predicted with the proposed model. For a more formal validation, a semi-physical system identification procedure may be performed, utilizing a complete dataset with more appropriate a priori within-person experimental procedures.

VI. Case Study: Predicting “Ambitious but Doable” Goals in a Physical Activity Behavioral Intervention

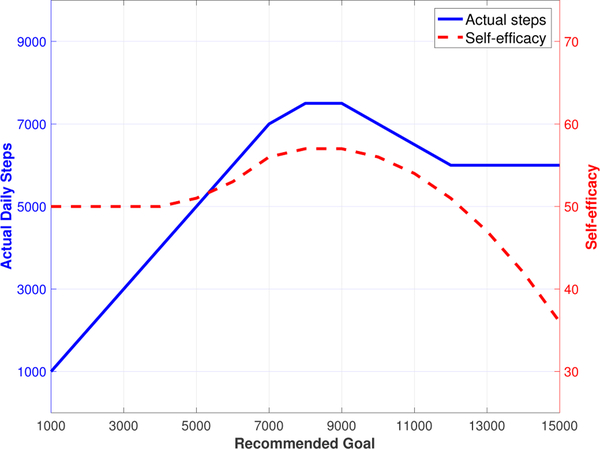
From a psychological standpoint, the continuous application of a positive stimulus may lead to a negative response; this response can take the shape of what is called an “inverted U” [39]. In the case of a behavioral intervention for promoting physical activity using step goals as the main driver for promoting sustained physical activity, prior clinical experience [40] suggests the existence of an ideal range at any given moment for a step goal (e.g., if a person walked 7000 steps per day last week, next week an ideal goal range might be 7500–8500 steps). In this context, individuals might react negatively to a high goal that they may consider difficult or impossible to reach; this effect can be represented through a steady state equilibrium curve such as Fig. 16.

Fig. 16.

Hypothetical steady state equilibrium curve depicting the tradeoff between physical activity (daily steps), goals, and self-efficacy. The x-axis corresponds to recommended goals (ξ₈), while the y-axis gives the actual performed steps (η₄) and self-efficacy (η₃).

Fig. 16 depicts a hypothetical equilibrium curve with numerical values chosen to resemble actual physical activity interventions [35], [40]. The x-axis represents the recommended daily step goals; one of the y-axes represents the achieved average daily steps (e.g., daily average for a full week), while the second y-axis represents the individual’s perceived self-efficacy. For this hypothetical case, a baseline initial behavior of 7000 steps for goals (e.g., average steps performed the last week) is assumed; hence, the ideal range of goals is positioned around this baseline. The “inverted U” shape of the curve is formed around the ideal goal range, since recommended goals that are above or below this range, result in lower achieved steps, and consequently inefficient responses. For the higher part of the range (i.e., higher goals) this result can be attributed to a state of pessimism in the individual caused by such a high goal setting.

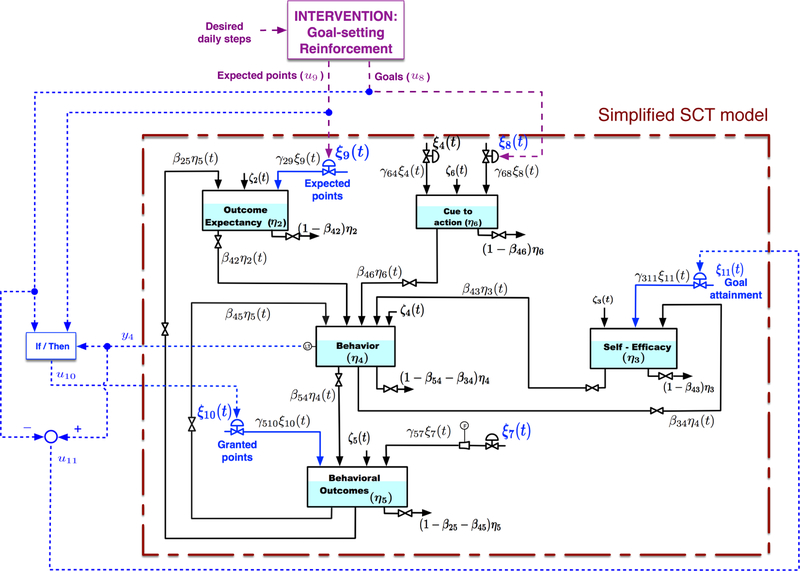
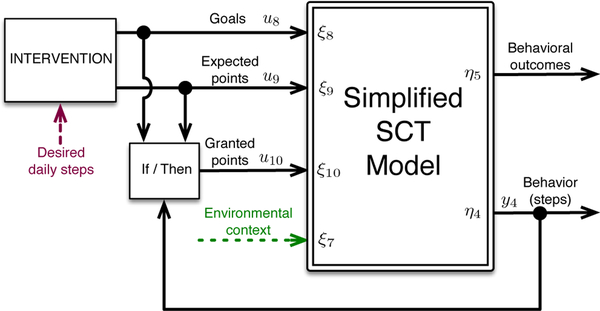
At first glance, and relying on a black-box, input-output perspective, it would appear like the relationship between goals and actual steps is nonlinear, with a process gain (denoted by the slope of a tangent line at any steady-state operating point) changing in sign from positive to negative as goals become too ambitious. This response is akin to what is seen in continuous-stirred tank reactors with reversible dynamics, and has been studied as a representative problem for nonlinear control in [41]. However, it is possible to show that relying on Social Cognitive Theory, particularly taking into account how self-efficacy influences what constitutes a doable goal, the phenomenon in Fig. 16 can be reproduced on the basis of linear models. We rely on a simplified version of the SCT model that considers inventories η₂, η₃, η₄, η₅, η₆, and incorporates additional inputs, as depicted in Fig. 18 and described subsequently in this section. The proposed intervention is depicted in Fig. 17, where the main goal for the participant is to achieve and sustain the desired level of daily steps by the end of the intervention; this can be reached by systematically delivering the following components:

• Daily goals u₈, these can be delivered as an external cue to action (ξ₈) to establish quantitatively the desired behavior (e.g., 10,000 steps per day). They can vary according to the intervention objectives or the desired rate of change.

• Expected points u₉, delivered as a new input to the model called outcome expectancy for reinforcement (ξ₉) connected directly to the outcome expectancy (η₂) inventory, allowing the participant to know the daily expected reward points that will be translated later into specific rewards (e.g., gift cards, gym subscriptions).

• Granted points u₁₀, delivered as an additional input to the model called reinforcement (u₁₀), that is fed to the behavioral outcomes (η₅) inventory, only if the performed behavior y₄ = η₄ (e.g., steps) is greater or equal than the specified goal u₈. This is achieved through an “If/Then block” that constitutes an inherent nonlinearity within the dynamical system.

Fig. 18.

Fluid analogy for the physical activity intervention based on a simplified SCT model that relies on a goal-attainment signal and the self-efficacy inventory η₃ to enable the model to predict the acceptable ranges for goal-setting.

Fig. 17.

Conceptual representation of the physical activity intervention, based on a simplified version of the SCT model.

The proposed approach to represent the ideal performance range, and hence goal setting, relies on the simplified SCT model. This is illustrated in Fig. 18 where the physical activity intervention is affecting the model through inputs: goals (u₈), expected and granted points (u₉, u₁₀), and a new signal called Goal attainment (u₁₁) that gives an indication of the amount of attainment to the established goals as:

$$u_{11}=y_4-u_8$$ (27)

This signal is fed into the self-efficacy inventory such that if the individual fails to reach a goal, a negative effect will be produced that ultimately will lead to a decrease in performed behavior. The magnitude of this negative effect is quantified through gains γ₃₁₁ and parameter β₄₃.

To show the capability of the proposed approach to achieve an “inverted U” and define the ideal range, a simulation was performed using the model depicted in Fig. 18 with goals (u₈) as the unique input, and considering ζ_i = 0 ∀i. Performing the stability analysis described in Appendix A and considering the effect from behavior (η₄) to self-efficacy (η₃), one of the necessary stability conditions detailed in (40) is:

$${\beta }_{34}<1$$ (28)

Considering that the added signal u₁₁ = y₄ − u₈ includes a linear dependency on the inventory behavior (y₄ = η₄), the total effect from η₄ to η₃ is now β₃₄ + γ₃₁₁; hence the previously discussed stability condition is modified as:

$${\beta }_{34}+{\gamma }_{311}<1$$ (29)

Using the hypothetical representation from Fig. 16 and the semi-physical identification procedure described in Section V, the following set of SCT model parameters is selected to represent the ideal range of step-goals feature, and to satisfy the stability sufficient conditions:

• $\begin{array}{l}{\tau }_2=28.26,{\tau }_3=876.07,{\tau }_4=20.19,{\tau }_5=25.98,\\ {\tau }_6=\mathrm{0.06.}\end{array}$

• $\begin{array}{l}{\gamma }_{29}=1,{\gamma }_{64}=1,{\gamma }_{68}=1.01,{\gamma }_{33}=1,{\gamma }_{510}=1,\\ {\gamma }_{57}=1,{\gamma }_{35}=1,{\gamma }_{36}=1,{\gamma }_{311}=\mathrm{0.2.}\end{array}$

• $\begin{array}{l}{\beta }_{25}=0.12,{\beta }_{34}=0.07,{\beta }_{42}=0.27,{\beta }_{45}=0.19,\\ {\beta }_{46}=0.13,{\beta }_{43}=0.06,{\beta }_{54}=\mathrm{0.01.}\end{array}$

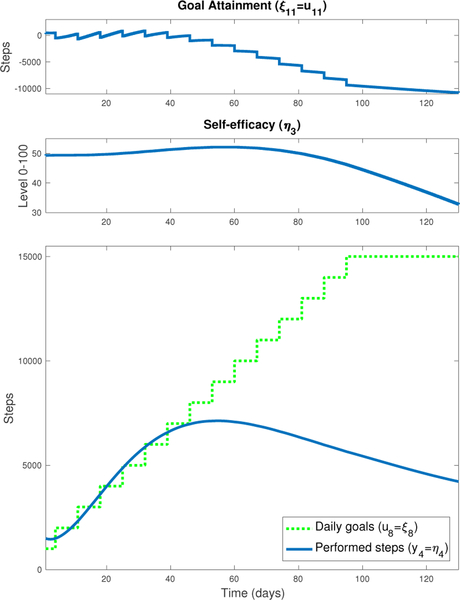
Simulation results are shown in Fig. 19. During a few initial cycles, the performed steps approximate the set goal. However, the magnitude of the difference between the goal and the steps increases as observed in the goal attainment (u₁₁) signal, causing a considerable reduction in self-efficacy (η₃) that eventually leads to a considerable reduction of performed steps (y₄ = η₄). This approach must be carefully verified via data obtained from system identification experiments, where it is crucial to obtain well validated measurements for self-efficacy and the other SCT model constructs.

Fig. 19.

Simulation results for a physical activity behavioral intervention, representing the ideal range of step-goals feature by influencing self-efficacy (η₃) through the goal attainment (u₁₁) signal.

VII. Conclusions, Current, and Future Work

This paper has described how Social Cognitive Theory (SCT) can be represented as a dynamical system that can be in turn be used for system identification and control design purposes, with the ultimate goal of improving intensively adaptive interventions in mHealth. Fluid analogies were utilized to represent the dynamic behavior portrayed in the theory. The result was a computational model which could support visualization and validation efforts. Simulations proved to be valuable for better specifying implicit assumptions made within SCT to ensure better operationalization; for example, the scenarios depicted the power of cue to action to strongly and rapidly influence behavior, much more so than the cognitive constructs of SCT (e.g., self-efficacy, outcome expectancies). There are additional details and approaches involved in the theory, such as the overflow of reward structures (behavioral outcomes), that could be modeled with nonlinear schemes that may improve the accuracy of the model.

While the SCT model has been motivated on the basis of applications to mHealth, its potential use is much larger. Some emerging applications that utilize the model developed in this paper include human-robot interaction [42] and human-in-the-loop behavior with HVAC systems [43].

Semiphysical identification using the MILES data demonstrated the ability of the model to depict a real behavioral problem like physical activity. In future work, the generalizability of this model for different behaviors should be examined in greater detail [44]; it can serve as a valuable tool in optimizing interventions and accomplishing agile science [45].

As a case study for demonstrating the usefulness of the model, the ability to estimate the ideal range of step goals, a well-known issue in physical activity interventions, was presented. This feature was incorporated into the model by defining a goal achievement signal that is then introduced in the self-efficacy inventory. Simulations showed the ability of this augmented model to display the characteristic “inverted U” response between goals and behavior through the relationships between behavioral constructs denoted by SCT, in lieu of having to introduce additional nonlinear functionality in the model. Consequently, this model can be used to predict the range of “ambitious but doable” goals in a behavioral intervention setting.

Current and future activities in the model involve examining experimental design issues and additional experimental validation. One important goal of the experimental input design is to satisfy identification requirements such as persistence of excitation, while at the same time keeping variations within user-defined, “patient-friendly” [46] constraints. An additional challenge is to obtain outputs that are consistent with the goals and practical demands of the intervention. One approach is to rely on standard input signals (i.e., random or pseudo-random signals, multisines) with sufficient excitation; however, this may cause undesired variations in the participant’s behavior. Therefore an initial judicious experiment is proposed; these inputs rely on an a priori study [35] designed to produce data according to an expected profile, combined with classical input signals that will facilitate capturing the dynamical relationships among variables. The informative model can also form the basis for subsequent optimization in experimental design; an optimized experimental design procedure is described in [47] and [48]. Drawing on these ideas is Just Walk, a pilot-scale mHealth intervention [49], which has implemented an informative identification test using multisine inputs to 22 participants, and which seeks to examine daily “ambitious but doable” step goals and reinforcements (i.e., points) for achieving goals. The experimental design and analysis procedure of this intervention relying on ARX models is described in [30]; estimating semi-physical SCT models is currently underway.

Ultimately, one of the principal uses of the SCT model is as an internal model in control system design. Hybrid Model Predictive Control (HMPC) algorithms [22] provide an effective framework for developing participant-friendly behavioral interventions [13], [14], [9], [7], [8]. This control technology effectively combines feedback feedforward control action by online optimization of a cost function using a receding horizon and is particularly suited for designing discrete levels inputs [50]. A Mixed Logical Dynamical (MLD) framework is used to represent linear hybrid systems which are systems with real and integer states. This controller formulation was motivated by the needs of nontraditional control applications that are suitably described by hybrid production-inventory systems like those described in the SCT fluid analogy. The application of HMPC to the SCT model (in simulation) with the goal of achieving a “perpetually adapting” intervention that includes both training and maintenance phases (the transition between these achieve by online controller reconfiguration) has been examined in [15], [51].

Biography

César A. Martín (M’15) was born Guayaquil, Ecuador in 1971. He received a B.S. degree in Electrical Engineering in 1993 and a M.B.A degree in 1996 from ESPOL Polytechnic University, Ecuador, and the M.S.E. and Ph.D. degrees in Electrical Engineering from Arizona State University, AZ, US in 2003 and 2016 respectively.

He has been working as an associate professor since 1996, and currently is the Associate Dean of the department of Electrical and Computing Engineer at ESPOL Polytechnic University in Guayaquil, Ecuador. He also worked in the Control Systems Engineering Laboratory at Arizona State University (2012–2016). His research interests include system identification, dynamic modeling, and control applications in behavioral medicine and agricultural settings.

Daniel E. Rivera (M’91-SM’05) received the B.S. degree in chemical engineering from the University of Rochester, New York in 1982, the M.S. degree in chemical engineering from the University of Wisconsin-Madison in 1984, and the Ph.D in chemical engineering from the California Institute of Technology, Pasadena, California in 1987.

He is a Professor of chemical engineering in the School for Engineering of Matter, Transport, and Energy at Arizona State University in Tempe, Arizona. Prior to joining ASU he was a member of the Control Systems Section of Shell Development Company in Houston, Texas. His research interests span the topics of system identification, robust process control, and applications of control engineering to problems in supply chain management and behavioral medicine.

Since 2014, Dr. Rivera has chaired the IEEE Control System Society’s (CSS’s) Outreach Task Force. He was the inaugural chair of the IEEE CSS technical committee on healthcare and medical systems (2013 – 2014) and has also chaired the IEEE CSS technical committee on system identification and adaptive control (2007 – 2012). He is past associate editor for the IEEE Transactions in Control Systems Technology (2003 – 2010) and the IEEE Control Systems Magazine (2003 – 2007). In 2007 he was awarded a K25 Mentored Quantitative Research Career Development Award from the National Institutes of Health to study the application of control systems engineering principles to optimize personalized prevention and treatment interventions for drug abuse.

Eric B. Hekler received the Ph.D. in Clinical Health Psychology from Rutgers University, and completed postdoctoral training at Stanford University.

He is an Associate Professor in the Department of Family Medicine and Public Health in the University of California, San Diego (UCSD), the Director of the Center for Wireless and Population Health Systems within the Qualcomm Institute at UCSD, and a faculty member of the Design Lab at UCSD. Prior to UCSD, he was a professor at Arizona State University. Dr. Hekler’s research is broadly focused on advancing methods in the design, creation, optimization, evaluation, and reuse (scaling up and out) of digital health technologies. His work is inherently transdisciplinary by advancing methods via melding approaches from behavioral science/psychology, public health, human-computer interaction (HCI), control systems engineering, and computer science. There are three interdependent themes to his research for advancing 1) methods for optimizing adaptive behavioral interventions, 2) methods and processes to help people help themselves, and 3) research pipelines to achieve efficient, rigorous, context-relevant solutions for complex problems.

William T. Riley was born in Gloucester, Virginia, USA in 1957. He received his B.S. in psychology and sociology from James Madison University, Harrisonburg, VA (1979) and his M.S. (1981) and Ph.D. (1984) in clinical psychology from Florida State University, Tallahassee, FL, USA. He completed an internship in Medical Psychology at Baylor College of Medicine, Houston, TX, USA.

He currently serves as Associate Director for Behavioral and Social Sciences Research and Director of the Office of Behavioral and Social Sciences Research at the National Institutes of Health (NIH), Bethesda, MD, USA. He has been at NIH since 2005 and has served at the National Institute of Mental Health (NIMH), the National Heart, Lung, and Blood Institute (NHLBI), and the National Cancer Institute (NCI) prior to his current appointment. He also holds an appointment as Professorial Lecturer in the School of Public Health at George Washington University. Prior to the NIH, he was Director of Research at PICS, a small research and development firm in Reston, Virginia. He previously served as assistant professor at the Medical College of Georgia and as associate professor at the Medical College of Virginia, Virginial Commonwealth University. His research interests include behavioral assessment, technology-based interventions for health risk factors, and the application of engineering and computer science methodologies to the behavioral sciences.

Matthew P. Buman was born in San Diego, CA in 1980. He received his B.S. in Exercise and Sport Science and Psychology from the University of Utah, Salt Lake City, UT (2002) and his M.S.in Counseling Psychology from Springfield College, Springfield, MA (2004) and his Ph.D. in Applied Physiology and Kinesiology from the University of Florida, Gainesville, FL (2008). He completed a postdoctoral fellowship in Cardiovascular Epidemiology from the Stanford University School of Medicine, Stanford, CA (2011).

He currently is an Associate Professor in the College of Health Solutions at Arizona State University, Phoenix, AZ. His research interests focus on the dynamic interplay of behaviors across the 24 hours - sleep, sedentary behavior, and physical activity - and how collectively these behaviors can be used to promote health. His work leverages wearable sensors, smartphone technologies, and other technological innovations to promote health in clinical and community populations.

Marc A. Adams was born in Oak Park, IL, USA in 1975. He received the B.A. degree in psychology in 2001 and the Masters of Public Health in 2003 from San Diego State University, San Diego, CA, USA and his Ph.D. in Public Health (health behavior) from a joint doctoral program between San Diego State University and University of California, San Diego, CA, USA in 2009.

He is currently an Associate Professor in the College of Health Solutions and a Senior Sustainability Scientist in the Global Institute of Sustainability at Arizona State University, Phoenix, AZ, USA. His research interests currently include adaptive interventions for behavior change and urban design determinants for physical activity and diet to improve public health, as guided by the Behavioral Ecological Model.

Alicia B. Magann was born in Phoenix, AZ, USA in 1994. She received her B.S.E. degree in chemical engineering from Arizona State University, Tempe, AZ, USA in 2016 and her M.A. degree in chemical and biological engineering from Princeton University, Princeton, NJ, USA in 2018. She is currently pursuing a Ph.D. degree in chemical and biological engineering at Princeton University, Princeton, NJ, USA.

Her undergraduate research as part of the Control Systems Engineering Laboratory at Arizona State University (2015–2016) focused on dynamic modeling of physical activity interventions. She was awarded the United States Department of Energy Computational Science Graduate Fellowship for her Ph.D. research at Princeton University, Princeton, NJ, USA in 2017. Her current research focuses on quantum dynamics and control.

Appendix A Necessary Conditions for Stability

Using the state space representation of the system based on the SCT model, the state matrix is:

$$\mathbf{A}=\left(\begin{array}{cccccc}-\frac{1}{{\tau }_1}& 0& 0& \frac{{\beta }_{14}}{{\tau }_1}& 0& 0\\ \frac{{\beta }_{21}}{{\tau }_2}& -\frac{1}{{\tau }_2}& 0& 0& \frac{{\beta }_{25}}{{\tau }_2}& 0\\ \frac{{\beta }_{31}}{{\tau }_3}& 0& -\frac{1}{{\tau }_3}& \frac{{\beta }_{34}}{{\tau }_3}& 0& 0\\ 0& \frac{{\beta }_{42}}{{\tau }_4}& \frac{{\beta }_{43}}{{\tau }_4}& -\frac{1}{{\tau }_4}& \frac{{\beta }_{45}}{{\tau }_4}& \frac{{\beta }_{46}}{{\tau }_4}\\ 0& 0& 0& \frac{{\beta }_{54}}{{\tau }_5}& -\frac{1}{{\tau }_5}& 0\\ 0& 0& 0& 0& 0& -\frac{1}{{\tau }_6}\end{array}\right)$$ (30)

The system is stable if all the eigenvalues of A have negative real parts. The characteristic equation of the matrix A is computed as:

$$D(s)=|s\mathbf{\text{I}}-\mathbf{\text{A}}|=a_{\text{5}}{s}^5+a_4{s}^4+a_3{s}^3+a_2{s}^2+a_{1}s+a_0$$ (31)

with:

$$a_5={\tau }_1{\tau }_2{\tau }_3{\tau }_4{\tau }_5$$ (32)

$$\begin{gathered} a_4={\tau }_1{\tau }_2{\tau }_3{\tau }_4+{\tau }_1{\tau }_2{\tau }_3{\tau }_5+{\tau }_1{\tau }_2{\tau }_4{\tau }_5+{\tau }_1{\tau }_3{\tau }_4{\tau }_5 \\ +{\tau }_2{\tau }_3{\tau }_4{\tau }_5 \end{gathered}$$ (33)

$$\begin{gathered} a_3={\tau }_1{\tau }_2{\tau }_5(1-{\beta }_{34}{\beta }_{43})+{\tau }_1{\tau }_2{\tau }_3(1-{\beta }_{45}{\beta }_{54}) \\ +{\tau }_1{\tau }_2{\tau }_4+{\tau }_1{\tau }_3{\tau }_4+{\tau }_1{\tau }_3{\tau }_5+{\tau }_2{\tau }_3{\tau }_4+{\tau }_1{\tau }_4{\tau }_5 \\ +{\tau }_2{\tau }_3{\tau }_5+{\tau }_2{\tau }_4{\tau }_5+{\tau }_3{\tau }_4{\tau }_5 \end{gathered}$$ (34)

$$\begin{gathered} a_2={\tau }_1{\tau }_5(1-{\beta }_{34}{\beta }_{43})+{\tau }_1{\tau }_2(1-{\beta }_{34}{\beta }_{43}-{\beta }_{45}{\beta }_{54}) \\ +{\tau }_2{\tau }_5(1-{\beta }_{34}{\beta }_{43}-{\beta }_{14}{\beta }_{31}{\beta }_{43}) \\ +{\tau }_1{\tau }_3(1-{\beta }_{45}{\beta }_{54}-{\beta }_{25}{\beta }_{42}{\beta }_{54}) \\ +{\tau }_2{\tau }_3(1-{\beta }_{45}{\beta }_{54})+{\tau }_3{\tau }_5(1-{\beta }_{14}{\beta }_{21}{\beta }_{42}) \\ +{\tau }_1{\tau }_4+{\tau }_2{\tau }_4+{\tau }_3{\tau }_4+{\tau }_4{\tau }_5 \end{gathered}$$ (35)

$$\begin{gathered} a_1={\tau }_1(1-{\beta }_{34}{\beta }_{43}-{\beta }_{45}{\beta }_{54}-{\beta }_{25}{\beta }_{42}{\beta }_{54}) \\ +{\tau }_2(1-{\beta }_{34}{\beta }_{43}-{\beta }_{45}{\beta }_{54}-{\beta }_{14}{\beta }_{31}{\beta }_{43})+{\tau }_4 \\ +{\tau }_3(1-{\beta }_{45}{\beta }_{54}-{\beta }_{14}{\beta }_{21}{\beta }_{42}-{\beta }_{25}{\beta }_{42}{\beta }_{54}) \\ +{\tau }_5(1-{\beta }_{34}{\beta }_{43}-{\beta }_{14}{\beta }_{21}{\beta }_{42}-{\beta }_{14}{\beta }_{31}{\beta }_{43}) \end{gathered}$$ (36)

$$\begin{gathered} a_0=1-{\beta }_{34}{\beta }_{43}-{\beta }_{45}{\beta }_{54}-{\beta }_{14}{\beta }_{21}{\beta }_{42}-{\beta }_{14}{\beta }_{31}{\beta }_{43} \\ -{\beta }_{25}{\beta }_{42}{\beta }_{54} \end{gathered}$$ (37)

A necessary condition for stability is that all the coefficients of D(s) are positive; therefore, a set of necessary conditions for stability is:

$$a_i>0,i=0,\cdots ,5$$ (38)

Considering that all time constants τ_j are positive, the only possibility for any term a_i to be negative is if one or more of its internal factors 1 − (β_iβ_j) − ··· − (β_kβ_lβ_m) are negative. To prevent this for any specific internal factor, the following condition must be met:

$$({\beta }_i{\beta }_j)+\cdots +({\beta }_k{\beta }_l{\beta }_m)<1$$ (39)

One general way to meet this requirement is to consider that each gain β is less than one, therefore to have a stable system it is necessary that all of the following conditions are met simultaneously:

$$\begin{array}{c}{\beta }_{21}<1,{\beta }_{31}<1,{\beta }_{42}<1,{\beta }_{43}<1,{\beta }_{54}<1,{\beta }_{34}<1,\\ {\beta }_{14}<1,{\beta }_{25}<1,{\beta }_{45}<1\end{array}$$ (40)