Diffusion MR Imaging in Multiple Sclerosis: Technical Aspects and Challenges

Abstract

SUMMARY: Diffusion tensor (DT) MR imaging has frequently been applied in multiple sclerosis (MS) because of its ability to detect and quantify disease-related changes of the tissue microstructure within and outside T2-visible lesions. DT MR imaging data collection places high demands on scanner hardware and, though the acquisition and postprocessing can be relatively straightforward, numerous challenges remain in improving the reproducibility of this technique. Although there are some issues concerning image quality, echo-planar imaging is the most widely used acquisition scheme for diffusion imaging studies. Once the DT is estimated, indexes conveying the size, shape, and orientation of the DT can be calculated and further analyzed by using either histogram- or region-of-interest–based analyses. Because the orientation of the DT reflects the orientation of the axonal fibers of the brain, the pathways of the major white matter tracts can also be visualized. The DT model of diffusion, however, is not sufficient to characterize the diffusion properties of the brain when complex populations of fibers are present in a single voxel, and new ways to address this issue have been proposed. Two developments have enabled considerable improvements in the application of DT MR imaging: high magnetic field strengths and multicoil receiver arrays with parallel imaging. This review critically discusses models, acquisition, and postprocessing approaches that are currently available for DT MR imaging, as well as their limitations and possible improvements, to provide a better understanding of the strengths and weaknesses of this technique and a background for designing diffusion studies in MS.

Over the past 15 years, diffusion-weighted (DW) MR imaging has increasingly been applied to the brain and is now available for the clinical investigation of numerous conditions, including multiple sclerosis (MS).^1–3 The contrast in DW MR imaging is based on the diffusional displacement of water molecules, which, in the presence of a strong magnetic field gradient, causes the signal intensity in an MR image to be attenuated.^4,5 The degree of attenuation depends on the strength of the gradient, the time over which it is applied, and the magnitude of water diffusion; increases in any of these will lead to a reduction in the MR signal intensity. An innovative form of pulse sequence to measure diffusion was introduced by Stejskal and Tanner.⁶ This uses a pair of gradient pulses for encoding diffusion, a form of pulse sequence that was compatible with later developments in MR image acquisition and is still used today.

Diffusion is, of course, a 3D phenomenon and can vary in magnitude depending on the direction in which the diffusional displacements are measured.^7,8 This directionality is introduced because water diffusion in and around cellular structures is not “free,” as it is in a bulk fluid, but is restricted as it comes into contact with cell membranes and other macromolecular structures.⁹ Any orientation of these cellular structures will be reflected in a corresponding directional dependence of diffusional displacements. Because the applied magnetic field gradient also has a specific direction, the degree of signal intensity attenuation depends on direction of the field gradient and the magnitude of diffusion in that direction.

To describe diffusion in the environment found in vivo, a mathematical notation known as a tensor is used.¹⁰ For diffusion in 3D, the 3 × 3 diffusion tensor (DT) matrix describes the mean square diffusion distance in any direction, under the assumption that the diffusional displacement profile is Gaussian. Other descriptions of water diffusion have been suggested, and the tensor may be seen as a simple but practical approach.¹¹ However, rather than trying to visualize the tensor in its entirety, it is often more useful to summarize its properties. These properties characterize the size, shape, and orientation of the DT.¹²

Conventional MR images of patients with MS show multiple focal abnormalities, which correspond to histopathologic lesions in the white matter (WM).^13–17 On proton density (PD) and T2-weighted images, lesions appear hyperintense compared with the background, whereas on postcontrast T1-weighted images, the same lesions may appear hyperintense (enhancing) if they are in the acute inflammatory phase,¹⁷ or hypointense (“black holes”) in case of severe tissue damage but no active inflammation.¹⁸ Beyond this, however, the images are largely nonspecific with respect to the degree of tissue damage within the lesions. It has also recently become apparent that the MS pathologic process has a diffuse component that is widespread throughout the entire central nervous system (CNS) and that may precede or accompany the more established pathologic condition that is seen in the focal lesions.¹⁹ DT MR imaging appears to offer improved pathologic specificity over conventional MR imaging for assessing the degree of damage in individual MS lesions, and its quantitative nature allows an assessment of the more widespread tissue damage occurring outside such lesions. A detailed description of the many contributions of DT MR imaging to the understanding of MS pathobiology are beyond the scope of this review and have been reported in another recent article.¹

Although DT MR imaging has great potential in MS research, the interpretation of diffusion data is not straightforward. Concomitant factors determine changes of DT-derived metrics, and it is difficult to relate such changes to the pathologic processes responsible for clinical impairment. In addition, the complexities of the underlying axonal architecture, even without the structural damage that occurs because of the disease, play an important role in determining the diffusion characteristics. For example, where the intravoxel orientational coherence of fibers is low (ie, at fiber bundle crossing points), damage to one of the fibers could lead to an increased anisotropy because the effect of this fiber is removed from the voxel average. All these shortcomings might be the reasons, at least partially, why preliminary postmortem studies²⁰ reported a relatively poor correlation between diffusion changes and pathologic features of MS-related tissue damage.

The aim of this review is to discuss critically current available models, acquisition techniques, and postprocessing techniques for DT MR imaging, to address their potential strengths and weaknesses, and to provide a background for designing ad hoc studies for MS research.

Diffusion Tensor MR imaging

Acquisition

A DT MR imaging experiment consists of acquiring a series of MR images, with the magnetic field gradient that encodes diffusion applied in different directions or with different amplitudes for each image.²¹ The DT is a 3 × 3 matrix of numbers that is symmetric and therefore has 6 unique elements. An estimate of the tensor therefore requires that at least 6 DW images are acquired, with another non-DW image needed to estimate the variations in signal intensity that are not caused by diffusion weighting (PD and T2 weighting). In practice, many more than 6 directions are often acquired to improve the quality of the estimate of the DT.²² Recent studies using numerical simulations²³ or a theoretic approach²⁴ suggested that a sampling scheme with at least 30 unique gradient orientations should give a robust estimate of the DT.

Echo-planar imaging (EPI) is a pulse sequence that acquires image data in a very short time (typically 30–60 ms per image section), thereby freezing any patient motion.²⁵ Because of freedom from motion artifacts caused by the diffusion weighting, which is a particular problem in the case of disabled patients, such as those with MS, EPI is the most widely used acquisition method for DT MR imaging studies. However, because of the rapid acquisition, it suffers from lower in-plane resolution and worse geometric distortions, as a result of magnetic field inhomogeneity, than conventional MR imaging. For qualitative studies, these may not be such a problem, because information from DT MR imaging is often complementary to that from higher resolution morphologic scans. However, in quantitative MS studies, when different types of tissue, such as T2 visible lesions, normal-appearing white matter (NAWM) and gray matter (GM) are analyzed after a segmentation procedure, there must be correspondence in position between different scans. The geometric distortions need to be corrected before there is correspondence between the anatomic locations in an EP image and a conventional image, as shown in Fig 1. Newer pulse sequences that suffer less from geometric distortion will be discussed in the “Future Perspectives” section. To prevent gross chemical shift artifacts caused by subcutaneous fat, fat suppression techniques must be used with EPI. Fat suppression normally relies on frequency-selective radio frequency (RF) pulses, and the quality of suppression depends on the uniformity of the magnetic field. This is particularly important for scanners used in routine clinical practice without adequate attention paid to maintaining the B₀ field homogeneity.

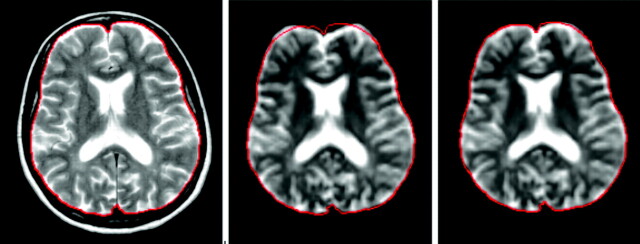
Fig 1.

Geometric distortions inherent in echo-planar imaging (EPI), evident from the comparison between a fast spin-echo (FSE) T2-weighted image (left) and the b = 0 image of a pulsed gradient SE-EPI experiment, after rigid (middle) and nonlinear transformation (right)⁶⁰ to match the anatomy of the FSE T2-weighted image. The cranial contents are outlined in red on the FSE image, and the same outline is superimposed on the other images to show the degree of distortion.

With EPI, a whole-brain DW MR imaging study with a single DW direction can be obtained in a very short acquisition time, though this process is usually repeated many times with diffusion-encoding along the different directions needed to estimate the DT. Furthermore, the data acquisition may need to be triggered by the subject's heart beat, because distortions of the brain that occur as a result of fluctuations in blood pressure can result in fluctuations in signal intensity that mimic those caused by diffusion. This influences the estimated orientation of the DT and, indirectly, the results from tractography, as has been demonstrated using the bootstrap technique.²⁶ Triggering the acquisition in this way further extends the data acquisition time, limiting the applicability in the most disabled patients with MS. However, although cardiac gated acquisition is to be preferred, many DT measurements of the brain are acquired without cardiac gating, because of time constraints.

As well as geometric distortions caused by magnetic field inhomogeneities, EPI is susceptible to other distortions caused by application of the gradient pulses that encode diffusion. These distortions are caused by eddy-current-induced residual magnetic fields that result from switching the magnetic field gradients on and off, and are different for every direction of diffusion encoding (Fig 2). However, they can either be reduced by using a modification of the Stejskal-Tanner sequence²⁷ or largely removed by image postprocessing methods, as described below.

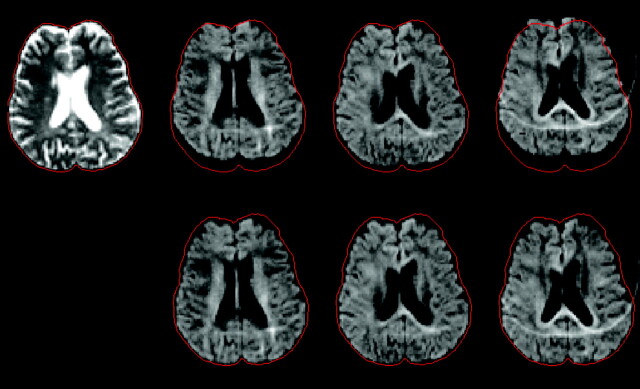
Fig 2.

Geometric distortions caused by eddy currents. A non–diffusion-weighted image (top left) and 3 diffusion-weighted images with gradients along independent directions are shown before (top row) and after (bottom row) correction by postprocessing. The cranial contents are outlined in red on the non diffusion-weighted image, and this same outline is superimposed on the other images to show the degree of distortion. The correction involves estimating and applying a shift, scaling and shearing along the phase encoding direction of each diffusion-weighted image. The ghost-artifact seen in the diffusion-weighted images is caused by poor fat suppression because of magnetic field inhomogeneity.

Image Postprocessing and Analysis

Geometric distortions caused by eddy currents first need to be corrected; several algorithms have been proposed, but they usually work by matching (registering) the distorted DW image to an undistorted image. They differ mainly in the way that they determine the goodness of registration and in the way that the spatial correction is accomplished.^28–30 Most schemes perform their correction on a section-by-section basis, using the acquisition without diffusion weighting as the undistorted reference image. Next, the DT is estimated for every image pixel, using the expression derived by Stejskal³¹ for the pulsed gradient spin-echo experiment in the presence of restricted diffusion, and developed subsequently by Basser et al²¹ in a more general scheme for anisotropic diffusion. The relationship between the applied magnetic field gradient and the echo intensity is ln[A/A₀] = −ΣΣb_ijD_ij, where A is the echo intensity, A₀ is the echo intensity with no applied gradients, D_ij is ij^th tensor component, and b_ij is the ij^th component of a symmetric matrix b, which depends on the time integral of the applied magnetic field gradient vector components. Because the acquisition experiment is designed to collect independent measurements of the echo intensities, the DT can be estimated using multivariate linear regression.

One practical way to visualize the DT is by calculating the diffusion tensor ellipsoid.³² This comes from the characterization of the diffusion process as a probability that a molecule starting at a position x₀ reaches a position x at time t. For a Gaussian probability distribution function, an assumption underlying DT MR imaging,^31,32 a surface of constant probability takes the form of an ellipsoid in 3D space: [(x − x₀)^T D⁻¹(t)(x − x₀)]/4t = constant. The directions parallel to the axes of the ellipsoid can be used to elucidate the underlying tissue fiber structure, because the diffusivity is at a maximum in the direction parallel to the longest axis of the ellipse. The axes of the ellipse are obtained by calculating the 3 eigenvectors of the tensor matrix, obtained as the 3 solutions for X_i of the equation DX_i = λ_iX_i. Here, the 3 eigenvalues λ_i are the diffusivities in the directions of the ellipse axes. Depending on the relative sizes of the eigenvalues, the tensor can be classified in a way that helps intuitive understanding of the underlying structure:

1. Linear (λ₁ ≫ λ₂ ≅ λ₃): diffusion is mainly in the direction of the eigenvector corresponding to the largest eigenvalue.

2. Planar (λ₁ ≅ λ₂ ≫ λ₃): diffusion is mainly in the plane spanned by the 2 eigenvectors corresponding to the 2 largest eigenvalues.

3. Spherical (λ₁ ≅ λ₂ ≅ λ₃): diffusion is largely isotropic.

The characteristics of the DT can also be summarized by using parameters that depend on the shape, not the orientation of the DT ellipsoid, and which are derived from operations on the DT.³³ Because they do not depend on the orientation, these parameters are called rotational invariants of the DT. To better understand the meaning of these invariants, it is worth remembering the definition of the magnitude of a tensor, which is equivalent to that used for vectors: (D:D)^1/2 ≡ (ΣΣD_ij²)^1/2, where : indicates the tensor product. It is also useful to rewrite the tensor as the sum of an isotropic tensor and an anisotropic tensor D = D_i + D_a by choosing the isotropic tensor as D_i = <D>I and the anisotropic tensor as D_a = (D − D_i), where <D> is the mean diffusivity, and I is the identity matrix.

The following scalar invariants can be then derived:

• Mean diffusivity (MD). This has already been introduced for the definition of the isotropic part of the tensor as follows: MD ≡ Tr(D)/3 = (Σλ_i)/3, where MD measures the average molecular motion independent of any tissue directionality. It is numerically equal to one third of the trace of the diffusion tensor (Tr(D)), where the trace is the sum of the 3 diagonal elements of the tensor.

• Fractional anisotropy (FA). This is a measure of the deviation from isotropy and is proportional to the ratio of the magnitude of the anisotropic part to the magnitude of the DT: FA ≡ (3/2)^1/2 (D_a:D_a/D:D)^1/2 = (3/2)^1/2(3 Var(λ)/(λ₁²+λ₂²+λ₃²))^1/2, where Var is the variance.

Once maps of these properties of the DT are formed, their values are usually averaged over regions of interest (ROIs) that are a priori considered to be associated in some way with the disease and its evolution. In MS, brain regions are classified as lesions because of their abnormal appearance on conventional MR images. Other regions may not appear abnormal but may have a particular functional significance. Abnormal regions may be best delineated on conventional images, and, because of the geometric distortion of the EPI images, the diffusion parameter maps must be registered to the conventional images.³⁴ Lesions can be outlined manually or semiautomatically by expert observers³⁵ and then superimposed on the DT parameter maps and the average properties within each lesion calculated. The same strategy can be used to sample values in the NAWM or in clinically eloquent anatomic sites, but the correct positioning of ROIs can be problematic: in subjects acquired with different section positioning or with different brain shapes because of atrophy,³⁶ it might be difficult to find the same anatomic markers to draw the ROIs. This makes the method very subjective and causes poor reproducibility. Registration into a standard anatomic space (Talairach space) can help when comparing different subjects.

The problem of poor correspondence between the brains of different subjects can be avoided by performing a more global analysis. In this case, a histogram of parameter values is usually formed from the whole of the brain tissue (or from segmented tissue classes), and then descriptors of the shape of the histogram are used to quantify the global properties. Such shape descriptors normally include the mean value, the peak position, and the peak height.³⁷ If the histogram is normalized (eg, by dividing the height of each histogram bin by the total number of pixels included), then the measures become largely independent of the size of the brain. It is also possible to obtain histograms from the GM and WM separately. However, care must be taken in all forms of histogram analysis of EP images, because the low spatial resolution will lead to a high degree of contamination of signal intensity from brain by CSF, thereby possibly enhancing the influence of atrophy (leading to enlarged ventricles and cortical sulci) on the changes of histogram-derived quantities.

Future Perspectives

Data Acquisition

Two recent developments have the potential to improve DT MR imaging acquisition considerably: 1) high-strength MR imaging magnets, particularly the ready availability of systems operating at 3T, and 2) multiple receiver coils with parallel imaging data acquisition techniques.²⁹ Both of these are likely to enhance the role of diffusion imaging in MS research by improving the spatial resolution that is achievable.

Higher magnetic field strengths intrinsically give better signal-to-noise ratio (SNR), which can be traded off for shorter acquisition times or better spatial resolution. However, it is important to be aware of some of the limitations of 3T systems and the implications for diffusion imaging:

1. The exciting and receiving RF field becomes increasingly inhomogeneous with increasing field strength.³⁸ Some of the quantitative parameters derived from DT MR imaging are not affected by these intensity modulations,²⁹ but others, such as FA, depend on the SNR, which varies with position in the subject.¹²

2. The T1 relaxation time of brain tissue, but not CSF, is prolonged significantly. Therefore, the repetition time intervals need to be lengthened to avoid T1-weighting.

3. The chemical shift between water and fat is greater and thus chemical shift artifacts can be more pronounced.

4. Field inhomogeneities and T2* decay are more severe. At 3T, higher order shimming³⁹ is very important for DT MR imaging to avoid artifacts from field perturbations. With EPI, the most obvious difference between 1.5T and 3T images is the more pronounced geometric distortion at air issue interfaces, such as around the auditory canals and the frontal sinuses, and above the base of the skull. Faster T2* decay can lead to blurring and considerable signal intensity loss. Parallel imaging can help to reduce these artifacts.²⁹

5. The acoustic noise and vibration inherent in MR imaging scanning, and particularly in DW EPI, are significantly worse.

Parallel imaging strategies combine the signal intensity from individual coil elements of an RF coil array to accelerate MR imaging data acquisition without interfering with the contrast mechanisms. This reduces the distortions seen in EPI, but has the disadvantage that the SNR is poorer. Because the intrinsic SNR of an MR imaging scanner is roughly proportional to the field strength, the combination of multicoil receiver arrays with parallel imaging techniques on high field magnets has produced good quality DT MR imaging data. Figure 3 shows how the use of sensitivity encoding (SENSE)⁴⁰ helps to reduce the strong EPI-related artifacts. Distortions are greatly improved, but the SENSE method also reduces the SNR. Several studies have already been conducted to compare the use of 3T and 1.5T MR imaging in MS, but none included DW MR imaging. These studies consistently showed that the better resolution achievable at higher magnetic field strengths allowed lesions to be seen that were not detected at 1.5 T.^41–44 Another benefit of improved resolution is the better spatial discrimination of GM and WM, further encouraging the combination of conventional and DW MR imaging at high field. This would allow a more accurate investigation of lesion heterogeneity and quantification of the extent of subtle tissue abnormalities in the NAWM and GM.

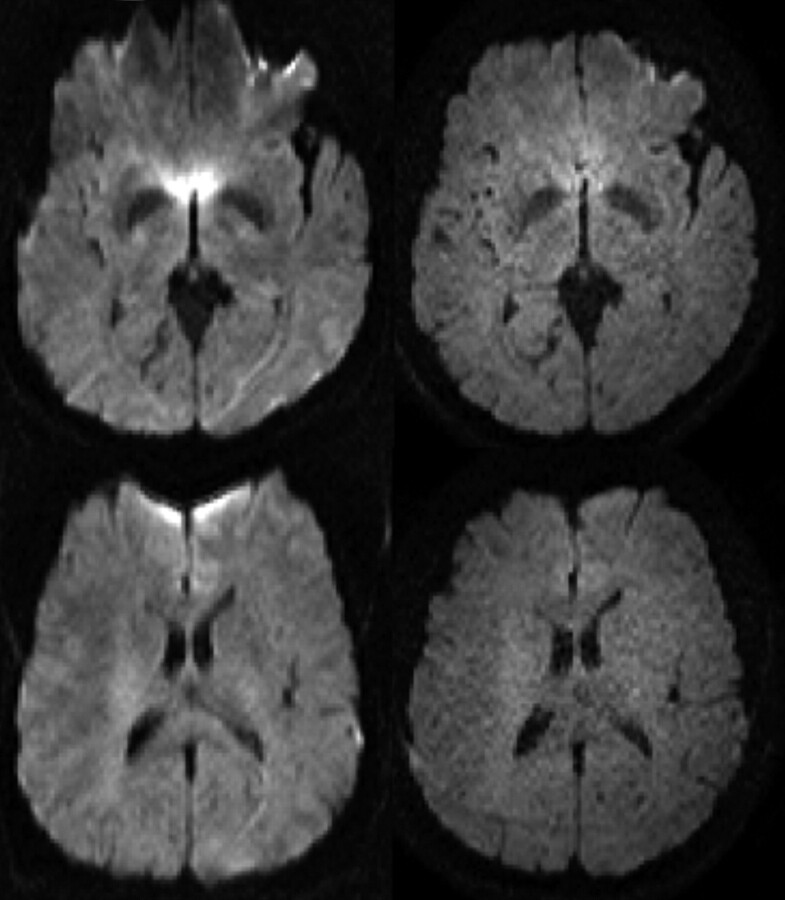
Fig 3.

Diffusion-weighted MR imaging at 3T: the left column shows 2 transverse sections acquired without sensitivity encoding (SENSE), whereas the right column shows the same sections acquired with a SENSE factor R = 3. Note the much smaller geometric distortion in the SENSE images because of the shorter acquisition time.

Certain anatomic areas, such as the optic nerve or the spinal cord, are particularly difficult to investigate because of the low resolution and image distortions inherent to EPI. Nevertheless, recent applications of DT MR imaging in the cervical cord have shown that DT-derived metrics averaged over the central sagittal section of the cervical cord are able to differentiate patients with MS from healthy subjects and correlate with clinical disability.^45,46 In the optic nerve, a significant increase of the principal diffusivity was found in the affected nerves of patients with MS with optic neuritis compared with the unaffected contralateral side; this was achieved using a technique specifically developed for application to the optic nerve.⁴⁷

One very elegant new development, called periodically rotated overlapping parallel lines with enhanced reconstruction (PROPELLER)⁴⁸ allows the acquisition of DW images at high spatial resolution and with minimal distortion. It is based on the fast spin-echo (FSE) sequence, but it is modified so that the image can be reconstructed without the usual motion artifacts that are seen when FSE is combined with diffusion weighting. This high resolution can be important for the study of these clinically eloquent CNS sites in MS, which might provide us with relevant information about the mechanisms underlying the accumulation of disability.

Image Postprocessing and Analysis

Pathologic changes in tissue microstructure are expected to be reflected in a deviation from normal diffusion anisotropy values, though details of the relationship are still unclear. More information can be obtained by analyzing the behavior of the eigenvalues together with the FA and MD. In a study of wallerian degeneration caused by a primary stroke lesion, it was shown that a slightly increased first eigenvalue together with a strong decrease of FA was the characteristic that discriminated between initial and secondary degeneration.⁴⁹ Application of a similar analysis to MS would provide us with useful information about the pathophysiologic processes occurring in tissue. However, knowledge of the underlying anatomy is a prerequisite of this type of analysis, so that misinterpretation can be avoided.⁵⁰

When comparing DT-derived values in patients with those in control subjects, it is imperative, therefore, to consider regions that match anatomically. One way to conduct such analyses is by using tractography, whereby specific fiber bundles can be extracted. In addition to improving the validity of the analysis, this method should increase the specificity by focusing on systems that have a particular functional significance.

The basic idea behind fiber tracking is that the principal diffusion direction matches the orientation of a fiber bundle, and a computer program can reconstruct the path of the bundle by starting from a seed point set by the user and moving in short steps along the principal diffusion direction. This class of algorithm is referred to as streamline following.^51–54 Streamline following suffers, however, from a major problem, which is the difficulty in passing through GM, areas where fibers cross, or (in patients with MS) through degenerated brain tissue, because of the greater uncertainty in the principal diffusion direction when FA decreases.^55–58 Recently, several methods have been described for handling this uncertainty in a probabilistic fashion. One method⁵⁸ estimates a probability distribution function (PDF) for fiber orientation at each point in the image and initiates tracking from the same seed point many times; however, by using the PDF, the exact fiber trajectory is decided in a random fashion, which results in a different path for every run. The result is a probability map of the tract of interest, calculated by adding the tracts obtained from the multiple runs.

Spatial normalization of DT MR imaging data into an anatomic reference frame⁵⁹ facilitates the positioning of ROIs and allows voxel-based assessment that does not require a priori hypotheses. However, when using spatial normalization and subsequent group comparisons, the results should be interpreted conservatively. Significant differences between subjects or groups may occur at the interfaces between GM and WM and between brain parenchyma and CSF due to slight misregistration. Although simple transformation can produce good results when applied to healthy subjects, more complex deformation^60–63 may be needed when compensating for brain atrophy, which is a frequent finding in patients with MS.³⁶ Registration may also be improved by matching based on the whole of the DT, rather than just a simple image intensity.⁶⁴

New Models of Diffusion Description

The Gaussian model of displacement profiles (ie, a tensor model) may not work well in places where there are complex fiber patterns, such as crossing and merging fibers; this limits what can be achieved when trying to track fibers over long connection pathways in the brain. In MS studies, this can be more of an issue for tracking over clinically eloquent fiber pathways, where disease-related tissue damage reduces tissue anisotropy. This problem has been addressed by using multicompartment models of diffusion,⁶⁵ where several fiber bundles can exist in each voxel, with Gaussian behavior for each bundle. However, this approach requires a priori information about the number of compartments.

There are approaches that do not require any assumptions about the diffusion within a voxel. One such is the so-called q-space formalism,⁶⁶ which measures the probability that a molecule at a certain initial position ends up at a different position after a certain amount of time (the displacement profile). The tissue microstructure determines the shape of this profile and its evolution over time. It has been shown that when this profile is a 3D Gaussian function, the DT is sufficient to fully describe diffusion, but that in the more general case, the profile itself must be examined for a full description of the diffusion characteristics.⁶⁷ By applying gradient pulses with different amplitudes and in different directions, the q-space concept has been used to estimate the 3D displacement distribution of water molecules in vivo.^68–71 Measuring this distribution in vivo at high q values would allow the characterization of the slow restricted diffusion component, which is probably mainly dependent on axonal membranes and modulated by myelin layers. This would, in principle, improve our ability to differentiate between demyelination, axonal loss, and inflammation in MS. Assaf et al⁷² showed that, by using parameters derived from the displacement profile, the difference of values in the NAWM of patients with MS was more pronounced than with DT MR imaging and that the correlation with N-acetylaspartate levels (a measure of neuronal and axonal viability) improved.⁷³ As an example, Fig 4 shows the probability map for zero displacement for a healthy control (bottom right) and an MS patient (bottom left); this parameter was derived for each pixel as the peak height of the displacement distribution function (Fig 5). This approach, however, is quite demanding of MR imaging scanner hardware, and requires long data acquisition times. Moreover, one of the essential requirements of the q-space formalism ie, the gradient pulse to be large and infinitely short, cannot be satisfied due to gradient hardware limitations, and because rapid switching of large gradients induces dangerous nerve stimulation.

Fig 4.

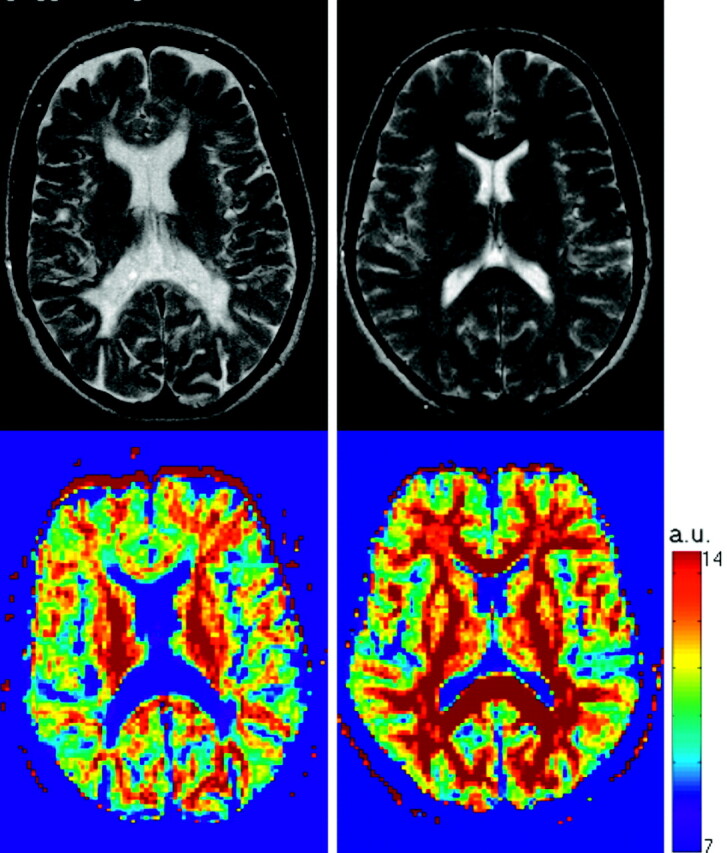
T2-weighted images (top row) and q-space probability for zero displacement (bottom row) are shown for a healthy control (right) and a multiple sclerosis patient (left). Both T2-weighted visible lesions and the normal appearing white matter are characterized by lower probability when compared with controls. a.u., arbitrary units.

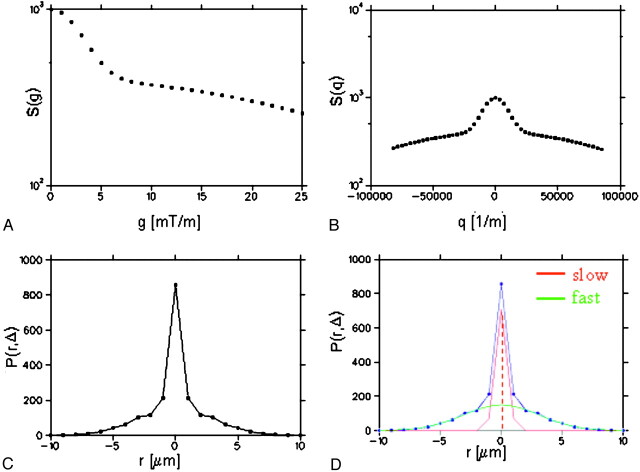
Fig 5.

The q-space approach illustrated using simulated data. First, diffusion weighted MR imaging data are acquired changing the diffusion gradient strength (g) along each direction considered (A). Then, using the relationship q = γ × δ × g, where γ is the gyromagnetic ratio and δ is the pulse duration, the measured signal intensity, S(g), is expressed as function of q (B). The probability P(r, Δ) that a molecule ends up at position r after a time Δ is then calculated as the inverse Fourier transform of S(q), Δ being the separation between the leading edges of the pulses (C). Finally, in one approach to characterizing P, the fast and slow diffusion components are extracted after Gaussian fitting to P(r, Δ) and the peak height of the slow component used as probability for zero displacement. The slow component is thought to reflect the integrity of the myelin sheath and cell membranes.

Other approaches measure the diffusion along different directions with a high angular resolution.⁷⁴ The resulting 3D representation of diffusivity can be decomposed into a set of orthogonal 3D functions, the so-called spherical harmonics.¹¹ The orientations of multiple axonal fiber populations can also be estimated directly from the DW attenuation sampled at high resolution.⁷⁵ However, these methods still retain the inherent assumption of Gaussian diffusion. An interesting approach to deriving multiple fiber populations without this assumption is that taken by Tuch,⁷⁶ where a transform of the DW intensities acquired with high angular resolution directly gives the distribution of fibers (Fig 6). However, relatively high diffusion weighting and long acquisition times are required.

Fig 6.

Q-ball image (axial orientation, inset)⁷⁶ with an enlargement of the area shown. The glyph at each voxel depicts the local diffusion orientation distribution function (ODF), which can resolve multiple intravoxel diffusion orientations. There is an intersection between the left-right fibers (shown in red) and the anteroposterior fibers (green). Superior-inferior fibers are shown in blue. Image kindly provided by Dr. David Tuch.

Diffusion MR Imaging and Multicenter MS Studies

Nowadays, MR imaging-derived measures represent an “established” outcome in clinical trials of experimental treatments for MS. In principle, the increased availability of powerful magnetic field gradient systems and EPI on commercial scanners makes it feasible to perform large-scale multicenter MS trials using both conventional and DT MR imaging to provide adjunctive in vivo measures of disease-related damage progression. However, all aspects of data acquisition and analysis should be taken into account when planning multicenter or longitudinal DT MR imaging-based studies.

It has been shown that biologic activity, pulse sequences, accuracy in section repositioning, observer reproducibility, and use of different scanners all influence the measurements of quantities derived from MR imaging.^77,78 In clinical trials, the use of a variety of MR scanners is hard to avoid and, given the duration of trials and the service life of an MR imaging scanner, it is also inevitable that some units will undergo a major upgrade or replacement during the course of a long-term study. Overall, quality assurance issues are 2-fold. First, the accuracy and precision of measurements should not change for the duration of a longitudinal study. Second, comparability across sites must be established. If we are only interested in longitudinal change in any given patient, comparability between sites is not so important. On the other hand, high measurement accuracy is required if data from multiple sites are to be pooled directly without correction for intersite differences.

The design of DW EPI sequences is relatively straightforward. Nevertheless, many factors vary between different MR scanners, or even between different models or release levels from a single vendor, which can significantly alter the measured quantities. These factors include: 1) the timing, strength and orientation of the gradients^22,79–81; 2) the details of the EPI readout; 3) the methods used to compensate image distortions caused by eddy currents^27,82,83; 4) the shimming techniques³⁹; 5) the way fat suppression is accomplished; 6) the way image⁸⁴ and diffusion encoding gradient nonlinearities are corrected⁸⁵; 7) whether acquisition is gated to the cardiac cycle and the method used for gating⁸⁶; and 8) the type of phase navigation in nonsingle-shot methods.^48,87–91

Because DT MR imaging analysis involves a significant amount of postprocessing, this can also affect the derived values. Thus, centralized analysis of MS trials using DT MR imaging should always be performed and all aspects of the processing reported. Moreover, the SNR can bias the tensor estimation, along with values derived from the tensor^92,93; therefore, the noise level should be always shown. Both accuracy and precision can be measured using a phantom made from substances that mimic the diffusivity and relaxation times of biologic tissues.⁹⁴ However, a standardized phantom that exhibits stable anisotropic diffusion and that can be shipped to participating trial sites has yet to be developed.

The impact of the use of different scanners and pulse sequences on histograms of DT MR imaging quantities was recently investigated in healthy volunteers to assess the intersequence and interscanner variabilities without the confounding factor of disease-induced biologic variation. This study⁹⁵ demonstrated that both different pulse sequences and different MR scanners introduce variability into DT MR imaging-derived quantities. However, the interscanner variability of similar, but not identical, pulse sequences was significantly better than the intersequence variability. The overall measurement variability was relatively low, giving encouragement for the use of diffusion in multicenter studies and trials for MS.

Conclusions

DT MR imaging has the potential to investigate tissue damage caused by MS, as has consistently been shown by several studies¹ conducted using acquisition and postprocessing procedures based on the DT model. New approaches for DW MR imaging acquisition and postprocessing are now available that might provide further insights into the different pathologic features of MS with improved reliability, as summarized in the Table. The optimal scheme for DT MR imaging in MS studies will inevitably be a compromise between acceptable acquisition times, increased pathologic specificity of derived parameters, sensitivity to change (both cross-sectionally and longitudinally), applicability to different CNS structures (ie, brain, spinal cord, and optic nerve) and feasibility in the context of large-scale studies. A multicenter research setting might represent the best environment to address some of the unsolved issues and run validation studies.

Summary of current challenges for DT imaging

	Current Challenges	Current Solutions	Future Directions
Acquisition	Low resolution		Higher static/gradient field
			PROPELLER
			Parallel acquisition
	Distortions by EPI	Postprocessing corrections	PROPELLER
			Parallel acquisition
	Cardiac/CSF pulsation	Cardiac triggering	Cardiac triggering in routine practice
	Robust estimate of the DT	More averages	Higher static field
			Optimized sequence parameters
			Increased number of DW directions
Postprocessing and analysis	Subjectivity of the ROI approach	Training of the neurologist	Registration to standard space
		Histogram analysis
	Correlations of DT derived metrics with clinical histopathology	ROI and histogram analysis of MD and FA maps	Include analysis of eigenvalues
			Focus on systems that have a functional significance (ie, specific fiber tracts)
			Voxel based assessment after normalization to standard space to avoid a priori hypotheses
Acquisition and analysis	Crossing/merging fibers		Multicompartment models
			Q-space formalism
			High angular resolution

Note:—PROPELLER indicates periodically rotated overlapping parallel lines with enhanced reconstruction; EPI, echo-planar imaging; DT, diffusion tensor; DW, diffusion-weighted; ROI, region of interest; MD, mean diffusivity; FA, fractional anisotropy.