Computational Simulations for Infrared Laser Sealing and Cutting of Blood Vessels

Abstract

Blood vessel burst pressures were simulated and predicted for sealing and cutting of vessels in a two-step process, using low (<25 W), medium (~100 W), and high (200 W) power lasers at a wavelength of 1470 nm. Monte Carlo optical transport, heat transfer, Arrhenius integral tissue damage simulations, and vessel pressure equations were utilized. The purpose of these studies was to first validate the numerical model by comparison with experimental results (for low and medium power) and then to use the model to simulate parameters that could not be experimentally tested (for high power). The goal was to reduce the large range of parameters (power, irradiation time, and linear beam dimensions) to be tested in future experiments, for achieving short vessel sealing/cutting times, minimal bifurcated seal zones (BSZ), and high vessel burst pressures. Blood vessels were compressed to 400 μm thickness. A wide range of linear beam profiles (1–5 mm widths and 8–9.5 mm lengths), incident powers (20–200 W) and clinically relevant irradiation times (0.5–5.0 s) were simulated and peak seal and cut temperatures as well as thermal seal zones, ablation zones, and BSZ computed. A simplistic mathematical expression was used to estimate vessel burst pressures based on seal width. Optimal low-power parameters were: 24W/5s/8×2mm (sealing) and 24W/5s/8×1mm (cutting), yielding a BSZ of 0.4 mm, corresponding to experimental burst pressures of ~450 mmHg. Optimal medium-power parameters were: 90W/1s/9.5×3mm (sealing) and 90W/1s/9.5×1mm (cutting), yielding a BSZ of 0.9 mm for burst pressures of ~1300 mmHg. Simulated only optimal high-power parameters were: 200W/0.5s/9×3 mm (sealing) and 200W/0.5s/9×1mm (cutting), yielding a BSZ of 0.9 mm and extrapolated to predict a seal strength of ~1300 mmHg. All lasers produced seal zones between 0.4–1.5 mm, corresponding to high vessel burst pressures of 300–1300 mmHg (well above normal systolic blood pressure of 120 mmHg). Higher laser powers enable shorter sealing/cutting times and higher vessel strengths.

I. Introduction

Radiofrequency (RF) and ultrasonic (US) energy-based devices are commonly used to expedite hemostasis and ligation of vascular tissues during numerous laparoscopic surgical procedures (e.g. hysterectomy, colonectomy, nephrectomy, cystectomy, splenectomy, lobectomy,..etc.) [1–6]. However, these devices have several limitations, including significant thermal spread (> 2 mm) and high device temperatures on the outside of the jaws (> 100–200 °C), which extends procedure times due to the slow cooling of jaws between applications (> 20 s). These high temperatures on the external surface of the device jaws must be taken into consideration to prevent injury when using RF and US devices during procedures involving confined spaces near delicate tissues (such as prostatectomy and thyroidectomy).

Our laboratory is developing an alternative optical approach utilizing infrared (IR) diode lasers for both sealing and bisection of blood vessels (Figure 1). This optical method has shown promising results during preliminary ex vivo tissue and in vivo porcine studies. Stronger vascular seals were observed in shorter time durations and with less thermal spread and lower temperatures on the outside of the device jaws [7–10].

Fig. 1.

(A) Representation of a compressed normal blood vessel; (B) Infrared laser vessel sealing/cutting method utilizing a laparoscopic device with jaws for clamping down on vascular tissues; (C) A compressed blood vessel which experienced a sequential optical process of first sealing (coagulation) and then cutting (vaporization) for bisection, with seal denoted by lighter zones.

During these preliminary studies, a linear beam profile oriented perpendicular to the length of the blood vessel was used to both seal and cut the vessel. The most effective linear beam profiles tested to date utilized the optical beam density in a two-step method, first sealing (coagulation) and second cutting (vaporization) of blood vessels [8]. The sealing beam profile had a wider dimension which created a lower fluence (energy density), providing sufficient coagulated temperatures to produce a seal. The cutting beam profile had a narrower dimension generating a higher fluence, which produced higher ablative temperatures for vaporization of the soft tissue, leaving two equally coagulated halves of a bisected blood vessel for hemostasis.

This IR laser sealing/cutting method has only been tested in laboratory experiments [7–10]. The purpose of these studies is to create a computer simulation to optimize specific parameters such as laser beam length and width, laser incident power, and laser irradiation time of low (<25 W), medium (~100 W), and high-power (200 W) lasers for creating a laser vessel sealing/cutting device with high burst pressures. By narrowing down this large range of parameters through computer simulations, it is possible to predict the expected burst pressures of varied parameters for different commercially available lasers, thus limiting the amount of experimental tests needed. The validity of the computer simulations were first confirmed by comparing simulations for low and medium powered lasers with experimental results. These numerical simulations then enabled evaluation of high power laser parameters (e.g. 200 W laser) when experimental studies were not readily available. To conduct these simulations, Monte Carlo optical transport, heat transfer, Arrhenius integral tissue damage simulations, and vessel pressure equations were used.

II. Methods

A. Bifurcated Seal Zone

A standard, linked, three-step method was used to simulate bifurcated seal zone widths in laser sealed blood vessels: (1) a Monte Carlo (MC) model of photon transport in tissue, (2) a heat transfer model to map maximum tissue temperatures, and (3) an Arrhenius integral tissue damage model to quantify thermal spread and coagulation zones. Coagulation and cutting laser beam profiles were optimized for specific temperatures based on optical beam density. The results were then used to compute burst pressures and also compared with experimental vessel burst pressures quantifying the effectiveness of optimizing the bifurcated seal zone (BSZ), when possible. The bifurcated seal zone (BSZ) was defined by the following formula (1):

$$\text{BSZ}=(\text{thermal seal zone }-\text{ ablation zone})/2$$ (1)

where thermal seal zone was total distance across the thermally coagulated and sealed vessel before bisection, and ablation zone was the central part of the thermal seal zone that had been vaporized and removed for cutting. After cutting, two separate segments of sealed tissue were left, one on each side of the bisected vessel, referred to as the BSZ (Figure 2).

Fig. 2.

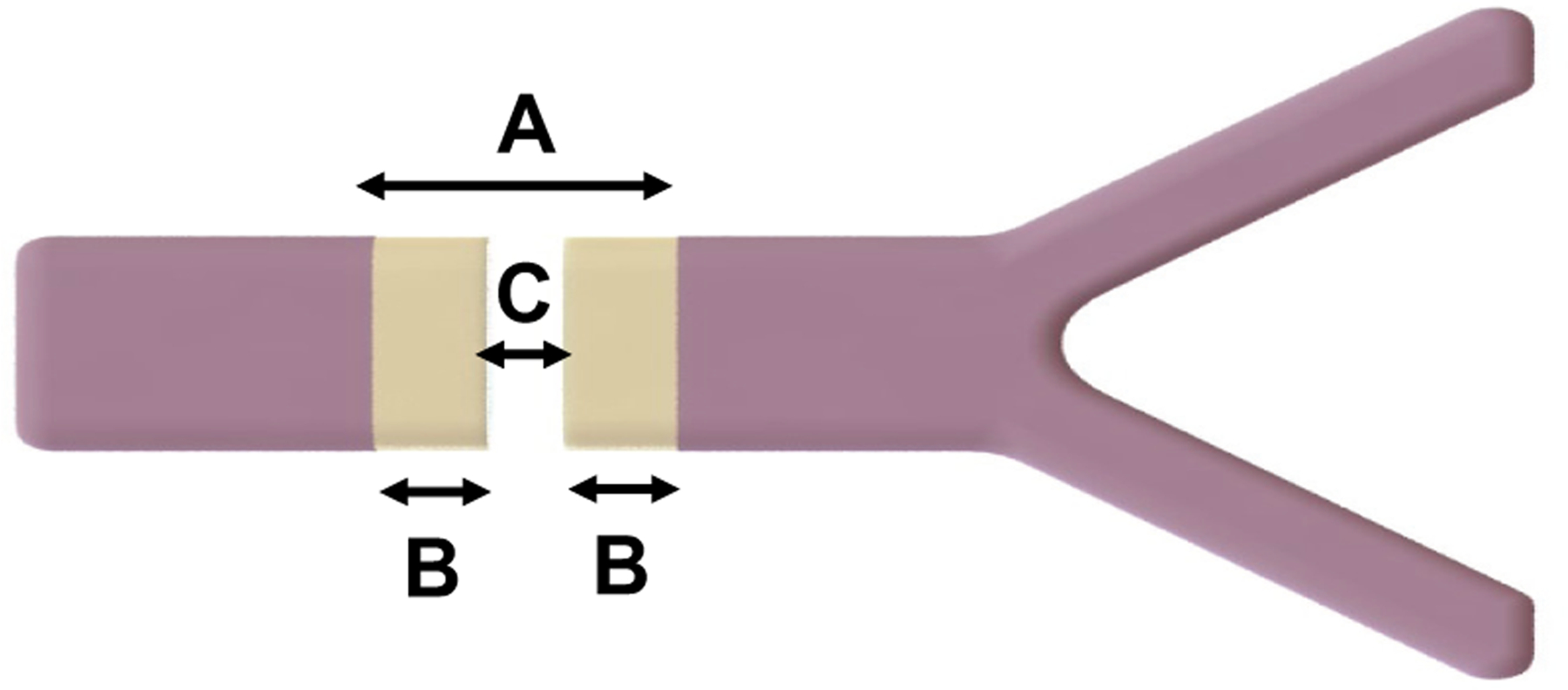
Representation of a sealed and cut vessel, showing how (A) thermal seal zone, (B) bifurcated seal zone, and (C) ablation zone were measured.

The BSZ is an important feature of a sealed and cut blood vessel. Once a blood vessel has been sealed and cut, the blood will reenter the treated area of the blood vessel lumen and create an internal pressure vessel at the end cap or BSZ. A healthy region of blood vessel can be approximated to be a thin walled pressure vessel [11]. However, unlike healthy blood vessel walls, the BSZ has been coagulated and has lost some of its elastic ability to stretch. This creates a weak point at the end cap of the pressure vessel. If the BSZ is not sufficiently thick to sustain the blood flow pressure, then the BSZ becomes the first point of failure and the vessel will burst. A simplistic mathematical expression was used to estimate internal pressure on BSZ as a longitudinal stress in a cylindrical case on a flat circular end cap, provided in (2) [12]:

$${\sigma }_{\text{max}}=\left[3{\text{a}}^2(3\text{m}+1)\text{P}\right]/8{\text{mt}}^2$$ (2)

where σ_max is the maximum stress at the center of the end cap, P is the pressure uniformly distributed over the end cap, a is the radius of the end cap, t is the thickness of the end cap, and m is the reciprocal of the Poisson’s ratio. Equation 2 is most accurate when the thickness of the plate is no thicker than one-quarter of the effective diameter (ED) of the vessel. The burst or failure of the vessel will occur when the maximum stress is equal to the tensile strength of the material. The internal pressure of the vessel increases when the longitudinal stress on the BSZ increases. For a large BSZ value (within one-quarter of the ED), it is possible to inflate the thickness value, t, and create a seal that can withstand larger internal pressures which can be estimated with (2).

Energy-based vessel sealing devices are commonly used for blood vessels with diameters of 2–6 mm [13]. In our experimental setup, the IR laser testing device, composed of bulk optics, compressed blood vessels of 2–6 mm to a fixed thickness of 400 μm, replicating the jaws of the laparoscopic device. Tissue compression displaces the blood away from the treatment zone and widens the effective vessel width beyond its normal diameter. Therefore, a layer of blood was not included in the simulations. The model instead consisted of a homogeneous 400-μm-thick vessel wall structure. The simulations also assumed a tissue with a widening effect of 50% of its original diameter (e.g. a 6 mm wide blood vessel was compressed to 9 mm width), consistent with values in the literature [14]. All simulations were performed with a compressed vessel width matching the beam length. A flat-top linear beam was used with a wide range of possible beam dimensions (1–5 mm widths and 8–9.5 mm lengths), incident powers (20–200 W), and irradiation times (0.5–5.0 s).

B. Monte Carlo Optical Transport Model

A standard Monte Carlo (MC) program in MATLAB [15] was adapted for these studies. MC simulations use a statistical “random walk” method to model light propagation, where tissues are assigned absorption and scattering coefficients as probability distributions that determine events [16]. The program determines scattering angle and tracks multiple events for each photon. These vectors are a function of the total attenuation coefficient μ_t which is the sum of absorption (μ_a) and scattering (μ_s) coefficients. The photon deposits an amount of its energy in each of these locations and is re-weighted based on the tissue optical properties. The change in the weight of the photon (ΔP) is given by (3):

$$\Delta \text{P}={\mu }_{\text{a}}/\left({\mu }_{\text{a}}+{\mu }_{\text{s}}\right)$$ (3)

The photon then carries its new weight when it takes its next step forward in the tissue. This process continues until the photon weight is reduced to a fraction of its original weight. MC output provides the radiated energy density distribution as a function of space in tissue.

To simulate distribution of photons deposited into a compressed blood vessel, a plane parallel geometry was used. This is a valid assumption for cylindrical vessels compressed and flattened within the device jaws. Three million photons were simulated to achieve sufficient (4 μm axial) spatial resolution and distribution of light absorbed in tissue. Optical properties of normal and coagulated aorta at 1470 nm under compression of 195.8 kPa were extrapolated from existing literature and used for these simulations [14,17]. When aorta tissue is transformed from its normal to coagulated state, the scattering coefficient at 1470 nm rises approximately 34%, while the absorption coefficient remains relatively constant [17]. At 1470 nm, the anisotropy factor was assumed to remain constant between normal and coagulated tissue, consistent with only small fluctuations reported in previous studies [18]. Therefore, compressed normal tissue optical properties were used in the first step (sealing beam) and coagulated compressed tissue optical properties were used in the second step (cutting beam) for all two-step simulated procedures (Table I). It should be noted that although the optical properties of laser irradiated tissue are dynamic and continuously change, for this study, simulations incorporated a discrete transformation of tissue optical properties.

TABLE I.

Optical Parameters of Normal and Thermally Coagulated, Compressed Tissue at a Wavelength of 1470 nm [14, 17, 19]

Parameter	Normal, Compressed	Coagulated, Compressed
Seal beam length (mm)	8.0 – 9.5	NA
Seal beam width (mm)	2.0 – 5.0	NA
Cut beam length (mm)	NA	8.0 – 9.5
Cut beam width (mm)	NA	1.0 – 1.5
Absorption coefficient, μa (mm−1)	2.04	2.04
Scattering coefficient, μs (mm−1)	26.7	35.7
Anisotropy factor, g	0.875	0.875
Refractive index, n	1.52	1.52
Tissue thickness (mm)	0.4	0.4

C. Heat Transfer Model

Tissue temperature simulations were conducted using an additional add-on module to the MATLAB program [15]. This model was directly integrated into the MC simulation inputs. The tissue layer was represented using thermal properties from the literature with a volumetric heat capacity of c = 3.5 J/cm³-°C and thermal conductivity of k = 0.0062 W/cm-°C (Table II) [20]. The initial tissue temperature was set at body temperature, T₀ = 37 °C.

TABLE II.

Thermal Parameters for Aorta Tissue [20]

Parameter	Value
Initial temperature, T0 (°C)	37
Volumetric heat capacity, c (J/cm3−°C)	3.5
Thermal conductivity, k (W/cm−°C)	0.0062

Temperature is an important parameter during laser tissue interactions, since it dictates if the tissue will be coagulated (sealed) or vaporized (cut). When soft tissue temperature rises, it experiences different stages which alter its physical and optical properties. At 100 °C, water begins to evaporate from the tissue. From 100–300 °C, a permanent seal of the vessel lumen starts to form. When tissue experiences temperatures of 300–400 °C, the tissue will begin to carbonize and form char. Temperatures of 400–600 °C are sufficient to vaporize the tissue [20–29]. In this study, the objective for the first step, sealing (thermal coagulation), is to achieve a maximum tissue temperature of between 100–300 °C with the sealing beam profile. For the second step, cutting (vaporization), the goal is to achieve a maximum tissue temperature of 400–600 °C.

D. Arrhenius Integral Thermal Damage Model

A standard Arrhenius integral model was used in MATLAB [15] to predict thermal injury using values for the frequency factor, ζ, and activation energy, E_a, from the literature, where ζ = 5.6 × 10⁶³ s⁻¹ and E_a = 4.3 × 10⁵ J/mol (Table III) [28].

TABLE III.

Tissue Damage Parameters for Aorta Tissue [28]

Parameter	Value
Frequency factor, ζ (s−1)	5.6 × 1063
Activation energy, Ea (J/mol)	4.3 × 105
Universal gas constant, R (J/mol-K)	8.32

Tissue damage was bundled into a single parameter given Ω(t) The temperature-time simulation data was compiled in a standard Arrhenius integral formulation in the form of a first-order chemical rate process equation used to determine thermal damage and tissue coagulation, as provided in (4) [30–32, 36].

$$\Omega (t)=\zeta \underset{0}{\overset{\tau }{\int }}\text{exp}\left(-\frac{E_a}{RT(t)}\right)dt$$ (4)

In (4), the integral time begins and ends with the laser irradiation time (t), where ζ is a frequency factor, E_a is activation energy of the transformation, R is universal gas constant, and T is absolute temperature. This integral is solved for each volume element, which will be predefined depending on the tissue geometry of the compressed blood vessel. This integral provides a ratio of damage of proteins before, C_b, and after heating, C_a. The ratio is calculated as (5):

$$\Omega (\text{T},\text{t})=-\text{ln}\left({\text{C}}_{\text{a}}/{\text{C}}_{\text{b}}\right)$$ (5)

The equation above can be transformed into a more meaningful form (6):

$$\%{\text{C}}_{\text{damage }}=\%{\text{C}}_{\text{b}}\left(-{\text{e}}^{-\Omega (\text{T},\text{t})}+1\right)$$ (6)

where %C_damage is percent damage to the proteins.

The simulated thermal damage sensor was placed in the center of the collapsed lumen, the most critical part of the blood vessel for the seal/cut procedure. Thermal damage was calculated for both sealed and cut beam profiles. The damaged cut profiles were observed as fully vaporized (ablated) tissue and subtracted from the thermal seal zone. The thermal seal zone was then divided by two because it would have been bisected by the cut profile (1). This final calculation provided an accurate representation of the bifurcated seal zone (BSZ) on a blood vessel bisected by the laser, as confirmed in previous experimental studies [8]. The BSZ was then correlated with experimental burst pressures to predict burst pressures for parameters that could not be tested in the laboratory. The BSZ was then substituted into (2), with an inverse Poisson ratio of 2 [33], and a tensile strength of 0.52 MPa [34], for an estimation of the burst pressure of a blood vessel with a diameter of 3.2 mm (the average experimental vessel size in our studies prior to compression).

E. Experimental setup

Both low and medium power 1470 nm laser diodes were tested experimentally in the laboratory. Porcine renal blood vessels with mean outer diameters of 3.2 ± 1.4 mm, and a total sample size of n = 94, were harvested from fresh porcine kidney pairs provided by a slaughterhouse (Animal Technologies, Tyler, TX) and then stored in saline prior to same day use. Blood vessels were tested on an experimental benchtop setup designed to mimic surgical instrumentation, compressing vessels to a fixed 0.4 mm thickness, as previously reported [7–8]. Each test was paired with two distinct spatial beam profiles: one for sealing and another for cutting. The change in beam size, which resulted in a change in fluence or energy density, was achieved by translating the vessel position along the optical axis. Beams were measured at FWHM and found to have small variations from the simulations, as a true flat-top beam profile could not be achieved in the laboratory. A representative example of the experimental laser spatial beam profiles incident on the vessel surface is shown in Figure 3 and is similar to previously published studies [8]. It should be noted that due to the high scattering coefficients for both native and coagulated blood vessels at the wavelength of 1470 nm (Table I), the photons undergo multiple scattering events through the compressed vessel thickness of 400 μm during the procedure, resulting in an altered and homogenized beam within the tissue, so small variations in the incident spatial beam profile probably are not significant.

Fig. 3.

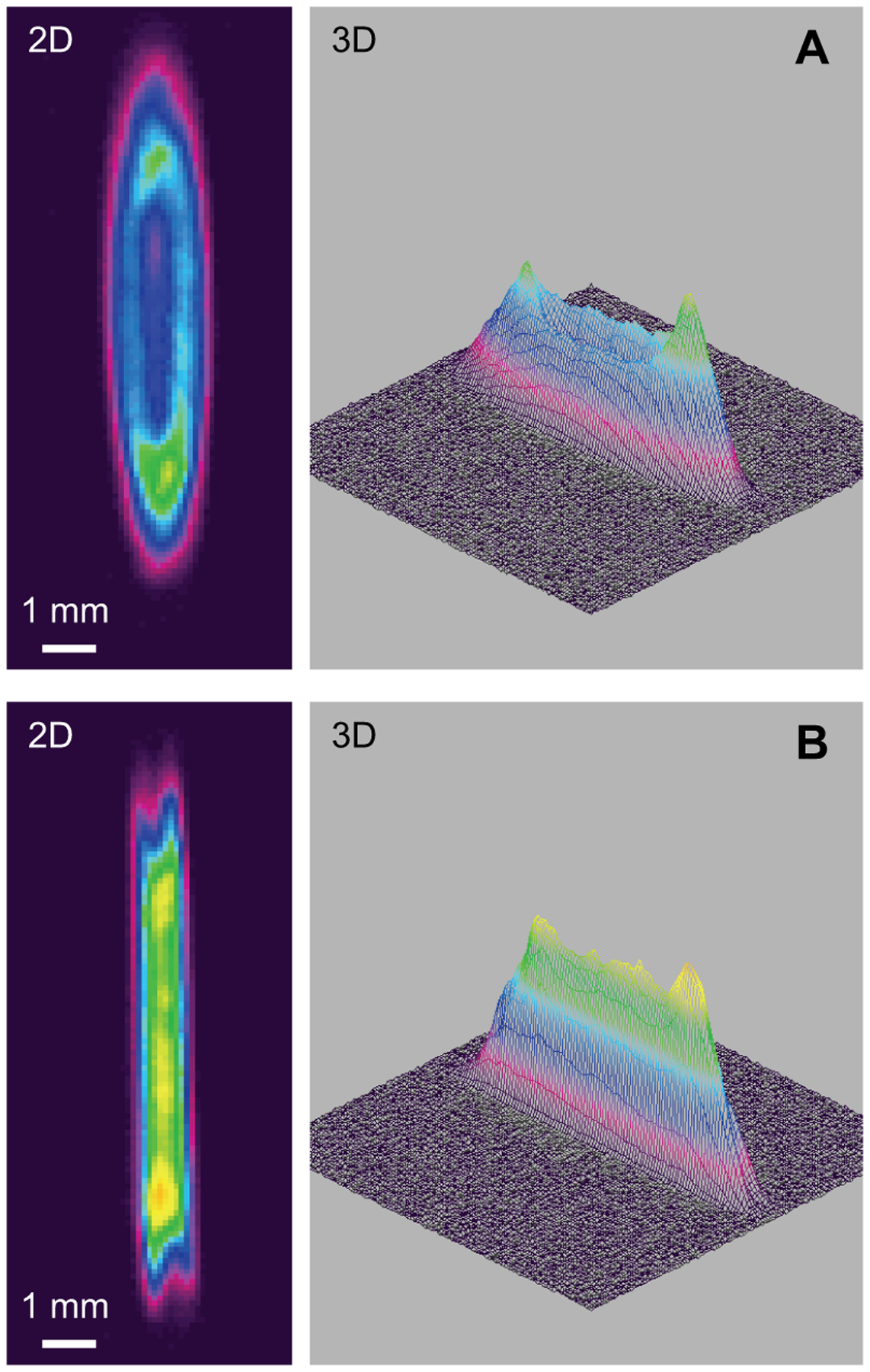
Two and three dimensional images of optimal low power beam shapes (A) 8 × 2 mm for sealing; (B) 8 × 1 mm for cutting, yielding a BSZ of 0.4 mm and corresponding to experimental vessel burst pressures of about 450 mmHg.

Vessel burst pressure measurements were performed using a pressure meter (Model 717 100 G, Fluke, Everett, WA), infusion pump (Cole Parmer, Vernon Hills, IL), and an iris clamp. Standard burst pressure measurements were conducted as previously reported, with the maximum pressure (in mmHg) corresponding to when a vessel seal bursts [7–8, 36–37]. A seal was judged to be successful if its burst pressure exceeded both normal systolic blood pressure (120 mmHg) and hypertensive blood pressure (180 mmHg). The maximum burst pressure was recorded and correlated to the simulated BSZ. The BSZ were then measured for randomly selected blood vessels using photographs and pixel counting in ImageJ software. The 200 W laser was not available for experimental testing in these studies, but was still simulated in these studies since 1470 nm diode lasers are commercially available at powers up to 200 W. It was possible to identify a trend in burst pressure versus BSZ data which helped to predict burst pressure results for the 200 W laser setting.

III. Results

A wide range of linear beam profiles (1–5 mm widths and 8–9.5 mm lengths), incident powers (20–200 W) and irradiation times (0.5–5.0 s) were simulated for low (< 25 W), medium (~ 100 W), and high (200 W) power, 1470 nm diode lasers. Table IV represents the optimal peak seal (coagulation) and cut (ablation) beam profiles with the shortest irradiation time for each laser power. Surgeons typically perform numerous blood vessel ligation applications during a single clinical procedure, so it is important to determine the optimal laser parameters which provide the shortest seal/cut times.

Figure 4 provides examples of both one and two dimensional plots of the Monte Carlo optical simulations for the 9 × 5 mm laser sealing beam. The fluence has a peak just below the surface of the vessel, due to contributions from back-scattered photons, and then follows an exponentially decaying trend. The chaotic color coded data on the left and right sides of the 2D plot is due to enhanced light scattering effects along the periphery or edges of the laser beam width.

Fig. 4.

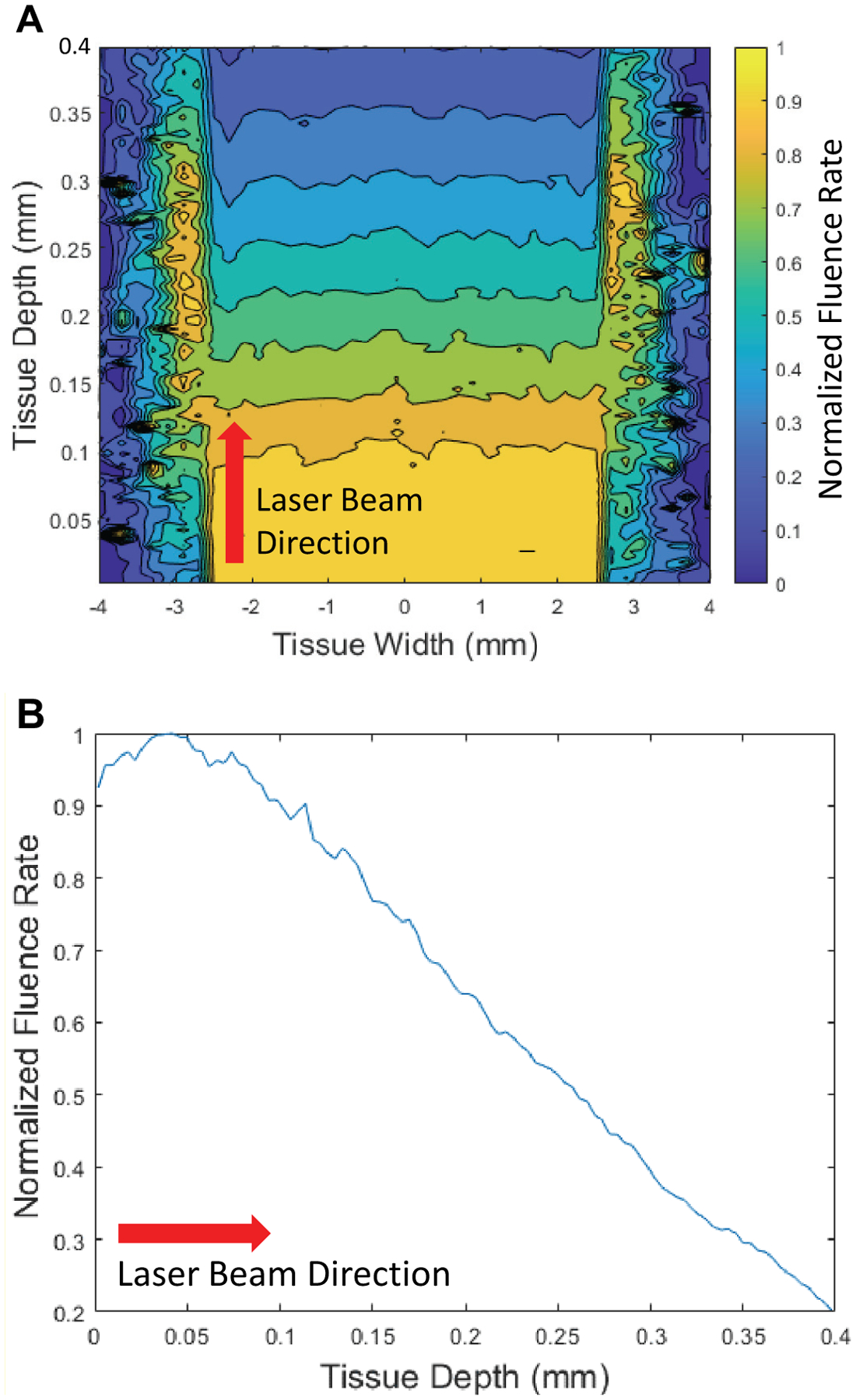
A center slice of the Monte Carlo plots of the optical absorption of three million photons in the vessel for the laser parameters of 9 × 5 mm. (A) 2D plot; (B) 1D plot. This distribution of absorbed photons correlates with temperature, where temperature on the backside of the vessel is the lowest.

The simulation results for the thermal seal zones and ablation zones are provided in Tables V and VI for the laser parameters studied. Maximum temperatures reported refer to the temperature at the backside of the vessel.

Table V shows the correspondence between fluence (energy density) and maximum temperature for the first step, laser coagulation and sealing of the vessel. Maximum tissue temperatures varied from 200 to 300 °C, within the temperature range necessary for successful seals. This table also shows the close correlation between the laser beam width (2–5 mm) and thermal seal zone or coagulated region on the vessel (2.2–4.8 mm).

TABLE V.

Thermal Seal Zones and Maximum Temperatures for Vessel Sealing

Fluence (J/cm2)	Max. Temp. (°C)	Seal Beam (mm)	Thermal Seal Zone (mm)
750	290	8 × 2	2.2
422	272	9 × 5	4.8
315	211	9.5 × 3	3.0
370	227	9 × 3	3.0

Similarly, Table VI shows the correspondence between fluence and maximum temperature for the second step, laser ablation and cutting of the vessel. Maximum tissue temperature ranged from 500 to 750 °C, above the minimum temperature necessary for successful vessel ablation. This table also shows the close correlation between the laser beam width (1.0–1.5 mm) and ablation zone or cut region on the vessel (1.2–1.8 mm).

TABLE VI.

Ablation Zones and Maximum Temperatures for Vessel Cutting

Fluence (J/cm2)	Max. Temp. (°C)	Cut Beam (mm)	Ablation Zone (mm)
1500	755	8 × 1	1.4
1407	682	9 × 1.5	1.8
947	496	9.5 × 1	1.2
1111	558	9 × 1	1.2

The BSZ was then calculated from (1) to be in the range of 0.4 to 1.5 mm (Table IV) which corresponded closely to previously measured and reported BSZ values (Figure 5A) [8]. These simulated BSZ were compared with gross images of BSZ and with both simulated and experimental burst pressures. A trend emerged of lower BSZ corresponding to lower burst pressure values (Figure 5B). Seal zones and burst pressures were plotted with error bars represented from both current and previously published experimental data [10]. It should be noted that experimental studies were performed with sealing beams tested without a second stage cutting beam present. Results showed high burst pressures, but no vessels were bifurcated. Similarly, cutting beams were tested without an initial sealing beam stage and blood vessels were all bifurcated, however, burst pressures were lower than accepted values (< 170 mmHg). These results confirmed that simulation temperatures were accurate and verified the need for a two-step, sequential, sealing and then cutting method.

TABLE IV.

Calculated and Experimental Bifurcated Seal Zones (BSZ) and Corresponding Experimental Burst Pressure (BP) Measurements for Low, Medium, and High Power Lasers [28]

Power (W)	Seal/Cut Time (s)	Seal/Cut Beams (mm)	Calculated BSZ (mm)	Measured BSZ (mm)	Measured BP (mmHg)
24	5 / 5	8 × 2 / 8 × 1	0.4	0.5 ± 0.2	457 ± 135
95	2 / 2	9 × 5 / 9 × 1.5	1.5	1.5 ± 0.4	1268 ± 771
90	1 / 1	9.5 × 3 / 9.5 × 1	0.9	0.9 ± 0.5	1305 ± 783
200	0.5 / 0.5	9 × 3 / 9 × 1	0.9	NA	NA

Fig. 5.

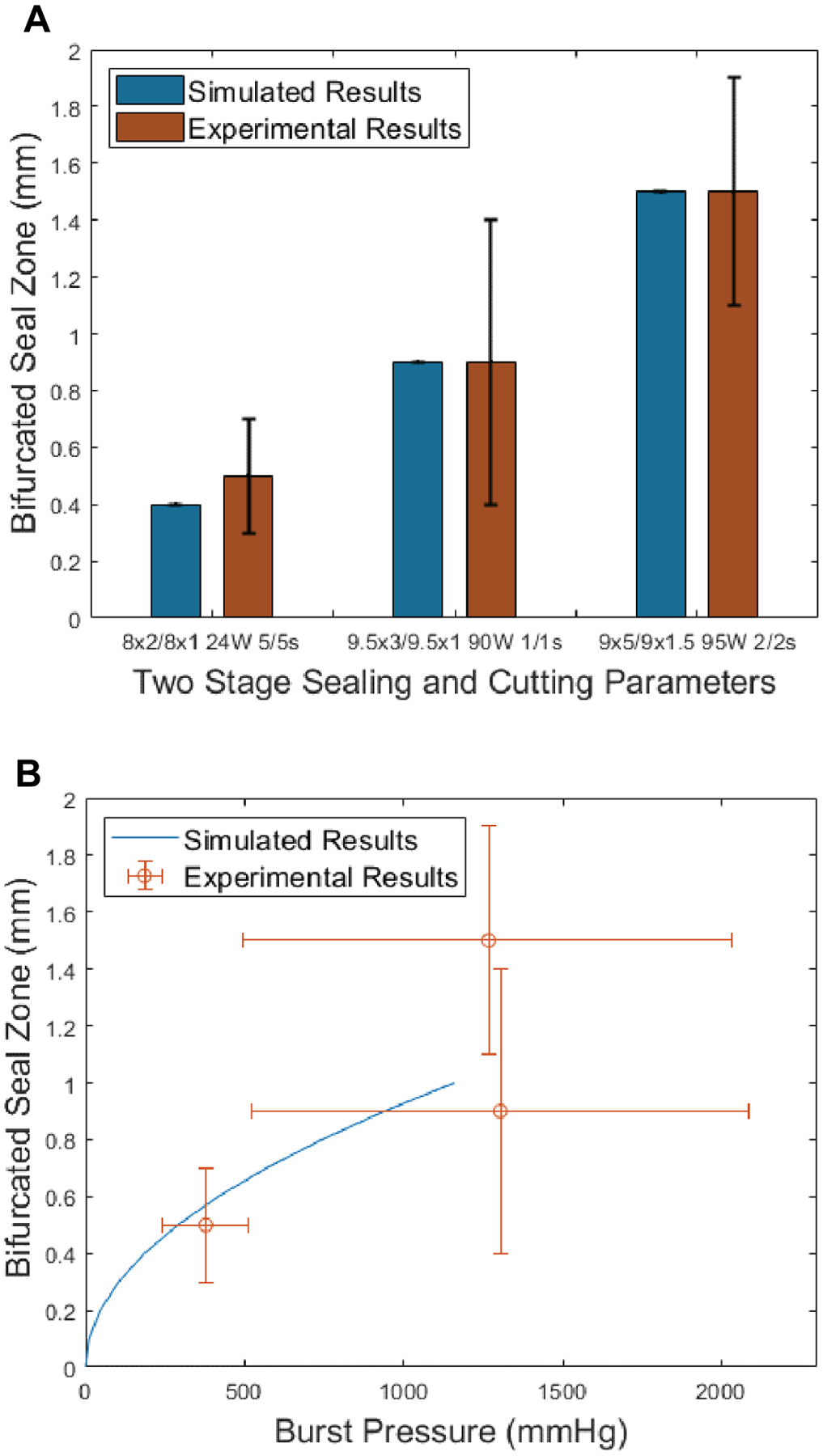
(A) Simulated BSZ (Blue) and gross measured experimental BSZ (Red) corresponding to optimum parameters in Table IV. (B) Prediction of burst pressures by using only simulated bifurcated seal zones (BSZ), where BSZ = (thermal seal zone − ablation zone) / 2 and Equation 2 up to one-quarter of the vessel width. These BSZ values were compared to experimental burst pressure measurements. These measurements show a trend where larger BSZ resulted in larger burst pressures. There is also a cap to this increase of burst pressures, which levels out at a simulated BSZ of about 0.9 mm.

Figure 6 shows representative photographs of the experimental BSZ for each of the three laser settings tested, corresponding to the laser parameters in Table IV and the simulated BSZ and burst pressure data points shown in Figure 5.

Fig. 6.

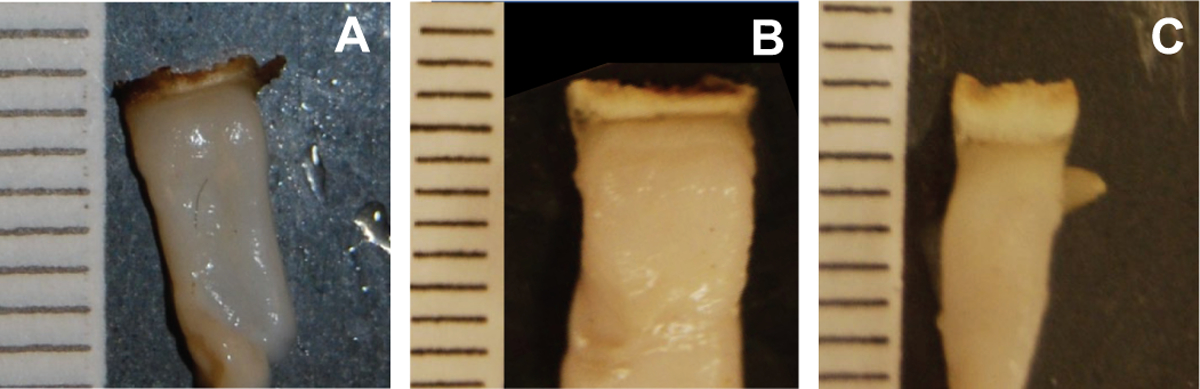
Photographs of experimental seals. Ruler lines are in millimeter scale. (A) 24 W (low power), 5 s seal / 5 s cut times, 8 × 2 mm seal beam, 8 × 1 mm cut beam dimensions, with BSZ of 0.47 mm; (B) 90 W (medium power, 1 s seal / 1 s cut times, 9.5 × 3 seal beam, 9.5 × 1 mm cut beam dimensions, with BSZ of 0.93 mm; (C) 95 W (medium power, 2 s seal / 2 s cut times, 9 × 5 mm seal beam, 6.5 × 1.5 cut beam dimensions, with BSZ of 1.6 mm.

IV. Discussion

Preliminary computer simulations demonstrated the ability to predict and optimize the optical linear beam profiles for both sealing and cutting of blood vessels, utilizing a two-step variable optical beam density technique. Use of higher power lasers shortened vessel seal and cut times, while lower power lasers yielded times similar to other clinical ultrasonic and radiofrequency energy-based devices (3–19 s) [36–41].

The trends and large error bars associated with the burst pressure measurements in Figure 5 can be explained. There were differences in burst pressures for BSZ lower than 0.9 mm. However, for a BSZ above 0.9 mm, burst pressures did not increase. The large standard deviation observed in the burst pressure measurements may be attributed to the range of vessel sizes tested. Vessels with larger diameters are exposed to higher tensions and are more likely to burst at lower pressures, which is confirmed by Laplace’s law [12,42]. However, a BSZ of 0.9 mm or higher makes this issue irrelevant since physiological blood pressures larger than 2000 mmHg are not encountered. Alternatively, when smaller blood vessels are compressed they do not stretch to the entire length of the laser beam and therefore do not absorb the entire laser energy deposited, which can also translate into lower experimental burst pressures. However, these are conflicting factors since blood pressure is proportional to blood vessel size, and smaller vessels only need to tolerate lower burst pressures to maintain hemostasis.

There are several limitations of these preliminary simulation studies. First, the optical properties of tissues are dynamic and non-linear in nature, and thus change at a continuous rate, an example of this being phase changes at temperatures above 100° C. However, these computer simulations only incorporated a discrete transformation of optical tissue properties, which occurred at the moment the beam shape changed from a sealing to a cutting beam. This discrepancy may affect how light is deposited in the tissue, which could also translate into different values for the thermal seal zone widths. The dynamic optical parameters may also affect the second, cutting beam step as well. The tissue may experience a carbonization phase with increasing temperatures before the ablation phase. Again, these dynamics could not be incorporated into the model, but may translate into a significant increase in the tissue absorption coefficient.

A second limitation concerns the laser beam dimensions during the simulations. It was necessary to model a collimated, flat-top beam incident on the tissue surface since this closely matched our benchtop studies. However, in our experimental studies, the laser output beam from the cylindrical lens was focused on the tissue, creating a variable spot width in the z direction of the tissue. The path length of the laser beam within the tissue is only 400 μm due to compression of the vessel to match the insert in the laparoscopic jaws, so the beam width change within the tissue is minimal. The benchtop study also did not achieve a full flat-top beam profile (Figure 3). This left a small region of lower power density on the beam periphery which, during the cutting beam process, could lead to a larger BSZ. However, despite this uncertainty, a close correlation was still observed between the results of the computer simulations and experimental results, as shown in Figure 5.

A third limitation of the simulations is due to the material that the blood vessel rests on, called the “back-plate” in the experimental setup. In particular, with smaller vessels, the back-plate material may affect the results. When the laser beam overfills the vessel and is incident on the back-plate without first interacting with the blood vessel, the back-plate directly absorbs the energy and heats up. The heat from the back-plate may then be reabsorbed by the back side of the blood vessel. For simplicity, these simulations assumed no laser beam overflow beyond the vessel width.

Finally, it should be noted that equation 2 used to simulate burst pressure strengths is a simplified version of the actual mechanism which occurs during vessel burst pressures. The geometry used assumes a flat plate which is not a realistic geometry which occurs in a sealed vessel. Future work can improve on the correlation of BSZ and burst pressures by improving the geometry of the seal in the model. The mechanical properties used in this equation are taken from the mechanical properties of healthy vessels. When these vessels are thermally coagulated during laser irradiation, their mechanical properties change. In future work, these mechanical properties should be measured after laser irradiation to provide a more accurate model. The model also uses an average size vessel, however, burst pressures are a function of vessel size. Overall, the model provides a close approximation to experimental burst pressure measurements, but future refinements may continue to improve on the model.

V. Conclusions

These preliminary simulation studies enabled identification of successful sealing and cutting optical linear beam dimensions based on temperature and tissue damage, optimization of laser parameters including power and irradiation time, and correlation of bifurcated seal zones with expected vessel burst pressures. Low (25 W), medium (100 W), and high-power (200 W), 1470-nm infrared lasers are capable of rapidly sealing and cutting blood vessels with acceptable burst pressures. The low power laser provides a less expensive, more compact, portable, and air-cooled system. The medium and high power lasers may enable shorter seal/cut treatment times in the operating room and the potential for treatment of larger blood vessels. A trend emerged which linked an optimal bifurcated seal zone with burst pressures. Future work will utilize these laser parameters to design a more efficient infrared laser vessel sealing and cutting device for laparoscopic surgical procedures.

Author Biographies

Nicholas C. Giglio received a Bachelor of Science degree with Honors in Physics and a Bachelor of Arts degree in Mathematics from the University of North Carolina at Charlotte, in 2013, and a Master of Science in Biomedical Engineering from the University of Rochester, in 2014. He is currently a Ph.D. student in the Optical Science and Engineering Program at the University of North Carolina at Charlotte.

Nathaniel M. Fried received a Bachelor of Arts degree in Physics from Swarthmore College, in 1992, a Master of Science degree in Physics from Rensselaer Polytechnic Institute, in 1994, and a Ph.D. in Biomedical Engineering from Northwestern University, in 1998. From 1998–2000, he was a joint postdoctoral fellow with the Applied Physics Laboratory and the Department of Biomedical Engineering at Johns Hopkins University. From 2000–2006, he was an Assistant Professor in the Urology Department at Johns Hopkins Medical School. He is currently a Professor in the Department of Physics and Optical Science at the University of North Carolina at Charlotte. His research interests include therapeutic and diagnostic applications of lasers in medicine.