Abstract
This article proposes a data-driven learning-based approach for shape sensing and Distal-end Position Estimation (DPE) of a surgical Continuum Manipulator (CM) in constrained environments using Fiber Bragg Grating (FBG) sensors. The proposed approach uses only the sensory data from an unmodeled uncalibrated sensor embedded in the CM to estimate the shape and DPE. It serves as an alternate to the conventional mechanics-based sensor-model-dependent approach which relies on several sensor and CM geometrical assumptions. Unlike the conventional approach where the shape is reconstructed from proximal to distal end of the device, we propose a reversed approach where the distal-end position is estimated first and given this information, shape is then reconstructed from distal to proximal end. The proposed methodology yields more accurate DPE by avoiding accumulation of integration errors in conventional approaches. We study three data-driven models, namely a linear regression model, a Deep Neural Network (DNN), and a Temporal Neural Network (TNN) and compare DPE and shape reconstruction results. Additionally, we test both approaches (data-driven and model-dependent) against internal and external disturbances to the CM and its environment such as incorporation of flexible medical instruments into the CM and contacts with obstacles in taskspace. Using the data-driven (DNN) and model-dependent approaches, the following max absolute errors are observed for DPE: 0.78 mm and 2.45 mm in free bending motion, 0.11 mm and 3.20 mm with flexible instruments, and 1.22 mm and 3.19 mm with taskspace obstacles, indicating superior performance of the proposed data-driven approach compared to the conventional approaches.
Keywords: Deep Neural Networks, Temporal Neural Networks, Continuum Manipulator, Fiber Bragg Grating, Data-driven Sensing, Shape Sensing
I. Introduction
FLEXIBLE robots have shown great potential in enhancing dexterity and reach in Minimally Invasive Surgery (MIS) and Laparo-endoscopic Single Site (LESS) interventions [1]. To this end, flexible medical devices such as Continuum Manipulators (CMs) have been the focus of attention to facilitate and address some of the challenges associated with rigid instruments in medical robotics. Compared to rigid-link robots, CMs can adopt to various shapes and exhibit compliance when interacting with obstacles and organs [2]. Although beneficial, the flexibility and conformity of CMs make accurate shape sensing (center-line or backbone position estimation along the manipulator body) and Distal-end Position Estimation (DPE) challenging.
CMs are typically guided to target locations inside the body, where embedded flexible sensing units are more suitable as compared to external tracking devices such as optical trackers. In recent years, optical fibers such as Fiber Bragg Grating (FBG) have been considered for shape and tip sensing of CMs, as well as other flexible devices such as biopsy needles and catheters [3]–[6]. FBGs are well-suited for medical applications, since they are small in size, lightweight, flexible, and immune to electromagnetic interference. They also have high sensitivity, fast response and high frequency streaming rate while compatible with medical imaging modalities [7].
A common technique for shape sensing and DPE using FBG sensors is to find the curvature at discrete locations, extrapolate curvature along the length of the sensor, compute slopes and reconstruct the shape from proximal to distal end (base to tip) by integration [3], [5], [7]. This method, however, faces several drawbacks: 1) it relies on many geometrical assumptions about the sensor or CM design, 2) it requires extraneous calibration procedures for system parameter identification, 3) due to limited number of active sensing locations on the fibers, the method is prone to error propagation during integration and shape reconstruction, 4) it uses only a subset of FBG measurements located at a particular active area cross section for estimation of local curvature. Moreover, due to the proximal to distal end integration approach for shape reconstruction, the error is accumulated toward the distal end, resulting in poor DPE accuracy. The distal end feedback, however, usually is the most critical part of the CM during control to desired surgical target sites.
Model-driven approaches require deep understanding of the system followed by simplifying assumptions to allow modeling of complex systems in a feasible manner. As such, perfect emulation of the system with a model containing sufficient complexity to capture the underlying physics of the system is challenging and a cumbersome task. Another drawback of the traditional model-driven approaches is that the key variables used in the model are sometimes difficult to measure online due to the complexity of the design and environment uncertainties.
Data-driven methods, however, provide stable and reliable online estimation of these variables based on historical measurements [14]. Deep learning has recently become a popular data-driven approach by showing the ability to capture richer information from raw input data and yielding improved representation [15]. To address the drawbacks associated with the conventional model-dependent shape reconstruction approach, we introduce a new data-driven paradigm for reconstructing the CM shape and DPE. We define the problem of CM shape reconstruction as a supervised regression problem for estimating the CM distal-end tip position, followed by an optimization method that reconstructs the shape of the manipulator. The input to this algorithm is the sensory data obtained from the embedded FBG sensor and the output is the DPE as well as the reconstructed shape. Similar to other supervised learning algorithms, the proposed method consists of an offline dataset creation step, during which the sensory data is labeled with correct distal-end position. Three different supervised machine learning algorithms (linear and nonlinear) are incorporated and trained on the collected dataset to learn the mapping from FBG measurements to CM’s distal-end position. This information is then passed to an optimization method that reconstructs the shape of the CM.
Table I summarizes the recent state of FBG-based CM shape sensing and DPE accuracy by different researchers using the conventional sensor-model-dependent approach. Roesthuis et al. [8] reconstructed the CM shape in free environment while using FBGs at four active areas along the sensor. They performed an additional calibration step to correct for inaccuracies in DPE by scaling the reconstructed values from the FBG sensor. Liu et al. [7] and Farvardin et al. [10] reported larger tip position errors when the CM was introduced to a constrained environment with obstacles. Ryu et al. [11] reported the shape reconstruction results only in free space. Other studies, such as [9], [12] and [13], lacked validation studies on the accuracy of the FBG-based shape reconstruction and DPE accuracy. For each study, the following are reported in Table I: number of fibers used in a sensor, number of inscribed Bragg gratings, sensor substrate material and outside diameter, number of sensors, configuration of fibers to substrate attachment, manipulator length, sensor/manipulator assembly, and DPE in free and constrained environment experiments. In order for the DPE errors to be comparable among studies with different manipulator lengths, we define the Deflection Ratio (DR) measure and denote it with ξ:
| (1) |
where δ is the maximum tip deflection applied to the manipulator in the study and L is the manipulator’s length. The DR for an experiment shows what percentage of the manipulator length, its tip has deflected. This measure along with the maximum curvature applied to the manipulator is useful for manipulator DPE error comparison among different studies.
TABLE I.
Review of FBG-based continuum manipulator distal-end position estimation (dpe) error by different research groups (cm = continuum manipulator, od = outside diameter, ξ = deflection ratio, κ = curvature, nr = not reported, na = not applicable).
| Research Group | FBG Sensor Design | CM | Free | Constrained | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| # Fibers (# FBG) | Substrate (OD) | # Sensors | Config. | Length (mm) | Sensor Assembly | DPE (mm) Mean (Std) | ξ (%) κ (m−1) | DPE (mm) Mean (Std) | ξ (%) κ (m−1) | |
| Roesthuis et al. [8] | 3 (4) | NiTi wire (1.0 mm) |
1 | Triangular | 160 | In Backbone | No Calib.: x: 2.04 (1.58) y: 2.03 (1.77) With Calib.: x: 0.96 (0.46) y: 0.44 (0.26) |
18.75 2.37 |
NR | NA |
| Liu et al. [7] | 1 (3) | 2 NiTi wires (0.125 mm) |
2 | Triangular | 35 | In Side Lumen |
0.41 (0.30) | 57.14 50.00 |
0.61 (0.15) 0.93 (0.05) 0.23 (0.1) |
42.86 27.00 |
| Xu et al. [9] | 3 (1) | NiTi tube (2.0 mm) |
1 | Helical | 90 | Wrapped on CM | NR | NA | NR | NA |
| Farvardin et al. [10] | 1 (3) | 2 NiTi wires (0.125 mm) |
2 | Triangular | 35 | In Side Lumen | 1.14 (0.77) 0.81 (0.99) 3.49 (1.13) |
42.86 27.00 |
2.73 (0.77) 0.96 (0.35) |
22.86 14.22 |
| Ryu et al. [11] | 1 (NR) | Polymer tube (1.05 mm) |
1 | Triangular | 80 | Along Substrate |
0.84 (0.62) | 50.39 14.00 |
NR | NA |
| Wei et al. [12] | 1 (4) | NiTi wire (0.3 mm) |
1 | Helical | 110 | Wrapped on CM | NR | NA | NR | NA |
| Chitalia et al. [13] | 1 (1) | NiTi spine (0.57 mm) |
1 | N/A | 20.5 100 |
In Backbone | NR | NA | NR | NA |
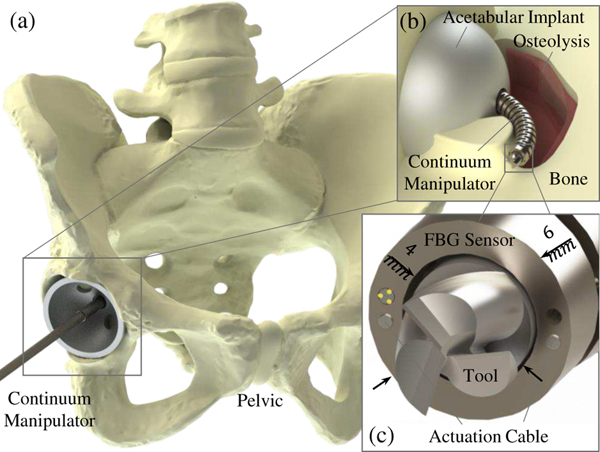
It can be observed from Table I that previous studies have generally focused more on the FBG sensor design perspectives and the shape reconstruction methods, while a comprehensive and unified evaluation of the shape reconstruction results is missing, specially during CM interaction with obstacles and contacts with the environment. Moreover, there are many differences associated with these studies with regard to the design specifications of the CM and FBG sensor (such as length, substrate material and geometry, number of optical fibers and FBGs, etc), as well as the design of the evaluation experiments. The maximum curvature and DR are helpful measures in comparing the DPE errors for different sensors and manipulators, however, with such variations in previous experimental studies, a thorough comparison study on a single sensor and CM assembly in various experimental scenarios (free and constrained environment) could be beneficial for the community. The main contributions of the paper are as follows: 1) development of a novel data-driven approach for CM shape sensing and DPE, 2) implementation of three data-driven models using linear regression, a Deep Neural Network (DNN), and a Temporal Neural Network (TNN), 3) a thorough comparative study for evaluation of the shape sensing and DPE results using the conventional sensor-model-dependent and data-driven approaches on a non-constant curvature planar CM with large deflections both in free and constrained environments. The CM was specifically designed for minimally invasive orthopedic interventions such as osteolysis or bone degradation behind the acetabular implant (Fig. 1).
Fig. 1.
(a) Robot-assisted treatment of pelvic osteolysis, (b) continuum manipulator interacting with bone behind the acetbular implant, and (c) debriding tool and FBG sensor integrated with the continuum manipulator (distal end view)
II. Methods
A. Model-Dependent Shape Sensing
In conventional model-dependent approaches, first the strain at each sensor cross section with FBG nodes is found by (2) and then based on the sensor’s geometry, a system of nonlinear equations (3) is solved at each cross section with three FBG nodes in a triangular configuration (see Fig. 2(d)) to find local curvature (κ), curvature angle (ϕ), and a strain bias (ϵ0) entailing the temperature effects or common mechanical strain at the cross section:
| (2) |
| (3) |
where subscripts a, b, and c correspond to the three fibers, λB is the Bragg wavelength, pe is the strain constant for the optical fiber and r, γ are geometrical parameters which can be obtained from design or estimated in a calibration procedure [3]. Assuming a relationship (typically linear) between curvature (κ) and arc length (s), and dividing the sensor length to n sufficiently small segments, curvature and its direction (ϕ) can be extrapolated at each segment (4). Using the curvature at each segment (κi for i = 1,..., n), the slope of each segment can be found using (5). Establishing an appropriate local coordinate frame to the beginning of each segment, the shape and consequently the distal-end position can be reconstructed segment by segment using (6):
| (4) |
| (5) |
| (6) |
where ρi = 1/κi is the radius of curvature and Rx,ϕ is the rotation of ϕ about the local x axis. Using (6) for i = 1,..., n, the tip position of the sensor (Pn) can be found. For CMs in which the FBG sensor is not placed on the center axis of the CM, all Pi should be shifted by the distance between sensor’s and CM’s centers to obtain the CM center-line shape.
Fig. 2.
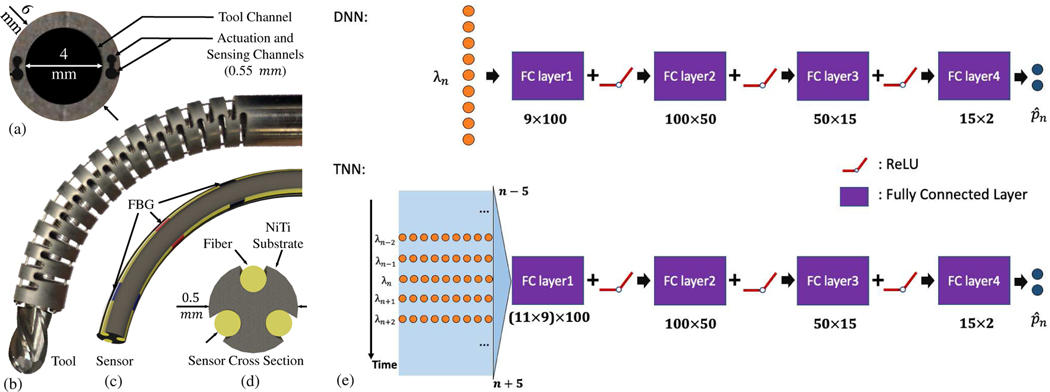
(a) CM tip cross sectional view showing the actuation, sensing, and tool channels, (b) tool integrated with the CM, (c) FBG sensor, (d) FBG sensor with the triangular configuration cross section view, and (e) Top: DNN architecture. λn is the raw FBG vector at the nth observation. is the network output CM tip position. Hyperparameters of the fully connected layers are listed under each block. Bottom: TNN architecture. The concatenation process is illustrated with the time-series data.
It must be noted that estimation of local curvature (4) can also be performed by calibrating the FBG sensor wavelength data (λ) against curvature (κ), typically using a 3-D-printed or laser-cut calibration jig with constant curvatures to find the mapping [7], [10]:
| (7) |
where f is the mapping between the raw wavelength data and the local curvature at sensor cross sections with FBG nodes.
B. Data-Driven DPE
In surgical applications, typically the distal end of the CMs are controlled to target locations in human anatomy for navigation of flexible instruments or manipulation of tissue [16]. One of the major drawbacks of the conventional model-dependent sensing approach outlined in section II-A is that the DPE is a byproduct of the shape reconstruction algorithm after integration of curvature information from proximal to distal end of the sensor. Consequently, the reconstruction error propagates toward the distal end of the manipulator [17]. This error can be reduced with high spatial resolution sensors containing several FBG nodes along the sensor length. For FBG sensors with limited number of active areas, however, the error propagation is more apparent. To remedy this problem in low spatial resolution FBG sensors, we introduce a novel data-driven paradigm for reconstructing the CM shape and DPE using supervised machine learning methods. The paradigm consists of two steps: 1) estimating the CM distal-end position using a supervised regression learning model with FBG measurements as input, and 2) reconstructing the shape of the CM via an optimization approach using the DPE from step 1) as input (desribed in section II-C). For the DPE step, we aim to find a regression model that predicts the CM’s distal-end tip position, given a set of raw FBG wavelength data along the sensor. Motivated by application to a planar CM designed for minimally invasive orthopaedic interventions such as osteolysis (Fig. 1), we formulate this problem as a regression problem with the FBG measurements (λ) as the independent variables and the CM distal position (p) as the dependent variables:
| (8) |
where p ∈ ℝ2 is the 2-D position of the CM tip, λ ∈ ℝm is the vector containing the raw wavelength data of the m FBG nodes on the sensor, β is the vector of unknown parameters, and Ψ : ℝm → ℝ2 is the regression model that predicts the CM tip position, given the wavelength information of the complete set of FBG nodes on the sensor at any given time. Of note, the effect of temperature change and common axial force in sensor readings for a single cross section can be eliminated by subtracting the common mode from Bragg wavelength shift of each sensor, as proposed in [18], [19]. Additionally, to avoid sensitivity of the data-driven algorithm to scale of the input features, we apply a normalization (standardization) to the sensor measurements to achieve a data distribution with mean of zero and standard deviation of one:
| (9) |
where is the expected mean, Var is the variance and is the normalized measurement input to the model at time step n. Depending on the degrees of freedom of the CM, complexity of the environment, and the shapes that the CM can obtain, different regression models could be incorporated to capture the unknown parameters β. We hereby propose, describe and evaluate three different models for this purpose: 1) linear least square model, 2) DNN, and 3) TNN.
1). Linear Regression:
Linear regression is a common regression method that models the dependent variables as a linear combination of the unknown parameters. The DPE can be modeled as a least squares optimization problem:
| (10) |
where rn is the residual error for the nth observation, Λ ∈ ℝN×m is a stack of N observations of the m FBG node data, P ∈ ℝN×2 is the stack of N ground truth CM distal-end position observation data, and B ∈ ℝm×2 is the matrix of unknown parameters. Using (10), the regression model can be trained preoperatively on N observations of the FBG and ground truth data to find the unknown parameters B using the MoorePenrose inverse:
| (11) |
The trained model can then be used intraoperatively to predict CM tip position values given the current FBG data:
| (12) |
where is the predicted the CM distal-end position, given the normalized FBG wavelength nth data observation ().
2). DNN:
DNNs are becoming popular due to their increased flexibility to fit complex models compared to traditional regression methods. Unknown parameters in the DNN model can be trained end-to-end in a data-driven manner through backpropagation. We define the trainable parameters in the DNN as with a corresponding bias vector , where i is the layer index and Fi is the layer size hyperparameter. For normalized raw FBG wavelength data vector at the nth observation, , we compute activations for with:
| (13) |
| (14) |
where f(·) is the Rectified Linear Unit (ReLU) non-linear activation function, l ∈ {2,..., L} are the second to the last layer of the network and F0 = m. The DNN output is the corresponding nth CM distal-end position . We use Mean Squared Error (MSE) as loss function to optimize , where pn ∈ ℝ2 is the ground truth tip position observation. Fig. 2 illustrates the architecture design of the DNN.
3). TNN:
All the aforementioned models are trained only with individual sensor observations at a particular time step, without consideration of the time-series information. In prior work, Temporal Convolutional Networks (TCN) have been proposed to improve video-based analysis models, which use time-varying features to make predictions [20], [21]. The intuition behind utilizing a time-series model lies with the observation that input data features are often changing continuously. In the present application, the CM manipulation and deformation also occur in a continuous manner, since the CM is usually controlled from its initial state to the desired target state. Thus, we take the inspiration from the design of the TCNs to propose a TNN for CM DPE.
Fig. 2 presents the hierarchical structure of the TNN. We follow the above notations and denote the input concatenated feature with respect to time as , where (2k+1) is the number of samples covered in this concatenated feature. The TNN is trained to predict the DPE corresponding to the middle data sample . In spite of introducing a small delay in predictions (in the order of a couple of milliseconds), the intuition behind the proposed embedding of the time-series is to incorporate information about changes in the sensory data as a result of potential contacts with the environment or stopping the CM actuation. For the TNN, we use the same MSE loss that is used in the DNN approach.
In general, the network architecture and choice of hyperparameters are application-dependent. Accordingly, in this work, the hyperparameters were chosen empirically based on the complexity of the FBG singal data. We perceived that four fully-connected layers both for the DNN and the TNN were sufficient to capture the complexity of the data. Fig. 2 (e) lists the input and output feature dimensions of each layer under each block. The input dimension of the first layer is consistent with the input size (number of FBG nodes). The second to fourth layers of the DNN and the TNN are designed to be the same in order to make the feature encodings comparable between the two methods.
C. Data-Driven Shape reconstruction
Once accurate estimate of the distal-end position of the CM is obtained from the regression model, the shape of the CM can be reconstructed. To do so, we model the CM as a series of rigid links connected by passive elastic joints using a pseudo-rigid body model. In particular, the CM in this study is modeled as a n-revolute-joint mechanism due to the planar motion of the CM. Depending on the design of the particular CM, spherical joints can also be assumed for the CM in a general case. At any given instance, the DPE () output from the regression model (section II-B) is passed as input to the constrained optimization (15) to solve for the joint angles and consequently the shape is reconstructed:
| (15) |
where Θc ∈ ℝn is the CM joint angles from the pseudo-rigid body model, d = Lc/n is the distance between two consecutive joints, f(Θc) : Θc → ℝ2 is the CM forward kinematics mapping from joint space to task space, and Θmax is the maximum angle each joint can take, which can be determined experimentally [22]. The trade-off between choosing a more complex pseudo-rigid body model (large number for n) and the computational complexity of (15) must be adjusted according to the application requirements and specifications.
III. Experimental Setup
A. Continuum Manipulator and Flexible Instruments
The CM used in this study was designed primarily for the MIS orthopedic interventions. It was constructed from a Nitinol (NiTi) tube with several notches to achieve flexibility (see Fig. 3, top right). One result of this design and choice of material was that the CM was very stiff perpendicular to the direction of bending while still flexible in the direction of bending. This is important to enable the CM to sustain large loads associated with the debriding/cutting process in orthopedic surgeries [22], [23]. As shown in Fig. 2(a), the CM’s wall contains four lengthwise channels with the Outside Diameter (OD) of 500 μm for passing actuation cables and fiber optic sensors. The overall length of the flexible part the CM was chosen as 35 mm, with OD of 6 mm to meet the requirements for the orthopedic applications such as the less invasive treatment of osteolysis or bone degradation [24]. The CM contains a 4 mm instrument channel for insertion of flexible debriding tools [24], [25]. From a shape sensing standpoint, the insertion of the flexible instruments into the open lumen of the CM alters the dynamic behaviour of the CM (i.e. the local curvatures), which should consequently be accounted for in the shape sensing algorithms [26]. The experimental setup is shown in Fig. 3, where the CM is mounted on an actuation unit and its cables are actuated with two DC motors (RE10, Maxon Motor Inc. Switzerland) with spindle drives (GP 10 A, Maxon Motor, Inc. Switzerland) on the actuation unit. A commercial controller (EPOS 2, Maxon Motor Inc. Switzerland) is used to control the individual Maxon motors.
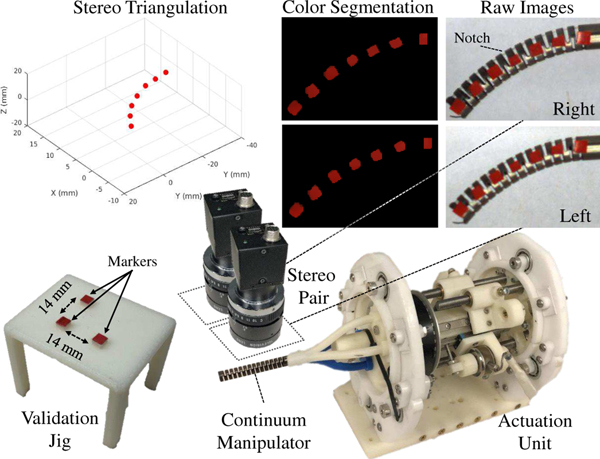
Fig. 3.
The experimental setup including the CM actuation unit integrated with a calibrated stereo camera pair. Raw images obtained from the camera pair are first color-segmented and then 3-D locations of the markers are computed by triangulation. The custom-designed jig for validation of the marker-based triangulation is shown on the bottom left.
B. FBG Sensor Design and Fabrication
The FBG sensor used for this study contains three FBG fibers attached to a flexible NiTi wire with an OD of 500 μm in a triangular configuration (see Fig. 2(d)). Three grooves (radially 120° apart from each other) are engraved by laser (Potomac, USA) along the length of the wire to hold three fibers each with three 3-mm Bragg grating, spaced 10 mm apart from one another (Technica S.A, China). The FBG cores are silica with polyimide coating. The fibers are glued into the engraved NiTi grooves using epoxy glue (J-B Clear Weld Quick Setting Epoxy). The NiTi wire is passed into the CM sensor channel and glued to the manipulator distal end, such that the first grating on each fiber is 5 mm apart from the CM tip. Due to its relatively small OD, the NiTi wire can withstand curvatures of as small as 20 mm radius during bending, which is sufficient to cover and sense large deflections of the CM [27].
C. Stereo Camera Pair
In order to generate ground truth data for the true shape of the CM at any given instance, a stereo camera setup with 1024 × 768 resolution was used to track colorized markers attached to the center-line of the CM. The markers were aligned with the CM notch geometry and attached under the microscope. The stereo camera pair was calibrated using the stereo camera calibration toolbox in MATLAB on a 8 × 6 checkerboard with 5 mm edge squares. The resulting overall mean error for the stereo pair calibration was 0.12 pixels. For each stereo image pair, the 2-D pixel locations of the marker centers were found in each image by applying a color segmentation with experimentally-determined thresholds. An interactive graphical user interface was written in Python to facilitate the process of determining the color segmentation thresholds. The intrinsic and extrinsic parameters from the calibration procedure were then used in custom-written Python code to find the corresponding markers within the two color-segmented images and obtain the 3-D locations of the markers by triangulation [28]. An erosion morphological operation, followed up with a dilation was applied to the segmented images to smooth out the color segmentation. Of note, a custom-designed jig containing three markers with known predetermined spatial locations was used for validation purposes (Fig. 3, bottom left). The jig was translated and rotated in the desired workspace of the stereo pair and a sequence of image pairs were recorded. Using the parameters obtained from the calibration process, a 0.02 mm mean 3-D position accuracy error was observed when triangulating and measuring the distance between the markers.
IV. Experiment Design and Evaluation Criteria
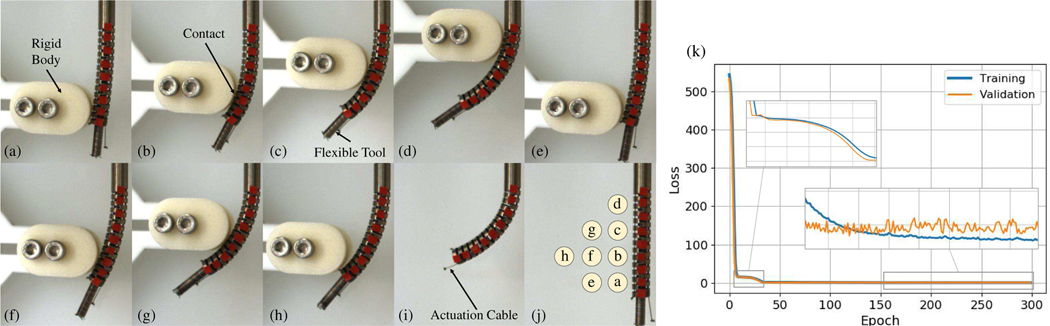
Inspired by CM motions in a MIS surgical procedure, three sets of experiments were considered and the shape reconstruction and DPE from both model-dependent and data-driven paradigms were evaluated and compared. In the first and second sets, the CM was bent in free environment to large curvatures up to κ = 50 m−1 with and without the tool. In the third set, 3-D printed obstacles were distributed at eight different locations along the body of the CM in its workspace (Fig. 4). Presence of obstacles enforced the CM to take on more complex shapes compared to free environment bending, resulting in more challenging shape sensing problems. These experiments were designed to imitate the behaviour of the CM in real surgical scenarios, where presence of obstacles such as bone, tissue, organs, etc. is inevitable. In each experiment, the CM started from its straight pose and the actuating cable was pulled for a maximum of 5.5 mm with a velocity of 0.2 mm/s to obtain training data with high resolution. On average, each experiment contained nearly 836 samples, with a total of 8,364 samples in all experiments. A K-fold cross validation technique (with K = 10) was used to evaluate the performance by splitting the data to training and validation sets. In particular, out of the ten experiments (Fig 4 (a) through (j)), one experiment was chosen as the validation dataset and the remaining nine experiments were used for the training phase. This process was repeated for all possible ten choices of the validation experiment to ensure generalization of each method in predicting unseen sensory data regardless of the type of experiment (i.e. free or constrained with varying obstacle location).
Fig. 4.
(a through h) CM bending experiments in constrained environment in presence of internal disturbance (flexible tool) and external disturbance (obstacles at various locations), (i) CM bending in free environment, (j) CM bending in free environment with tool, as well as the demonstration of the obstacle locations relative to the CM for experiments a through h. (k) loss trend during training and validation.
A. Data Collection
FBG data was streamed by an optical sensing interrogator (Micron Optics sm 130) at a frequency of 100 Hz, while the images from the stereo pair camera system (Flea2 1394b, FLIR Integrated Imaging Solutions Inc.) were obtained at 30 Hz frequency. A thread-safe mechanism from open source C++ cisst-saw libraries [29] was used to record the data for each of these sensor sources in parallel, using a separate CPU thread for each source. All the data was time-stamped and pre-processed during the training phase to pair the FBG data with the corresponding image sample. All experiments were run on a computer with an Intel 2.3 GHz core i7 processor with 8 GB RAM, running Ubuntu 16.04.
B. Network Training Hyperparameters
Both the DNN and the TNN were trained with learning rate of 1.0 × 10−3, and batch size of 128. We used the Adam optimizer with a weight decay of 1.0×10−5, obtained empirically. Fig. 4(k) presents an example of the reduction of the loss function during training and validation of the DNN model as the number of epochs (each epoch correspond to one cycle through the full training dataset) evolves. Of note, the concatenation feature length 2k+1 in the TNN model controls how much temporal information is included for prediction. The k value was chosen experimentally as 5. Thus, a concatenation feature covers 2k + 1 = 11 samples in the TNN model.
V. Results and Discussion
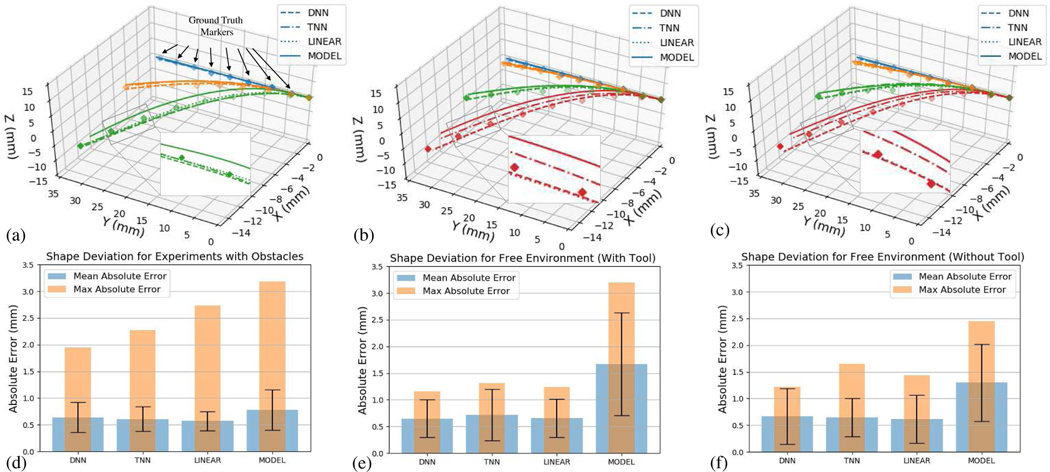
A summary of the performance of the data-driven and sensor-model-dependent approaches in shape sensing and DPE is presented in Table II. For each method, the DPE error for any point along the length of the manipulator (parametrized by the distance from the manipulator base) is defined as the euclidean distance between the method estimation and the ground truth data for that particular point. For instance, the distal-end (tip) position error is the euclidean distance between the estimation for the tip of the manipulator and the ground truth tip position. For shape, the mean absolute error is used for all the points with available ground truth data (i.e. the markers) along the length of the manipulator. In addition, the standard deviations and the maximum absolute errors are reported for the shape estimations. In particular, using the DNN, TNN, linear regression, and the sensor-model-dependent model, the mean, standard deviation, and maximum error for shape reconstruction and DPE in both constrained spaces and free environment are presented. Motivated by orthopedic applications, the CM was equipped with a flexible instrument (Fig. 2(b)) during the constrained space experiments with obstacles, while the free environment experiments were performed both in presence and absence of the flexible instrument. From a shape sensing and DPE perspective, the presence of a flexible instrument is regarded as internal disturbance while the presence of obstacles in the surrounding of the CM is regarded as external disturbance. The last three columns of the table demonstrate the average errors observed in the constrained cases (in presence of obstacle) as well as the free environment with and without flexible instruments. A comparison of the DPE results reveals that the DNN model achieves better generalization and outperforms the other models on average with sub-millimeter accuracy performance in constrained and free spaces. The linear and TNN models also show relatively good performance, while the sensor-dependent-model approach can lead to DPE with maximum error as high as 3.20 mm and 3.19 mm in large deflection bendings of the CM in presence of internal and external disturbances, respectively. For the experiments with presence of obstacles (external disturbance), the maximum observed DPE errors using the DNN, TNN, linear, and sensor-model-dependent approach are 1.22 mm, 1.72 mm, 2.74 mm, and 3.19 mm, respectively.
TABLE II.
Comparison of results for model-dependent and data-driven dpe and shape sensing in free and constrained environments. errors for individual constrained experiments (a to h) from Fig. 4 Are also reported. All units are millimeter.
| Method | Exp a | Exp b | Exp c | Exp d | Exp e | Exp f | Exp g | Exp h | Constrained | Free (Tool) | Free (No Tool) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Shape | DNN | Mean | 0.32 | 0.89 | 1.16 | 0.49 | 0.39 | 0.48 | 0.53 | 0.90 | 0.64 | 0.65 | 0.67 |
| Std. | 0.21 | 0.60 | 0.71 | 0.32 | 0.25 | 0.22 | 0.29 | 0.50 | 0.28 | 0.35 | 0.52 | ||
| Max | 0.65 | 1.74 | 1.95 | 1.22 | 0.81 | 0.65 | 0.98 | 1.51 | 1.95 | 1.16 | 1.22 | ||
| TNN | Mean | 0.37 | 0.82 | 1.10 | 0.58 | 0.40 | 0.48 | 0.49 | 0.62 | 0.61 | 0.72 | 0.65 | |
| Std. | 0.24 | 0.55 | 0.83 | 0.42 | 0.25 | 0.28 | 0.27 | 0.32 | 0.23 | 0.48 | 0.36 | ||
| Max | 0.70 | 1.70 | 2.27 | 1.25 | 0.76 | 0.84 | 0.93 | 0.98 | 2.27 | 1.31 | 1.65 | ||
| LIN | Mean | 0.32 | 0.73 | 0.81 | 0.54 | 0.40 | 0.40 | 0.62 | 0.77 | 0.57 | 0.66 | 0.62 | |
| Std. | 0.22 | 0.46 | 0.98 | 0.78 | 0.25 | 0.19 | 0.36 | 0.41 | 0.18 | 0.36 | 0.45 | ||
| Max | 0.66 | 1.52 | 2.74 | 1.74 | 0.84 | 0.65 | 1.19 | 1.31 | 2.74 | 1.24 | 1.44 | ||
| MODEL | Mean | 0.23 | 1.14 | 0.78 | 1.08 | 0.32 | 0.42 | 1.07 | 1.24 | 0.78 | 1.67 | 1.30 | |
| Std. | 0.12 | 1.13 | 0.84 | 0.63 | 0.19 | 0.28 | 0.62 | 0.67 | 0.38 | 0.96 | 0.72 | ||
| Max | 0.41 | 3.19 | 2.40 | 2.14 | 0.57 | 1.03 | 2.20 | 2.19 | 3.19 | 3.20 | 2.45 | ||
| DPE | DNN | Error | 0.23 | 0.48 | 0.16 | 1.22 | 0.36 | 0.38 | 0.93 | 1.11 | 0.61 | 0.11 | 0.78 |
| TNN | Error | 0.23 | 0.64 | 1.72 | 0.50 | 0.52 | 0.34 | 0.93 | 0.78 | 0.71 | 0.28 | 0.68 | |
| LIN | Error | 0.21 | 0.98 | 2.74 | 0.87 | 0.32 | 0.13 | 0.49 | 1.31 | 0.88 | 0.29 | 0.86 | |
| MODEL | Error | 0.41 | 3.19 | 2.40 | 2.14 | 0.57 | 1.03 | 2.21 | 2.19 | 1.76 | 3.20 | 2.45 | |
The slightly superior performance of the DNN compared to the TNN in maximum reported errors (maximum CM bend) can be explained by noting that the network mostly experiences continuous changes in data during motion of the CM, whereas there is only one appearance of a motion stop in each experiment (at maximum CM bend). Given the limited number of data associated with motion stops, the TNN model may not be able to predict the stops and as a result may slightly overshoot the predicted DPE. Such behaviour could be mediated by either adding more stop/motion occurrences in the data set or by incorporating action information (e.g. actuation cable displacement or motor current) in the input to the network. Another possible reason is that DNN and TNN have different learnable parameters. DNN has 6,847 learnable parameters, while TNN has 15,847 learnable parameters. TNN is more likely to overfit to the training data. Of note, The learnable parameters of the linear regression is 18 (number of FBG nodes times the output dimension).
Fig. 5 shows the shape reconstruction results using the four approaches and their comparison with the ground truth data obtained from the markers attached to the CM. Figs. 5(a), 5(b), and 5(c) correspond to the shape reconstruction in presence of obstacle, free environment with embedded flexible tool, and free environment without flexible tool, respectively. The quantitative shape reconstruction results are shown in Figs. 5(d), 5(e), 5(f), where the mean, standard deviation and maximum errors in shape reconstruction using each method are plotted in constrained environment, free environment with flexible tool, and free environment without flexible tool, respectively. It can be observed that the sensor-model-dependent approach yields to maximum shape deviations of 3.20 mm and 2.45 mm from the ground truth markers in free environment with and without flexible tool, respectively. The increased error in presence of flexible tool can be explained by the variations that the flexible tool may impose on the local curvature profile of the CM which may not be captured by the limited number of sensing nodes along the length of the sensor. Moreover, the model-dependent approach results in average maximum error of 1.76 mm in all obstacle cases, with the worst performance in case of obstacle (b) with 3.19 mm maximum error. For the data-driven approaches, the DNN model outperforms the TNN and linear model with smaller maximum shape deviation error in comparison. For the cases with obstacle, the DNN, TNN, and linear models yield maximum shape deviation errors of 1.95 mm, 2.27 mm, and 2.74 mm, respectively. For the free environment experiments, with and without the presence of tool, all three methods result in similar accuracy performance, with the DNN model showing slight superior performance over the TNN and linear models.
Fig. 5.
Shape reconstruction results using the DNN, TNN, linear, and physics-based methods for the constrained environment experiments with obstacle contacts (a and d), free environment experiment with tool (b and e), free environment experiment without tool (c and f).
Of note, we have tried the TNN approach both by using the temporal information only from the past observations, as well as the combination of the future and the past observations. The results demonstrated better performance when using both past and future observations, increasing the DPE estimation accuracy by 0.4 mm on average, compared to using only the past observations. This finding is consistent with prior work on temporal convolutional networks ([21]), where it was demonstrated that including both the past and future information helps with better encoding of the signal. There is clearly a trade-off between accuracy and real-time performance that could be determined based on the application and performance criteria. With 100 Hz FBG data streaming frequency and k = 5 number of future samples, a 50 ms delay is introduced in the estimations, which could still be acceptable for many applications.
The CM used in this study is non-constant curvature, which makes the modeling of the CM and sensor more challenging due to more complex underlying behaviour. An overview of the previous studies (Table I) reveals that compared to other studies where the fibers are directly attached to the CM or the backbone, the integration of the FBG sensor into the side lumens of the manipulator used in this study increases the modeling complexities further. As such, a data-driven approach could be beneficial by skipping the step for making several geometrical assumptions. In addition, a segment by segment shape reconstruction in conventional model-dependent methods suffers from error propagation especially in CMs with large deflection (similar to the CM used in this study), since any inaccuracy in curvature estimation at cross sections close to the base of the CM will establish an incorrect direction for the remainder of shape reconstruction, resulting in inaccurate DPE.
For the experiments reported in this study, the CM underwent a maximum curvature of 50 m−1, with a DR of 58, while both intrinsic (flexible tool) and extrinsic (contact at multiple locations in the workspace) disturbances were present during the experiments. Referring to Table I, the maximum curvature and the DR reported in this study are larger than or equal to any of the previously reported work in the literature, with enhanced variation in the free and constrained environment experiments. Considering the larger maximum curvature and DR, the DNN results reported in this study are superior than those reported in the literature. The constrained environment bending shape sensing errors in [7] is comparable to the DNN results, however, the variety of contact location in [7] is limited compared to our study (three compared to eight contact locations).
While previous studies have demonstrated valuable insight into the design considerations of the FBG sensor and integration into different CMs, they have not provided thorough evaluation experiments on the shape sensing method accuracy in practical cases. The comprehensive results presented in this study can therefore be used as a baseline for the performance and accuracy of the FBG-based shape sensing with limited number of sensing locations for CMs with large curvature bending in free and constrained environments. Moreover, the proposed data-driven approaches for DPE and shape reconstruction have proven valuable for such manipulators. One reason for the observed outperformance is that on the contrary to the conventional shape reconstruction methods where only wavelength information of a few FBG nodes at a certain cross section are used to predict curvature locally, in the data-driven approach, the wavelength information of all FBG nodes on the sensor is incorporated into the model during each tip position prediction. Of note, the data-driven method can also be applied to CMs with multiple backbones by incorporating separate data-driven models for each segment and sequentially estimating the distal-end position of the next segment.
One important aspect of the data-driven approaches lies at the creation of the dataset, as with any supervised machine learning approach. While this can be considered an additional step in preparation and use of the sensor, the benefit of learning the parameters from real data rather than imperfect geometrical and mechanical assumptions and conjectures, outweighs the hardships associated with dataset creation. Additionally, for the conventional mechanics-based model-dependent approaches, performing a calibration experiment of some sort is inevitable. The calibration could be done for establishing a wavelength-curvature relationship or estimating the parameters present in the model (system identification).
For the data-driven approaches, the average required time for collecting the data associated with each experiment in this study was less than one minute. As a result, a combination of e.g. ten experiments could be carried out in the order of 10 to 15 minutes. Using a system with core i7 Intel CPU and 8 GB of RAM running Ubuntu 16.04, the average training time for the DNN, and the TNN were 14.82 s and 28.93 s, respectively, while estimating the least squares linear model was in the order of a couple of milliseconds depending on the size of training data. The forward pass time for the DNN and the TNN were on average measured at 0.41 ms and 0.72 ms, respectively, which is sufficient for real-time applications. Of note, in a practical setting (e.g. surgical scenario), the required data for the data-driven approach can be generated on the fly by articulation of the CM (and consequently the embedded FBG sensor) and incorporation of an external source of information such as X-ray or camera images. In another scenario, a baseline data-driven model could be established preoperatively, while the model is updated intraoperatively as additional data (such as ground truth data from intermittent X-ray) is incorporated into the model for updating the network parameters (weights).
VI. CONCLUSION
In this study, we evaluated the performance of the conventional mechanics-based sensor-model-dependent approach for reconstructing the shape of a large curvature CM in free and constrained environments. In these experiments, the CM was articulated to curvatures as large as 50 m−1 (corresponding to radius of curvatures as small as 20 mm), which is larger than the reported maximum curvatures for CMs with similar scale in previous studies. In addition, we proposed a novel data-driven paradigm for DPE and shape sensing which did not require calibration or any prior assumptions regarding the sensor or CM model (FBG node location, substrate geometry, sensor-CM integration). Particularly, a DNN, a TNN, and a linear regression model were designed, trained and evaluated in combination with a data-driven optimization-based shape sensing method, resulting in superior performance compared to conventional model-dependent approaches.
While in this study, we incorporated an FBG sensor embedded in the CM and used a stereo pair camera system for obtaining the ground truth data, other sensing modalities such as EM trackers for sensing and optical trackers or X-ray images for ground truth data could potentially be used. In future work, other optical fiber sensing such as the polymer FBG [30] or Random Optical Gratings by Ultraviolet laser Exposure (ROGUEs) [31] will be explored to enhance the sensitivity and estimation accuracy. Additionally, the combination of the data-driven and the physics-based methods should be explored in the future to take advantage of the strengths of each method.
Acknowledgments
Research supported by NIH/NIBIB grant R01EB016703 and Johns Hopkins university internal funds.
Biography

Shahriar Sefati received his M.S.E. in Computer Science and Ph.D. in Mechanical Engineering from the Johns Hopkins University in 2017 and 2020, respectively. He has been a member of the Biomechanical- and Image-Guided Surgical Systems (BIGSS) Laboratory, as part of the Laboratory for Computational Sensing and Robotics (LCSR), where he is currently serving as a postdoctoral researcher at the Autonomous Systems, Control, and Optimization (ASCO) laboratory. Prior to joining Johns Hopkins, he received his B.Sc. in Mechanical Engineering from Sharif University of Technology, Tehran, Iran, in 2014. His research interests include robotics and artificial intelligence for development of autonomous systems.

Cong Gao received his B.E. in Electronic Engineering from Tsinghua University in 2017. He is currently a Ph.D. candidate in Computer Science in the Johns Hopkins University. He is a member of the Biomechanical- and Image-Guided Surgical Systems (BIGSS) Laboratory and the Advanced Robotics and Computationally AugmenteD Environments (AR-CADE) Laboratory, as part of the Laboratory for Computational Sensing and Robotics (LCSR). His research interest lies in medical robotics vision and deep learning.

Iulian Iordachita (IEEE M08, S14) is a faculty member of the Laboratory for Computational Sensing and Robotics, Johns Hopkins University, and the director of the Advanced Medical Instrumentation and Robotics Research Laboratory. He received the M.Eng. degree in industrial robotics and the Ph.D. degree in mechanical engineering in 1989 and 1996, respectively, from the University of Craiova. His current research interests include medical robotics, image guided surgery, robotics, smart surgical tools, and medical instrumentation.

Russell H. Taylor received the Ph.D. degree in computer science from Stanford University, in 1976. After working as a Research Staff Member and Research Manager with IBM Research from 1976 to 1995, he joined Johns Hopkins University, where he is the John C. Malone Professor of Computer Science with joint appointments in Mechanical Engineering, Radiology, and Surgery, and is also the Director of the Engineering Research Center for Computer-Integrated Surgical Systems and Technology and the Laboratory for Computational Sensing and Robotics. He is an author of over 500 peer-reviewed publications and has 80 US and International patents.

Mehran Armand received Ph.D. degrees in mechanical engineering and kinesiology from the University of Waterloo, Ontario, Canada. He is a Professor of Orhtopaedic Surgery and Research Professor of Mechanical Engineering at the Johns Hopkins University (JHU) and a principal scientist at the JHU Applied Physics Laboratory. Prior to joining JHU/APL in 2000, he completed postdoctoral fellowships at the JHU Orthopaedic Surgery and Otolaryngology-head and neck surgery. He currently directs the laboratory for Biomechanical- and Image-Guided Surgical Systems (BIGSS) at JHU Whiting School of Engineering. He also co-directs the AVECINNA Laboratory for advancing surgical technologies, located at the Johns Hopkins Bayview Medical Center. His lab encompasses research in continuum manipulators, biomechanics, medical image analysis, and augmented reality for translation to clinical applications of integrated surgical systems in the areas of orthopaedic, ENT, and craniofacial reconstructive surgery.
Contributor Information
Shahriar Sefati, Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA, 21218.
Cong Gao, Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA, 21218.
Iulian Iordachita, Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA, 21218.
Russell H. Taylor, Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA, 21218.
Mehran Armand, Department of Orthopedic Surgery, The Johns Hopkins Medical School, Baltimore, MD, USA, 21205; Laboratory for Computational Sensing and Robotics, Johns Hopkins University, Baltimore, MD, USA, 21218.
REFERENCES
- [1].Vyas L, Aquino D, Kuo C-H, Dai JS, and Dasgupta P, “Flexible robotics,” BJU international, vol. 107, no. 2, pp. 187–189, 2011. [DOI] [PubMed] [Google Scholar]
- [2].Burgner-Kahrs J, Rucker DC, and Choset H, “Continuum robots for medical applications: A survey,” IEEE Transactions on Robotics, vol. 31, no. 6, pp. 1261–1280, 2015. [Google Scholar]
- [3].Roesthuis RJ, Kemp M, van den Dobbelsteen JJ, and Misra S, “Three-dimensional needle shape reconstruction using an array of fiber bragg grating sensors,” IEEE/ASME transactions on mechatronics, vol. 19, no. 4, pp. 1115–1126, 2013. [Google Scholar]
- [4].Khan F, Denasi A, Barrera D, Madrigal J, Sales S, and Misra S, “Multi-core optical fibers with bragg gratings as shape sensor for flexible medical instruments,” IEEE sensors journal, 2019. [Google Scholar]
- [5].Shi C, Luo X, Qi P, Li T, Song S, Najdovski Z, Fukuda T, and Ren H, “Shape sensing techniques for continuum robots in minimally invasive surgery: A survey,” IEEE Transactions on Biomedical Engineering, vol. 64, no. 8, pp. 1665–1678, 2016. [DOI] [PubMed] [Google Scholar]
- [6].Beisenova A, Issatayeva A, Tosi D, and Molardi C, “Fiber-optic distributed strain sensing needle for real-time guidance in epidural anesthesia,” IEEE Sensors Journal, vol. 18, no. 19, pp. 8034–8044, 2018. [Google Scholar]
- [7].Liu H, Farvardin A, Grupp R, Murphy RJ, Taylor RH, Iordachita I, and Armand M, “Shape tracking of a dexterous continuum manipulator utilizing two large deflection shape sensors,” IEEE sensors journal, vol. 15, no. 10, pp. 5494–5503, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Roesthuis RJ, Janssen S, and Misra S, “On using an array of fiber bragg grating sensors for closed-loop control of flexible minimally invasive surgical instruments,” in 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 2545–2551, IEEE, 2013. [Google Scholar]
- [9].Xu R, Yurkewich A, and Patel RV, “Curvature, torsion, and force sensing in continuum robots using helically wrapped fbg sensors,” IEEE Robotics and Automation Letters, vol. 1, no. 2, pp. 1052–1059, 2016. [Google Scholar]
- [10].Farvardin A, Murphy RJ, Grupp RB, Iordachita I, and Armand M, “Towards real-time shape sensing of continuum manipulators utilizing fiber bragg grating sensors,” in 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), pp. 1180–1185, IEEE, 2016. [Google Scholar]
- [11].Ryu SC and Dupont PE, “Fbg-based shape sensing tubes for continuum robots,” in Robotics and Automation (ICRA), 2014 IEEE International Conference on, pp. 3531–3537, IEEE, 2014. [Google Scholar]
- [12].Wei J, Wang S, Li J, and Zuo S, “Novel integrated helical design of single optic fiber for shape sensing of flexible robot,” IEEE Sensors Journal, vol. 17, no. 20, pp. 6627–6636, 2017. [Google Scholar]
- [13].Chitalia Y, Deaton NJ, Jeong S, Rahman N, and Desai JP, “Towards fbg-based shape sensing for micro-scale and meso-scale continuum robots with large deflection,” IEEE Robotics and Automation Letters, vol. 5, no. 2, pp. 1712–1719, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Shang C, Yang F, Huang D, and Lyu W, “Data-driven soft sensor development based on deep learning technique,” Journal of Process Control, vol. 24, no. 3, pp. 223–233, 2014. [Google Scholar]
- [15].Yuan X, Gu Y, Wang Y, Yang C, and Gui W, “A deep supervised learning framework for data-driven soft sensor modeling of industrial processes,” IEEE Transactions on Neural Networks and Learning Systems, 2019. [DOI] [PubMed] [Google Scholar]
- [16].Sefati S, Murphy R, Alambeigi F, Pozin M, Iordachita I, Taylor R, and Armand M, “Fbg-based control of a continuum manipulator interacting with obstacles,” in Intelligent Robots and Systems (IROS), 2018 IEEE/RSJ Int. Conference, pp. 1–7, 2018. [Google Scholar]
- [17].Sefati S, Hegeman R, Alambeigi F, Iordachita I, and Armand M, “Fbg-based position estimation of highly deformable continuum manipulators: Model-dependent vs. data-driven approaches,” in 2019 International Symposium on Medical Robotics (ISMR), pp. 1–6, IEEE, 2019. [Google Scholar]
- [18].Gonenc B, Chamani A, Handa J, Gehlbach P, Taylor RH, and Iordachita I, “3-dof force-sensing motorized micro-forceps for robot-assisted vitreoretinal surgery,” IEEE sensors journal, vol. 17, no. 11, pp. 3526–3541, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Iordachita I, Sun Z, Balicki M, Kang JU, Phee SJ, Handa J, Gehlbach P, and Taylor R, “A sub-millimetric, 0.25 mn resolution fully integrated fiber-optic force-sensing tool for retinal microsurgery,” International journal of computer assisted radiology and surgery, vol. 4, no. 4, pp. 383–390, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Lea C, Vidal R, Reiter A, and Hager GD, “Temporal convolutional networks: A unified approach to action segmentation,” in European Conference on Computer Vision, pp. 47–54, Springer, 2016. [Google Scholar]
- [21].Gao C, Liu X, Peven M, Unberath M, and Reiter A, “Learning to see forces: Surgical force prediction with rgb-point cloud temporal convolutional networks,” in OR 2.0 Context-Aware Operating Theaters, Computer Assisted Robotic Endoscopy, Clinical Image-Based Procedures, and Skin Image Analysis, pp. 118–127, Springer, 2018. [Google Scholar]
- [22].Murphy RJ, Kutzer MD, Segreti SM, Lucas BC, and Armand M, “Design and kinematic characterization of a surgical manipulator with a focus on treating osteolysis,” Robotica, vol. 32, no. 6, pp. 835–850, 2014. [Google Scholar]
- [23].Kutzer MD, Segreti SM, Brown CY, Armand M, Taylor RH, and Mears SC, “Design of a new cable-driven manipulator with a large open lumen: Preliminary applications in the minimally-invasive removal of osteolysis,” in 2011 IEEE International Conference on Robotics and Automation, pp. 2913–2920, IEEE, 2011. [Google Scholar]
- [24].Alambeigi F, Sefati S, Murphy RJ, Iordachita I, and Armand M, “Design and characterization of a debriding tool in robot-assisted treatment of osteolysis,” in 2016 IEEE International Conference on Robotics and Automation (ICRA), pp. 5664–5669, IEEE, 2016. [Google Scholar]
- [25].Alambeigi F, Wang Y, Sefati S, Gao C, Murphy RJ, Iordachita I, Taylor RH, Khanuja H, and Armand M, “A curved-drilling approach in core decompression of the femoral head osteonecrosis using a continuum manipulator,” IEEE Robotics and Automation Letters, vol. 2, no. 3, pp. 1480–1487, 2017. [Google Scholar]
- [26].Murphy RJ, Otake Y, Wolfe KC, Taylor RH, and Armand M, “Effects of tools inserted through snake-like surgical manipulators,” in 2014 36th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, pp. 6854–6858, IEEE, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Sefati S, Pozin M, Alambeigi F, Iordachita I, Taylor RH, and Armand M, “A highly sensitive fiber bragg grating shape sensor for continuum manipulators with large deflections,” in 2017 IEEE SENSORS, pp. 1–3, IEEE, 2017. [Google Scholar]
- [28].Hartley R and Zisserman A, Multiple view geometry in computer vision. Cambridge university press, 2003. [Google Scholar]
- [29].Deguet A, Kumar R, Taylor R, and Kazanzides P, “The cisst libraries for computer assisted intervention systems,” in MICCAI Workshop on Systems and Arch. for Computer Assisted Interventions, Midas Journal, vol. 71, 2008. [Google Scholar]
- [30].Broadway C, Min R, Leal-Junior AG, Marques C, and Caucheteur C, “Toward commercial polymer fiber bragg grating sensors: Review and applications,” Journal of Lightwave Technology, vol. 37, no. 11, pp. 2605–2615, 2019. [Google Scholar]
- [31].Monet F, Sefati S, Lorre P, Poiffaut A, Kadoury S, Armand M, Iordachita I, and Kashyap R, “High-resolution optical fiber shape sensing of continuum robots: A comparative study,” in 2020 IEEE International Conference on Robotics and Automation (ICRA), pp. 8877–8883, IEEE, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]