Quantile Regression for Survival Data

Abstract

Quantile regression offers a useful alternative strategy for analyzing survival data. Compared to traditional survival analysis methods, quantile regression allows for comprehensive and flexible evaluations of covariate effects on a survival outcome of interest, while providing simple physical interpretations on the time scale. Moreover, many quantile regression methods enjoy easy and stable computation. These appealing features make quantile regression a valuable practical tool for delivering in-depth analyses of survival data. In this paper, I review a comprehensive set of statistical methods for performing quantile regression with different types of survival data. This review covers various survival scenarios, including randomly censored data, data subject to left truncation or censoring, competing risks and semi-competing risks data, and recurrent events data. Two real examples are presented to illustrate the utility of quantile regression for practical survival data analyses.

1. Background and motivation

The problem of analyzing survival (or time-to-event) data arises in a number of scientific fields. For example, an event time of interest can be survival time of a cancer patient recorded in a medical study, time to high school dropout studied by sociologists, “survival” time of new business addressed in economic research, or lifetime of a part under stress evaluated in an engineering reliability study. A common feature of survival data is that they often contain incomplete time-to-event information due to censoring or truncation. Censoring occurs when an event time is known to have occurred only within certain intervals. Truncation is defined as a condition which excludes certain subjects from the study population. Statistical methods for analyzing survival data need to appropriately account for various forms of censoring and truncation.

To evaluate the association between a survival outcome and a set of explanatory variables (or covariates), the accelerated failure time (AFT) model has been extensively studied in literature as a counterpart of linear regression in survival analysis (Miller 1976, Buckley & James 1979, Prentice 1978, Wei & Gail 1983, Tsiatis 1990, Ritov 1990, Wei et al. 1990, among others). Consider an event time T and a p × 1 covariate vector $\tilde{Z}$. The AFT model regresses a survival response, Y ≐ log(T), or another monotone transformation of T, over $\tilde{Z}$; that is,

$$Y={\tilde{Z}}^{\top }b+ϵ,$$

where b is a vector of unknown regression coefficients and ϵ is an error term with an unknown distribution independent of $\tilde{Z}$. The assumption that ϵ is independent of $\tilde{Z}$ confines covariates to affect only the location of the distribution of Y. However, this is often too restrictive in real applications. For example, an analysis of a dialysis dataset presented in Section 5.1 suggests that the symptom severity of restless leg syndrome (RLS) may only impact the lower range but not the upper range of the survival function of dialysis patients. The AFT model, which assumes pure location shift effects, would fail to accommodate such an inhomogeneous effect of RLS.

An alternative regression strategy for survival data is to use the Cox proportional hazards (PH) model (Cox 1972, Andersen & Gill 1982) Specifically, the Cox PH model relates the conditional hazard function of T, $\lambda (t\mid \tilde{Z})\doteq {\text{lim}}_{\Delta \to 0}{\Delta }^{-1}\text{Pr}\{t\in (t,t+\Delta ]\mid T⩾t,\tilde{Z}\}$, to covariates in $\tilde{Z}$ multiplicatively without specifying a parametric baseline hazard; that is,

$$\lambda (t\mid \tilde{Z})={\lambda }_0(t)\text{exp}\left\{{\tilde{Z}}^{\top }b\right\},$$

where λ₀(t) is an unspecified baseline hazard function, and b is an unknown regression coefficient vector. The Cox PH model is widely used in the practice of survival analysis. Nevertheless, the Cox regression model requires covariate-specific hazards be proportional. This key assumption essentially exerts a location shift model for a monotonically transformed survival function of T. This limits the applications of the Cox PH model in scenarios with inhomogeneous covariate effects as exemplified above. Under the Cox PH model, covariate effects are formulated on the conditional hazard function of T, which lacks a physical interpretation on event times (Reid 1994).

Quantile regression (Koenker & Bassett 1978) offers a natural remedy for accommodating heterogeneous covariate effects, while retaining straightforward physical interpretations. A comprehensive review of quantile regression methodology was provided by Koenker (2017). Quantile regression has received increased attention in survival analysis because event times themselves are often of scientific interest, and quantiles are more flexible and robust quantitative tools for characterizing event times than mean-based devices. For example, in the presence of censoring with bounded support, mean survival time may not be identifiable, while quantiles may be identifiable.

For a survival time T, a standard quantile regression model assumes that the τ-th conditional quantile of Y ≐ log(T) given $\mathit{Z}={\left(1,{\tilde{\mathit{Z}}}^{\top }\right)}^{\top }$, defined as Q_Y (τ|Z) ≐ inf{t : Pr(Y ⩽ t|Z) ⩾ τ), is linearly related to covariates in Z. That is,

$$Q_Y(\tau \mid Z)=Z^{\top }{\beta }_0(\tau ),\tau \in \left[{\tau }_L,{\tau }_U\right],$$ (1)

where 0 ⩽ τ_L ⩽ τ_U < 1 and β₀(τ) is a (p + 1) × 1 vector of unknown regression coefficients. A non-intercept coefficient in β₀(τ) represents a covariate effect on the τ-th conditional quantile of log(T). By allowing β₀(τ) to change with τ, quantile regression permits varying covariate effects on different segments of the response distribution. This feature renders the flexibility to accommodate inhomogeneous covariate effects

When τ_L = τ_U, model (1) is referred to as a locally linear quantile regression model because it only asserts “local” linearity between the conditional quantile of log(T) and Z at a single quantile level. When τ_L < τ_U, model (1) imposes a “global” linearity for the conditional quantile of log(T) throughout the τ-interval [τ_L, τ_U], and thus is referred to as a globally linear quantile regression model. A globally linear quantile regression model can provide a platform for investigating the dynamic pattern of covariate effects, while paying the price of imposing a stronger model assumption compared to a locally linear quantile regression model.

It is easy to see that the AFT model is a special case of model (1) with β₀(τ) = {Q_ϵ(τ), b^⊤}^⊤, where Q_ϵ(τ) denotes the τth-percentile of ϵ. Under the standard Cox PH model, $Q_{\text{log }{\Lambda }_0(T)}(\tau \mid \mathit{Z})=\text{log}\{-\text{log}(1-\tau )\}+{\tilde{Z}}^{\top }b$, where ${\Lambda }_0(t)={\int }_0^t{\lambda }_0(u)du$. Given Λ₀(·) is an unknown function, the quantile interpretation of the Cox PH model is vague. Moreover, many interesting forms of heterogeneous covariate effects are excluded by the restrictive forms of Q_T (τ|Z) designated by the AFT model and the Cox PH model. In contrast, quantile regression modeling offers straightforward physical interpretations as well as greater flexibility to accommodate heterogeneous associations between covariates and the survival response. This serves as the key motivation for considering quantile regression as an alternative approach to analyzing survival data.

In this paper, we present a comprehensive methodological framework that has been developed to perform quantile regression with survival data. Due to space limit, the review is rather selective but yet cover a wide range of survival scenarios. More specifically, section 2 is focused on the standard survival setting with randomly censored data. Section 3 includes discussions of quantile regression methods applicable to more complex survival settings that involve left truncation or left censoring, competing risks and semi-competing risks. Recent method developments for recurrent events data are presented in Section 4. Two real data examples are presented in section 5 to illustrate the practical utility of quantile regression methods for survival analyses. Section 6 concludes this paper with a brief summary and a few remarks.

2. Quantile regression for randomly censored data

Let T denote time to event subject to right censoring by C, and let Y = log(T). Define $\tilde{T}=T\wedge C$ and Δ = I(T ⩽ C), where ∧ is the minimum operator. The observed data consist of n i.i.d. replicates of ($\tilde{T}$, Δ, Z), denoted by (${\tilde{T}}_i$, Δ_i, Z_i), i = 1, …, n. Define $\tilde{Y}=\text{log}(\tilde{T})$, ${\tilde{Y}}_i=\text{log}\left({\tilde{T}}_i\right)$, U = log(C), and U_i = log(C_i).

2.1. Random right censoring with C always known

In the absence of censoring, the regression quantile β₀(τ) in model (1) is defined as the minimizer of the standard quantile loss function, ${\sum }_{i=1}^n{\rho }_{\tau }\left\{Y_i-\left(Z_i^{\top }b\right)\wedge U_i\right\}$, with respect to b, where ρ_τ(x) = x{τ − I(x < 0)} (Koenker & Bassett 1978).

When censoring is present and the censoring time C is fixed at prespecified values, by utilizing the fact that $Q_{\tilde{Y}}(\tau \mid \mathit{Z})=\left\{{\mathit{Z}}^{\top }{\mathit{\beta }}_0(\tau )\right\}\wedge U$, Powell (1984, 1986) proposed an adaptation of the standard quantile loss function, which led to an estimator of β₀(τ) given by arg min_b r(b, τ), where

$$r(b,\tau )=\sum _{i=1}^n{\rho }_{\tau }\left\{{\tilde{Y}}_i-\left(Z_i^{\top }b\right)\wedge U_i\right\}.$$

This estimation method is directly applicable to a more general case where C is always known but not necessarily fixed, and is independent of T given Z. Unlike the standard quantile loss function, r(b, τ) is not convex in b and thus it may have multiple local minima. Several authors, for example, Fitzenberger (1997), Buchinsky & Hahn (1998), Chernozhukov & Hong (2001), contributed strategies to improve the numerical performance of Powell’s estimator. An implementation of Powell’s method is available in the crq function in the R package quantreg (Koenker et al. 2019).

2.2. Unconditionally random right censoring

Censoring time C is not always observed in most survival settings. Under the assumption that T and C are independent and C is independent of Z (i.e. unconditionally random right censoring), Ying et al. (1995) proposed to estimate β₀(τ) by solving the following estimating equation,

$$n^{-1/2}\sum _{i=1}^n{\mathit{Z}}_i\left[\frac{I\left\{{\tilde{Y}}_i-{\mathit{Z}}_i^{\top }\beta (\tau )>0\right\}}{\widehat{G}\left\{Z_i^{\top }\beta (\tau )\right\}}-(1-\tau )\right]=0,$$ (2)

where $\widehat{G}(\cdot )$ is the Kaplan-Meier estimate for G(·), which denotes the survival function of U. Since equation (2) is not continuous and may not have an exact zero-crossing, Ying et al. (1995) suggested obtaining the estimator of β₀(τ) by minimizing the L₂ norm of the estimating function in (2). The resulting objective function however may have multiple minima.

Employing the inverse probability of censoring weighting (IPCW) technique (Robins & Rotnitzky 1992), Zhou (2006) studied an alternative estimating equation for β₀(τ), which is given by

$$n^{-1/2}\sum _{i=1}^n{Z}_i\left[\frac{I\left\{{\tilde{Y}}_i⩽Z_i^{\top }\beta (\tau ),{\Delta }_i=1\right\}}{\widehat{G}\left({\tilde{Y}}_i\right)}-\tau \right]=0.$$ (3)

The estimating function in (3) is monotone (Fygenson & Ritov 1994). Consequently, the solution to equation (3) can be reformulated as the minimizer of a convex L₁-type convex function of b,

$$\sum _{i=1}^n\left\{I\left({\Delta }_i=1\right)\left|\frac{{\tilde{Y}}_i}{\widehat{G}\left({\tilde{Y}}_i\right)}-b^{\top }\frac{Z_i}{\widehat{G}\left({\tilde{Y}}_i\right)}\right|\right\}+\left|M^{*}-b^{\top }\sum _{l=1}^n\left(-\frac{Z_{l}I\left({\Delta }_l=1\right)}{\widehat{G}\left({\tilde{Y}}_l\right)}+2Z_l\tau \right)\right|,$$

where M* is an extremely large positive number selected to bound $b^{\top }{\sum }_{l=1}^n\left(-\frac{Z_{l}I\left({\Delta }_l=1\right)}{\widehat{G}\left({\tilde{Y}}_l\right)}+2Z_l\tau \right)$ for all b’s in a compact parameter space. This minimization problem can be readily solved by the l1fit() function in S-PLUS or the rq() function in the R package quantreg (Koenker et al. 2019).

2.3. Conditionally random right censoring

Conditionally random right censoring, which assumes C is independent of T given Z, is the most commonly adopted random censoring mechanism. This censoring mechanism is less restrictive than those considered in Sections 2.1 and 2.2.

In this section, we first consider a globally linear quantile regression model,

$$Q_Y(\tau \mid Z)=Z^{\text{T}}{\beta }_0(\tau ),\tau \in \left[0,{\tau }_U\right],$$ (4)

and then discuss a locally linear quantile regression model with τ_L = τ_U.

2.3.1. Self-consistent approaches.

By adapting the idea of redistributing censoring probability in the self-consistent Kaplan-Meier estimator (Efron 1967), Portnoy (2003) made the first attempt to estimate the globally linear quantile regression model (4) under the conditionally random right censoring assumption. The initial iterative self-consistent algorithm (Portnoy 2003) was simplified into a grid-based sequential estimation procedure (Neocleous et al. 2006), and the corresponding asymptotic studies was conducted by Portnoy & Lin (2010).

The grid-based estimation procedure of Neocleous et al. (2006) is outlined as follows. First, define a grid of τ-values, ${\mathcal{G}}_n$, as $0={\tau }_0<{\tau }_1<\dots <{\tau }_{M_n}={\tau }_U$. Let $\Vert {\mathcal{G}}_n\Vert =\text{max}\{{\tau }_k-{\tau }_{k-1}:k=1,\dots ,M_n\}$. Without further mentioning, ${\mathcal{G}}_n$ will be adopted throughout Section 2.3. Assuming no censoring occurs below the τ₁-th conditional quantile of T, one can obtain an estimate for β₀(τ₁) from applying uncensored quantile regression. Next, one can estimate β₀(τ_k+1) sequentially for k = 1, 2, …, M_n by minimizing

$$\sum _{i\in K^c}{\rho }_{{\tau }_{k+1}}\left({\tilde{Y}}_i-{\mathit{Z}}_i^{\top }\mathit{b}\right)+\sum _{i\in K}\left\{w_{k+1,i}\cdot {\rho }_{{\tau }_{k+1}}\left({\tilde{Y}}_i-{\mathit{Z}}_i^{\top }\mathit{b}\right)+\left(1-w_{k+1,i}\right){\rho }_{{\tau }_{k+1}}\left(Y^{*}-{\mathit{Z}}_i^{\top }\mathit{b}\right)\right\},$$ (5)

where Y* is an extremely large value and K denotes the set of indices of censored observations that have been previously crossed (i.e. $C_i⩽Z_i^{\top }\widehat{\beta }(\tau )$). The weight w_k+1,i takes the form (τ_k+1−τ_l)/(1−τ_l) to approximate the conditional probability, Pr(C_i < T_i < exp{Z_iβ₀(τ_k+1)}|C_i < T_i, Z_i) based on the estimates for β₀(τ₁), …, β₀(τ_k).

Peng (2012) proposed alternative formulations of the self-consistent approach based on stochastic integral equations. First, using stochastic integral formulation and applying stochastic integral by parts, Efron (1967)’s self-consistent estimating equation for F_Y (t) in the one-sample case can be re-expressed as

$$F_Y(t)=n^{-1}\sum _{i=1}^n\left[N_i(t)+R_i(t)\left\{1-F_Y(t)\right\}{\int }_0^t\frac{R_i(u)}{{\left\{1-F_Y(u)\right\}}^2}d{F}_Y(u)\right],$$

where $N_i(t)=I\left({\tilde{Y}}_i⩽t,{\Delta }_i=1\right)$, $R_i(t)=I\left({\tilde{Y}}_i⩽t,{\Delta }_i=0\right)$, and F_Y (t) = Pr(Y ⩽ t).

With t replaced by ${\mathit{Z}}_i^{\top }\beta (\tau )$, this equation evolves into an estimating equation for β₀(τ),

$$n^{1/2}{\mathit{S}}_n^{(SC)}(\mathit{\beta },\tau )\doteq n^{-1/2}\sum _{i=1}^n{\mathit{Z}}_i\left[N_i\left\{{\mathit{Z}}_i^{\top }\beta (\tau )\right\}+R_i\left\{Z_i^{\top }\beta (\tau )\right\}(1-\tau ){\int }_0^{\tau }\frac{R_i\left\{Z_i^{\top }\beta (u)\right\}}{{(1-u)}^2}du-\tau \right]=0.$$ (6)

Peng (2012) further justified several asymptotically equivalent variants of the estimating equation (6), one of which takes the form of

$$n^{1/2}{S}_n^{(MSC)}(\beta ,\tau )\doteq n^{-1/2}\sum _{i=1}^n{Z}_i\left[N_i\left\{Z_i^{\top }\beta (\tau )\right\}+R_i\left\{Z_i^{\top }\beta (\tau )\right\}\frac{\tau -{\psi }_i(\beta ,\tau )}{1-{\psi }_i(\beta ,\tau )}-\tau \right]=0.$$ (7)

Here ψ_i(β, τ) = sup{A_i(β, τ)} · I(A_i(β, τ) is not empty) + τI(A_i(β, τ) is empty) with $A_i(\beta ,\tau )=\left\{u:0⩽u<\tau ,{\mathit{Z}}_i^{\top }\beta (u-)⩽{\tilde{Y}}_i⩽Z_i^{\top }\beta (u)\right\}$. The estimation procedure derived from equation (7) is identical to Neocleous et al. (2006)’s procedure except for the estimation of β₀(τ₁). That is, Neocleous et al. (2006)’s procedure estimates β₀(τ₁) as the minimizer of (5) with w_1,i = 1, while estimating β₀(τ₁) based on equation (7) is equivalent to minimizing (5) with w_1,i = 0.

Large sample studies for the estimator ${\widehat{\beta }}_{SC}(\tau )$ obtained from solving equation (6) are facilitated by the stochastic integral equation representation of $S_n^{(SC)}(\beta ,\tau )$. Specifically, under certain regularity conditions and given ${\text{lim}}_{n\to \infty }\Vert {\mathcal{G}}_n\Vert =0$, ${\text{sup}}_{\tau \in \left[\nu ,{\tau }_U\right]}\Vert {\widehat{\beta }}_{SC}(\tau )-{\beta }_0(\tau )\Vert {\to }_{p}0$, where 0 < ν < τ_U. If $n^{1/2}{\text{lim}}_{n\to \infty }\Vert {\mathcal{G}}_n\Vert =0$ is further satisfied, then $n^{1/2}\left\{{\widehat{\beta }}_{SC}(\tau )-{\beta }_0(\tau )\right\}$ converges weakly to a Gaussian process for τ ∈ [ν, τ_U]. Estimator defined based on (7) is asymptotically equivalent to ${\widehat{\beta }}_{SC}(\cdot )$.

2.3.2. Martingale-based approach.

Peng & Huang (2008) proposed to utilize the martingale structure underlying randomly censored data to construct an estimating equation for model (4). Define Λ_Y (t|Z) = −log{1−Pr(Y ⩽ t|Z)}, $N(t)=I(\tilde{Y}⩽t,\Delta =1)$, and M(t) = N(t) − Λ_Y (t ∧ Y|Z). Let N_i(t) and M_i(t) be sample analogs of N(t) and M(t) respectively, i = 1, …, n. Note that M_i(t) is the martingale process associated with the counting process N_i(t). Thus, E{M_i(t)|Z_i} = 0 for all t > 0, and $E\left\{{\sum }_{i=1}^n{\mathit{Z}}_i\left[N_i\left\{Z_i^{\top }{\beta }_0(\tau )\right\}-{\Lambda }_Y\left\{Z_i^{\top }{\beta }_0(\tau )\wedge {\tilde{Y}}_i\mid Z_i\right\}\right]\right\}=0$ for τ[0, τ_U]. Since $Z_i^{\top }{\beta }_0(\tau )$ is monotone in τ ∈ [0, τ_U], we have ${\Lambda }_Y\left\{Z_i^{\top }{\beta }_0(\tau )\wedge {\tilde{Y}}_i\mid Z_i\right\}={\int }_0^{\tau }I\left\{{\tilde{Y}}_i⩾Z_i^{\text{T}}{\beta }_0(u)\right\}dH(u)$, where H(x) = −log(1 − x). These findings suggest a stochastic integral based estimating equation,

$$n^{1/2}{S}_n^{(PH)}(\beta ,\tau )\doteq n^{-1/2}\sum _{i=1}^n{Z}_i\left[N_i\left\{Z_i^{\top }\beta (\tau )\right\}-{\int }_0^{\tau }I\left\{{\tilde{Y}}_i⩾Z_i^{\top }\beta (u)\right\}dH(u)\right]=0.$$ (8)

An estimator of β₀(τ), denoted by ${\widehat{\beta }}_{PH}(\tau )$, can be obtained through approximating the stochastic solution to equation (8). Specifically, let ${\widehat{\beta }}_{PH}(\tau )$ be a cadlag (i.e. right continuous with finite left limits) step function of τ that jumps only at the grid points of ${\mathcal{G}}_n$. The procedure to obtain ${\widehat{\beta }}_{PH}(\tau )$ follows.

1. Set $\text{exp}\left\{Z_i^{\top }{\widehat{\beta }}_{PH}\left({\tau }_0\right)\right\}=0$ for all i. Set k = 0.

2. Given $\text{exp}\left\{Z_i^{\text{T}}{\widehat{\beta }}_{PH}\left({\tau }_l\right)\right\}$ for l ⩽ k, obtain ${\widehat{\beta }}_{PH}\left({\tau }_{k+1}\right)$ as the minimizer of the following L₁-type convex objective function:

   $$l_{k+1}(h)=\sum _{i=1}^n\left|{\Delta }_i{\tilde{Y}}_i-{\Delta }_i{Z}_i^{\top }h\right|+\left|Y^{*}-\sum _{l=1}^n\left(-{\Delta }_l{Z}_l^{\top }h\right)\right|+\left|Y^{*}-\sum _{r=1}^n\left[\left(2Z_r^{\top }h\right)\sum _{l=0}^{k}I\left\{{\tilde{Y}}_r⩾Z_r^{\top }{\widehat{\beta }}_{PH}\left({\tau }_l\right)\right\}\left\{H\left({\tau }_{l+1}\right)-H\left({\tau }_l\right)\right\}\right]\right|,$$

   where Y* is an extremely large value.

3. Replace k by k + 1 and repeat step 2 until k = M_n or no feasible solution can be found for minimizing l_k(h).

Peng & Huang (2008) established the uniform consistency and weak convergence of ${\widehat{\beta }}_{PH}(\cdot )$. Moreover, Peng (2012) showed that ${\widehat{\beta }}_{PH}(\cdot )$ is asymptotically equivalent to the self-consistent estimator ${\widehat{\beta }}_{SC}(\cdot )$ in that ${\text{sup}}_{\tau \in \left[\nu ,{\tau }_U\right]}\Vert n^{1/2}\left\{{\widehat{\beta }}_{PH}(\tau )-{\widehat{\beta }}_{SC}(\tau )\right\}\Vert =o_p(1)$ with 0 < ν < τ_U. This theoretical result is consistent with the numerical results reported in Koenker (2008) and Peng (2012).

The crq() function in the R package quantreg (Koenker et al. 2019) provides an implementation of ${\widehat{\beta }}_{PH}(\tau )$ based on an algorithm slightly different from the one presented above. An asymptotically equivalent grid-free estimation procedure for model (4) was developed by Huang (2010).

2.3.3. Data augmentation approach.

Yang et al. (2018) employed a variation of the data augmentation algorithm to tackle the estimation of model (4) with τ_U = 1. The basic idea is to apply the general principle of data augmentation (Tanner & Wong 1987), and employ an alternating process between imputation of censored values from the quantile functions and refitting of the quantile model using the imputed values. More specifically, the algorithm starts with a set of initial values, ${\widehat{\beta }}^{(0)}\left({\tau }_k\right)\left(k=1,\dots ,M_n\right)$, obtained by parallel quantile regression estimators or existing quantile regression estimators. For h = 1, …, H, draw $Y_i^{(h)}$ from the quantile process approximated by $Z_i^{\text{T}}{\widehat{\beta }}^{(h-1)}\left({\tau }_k\right)$ conditional on the set of possible values for Y_i. Then, based on a pairwise bootstrapping sample of size n from ${\left\{Z_i,Y_i^{(h)}\right\}}_{i=1}^n$, obtain updated estimates ${\widehat{\beta }}^{(h)}\left({\tau }_k\right)$ via standard uncensored quantile regression. Lastly, take the final estimates as $\widehat{\beta }(\tau )=H^{-1}{\sum }_{h=1}^H{\widehat{\beta }}^{(h)}(\tau )$.

An appealing feature of Yang et al. (2018)’s approach is that it can handle different forms of censoring, including random censoring, double censoring, and interval censoring. As demonstrated by Monte Carlo simulations, the resulting estimator can achieve significant efficiency gains over the existing methods. The algorithm of Yang et al. (2018) is implemented by the R function DArq().

2.3.4. Adjusted loss function methods.

Assume a locally linear quantile regression model, which is model (1) with τ_L = τ_U equal to a prespecified τ, i.e.

$$Q_Y(\tau \mid Z)=Z^{\top }{\beta }_0(\tau ).$$ (9)

To account for random censoring in the estimation of model (9), Wang & Wang (2009) proposed to modify the standard quantile loss function by twisting the idea of the self-consistent Kaplan-Meier estimator (Efron 1967). That is, one may redistribute the probability mass associated with each censored case, Pr(T_i > C_i|C_i, Z_i), to the right through a local weighting scheme by w_i(F₀), where

$$w_i\left(F_0\right)=\{\begin{array}{ll}1\hfill & {\Delta }_i=1\text{ or }{F}_0\left(C_i\mid Z_i\right)>\tau \hfill \\ \frac{\tau -F_0\left(C_i\mid Z_i\right)}{1-F_0\left(C_i\mid Z_i\right)}\hfill & {\Delta }_i=0\text{ and }{F}_0\left(C_i\mid Z_i\right)<\tau \hfill \end{array}$$

with F₀(t|z) = Pr(T > t|Z = z). Suppose F₀(t|z) is known. An estimator of β₀(τ) in model (9) can be obtained by minimizing the following objective function of β:

$$n^{-1}\sum _{i=1}^n\left[w_i\left(F_0\right){\rho }_{\tau }\left({\tilde{Y}}_i-{\mathit{Z}}_i^{\top }\beta \right)+\left\{1-w_i\left(F_0\right)\right\}{\rho }_{\tau }\left(Y^{*}-{\mathit{Z}}_i^{\top }\beta \right)\right].$$ (10)

In practice, F₀(t|z) is usually unknown. In this case, Wang & Wang (2009) proposed to minimize the objective function (10) with F₀(·) replaced by $\widehat{F}(\cdot )$, the local Kaplan-Meier estimator, namely,

$$\widehat{F}(t\mid z)=1-\prod _{j=1}^n{\left\{1-\frac{B_{nj}(z)}{{\sum }_{k=1}^{n}I\left({\tilde{Y}}_k⩾{\tilde{Y}}_j\right)B_{nk}(z)}\right\}}^{N_j(t)}.$$

Here B_nk(z) is a sequence of nonnegative weights adding up to 1, for example, Nadaraya-Watson’s type weight, $B_{nk}(z)=K\left(\frac{z-z_k}{h_n}\right)/{\sum }_{i=1}^{n}K\left(\frac{z-z_i}{h_n}\right)$, where K(·) is a density kernel function and h_n is a positive bandwidth converging to 0 as n → ∞. The resulting estimator is shown to be consistent and asymptotically normal with root n rate under regularity conditions.

De Backer et al. (2019) and De Backer et al. (2020) investigated different strategies for adjusting the standard quantile loss function in order to accommodate randomly censored data. More specifically, letting G_U(u|Z) = Pr(U > u|Z), De Backer et al. (2019) noted that the derivative of ${\varphi }_{\tau }\left(a;Y,G_U(\cdot \mid Z)\right)\doteq (Y-a)\{\tau -I(Y⩽a)\}-(1-\tau ){\int }_0^a\left\{1-G_U(s\mid Z)\right\}ds$ with respect to a equals −{I(Y > a) − G_U(a|Z)(1 − τ)}, which, conditional on Z, has expectation zero with $a={\mathit{Z}}^{\top }{\beta }_0(\tau )$ under model (9). This key fact leads to an adjusted loss function for censored quantile regression,

$$\sum _{i=1}^n{\varphi }_{\tau }\left(Z_i^{\top }\beta ;Y_i,{\widehat{G}}_U\left(\cdot \mid Z_i\right)\right),$$ (11)

where ${\widehat{G}}_U(\cdot \mid z)$ is a consistent estimator of G_U(·|z). When C is independent Z, ${\widehat{G}}_U(\cdot \mid z)$ can be obtained through the Kaplan-Meier estimator of the survival distribution of C. Without assuming the independence between C and Z, ${\widehat{G}}_U(\cdot \mid z)$ can be obtained through semiparametric modeling of C given Z, or by directly using Beran’s conditional Kaplan-Meier estimator (Beran 1981). De Backer et al. (2019) developed a numerically robust MM algorithm to solve the minimization of the non-convex adjusted loss function (11). Following a different view, De Backer et al. (2020) proposed to estimate model (9) based on a minimum distance loss function, given by ${{\sum }_{i=1}^n\left\{1-\widehat{F}\left(Z_i^{\top }\beta (\tau )\mid Z_i\right)-\tau \right\}}^2$. De Backer et al. (2020) further suggested using a smooth double kernel version of $\widehat{F}\left(\cdot \mid {\mathit{Z}}_i\right)$. They also discussed how to handle high-dimensional covariates by employing the effective dimension reduction technique (Li et al. 1999, Xia et al. 2010). Desirable asymptotic properties, consistency and asymptotic normality, were established for these estimators of β₀(τ) in model (9).

2.4. Inference procedures

2.4.1. Variance estimation.

Bootstrapping procedures have been justified and commonly used to make inferences under quantile regression with either uncensored response or censored survival response. For example, to estimate the asymptotic variance of the estimators discussed in sections 2.1–2.3, one may use resampling methods that follow the idea of Parzen & Ying (1994) or apply the standard bootstrapping procedures that use resampling with replacement (Koenker 2005, Peng & Huang 2008).

Alternative methods without involving resampling have been developed for variance estimation under quantile regression. A main challenge is how to estimate the unknown densities involved in the formulas for asymptotic variances. Under random right censoring with known censoring time or unconditionally random censoring, Huang (2002)’s technique can be directly applied to avoid smoothing-based density estimation, which may be unstable with small or moderate sample sizes. Specifically, let $\widehat{\beta }(\tau )$ denote an estimator of β₀(τ), and S_n{β(τ), τ} denote the estimating function associated with $\widehat{\beta }(\tau )$, for example, the left-hand side of (2) and (3). Generally it can be shown that S_n{β₀(τ), τ} converges to a mean-zero multivariate normal distribution with covariance matrix Σ(τ), which may be consistently estimated by $\widehat{\Sigma }(\tau )$. The following are the main steps to obtain a sample-based variance estimator:

• A.1Find a symmetric and nonsingular (p + 1) × (p + 1) matrix E_n(τ) ≐ {e_n,1(τ), …, e_n,p+1(τ)} such that $\widehat{\Sigma }(\tau )={\left\{E_n(\tau )\right\}}^2$.
• A.2Calculate $D_n(\tau )=\left(S_n^{-1}\left\{e_{n,1}(\tau ),\tau \right\}-\widehat{\beta }(\tau ),\dots ,S_n^{-1}\left\{e_{n,p+1}(\tau ),\tau \right\}-\widehat{\beta }(\tau )\right)$, where $S_n^{-1}(e,\tau )$ is defined as the solution to S_n(b, τ) − e = 0.
• A.3Estimate the asymptotic variance matrix of $n^{1/2}\left\{\widehat{\beta }(\tau )-{\beta }_0(\tau )\right\}$ by n{D_n(τ)}^⊗2.

Under conditionally random censoring, the self-consistent estimators and the martingale-based estimator for model (4) take much more complex forms than those developed under the stronger censoring mechanism with either known censoring time or unconditionally independent censoring. To estimate the asymptotic variances of these estimators, it requires much more sophisticated twists of Huang (2002)’s technique to address the challenge associated with unknown densities. A sample-based variance estimation procedure for Peng & Huang (2008)’s estimator is available through adapting Sun et al. (2016)’s sample-based inference procedure for recurrent events data to the setting with randomly censored data.

2.4.2. Second-stage inference.

Globally linear quantile regression model (4) provides a platform to explore the varying pattern of covariate effects across different quantile levels. Second-stage inference can be performed to address such interests. For example, one may estimate a functional of β₀(·), say Ψ(β₀), to provide a meaningful summary of covariate effects over a range of τ. It is often of interest to determine whether some covariates have constant effects so that a simpler model may be considered. In this case, the problem can be formulated as testing the null hypothesis $H_{0,j}:{\beta }_0^{(j)}(\tau )={\rho }_0$, τ ∈ [τ_L, τ_U], where the superscript ^(j) indicates the jth component of a vector, and ρ₀ is an unspecified constant, j = 2, …, or p+1. Of note, accepting H_0,j for all j ∈ {2, …, p+1} may indicate the adequacy of an AFT model. Peng & Huang (2008) presented second-stage inference procedures for estimating Ψ(β₀) and testing H₀ under model (4), which can be readily adapted to many other quantile regression settings.

3. Quantile regression in complex survival settings

In practice, survival data often involve complications beyond random censoring, such as truncation, competing risks or semi-competing risks. Various methods have developed for quantile regression in more complex survival scenarios. In this section, we present a set of quantile regression methods developed for analyzing for doubly censored data with left truncation, competing risks data, and semi-competing risks data.

3.1. Quantile regression with doubly censored data with left truncation

Ji et al. (2012) proposed an extension of Peng & Huang (2008)’s method to handle doubly censored data subject to left truncation. Such survival scenarios often arise in observational studies, where the event of interest can occur before study entry. Let T denote the event time of interest and C denote time to random right censoring. In addition, let L denote left censoring time, always observed, and A denote left truncation time. Define X = L ∨ (T ∧ C) and Δ as the censoring indicator which equals 1 if L < T ⩽ C, 2 if T ⩽ L, and 3 if T > C, where ∨ is the maximum operator. When X is subject to left truncation by A, the observed data include n i.i.d. replicates of (X′, L′, A′, δ′, Z), denoted by ${\left\{\left(X_i^{\prime },L_i^{\prime },A_i^{\prime },{\delta }_i^{\prime },Z_i\right)\right\}}_{i=1}^n$, where {X′, L′, A′, δ′, Z′} follows the conditional distribution of {X, L, A, δ, Z} given X ⩾ A. It is assumed that (L, C, A) is independent of T given Z. We refer to such data as doubly censored data with left truncation. With L = 0, the data reduce to the usual randomly left truncated right censored data.

To estimate model (4) with doubly censored data subject to left truncation, an estimating equation can be constructed based on the martingale structure underlying the observed survival data, namely, $M^{\prime }\left(t\right)=N^{\prime }\left(t\right)-{\int }_0^t{R}^{\prime }\left(s\right)d{\Lambda }_Y\left(s\mid Z\right)$, where N′(t) = I(log(X′) ⩽ t, δ′ = 1), R′(t) = I{log(L′ ∨ A′) < t ⩽ log(X′)) denoting an at-risk process, and Λ_Y (·|Z) denotes the cumulative hazard function of Y ≐ log(T) given Z. It can be shown that M′(t) is a martingale process. This fact suggests an estimating equation for β₀(·),

$$n^{1/2}{S}_n^{\prime }\left(\beta ,\tau \right)\doteq n^{-1/2}\sum _{i=1}^n{Z}_i\left(N_i^{\prime }\left\{Z_i^{\top }\beta \left(\tau \right)\right\}-{\int }_0^{\tau }{R}^{\prime }\left\{Z_i^{\top }\beta \left(u\right)\right\}dH\left(u\right)\right)=0.$$ (12)

To obtain an estimator of β₀(τ) based on equation (12), denoted by ${\widehat{\beta }}_{PH,*}\left(\tau \right)$, one may follow the algorithm for ${\widehat{\beta }}_{PH}\left(\tau \right)$ (presented in section 2.3) with the objective function in Step 2 modified to

$$\begin{gathered} l_{k+1}^{*}\left(h\right)=\sum _{i=1}^n\left|I\left({\Delta }_i=1\right)\text{log}\left(X_i^{\prime }\right)-I\left({\Delta }_i=1\right)Z_i^{\top }h\right|+\left|Y^{*}-\sum _{l=1}^n\left(-I\left({\Delta }_l=1\right)Z_l^{\top }h\right)\right| \\ +\left|Y^{*}-\sum _{r=1}^n\left[\left(2Z_r^{\top }h\right)\sum _{l=0}^{k}I\left\{\text{log}\left(X_r^{\prime }\right)⩾Z_r^{\top }{\widehat{\beta }}_{PH,*}\left({\tau }_l\right)⩾\text{log}\left(L_r^{\prime }\right)\right\}\left\{H\left({\tau }_{l+1}\right)-H\left({\tau }_l\right)\right\}\right]\right|. \end{gathered}$$

Theoretical properties, such as uniform consistency and weak convergence to a Gaussian process, can be established for ${\widehat{\beta }}_{PH,*}\left(\tau \right)$ with similar lines of Peng & Huang (2008).

3.2. Quantile regression with competing risks data

Competing risks data arise in scientific studies involving multiple types of failures that are mutually exclusive. For example, a cancer patient may die from tumor recurrence or nonrecurrence-related reasons. This gives rise to a competing risks scenario, where death from tumor recurrence and death from nonrecurrence-related reasons are two competing failure types.

We adopt standard formulation of competing risks data. Let T_k denote the latent time to failure of type k (k = 1, …, K). Define T = min(T₁, …, T_K). Let ϵ denote the failure type corresponding to T (i.e. T = T_ϵ), C denote independent censoring to T, and $\tilde{Z}$ denote a p×1 vector of covariates. Define X = T ∧ C, δ = I(T ⩽ C)ϵ, and $Z={\left(1,{\tilde{Z}}^{\top }\right)}^{\top }$. Here ∧ is the minimum operator and I(·) is the indicator function. The observed competing risks data consist of n iid replicates of (X, δ, Z), denoted by {(X_i, δ_i, Z_i), i = 1, …, n}.

Analysis of competing risks data generally follows two different perspectives. One perspective focuses on crude quantities, such as the cumulative incidence function or cause-specific hazard function. Studying crude quantities for a failure type naturally accounts for the presence of competing risks from the other types of failure. The other perspective concerns net quantities defined upon latent failure times T_k’s. Inference on the latent failure time for a failure type however implicitly hypothesizes a setting where the other types of failure do not exist. Such a setting may be controversial but can be meaningful in some situations. For example, patient dropouts can be a competing risk for time to death but may be avoided by diligent follow-up efforts. When the elimination of other types of failures is not possible, competing risks analysis oriented to crude quantities would be more appropriate. In the following, we discuss quantile regression methods for competing risks data developed under these two different perspectives.

3.2.1. Competing risks quantile regression based on cumulative incidence functions.

Peng & Fine (2009) proposed to formulate competing risks quantile regression using cumulative incidence function, which is the cause-specific analog of the usual survival function for an event time. Specifically, the type-k cumulative incidence conditional quantile function is defined as Q_k(τ|Z) ≐ inf{t : F_k(t|Z) ⩾ τ}, where F_k(t|Z) ≐ Pr(T ⩽ t, ϵ = k|Z) denotes the type-k cumulative incidence function (k = 1, …, K). This quantity can be interpreted as the first time given covariate Z at which the probability of type-k failure having occurred exceeds τ, in the presence of other types of failures.

A competing risks quantile regression model based on type-k cumulative incidence function takes the form,

$$Q_k\left(\tau \mid Z\right)=\text{exp}\left\{Z^T{\beta }_0\left(\tau \right)\right\},\tau \in \left[{\tau }_L,{\tau }_U\right],$$ (13)

where β₀(τ) is a (p+1)×1 vector of unknown regression coefficients, and 0 ⩽ τ_L ⩽ τ_U < 1. Under model (13), the non-intercept coefficients in β₀(τ) represent covariate effects on the τth-cumulative incidence quantile, Q_k(τ|Z), which may change with τ. The exp(·) function in (13) can be replaced by any other monotone link function.

To estimate β₀(τ) in model (13), Peng & Fine (2009) proposed the following estimating equation,

$$n^{-1/2}\sum _{i=1}^n{Z}_i\left(\frac{I\left\{X_i⩽\text{exp}\left(Z_i^{T}b\right)\right\}I\left({\delta }_i=1\right)}{\widehat{G}\left(X_i\mid Z_i\right)}-\tau \right)=0,$$ (14)

where $\widehat{G}\left(\cdot \mid Z\right)$ is a reasonable estimate for G(x|Z) ≐ Pr(C ⩾ x|Z), which can be obtained by following the discussions about ${\widehat{G}}_U\left(\cdot \mid Z\right)$ in Section 2.3.4.

Solving equation (14) can be reformulated as locating the minimizer of the convex L₁-type function,

$$\sum _{i=1}^{n}I\left({\delta }_i=1\right)\left|\frac{\text{log}\left(X_i\right)}{\widehat{G}\left(X_i\mid Z_i\right)}-b^T\frac{Z_i}{\widehat{G}\left(X_i\mid Z_i\right)}\right|+\left|M^{*}-b^T\sum _{l=1}^n\frac{-Z_{l}I\left({\delta }_l=1\right)}{\widehat{G}\left(X_l\mid Z_l\right)}\right|+\left|M^{*}-b^T\sum _{k=1}^n\left(2Z_k\tau \right)\right|,$$

where M* is an extremely large positive number.

Peng & Fine (2009) showed that the resulting estimator is uniformly consistent in τ ∈ [τ_L, τ_U], and converges weakly to a tight mean-zero Gaussian process. They developed inference procedures about β₀(τ) in model (13), which follow similar lines to those presented in section 2.4 for randomly censored data with known or unconditional independent censoring. Following the same framework, Sun et al. (2012) studied model (13) for the competing risks setting with missing failure types, where IPCW technique was used to to deal with unobserved failure types under the missing at random assumption.

3.2.2. Quantile regression based on latent failure time distributions in the presence of competing risks.

The analysis of competing risks data based on net quantities, such as the marginal distributions of T_k’s (k = 1, …, K), is complicated by their nonparametric nonidentifiability (Tsiatis 1975). Without loss of generality, we consider the situation with K = 2. This special case coincides with the typical dependent censoring scenario, where the dependent censoring event and the event of interest can be viewed as a pair of competing risks.

Concerning the latent failure times T₁ and T₂, one may consider the following quantile regression models:

$$Q_{T_k}\left(\tau \mid Z\right)=\text{exp}\left\{Z^{\top }{\beta }_{0,k}\left(\tau \right)\right\},\tau \in \left(0,1\right),k=1,2,$$ (15)

where β_0,k(τ) is an vector of unknown coefficients, representing covariate effects on $Q_{T_k}\left(\tau \mid Z\right)$. Here, exp(·) can be replaced by another monotone link function, which may take different forms in the models for $Q_{T_1}\left(\tau \mid Z\right)$ and $Q_{T_2}\left(\tau \mid Z\right)$.

Ji et al. (2014) studied the estimation of the marginal quantile regression models (15) with competing risks data. To mitigate the identifiability issue, additional modeling is imposed for the dependence structure between T₁ and T₂. Specifically, it is assumed that

$$\text{Pr}\left(T>t_1,D>t_2\mid Z\right)=H\left\{\text{Pr}\left(T>t_1\mid Z\right),\text{Pr}\left(D>t_2\mid Z\right)\right\},$$ (16)

where H(·, ·) is a known copula function, for example, the Clayton copula (Clayton 1978), i.e. $H\left(u,v\right)={\left\{u^{-r}+v^{-r}-1\right\}}^{-\frac{1}{r}}$, r > 0, and the Frank copula (Genest 1987), i.e., $H\left(u,v\right)={\text{log}}_r\left\{1+\frac{\left(r^u-1\right)\left(r^v-1\right)}{r-1}\right\}$, r > 0 and r ≠ 1. Here r is a known copula parameter, which may be specified based on prior knowledge on the strength of the association between T₁ and T₂. In practice, one may perform a sensitivity analysis to obtain bounds for Q_T (τ|Z) by varying r in a plausible range.

To estimate β_0,k(τ) in (15), Ji et al. (2014) utilized the martingales associated with cause-specific hazard functions. Let N_k(t) ≐ I(X ⩽ t, ϵ = k) denote the counting process for T_k and define $M_k\left(t\right)=N_k\left(t\right)-{\int }_0^{t}I\left(X⩾u\right){\lambda }_k^{*}\left(u\mid Z\right)\text{d}u$, where ${\lambda }_k^{*}\left(t\mid Z\right)={\text{lim}}_{h\to 0}\text{Pr}\left(t⩽T_k<t+h,ϵ=k\mid T_1⩾t,T_2⩾t;Z\right)/h$, which is the cause-specific hazard function for type-k failure. As shown by Kalbfleisch & Prentice (2002), M_k(t) is a martingale with respect to the filtration, ${\mathcal{F}}_{t,k}=\left\{N_k\left(t\right),Y\left(t+\right),Z\right\}$. This implies $E\left\{N_k\left(t\right)-{\int }_0^{t}I\left(X⩾s\right){\lambda }_k^{*}\left(s\mid Z\right)\text{d}s\right\}=0$ for all t ⩾ 0. Under models (15) and (16), it can be shown with stochastic integral manipulations that

$${\int }_0^{t}I\left(X⩾s\right){\lambda }_k^{*}\left(s\mid Z\right)\text{d}s={\int }_0^{F_{T_k}\left(t\mid Z\right)}I\left\{X⩾Q_{T_k}\left(u\mid Z\right)\right\}{\varphi }_k\left(1-u,1-{\int }_0^{1}I\left[\text{exp}\left\{Z_i^T{\beta }_{0,3-k}\left(v\right)\right\}⩽Q_{T_k}\left(u\mid Z\right)\right]dv\right)du,$$

where $F_{T_k}\left(t\mid Z\right)=\text{Pr}\left(T_k⩽t\mid Z\right)$, ${\varphi }_k\left(v_1,v_2\right)=\partial \text{log}\left\{H\left(v_1,v_2\right)\right\}/\partial v_k$, and k = 1, 2. These facts motivate the estimating equations,

$$n^{\frac{1}{2}}{S}_n^{\left(k\right)}\left({\beta }_1,{\beta }_2,\tau \right)=0,k=1,2,$$ (17)

where $S_n^{\left(k\right)}\left({\beta }_1,{\beta }_2,\tau \right)=n^{-1}{\sum }_{i=1}^n{Z}_i\left\{N_{ki}\left[\text{exp}\left\{Z_i^{\top }{\beta }_k\left(\tau \right)\right\}\right]-{\int }_0^{\tau }I\left(X_i⩾\text{exp}\left\{Z_i^{\top }{\beta }_{3-k}\left(u\right)\right\}\right)\times {\varphi }_k\left(1-u,1-{\int }_0^{1}I\left\{Z_i^T{\beta }_{3-k}\left(v\right)⩽Z_i^{\top }{\beta }_k\left(u\right)\right\}\text{d}v\right)\text{d}u\right\}$.

Note that β_0,k(τ) may not be identifiable for all τ ∈ (0, 1) due to censoring to T_k (k = 1, 2). Truncating the time scale by an upper bound, min(exp{Z^⊤β_0,1(τ_U,1)}, exp{Z^⊤β_0,2(τ_U,2)}), leading to a modified estimating equation,

$$n^{\frac{1}{2}}{S}_n^{*\left(k\right)}\left({\beta }_1,{\beta }_2,\tau \right)=0,k=1,2,$$ (18)

where $S_n^{*\left(k\right)}\left({\beta }_1,{\beta }_2,\tau \right)=n^{-1}{\sum }_{i=1}^n{Z}_i\left\{N_{ki}\left[\text{exp}\left\{Z_i^{\top }{\beta }_k\left(\tau \right)\right\}\right]I\left\{\text{log}\left(X_i\right)⩽Z_i^{\top }{\beta }_{3-k}\left({\tau }_{U,3-k}\right)\right\}-{\int }_0^{\tau }I\left(X_i⩾\text{exp}\left\{Z_i^{\top }{\beta }_k\left(u\right)\right\}\right)I\left\{Z_i^{\top }{\beta }_k\left(u\right)⩽Z_i^{\top }{\beta }_{3-k}\left({\tau }_{U,3-k}\right)\right\}\times {\varphi }_k\left(1-u,1-{\int }_0^{{\tau }_{U,3-k}}I\left\{Z_i^{\top }{\beta }_{3-k}\left(v\right)⩽Z_i^{\top }{\beta }_k\left(u\right)\right\}\text{d}v\right)\text{d}u\right\}$.

Equations in (18) may be solved via an iterative algorithm:

• Step B.1

  Set m = 0. Choose the initial value ${\widehat{\beta }}_2^{\left[m\right]}\left(\tau \right),\tau \in \left(0,{\tau }_{U,2}\right]$.

• Step B.2

  Solve $S_n^{*\left(1\right)}\left({\beta }_1,{\widehat{\beta }}_2^{\left[m\right]},\tau \right)=0$ for ${\widehat{\beta }}_1^{\left[m+1\right]}\left(\tau \right),\tau \in \left(0,{\tau }_{U,1}^{\left[m+1\right]}\right]$. Update τ_U,1 with ${\tau }_{U,1}^{\left[m+1\right]}$.

• Step B.3

  Solve $S_n^{*\left(2\right)}\left({\widehat{\beta }}_1^{\left[m+1\right]},{\beta }_2,\tau \right)=0$ for ${\widehat{\beta }}_2^{\left[m+1\right]}\left(\tau \right),\tau \in \left(0,{\tau }_{U,2}^{\left[m+1\right]}\right]$. Update τ_U,2 with ${\tau }_{U,2}^{\left[m+1\right]}$.

• Step B.4

  Let m = m + 1. Repeat Steps B.2 and B.3 until convergence criteria are met.

Here, the initial value in Step B.1 can be set as Peng & Huang (2008)’s estimator which treats T₁ and T₂ are independent. The equations in Steps B.2–B.3 can be solved by L₁ minimization problems along similar lines of Peng & Huang (2008).

Asymptotic properties were established for the resulting estimators of β_0,k (k = 1, 2), including uniform consistency and weak convergence to a Gaussian process. Inference can be conducted through a standard bootstrapping procedure.

3.3. Quantile regression with semi-competing risks data

Semi-competing risks (Fine et al. 2001) refers to as a situation where time to a nonterminal event (e.g. a non-fetal disease landmark event) can be censored by time to a terminal event (e.g. death or dropout) but not vice versa. Let T₁, T₂, and C denote time to the nonterminal event, time to the terminal event, and time to random censoring, respectively. Let $\tilde{Z}$ be a p × 1 vector of covariates and $Z={\left(1,{\tilde{Z}}^{\top }\right)}^{\top }$. Define X = T₁ ∧ T₂ ∧ C, Y = T₂ ∧ C, δ = I(T₁ < Y), and η = I(T₂ < C). The standard semi-competing risks data consist of n replicates of (X, Y, δ, η, $\tilde{Z}$), denoted by {(X_i, Y_i, δ_i, η_i, ${\tilde{Z}}_i$), i = 1, …, n}. In a standard semi-competing risks setting, T₂ is only subject to random censoring by C; thus quantile regression for T₂ can follow the approaches developed for randomly censored data; see section 2.

Semi-competing risks methods are usually focused on the inference about T₁, which is complicated by the dependent censoring by T₂. Intuitively, one may first coerce semi-competing risks data into classic competing risk data by ignoring the extra information on T₂ when δ = 1, and then apply quantile regression approaches developed for competing risks data. For example, targeting crude quantities for the nonterminal event, one can directly perform competing risks cumulative incidence quantile regression presented in section 3.2.1. Of note, this approach does not incur information loss from only using the competing risks portion of the data. This is because when δ = 1, the cumulative incidence function for the non-terminal event, by definition, does not involve the extra information on the terminal event after the occurrence of the non-terminal event. An exception arises when left truncation is present. In that case, the semi-competing risks data are observable only when Y > L, where L is a known left truncation time. Coercing semi-competing risks data into competing risks data induces artificial left truncation defined as X > L, thereby leading to information loss.

Li & Peng (2011) developed an extension of Peng & Fine (2009)’s method for competing risks cumulative incidence quantile regression tailored to semi-competing risks data subject to left truncation. In this case, the observed data include n i.i.d. replicates of (X*, Y*, δ*, η*, L*, Z*), which follow the conditional distribution of (X, Y, δ, η, L, Z) given L < Y. Assume the cumulative incidence quantile regression model for T₁, which is model (13) with k = 1. The basic estimation idea is to employ the IPCW technique with an inverse weight derived to properly account for both censoring by C and left truncation Y. Under the assumption of (L, C) is independent of (T₁, T₂, Z), an estimating equation is given by

$$n^{-1/2}\sum _{i=1}^n{Z}_i^{*}\left[\frac{I\left\{X_i^{*}⩽\text{exp}\left(Z_i^{*T}b\right),{\delta }_i^{*}=1,{\eta }_i^{*}=1\right\}}{\widehat{W}\left(Y_i^{*},Z_i^{*}\right)}-\tau \right]=0,$$ (19)

where $\widehat{W}\left(y,z\right)=\widehat{G}\left(y\right)/\widehat{G}\left(z\right)$ with

$$\widehat{\alpha }\left(z\right)={\int }_0^{\nu }{\widehat{S}}_{T_2}\left(u\mid z\right){\widehat{F}}_L\left(\text{d}u\right),\widehat{G}\left(y\right)=\frac{1}{n}\sum _{i=1}^n\frac{I\left(L_i^{*}<y⩽Y_i^{*}\right)\widehat{\alpha }\left(Z_i^{*}\right)}{{\widehat{S}}_{T_2}\left(y-\mid Z_i^{*}\right)}.$$

Here ${\widehat{F}}_L\left(y\right)$ represents the Lynden-Bell estimator of $F_L\left(y\right)\doteq P\left(L⩽y\right)$, and ${\widehat{S}}_{T_2}\left(u\mid z\right)$ is an adequate estimator of P(T₂ > u|z). In practice, given T₂ is only subject to random right censoring by C and random left truncation by L, ${\widehat{S}}_{T_2\mid Z=z}\left(t\right)$ may be obtained by using any existing regression method for left truncated and right censored data, such as the Cox proportional hazards model. After obtaining $\widehat{W}\left(Y_i^{*},Z_i^{*}\right)$, equation (19) can be solved by an algorithm similar to that presented for equation (14). Desirable theoretical properties, including uniform consistency and weak convergence to a Gaussian process, can also be established for the resulting estimator.

When interests lie in net quantities related to the latent time to nonterminal event T₁, utilizing the extra information in semi-competing risk data (beyond its competing risks portion) generally leads to better identifiability as well as improved statistical efficiency. Along this line, Li & Peng (2015) developed a quantile regression method tailored to study the conditional quantile of T₁ in the semi-competing risks setting. Specifically, Li & Peng (2015) assumed the following models:

$$\text{Pr}\left(T_1>s,T_2>t\mid Z\right)=C\left\{1-F_{T_1}\left(s\mid Z\right),1-F_{T_2}\left(t\mid Z\right);g\left({\overline{Z}}^T{r}_0\right)\right\},$$ (20)

$$Q_{T_1}\left(\tau \mid Z\right)=\text{exp}\left\{Z^T{\beta }_0\left(\tau \right)\right\},Q_{T_2}\left(\tau \mid Z\right)=\text{exp}\left\{Z^T{\alpha }_0\left(\tau \right)\right\},0<\tau <1,$$ (21)

where $\overline{Z}$ is a subvector of Z or Z itself, C(·, ·; α) is a known copula function with a given copula parameter α, and g(·) is a known function. In copula model (20), the unknown parameter r₀ depicts how covariates may influence the copula parameter, which is often closely linked to the association between T₁ and T₂. In (21), the non-intercept coefficients in β₀(τ) and α₀(τ) represent covariate effects on the τ-th quantile of T₁ and T₂ respectively, which are permitted to change with τ. When these coefficients are constant over τ, the models in (21) reduce to AFT models for T₁ and T₂.

To estimate models (20) and (21), a useful fact is that (20) implies

$$\text{Pr}\left(X>t\mid Y>t,Z\right)=K_A\left\{\text{Pr}\left(T_1>s\mid Z\right),\text{Pr}\left(T_2>t\mid Z\right),g\left({\overline{Z}}^{\top }{r}_0\right)\right\},t>0,$$ (22)

$$\text{Pr}\left(X⩽s\mid Y>t,Z\right)=K_B\left\{\text{Pr}\left(T_1>s\mid Z\right),\text{Pr}\left(T_2>t\mid Z\right),g\left({\overline{Z}}^{\top }{r}_0\right)\right\},s⩽t,$$ (23)

where K_A(u, v, θ) = C(u, v; α)/v and K_B(u, v, α) = {v – C(u, v; α)}/v. In addition, the model assumptions in (21) imply Pr(T₁ ⩽ exp{Z^Tβ₀(τ)} | Z) = τ and $\text{Pr}\left(T_2⩽t\mid Z\right))={\int }_0^{1}I\left[t⩾\text{exp}\left\{Z^T{\alpha }_0\left(u\right)\right\}\right]\text{d}u$. Li & Peng (2015) utilized these results to construct the following estimating equations,

$$n^{-1/2}\sum _{i=1}^n{\tilde{Z}}_{i}I\left\{{\tilde{Z}}_i^T\beta \left(\tau \right)⩽{\tilde{Z}}_i^T\widehat{\alpha }\left({\tau }_{U,2}\right)\right\}{P}_i\left(\beta ,\widehat{\alpha },r,\tau \right)=0,n^{-1/2}\sum _{i=1}^n{\int }_{{\tau }_a}^{{\tau }_b}{\overline{\tilde{Z}}}_i{Q}_i\left(\beta ,\widehat{\alpha },r,\tau \right)=0,$$

where $\widehat{\alpha }(\cdot )$ is Peng & Huang (2008)’s estimator of α₀(·) given T₂ is only subject to random censoring by C, τ_U,2 is an upper bound of a τ-range where α₀(τ) is identifiable, and

$$P_i\left(\beta ,\alpha ,r,\tau \right)=I\left\{\text{log }{X}_i>{\tilde{Z}}_i^T\beta \left(\tau \right)\right\}-I\left\{\text{log }{Y}_i>{\tilde{Z}}_i^T\beta \left(\tau \right)\right\}\times K_A\left\{\tau ,{\int }_0^{{\tau }_{U,2}}I\left\{{\tilde{Z}}_i^T\beta \left(\tau \right)⩾{\tilde{Z}}_i^T\alpha \left(u\right)\right\}du,g\left({\overline{\tilde{Z}}}_i^{T}r\right)\right\},$$

$$Q_i\left(\beta ,\alpha ,r,\tau \right)={\int }_{t\in \left(0,\infty \right)}I\left\{{\tilde{Z}}_i^T\beta \left(\tau \right)⩽\text{log }t⩽{\tilde{Z}}_i^T\alpha \left({\tau }_{U2}\right)\wedge \text{log }{Y}_i\right\}\times \left(I\left\{\text{log }{X}_i⩽{\tilde{Z}}_i^T\beta \left(\tau \right)\right\}-K_B\left[\tau ,{\int }_0^{{\tau }_{U,2}}I\left\{\text{log }t⩾{\tilde{Z}}_i^T\alpha \left(u\right)\right\}\text{d}u,g\left({\overline{\tilde{Z}}}_i^{T}r\right)\right]\right)dt.$$

To compute Q_i(β, $\widehat{\alpha }$, r, τ), one only needs to evaluate the integration over $t\in (0,{\text{max}}_{i=1}^n{Y}_i\wedge \text{exp}\left\{Z_i^{\top }\widehat{\alpha }\left({\tau }_{U,2}\right)\right\}$. Confining β(·) to be a cadlag step function, the integrand in Q_i(β, $\widehat{\alpha }$, r, τ) is a piecewise constant function of τ, and hence Q_i(β, $\widehat{\alpha }$, r, τ) can be calculated as a finite sum. Li & Peng (2015) presented an iterative algorithm to solve these estimating equations. Li & Peng (2015) showed that the resulting estimator of r₀ is consistent and asymptotic normal. Desirable theoretical properties, including uniform consistency and weak convergence to a Gaussian process, were established for the resulting estimator of β₀(τ) for τ ∈ [ν₁, τ_U,1], where 0 < ν₁ < τ_U,1 < 1.

4. Quantile Regression and Its Adaptations for Recurrent events data

Recurrent events data are frequently encountered in clinical or epidemiological studies when the event of interest, such as infection and hospitalization, can occur repeatedly over time. Consider a general recurrent events data setting, where the observation of recurrent events is subject to an observation window specified as a time interval (L, R] (Nelson 2003). The counting process for the observed recurrent events is given by $N^{re}\left(t\right)={\sum }_{j=1}^{\infty }I\left(L⩽T_j^{\left(i\right)}⩽t\wedge R\right)$, where T^(j) denotes time to the jth recurrent event (j = 1, 2, …), and the at-risk process is given by Y^re(t) = I(L < t ⩽ R). Let $\tilde{Z}$ be a p×1 vector of covariates and $Z={\left(1,{\tilde{Z}}^{\top }\right)}^{\top }$. The observed recurrent events data include n i.i.d. replicates of N^re(·), Z, L, and R, denoted by ${\left\{N_i^{re}(\cdot ),Z_i,L_i,R_i\right\}}_{i=1}^n$. In this section, we introduce three different ways to apply or adapt quantile regression to recurrent events data.

4.1. Quantile regression of recurrent event gap time.

Luo et al. (2013) proposed to model the gap time between recurrent events, namely, $G_{i,j}\doteq T_i^{\left(j\right)}-T_i^{\left(j-1\right)}$. By this approach, it is assumed that conditioning on Z_i and a nonnegative subject-specific frailty variable ${\gamma }_i,N_i^{re}(\cdot )$ is a renewal process, and furthermore,

$$Q_{G_{i,j}}\left(\tau \mid Z_i\right)=\text{exp}\left\{Z_i^{\top }{\beta }_0\left(\tau \right)\right\},\tau \in \left(0,{\tau }_U\right].$$ (24)

Consider the case where L_i = 0 and R_i is independent of γ_i and ${\left\{T_i^{\left(j\right)}\right\}}_{j=1}^{\infty }$ given Z_i. Let $m_i=N_i^{re}\left(R_i\right),m_i^{*}=\text{max}\left(m_i-1,1\right)$ and Δ_i = I(m_i > 1). Define X_i,j = G_i,j if j < m_i and $X_{i,j}=R_i-T_i^{\left(m_i-1\right)}$ if j = m_i. Define N_i,j(t) = I(G_i,j ⩽ t, Δ_i = 1), R_i,j(t) = I(G_i,j ⩾ t), H(x) = −log(1 – x). Note that uncensored gap times, {X_i,j, j = 1, …, m_i − 1}, combined with the censored first gap time, X_i,1 with Δ_i = 0, can be viewed as clustered event times subject to random censoring. Under this view and by adapting the estimation framework of Peng & Huang (2008), Luo et al. (2013) proposed the following estimating equation for model (24):

$$n^{-1/2}\sum _{i=1}^n{Z}_i\left[N_i^{*}\left(\text{exp}\left\{Z_i^{\top }\beta \left(\tau \right)\right\}\right)-{\int }_0^{\tau }{R}_i^{*}\left(\text{exp}\left\{Z_i^{\top }\beta \left(u\right)\right\}\right)dH\left(u\right)\right]=0,$$ (25)

where $N_i^{*}\left(t\right)={\left(m_i^{*}\right)}^{-1}{\sum }_{j=1}^{m_i^{*}}{N}_{i,j}\left(t\right)$ and $R_i^{*}\left(t\right)={\left(m_i^{*}\right)}^{-1}{\sum }_{j=1}^{m_i^{*}}{R}_{i,j}\left(t\right)$. An efficient algorithm to solve equation (25) can be developed along the lines of Peng & Huang (2008).

4.2. Generalized accelerated recurrence time model.

Huang & Peng (2009) and Sun et al. (2016) adopted a different strategy to adapt quantile regression modeling to recurrence events data. The main idea is to utilize the concept of time to expected frequency, which is a generalized version of conditional quantile that fits the recurrent events setting. Specifically, time to expected frequency is defined as ${\tau }_Z\left(u\right)\doteq \text{inf}\left\{t⩾0:{\mu }_Z\left(t\right)⩾u\right\}$ for u > 0, where $\tilde{N}\left(t\right)={\sum }_{j=1}^{\infty }I\left(T^{\left(j\right)}⩽t\right)$ and ${\mu }_Z\left(t\right)=E\left\{\tilde{N}\left(t\right)\mid Z\right\}$. It is easy to see that when the event of interest is not recurrent (i.e. T^(j) = ∞ for j ⩾ 2), τ_Z(u) becomes the conditional quantile Q_T⁽¹⁾(τ|Z). With recurrent events data, an adaptation of quantile regression modeling is to formulate covariate effects on τ_Z(u). This leads to the generalized accelerated recurrence time model, which is given by

$${\tau }_Z(G(u))=\text{exp}\left\{Z^{\top }{\beta }_0\left(u\right)\right\},u\in \left(0,U\right],$$ (26)

where G(·) is a known positive increasing function, the non-intercept coefficients in β₀(u) represent covariate effects on time to expected frequency G(u), and U > 0 is a prespecified constant.

The estimation of model (26) is facilitated by the counting process representation of model (26) justified in Sun et al. (2016). That is, model (26) is equivalent to

$$E\left\{N^{re}\left(\text{exp}\left\{Z^{\top }{\beta }_0\left(u\right)\right\}\right)\mid Z\right\}=E\left\{{\int }_0^u{Y}^{re}(\text{exp}\left\{Z^{\top }{\beta }_0\left(s\right)\right\}g\left(s\right)ds\mid Z\right\},u\in \left(0,U\right],$$ (27)

where g(u) = dG(u)/du. This motivates a stochastic integral equation taking the form,

$$n^{-1/2}\sum _{i=1}^n{X}_i\left\{N_i^{re}\left(\text{exp}\left\{X_i^{\top }\beta \left(u\right)\right\}\right)-{\int }_0^u{Y}_i^{re}\left(\text{exp}\left\{X_i^{\top }\beta \left(s\right)\right\}\right)g\left(s\right)ds\right\}=0,u\in (0,U].$$ (28)

As commented in Sun et al. (2016), the theoretical and computational framework of Peng & Huang (2008) can be readily extended to study the recurrent events model (26). The algorithm to solve equation (28) is very similar to that for Peng & Huang (2008)’s martingale-based estimator (see section 2). The key modifications include adopting a grid on the frequency scale (instead of the τ-scale), {0 = u₀ < u₁ < ⋯ < u_L(n) = U}, and replace the objective function in Step 2 by

$$\begin{gathered} l_k\left(h\right)=\sum _{i=1}^n\sum _{j=1}^{\infty }I\left(L_i⩽T_i^{\left(j\right)}⩽R_i\right)\left|\text{log }{T}_i^{\left(j\right)}-X_i^{\top }h\right|+\left|R^{*}-\left\{\sum _{i=1}^n\sum _{j=1}^{\infty }I\left(L_i⩽T_i^{\left(j\right)}⩽R_i\right){\left(-X_i\right)}^{\top }h\right\}\right| \\ +\left|R^{*}-\left\{\sum _{i=1}^{n}2X_i^{\top }h\sum _{m=0}^{k-1}{Y}_i\left(\text{exp}\left\{X_i^{\top }\widehat{\beta }\left(u_m\right)\right\}\right){\int }_{u_m}^{u_{m+1}}g\left(s\right)ds,\right\}\right|, \end{gathered}$$

where R* is an extremely large number. Theoretical arguments for Peng & Huang (2008)’ estimator can also be generalized to establish the asymptotic properties of the estimator derived based on equation (28), including the uniform consistency for u ∈ [v, U], where 0 < v < U, and weak convergence to a Gaussian process at the root n rate.

4.3. Quantile regression of individual recurrent risk measure.

More recently, Ma et al. (2020) proposed quantile regression of a sensible individual risk measure formulated upon the intensity process of recurrent events. Let $\tilde{N}\left(t\right)\doteq {\sum }_{j=1}^{\infty }I\left(T^{\left(j\right)}⩽t\right)$ denote the underlying recurrent event process. Ma et al. (2020) assumed that given a nonnegative random variable γ_i, ${\tilde{N}}_i\left(t\right)$ is a nonstationary Poisson process with the intensity function,

$$\lambda \left(t\mid {\gamma }_i\right)={\gamma }_i\cdot {\lambda }_0\left(t\right).$$ (29)

Here λ₀(t) stands for an unknown baseline intensity function, which is nonnegative and continuous, and is subject to the constraint, ${\int }_0^{\nu *}{\lambda }_0\left(t\right)dt=1$, with a predetermined constant ν*. This constraint is necessary for the purpose of model identifiability.

Under model (29), γ_i captures the scale shift of subject i’s intensity process from the unknown baseline intensity λ₀(t). A special case of model (29) is Wang et al. (2001)’s semi-parametric multiplicative intensity model, where ${\gamma }_i={\xi }_i\text{exp}\left({\tilde{Z}}_i^{\top }{b}_0\right)$, and ξ_i is an unobservable frailty. This connection suggests that γ_i can serve as a sensible measure of the latent subject-specific risk of recurrent events, which may naturally account for both observed covariates and unobservable frailty.

Ma et al. (2020) proposed to use quantile regression to explore the heterogeneity in γ_i which quantifies the subject-specific risk of recurrent events. Specifically, it is assumed that

$$Q_{{\gamma }_i}\left(\tau \mid Z_i\right)=\text{exp}\left\{Z_i^{\top }{\beta }_0\left(\tau \right)\right\}.$$ (30)

The non-intercept coefficients in β₀(τ) represent covariate effects on the τ-th quantiles of γ_i.

A main challenge to estimate model (30) is that γ_i’s are not observed. Considering the setting with L_i = 0 and assuming R_i is independent of ${\tilde{N}}_i(\cdot )$ given γ_i, and R_i is independent of γ_i given Z_i, Ma et al. (2020) employed the principle of conditional score (Stefanski & Carroll 1987) and proposed the estimating equation,

$$n^{1/2}{S}_n\left(\beta ,\widehat{\mu },\tau \right)=0,$$ (31)

where $S_n\left(\beta ,\mu ,\tau \right)\doteq n^{-1}{\sum }_{i=1}^n{\int }_r{Z}_i\cdot {\psi }_{\tau }\left\{\text{log}\left(r\right)-Z_i^{\top }\beta \left(\tau \right)\right\}f\left\{r\mid m_i,C_i,Z_i;\beta (\cdot ),\mu (\cdot )\right\}dr$ and $\widehat{\mu }\left(t\right)=\text{exp}\left\{\widehat{H}\left(t\right)\right\}$ with $\widehat{H}\left(t\right)=-{\int }_t^{\nu *}\frac{{\sum }_{i=1}^{n}d{N}_i^{re}\left(s\right)}{{\sum }_{i=1}^{n}I\left(R_i⩾s\right)N_i^{re}\left(s\right)}$. Here ψ_τ(v) = τ – I(v < 0), and

$$f\left\{\gamma \mid m,C,X;\beta (\cdot ),\mu (\cdot )\right\}=\frac{\rho \left\{m\mid \gamma ,C;\mu (\cdot )\right\}g\left\{\gamma \mid X;\beta (\cdot )\right\}}{{\int }_r\rho \left\{m\mid r,C;\mu (\cdot )\right\}g\left\{r\mid X;\beta (\cdot )\right\}dr},$$

where $\rho \left\{m\mid \gamma ,C;\mu (\cdot )\right\}=\frac{{\left\{\gamma \mu \left(C\right)\right\}}^m}{m!}\text{exp}\left\{-\gamma \mu \left(C\right)\right\}$ and $g\left\{\gamma \mid \mathit{X};\mathit{\beta }(\cdot )\right\}={\text{lim}}_{\delta \to 0}\frac{\delta }{\text{exp}\left\{X^{\top }\beta \left({\tau }_{\gamma }+\delta \right)\right\}-\text{exp}\left\{X^{\top }\beta \left({\tau }_{\gamma }\right)\right\}}$, with τ_γ = {τ ∈ (0, 1) : exp{X^Tβ(τ) = γ}. It can be shown that f{γ|m, C, X; β₀(·), μ₀(·)} denotes the conditional density of γ given m, C and X under the assumed models, and hence E[S_n(β₀, μ₀, τ)] = 0.

To solve equation (31), Ma et al. (2020) approximated β(τ) by using splines with K(n) knots, and developed an iterative algorithm to find an estimate for the β₀(τ) in model (30) based on equation (31). The details are omitted here. Under certain regularity conditions, the resulting estimator was shown to be uniformly consistent for τ ∈ [ζ₁, ζ₂], where 0 < ζ₁ < ζ₂ < 1. Weak convergence to a Gaussian process was also established.

5. Illustrations of quantile regression for survival data

5.1. An example of quantile regression analysis with randomly censored data

We use a dataset from a dialysis study that investigated predictors of mortality in a cohort of 191 incident dialysis patients with chronic renal failure, aged 20 years and older, who started on chronic hemodialysis or peritoneal dialysis therapy between July 1996 and August 1997, recruited from metro-Atlanta area (Kutner et al. 2002). Of particular interest is a risk factor on symptoms of restless legs syndrome (RLS), which negatively affect quality of life and mortality risk as evidenced by prior studies. In this study, baseline measures were collected between 1996 and 1997 and vital status was monitored to December, 2005. In this dataset, the survival time T of 35% dialysis patients were censored due to renal transplant or end of study.

Figure 1 plots the Kaplan-Merier curves for survival time stratified by the binary variable indicating moderate to severe RLS symptoms versus mild RLS symptoms (denoted by BLEGS). It is noted that the 25th percentiles of survival time for the the severe RLS group and the mild RLS groups are 0.95 versus 2.45 years, which are statistically significantly different. The 75th survival time percentiles for these two groups are rather similar, both between 7 and 8 years. This observation suggests that BLEGS may have an inhomogeneous effect on the distribution or quantile function of T. We next consider BLEGS, along with other potential predictors including patient’s age (AGE), the indicator of fish consumption over the first year of dialysis (FISHH), the indicator of baseline HD dialysis modality (BHDPD), the indicator of eduction equal or higher than college (HIEDU), and the indicator of being black (BLACK). We fit the data with the standard Cox PH model and AFT model. In Table 1, we present the estimation results including the estimated coefficients and the associated p values. It is shown that both Cox PH model and AFT model do not suggest a significant effect of BLEGS on dialysis survival, though Figure 1 demonstrates its potential influence on the lower part of the survival distribution.

Figure 1.

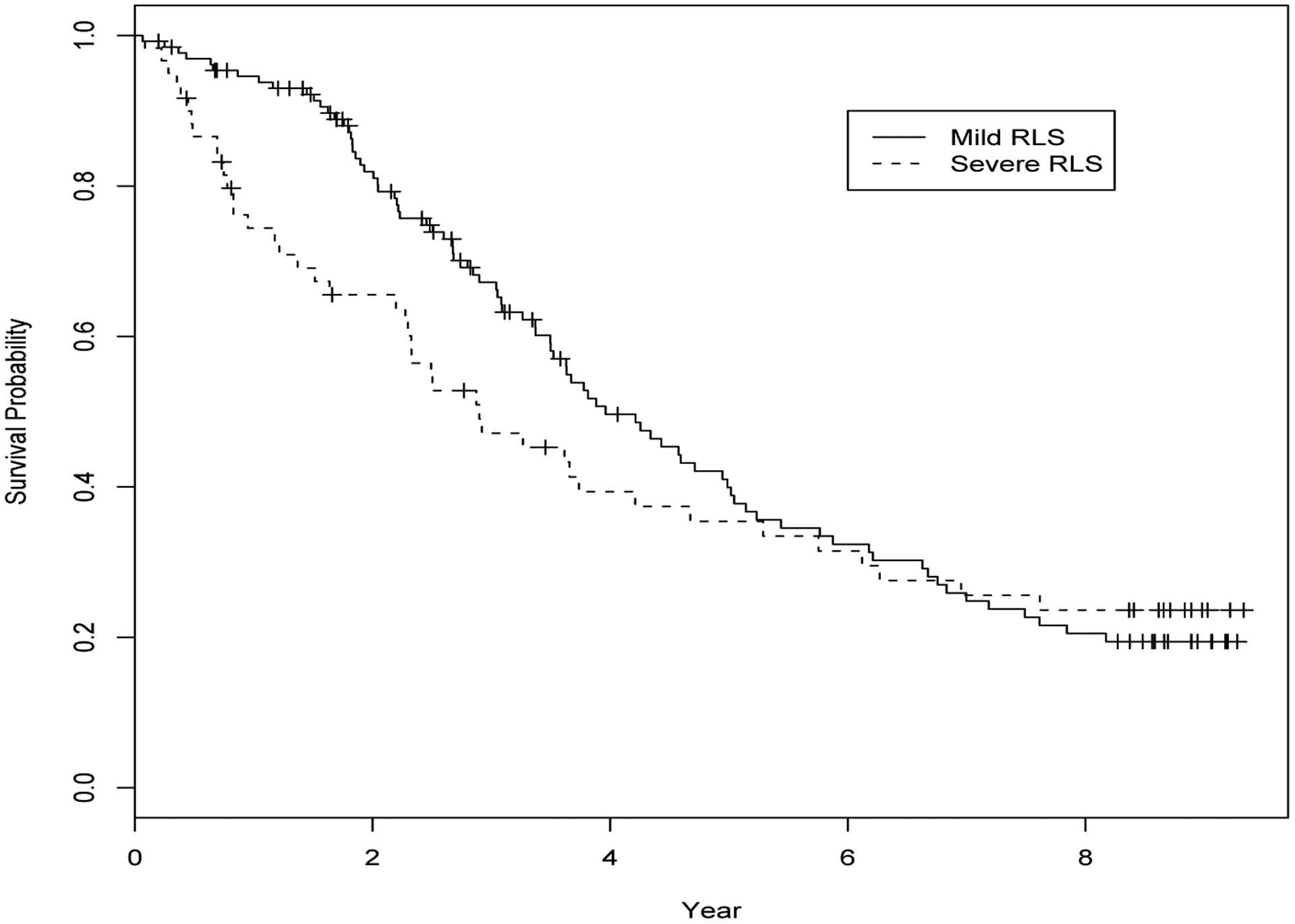
The dialysis example: Kaplan Meier curves of survival time stratified by the status of RLS symptoms

Table 1.

Results from fitting the Cox PH model and AFT model to the dialysis dataset.

	Cox Model		AFT Model
	Coef	p value	Coef	p value
AGE	0.059	<0.001	−0.035	<0.001
FISHH	−0.831	<0.001	0.485	<0.001
BHDPD	0.837	<0.001	−0.473	<0.001
BLEGS	0.264	0.197	−0.173	0.232
HIEDU	0.625	0.009	0.364	0.024
BLACK	−1.014	<0.001	0.591	<0.001

Coef: coefficient estimate; SE: standard error

We next conduct quantile regression based on model (4) using Peng & Huang (2008)’s method for the same dataset. Figure 2 displays Peng & Huang (2008)’s estimator of β₀(τ) along with 95% pointwise confidence intervals. In Figure 2, we observe that the coefficient for BLEGS diminishes gradually with τ whereas estimates for the other coefficients seem to be fairly constant. We apply the second-stage inference to formally investigate the constancy of each coefficient. The results confirm our observation from Figure 1, suggesting a varying effect of BLEGS and constant effects of the other covariates. This may lead to an interesting scientific implication that BLEGS may affect the survival experience of dialysis patients with short survival times but may have little impact on that of long-term survivors. The confirmed nonconstancy of the BLEGS coefficients further indicates the lack-of-fit of an AFT model for this dialysis data.

Figure 2.

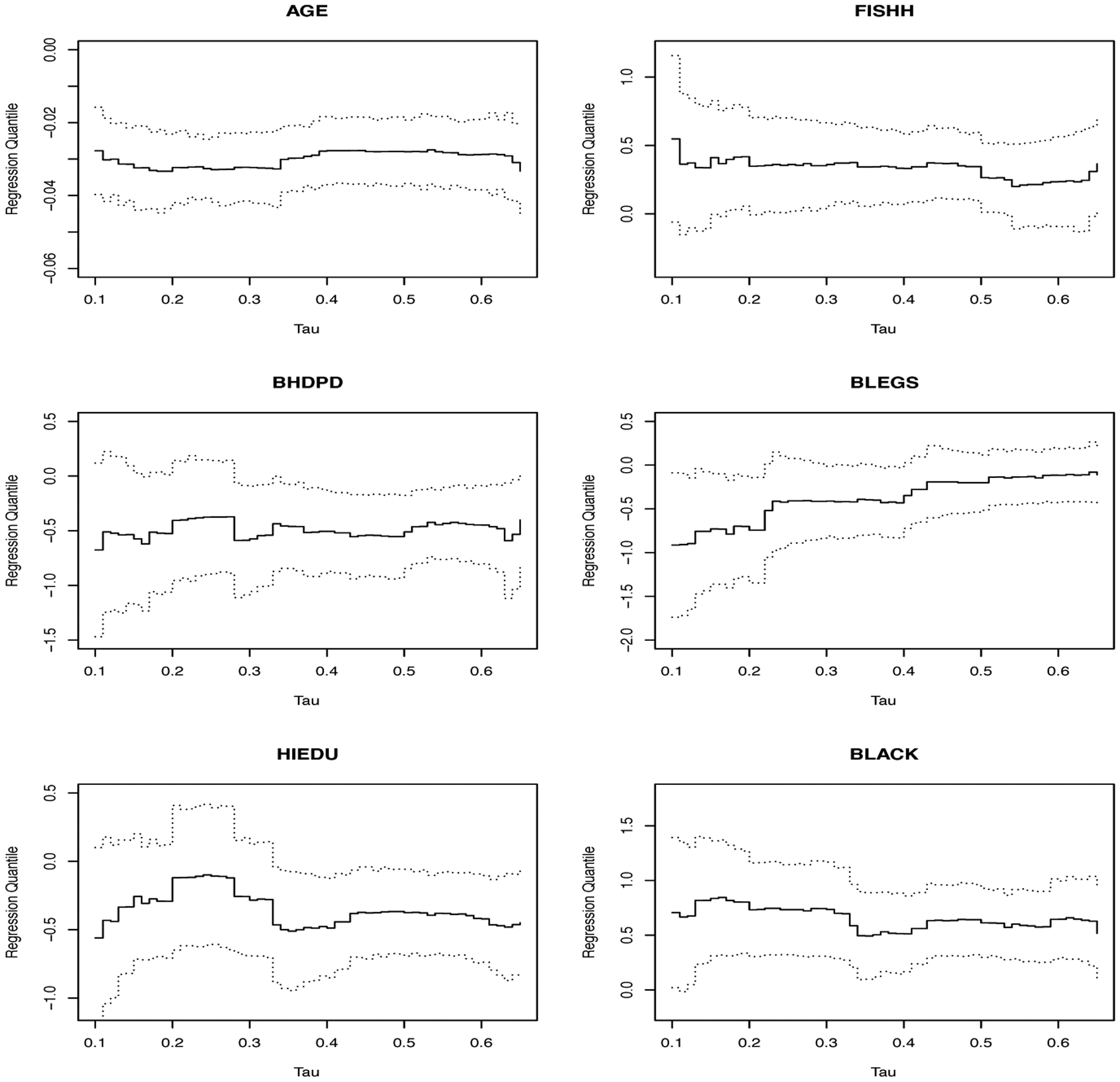
The dialysis example: Peng and Huang’s estimator (solid lines) and 95% pointwise confidence intervals (dotted lines) of regression quantiles.

We also estimate the average quantile effects defined as ${\int }_l^u{\beta }_0^{\left(i\right)}\left(u\right)du\left(i=2,\dots ,7\right)$. The results are given in Table 2. We observe that the estimated average effect of BLEGS based on quantile regression has a larger magnitude compared to that based on the AFT model. The associated p value is less than 0.05, providing some evidence for the association between RLS and dialysis survival. This example suggests that naively treating varying effects as constant ones may lead to attenuated covariate effect estimates and consequently result in biased conclusions.

Table 2.

Estimation of average covariate effects based on quantile regression.

	AveEff	SE	p value
AGE	−0.030	0.003	< 0.001
FISHH	0.327	0.116	0.005
BHDPD	−0.489	0.162	0.003
BLEGS	−0.369	0.161	0.022
HIEDU	−0.350	0.137	0.011
BLACK	0.654	0.144	< 0.001

AveEff: Estimated average effect; SE: standard error

5.2. An example of quantile regression analysis with competing risks data

We use the dataset from the breast cancer trial E1178 by the Eastern Cooperative Oncology Group (Cummings et al. 1993). In this study, patients were followed-up until breast cancer recurrence (BCR) or non-recurrence related death (NRD), whichever occurred first. This dataset includes 82 patients assigned to placebo and 85 patients assigned to tamoxifen. In the tamoxifen group, 42 patients experienced breast cancer recurrence and 23 died without recurrence; in the placebo group, 59 patients had breast cancer recurrence and 19 died without recurrence.

We apply the quantile regression strategy to evaluate the difference between two-year tamoxifen therapy versus placebo, while adjusting for other potential risk factors, including age, tumor size, number of positive nodes. Since it is more clinically relevant to evaluate BCR in the presence of NRD than with the unrealistic exclusion of NRD, we choose to use the cumulative incidence quantile regression method (Peng & Fine 2009) to analyze this competing risks dataset.

In Figure 3, we plot the BCR and NRD cumulative incidence functions separately for patient groups stratified by treatment, or age, number of positive nodes, and tumor size dichotomized at their median values, which are 71 years, 3, and 25mm, respectively. From Figure 3, we observe that all BCR cumulative incidence curves exceed 0.45 in the right tails. In contrast, the cumulative incidence curves for NRD are below 0.20. A visual impression from Figure 3 is that tamoxifen, number of positive nodes and tumor size may impact the cumulative incidence of BCR but not NRD, and their effects on BCR may not be constant.

Figure 3.

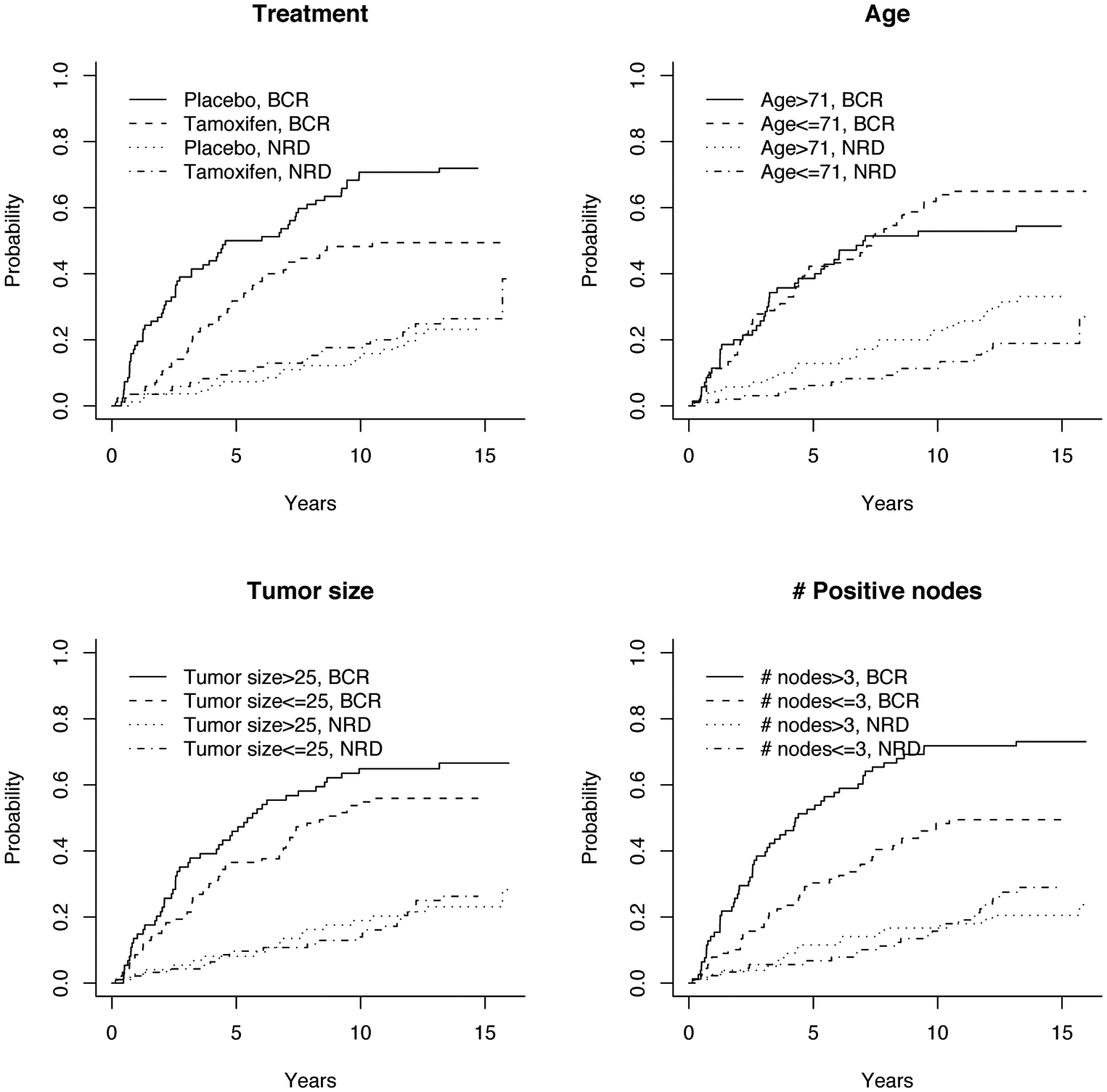
E1178 Trial Example: Estimated Cumulative Incidence Functions.

We apply Peng & Fine (2009)’s method to fit the data with the competing risks quantile regression model (13), where the failure type corresponds to BCR and the exponential link function is replaced by the identify function. The number of positive nodes is incorporated into the model after log-transformation. Based on the results in Figure 3, we let [τ_L, τ_U] = [0.10, 0.45]. The analysis results displayed in Figure 4 suggest that patients who received placebo tend to experience breast cancer recurrence sooner than those on tamoxifen. In this example, age does not show a significant effect on the timing of breast cancer recurrence in the presence of nonrecurrence death. The effects of tumor size and number of nodes demonstrate some interesting increasing trend. The coefficient estimates, coupled with the 95% confidence intervals, suggest that tumor size and node number may only have a significant influence on the BCR cumulative incidence quantiles with relatively larger τ’s, such as τ = 0.35 or 0.4. The changing trend of the effects of tumor size and node number over τ is confirmed by second-stage constancy tests. The clinical implication may be that either tumor size or number of positive nodes may significantly shorten the time to BCR for patients with moderate or low risk of BCR (corresponding to large τ’s), while such an impact may vanish when patients are subject to high risk of BCR (corresponding to small τ’s) possibly due to worse pre-existing health condition or other unknown factors. The treatment coefficients are rather constant, and are significantly above zero for many τ’s. This reflects the beneficial effect of Tamoxifen treatment in term of prolonging the progression to BCR.

Figure 4.

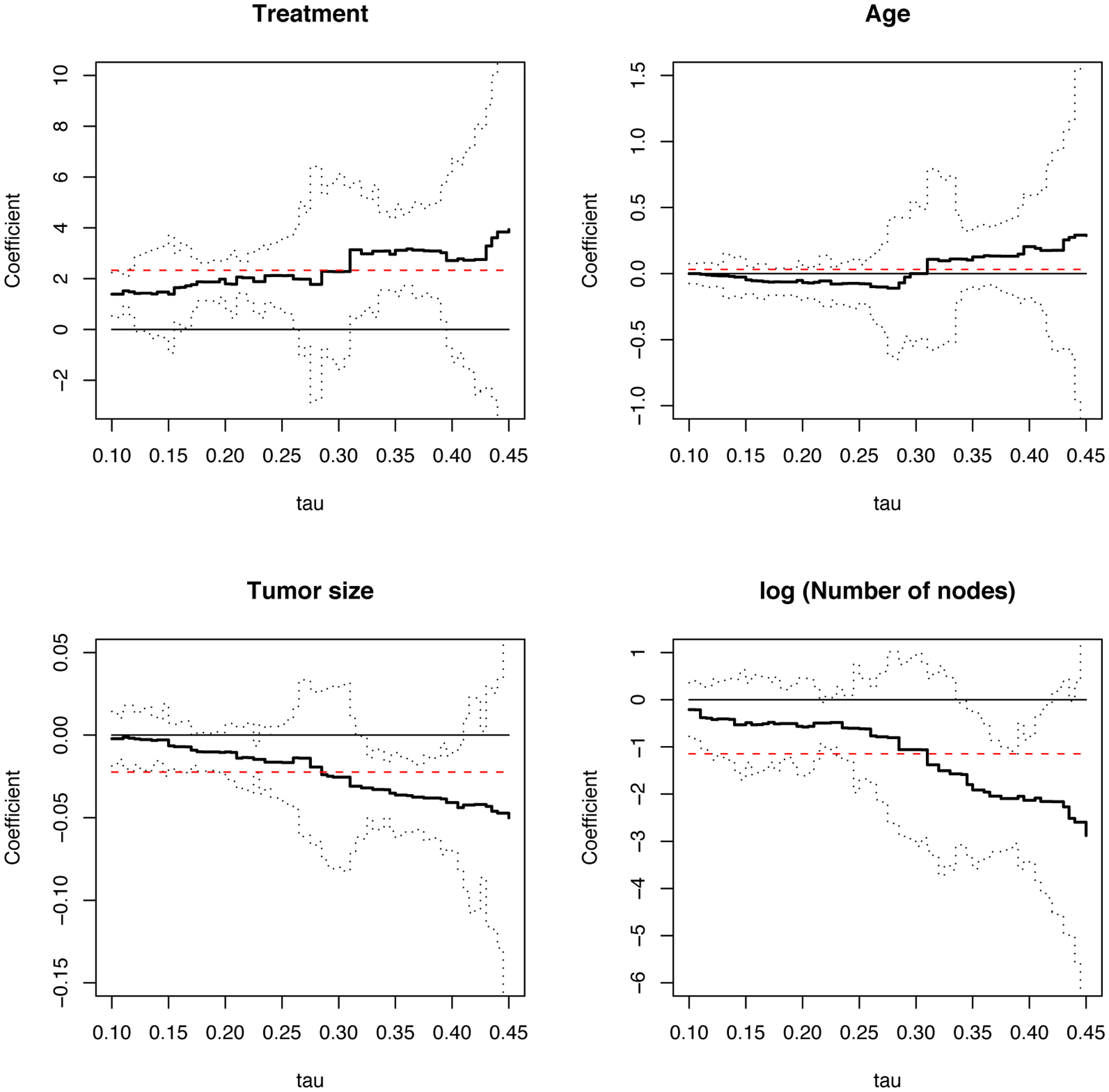
E1178 Trial Example: Estimated Regression Coefficients for the Breast Cancer Recurrence Endpoint. Bold Solid Lines Represent Coefficient Estimates; Dotted Lines Represent 95% Pointwise Confidence Intervals; Dashed Lines Represent Estimates for Trimmed Mean Covariate Effects.

6. Remarks

Applying quantile regression to analyze survival data can provide robust and dynamic insight about the association between covariates and survival outcomes, which may not be offered by traditional survival regression methods. There have been rich developments of quantile regression methods for survival data in the last two decades. In this paper, we provide a selective review of approaches available to handle various types of survival data, including randomly censored data, competing and semi-competing risks data, truncated data, recurrent events data. Most of these methods are easy and stable to implement. This feature can help foster the applications of quantile regression in survival analysis.

Due to space limit, we omit many important relevant method developments. These include, but are not limited to, cure rate quantile regression methods (Wu & Yin 2013, 2017b,a) and censored quantile regression methods attending to regression quantile monotonicity across quantile levels, such as semiparametric copula quantile regression (De Backer et al. 2017).

Some important problems not covered in this paper but worth attention are quantile regression for survival data with high-dimensional covariates, survival data with time-dependent covariates, and survival data with missing covariates. This paper also does not discuss scenarios where the collection of survival data is attached to a special epidemiologic design, such as case-cohort design, and nested case-cohort design. Another interesting direction for extending survival quantile regression is to integrate quantile regression with causal inference. Work has emerged along these directions and merits further research efforts.