Robust Inference for the Stepped Wedge Design

Summary:

Stepped wedge designed trials are a type of cluster-randomized study in which the intervention is introduced to each cluster in a random order over time. This design is often used to assess the effect of a new intervention as it is rolled out across a series of clinics or communities. Based on a permutation argument, we derive a closed form expression for an estimate of the intervention effect, along with its standard error, for a stepped wedge design trial. We show that these estimates are robust to mis-specification of both the mean and covariance structure of the underlying data-generating mechanism, thereby providing a robust approach to inference for the intervention effect in stepped wedge designs. We use simulations to evaluate the type I error and power of the proposed estimate and to compare the performance of the proposed estimate to the optimal estimate when the correct model specification is known. The limitations, possible extensions, and open problems regarding the method are discussed.

1. Introduction

Stepped wedge designed trials (e.g. figure 1) are a type of cluster-randomized study in which all clusters (clinics, communities, etc.) receive the intervention but the time when the intervention is introduced to each cluster is randomized. Once introduced, the intervention continues in the cluster for the duration of the study (i.e. one-way crossover). Stepped wedge designs are often used to assess the effect of a new treatment or intervention as it is rolled out across a series of clinics or communities (Hussey and Hughes, 2007; Mdege et al., 2011; Hemming et al., 2015). Estimation of the intervention effect in a stepped wedge design is more difficult, and generally model dependent, compared to a simple parallel cluster-randomized trial since the stepped wedge design induces a conlinearity between time and the intervention. Mixed effects regression analyses are often used to disentangle these effects (e.g. Hemming et al. (2015); Hooper et al. (2016)) but this approach depends heavily on modelling assumptions, including the functional form chosen for time, the assumption of similar time trends across clusters, and the covariance structure within and between cluster-periods. Misspecification of any of these factors may result in incorrect inference (Thompson et al., 2017). Generalized estimating equations (GEE) provide an alternative analysis approach that is robust to misspecification of the covariance structure; however, GEE still requires correct modelling of the time trend and gives inflated type I error rates when the number of clusters is small (Scott et al., 2017).

Figure 1.

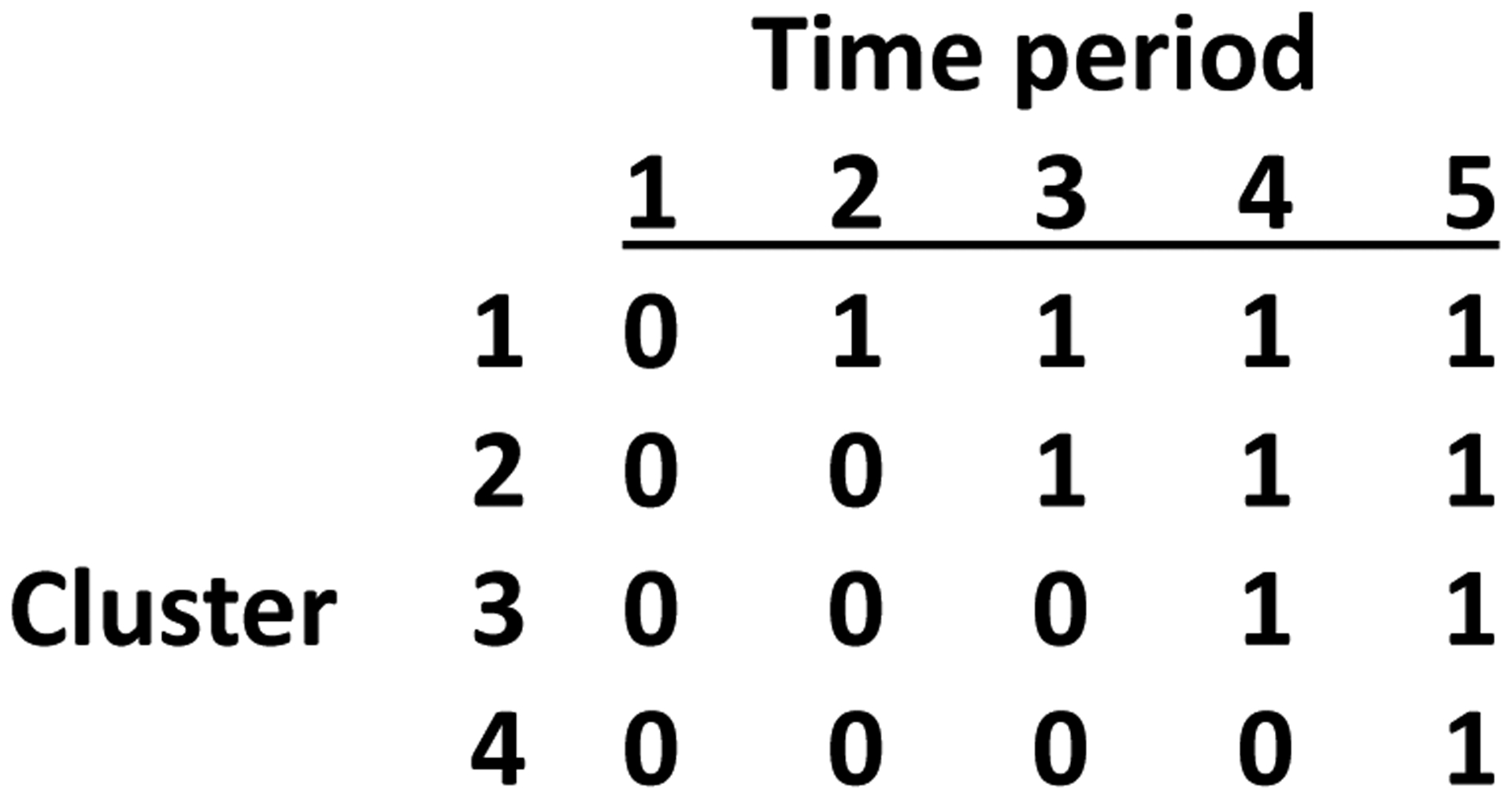
Schematic representation of stepped wedge designs with 4 intervention sequences, one cluster per sequence, and 5 time periods. 0 indicates control condition and 1 represents treatment.

Since the cluster is the unit of randomization in a stepped wedge trial, an alternative approach to evaluating the intervention may be based on a permutation test that permutes the treatment sequences among the clusters. Ji et al. (2017) considered properties of permutation tests for stepped wedge designs when the underlying mean (fixed effect) structure of the data-generating process is correctly specified, although they do consider situations in which the variance structure is misspecified. Wang and DeGruttola (2017) also investigated the behavior of permutation tests compared to mixed effects models when the mixed effect model fixed effects and variance structure are correctly specified but the error distribution may be misspecified. Most recently, Thompson et al. (2018) derive an estimator based on combining weighted within-period comparisons (so-called “vertical” comparisons (Davey et al., 2015)) of cluster-level summaries, similar in spirit to the estimate we define below. They develop both a nonparametric test using a permutation procedure and a parametric procedure in which the variance-covariance components of the proposed estimator are derived using generalized estimating equations. In the following we consider the characteristics of a design-based estimate of the treatment effect when both the mean and variance structure of the data-generating model may be misspecified. We show that even with such a highly misspecified model the proposed estimate is unbiased for the intervention effect and provides valid hypothesis tests and confidence intervals. Further, the estimate and test statistic can be computed from closed-form expressions i.e. no computer intensive permutation procedure is necessary. The result is a broadly robust procedure for inference in stepped wedge randomized trials.

2. Methods

Consider a stepped wedge design with N clusters and T time periods (e.g. in figure 1 N = 4, T = 5). Often, N is an integer multiple of T − 1, although that is not required (i.e. the number of clusters assigned to each intervention sequence need not be the same). Let y_ijk be the observation on individual k in cluster i at time j. Assume that clusters are independent and that the number of individuals measured in each cluster-period is constant i.e. n_ij = n (we evaluate the sensitivity to this second assumption using simulations in Section 3). Let y denote the NTn-vector (y₁₁₁, y₁₁₂ … y_NTn) of outcomes. Let x_ij indicate whether the intervention is provided (x_ij = 1) or not (x_ij = 0) in cluster i at time j and let x denote the corresponding NTn individual-level vector where each x_ij is replicated n times.

Assume that y has been generated with mean and variance

$$\begin{gathered} E_Y(y)=\mu +x\delta +z\beta \\ {V}_Y(y)=\Sigma \end{gathered}$$ (1)

where z is the design matrix for the temporal trend, Σ is a (block diagonal) variance-covariance matrix, and μ, δ and β are the parameters for the baseline mean, intervention effect and time effect, respectively. We explicitly do not make any distributional assumptions in (1).

Suppose we completely ignore the underlying time trend, zβ, and the true covariance structure, Σ and fit the following model

$$y~\left({\mu }^{\star }+x{\delta }^{\star },{\sigma }^{2}I\right).$$ (2)

In this model, provided n_ij = n, identical estimates are obtained regardless of whether the model is fit based on individual-level data or cluster-period means. Therefore, let Y be the vector of cluster-period level means, (Y₁₁, Y₁₂, … Y_NT), where $Y_{ij}={\sum }_k{y}_{\mathit{\text{ijk}}}/n$ and, similarly, let X denote the cluster-period level vector (x₁₁, x₁₂, … x_NT). The least squares estimate of (μ^⋆, δ^⋆) is

$$\left({\widehat{\mu }}^{\star },{\widehat{\delta }}^{\star }\right)={\left(W^{T}W\right)}^{-1}{W}^{T}Y$$ (3)

where W = [1, X] is a NT × 2 matrix with the first column all ones and the second column equal to X. Letting f denote the proportion of the cluster-periods that are assigned to the intervention condition (often, f = 1/2) (e.g., in figure 1, f = 1/2), it is straightforward to show that

$$\left(W^{T}W\right)=NT\left(\begin{array}{cc}1& f\\ f& f\end{array}\right)$$

so

$${\left(W^{T}W\right)}^{-1}=\frac{1}{f(1-f)NT}\left(\begin{array}{cc}f& -f\\ -f& 1\end{array}\right).$$

Then, based on (3),

$${\widehat{\delta }}^{\star }=\frac{1}{f(1-f)NT}\sum _{ij}{Y}_{ij}\left(x_{ij}-f\right).$$ (4)

${\widehat{\delta }}^{\star }$ is, of course, a biased estimate of δ (Rao, 1971). However, consider the distribution of ${\widehat{\delta }}^{\star }$ with respect to the permutation distribution of the stepped wedge design. As noted above, the permutation distribution is obtained by permuting the sequences (rows) of the stepped wedge design matrix in figure 1. Importantly, (W^TW)⁻¹ is the same for any permutation of the rows in figure 1. sequences.

Let $E_{\mathcal{P}}$ and $V_{\mathcal{P}}$ denote expectation and variance, respectively, under the permutation distribution. Then

$$E_{\mathcal{P}}\left(x_{ij}\right)={\overline{x}}_j$$ (5)

$$V_{\mathcal{P}}\left(x_{ij}\right)={\overline{x}}_j\left(1-{\overline{x}}_j\right)$$ (6)

$$\begin{gathered} {\mathit{\text{Cov}}}_{\mathcal{P}}\left(x_{ij},x_{i^{\prime }{j}^{\prime }}\right)=\begin{array}{cc}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)& i=i^{\prime },j<j^{\prime }\end{array} \\ =\begin{array}{cc}-\frac{1}{N-1}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)& i\ne i^{\prime },j⩽j^{\prime }\end{array} \end{gathered}$$ (7)

where ${\overline{x}}_j={\sum }_i{x}_{ij}/N$. These results make use of the stepped wedge design feature that an intervention is never removed once introduced (i.e. x_ij ⩽ x_ij′ for j < j′).

Since Y is constant with respect to the permutation distribution then, based on (5),

$$E_{\mathcal{P}}\left({\widehat{\delta }}^{\star }\right)=\frac{1}{f(1-f)NT}\sum _{ij}{Y}_{ij}\left({\overline{x}}_j-f\right)$$ (8)

and combining (4) and (8) gives

$$\Delta ={\widehat{\delta }}^{\star }-E_{\mathcal{P}}\left({\widehat{\delta }}^{\star }\right)=\frac{1}{f(1-f)NT}\sum _{ij}{Y}_{ij}\left(x_{ij}-{\overline{x}}_j\right).$$ (9)

Now consider the expectation of Δ under the (true) distribution of Y. From (1)

$$E_Y\left(Y_{ij}\right)=\mu +x_{ij}\delta +z_{ij}\beta$$ (10)

where z_ij is the row (vector) of z corresponding to the i, j’th observation. Most stepped wedge models assume that the temporal component of the model is constant across all clusters. This implies that z_ijβ does not depend on i. Then, since ${\sum }_i\left(x_{ij}-{\overline{x}}_j\right)=0$ and $x_{ij}^2=x_{ij}$,

$$E_Y(\Delta )=\delta \frac{1}{f(1-f)NT}\sum _{ij}{x}_{ij}\left(1-{\overline{x}}_j\right)=\delta \frac{1}{f(1-f)T}\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)$$ (11)

Importantly, this implies that, using the permutation distribution, the treatment effect, δ, can be estimated unbiasedly even if the temporal portion of the model is ignored. Specifically,

$$\widehat{\delta }=\frac{\Delta }{\frac{1}{f(1-f)T}\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)}=\frac{\sum _{ij}{Y}_{ij}\left(x_{ij}-{\overline{x}}_j\right)}{N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)}.$$ (12)

If the assumption of temporal constancy across clusters is violated then permutations could be done within strata for which the assumption is met, and the argument carries through (see the appendix A1 for formulas).

Now consider the variance of $\widehat{\delta }$. Assuming independence between clusters, straightforward calculations based on (12) give

$$V_Y(\widehat{\delta })=\frac{\sum _i\left\{\sum _j\text{Var}\left(Y_{ij}\right){\left(x_{ij}-{\overline{x}}_j\right)}^2+2\sum _{j<j^{\prime }}\text{Cov}\left(Y_{ij},Y_{i{j}^{\prime }}\right)\left(x_{ij}-{\overline{x}}_j\right)\left(x_{i{j}^{\prime }}-{\overline{x}}_{j^{\prime }}\right)\right\}}{{\left\{N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right\}}^2}$$ (13)

In the special case where the covariance matrix of Y does not depend on cluster (i.e. $\text{Var}\left(Y_{ij}\right)={\sigma }_j^2$ and Cov(Y_ij, Y_ij′) = σ_j,j′) (13) reduces to

$$V_Y(\widehat{\delta })=\frac{\left\{\sum _j{\sigma }_j^2{\overline{x}}_j\left(1-{\overline{x}}_j\right)+2\sum _{j<j^{\prime }}{\sigma }_{j,j^{\prime }}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)\right\}}{N{\left\{\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right\}}^2}$$ (14)

Expressions (13) and (14) depend on the true variance-covariance matrix and are, therefore, of limited utility in practice. Instead, we seek a variance estimator that does not depend on knowledge of the true variance of the data-generating process. We accomplish this by considering the variance of $\widehat{\delta }$ across the permutation distribution and derive two unbiased variance estimates that can be used for inference (see appendix A2 for derivation).

The first is suitable for any stepped wedge design and is given by

$$V_{\delta }^1(\widehat{\delta })=[\sum _i\left\{\sum _j{\left(Y_{ij}-x_{ij}\delta \right)}^2{\overline{x}}_j\left(1-{\overline{x}}_j\right)+2\sum _{j<j^{\prime }}\left(Y_{ij}-x_{ij}\delta \right)\left(Y_{i{j}^{\prime }}-x_{i{j}^{\prime }}\delta \right){\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)\right\}-\frac{2}{N-1}\sum _{i<i^{\prime }}\sum _{j,j^{\prime }}\left(Y_{ij}-x_{ij}\delta \right)\left(Y_{i^{\prime }{j}^{\prime }}-x_{i^{\prime }{j}^{\prime }}\delta \right){\overline{x}}_{\text{min}\left(j,j^{\prime }\right)}\left(1-{\overline{x}}_{\text{max}\left(j,j^{\prime }\right)}\right)]/{\left\{N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right\}}^2.$$ (15)

$V_{\delta }^1(\widehat{\delta })$ has expectation (with respect to the distribution of Y) equal to $V_Y(\widehat{\delta })$ when the covariance matrix of Y_i does not depend on cluster (i.e. (14)). If $\widehat{\delta }$ is used in place of δ in (15) then $V_{\widehat{\delta }}^1(\widehat{\delta })$ is a biased estimate of $V_Y(\widehat{\delta })$. The bias is a complex expression that depends in part on the true variance of Y (see appendix A3). Nonetheless, in simulations we have run so far, the simple adjustment of multiplying $V_{\widehat{\delta }}^1(\widehat{\delta })$ by N/(N − 1) provides an approximately unbiased estimate, especially for large N (some justification for this choice is given in the appendix). We investigate the behavior of both $V_{\delta }^1(\widehat{\delta })$ and $V_{\widehat{\delta }}^1(\widehat{\delta })$ in simulations in Section 3.

The restriction that (15) is unbiased only when the variance of Y_i does not depend on cluster is non-trivial. Two examples where this assumption is violated are i) there is a cluster × intervention interaction (random intervention effect); in the presence of a random intervention effect the covariance of Y_i depends on the intervention sequence and hence on cluster; ii) the sample size varies by cluster. The second proposed variance estimate does not depend on the assumption that the variance of Y_i is independent of i. However, this alternative variance estimate does require that each intervention sequence (each row of figure 1) is replicated at least once (i.e. there are two or more clusters with each sequence). Specifically, suppose there are m(h) clusters with intervention sequence h (m(h) > 1 for all h). Let Y_hij denote the cluster-period mean for cluster i in sequence h (i = 1 … m(h)) at time j and similarly for the intervention indicators x_hij. Then

$$V^2(\widehat{\delta })=\sum _h[\sum _{i=1}^{m(h)}\left\{\sum _j{Y}_{\mathit{\text{hij}}}^2{\left(x_{\mathit{\text{hij}}}-{\overline{x}}_j\right)}^2+2\sum _{j<j^{\prime }}{Y}_{\mathit{\text{hij}}}{Y}_{{\mathit{\text{hij}}}^{\prime }}\left(x_{\mathit{\text{hij}}}-{\overline{x}}_j\right)\left(x_{{\mathit{\text{hij}}}^{\prime }}-{\overline{x}}_{j^{\prime }}\right)\right\}-\frac{2}{m(h)-1}\sum _{i<i^{\prime }}\sum _{j,j^{\prime }}{Y}_{\mathit{\text{hij}}}{Y}_{h{i}^{\prime }{j}^{\prime }}\left(x_{\mathit{\text{hij}}}-{\overline{x}}_j\right)\left(x_{h{i}^{\prime }{j}^{\prime }}-{\overline{x}}_{j^{\prime }}\right)]/{\{N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\}}^2$$ (16)

has expectation equal to (13) for any covariance matrix structure. In addition, $V^2(\widehat{\delta })$ does not depend on δ. We evaluate the performance of $V^2(\widehat{\delta })$ using simulations in Section 3.

No distributional assumptions have been necessary for the development thus far. For inference, we assume that either individual observations are normally distributed or the central limit theorem holds, which is a reasonable assumption in most cases since the analysis is based on (sums of) cluster-period level means. In that case, the estimates and variances derived above can be used to test the hypothesis Ho: δ = δ_o using a Z statistic such as

$$Z_1=\frac{\widehat{\delta }-{\delta }_o}{\sqrt{V_{{\delta }_o}^1(\widehat{\delta })}}\text{\hspace{1em}or\hspace{1em}}{Z}_2=\frac{\widehat{\delta }-{\delta }_o}{\sqrt{V^2(\widehat{\delta })}}$$ (17)

Further, a 100 * (1 – α)% confidence interval for $\widehat{\delta }$ may be defined as

$$\left\{\delta :Z_{\alpha /2}⩽(\widehat{\delta }-\delta )/\sqrt{V_{\delta }^1(\widehat{\delta })}⩽Z_{1-\alpha /2}\right\}$$ (18)

or by the interval

$$\widehat{\delta }\pm Z_{1-\alpha /2}*\sqrt{V^2(\widehat{\delta })}$$ (19)

where Z_α is the α’th percentile of the standard normal distribution.

3. Simulation Results

We simulate datasets for a stepped wedge design with T = 5 time periods and varying numbers of clusters. Data were simulated from a mixed model that includes random cluster, time and intervention effects:

$$Y_{\mathit{\text{ijk}}}=\mu +{\beta }_j+x_{ij}\delta +a_i+b_{ij}+c_i{x}_{ij}+e_{ijk}$$ (20)

where μ = 10, β = (0, −0.1, −0.2, −0.3, −0.4) in all simulations and

$$a_i~N\left(0,{\tau }^2\right)$$

$$b_{ij}~N\left(0,{\psi }^2\right)$$

$$c_i~N\left(0,{\eta }^2\right)$$

$$e_{\mathit{\text{ijk}}}~N\left(0,{\sigma }^2\right)$$

Table 1 gives the values of the variance components used in five specific simulation scenarios.

Table 1.

Scenarios for stepped wedge simulations

	Scenario
	1	2	3	4	5
Random Effects	None	Cluster	Cluster Intervention	Cluster Time	Cluster Intervention Time
σ2	1	1	1	1	1
τ2	0	0.2	0.2	0.2	0.2
η2	0	0	0.1	0	0.1
ψ2	0	0	0	0.04	0.04

Table 2 shows bias and confidence interval coverage of the proposed estimator across the five scenarios shown in table 1 for N = 12, 24 and 36 clusters and where the number of observations per cluster per time period (n) is either constant (n = 10) or varies between clusters (with average = 10) according to a lognormal distribution (rounded to the nearest integer) with standard deviation 0.2 (low var) or standard deviation 1.0 (high var). The estimator is approximately unbiased for all cluster sizes, sample sizes and scenarios. Coverage using the variance estimator $V_{\delta }^1(\widehat{\delta })$ achieves the nominal 95% across all scenarios, even in the scenarios where Var(Y_i) varies across clusters (scenarios 3 and 5, and the scenarios with nonconstant n). $V_{\widehat{\delta }}^1(\widehat{\delta })$ (multiplied by the correction factor N/(N − 1)) also generally gives good coverage although we note some undercoverage when N = 12 (the undercoverage is much more severe if $V_{\widehat{\delta }}^1(\widehat{\delta })$ is used without the correction factor - data not shown). In contrast, use of the variance estimator $V^2(\widehat{\delta })$ generally results in confidence intervals with greater undercoverage, although this also improves as N increases.

Table 2.

Bias (a) and confidence interval coverage (b), based on 10000 simulations, of the proposed estimator for the five simulation scenarios described in table 1. Number of clusters (N) is 12, 24 or 36. Number of time periods (T) is 5 with a linearly decreasing time effect (β = 0, −0.1, −0.2, −0.3, −0.4). Intercept (μ) is 10 and treatment effect (δ) is 5. Number of individuals per cluster per time period (n) is either constant (n = 10) or varies between clusters (average = 10) according to a lognormal with standard deviation 0.2 (low var) or lognormal with standard deviation 1.0 (hi var). Coverage is shown for the three variance formulas described in the text; nominal coverage is 95%.

(a) Bias
		Simulation scenario
N	n	1	2	3	4	5
12	constant	0.000	−0.002	0.000	0.003	−0.004
	low var	0.001	0.002	0.007	−0.003	0.004
	hi var	0.000	0.002	−0.003	0.003	0.004
24	constant	0.000	0.001	−0.004	0.001	0.001
	low var	0.001	0.002	0.000	0.001	0.001
	hi var	0.000	−0.003	0.002	0.001	0.001
36	constant	−0.001	0.000	−0.001	0.000	0.000
	low var	0.000	0.000	0.000	−0.002	−0.002
	hi var	0.000	−0.004	0.003	−0.001	0.003

(b) Coverage
		$V_{\delta }^1(\widehat{\delta })$					$\frac{N}{N-1}{V}_{\widehat{\delta }}^1(\widehat{\delta })$					$V^2(\widehat{\delta })$
		Simulation scenario
N	n	1	2	3	4	5	1	2	3	4	5	1	2	3	4	5
12	constant	0.96	0.96	0.95	0.96	0.95	0.94	0.93	0.92	0.93	0.93	0.91	0.90	0.90	0.90	0.90
	low var	0.95	0.96	0.95	0.96	0.95	0.94	0.93	0.92	0.93	0.92	0.91	0.90	0.90	0.90	0.90
	hi var	0.94	0.95	0.95	0.95	0.95	0.93	0.93	0.92	0.93	0.92	0.90	0.90	0.90	0.90	0.90
24	constant	0.95	0.96	0.95	0.95	0.95	0.95	0.94	0.93	0.94	0.94	0.93	0.93	0.93	0.93	0.93
	low var	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.94	0.94	0.94	0.94	0.93	0.94	0.93	0.93
	hi var	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.94	0.94	0.94	0.94	0.93	0.93	0.93	0.93
36	constant	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.94	0.94	0.94	0.94	0.94	0.94	0.94	0.94
	low var	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.95	0.94	0.94	0.94	0.94	0.94	0.94
	hi var	0.95	0.95	0.95	0.95	0.95	0.95	0.95	0.94	0.95	0.95	0.94	0.94	0.94	0.94	0.94

Table 3 gives type I error rates and power from 10,000 simulations for tests of the null hypothesis Ho: δ = 0 using the variance estimators in equations (15) and (16). When $\delta =\widehat{\delta }$ is used in (15) a correction factor of N/(N−1) is applied to the variance estimate. Interestingly, even though the assumptions for using $V_{\delta }^1(\widehat{\delta })$ are only met when n is constant and η² = 0, the type I error rates using this variance estimate are quite close to nominal levels under all scenarios. The type I error rates for $V_{\delta }^1(\widehat{\delta })$ show only slight sensitivity to the variance of the random treatment effect and essentially none to the variation in the number of individuals per cluster-time period, at least across the ranges investigated in these simulations. When $V_{\widehat{\delta }}^1(\widehat{\delta })$ is used some slight type I error inflation is observed across all N, particularly for N = 12 (we speculate that use of a t-distribution as a reference may produce type I error rates close to nominal levels over the entire range of N; however, the correct degrees of freedom calculation is unclear). Use of the variance estimate $V^2(\widehat{\delta })$ results in substantial type I error inflation for N = 12 (type I error rates of 0.08 – 0.10); the type I error rates approach, but do not achieve, nominal levels as N increases to 36.

Table 3.

Type I error rate (a) and power (b) for testing the null hypothesis Ho: δ = 0 based on 10000 simulations. Data are simulated from equation (20) with a random cluster effect (τ² = 0.2), random treatment effect (η² = 0, 0.1, 0.4) and random error (σ² = 1). Number of individuals per cluster per time period (n) is either constant (n = 10) or varies between clusters (average = 10) according to a lognormal with standard deviation 0.2 (low var) or lognormal with standard deviation 1.0 (hi var). Number of clusters (N) is 12, 24 or 36. Number of time periods (T) is 5 with a linearly decreasing time effect (−0.1 per time period).

(a) Type I error rate (nominal level = 0.05)
		$V_{\delta =0}^1(\widehat{\delta })$			$\frac{N}{N-1}{V}_{\delta =\widehat{\delta }}^1(\widehat{\delta })$			$V^2(\widehat{\delta })$
		Treatment variance (η2)
N	n	0	0.1	0.4	0	0.1	0.4	0	0.1	0.4
12	constant	0.05	0.05	0.05	0.06	0.07	0.07	0.09	0.09	0.10
	low var	0.05	0.05	0.05	0.06	0.07	0.07	0.10	0.09	0.09
	hi var	0.05	0.05	0.05	0.07	0.07	0.07	0.09	0.08	0.08
24	constant	0.05	0.05	0.06	0.06	0.06	0.06	0.07	0.07	0.07
	low var	0.05	0.05	0.06	0.06	0.06	0.06	0.07	0.07	0.07
	hi var	0.04	0.04	0.05	0.05	0.05	0.05	0.07	0.06	0.06
36	constant	0.05	0.05	0.06	0.05	0.06	0.06	0.06	0.06	0.06
	low var	0.05	0.05	0.06	0.06	0.06	0.06	0.06	0.06	0.06
	hi var	0.05	0.06	0.06	0.06	0.06	0.07	0.06	0.06	0.06
(b) Power (for the alternative Ha : δ = 1)
		$V_{\delta =0}^1(\widehat{\delta })$			$\frac{N}{N-1}{V}_{\delta =\widehat{\delta }}^1(\widehat{\delta })$			$V^2(\widehat{\delta })$
		Treatment variance (η2)
N	n	0	0.1	0.4	0	0.1	0.4	0	0.1	0.4
12	constant	0.59	0.57	0.51	0.64	0.61	0.55	0.65	0.62	0.55
	low var	0.59	0.56	0.49	0.63	0.60	0.53	0.64	0.60	0.54
	hi var	0.42	0.41	0.38	0.46	0.45	0.42	0.48	0.47	0.42
24	constant	0.90	0.87	0.81	0.90	0.88	0.82	0.90	0.88	0.80
	low var	0.89	0.87	0.81	0.90	0.88	0.82	0.90	0.88	0.81
	hi var	0.78	0.76	0.71	0.79	0.78	0.72	0.82	0.79	0.73
36	constant	0.97	0.97	0.94	0.98	0.97	0.94	0.97	0.97	0.93
	low var	0.97	0.96	0.93	0.97	0.96	0.94	0.97	0.96	0.93
	hi var	0.84	0.83	0.79	0.85	0.84	0.80	0.84	0.82	0.78

In all cases, power declines as either cluster size variance or treatment effect variance increases. We note, however, that power must be interpreted cautiously and is not comparable between the different variance estimates since the type I error rates are not uniformly maintained at the nominal level.

Figure 2 shows power curves (power vs effect size), based on 1000 simulations, of a test based on the proposed estimator (using variance equation (15)) for testing Ho: δ = 0 versus a test based on the correct model that includes an appropriate time effect and within-cluster correlation structure, implemented using the R function lmer() (Bates et al., 2015), for five scenarios - i) independence, ii) random cluster effect iii) random cluster and treatment effects iv) random cluster and time effects v) random cluster, treatment and time effects (table 1). Across the five scenarios the variance components were chosen so that the power curves for the robust test (solid line in figure 2) are (virtually) identical (specifically, σ² was varied and the intracluster correlations (ICC) for the cluster, treatment and time random effects were set at 0.17, 0.091 and 0.038, respectively). Except for the independence scenario, the proposed estimator is less efficient than the maximum likelihood estimate based on the correct model since the latter uses both within-cluster and between-cluster information to estimate the treatment effect. However, this gain in efficiency must be balanced against the potential for inflation of the type I error rate when the covariance structure used for the analysis does not match the data generating mechanism. In general, the type I error will be inflated if the model used for analysis does not include all the random effects from the data-generating mechanism. The proposed estimator is robust to such model misspecification, as well as misspecification of the time trend.

Figure 2.

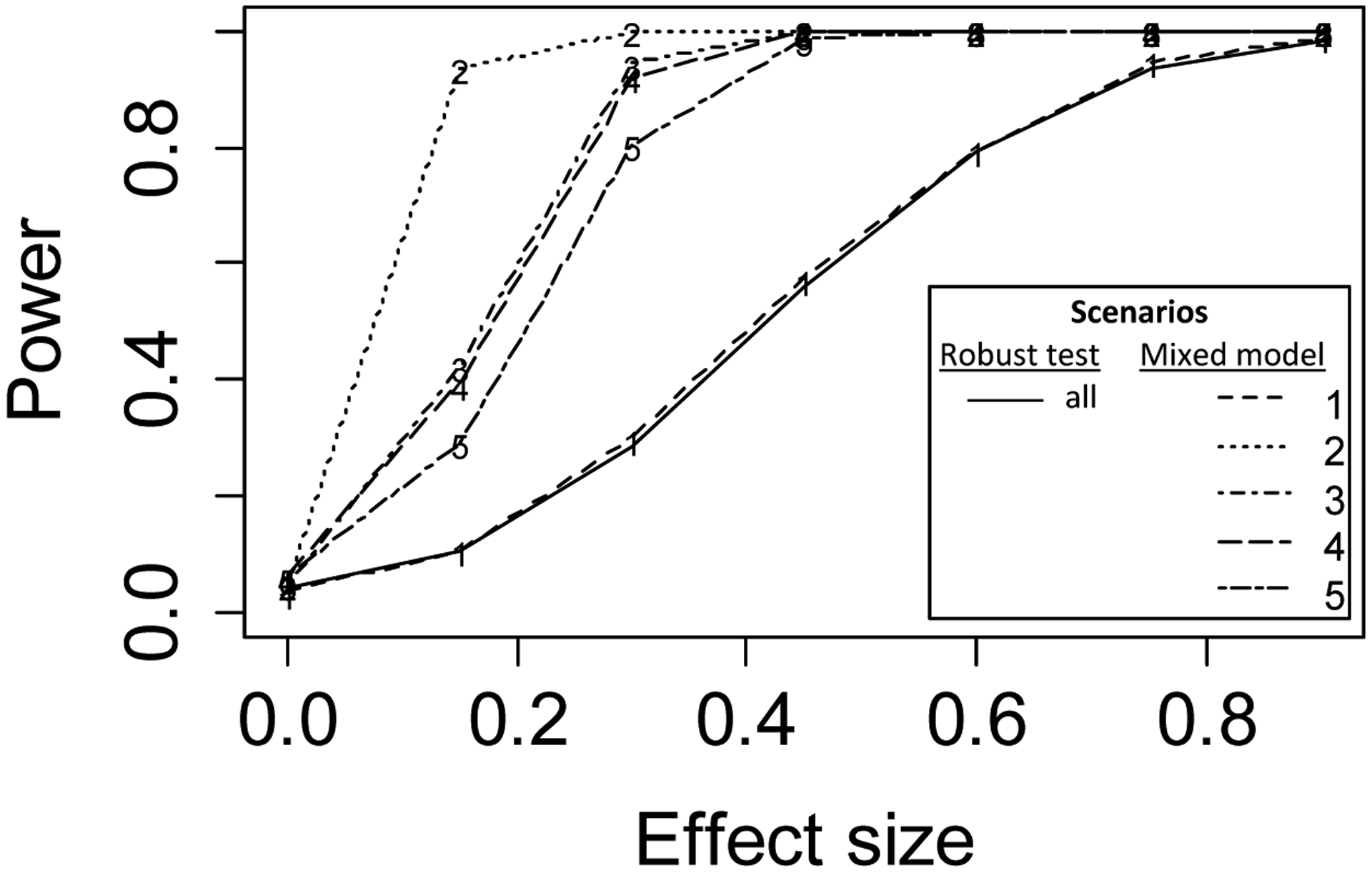
Power curves for testing Ho: δ = 0 computed across 1000 simulations for the robust test proposed here (solid line, using $V_{\delta =0}^1(\widehat{\delta })$ versus an asymptotic test based on the correctly specified model for the five scenarios described in table 1 (dashed and dotted lines labeled 1 – 5). Note: The scenarios were constructed so that the power curves for the robust test were identical across scenarios; specifically, the intraclass correlations (ICC) for the cluster, intervention and time random effects (when included) were set at 0.17, 0.091 and 0.038, respectively, and σ² was varied by scenario.

As noted previously, no assumptions are made about the distribution of y in (1). Thus, motivated by the example in the next Section, we conducted a second set of simulations with a binomial endpoint. Specifically, datasets were generated with 22 clusters and 5 time intervals (with 6, 6, 6 and 4 clusters following the four possible sequences - identical to the design of the Washington EPT trial discussed in the next Section). Binomial observations for each cluster-period were simulated from a linear model with μ = 0.09, a linearly decreasing time effect (−0.005 per time period), a random cluster effect (τ = 0.015) and varying random treatment effects (η = 0, 0.002, 0.008). Two different sample size scenarios were simulated. In the first, all clusters had a fixed size of 305. In the second, cluster size followed a lognormal distribution with mean equal to log(171) and standard deviation equal to 1.06, giving a mean sample size of 305 (these parameters and sample size variation reflect values estimated from the Washington EPT trial). We evaluated type I error rate for the hypothesis Ho: δ = 0 and power against the alternative Ha: δ = −.01 where δ represents a risk difference. Results are shown in table 4. Absolute bias in δ (not shown) was less then 10⁻⁴ across all all sample size and random treatment effect scenarios. Similar to the results shown in table 3 type I error rates were maintained across scenarios for tests based on $V_{\delta }^1(\widehat{\delta })$ and slightly inflated for tests based on $V_{\delta =\widehat{\delta }}^1(\widehat{\delta })$ and $V^2(\widehat{\delta })$. Power declined as the treatment effect standard deviation increased and with increased cluster size variability.

Table 4.

Type I error rate (a) and power (b) for testing the null hypothesis Ho: δ = 0 based on 10000 simulations with characteristics similar to the WA EPT study. Binomial observations for 22 clusters in 5 times intervals are simulated from a linear model with μ = 0.09, a linearly decreasing time effect (−0.005 per time period), a random cluster effect (τ = 0.015) and random treatment effect (η = 0, 0.002, 0.008). Number of individuals per cluster per time period (n) is either constant (n = 305) or variable between clusters according to a lognormal distribution with mean log(171) and standard deviation 1.06 (giving a mean cluster size of 305).

(a) Type I error rate (nominal level = 0.05)
	$V_{\delta =0}^1(\widehat{\delta })$			$\frac{N}{N-1}{V}_{\delta =\widehat{\delta }}^1(\widehat{\delta })$			$V^2(\widehat{\delta })$
	Treatment standard deviation (η)
n	0	0.002	0.008	0	0.002	0.008	0	0.002	0.008
constant	0.05	0.05	0.05	0.06	0.06	0.06	0.07	0.07	0.08
variable	0.04	0.05	0.05	0.05	0.05	0.06	0.06	0.07	0.07
(b) Power (for the alternative Ha : δ = −0. 01)
	$V_{\delta =0}^1(\widehat{\delta })$			$\frac{N}{N-1}{V}_{\delta =\widehat{\delta }}^1(\widehat{\delta })$			$V^2(\widehat{\delta })$
	Treatment standard deviation (η)
n	0	0.002	0.008	0	0.002	0.008	0	0.002	0.008
constant	0.29	0.29	0.26	0.31	0.31	0.28	0.33	0.32	0.30
variable	0.18	0.17	0.08	0.20	0.18	0.09	0.22	0.20	0.12

4. Example

The Washington state EPT trial was a stepped wedge trial of expedited partner treatment (the practice of treating the sex partners of persons with sexually transmitted infections without prior medical evaluation of the partner) for the prevention of chlamydia and gonorrhea infection. The trial was conducted between July, 2007 and August, 2010. The primary outcome for the trial was chlamydia positivity, measured in sentinel sites throughout Washington state during the course of the trial, and incidence of reported gonorrhea, both in women aged 14–25. Twenty two local health jurisdictions (LHJs - equal to counties or clusters of counties in the state) were randomized to one of four different intervention sequences which were initiated in 7–8 month intervals. Outcomes were measured during the last 3 months of each interval. Additional details are provided in Golden et al. (2015).

Tables Web 1 and Web 2 in the supporting information show the trial design and chlamydia positivity by LHJ and time. The median sample size per cluster-period was 171 (IQR: 78 – 396). We tested the hypothesis of no intervention effect (i.e. H_o: δ = 0) using $V_{\delta =0}^1(\widehat{\delta })$ as in equation (17) and constructed a 95% confidence interval for the risk difference using equation (18). The intervention risk difference was estimated as −0.015 (95% CI: −0.033 – 0.003; p = 0.10). For comparison, Golden et al. (2015) reported a relative risk of 0.89 (95% CI: 0.77 – 1.04; p = 0.15) from a baseline positivity rate of 0.082, equivalent to a risk difference of −0.009 (95% CI: −0.019 – 0.009). The results from both analyses are qualitatively similar and show a small, non-significant intervention effect.

5. Discussion

We have developed a design-based approach for obtaining unbiased estimates of the intervention effect and robust inference (confidence intervals and hypothesis tests) in a stepped wedge study design. Although the methods are motivated by permutation arguments, closed form expressions for the intervention effect estimate and its variance are derived, so the approach is computationally simple. The proposed methods do not depend on detailed knowledge of the temporal mean structure, covariance structure or distribution of the data-generating mechanism. Similar to Thompson et al. (2018), the intervention effect estimate derived here is a “vertical” estimate (Davey et al., 2015) i.e. it relies only on between-cluster information on the intervention effect. This explains the robustness to misspecification of the time-trend - a comparison of intervention and control clusters at a point in time (between-cluster comparison) does not depend on the underlying time trend whereas any within-cluster comparison of intervention and control periods must first correct for time trends. While the reliance on between-cluster comparisons helps explain the robustness of the proposed intervention effect estimate, this also explains the loss of efficiency relative to the intervention effect estimate from a correctly specified model that uses both between-cluster and within-cluster information.

We have developed three variance estimates that can be used for inference, namely, $V_{\delta }^1(\widehat{\delta })$, $V_{\widehat{\delta }}^1(\widehat{\delta })$ and $V^2(\widehat{\delta })$. The first two (collectively, V¹) assume that Var(Y_i) does not depend on i while the last (V²) does not depend on this assumption. However, V¹ appears to be relatively insensitive to violations of this assumption and in simulations $V_{\delta }^1(\widehat{\delta })$ performs well across a range of scenarios and maintains the nominal type I error rate better than either of the other two variance estimates. Thus, we recommend the use of $V_{\delta }^1(\widehat{\delta })$ in practice. $V_{\widehat{\delta }}^1(\widehat{\delta })$ is a biased estimate of $V_Y(\widehat{\delta })$ and the bias depends on the true variance. Although multiplying $V_{\widehat{\delta }}^1(\widehat{\delta })$ by a correction factor of N/(N − 1) improves the performance, further research is needed before this approach can be broadly recommended.

In developing the proposed estimator, we assumed constant sample size across all clusters. This assumption greatly facilitates the computation of expectations and variances under the permutation distribution. Nonetheless, as demonstrated in our simulations, the proposed estimator is approximately unbiased and maintains type I error rate control and confidence interval coverage across a range of scenarios (particularly for $V_{\delta }^1(\widehat{\delta })$) even when sample sizes vary, assuming cluster size is uninformative for the treatment effect (Williamson et al., 2003). We do note, however, a loss of power in table 3 as cluster size variation increases.

A key assumption (which is necessary for all approaches to the analysis of stepped wedge trials) is that the underlying time trend is the same for all clusters. If this assumption is violated then $\widehat{\delta }$ may be biased and estimates of $V(\widehat{\delta })$ may be incorrect as well. However, if clusters can be grouped into strata with similar temporal trends (ideally, these strata would be defined apriori) then it is possible to derive an estimate of the intervention effect and its sampling variance based on a stratified permutation distribution. The resulting estimate is unbiased and has correct sampling variance (under the same constraints/assumptions as (15) and (16)). As previously noted, formulas for these stratified estimates are given in appendix A1.

The approach outlined here uses cluster-period level summaries and should, therefore, be robust to the underlying distribution of individual data points, provided the cluster-period sample sizes are moderately large. Thus, the proposed methods may be used with continuous, binary or count data, and the intervention effect will be interpretable as a mean difference, risk difference, or rate difference, respectively. Critically, however, the equivalence between an individual-level analysis and an analysis of cluster-period means used to derive $\widehat{\delta }$ only holds for the identity link (with equal cluster sizes). Specifically, if $\widehat{\delta }$ is computed using (nonlinearly) transformed cluster-period level summaries (e.g., log(Y_ij) or logit(Y_ij)), it will be a biased estimate of the intervention effect from an individual-level model with the corresponding nonlinear link. An extension of the proposed methods to other links to allow unbiased estimation of e.g. risk ratios is an area of ongoing research.

Appendix

A1. Stratified Estimation

The following estimators can be used for stratified estimation, where Y_hij represents the observation on the i’th cluster in stratum h at time j (note that i takes on values from 1 … m_h in these formulae):

$$\widehat{\delta }=\frac{\sum _{\mathit{\text{hij}}}{Y}_{\mathit{\text{hij}}}\left(x_{\mathit{\text{hij}}}-{\overline{x}}_{hj}\right)}{\sum _h{N}_h\sum _j{\overline{x}}_{hj}\left(1-{\overline{x}}_{hj}\right)}.$$

$$V_{\delta }(\widehat{\delta })=\{\sum _{hi}\left[\sum _j{\left(Y_{\mathit{\text{hij}}}-x_{\mathit{\text{hij}}}\delta \right)}^2{\overline{x}}_{hj}\left(1-{\overline{x}}_{hj}\right)+2\sum _{j<j^{\prime }}\left(Y_{\mathit{\text{hij}}}-x_{\mathit{\text{hij}}}\delta \right)\left(Y_{{\mathit{\text{hij}}}^{\prime }}-x_{{\mathit{\text{hij}}}^{\prime }}\delta \right){\overline{x}}_{hj}\left(1-{\overline{x}}_{h{j}^{\prime }}\right)\right]-\frac{2}{N_h-1}\sum _h\sum _{i<i^{\prime }}\sum _{j,j^{\prime }}\left(Y_{\mathit{\text{hij}}}-x_{\mathit{\text{hij}}}\delta \right)\left(Y_{h{i}^{\prime }{j}^{\prime }}-x_{h{i}^{\prime }{j}^{\prime }}\delta \right){\overline{x}}_{h,\text{min}\left(j,j^{\prime }\right)}\left(1-{\overline{x}}_{h,\text{max}\left(j,j^{\prime }\right)}\right)\}/{(\sum _h{N}_h\sum _j{\overline{x}}_{hj}(1-{\overline{x}}_{hj}))}^2.$$

A2. Permutation variance of $\widehat{\delta }$

The estimated intervention effect is

$$\widehat{\delta }=\frac{\sum _{ij}{Y}_{ij}\left(x_{ij}-{\overline{x}}_j\right)}{N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)}.$$

Letting $V_{\mathcal{P}}$ denote variance with respect to the permutation distribution,

$$V_{\mathcal{P}}(\widehat{\delta })=\frac{V_{\mathcal{P}}\left(\sum _{ij}{Y}_{ij}\left(x_{ij}-{\overline{x}}_j\right)\right)}{{\left(N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^2}$$

since ${\overline{x}}_j$ is constant across permutations. Further, since Y_ij is also constant with respect to the permutation distribution, one can use equations 5 – 7 to show that the variance of $\widehat{\delta }$ over all possible permutations is

$$V_{\mathcal{P}}(\widehat{\delta })=\{\sum _i\left[\sum _j{Y}_{ij}^2{\overline{x}}_j\left(1-{\overline{x}}_j\right)+2\sum _{j<j^{\prime }}{Y}_{ij}{Y}_{i{j}^{\prime }}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)\right]-\frac{2}{N-1}\sum _{i<i^{\prime }}\sum _{j,j^{\prime }}{Y}_{ij}{Y}_{i^{\prime }{j}^{\prime }}{\overline{x}}_{\text{min}\left(j,j^{\prime }\right)}\left(1-{\overline{x}}_{\text{max}\left(j,j^{\prime }\right)}\right)\}/{(N\sum _j{\overline{x}}_j(1-{\overline{x}}_j))}^2.$$

Unfortunately, however, $V_{\mathcal{P}}(\widehat{\delta })$ is a biased estimator of $V_Y(\widehat{\delta })$. To find the expected value of $V_{\mathcal{P}}(\widehat{\delta })$ with respect to the distribution of Y we make use of

$$\begin{array}{ccc}\hfill E_Y\left(Y_{ij}^2\right)& \hfill =\hfill & \text{Var}\left(Y_{ij}\right)+E{\left(Y_{ij}\right)}^2\hfill \\ \hfill E_Y\left(Y_{ij},Y_{i{j}^{\prime }}\right)& \hfill =\hfill & \text{Cov}\left(Y_{ij},Y_{i{j}^{\prime }}\right)+E\left(Y_{ij}\right)E\left(Y_{i{j}^{\prime }}\right)\hfill \\ \hfill E_Y\left(Y_{ij},Y_{i^{\prime }{j}^{\prime }}\right)& \hfill =\hfill & E\left(Y_{ij}\right)E\left(Y_{i^{\prime }{j}^{\prime }}\right)\hfill \end{array}$$

as well as $x_{ij}^2=x_{ij}$ and x_ijx_ij′ = x_ij for j < j′, to derive

$$\begin{gathered} E_Y\left(V_{\mathcal{P}}(\widehat{\delta })\right)=\frac{{\sum }_i\left[{\sum }_j\text{Var}\left(Y_{ij}\right){\overline{x}}_j\left(1-{\overline{x}}_j\right)+2{\sum }_{j<j}\text{Cov}\left(Y_{ij},Y_{i{j}^{\prime }}\right){\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)\right]+{\delta }^{2}C}{{\left(N\sum _j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^2} \\ C=\sum _i\left[\sum _j{x}_{ij}{\overline{x}}_j\left(1-{\overline{x}}_j\right)+2\sum _{j<j^{\prime }}{x}_{ij}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right)\right]-\frac{2}{N-1}\sum _{i<i^{\prime }}\sum _{j,j^{\prime }}{x}_{ij}{x}_{i^{\prime }{j}^{\prime }}{\overline{x}}_{\mathit{\text{min}}\left(j,j^{\prime }\right)}\left(1-{\overline{x}}_{\mathit{\text{max}}\left(j,j^{\prime }\right)}\right). \end{gathered}$$

Comparing this to equation (13), we see that the bias depends only on δ and not other parameters of the mean model for Y. In fact, the bias of $V_{\mathcal{P}}(\widehat{\delta })$ does not depend on any covariate that is constant within a column of the stepped wedge design matrix (e.g. the time parameters β_j). Using this same approach, one may show that $V_{\delta }^1(\widehat{\delta })$ is unbiased i.e.

$$\mathbf{\text{E}}\left(V_{\delta }^1(\widehat{\delta })\right)=V_Y(\widehat{\delta }).$$

A3. Bias of the plug-in variance estimator

Assume, as in equation (14), that Var(Y_i) does not depend on cluster. Although $V_{\delta }^1(\widehat{\delta })$ is unbiased for $V_Y(\widehat{\delta })$, $V_{\widehat{\delta }}^1(\widehat{\delta })$ is biased. Specifically,

$$\mathbb{E}\left(V_{\widehat{\delta }}(\widehat{\delta })\right)=[1+\frac{1}{N-1}\frac{{\Sigma }_j{\overline{x}}_j^2{\left(1-{\overline{x}}_j\right)}^2+2{\Sigma }_{j<j^{\prime }}{\overline{x}}_j^2{\left(1-{\overline{x}}_{j^{\prime }}\right)}^2}{{\left({\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^2}]V_Y(\widehat{\delta })-\frac{2N}{N-1}\frac{B1+B2+B3}{{\left(N{\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^3}$$

where

$$\begin{gathered} B1={\Sigma }_i{\Sigma }_j{x}_{ij}{\overline{x}}_j\left(1-{\overline{x}}_j\right){\Sigma }_l\left(x_{il}-{\overline{x}}_l\right){\sigma }_{j,l} \\ B2={\Sigma }_i{\Sigma }_{j<j^{\prime }}{x}_{ij}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right){\Sigma }_l\left(x_{il}-{\overline{x}}_l\right){\sigma }_{j^{\prime },l} \\ B3={\Sigma }_i{\Sigma }_{j<j^{\prime }}{x}_{i{j}^{\prime }}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right){\Sigma }_l\left(x_{il}-{\overline{x}}_l\right){\sigma }_{j,l} \end{gathered}$$

and σ_j,l is the covariance between Y_ij and Y_il. Dividing both sides by $V_Y(\widehat{\delta })$ gives the relative bias

$$\mathit{\text{bias}}=1+\frac{1}{N-1}\frac{{\Sigma }_j{\overline{x}}_j^2{\left(1-{\overline{x}}_j\right)}^2+2{\Sigma }_{j<j^{\prime }}{\overline{x}}_j^2{\left(1-{\overline{x}}_{j^{\prime }}\right)}^2}{{\left({\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^2}-\frac{2}{N-1}\frac{B1+B2+B3}{\left({\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)\left({\Sigma }_i{\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right){\sigma }_j^2+2{\Sigma }_i{\Sigma }_{j<j^{\prime }}{\overline{x}}_j\left(1-{\overline{x}}_{j^{\prime }}\right){\sigma }_{j,j^{\prime }}\right)}$$

In the special case where the covariance matrix is diagonal with ${\sigma }_j^2={\sigma }^2$, however, the third term on the right hand side equals the second, aside from the leading 2/(N − 1). Therefore, in this special case, the relative bias is

$$\mathit{\text{bias}}=1-\frac{1}{N-1}\frac{{\Sigma }_j{\overline{x}}_j^2{\left(1-{\overline{x}}_j\right)}^2+2{\Sigma }_{j<j^{\prime }}{\overline{x}}_j^2{\left(1-{\overline{x}}_{j^{\prime }}\right)}^2}{{\left({\Sigma }_j{\overline{x}}_j\left(1-{\overline{x}}_j\right)\right)}^2}$$

For a regular stepped wedge design in which N = k(T − 1) (k an integer) and each sequence occurs in an equal number of clusters (so ${\overline{x}}_j=j/T$), the relative bias becomes

$$\mathit{\text{bias}}=1-\frac{1}{N-1}\frac{2{(T-1)}^4+5{(T-1)}^2-7}{5{(T-1)}^4-10{(T-1)}^2+5}$$

Remarkably, this function is reasonably well approximated by 1 − 1/N for any k, suggesting that the plug-in estimator is biased down by a factor of approximately $\frac{N-1}{N}$ under these conditions. Our simulations suggest that this approximation holds even when then the covariance matrix is not diagonal.