Abstract
Post COVID-19 vaccine development, nations are now getting ready to face another challenge: how to effectively distribute vaccines amongst the masses to quickly achieve herd immunity against the infection. According to some experts, herd immunity for COVID-19 can be achieved by inoculating 67% of the population. India may find it difficult to achieve this service level target, owing to several infrastructural deficiencies in its vaccine supply chain. Effect of these deficiencies is to cause frequent lead time disruptions. In this context, we develop a novel modelling approach to identify few nodes, which require additional inventory allocations (strategic inventory reserves) to ensure minimum service level (67%) under the possibility of lead time disruptions. Later, through an illustrative case study on distribution of Japanese Encephalitis vaccine, we identify conditions under which strategic inventory reserve policy cannot be practically implemented to meet service level targets. Nodes fulfilling these conditions are termed as critical nodes and must be overhauled structurally to make the implementation of strategic inventory policy practically viable again. Structural overhauling may entail installation of better cold storage facilities, purchasing more quality transport vans, improving reliability of transport network, and skills of cold storage manager by training. Ideally, conditions for identifying critical nodes for COVID-19 vaccine distribution must be derived separately by substituting COVID-19 specific parametric values in our model. In the absence of the required data for COVID-19 scenario, JE specific criteria can be used heuristically to identify critical nodes and structurally overhaul them later for efficiently achieving service level targets.
Keywords: Humanitarian logistics (O), Structural resilience, COVID-19, Lead time disruption, Herd immunity, Vaccine supply chain
1. Introduction
This study aims to address an important question “Are there any ways to mitigate the impact of COVID-19?” raised in the special issue of EJOR on “The role of Operational Research in the future epidemics/pandemics”. This question is addressed by developing cost effective vaccine distribution strategies for the masses in India. Vaccination is widely recognised as one of the most effective methods in controlling the spread of epidemics/pandemics like SARS, Ebola, COVID-19. Massive global efforts are already underway to develop a potent COVID-19 vaccine. Post vaccine development, primary concern of all nations will be to acquire herd immunity in the least possible time. Importance of achieving herd immunity stems from the fact that infection is effectively contained if the population acquires it. Formally, herd immunity is defined by Randolph and Barreiro (2020) as “the indirect protection from infection conferred to susceptible individuals when a sufficiently large proportion of immune individuals exist in a population”.
Herd immunity is acquired by a population when the proportion of individuals, who are immune to the infection, is greater than or equal to herd immunity threshold (Metcalf, Ferrari, Graham & Grenfell, 2015). Under some simplistic assumptions, researchers (Park & Kim, 2020); Randolph & Barreiro, 2020 have estimated herd immunity threshold for COVID-19 to be 67% of total population. In other words, vaccine supply chains across the globe will be required to ensure inoculation of 67% of the population for acquiring herd immunity against COVID-19 infection. However, low-income, and middle-income countries (like India, Kenya, Nigeria, etc.) may find it difficult to ensure these service level targets owing to the frequent lead time disruptions in their vaccine supply chain. Lead time disruptions render supply chain nodes non-operational for a period, which is known as disruption recovery time in supply chain literature (Ivanov, Dolgui, Sokolov & Ivanova, 2017). Hence, when a disruption is realized, the total supply lead time for a node will increase by the amount of disruption recovery time of the preceding node. Increment in supply lead time has a direct effect on the service level in the vaccine supply chain as demonstrated later. Our following discussion will be focussed on evaluating the effects of lead time disruptions on the performance of vaccine supply chain in the Indian context.
We do not consider the effects of other disruptions (production/yield, quality) in our study as these disruptions mostly occur during the production phases (Shao, 2018). Since vaccines are often manufactured abroad and later imported in India, these disruptions cannot be entirely mitigated by the Indian government. On the contrary, lead time disruptions occur during vaccine distribution, and must be mitigated by the Indian government to meet the minimum service level targets.
Lead time disruptions are primarily caused due to various infrastructural deficiencies in the Indian vaccine supply chain (IVSC). Some of them are unavailability of reliable power supply in rural areas, absence of spare parts for maintaining cold storage, acute shortage of trained manpower, and inadequate number of transport vans.1 Apart from causing frequent disruptions, these infrastructural deficiencies are also responsible for reducing the effective shelf life of the vaccines. In some cases, effective shelf life of vaccine is reduced from 36 months to 2 weeks (Lala, 2003). The combined effect of reduced shelf life of a vaccine along-with increase in supply lead time (due to lead-time disruptions), is to cause huge wastage of vaccines due to expiration, and at the same time, a loss in the customer service level. The current vaccine wastage due to perishability in Indian vaccine supply chain (IVSC) is nearly 30% (Chakraborty & Joardar, 2019).
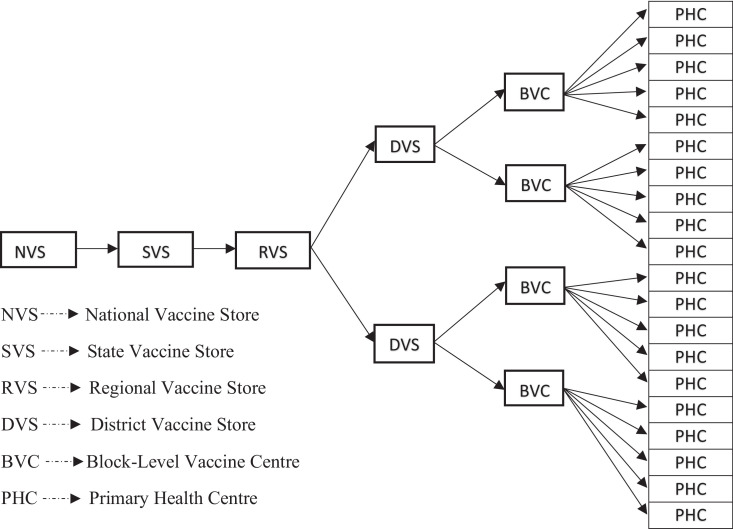
Lead-time disruptions are rapidly transmitted across the IVSC due to its extensive and scattered structure. IVSC comprises of about 27,000 nodes with about 95% of the nodes pertaining to the Primary Health Centre (PHC) level, while only 5% pertain to higher echelons (Block level or above)2 (Fig. 1 ). Due to highly scattered structure, failure of a single higher echelon node affects the performance of many lower echelon nodes (Atlay & Green, 2006). In other words, disruptions at any higher echelon node are readily transmitted rapidly across supply chain.
Fig. 1.
Vaccine Supply Chain in India.
To sum up, addressing the infrastructural deficiencies is crucial for minimizing the lead time disruptions, and consequently improving the service level in IVSC. Service level improvement in IVSC will help India in rapidly achieving herd immunity for COVID-19 in future. Ideally, infrastructural resilience should be increased on all supply chain nodes, as all of them are susceptible to frequent disruptions due to infrastructural deficiencies. However, such a solution would be cost-prohibitive and practically infeasible for low-income/middle income country like India. In this context, our main contribution in this paper is development of a modelling approach which can be utilized to identify few critical nodes, such that increasing infrastructural resilience of them will be sufficient to meet the required service level targets for achieving herd immunity. Increasing infrastructural resilience of few critical nodes is obviously more cost-effective solution in comparison to increasing infrastructural resilience of all the nodes.
In our modelling approach, we first propose a demand forecasting model to minimize vaccine wastage. Further, a cost-effective multi-echelon inventory model under no disruption scenario is proposed, to fulfil forecasted demand. Later, a game theoretic model is developed to identify major disruption scenarios, under which service level targets cannot be met. Inventory hedging strategy should be implemented to protect service level in these disruption scenarios. Finally, through an illustrative case study on the distribution of Japanese Encephalitis (JE) vaccine in Gorakhpur, India; we develop exact condition under which inventory hedging strategy becomes infeasible. At this point, service level can only be restored by increasing the infrastructural resilience of some critical nodes. JE has been recognized as an epidemic for many years in this area (Gorakhpur, India), and Indian government has not been able to eradicate it due to infrastructural deficiencies in Indian vaccine supply chain. Our case study demonstrates how proposed model can be used to identify critical nodes for JE, which can be structurally overhauled to eradicate this disease. To develop criteria for identifying critical nodes in context to COVID-19, our model can be executed with COVID-19 specific parameters. In the absence of any COVID-19 specific data, JE specific criteria for identifying critical nodes can be used heuristically for COVID19 vaccine distribution scenario.
2. Literature review
IVSC is almost entirely controlled by the government of India, with only 3%−5% of the demand being met by the private sector (Sharma, Kaplan, Chokshi & Zodpey, 2016). Hence, the onus of its efficient operation solely lies with the government. Recently, the Indian government has taken several initiatives, including the implementation of a vaccine intelligence network program (VIN) and a cold chain tracking program to prevent stock-outs and improve the performance of IVSC. Nevertheless, these initiatives have only been marginally successful in improving the operational efficiency of IVSC. Marginal or unsatisfactory success of these initiatives can be attributed to acute lack of infrastructure in terms of number and capacity of cold storages, transport vans, lack of trained personnel, etc.3 Capacity issues, along with their prospective solutions, have been discussed in several assessment studies.4 , 5 However, none of these assessment studies or government initiatives have addressed the frequent lead time disruptions, their affect, and their mitigation in IVSC.
In literature too, researchers have only focused on yield/production disruptions in vaccine supply chains, while completely disregarding other forms of disruptions (Duijzer, van Jaarsveld & Dekker, 2018). Some important researches addressing the production disruptions in vaccine supply chains are Begen, Pun and Yan (2016), Chick, Mamani and Simchi-Levi (2008), De Treville et al. (2014), Federgruen and Yang (2009), Kazaz, Webster and Yadav (2016), Teunter and Flapper (2006), Cho and Tang (2013), Eskandarzadeh, Eshghi and Bahramgiri (2016), etc. These studies have focused on evaluating and minimizing the effects of production disruption on supply chain performance through various strategies (contracts, support prize, etc.), and cannot be extended to mitigate the lead-time disruption in our problem, as IVSC only comprises of distribution nodes (none of the nodes is dedicated to vaccine manufacturing).
Some prominent studies in literature focusing on lead time disruption in supply chain /transportation network are Cannella, Dominguez and Framinan (2017), Garcia, Ibeas, Herrera and Vilanova (2012), Konstantaras, Skouri and Lagodimos (2019), Sawik (2015), Schmitt, Kumar, Stecke, Glover and Ehlen (2017), Paz and Escobar (2018), Wichapa and Khokhajaikiat (2018), Granada-Echeverri, Toro and Santa (2019), Bhuiyan, Medal and Harun (2020), Paquay, Crama and Pironet (2020), Prak, Teunter and Syntetos (2017), Gupta, Starr, Farahani and Matinrad (2016), Li, Chen, Collignon and Ivanov (2020).
Garcia et al. (2012) have used adaptive control methodology to optimize inventory stock sizes under lead time uncertainty. It is assumed that the global demand parameters are known to each supply chain node in advance. Contrarily, demand information in IVSC is transmitted upstream from the PHC nodes. Our forecasting model in Section 3.1 minimizes the forecasting deviation or the bullwhip effect in this setting, which would otherwise be significant for a large supply chain in the absence accurate demand information on each node. Schmitt et al. (2017) have conducted simulation-based study to evaluate the performance of the supply chain in terms of effectiveness and efficiency under lead time disruptions. Sawik (2015) has proposed a combinational stochastic model to optimize efficiency and effectiveness under lead time disruptions. These studies have evaluated the effect lead time disruptions have on performance metrics like stock levels, service levels, cost, etc. In our study, we have measured the effects of lead time disruptions on the service level. An important difference in our modelling approach is that we have integrated our inventory model with a novel multi echelon demand forecasting model. This difference in modelling approach is aimed at minimizing the vaccine wastage in IVSC.
We also propose a game-theoretic model to identify the major disruption scenarios from the disruption scenario set. This model is motivated by the work of Jalali, Seifbarghy and Niaki (2018), Zahiri, Zhuang and Mohammadi (2017), and Zhang, Snyder, Ralphs and Xue (2016). Jalali et al. (2018) has proposed an interdictor game-based model for identifying vulnerabilities and addressing them through optimal supply chain design. Zahiri et al. (2017) has used novel metric for measuring resilience and sustainability and later propose a model to evaluate the performance of supply chain design according to these metrics under production uncertainty. Zhang et al. (2016) have proposed a bilevel optimization model to represent the supply chain designing problem under the disruption risk, when two competitors are competing for the same market space. Problem is modelled as Stackelberg game. These studies use game-theoretic based models to optimally design supply chains through efficient location of sites. In contrast, objective of our game theoretic model is to identify major disruption scenarios in a vaccine supply chain which is already in operation.
Major disruption scenarios are characterised by the failure of one or more nodes such that the intended service level cannot be met. To ensure service level in these scenarios, appropriate protection strategy must be implemented. Protection strategies in literature can be broadly classified as proactive strategies and reactive strategies. Reactive strategies are implemented to minimize the loss after the occurrence of disruptions, while proactive strategies are implemented to protect the supply chains from any future disruptions.
Tomlin (2009), in this context, has provided an excellent exposition on several protection strategies (proactive and reactive) like inventory hedging, contingent sourcing, supplier diversification, demand switching, etc. Inventory hedging strategy is defined as extra inventory carried by the nodes to hedge against disruption risk (Ivanov, 2020). It is usually not considered appropriate for perishable products, as its implementation under a no disruption scenario might result in huge wastage due to perishability (Tomlin, 2009). Since shelf life of vaccines is greater than other conventional perishable products (fruits, vegetable, dairy), we consider this strategy to be appropriate for our case. Further, our forecasting model and perishability constraints in the inventory model ensures that no vaccine is wasted due to perishability.
Other protection strategies suggested by Tomlin (2009) are not appropriate to IVSC due to the following reasons. Demand switching (reactive strategy) cannot be used as it is inconsistent with the government target of achieving the herd immunity for COVID-19, or complete eradication of JE infection. Implementing supplier diversification (proactive strategy) strategy requires working in partnership with many suppliers for the same products, which is not feasible in IVSC as it must adhere to a strict regulatory requirement related to suppliers. Contingent sourcing strategy (reactive strategy) requires sourcing the supplies from an alternate supplier in an event of disruption (Paranjuli et al., 2017). This strategy is also not recommended for IVSC, as its implementation may lead to several quality assurance issues (Gray, Roth & Leiblein, 2011).
Summing up, we implement inventory hedging strategy to protect customer service level under major disruption scenarios. Our case study on distribution of Japanese Encephalitis vaccine enables us to identify critical disruption scenarios, in which inventory hedging strategy fails. Critical disruption scenarios are characterised by failure of one or more critical nodes. Infrastructural resilience of these critical nodes can be increased to ensure minimum service level.
3. Model development
Important model assumptions are listed in Table 1
Table 1.
Model assumptions.
| 1 | Multi-echelon, multi-period, single product supply chain is considered. |
| 2 | Periodic inventory policy under lost sales case is considered. |
| 3 | There is exactly one path between the initial supply node and PHC node (consistent with the divergent supply chain structure, Dominguez et al., 2014). |
| 4 | Expiration time of vaccine is greater than the maximum lead time on any path under no disruption scenario. |
| 5 | Failure of each node is independent of the failure of other nodes. |
Periodic review inventory model is suitable for IVSC as vaccine transport vans are shared amongst the nodes and are not available to any node in all time periods. Supply chain nodes can only replenish their stock in the periods when the van is available.
As stated, earlier IVSC has a divergent structure. Therefore, we focus only on vaccine distribution, while discounting its manufacturing. Vaccines are often imported; hence it is not possible for the government to directly address the manufacturing uncertainties. Moreover, as discussed in the previous section, yield uncertainty in vaccine supply chain has already been addressed by many researchers.
Our assumption of lost sales case is motivated by the fact that IVSC majorly serves the poor, for whom, getting any family member vaccinated could mean the loss of single day wages. Loosing daily wages for more than one day for getting vaccinated, is unaffordable to many and consequently demand cannot be backordered.
We further consider only single product type (vaccine) distribution, as all vaccines have different demand, shelf life, in transit recommended temperature, and service level requirements. Vaccines with different recommended storage temperature cannot be transported in a single batch by a refrigerated van, as no single temperature setting will be ideal for all vaccines. We further consider that a disruption scenario can only be realized after the supply chain has fully recovered from the preceding disruption scenario. This assumption is consistent with other models in literature (Li et al., 2020; Sinha, Kumar & Prakash, 2020). We discuss a novel demand forecasting model in the next section. Problem notations are described in Table 5.
Table 5.
Notations used in model.
| Forecast horizon. | |
| Time period for which inventory model is valid. | |
| Node set in a supply chain network. | |
| Cardinality of the set . | |
| Time period such that . | |
| Demand forecast in period for the period . | |
| Estimated demand in the period . | |
| Node in supply chain network. | |
| Forecast deviation in the period for period . | |
| Expected value forecast deviation over forecast horizon . | |
| Node processing lead time. | |
| Service time of the node for node . | |
| Inventory replenishment time of node when node and node are its predecessor node and successor node respectively on a specific path. | |
| NVS node. | |
| PHC node. | |
| Set of demand node such that . | |
| Path connecting the demand node . | |
| Lead time for the node for the path . | |
| Estimated demand at the node at time due to lead time along the path . | |
| Set of all valid path in the supply chain network. | |
| Estimated demand at the node at time due to lead time along the path in disruption scenario . | |
| Cumulative demand at the node in the time period. | |
| Cumulative demand at the node in the time period in disruption scenario . | |
| Set of nodes in the higher echelon connected to node . | |
| Set of nodes in the lower echelon connected to node . | |
| Maximum order that can be placed by node at node such that | |
| Actual order size by the node to the node at time period. | |
| Age of the inventory when at the node . | |
| Set of initial supply nodes. | |
| Number of aged inventory at the node at time period. | |
| Total inventory at the node at time period of all ages. | |
| Total inventory at the node at time period of all ages in disruption scenario . | |
| Number of age inventories in the order . | |
| Ordering cost of the node . | |
| Total inventory at the node at time period of all ages when all the nodes place maximum orders after the initiation of disruption scenario . | |
| Inventory holding cost at the node . | |
| Excess inventory holding cost at the node . | |
| Binary variable whose value depends on whether an order is placed by node to the node such that . | |
| Space available for inventory storage at node . | |
| Total additional space available at node by incurring extra cost for allocating strategic inventory reserves. | |
| Binary value variable whose value depend on whether any age inventories supplied by node to node in time period has been allocated to path such that . | |
| Expiration constant in terms of number of time periods. | |
| Disruption scenario set. | |
| Set of critical disruption scenarios. | |
| Disruption scenario such that . | |
| Disruption recovery time for the node for the disruption scenario . | |
| Lead time of the node for the path in disruption scenario . | |
| No disruption scenario. | |
| Time period at which disruption is initiated. | |
| Binary variable (0,1) whose value depends on whether a node has been disrupted in scenario . | |
| Total strategic inventory reserve allocated at node . | |
| Maximum strategic inventory reserve to be allocated on the path connecting. | |
| Lead time of the node for the path in disruption scenario . | |
| Fixed cost of creating an excess fixed inventory space from to . | |
| Design parameter for service level. | |
| Large number (Model constant). | |
| Maximum service level loss at the demand node due to disruption at the node . | |
| Efficiency of heuristic H1. | |
| Transportation cost per unit from node to node |
3.1. Demand forecasting modelling
We refer to Graves and Willems (2000), and Schoenmeyr and Graves (2009) when developing this model. Graves and Willems (2000) have developed a forecasting model for a convergent type multi-echelon supply chain. Later, they use a dynamic programming-based algorithm to allocate safety stock at various nodes in the supply chain. Schoemeyr and Graves (2009) have extended this model to a generic case of convergent supply chain in which the demand forecast evolves over time. Although, these models are typically valid for the assembly type supply chain as described in Ben-Ammar, Dolgui and Wu (2018), they can be modified, and later extended to divergent supply chain structure of IVSC (Fig. 1), as discussed below.
Let represent the IVSC network consisting of node set , and arc set . Further, let denote the demand forecast in the period for the period , where ; represents the forecasting horizon and is defined as the length of time in the future for which our model can forecast or estimate demand. Similarly, denotes the total time periods for which inventory is planned. Actual demand in the period is denoted by random variable . By convention, we know . We make a demand forecast in period for period , and revise our forecast in each period according to the realized demand. Forecast deviation can be expressed as
| (1) |
Demand can be estimated as a function of according to the following expression
| (2) |
We assume forecast deviation to be random (independent of any special cause6 ), hence
| (3) |
By intuition, we know that the variance in forecasting error (denoted by ) increases as we increase .
We discuss our results for the sequential multi-stage supply chain as depicted in Fig. 2 , and later extend these results to multi-echelon IVSC as depicted in Fig. 1. represents an end customer node (PHC, Fig. 1). We assume a constant node processing time of as (in no disruption scenario).
Fig. 2.
Node sequence.
Node processing time may vary for each node and is the time taken by each cold storage to process and appropriately stock the vaccines, after the receipt of orders. Under a no disruption scenario, each node is required to fulfil an order in a service time denoted by , where is the successive node being supplied by node .
Service time may also vary for different lower echelon nodes ( in a multi-echelon system due to various operational constraints (number of transport vans, terrain to be traversed, number of trained inventory managers at each node, etc.). When a node places an order to upstream node at time period , then the order must be fulfilled by time period . Node after receiving this order at time period incurs time periods to process it and makes the product available for node at time period (Fig. 2). Similarly, an order received by node at time period from the downstream node (lower echelon node) must be fulfilled in . Therefore, order lead time can be expressed as
| (4) |
We assume that in our model. If this condition is not met, then there is no need to carry any inventory at node . In this case, to fulfil any order from the node at time period, node can place the same order to node at time period. In other words, if this condition is violated, our system will function as a JIT system (Lee & Ebrahimpour, 1984). Obviously, JIT implementation is not possible for IVSC, hence we completely discount this possibility.
It should be noted that processing time depends substantially on node infrastructure like the number of trained personnel, capacity, and efficiency of stocking facilities, etc.; while service time chiefly depends on the transportation infrastructure between nodes. Order lead time, as given in Eq. (4), can be summed over all the successive nodes in the path to obtain cumulative lead time for a node. Mathematically, it can be expressed as
| (5) |
represents the time required for the vaccines at node to reach PHC node along the path under no disruptions. Hence, estimated demand at the node along the path during the lead time is given by
| (6) |
In multi echelon divergent IVSC (Fig. 1), each node is connected to multiple PHC nodes through several paths. Hence, the total estimated demand for each node at the time period is given as
| (7) |
As stated earlier, for a non-JIT implementation, is non-increasing as we move downstream and . Further, while deriving the above expression, we have assumed that no cycles are present in the supply chain. This enables us to topologically order the supply chain network (Haeupler, Kavitha, Mathew, Sen & Tarjan, 2012). In a topologically ordered supply chain network, . We further assume that a PHC is supplied by a single precursor node. Hence, there is a maximum of one path between the NVS node and PHC node pair). This assumption is consistent with the divergent structure of IVSC (Dominguez, Framinan & Cannella, 2014).
denotes the forecasted demand at the node along path at time period. denotes the total forecasted demand at the node in time period. Hence order size must be optimized to fulfil under space, expiration, and service level constraints. An appropriate periodic review multi-echelon inventory model is proposed in the next section for this purpose.
3.2. Optimal ordering policy in no disruption scenario
Let be the maximum order size which can be placed by node at the node such that denotes the set of lower echelon nodes directly connected to node by arc. is the actual order size of the node to the node at time, and is the summation of all aged inventory from the higher echelon node , hence . denotes the quantity of age inventories in the order . We defined the age of the inventory as the number of time periods for which it stays in the system, hence we have
| (8) |
At time period , inventory level at all nodes is 0, hence
| (9) |
And,
| (10) |
Also,
| (11) |
denotes the initial supply node (NVS node in our case, (Fig. 1)). Total inventory level at a node in time period is the sum of inventories of all ages
| (12) |
As stated earlier, due to inadequate storage facilities in IVSC, shelf life and potency of vaccines are rapidly deteriorated (from 36 weeks to 2–3 weeks). Our modelling approach ensures that the total time taken by vaccines to traverse the distribution network should not exceed their reduced shelf life.
If 67% service level is required by all nodes, then
| (13) |
In Eq. (13), is the binary variable (0,1) which denotes whether an order was placed or not at the time period, that is scheduled to arrive at period. denotes weather an order was placed in this time period which is expected to be received in the nth time period. Further, as L.H.S. R.H.S, we ensure that a 67% service level is maintained according to the designated target in IVSC. Let , and denote the ordering cost, and inventory holding cost per unit respectively at node . Let further denote transportation cost per unit from and node. Multi-echelon inventory problem (1) aims to minimize the total cost while maintaining a 67% service level under the no disruption scenario.
Problem (1):
| (14) |
Subjected to:
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
Eq. (14) represents the total inventory cost comprising of total ordering, inventory holding costs, and transportation cost of all the nodes over planning horizon . Constraint (15) makes sure that all nodes can place their maximum order size in any valid time period . If this constraint is not satisfied, then the maximum order size parameter () becomes meaningless. Constraint (16) is the service level constraint and ensures a 67% service level on all the customer nodes over . Constraint (17) ensures that the maximum order size limitation is not violated by any node in any time period. Constraint (18) addresses space limitation on each node. Inventory stock in any time period and at any node should not be larger than what is permitted by available space for storage denoted by . Constraint (19) ensures that the inventory replenishment time is strictly nonnegative (following our arguments from Section 3.1). Constraint (20) ensures that the summation of age of inventory and the allocated path lead time does not exceed the reduced shelf life denoted by . Hence, this constraint ensures that higher aged inventories on a node are allocated to the path with less lead time. Eq. (21) defines the range of values for decision variables respectively.
The optimal solution to problem (1) minimizes the total cost, while ensuring a designated service level under the no disruption scenario. It must be noted that multi-echelon inventory problem must ideally be solved through backward optimization-based method as ensuring service level at the PHC node is more important than the service level at any preceding node. However, our cost minimization inventory model is integrated with a forecasting model (proposed earlier) in which demand forecasts at the higher echelon nodes are derived from the demand forecasts at the PHC nodes. Therefore, MATLAB solution to our integrated model is same as the solution that would be obtained by solving multi-echelon inventory problem through any backward optimization-based algorithm. In the next section, we propose a game-theoretic model to identify disruption scenarios in which minimum service level cannot be ensured.
3.3. Game theoretic model to identify major disruption scenarios
A major disruption scenario is defined as the one in which the service levels cannot be met even when order size at each node is maximized. Due to the extensiveness of the IVSC, size of the disruption scenario set is very large. Therefore, identifying major disruption scenarios is computationally non-trivial task as service level of the supply chain must be evaluated under each disruption scenario. To reduce the computational complexity of the problem, we propose a novel game-theoretic model which efficiently identifies major disruption scenario from the disruption scenario set. In our game-theoretic setting, two agents namely leader and follower have conflicting objectives. At the onset of disruption, the follower increases the order size to maintain the service level. The leader is aware of the follower's response and tries to identify a disruption scenario under which the follower's best response (maximization of order size within the permissible limits so that constraint (17) is not violated) will be insufficient in meeting service level targets. Problem (2) (described by (27), (28), (29), (30), (31)) is formulated to maximize the leader objective (disrupting the service level), and its feasibility implies that minimum customer service level cannot be ensured over all disruption possibilities. Each feasible solution to Problem (2) corresponds to a major disruption scenario, if it fulfils the conditions stated in Section 3.3.1.
To represent disruption possibilities, we use scenario-based modelling. In scenario-based modelling, each disruption scenario is characterized by a failure of one or several nodes simultaneously and is denoted by . Each node failure is associated with the failure probability and disruption recovery time as described by Babai, Syntetos, Dallery and Nikolopoulos (2009), and Paul, Sarker and Essam (2015). Disruption recovery time of the node is defined as the time required by a supply node to resume its normal operation after the onset of disruption, and is denoted by . Disruption scenario set comprises of all the possible disruption scenarios.
The failure probability of a node is determined by some random discrete probability distribution. Disruption at each node is considered an independent event, and joint probability of simultaneous disruptions at multiple nodes is calculated accordingly. Joint probability value is compared with design parameter to identify critical disruption scenarios. Parameter denotes the probability at which designated service level targets (67% in our case) should be met over the entire planning period .
As discussed earlier, lead time along the path increases when a disruption scenario is realized. Numerically, under any disruption scenario, it can be obtained by modifying the Eq. (5) as under
| (22) |
Intuitively, for no disruption scenario ,. Hence, Eq. (22) reduces to Eq. (5) for . Further, we have . When disruption scenario is realised, then Eq. (6), (7), and (13) transforms to Eq. (23), (24), and (25) respectively.
| (23) |
| (24) |
| (25) |
Inventory level at nodes under the follower's best response (maximization of order size)
| (26) |
For a PHC node , we have
| (26a) |
We have slightly abused the notation of maximum order size in Eq. (26) to emphasize that after the onset of disruption scenario at the time such that , maximum orders are placed by every node to maintain the service level. Eq. (26a) reiterates this condition for a PHC node. To identify major disruption scenarios, Problem (2) is formulated as under -Problem (2):
| (27) |
Subjected to:
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
Eq. (27) chooses a disruption scenario from the set with maximum probability of occurrence along a path. Each disruption scenario is characterised by a failure of some nodes, and non-failure of others across the path. Constraint (28), (30), and (31), are the same as constraint (18), (19), and (20), respectively. Constraint (29) ensures that the intended customer service level at a PHC is not satisfied for a disruption scenario. Eq. (32) defines the range of values for decision variables respectively.
In other words, any feasible solution to the above problem would imply that for at least one disruption scenario, the service level at any PHC node in a particular time period could not be met, even by maximizing the order size for all the nodes.
3.3.1. Total number of major disruption scenarios
Problem (2) in the previous section enabled us to identify disruption scenarios under which service level cannot be ensured. These disruption scenarios can be further classified as major disruption scenarios if their probability of occurrence is significantly high, or in other words objective_function (Problem (2)) . We now describe a simple method (procedure 2.1), for extracting all such critical disruption scenarios from the set. Let us define as the set of critical disruption scenarios such that .
| Procedure 2.1: |
| Step 0: |
| Step 1: Identify for which problem (2) is feasible and optimum such that , or else go to step 4. |
| Step 2: If objective function (Problem (2)) then , or else go to step 4. |
| Step 3: Go to step 1. |
| Step 4: Stop. |
Emptiness of set , and feasibility of problem (2) indicate the presence of disruption scenarios under which service level at all customer nodes (PHC) cannot be fulfilled. However, likelihood of the occurance of these disruptions is not significantly high. Hence, presence of these disruption scenarios does not warrant any additional response.
On the other hand, non-emptiness of set indicates the presence of major disruption scenarios which are capable of disrupting the service level with a significantly high probability. It must be noted that for set to be non-empty , problem (2) must be feasible. To protect the service level in major disruption scenarios, we recommend the use of inventory hedging strategy as described in the following section.
3.4. Inventory hedging strategy when
Inventory hedging strategy refers to allocating extra inventory at some nodes to protect the customer service level in major disruption scenarios. In our earlier model, maximum inventory size at each node was restricted by space constraints. We now assume that additional inventory space can be created at some nodes at some incremental cost. This may require purchasing an extra refrigerator (for vaccine storage) in our context.
Purpose of this model is to cost effectively allocate additional inventories at several nodes to protect the customer service level in the major disruption scenarios. In other words, this strategy aims to render the problem (2) infeasible over disruption scenario set. The amount of excess inventory to be carried for protection against disruption has been termed as strategic inventory reserve by Schmitt (2011). It must be noted that we don't explore the possibility of holding strategic inventory reserve in a central warehouse as it aggregates the risk of disruption (Pan et al., 2002; Schmitt, Sun, Snyder & Shen, 2015). Factors like regulatory requirements and counterfeiting measures may also make the centralized strategic inventory warehousing solution infeasible. Further, cost of building and operating a central warehouse may be prohibitive while fortifying against disruption scenarios which are ever changing in magnitude and probability of occurrence.
Let be the maximum allowable space over designated inventory space such that . We define as the integer decision variable whose value depends on whether excess inventory space of the node is utilized for strategic inventory allocation. Let the holding cost for excess inventory be. Total strategic inventory reserve allocated at the node is denoted by . is the fixed cost of increasing the inventory space of a node from to . If excess space cannot be created on any node, then we substitute . Cost optimal strategic inventory allocation problem (3) is formulated as below.
Problem (3)
| (33) |
Subjected to:
| (34) |
| (35) |
| (36) |
| (37) |
| (38) |
Constraint (33) minimizes the total inventory cost of carrying excess inventory. Constraint (34) allocates strategic inventory quantities on the lower echelon nodes if a major disruption scenario is characterised by a failure of a higher echelon node. Hence, it is ensured that the movement of vaccines across IVSC is not disrupted. Constraint (35) ensures that total excess inventory allocations along a path are greater than or equal to the maximum quantity disrupted over all major disruption scenarios. Constraint (36) ensures that such allocations protect the customer service level for all the subsequent time periods after the onset of disruption. Constraint (37) honours the excess space allocation constraint. Constraint (38) defines the range of values that decision variables can take.
By intuition, we see that problem (2) and problem (3) are mutually exclusive in terms of feasibility. Feasibility of problem (2) implies infeasibility of the problem (3) and vice versa. Problem (3) is feasible if objective_function(Problem (3))<<M. Feasibility of the problem (3) depends on total allowable excess space for the excess strategic inventory level. It is feasible if the total excess space allocated can accommodate strategic inventory reserves greater than or equal to the total service level loss over scenario set. A heuristic H1 is described next to efficiently solve the problem (3).
| H1: |
| Step 0: Compute , |
| Step 1: For a node , identify a scenario such that |
| Step 2: Compute . |
| Step 3: Allocate ; if |
| Step 4: . |
| Step 5: If then go to step 6 else repeat step 3 and step 4. |
| Step 6: Repeat step 1 to step 5 for all nodes. |
| Step 7: Repeat the step 0 to step 6 for all |
| Step 8: Compute |
| Step 9: Stop |
Proposition
Optimality gap of heuristics H1 is proportional to
Proof
represents the maximum service level loss of the demand node over disruption scenario . Hence an optimal solution will allocate no more than units (strategic inventory reserves) to ensure service level greater than or equal to 67% (herd immunity threshold for COVID-19). Therefore, optimality gap of H1 is proportional to. An exact algorithm must reallocate the strategic inventory reserves by ensuring that the condition is not violated. However, computational effort required for exact algorithm in a large supply chain network is prohibitively large. Efficiency of heuristic H1 can be evaluated by expression . Clearly, , if . In other words, efficiency of the heuristic depends upon the number of strategic inventory reserves units allocated at various nodes in comparison to the number of strategic inventory reserve units allocated by the optimal algorithm. Computational time comparison and efficiency comparison on 10 sample problem instances are given in Table 4 for illustrative purposes.
Table 4.
Performance of heuristic (H1).
| Problem instance | (%) | Computational time advantage (%) |
|---|---|---|
| 1 | 83.5 | 22.4 |
| 2 | 77.6 | 27.1 |
| 3 | 86.3 | 19.2 |
| 4 | 84.0 | 22.8 |
| 5 | 85.2 | 21.1 |
| 6 | 80.9 | 24.7 |
| 7 | 81.2 | 23.5 |
| 8 | 89.5 | 25.5 |
| 9 | 79.6 | 22.2 |
| 10 | 83.4 | 19.8 |
4. Illustrative case study on distribution of Japanese Encephalitis (JE) vaccine
In this section, we demonstrate the efficacy of our model in evaluating performance of IVSC. An instance of IVSC for distribution of Japanese Encephalitis vaccines is considered for this purpose. Japanese Encephalitis (JE) is a common mosquito borne viral encephalitis, mostly prevalent in south-east Asia due to its temperate climate. It mostly affects children and young adults causing them long term serious neurological morbidities like frequent tremors, paralysis, learning and behavioural problems, etc. (Vashishtha & Ramachandran, 2015). The mortality rate from the infection is reported to be 25%−30% across south-east Asia (Tiwari, Singh, Tiwari & Dhole, 2012). Though underreported, 67,000 children get infected and 15,000 die annually of JE (Hills et al., 2019). Underreporting of JE cases can be chiefly attributed to the fact that clinical diagnosis of the infection is very difficult. Only 1 in 300 cases develops the detectable clinical symptoms (Tiwari et al., 2012). Consequently, preventive measures like vaccination, proper sanitation, etc. are recognized as the most effective interventions for controlling the JE outbreak.
In India, JE vaccines were introduced into the IVSC schedule in the year 2006, after a significant outbreak of infection in many districts of eastern Uttar Pradesh and Bihar states, which affected 5737 children and caused 1344 deaths.7 Since 2006, Gorakhpur district, in the state of Uttar Pradesh, has been regarded as the epicentre of the JE outbreak in Northern India. According to some estimates, at least 50,000 children have died of the infection in Gorakhpur in the last four decades. Actual morbidity figures are expected to be much higher.
Gorakhpur district is located in eastern Uttar Pradesh at about 100 kilometers from Nepal border. It is one of the most flood vulnerable district in eastern Uttar Pradesh due to its unique location alongside the rivers Rapti and Ami. Any increase in water level of Ghaghara river blocks the flow of Rapti and Ami leading the flooding of nearby villages and towns. At least two flood incidents are recorded each year. Outbreak of the infection in the Gorakhpur occurs every year between the months of April and October due to irrigation patterns (Tiwari et al., 2012), and the ongoing rainy season which causes the river Rapti and Ami to flood. During this time of year, paddy fields are waterlogged and provide excellent breeding sites for mosquitoes. To contain the outbreak during this period, the government ramps up the vaccine supply to meet the increased service level requirements. However, supply side disruptions, due to the ongoing rainy season, prevents any significant improvement in the service level through an increased supply. The rainy season during this period causes frequent power cuts, reduced accessibility to rural areas by roads due to water clogging, flooding etc. These disruptions increase the supply lead time as discussed earlier. Further, frequent power cuts in cold storages during this period also reduce the shelf life of the vaccine from 18 months to only 2 weeks.8 Reduced shelf life coupled with frequent lead time disruptions result in huge wastage of vaccines, and poor vaccine coverage during peak months (April-October) in the district each year.
We consider three stages of IVSC (comprising of DVS, BVC, and PHC nodes) for our further analysis. The DVS node represents vaccine storage in the district of Gorakhpur. We have randomly selected five blocks within the Gorakhpur district (represented as BVC nodes in Fig. 1) namely Sardarnagar, Urwa, Belghat, Bansgaon, and Bhathat, and three PHC nodes under each BVC node. Selection of Gorakhpur district for our analysis is motivated by the fact that government's inability to inoculate children in or before peak season due to infrastructural deficiencies of IVSC, is one of the important reasons for not being able to eradicate this infection in this area. Therefore, if not addressed properly, these deficiencies will prevent the attainment of herd immunity targets for COVID-19.
4.1. Problem parameters
As stated earlier, demand in IVSC is forecasted. Initial demand forecasts are generated by the population estimates considering the net migration rate, and birth cohorts each year. Population growth is considered as 1% while mortality rate is assumed to be 25 per 1000 (Debellut et al., 2019). These forecasts are revised monthly by the PHC manager, according to their judgement on the net migration rate and demand in earlier months. In the peak months (April-October), order size is increased by additional 15%−20% to address the seasonality in demand. We accessed the records of the last two years on demand forecasts of all 15 PHC's (Table 2 ) and used our model to generate forecasts at higher echelon nodes. Due to seasonality of the demand, we consider the forecasting horizon as months (April-October). The total time period for which the inventory model is valid is months. Vaccine shelf life is further assumed to be days.
Table 3.
Model parameters representative values.
| Model parameter | DVS nodes | BVC nodes | PHC nodes |
|---|---|---|---|
| Inventory holding cost (including syringes) (Rupees/unit-period) | 4–5 | 7–9 | 10–12 |
| Ordering cost (Rupees/order) | 85–125 | 170–220 | 230–280 |
| Disruption lead time (days) | 2–3 | 4–5 | – |
| Disruption probability | 0.21–0.28 | 0.43–0.57 | – |
| Maximum order quantity (units/order) | 775–850 | 350–425 | 100–130 |
| Node processing lead time (days) | 1–2 | 0.25–0.75 | – |
| Service Time (days) | 3–5 | 2–4 | – |
| Inventory holding capacity (number of units) | 990–1050 | 450–600 | 100–350 |
| Enhanced inventory capacity at additional cost (Number of increased units) | 150–250 | 80–150 | 40–60 |
| Cost of additional inventory space (Rupees) | 2000 | 2500 | 3200 |
| Service level coefficient | |||
Table 2.
Demand forecast by PHC managers during the peak demand time (As per the records).
| M | Sadarnagar |
Urwa |
Belghat |
Bansgaon |
Bhathat |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | P1 | P2 | P3 | ||
| Year 2017 (April-October) | 1 | 142 | 155 | 120 | 166 | 176 | 130 | 179 | 156 | 180 | 128 | 123 | 107 | 117 | 107 | 113 |
| 2 | 157 | 107 | 118 | 162 | 168 | 132 | 103 | 117 | 114 | 100 | 152 | 164 | 165 | 134 | 179 | |
| 3 | 153 | 140 | 173 | 114 | 141 | 112 | 178 | 104 | 174 | 163 | 135 | 104 | 159 | 167 | 167 | |
| 4 | 153 | 111 | 129 | 113 | 152 | 102 | 154 | 133 | 157 | 120 | 137 | 156 | 125 | 138 | 121 | |
| 5 | 147 | 102 | 124 | 160 | 126 | 104 | 171 | 138 | 110 | 128 | 128 | 139 | 146 | 108 | 144 | |
| 6 | 117 | 155 | 173 | 106 | 142 | 153 | 176 | 167 | 114 | 136 | 114 | 179 | 159 | 166 | 106 | |
| 7 | 155 | 142 | 156 | 141 | 117 | 125 | 145 | 125 | 135 | 105 | 144 | 133 | 106 | 143 | 107 | |
| Year 2018 (April-October) | 1 | 115 | 159 | 121 | 102 | 120 | 116 | 165 | 165 | 147 | 100 | 118 | 154 | 135 | 172 | 157 |
| 2 | 154 | 133 | 152 | 100 | 109 | 157 | 103 | 129 | 134 | 145 | 103 | 125 | 166 | 152 | 121 | |
| 3 | 133 | 137 | 173 | 110 | 169 | 135 | 130 | 110 | 107 | 154 | 126 | 127 | 137 | 137 | 101 | |
| 4 | 144 | 114 | 158 | 150 | 168 | 129 | 115 | 128 | 179 | 119 | 100 | 155 | 135 | 134 | 148 | |
| 5 | 105 | 174 | 147 | 100 | 173 | 159 | 165 | 114 | 115 | 160 | 117 | 135 | 126 | 117 | 124 | |
| 6 | 115 | 105 | 146 | 155 | 122 | 148 | 165 | 154 | 127 | 164 | 105 | 129 | 108 | 157 | 146 | |
| 7 | 162 | 119 | 177 | 116 | 114 | 132 | 163 | 118 | 110 | 112 | 157 | 171 | 161 | 123 | 108 | |
M- Month corresponding to peak demand in two years (April-October).
P- PHC node under various BVC.
To limit the complexity of the problem, we consider only one disruption possibility at each node, characterized by a fixed disruption recovery time and associated probability value. Recovery time and associated probability values have been estimated through discussions with cold storage managers. A more accurate analysis can be carried out by assuming that disruption recovery time varies with probability according to geometric distribution as described by Warsing Jr, Wangwatcharakul and King (2013). Parameters of geometric distribution can be estimated using the moment generating method on the disruption data as explained by Mallick and Joshi (2018).
The representative values of other relevant parameters (as per the discussion with PHC, and BVC managers) is given in Table 4 . We vary the parameters within the range as described in Table 4 to generate 78 random feasible instances of the problem, out of which major disruption scenarios are identified in 50 instances. Service level of each problem instance is evaluated over entire forecasting horizon (). It must be noted that these problem instances (generated by varying the parameters within the range described in Table 4) are representative of an actual scenario. These problems are implemented on MATLAB and results are analysed to develop important managerial insights in the next section.
4.2. Data analysis and managerial insights
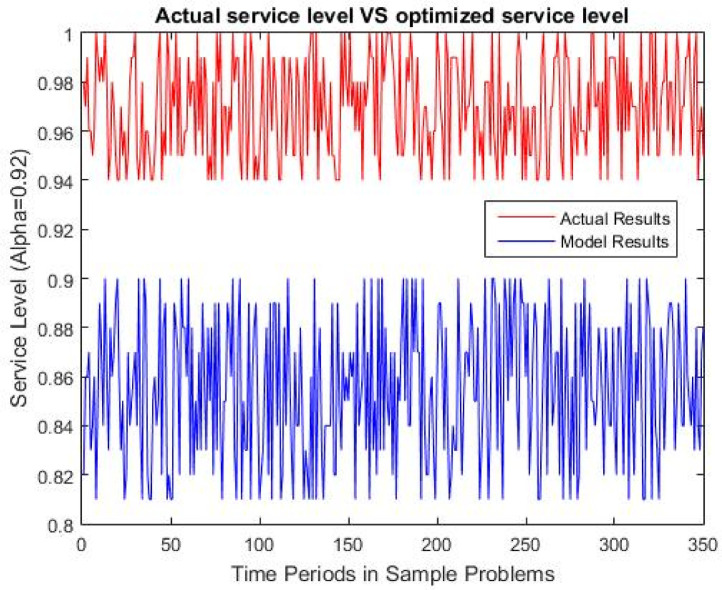
We first discuss the problem instances in which no critical disruption scenario was identified (problem (2) in Section 3.3 is not feasible for these problem instances). Disruptions (if encountered) are small in magnitude and the service level can be protected by increasing the order size within the permissible levels. From Fig. 3 (a, b) below, it is apparent that our multi echelon inventory model is effective in reducing the cost in IVSC under both conditions (disruption and no disruption scenarios). Under disruption possibilities however, the total inventory cost of our policy is slightly higher (Fig. 3b), due to the cost of carrying extra inventory (strategic inventory reserve) for protecting customer service level under disruptions. According to Fig. 4 , our model is effective in improving the service levels also. In Fig. 4, service level is evaluated for all 50 problem instances over entire forecasting horizon of 7 periods (). In other words, service level is evaluated over 350 (=50×7) time periods.
Fig. 3.
(a) and (b). Comparison of total inventory cost.
Fig. 4.
Service level comparison.
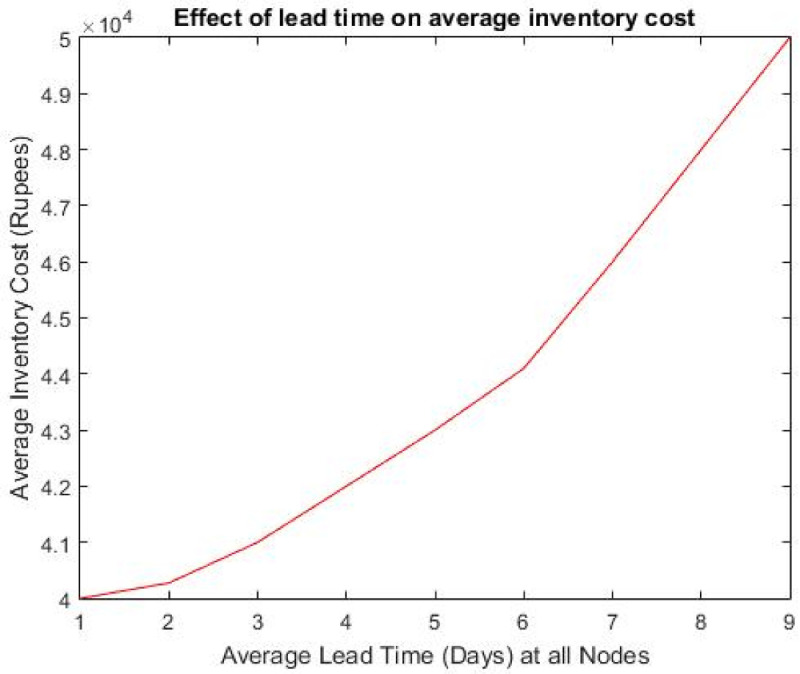
An in-depth understanding of model behaviour with respect to disruption intensity (measured as lead time increment), is essential for generating practical insights, that might be useful in addressing future COVID-19 related challenges. To understand the relationship better, we vary the disruption lead time and examine the trend of inventory size at various nodes. Our analysis shows that as we increase the lead time, inventory size at the lower echelon starts increasing. In Fig. 5 , high average inventory cost corresponds with larger inventory allocations at lower echelon nodes (PHC). Lower echelon nodes (PHC) are characterised by large inventory carrying costs. This result can be explained as follows. Large lead time increases the risk of vaccine wastage due to expiration. Hence, our model allocates the inventories at lower echelon nodes so that the total transit time does not violate the expiration time constraint. Consequently, it is seen that even without the realization of a major disruption scenarios, inventory cost increases rapidly as disruption recovery time increases. From our analysis on sample problems, it is seen that our model allocates all the strategic inventory reserve on PHC nodes for disruption scenarios characterised by probability greater than or equal 0.28, and disruption recovery time greater than or equal to 18% of service time. These disruption scenarios are termed as critical disruption scenarios, and nodes failing in them are termed as critical nodes. Entire allocation of strategic inventory reserves on PHC nodes can be interpreted as the failure of inventory hedging strategy.
Fig. 5.
Effect of disruption lead time on inventory cost`.
Large inventory allocations on PHC nodes is cost prohibitive and practically infeasible solution for the IVSC due to its skewed structure. Skewed structure of IVSC also restricts the reallocation of inventories from one PHC to other, during the demand disruption. Hence inventory hedging strategy fails if critical disruption scenarios are present. To protect the customer service level in these scenarios, increasing infrastructural resilience of the critical nodes is necessary. Increasing infrastructural resilience of the nodes may entail installation of better cold storage facilities, purchasing more quality transport vans, improving reliability of transport network, and skills of cold storage manager by training, etc., which is aimed at reducing the probability of occurrence of critical disruption scenarios. This is an interesting insight as it lets us identify exact conditions under which infrastructural investment to improve IVSC becomes necessary.
It must be noted that disruption parameters (especially the probability of disruption) are prone to misestimation. These parameters determine the size of strategic inventory reserve on nodes, which in turn enable us to classify a node as critical or non-critical. Robustness of the model in this sense is the ability to correctly identify critical nodes under the possibility of misestimation in the disruption parameters. To measure the robustness of the model, we vary the probability value, and disruption recovery time separately within the range of , and record the corresponding changes in the size of strategic inventory reserve on various nodes. Our numerical analysis suggest that the quantity of strategic inventory reserves is less sensitive to the variations in probability values of disruptions as compared to the variations in disruption recovery lead time. This can be attributed to our modelling approach in which we focus only on major disruption scenarios. As stated earlier, a major disruption scenario is one which satisfies the conditions stated in Section 3.3.1. Hence, overestimation and underestimation in the probability value of major disruption scenarios, and non-major disruption scenarios respectively, affect the quantity of strategic inventory reserves on PHC nodes for a very small range of values. Misestimation of probability values beyond this range does not cause strategic inventory level quantities to change. Robustness of our model, with respect to variation in probability values, increases its practical utility as estimating disruption probabilities in IVSC is very difficult.
Our forecasting model is valid if . Simply put, the total cumulative lead time along any path cannot be greater than the forecasting horizon. This condition may get violated during large epidemic breakouts, as forecasting horizon must be reduced to maintain the forecasting accuracy (Petropoulos, Makridakis, Assimakopoulos & Nikolopoulos, 2014). According to our data analysis, reduction in forecasting horizon from 7 months to 5 months, makes 69 out of 78 problem instances infeasible. Further, our data analysis also suggests that about 60%−70% of the useful life of the vaccine is already exhausted by the time the vaccine reaches PHC. The cumulative effect of these two factors may result in a major supply-demand mismatch and wastage due to expiration, while distributing the COVID-19 vaccine in the future. Hence, the Indian government must invest in developing better forecasting techniques (to increase the forecasting horizon) and transportation infrastructure (to reduce the extent of total useful life spent during transportation) for addressing the future challenges related to the distribution of the COVID-19 vaccine.
6. Theoretical contribution
An important theoretical contribution of this paper is the development of strategic inventory model for divergent supply chain. As mentioned earlier, constraint (34) in our model allocates strategic inventory quantities on the lower echelon nodes if a major disruption scenario is characterised by a failure of a higher echelon node. Hence, it is ensured that the movement of vaccines across IVSC is not disrupted. This would require an optimal algorithm to identify the disruption scenarios under which a node fails and update strategic inventory at all downstream nodes for each disruption scenario. Therefore, complexity of the optimal algorithm will depend on the number of supply chain nodes and the size of disruption scenario set. Hence, for an extensive supply chain like IVSC, an optimal algorithm will incur a huge computational time.
To reduce the computational time, we propose an efficient heuristic which starts allocation at the higher nodes and reallocates strategic inventory reserves only when downstream nodes fail under major disruption scenario. While developing this heuristic, we have exploited an important property of the IVSC that inventory carrying cost of downstream node is higher as compared to the inventory holding cost at upstream node, and failure of downstream node is less critical to service level than the failure of upstream node (due to divergent structure of IVSC). Our heuristic can be implemented to allocate strategic inventory reserves on any divergent supply chain with similar characteristics. For general extensive supply chains with divergent structure (without this property), evolutionary heuristics can be developed. Recent advances in literature on application of these methods on extensive supply chains can be referred for this purpose. For example, Khishtandar (2019) has developed chance constrained model for a biogas supply chain, and later proposed a hybrid Monte Carlo – genetic algorithm-based method to solve it. Similarly, Cheraghalipour, Paydar and Hajiaghaei-Keshteli (2019) has developed a bi-level mathematical model for rice supply chain, and later proposed a hybrid Taguchi-genetic algorithm-based method to solve it.
We have compared the performance of our heuristic, on randomly chosen 10 problem instances and solved them optimally and heuristically in MATLAB. Comparison results are shown in Table 4. It can be clearly seen for small number of sample problem instances, heuristic H1 renders a significant computational time advantage at the cost of smaller loss in efficiency.
7. Limitations and future developments
Demand for JE vaccine at PHC node is forecasted according to the factors like birth rate, infant mortality rate, etc. Since the objective of the Indian government is the complete eradication of the infection, ideally 100% service level is desired. In other words, demand for JE vaccine in a region is equal to the number of eligible children who have not been inoculated up till now. In contrast, objective of COVID-19 vaccine distribution is attainment of herd immunity which can be achieved by inoculating 67% of the population. Therefore, to make our analysis more representative for the COVID-19 vaccine distribution, we have used 67% as the desired service level instead of 100%. In other words, we evaluate the effects of infrastructural deficiencies on achieving herd immunity targets for COVID-19 infection.
However, certain limitations still persist which can be addressed to make the analysis more accurate for COVID-19 scenario. For instance, some parameters for the distribution of COVID-19 vaccine may not honour the representative values for the distribution of JE vaccine in our case study (ordering cost, shelf life, service time, maximum order quantity, may be different for JE and COVID-19 scenario). Hence, we recommend to analyse small section of IVSC by using COVID-19 specific parameters in our model to develop COVID-19 specific criteria for identifying nodes as critical or non-critical. In the absence of COVID-19 specific data, criteria developed for JE can be used heuristically to identify critical nodes in COVID-19 vaccine distribution scenario. Nodes identified as critical, must then be considered for infrastructural overhaul to ensure service level targets for achieving herd immunity.
In contrast with JE, COVID-19 is a contagious disease, so demand of the vaccine would depend upon other factors like reproduction number, transmission rate, etc. Since immunological memory of the human body from the infection is now estimated to be 8 months (Dan et al., 2021), efficient delivery schedules can be developed by prioritizing the inoculation in people who have never got infected or have recovered from the infection since more than 8 months. In this context, SIR and SIS models must be used to forecast demand at the PHC node for COVID-19. Demand forecast at the upstream nodes can later be calculated by our forecasting model as described in Section 3.1. In our case study, we have used factors like birth rate, infant mortality rate, etc. to forecast demand on the PHC node to illustrate the traditional forecasting as done by PHC manager in Indian Vaccine Supply Chain. It must be mentioned here that our modelling approach assumes demand forecast at the PHC nodes to be already given and hence there is no restriction on using any forecasting technique (SIS and SIR models) to forecast demand at the PHC node.
Footnotes
Sharma B.P. National Cold Chain Assessment, 2015. http://www.nccmis.org/document/UNICEF_Cold%20Chain%20Assessment%20Book2014.pdf.
Dr Bhrigu Kapuria. Immunization Supply Chain in India. https://www.technet-21.org/images/TC2015/10_Country_Innovations_India_Bhrigu_Kapuri.pdf.
Jhalani et al. (2018). Techno-Economic Assessment of Electronic Vaccine Intelligence Network. https://nhm.gov.in/New_Updates_2018/NHM_Components/Immunization/Guildelines_for_immunization/eVIN_Assessment_Report.pdf.
is an unbiased estimator of demand in the period .
World Health Organization. Outbreak Encephalitis 2005: Cases of Japanese Encephalitis in Gorakhpur, Uttar Pradesh, India. 2005. Core Programme Clusters. Communicable Diseases and Disease Surveillance. 21 October 2005.
Tsai (1990). Japanese Encephalitis Vaccines. https://wonder.cdc.gov/wonder/prevguid/p0000008/p0000008.asp
References
- Altay N., Green III W.G. OR/MS research in disaster operations management. European Journal of Operational Research. 2006;175(1):475–493. [Google Scholar]
- Babai M.Z., Syntetos A.A., Dallery Y., Nikolopoulos K. Dynamic re-order point inventory control with lead-time uncertainty: Analysis and empirical investigation. International Journal of Production Research. 2009;47(9):2461–2483. [Google Scholar]
- Begen M.A., Pun H., Yan X. Supply and demand uncertainty reduction efforts and cost comparison. International Journal of Production Economics. 2016;180:125–134. [Google Scholar]
- Ben-Ammar O., Dolgui A., Wu D.D. Planned lead times optimization for multi-level assembly systems under uncertainties. Omega. 2018;78:39–56. [Google Scholar]
- Bhuiyan T.H., Medal H.R., Harun S. A Stochastic Programming Model with Endogenous and Exogenous Uncertainty for Reliable Network Design Under Random Disruption. European Journal of Operational Research. 2020 doi: 10.1016/j.ejor.2020.02.016. [DOI] [Google Scholar]
- Cannella S., Dominguez R., Framinan J.M. Inventory record inaccuracy–The impact of structural complexity and lead time variability. Omega. 2017;68:123–138. [Google Scholar]
- Chakraborty N., Joardar G.K. Assessment of vaccine wastage in an immunization clinic of a tertiary care hospital, Kolkata, West Bengal. International Journal of Community Medicine and Public Health. 2019;6(11):4959–4963. [Google Scholar]
- Cheraghalipour A., Paydar M.M., Hajiaghaei-Keshteli M. Designing and solving a bi-level model for rice supply chain using the evolutionary algorithms. Computers and Electronics in Agriculture. 2019;162:651–668. [Google Scholar]
- Chick S.E., Mamani H., Simchi-Levi D. Supply chain coordination and influenza vaccination. Operations Research. 2008;56(6):1493–1506. [Google Scholar]
- Dan J.M., Mateus J., Kato Y., Hastie K.M., Yu E.D., Faliti C.E., et al. Immunological memory to SARS-CoV-2 assessed for up to 8 months after infection. Science (New York, N.Y.) 2021 doi: 10.1126/science.abf4063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Treville S., Bicer I., Chavez-Demoulin V., Hagspiel V., Schürhoff N., Tasserit C., et al. Valuing lead time. Journal of Operations Management. 2014;32(6):337–346. [Google Scholar]
- Debellut F., Hendrix N., Pitzer V.E., Neuzil K.M., Constenla D., Bar-Zeev N., et al. Forecasting demand for the typhoid conjugate vaccine in low-and middle-income countries. Clinical Infectious Diseases. 2019;68(2):154–160. doi: 10.1093/cid/ciy1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dominguez R., Framinan J.M., Cannella S. Serial vs. divergent supply chain networks: A comparative analysis of the bullwhip effect. International Journal of Production Research. 2014;52(7):2194–2210. [Google Scholar]
- Duijzer L.E., van Jaarsveld W., Dekker R. Literature review: The vaccine supply chain. European Journal of Operational Research. 2018;268(1):174–192. [Google Scholar]
- Eskandarzadeh S., Eshghi K., Bahramgiri M. Risk shaping in production planning problem with pricing under random yield. European Journal of Operational Research. 2016;253(1):108–120. [Google Scholar]
- Federgruen A., Yang N. Competition under generalized attraction models: Applications to quality competition under yield uncertainty. Management Science. 2009;55(12):2028–2043. [Google Scholar]
- Garcia C.A., Ibeas A., Herrera J., Vilanova R. Inventory control for the supply chain: An adaptive control approach based on the identification of the lead-time. Omega. 2012;40(3):314–327. [Google Scholar]
- Granada-Echeverri M., Toro E., Santa J. A mixed integer linear programming formulation for the vehicle routing problem with backhauls. International Journal of Industrial Engineering Computations. 2019;10(2):295–308. [Google Scholar]
- Graves S.C., Willems S.P. Optimizing strategic safety stock placement in supply chains. Manufacturing & Service Operations Management. 2000;2(1):68–83. [Google Scholar]
- Gray J.V., Roth A.V., Leiblein M.J. Quality risk in offshore manufacturing: Evidence from the pharmaceutical industry. Journal of Operations Management. 2011;29(7–8):737–752. [Google Scholar]
- Gupta S., Starr M.K., Farahani R.Z., Matinrad N. Vol. 25. Production and Operations Management; 2016. pp. 1611–1637. (Disaster management from a POM perspective: Mapping a new domain). [Google Scholar]
- Haeupler B., Kavitha T., Mathew R., Sen S., Tarjan R.E. Incremental cycle detection, topological ordering, and strong component maintenance. ACM Transactions on Algorithms (TALG) 2012;8(1):1–33. [Google Scholar]
- Hills S.L., Walter E.B., Atmar R.L., Fischer M., Group A.J.E.V.W., Group A.J.E.V.W., et al. Japanese encephalitis vaccine: Recommendations of the advisory committee on immunization practices. MMWR Recommendations and Reports. 2019;68(2):1–33. doi: 10.15585/mmwr.rr6802a1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transportation Research Part E: Logistics and Transportation Review. 2020;136 doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D., Dolgui A., Sokolov B., Ivanova M. Literature review on disruption recovery in the supply chain. International Journal of Production Research. 2017;55(20):6158–6174. [Google Scholar]
- Jalali S., Seifbarghy M., Niaki S.T.A. A risk-averse location-protection problem under intentional facility disruptions: A modified hybrid decomposition algorithm. Transportation Research Part E: Logistics and Transportation Review. 2018;114:196–219. [Google Scholar]
- Kazaz B., Webster S., Yadav P. Vol. 25. Production and Operations Management; 2016. pp. 1576–1600. (Interventions for an artemisinin-based malaria medicine supply chain). [Google Scholar]
- Khishtandar S. Simulation based evolutionary algorithms for fuzzy chance-constrained biogas supply chain design. Applied Energy. 2019;236:183–195. [Google Scholar]
- Konstantaras I., Skouri K., Lagodimos A.G. EOQ with independent endogenous supply disruptions. Omega. 2019;83:96–106. [Google Scholar]
- Lala K.R., & Vaccine Viral Monitor Thermostability of Vaccines Mrudula K. Lala. Indian Pediatrics. 2003;40:311–319. [PubMed] [Google Scholar]
- Lee S.M., Ebrahimpour M. Just-in-time production system: Some requirements for implementation. International Journal of Operations & Production Management. 1984;4(4):3–15. [Google Scholar]
- Li Y., Chen K., Collignon S., Ivanov D. Ripple effect in the supply chain network: Forward and backward disruption propagation, network health and firm vulnerability. European Journal of Operational Research. 2020 doi: 10.1016/j.ejor.2020.09.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallick A., Joshi R. Parameter estimation and application of generalized inflated geometric distribution. Journal of Statistical Theory and Applications. 2018;17(3):491–519. [Google Scholar]
- Metcalf C.J.E., Ferrari M., Graham A.L., Grenfell B.T. Understanding herd immunity. Trends in immunology. 2015;36(12):753–755. doi: 10.1016/j.it.2015.10.004. [DOI] [PubMed] [Google Scholar]
- Paquay C., Crama Y., Pironet T. Recovery management for a dial-a-ride system with real-time disruptions. European Journal of Operational Research. 2020;280(3):953–969. [Google Scholar]
- Park H., Kim H. A study on herd immunity of COVID-19 in South Korea: Using a stochastic economic-epidemiological model. Environmental and Resource Economics. 2020;76:665–670. doi: 10.1007/s10640-020-00439-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul S.K., Sarker R., Essam D. A disruption recovery plan in a three-stage production-inventory system. Computers & Operations Research. 2015;57:60–72. [Google Scholar]
- Paz J., Granada-Echeverri M., Escobar J. The multi-depot electric vehicle location routing problem with time windows. International Journal of Industrial Engineering Computations. 2018;9(1):123–136. [Google Scholar]
- Petropoulos F., Makridakis S., Assimakopoulos V., Nikolopoulos K. ‘Horses for Courses’ in demand forecasting. European Journal of Operational Research. 2014;237(1):152–163. [Google Scholar]
- Prak D., Teunter R., Syntetos A. On the calculation of safety stocks when demand is forecasted. European Journal of Operational Research. 2017;256(2):454–461. [Google Scholar]
- Randolph H.E., Barreiro L.B. Herd Immunity: Understanding COVID-19. Immunity. 2020;52(5):737–741. doi: 10.1016/j.immuni.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawik T. On the fair optimization of cost and customer service level in a supply chain under disruption risks. Omega. 2015;53:58–66. [Google Scholar]
- Schmitt A.J., Sun S.A., Snyder L.V., Shen Z.J.M. Centralization versus decentralization: Risk pooling, risk diversification, and supply chain disruptions. Omega. 2015;52:201–212. [Google Scholar]
- Schmitt A.J. Strategies for customer service level protection under multi-echelon supply chain disruption risk. Transportation Research Part B: Methodological. 2011;45(8):1266–1283. [Google Scholar]
- Schmitt T.G., Kumar S., Stecke K.E., Glover F.W., Ehlen M.A. Mitigating disruptions in a multi-echelon supply chain using adaptive ordering. Omega. 2017;68:185–198. [Google Scholar]
- Schoenmeyr T., Graves S.C. Strategic safety stocks in supply chains with evolving forecasts. Manufacturing & Service Operations Management. 2009;11(4):657–673. [Google Scholar]
- Shao X.F. Production disruption, compensation, and transshipment policies. Omega. 2018;74:37–49. [Google Scholar]
- Sharma A., Kaplan W.A., Chokshi M., Zodpey S.P. Role of the private sector in vaccination service delivery in India: Evidence from private-sector vaccine sales data, 2009–12. Health Policy and Planning. 2016;31(7):884–896. doi: 10.1093/heapol/czw008. [DOI] [PubMed] [Google Scholar]
- Sinha P., Kumar S., Prakash S. Measuring and mitigating the effects of cost disturbance propagation in multi-echelon apparel supply chains. European Journal of Operational Research. 2020;282(1):148–160. [Google Scholar]
- Teunter R.H., Flapper S.D. A comparison of bottling alternatives in the pharmaceutical industry. Journal of Operations Management. 2006;24(3):215–234. [Google Scholar]
- Tiwari S., Singh R.K., Tiwari R., Dhole T.N. Japanese encephalitis: A review of the Indian perspective. The Brazilian Journal of Infectious Diseases. 2012;16(6):564–573. doi: 10.1016/j.bjid.2012.10.004. [DOI] [PubMed] [Google Scholar]
- Tomlin B. Impact of supply learning when suppliers are unreliable. Manufacturing & Service Operations Management. 2009;11(2):192–209. [Google Scholar]
- Vashishtha V.M., Ramachandran V.G. Vaccination policy for Japanese encephalitis in India: Tread with caution! Indian. Paediatrics. 2015;52(10):837–839. doi: 10.1007/s13312-015-0728-5. [DOI] [PubMed] [Google Scholar]
- Warsing Jr D.P., Wangwatcharakul W., King R.E. Computing optimal base-stock levels for an inventory system with imperfect supply. Computers & Operations Research. 2013;40(11):2786–2800. [Google Scholar]
- Wichapa N., Khokhajaikiat P. Solving a multi-objective location routing problem for infectious waste disposal using hybrid goal programming and hybrid genetic algorithm. International Journal of Industrial Engineering Computations. 2018;9(1):75–98. [Google Scholar]
- Zahiri B., Zhuang J., Mohammadi M. Toward an integrated sustainable-resilient supply chain: A pharmaceutical case study. Transportation Research Part E: Logistics and Transportation Review. 2017;103:109–142. [Google Scholar]
- Zhang Y., Snyder L.V., Ralphs T.K., Xue Z. The competitive facility location problem under disruption risks. Transportation Research Part E: Logistics and Transportation Review. 2016;93:453–473. [Google Scholar]