Frequency of theta rhythm is controlled by acceleration, but not speed, in running rats

Summary

The theta rhythm organizes neural activity across hippocampus and entorhinal cortex. A role for theta oscillations in spatial navigation is supported by half a century of research reporting that theta frequency encodes running speed linearly so that displacement can be estimated through theta frequency integration. We show that this relationship is an artifact caused by the fact that the speed of freely moving animals could not be systematically disentangled from acceleration. Using an experimental procedure that clamps running speed at pre-set values, we find that the theta frequency of local field potentials and spike activity is linearly related to positive acceleration, but not negative acceleration or speed. The modulation by positive-only acceleration makes rhythmic activity at theta frequency unfit as a code to compute displacement or any other kinematic variable. Temporally precise variations in theta frequency may instead serve as a mechanism for speeding up entorhinal-hippocampal computations during accelerated movement.

Highlights

• •Entorhinal-hippocampal theta frequency is not modulated by speed
• •Theta frequency is linearly related to positive, but not negative, acceleration
• •Rhythmic spiking modulation by acceleration is expressed across functional cell types
• •Slow decay of theta frequency after acceleration creates spurious speed correlation

Kropff et al. find that the frequency of the theta rhythm, one of the most prominent oscillations in the mammalian brain, does not vary with running speed as previously thought. Instead, it responds with high temporal precision to positive (but not negative) acceleration.

Introduction

Local field potential (LFP) oscillations provide clues to understanding the dynamics of large populations of neurons. In the hippocampus and associated areas of the rodent brain, one of the most prominent LFP oscillations occurs in the theta frequency band, between 6 and 12 Hz (Buzsáki et al., 1983; Buzsáki and Moser, 2013; Colgin, 2013; Green and Arduini, 1954; Hasselmo and Stern, 2014; Jung and Kornmüller, 1938; Vanderwolf, 1969). Theta oscillations, which are especially robust when animals are actively navigating, are thought to reflect synchronization across neural populations. They are believed to result from the interplay between a driving force originating in the medial septum and acting as an external pattern generator, and the internal dynamics provided by local networks tuned to resonate inside this frequency band (Buzsáki, 2002; Colgin, 2013; Petsche et al., 1962).

Because of its salience in the hippocampus, the theta rhythm has long been thought to be essential for memory and navigation (Buzsáki and Moser, 2013). In agreement with this, lesion or inactivation of the medial septum in rats causes both suppression of hippocampal theta oscillations and impairment in a number of spatial memory tasks (Brioni et al., 1990; Leutgeb and Mizumori, 1999; Mizumori et al., 1990; Winson, 1978), as well as loss of the characteristic hexagonal firing pattern of entorhinal grid cells (Brandon et al., 2011; Koenig et al., 2011). In navigating rodents, evidence has pointed to a relationship between theta oscillations and moment-to-moment changes in the animal’s locomotion (Buzsáki et al., 1983). The amplitude or power of theta oscillations has been associated with kinematic variables such as the running speed (Whishaw and Vanderwolf, 1973) and acceleration (Long et al., 2014). Similarly, decades of evidence has reported a strong linear relationship between the frequency of theta oscillations and running speed, potentially enabling distance of movement to be read out by integration of theta frequency (Bland and Vanderwolf, 1972; Gupta et al., 2012; Hinman et al., 2011, 2016; Jeewajee et al., 2008; McFarland et al., 1975; Winter et al., 2015). Although theta amplitude is a local variable, in the sense that it shows strong variations across neighboring recording sites in the hippocampus (Montgomery et al., 2009), theta frequency is strikingly stable between neighboring sites, across hippocampal subfields, and along the dorso-ventral axis of the hippocampus (Patel et al., 2012), as expected from a wave traveling in an unpartitioned medium (Lubenov and Siapas, 2009). This points to theta frequency as a global variable and an important element of the circuit implementation of theta oscillations.

Recording LFP and single-cell activity in the entorhinal cortex and hippocampus in behaving rats, we sought to determine how theta frequency varies with the kinetics of behavior. In the majority of past studies where a linear relationship between theta frequency and running speed was reported, the frequency of theta oscillations was studied under conditions in which speed and acceleration changed simultaneously (Bland and Vanderwolf, 1972; Gupta et al., 2012; Hinman et al., 2011, 2016; Jeewajee et al., 2008; McFarland et al., 1975; Winter et al., 2015). This can lead to conflation of the relationship of theta to the two variables. During spontaneous behavior, rats exhibit a concatenation of brief speed peaks, each triggered by a positive acceleration peak and succeeded by a negative acceleration trough, often all within less than a second. Because changes in theta frequency during spontaneous speed peaks could reflect changes in either variable, we recorded theta activity in a bottomless car task (Kropff et al., 2015), in which the speed profile of rats running along a linear track can be decided by the experimenter. Speed and acceleration were disentangled by training rats to run for several seconds at constant speed, with acceleration close to zero, and with pre-determined acceleration or deceleration events between successive constant-speed segments. Data within uniform motion segments with zero acceleration were used to study the role of speed in modulating theta frequency, while the role of acceleration was assessed from the temporally precise and repeatable transitions between speed levels.

Results

Theta frequency is linearly related to positive acceleration and not modulated by negative acceleration or speed

In order to disentangle the contribution of speed and acceleration to modulation of theta frequency, we trained rats to run within a rat-sized computer-driven frame that moves along a 4-m linear track at an experimenter-controlled speed (Figure 1A) (Kropff et al., 2015). Because this “bottomless car” has no floor, rats need to actively run following the pre-set speed profile to reach the end of the track, where they get a chocolate cereal reward. Speed was kept constant within segments of the track so that accelerations only took place at transitions between segments with different speed. LFP and single unit activity were recorded from the medial entorhinal cortex (MEC) and the hippocampus during performance of this task. Data were also collected from these regions during free foraging sessions in a 1-m wide square enclosure. In both tasks, instantaneous speed and acceleration were estimated from the position tracking signal, while instantaneous theta frequency was obtained from the Hilbert transform of the band-passed LFP (STAR methods). Given that theta frequency is not a local variable (Lubenov and Siapas, 2009; Montgomery et al., 2009; Patel et al., 2012), data from different MEC layers or different hippocampal subfields were pooled for all analyses.

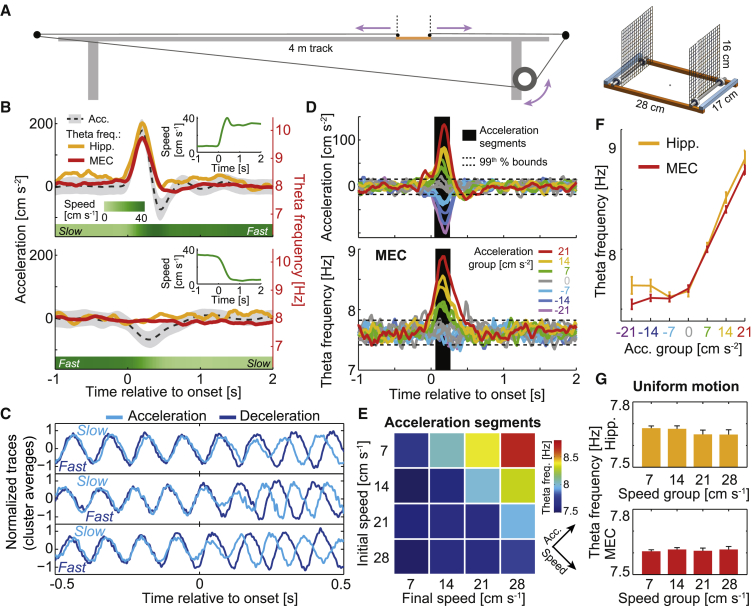
Figure 1.

Theta frequency during isolated acceleration events correlates with positive acceleration, but not with negative acceleration or speed

(A) Left: scheme of the bottomless car running along a 4-m linear track and pulled by a motor. Right: detail showing the minimalistic design of the bottomless car.

(B) Instantaneous acceleration (left axes, mean: black dashed line, SD: gray area) and theta frequency (right axes, hippocampus: orange, MEC: red) averaged over 544 repetitions of an accelerating (top) or decelerating (bottom) speed step (rat 14,570). Instantaneous speed is shown underneath in shades of green (horizontal bars; transitions between 6 cm/s and 36 cm/s) and in insets at the top right.

(C) Examples of 1-s long EEG traces cut around the acceleration (light blue) or deceleration (dark blue) onsets, averaged over >20 similar repetitions and paired by similarity (high Pearson correlation) during the first half of the plot (one pair of average examples per row).

(D) Mean acceleration (top) and MEC theta frequency (bottom) for all possible speed steps obtained from pseudo-randomly alternating between four speeds in a four-speed protocol (7, 14, 21, and 28 cm s⁻¹; color code indicates acceleration group independently of speed). Dashed lines indicate 1^st and 99^th percentiles of the data during uniform motion. Black area: acceleration segment (60–260 ms after onset) used for quantification.

(E) MEC theta frequency (color coded) averaged across acceleration segments for the 16 curves in (D), arranged according to initial and final speed. Arrows indicate the direction of diagonals along which mean speed and acceleration increase.

(F) MEC (red) and hippocampal (orange) theta frequency as in (E) but pooling together all events belonging to the same acceleration group (mean ± SEM).

(G) Theta frequency during uniform motion at each of the four speeds for hippocampus (Hipp.) and MEC (mean ± SEM).

First, 3 rats were trained to run at a high speed on one half of the car track and at a low speed on the other half, with sudden transitions between the two levels (two-speed step protocol). These transitions, lasting around 500 ms, represented isolated acceleration episodes (Figure 1B for transitions between 6 cm s⁻¹ and 36 cm s⁻¹, averaged over 544 repetitions; Figure S1A for transitions with smaller speed steps; transitions from resting state to running are not shown or analyzed in order to exclude potential effects related to states of arousal, although these were qualitatively similar to transitions between uniform motion segments). Positive acceleration peaks, surrounded by periods of slow and fast uniform motion with near-zero acceleration, were mirrored by theta-frequency peaks with largely similar dynamics, in both hippocampus and MEC (Figure 1B, top). The similarity in time course was particularly precise during the rising phase of the acceleration peak, whereas the decay was slightly slower for theta frequency than acceleration (Figures S1A–S1D). In striking contrast, opposite negative acceleration troughs, during transitions from fast to slow running speeds, had no influence on theta frequency (Figure 1B, bottom), nor did running at different constant speeds before and after each acceleration event (Figure 1B, t < 0 s or t > 1 s). To rule out the possibility that the relationship between theta frequency and acceleration was an artifact related to the method used to estimate instantaneous theta frequency, we studied 1-s raw LFP windows cut around the onset of each event, grouped by similarity and averaged (STAR methods). Faster oscillations during positive acceleration were directly observable from these group averages (Figures 1C and S1E). A similar enhancement of theta frequency was observed at the level of individual acceleration episodes, with minimal variation in time course from episode to episode (Figure S1F). The effect was also observable in average spectrograms based on the fast Fourier transform (Figure S1G).

To determine whether theta frequency increases linearly with acceleration, we next analyzed acceleration segments in a protocol with four speed levels (8 rats, 174 sessions). Speed was pseudo-randomly alternated between 7, 14, 21, and 28 cm s⁻¹ to produce 16 possible step-like transitions, grouped in 7 levels of mean acceleration (0, ±7, ±14, and ±21 cm s⁻²) (Figure 1D; see STAR methods for full description of the protocol). As expected from the two-speed experiment, theta frequency in MEC was consistently above the 99^th percentile of the uniform motion distribution only during positive acceleration events. Entorhinal theta frequency, averaged between 60 and 260 ms after the onset of each event (black area), correlated significantly with acceleration level across the pool of all events (7 levels of acceleration; Pearson correlation: r = 0.31, two-tailed t test of H₀: r = 0, t(8,026) = 29, p: 10⁻¹⁷⁵) (Figures 1E, 1F, and S2). This correlation was significant for positive, but not negative, acceleration events considered separately (respective Pearson correlations: r = 0.24, t(3,387) = 14.6, p: 10⁻⁴⁶ and r = 0.01, t(3,331) = 0.8, p: 0.42). A regression analysis testing for a non-linear dependence on acceleration including up to cubic polynomials revealed that the dependence of theta frequency on acceleration (≥0 cm s⁻²) was linear (H₀: no linear contribution, t(4,691) = 3.2; p: 0.001), with no significant contribution of higher order terms (H₀: no quadratic contribution, t(4,691) = 0.08; p: 0.94; H₀: no cubic contribution, t(4,691) = −0.07; p: 0.94). A similar correlation between theta frequency and positive, but not negative, acceleration was obtained for LFP in the hippocampus (91 sessions) (Figure S2). Theta frequency was not modulated by speed during acceleration events (MEC: r = 0.01, t(8,026) = 1.0, p: 0.33; hippocampus: r = 0.00, t(3,662) = 0.0, p: 0.84) or during uniform motion segments (MEC: r = 0.02, t(7,909) = 1.7, p: 0.10; hippocampus: r = −0.03, t(3,523) = −1.5, p: 0.13) (Figure 1G).

Modulation by acceleration is similarly present in rhythmic spiking activity of neurons

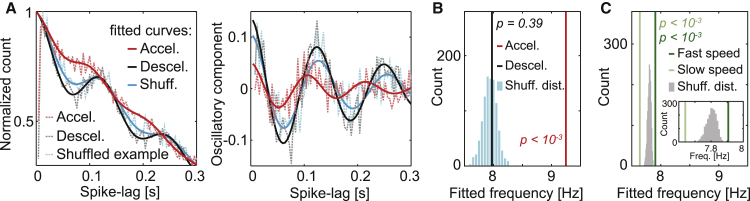
We next asked whether the linear increase in theta frequency with positive acceleration was present not only in LFP signals but also in the rhythmic spiking activity of individual neurons. We first examined spike-lag histograms (Climer et al., 2015) of the cumulative activity of 167 MEC neurons recorded in the two-speed step protocol (Figure 1B) and constructed exclusively with data from windows of 500 ms after each acceleration or deceleration onset (Figure 2A; window size optimized for spike-lag analysis). We fitted each curve with a decaying oscillatory function, obtaining intrinsic firing frequency within the theta band as one of the fitting parameters (Figure S2D). We also shuffled the windows 1,000 times (see example in Figure 2A) so they would randomly fall into slow or fast uniform motion periods with equal probability. Fitted intrinsic frequency was not different from the shuffled distribution during deceleration episodes (Figure 2B; deceleration, black line: 7.97 Hz, right-tail p: 0.39 by comparison with 1,000 shuffles) but increased significantly during positive acceleration episodes (red line: 9.25 Hz, p < 0.001). Similar results were obtained for hippocampal neurons (Figure S2E).

Figure 2.

Intrinsic firing frequency is strongly modulated by positive acceleration and weakly modulated by speed

(A) Left: normalized population spike-lag histograms (dashed lines) showing pooled data from 167 MEC neurons recorded in sessions contributing to Figure 1B during events of acceleration (red) or deceleration (black), together with a shuffled example (blue). Fits are shown in solid lines (same color code). Right: similar plot for the oscillatory component alone (i.e., subtracting the fitted decay term; Figure S2D). Note that the red curve exhibits lower theta modulation (wider range of frequencies) and a shift toward zero, suggesting a transient increase in frequency similar to the one observed in Figure 1B for LFP.

(B) Quantification of the intrinsic theta frequency obtained from fits in (A) for the pooled activity of all 167 cells (same color code). Significance p values obtained from direct comparison with the shuffled distribution (light blue; 1,000 shuffles) are indicated.

(C) As (B) but dividing data into windows of fast (dark green) and slow (light green) uniform motion for the same cells and sessions. The distribution obtained for 1,000 shuffles of speed tags (gray bars) falls entirely inside the segment delimited by the slow and fast intrinsic frequencies, indicating that, although small, the modulation by speed is significant (p < 0.001). Inset: same data zooming over the relevant range of frequencies.

When applying these analyses to uniform motion episodes we found that, unlike LFP, intrinsic theta frequency exhibited a small but significant modulation by speed (Figure 2C; fast: 7.91 Hz, slow: 7.64 Hz, respectively higher and lower than any values for 1,000 shuffles of speed tags, p < 0.001). The modulation by speed was only one-fifth in size of the modulation by acceleration for the same neurons in the same experimental sessions (0.27 Hz difference between speed groups in Figure 2C versus 1.28 Hz difference between acceleration groups in Figure 2B). Similar analyses applied to data from the four-speed step protocol (Figure S3) and the open field (Figure S4) showed that the speed modulation of rhythmic spiking activity was consistent with theta phase precession: It was restricted to a subset of cell types, absent in grid cells that did not exhibit phase precession, and for the pool of all grid cells, 98% of the variance of intrinsic firing period across speed bins was explained by a change in spiking theta phase. Together, these results suggest that positive acceleration strongly modulates the frequency of rhythmic spiking in the theta band, whereas spatial coding, through phase precession, adds an independent and rather mild source of modulation by speed.

Acceleration modulates theta frequency also during spontaneous running in two-dimensional environments

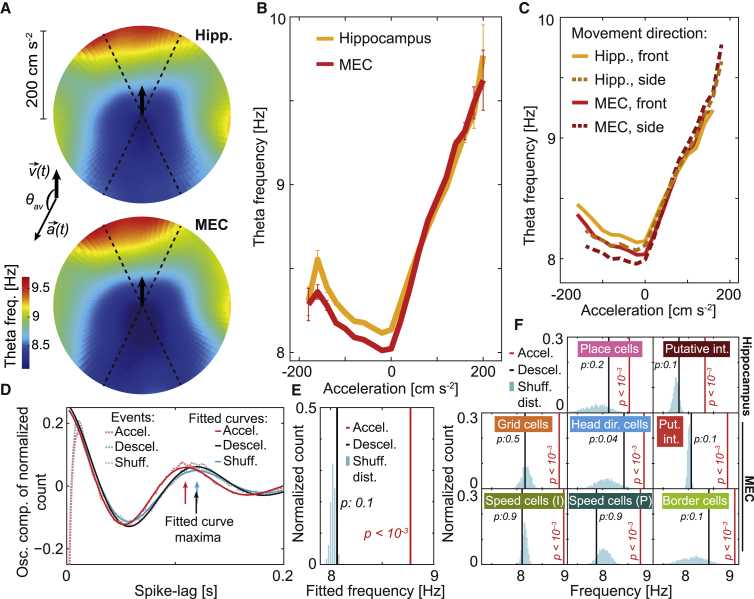
To rule out the possibility that the effects of acceleration reflect exclusive features of the bottomless-car procedure, we next determined the relationship between theta frequency and instantaneous acceleration in pooled data from 17 rats foraging freely in a 1-m wide square enclosure. Unlike for the car data, where stereotypical behavior allowed for averaging over many identical trials, the spontaneous open field data were smoothed along the temporal domain in order to obtain reliable one-shot instantaneous estimations of speed, acceleration, and theta frequency, whereas episodes of resting, grooming, and other non-navigational behaviors were removed (Figure S5; STAR methods). Because velocity and acceleration are vectors with direction and magnitude in the 2D condition, we plotted theta frequency as a function of the acceleration vector in polar coordinates, where the radial axis corresponds to the acceleration magnitude a and the angular axis to its direction relative to that of the velocity vector (θ_av) (Figure 3A; north corresponds to θ_av = 0°). Acceleration describes all changes in the velocity vector, both in its magnitude or its direction. Because we were specifically interested in variations in the magnitude (speeding up or slowing down), we defined the linear acceleration as a^∗sign(cos(θ_av)) only for timestamps in which cos(θ_av) was either >0.9 (positive acceleration; north) or <−0.9 (negative acceleration; south), and used this definition for all analyses in the 2D open-field condition.

Figure 3.

Theta frequency is linearly related to positive acceleration during free foraging in an open field

(A) Polar color maps of hippocampal (top) and entorhinal (bottom) theta frequency as a function of the acceleration vector $\overrightarrow{a}$, plotted relative to a north-pointing velocity vector $\overrightarrow{v}$ (schematically represented by a black arrow). Dashed lines limit the regions where the sign of acceleration is defined as positive (north) or negative (south).

(B) Theta frequency (mean ± SEM) as a function of linear acceleration in the hippocampus (orange) and MEC (red).

(C) As (B) but discriminating frontward (solid) and sideward (dashed) movements (cutoff: 45° relative to the head direction; error bars omitted for visualization purposes).

(D) As in Figure 2A, oscillatory part of the normalized population spike-lag histograms (dashed lines) and corresponding fits (solid lines) for the pooled activity of 2,497 cells recorded in the open field. Shown are a shuffled example (blue) and episodes of high (>50 cm s⁻²) positive (red) or negative (black) acceleration. Arrows indicate positions of the maxima of each fitted curve; note red arrow at a shorter time interval.

(E) As in Figure 2B, fitted theta frequency for positive (red) and negative (black) acceleration, together with the distribution of values for 1,000 shuffles (cyan; p values indicated).

(F) As in (E) but grouping the data by functional cell type.

When we plotted LFP theta frequency as a function of vector (Figure 3A) or linear (Figure 3B) acceleration in the open field, an asymmetrical relationship similar to the one obtained in the car experiments (Figure 1F) was observed. This occurred irrespective of whether movements were parallel or perpendicular to the head direction (Figure 3C). However, in contrast with results from the bottomless car, a small increase in theta frequency for negative acceleration was also observed. This effect is related to the slow decaying dynamics of theta frequency (Figure S1) and will be analyzed below.

To determine whether acceleration modulated also the rhythmicity of spiking in individual neurons during spontaneous behavior, we performed analyses similar to those used for the car data (Figures 2A and 2B) but selecting windows of high positive or negative linear acceleration (>50 cm s⁻²; variable window length, see STAR methods). We found a substantial increase in intrinsic frequency relative to shuffled data (1,000 shuffles of window timestamps) during positive acceleration (8.77 Hz versus a shuffle mean of 8.02 Hz, right-tail p < 0.001 obtained by direct comparison with the shuffled distribution), but not when acceleration was negative (8.06 Hz versus 8.03 Hz, p: 0.1) (Figures 3D and 3E). Similar observations were made when entorhinal and hippocampal functional cell types—grid cells, head direction cells, speed cells, border cells, place cells, and putative interneurons—were analyzed separately (Figure 3F; positive acceleration range: 8.33–8.93 Hz, p against shuffled window timestamps <0.001 for all functional cell types; negative acceleration range: 7.81–8.42 Hz, p > 0.04 for all cell types, Bonferroni adjusted alpha: 0.05/8 = 0.006).

Acceleration-related theta frequency changes persist under conditions that compromise spatial coding in grid cells

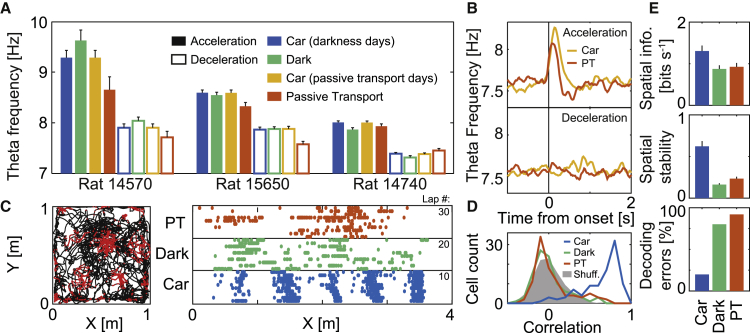
In a final set of experiments, we explored whether modulation of LFP theta frequency by acceleration depends on specific self-motion feedback signals. In these experiments, rats ran inside the bottomless car in the absence of visual input and optic flow (dark condition) or proprioceptive ambulatory feedback (passive transport on platform) (STAR methods). Both conditions led to acceleration modulation of theta frequency in MEC similar to the effect observed in regular car experiments, in step protocols with two speeds (Figures 4A and S6A–S6C; 3 rats) or four speeds (Figures 4B and S6D; pooled data from 7 rats). Grid cells remapped during both conditions (Figures 4C and 4D). The new maps in the dark and passive transport conditions had low spatial information and stability, which resulted in poor decoding of rat position (Figures 4E and S6E). These observations suggest that although the spatial firing pattern of grid cells on the car relies on both visual and proprioceptive ambulatory feedback signals, as expected (Campbell et al., 2018; Hafting et al., 2005), modulation of theta frequency by acceleration does not. The results complement the dissociation between theta frequency and spatial representation through phase precession in MEC (Figures S3 and S4).

Figure 4.

Visual and proprioceptive self-motion cues are not crucial for theta frequency modulation by acceleration but are crucial to maintain grid maps

(A) Distribution (mean ± SEM) of LFP theta frequency (averaged from 60–260 ms after each onset as in Figures 1D and 1E) during episodes of acceleration (filled bars) or deceleration (hollow bars) for 3 rats trained in the two-speed step protocol (step size for each rat, from left to right: 30, 20, and 14 cm s⁻¹). Dark (green) and passive transport (red) experiments were performed in the bottomless car under visual deprivation or restraint, respectively. Regular car sessions (Car) recorded on the same day as dark (blue) or passive transport (yellow) sessions are also shown.

(B) Four-speed step protocol pooled average of theta frequency relative to acceleration (left) or deceleration (right) onsets during passive transport (PT; red) or same-day car (gray) sessions (7 rats, 38 sessions of each type).

(C) Spike map (one color dot per spike) for a representative grid cell in open field (left; black line: trajectory) and block of car (right; raster plot) experiments (two-speed protocol, step size 20 cm s⁻¹), including regular car (bottom), dark (middle), and passive transport (top) conditions (same color code; 10 right runs for each condition).

(D) Distribution of correlations between spatial grid maps obtained from the first half of the car session versus maps obtained from the second half of either the car (blue), dark (green) or passive transport (red) sessions. The gray area shows the shuffled distribution for the car condition (100 independent shuffles of every run; normalized by 100). Only this condition exhibited significantly elevated correlations (Mann-Whitney U test two-tailed z = 15.7, p: 10⁻⁵⁴), indicating stability, while the other two were not different from the shuffled distribution (dark z = 0.3, p: 0.75, passive transport z = −0.7, p: 0.5), indicating full remapping across conditions.

(E) Grid cells in the regular car condition exhibited maps with higher spatial information rate (top) and stability (center) than in dark or passive transport conditions (same color code; mean ± SEM). This allows for a more accurate spatial decoding in the car session (fewer decoding errors) compared to the other two conditions (bottom; Figure S6E).

Positive acceleration mediates spurious correlations between theta frequency, speed, and negative acceleration

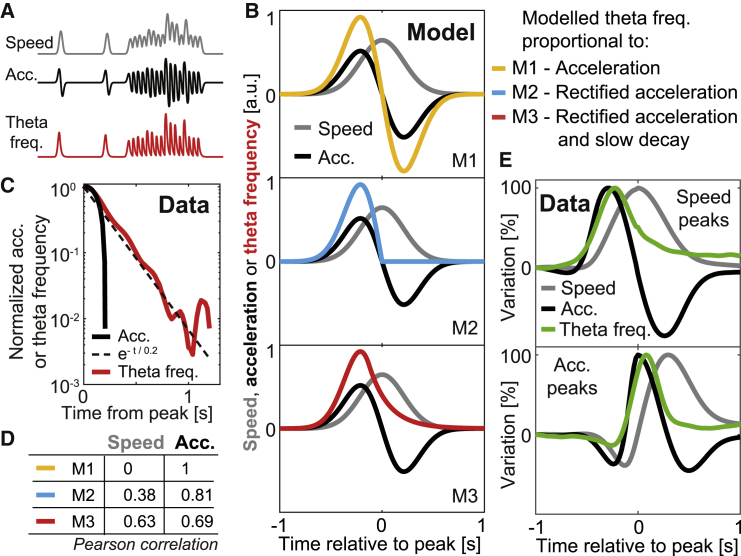
Our car experiments show that when speed and acceleration are carefully disentangled, there is no speed modulation of theta frequency. However, such a modulation has been reported in a number of thoroughly conducted experiments, sharing a common spontaneous behavior framework (Bland and Vanderwolf, 1972; Gupta et al., 2012; Hinman et al., 2011, 2016; Jeewajee et al., 2008; McFarland et al., 1975; Winter et al., 2015). The discrepancy of present and past data led us to ask whether the correlation with speed in past studies reflects conflation of speed and acceleration. During spontaneous behavior, rats do not preserve a constant speed for prolonged periods of time, but rather exhibit a concatenation of speed peaks each lasting around 1 s on average (Figures S5E and S5F; mean half decay of speed autocorrelation: 0.46 s). By the laws of kinematics, such peaks cannot occur without the simultaneous trigger of positive acceleration peaks, immediately followed by negative acceleration troughs (Figure 5A). This temporal coincidence may lead to a spurious correlation between theta frequency and speed. To investigate this possibility, we modeled theta frequency during a Gaussian speed peak as (M1) having a purely linear dependence on acceleration, (M2) restricting this linear relationship to positive acceleration alone, and (M3) further adding a slow decay in theta frequency (Figure 5B). The decay constant for the exponential decay was set to 0.2 s, which was a good fit for open field data (Figure 5C) and most car data (Figure S1D). Although in the first case (M1) the correlation with speed was strictly null (because acceleration is the temporal derivative of speed; see appendix in STAR methods), both modifications (M2 and M3) increased it, in M3 to a value similar to the correlation with acceleration (Figure 5D). When data in the pool of all of our open field sessions were cut into similar windows spanning 1 s to each side of speed or acceleration peaks, the average dynamics of speed, acceleration, and theta frequency resembled the one exhibited by M3 (Figure 5E). In both cases, theta frequency peaks coincided with acceleration peaks, while speed peaks followed 220 ms later (sampling period: 20 ms).

Figure 5.

Emergence of a spurious correlation with speed during spontaneous behavior

(A) Hypothetical scenario of the confusion emerging from the concatenation of multiple speed peaks. From top to bottom in arbitrary units: speed (gray), acceleration (black), theta frequency responding only to acceleration (red).

(B) Three versions of a simple model for the evolution of theta frequency (color) during a Gaussian speed peak (gray) and corresponding acceleration (black). From top to bottom, the relationship between theta frequency and acceleration is modeled in arbitrary units as linear (M1, yellow), rectified linear (M2, cyan), or rectified linear with a slow decay (M3, red, used in A).

(C) Average post-peak decay of acceleration (black) or theta frequency (red) for the pool of all open field data (as in Figure S1D, bottom). Variables are normalized so that 1 corresponds to the value at the peak, whereas 0 corresponds to 0 cm s⁻² or baseline theta frequency. The slow decay dynamics of theta frequency is described as decaying exponentially with a constant of 0.2 s (dashed line).

(D) Pearson correlation between modeled theta frequency and speed or acceleration for M1 to M3 (color coded).

(E) For the pool of all open field data, windows of 1 s to each side of a speed peak (top) or an acceleration peak (bottom) are defined. Averages over all such windows of recorded speed (gray), acceleration (black) and MEC theta frequency (green) are shown. y axis: percentage of variation between minimum and maximum positive values. Note resemblance with M3.

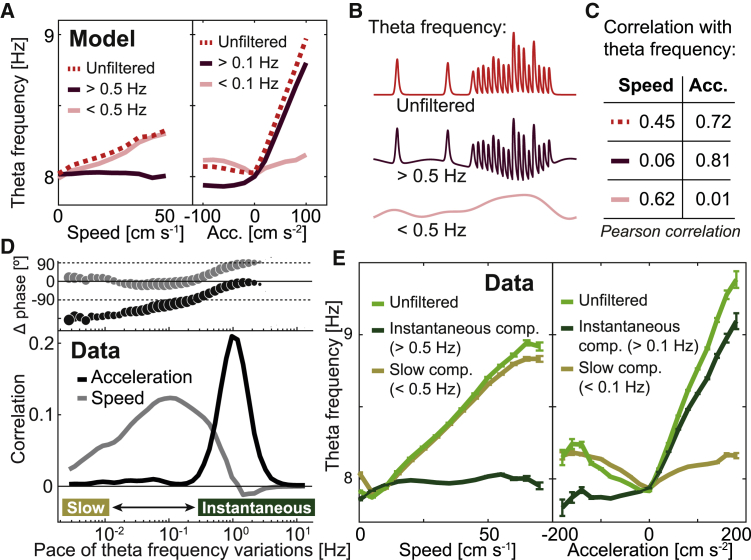
Our simple model (M3) correctly described the dynamics of the main variables, exhibiting a strong correlation between theta frequency and speed despite the fact that theta frequency was set explicitly to depend on positive acceleration alone. We next applied M3 to the acceleration during a 15-min session of actual tracked spontaneous behavior, finding that modeled theta frequency increased not only with positive acceleration as in Figure 1, but also with speed and negative acceleration, although no such causal relationship had been imprinted on the model (Figure 6A). To unmask this spurious correlation, taking into account the key role played by the dynamics of slow decay in M3, we decomposed the curve describing modeled theta frequency as a function of time into a slow varying baseline (low-pass filter) and an instantaneous component (high-pass filter) (Figures 6A and 6B; high- and low-pass filters were used with different ad hoc cutoff values, as indicated, selected in each case to maximize the contrast between slow and fast-varying components). Although the increase in theta frequency with speed was mostly due to changes in the slow varying baseline, instantaneous theta frequency correlated exclusively with acceleration (Figure 6C). In other words, the confound could be eliminated by selectively observing fast variations of theta frequency, a procedure that could be applied to recorded data.

Figure 6.

Only positive acceleration correlates with instantaneous variations of theta frequency

(A) The M3 model (red, Figure 5B, rectified linear with slow decay) is applied to the acceleration tracked during a 15-min representative session, and decomposed into its slow-varying (pale) and instantaneous (dark) dynamics utilizing high- and low-pass filters (cutoff values indicated). Average modeled theta frequency and its individual components are shown as a function of speed (left) and acceleration (right).

(B) Schematics of the decomposition of theta frequency (top) into its fast (center) and slow (bottom) components.

(C) Pearson correlation between speed or acceleration on one hand and modeled theta frequency and its components on the other (same color code).

(D) For the pool of all open field data, correlation of speed (gray) or acceleration (black) with Morlet wavelet components of the curve describing theta frequency as a function of time, plotted versus the wavelet frequency. Top subpanel: circular mean of the phase difference between Morlet wavelet components of theta frequency and speed (gray) or acceleration (black). The marker size is proportional to the mean vector length (1 – circular variance) (Figure S7D).

(E) Recorded MEC theta frequency (green; mean ± SEM), its slow baseline (pale), and instantaneous (dark) components (cutoff boundaries indicated) as a function of speed (left) and acceleration (right). Note resemblance with (A).

To better understand the correlation between variables at different dynamic ranges along the slow-varying to instantaneous dimension, we obtained the Morlet wavelet components of the curve describing recorded theta frequency as a function of time in the pool of all our open field data and correlated them with speed or acceleration (Figure 6D, bottom). Although the correlation of wavelet-filtered theta frequency with acceleration was maximal for variations occurring at a pace of around 1 s (1 Hz), spanning over a window of frequencies typical of instantaneous behavior (Figures S5E and S5F), its correlation with speed had a broader peak with maximum at around 0.1 Hz and was actually negative for fluctuations in theta frequency lasting less than 1 s (>1 Hz). In the regions of high correlation, a synchronization between the wavelet transforms of theta frequency on one hand and speed or acceleration on the other were observed, as evidenced by a 0° lag in their relative phase (Figures 6D, top, and S7).

We next plotted theta frequency, together with its slow and instantaneous components (as in Figures 6A–6C), as a function of speed and acceleration for the pool of all our open field data (Figure 6E). Although, as shown extensively in previous studies, theta frequency increased as a function of speed, most of this variation was due to the slow baseline component and vanished when only instantaneous variations in theta frequency (faster than 0.5 Hz) were considered. As captured by our model, the opposite was observed for acceleration. Instantaneous variations of theta frequency (faster than 0.1 Hz) had the kind of asymmetric behavior expected from the study of isolated positive and negative acceleration events (Figure 1), with no variation for negative acceleration. In contrast, the slow baseline of theta frequency exhibited symmetric (but weak) modulation by acceleration (see Figure S7 for cutoff values other than 0.1 and 0.5 Hz). These analyses suggest that during spontaneous navigation, when behavioral events are concatenated, the slow decay in theta frequency after each acceleration peak produces an effective slow-varying baseline that increases with the overall amount of locomotor activity, creating a spurious correlation between theta frequency and speed.

Could our model explain the numerous past reports of a correlation between speed and theta frequency? Most reports of a relationship between these variables estimated them over large temporal windows (>1 s), a manipulation that effectively filters the instantaneous component and keeps only the slow varying one (Bland and Vanderwolf, 1972; Carpenter et al., 2017; Hinman et al., 2011, 2016; McFarland et al., 1975; Richard et al., 2013; Rivas et al., 1996; Sławińska and Kasicki, 1998; Winter et al., 2015). A few more recent works have described a correlation between theta frequency and speed using higher temporal resolution (Gupta et al., 2012; Jeewajee et al., 2008; Newman et al., 2013; Wells et al., 2013), but these did not examine the potential role of acceleration as a source of confound. Our results suggest that all reported correlations are artifacts mediated by acceleration, as exemplified by our model. When acceleration events are sufficiently isolated (Figure 1) or when only instantaneous variations in theta frequency are considered (Figure 6), these spurious correlations disappear.

Discussion

Our main result is that instantaneous fluctuations in the frequency of theta band oscillations, described for many decades as correlating with running speed in the hippocampus (Bland and Vanderwolf, 1972; Gupta et al., 2012; Hinman et al., 2011; McFarland et al., 1975) and MEC (Hinman et al., 2016; Jeewajee et al., 2008; Winter et al., 2015), can instead be explained by acceleration, at the level of both LFP and single unit rhythmic spiking activity. The relationship to acceleration has unprecedented temporal precision and is highly non-linear: whereas positive acceleration generates a proportional variation in theta frequency, negative acceleration has no modulatory effect. It is unlikely that such a precise and graded relationship to intermittent acceleration events is caused by changes in the state of arousal or by other cognitive variables not directly linked to motion. Although speed does not correlate with the frequency of LFP oscillations, it does modulate to a lower extent the rhythmic spiking of certain cell types, such as grid cells and place cells, consistent with the idea that the LFP theta phase at which spikes of these cells occur, contains information about the position of an animal within a spatial field (Hafting et al., 2008; O’Keefe and Recce, 1993; Skaggs et al., 1996).

We have presented a model that accounts for the modulation of theta frequency by speed in past observations of spontaneous behavior, based on the dynamics of these variables along short temporal windows. The two key ingredients in our model are asymmetry of the theta frequency response with respect to the sign of acceleration and a dynamics characterized by fast rise but slow decay of the theta frequency. During spontaneous behavior, peaks of positive acceleration and theta frequency occur almost simultaneously, while speed tends to peak a fraction of a second later. The slow decay of theta frequency after peaking and the lack of modulation by negative acceleration result in the emergence of a spurious correlation between theta frequency and speed. If only the spontaneous behavior data in the open field had been available, it could have been posed as an alternative explanation that theta frequency codes for speed prospectively, with around 200 ms of anticipation. However, this is incompatible with our observations under controlled conditions in the car, where speed has a step profile but theta frequency exhibits a peak confined to the rising phase of the step, or no modulation at all if the transition is to a lower speed (Figure 1B). Instead, our model brings together classical results and observations from the bottomless car under a single parsimonious explanation. The spurious correlation between theta frequency and speed disappears when acceleration episodes are isolated or when only fast, temporally local variations of frequency are considered. Interestingly, correlations between speed and theta frequency have been observed to be absent during running in a wheel (Czurkó et al., 1999; Whishaw and Vanderwolf, 1973), during virtual-reality navigation in physically restrained animals (Ravassard et al., 2013), or under pharmacological inactivation of vestibular inputs (Jacob et al., 2014). These findings point to a possible role for vestibular information in the control of theta frequency during acceleration, especially in the light of our results regarding the non-crucial role played by visual and motor cues in this modulation. A potential role of acceleration in mediating other brain correlates of speed, such as gamma frequency (Ahmed and Mehta, 2012), still needs to be investigated.

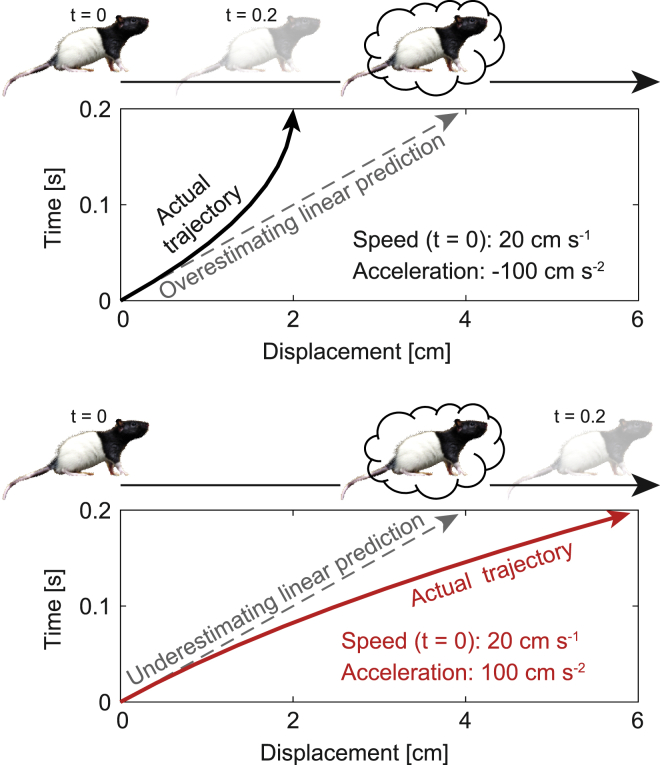
A temporally precise increase in theta frequency during acceleration events could be advantageous in at least two possible ways. First, the effect could help reducing errors in estimates of displacement on the basis of a single theta cycle. During navigation, rats are thought to perform path integration by updating the firing of grid cells in MEC using information coded by neighboring speed cells (McNaughton et al., 2006). However, the apparent lack of acceleration-coding cells in this circuit (Kropff et al., 2015) raises the possibility of impaired accuracy in the representation of non-inertial routes. A linear path integrator, guided by speed alone, would make systematic errors of magnitude a^∗Δt²/2, where a is acceleration and Δt the temporal window for integration. In navigating animals, the consequences of such errors would strongly depend on the sign of acceleration (Figure 7). In particular, underestimated displacement (during positive acceleration) would endanger the animal of running into obstacles that it plans to avoid. If Δt was related to the theta period, as proposed in theoretical models (Navratilova et al., 2012), an increase in theta frequency (i.e., a reduction of Δt) could reduce this error quadratically.

Figure 7.

Possible advantage of increasing temporal resolution specifically during navigation with positive acceleration

Simulated trajectory of a rat running for 0.2 s with an initial speed of 20 cm⁻¹ and a constant acceleration of either −100 cm s⁻² (top, black) or 100 cm s⁻² (bottom, red). In each panel, the bottom plots show the actual trajectory of the rat in an elapsed time versus displacement representation (solid line), together with the trajectory projected at time 0 by a linear path integrator (dashed line). The top plots in each panel depict initial position (t = 0 s), final position (t = 0.2 s; semi-transparent rat), and final position estimated by a linear path integrator at time 0 (rat in a cloud). Negative acceleration results in overestimation of displacement by the path integrator, which represents a conservative error because the actual final position is bounded between the initial position and the estimated one. In contrast, positive acceleration results in an underestimation of displacement, which represents a dangerous error because the actual final position is unbounded. The error (a^∗Δt²/2, where a is acceleration and Δt the temporal window for integration) could be selectively reduced by reducing Δt.

A second consequence of an increase in theta frequency during positive acceleration is a higher rate of computation. Theta cycles are thought to pack chunks of related information into discrete events to perform epochs of local computation (Brandon et al., 2013; Buzsáki and Moser, 2013; Colgin, 2013; Dragoi and Buzsáki, 2006; Gupta et al., 2012; Harris et al., 2003; Hasselmo et al., 2002; Jezek et al., 2011; Mizuseki et al., 2009; Skaggs et al., 1996). If this is the case, an increase of the oscillation frequency in response to a given contextual or behavioral demand could be interpreted as a way to raise the pace at which local computations are performed, so as to obtain a higher number of operations per second. This represents in our controlled car experiments a 25% boost during strong positive acceleration episodes, a number that could increase even more for the full range of natural behaviors. The absence of modulation by speed or negative acceleration suggests that episodes of increased theta frequency, while entraining a global system of networks including at least the MEC and the hippocampus, are triggered by behavioral variables much more specifically than previously thought.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Spike-time, EEG and position data	This paper	https://doi.org/10.12751/g-node.c84f73
Experimental models: organisms/strains
Long Evans rats	NTNU Kavli Institute vivarium	N/A
Software and algorithms
MATLAB	MathWorks	https://www.mathworks.com/
Kalman filter toolbox for MATLAB	Kevin Murphy	https://www.cs.ubc.ca/∼murphyk/Software/Kalman/kalman.html#other
Custom-made analysis code	This paper	https://doi.org/10.12751/g-node.c84f73

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Edvard I. Moser (edvard.moser@ntnu.no).

Materials availability

This study did not generate new unique materials.

Data and code availability

This study adapts built-in MATLAB functions to analyze data. Specific adaptations, customized code, and data are available from the corresponding authors on request. The spike time, EEG, and position data have been deposited in G-Node: https://doi.org/10.12751/g-node.c84f73. Custom-made analysis code can be found in G-Node: https://doi.org/10.12751/g-node.c84f73.

Source of the data

All open field data and part of the bottomless car data are taken from a previous publication (Kropff et al., 2015), in which firing rates of neurons in MEC and hippocampus were shown to be modulated by speed. LFP theta frequency was not investigated in that study. Data reported in the present study concerning visual deprivation and passive transport in the car (Figures 4 and S6) have not been published before.

Experimental model and subject details

Subjects

Seventeen male Long Evans rats (aged 3–6 months; 350–500 g at implantation and testing) were housed individually in transparent Plexiglass cages (54 × 44 × 35 cm). All rats were maintained on a 12-h light/12-h dark schedule and tested in the dark phase. After surgery, the rats were placed on a food deprivation schedule that initially kept them at ∼90% of their free-feeding body weight but was progressively loosened depending on task performance.

The experiments were approved by the National Animal Research Authority and performed in accordance with the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes. The study contained no grouping into experimental treatments, and thus no randomization or blinding. Sample size (number of animals) was not increased over the one used for the work presented in Kropff et al. (2015).

Method details

Electrode implantation and surgery

Tetrodes were constructed from four twisted 17-μm polyimide-coated platinum-iridium (90%–10%) wires (California Fine Wire) and mounted in groups of four into microdrives with a single turning screw and no separation between tetrodes. The electrode tips were plated with platinum to reduce electrode impedances to between 150–300 kΩ at 1 kHz.

Anesthesia was induced by placing the animal in a closed glass box filled with isoflurane vapor. Following this, the animals were rapidly moved into the stereotaxic frame, which had a mask connected to an isoflurane pump. Air flow was kept at 1 l per minute with 0.5%–3.5% isoflurane as determined by physiological monitoring. Local anesthetic (Xylocain) was applied on the skin before making the incision. Holes were drilled on the dorsal skull anterior to the transverse sinus to reach the entorhinal cortex, and posterior to bregma to reach the hippocampus. Rats were implanted with two microdrives aiming at entorhinal cortex alone bilaterally and a third microdrive aimed at the right hippocampus. The coordinates for entorhinal implants were: 4.5–4.8 mm medio-lateral relative to lambda, 0.2–0.7 mm anterior to the border of the sinus depending on the target layer, and 1.5–1.8 mm dorso-ventral relative to the surface of the brain. The inclination of the entorhinal tetrodes was 8°, with the tips pointing in the anterior direction. The coordinates for hippocampal implants were: 2.7 mm medio-lateral, −3.3 mm antero-posterior relative to bregma, and 1.5 mm dorso-ventral relative to the brain surface. These tetrodes were implanted vertically. Jeweller’s screws and dental cement were used to secure the drive to the skull. Two screws per microdrive were additionally connected to the system ground.

Data collection

For data collection, the rat was connected to the recording equipment (Axona Ltd) via a.c.-coupled unity-gain operational amplifiers close to its head, using a counterbalanced cable that allowed the animal to move freely within the available space. Tetrodes were lowered in steps of 50 μm every day and unit activity and LFP were recorded in parallel at each location. Given that, unlike power, theta frequency is not a local phenomenon (Lubenov and Siapas, 2009; Montgomery et al., 2009; Patel et al., 2012), all LFP analyses were conducted on data pooled into two groups (MEC and hippocampus), independently of layer or subfield. EEG was recorded single-ended from one electrode per microdrive. The EEG was amplified 1000–10,000 times, lowpass-filtered at 500 Hz, sampled at 4,800 Hz, and stored with the unit data. For single unit activity, recorded signals were amplified 5,000–25,000 times and band-pass filtered between 0.8 and 6.7 kHz. Triggered spikes were stored to disk at 48 kHz (50 samples per waveform, 8 bits per sample) with a 32-bit time stamp (clock rate at 96 kHz). A tracker system (Axona Ltd) was used to record the position of a pair of LEDs attached to the head stage at a rate of 50 samples per second, allowing to track for position and head direction.

Behavioral training

Every day the rats were first trained in an open field (1 m × 1 m × 50 cm box) and then in a bottomless car on a 4 m long linear track, with possible repetition of both types of trials. On some days, repetitions of the car trial were conducted in darkness or during passive transport (Dark and Passive Transport conditions; see below). In the open field, the animal was trained to collect chocolate crumbs thrown randomly into the box, one at a time, in trials that lasted at least 20 min and as long as the animal would exhibit active foraging behavior. Bottomless car trials varied depending on the protocol. With very few exceptions, a given rat was always trained with the same protocol. In general terms, sessions consisted of 10 to 25 runs on the linear track lasting at most 25 min. Naive rats generally explored the possibility of jumping over the limits of the car. This behavior was discouraged by placing the animals back in the correct position inside the car. Escape attempts typically stopped after one or two runs, when rats discovered that a chocolate crumb was placed at each end of the track to motivate running. On rare occasions, for training purposes, additional ground chocolate was distributed randomly along the track. This made the rat focus on the track and prevented it from taking alternative strategies such as jumping over the car. Between runs the rat rested on the end of the track for a random interval between 10 and 20 s. A 6 s beep of increasing pitch indicated the beginning of the next run. Between trials, the rat rested on a towel in a large flower pot on a pedestal.

The bottomless car had a minimalistic design to prevent the rat from using it as a sitting platform or spatial reference frame (Kropff et al., 2015). It was 28 cm long and 17 cm wide, with two ball-bearing wheels at each end. The car was supported by Plexiglas rails running slightly below the track along the sides. These lateral rails could barely be seen by the rat, giving support to the car without the need of lateral walls. At each end of the car was a wide mesh fence measuring 17 cm × 16 cm to prevent the rat from moving ahead or behind the car while not obscuring their vision or sensation of velocity. A 25 W battery-powered motor (Japan Servo) under the track was attached to two sets of guide lines, each one pulling from one end of the car. A motorcycle battery was used as an isolated power source to avoid 50 Hz a.c. noise. Braided fishing line (> 20 lb) was used as the guidance line. While the car was constructed in a minimalistic fashion, curtains were placed at both sides of the track and filled with a variety of salient visual cues, so as to make the laboratory the most salient spatial reference frame. Different scripts within the DacqUSB acquisition software (Axona Ltd) were used to control the motor that moved the bottomless car through the digital I/O port. The digital output of the recording system was transformed into analog by means of a custom-built digital-to-analog converter and fed as a control signal to the motor. To park the car consistently in the same position at the beginning of each run, two mechanical sensors were placed at the extremes of the track, and their output was fed to the digital input of the recording system.

Two-speed step protocol

The track was divided into two equal halves and different speeds were chosen for each half. The transition between them was sudden and occurred always in the same place.

Four-speed step protocol

This protocol was designed to obtain multiple transitions between four different speed groups: 7, 14, 21 and 28 cm s^-1. Every run was divided into six segments (S1–6), three of them corresponding to the outbound run and the other three to the inbound run. S1: the speed was set at 7 cm s^-1 for a fixed amount of time so as to cover roughly the first third of the track. S2: the speed was pseudo-randomly chosen among the four options, including the repetition of the previous speed. The point for the next transition was also chosen pseudo-randomly and varied from run to run within a range of ∼75 cm. S3: the speed was chosen pseudo-randomly again and kept until the end of the track was reached. S4: as in S2, the speed and the transition point toward S5 were chosen pseudo-randomly. The range of transition positions was the same as in the transition from S2 to S3. S5: the speed was chosen pseudo-randomly and kept until a fixed position (the same as for the transition between S1 and S2). S6: the speed was set to 28 cm s^-1 until the end of the track. This protocol biased the sampling in some transitions (S1 to S2 and S5 to S6) toward positive acceleration, but these transitions were not used for analyses (only unbiased transitions were used: S2 to S3 and S4 to S5). Transitions from resting state to S1 or S4 were not included in any analysis, to exclude potential effects related to state of arousal rather than to pure navigational factors. In analyses of behavior at different constant speeds, only the central segments S2 and S5 were taken into account, excluding windows of 1 s after each transition.

Dark and passive transport conditions

In some cases, additional car sessions were conducted on the same day and with the same speed protocol but during darkness or passive transport.

In the Dark condition, all lights in the room were turned off and the car was covered with a black box. The top of the box was made of black curtain cloth with an adjustable hole, so that the rat could pass through the hole before tightening it around the recording cable. When the rat was placed in the car, the box was placed around it so that there was no exchange of light between the inside and the outside. While this ensured that rats had no visual information even from faint distal room cues, the LEDs normally used for tracking purposes illuminated the space inside the box, providing minimal but vital cues for rats to be able to follow the car. Only animals subject to a fixed and predictable speed protocol (2-speed step) were recorded in the Dark condition, while we judged that the unpredictable 4-speed step protocol would have added too much stress to the task.

In the Passive Transport condition, a small platform made of the same material as the track floor was added on the bottom of the frame so that the car now had a floor around 2 cm above the track. The rat sat on the added floor and was passively transported along the track when the car moved.

Histology

Electrodes were not moved after the final recording session. Anesthesia was induced by placing the animal in a closed glass box filled with isoflurane vapor. The rats then received an overdose of Equithesin and were perfused intracardially with saline and 4% formaldehyde. The brains were extracted and stored in formaldehyde, and frozen sagittal sections (30 μm) were cut. All sections were mounted on glass slides and stained with cresyl violet. With the use of a light microscope, equipped with a digital camera, the positions of the recording electrodes were registered in relation to relevant borders between subfields. Final positions of the recording electrodes were indicated on photomicrographs obtained in AxioVision. The exact position of the electrodes at recording was extrapolated using the readout of the tetrode turning protocol.

Quantification and statistical analysis

LFP rejection criterion

One channel of every microdrive (with 4 tetrodes) was used for LFP recordings. Sessions where theta oscillations had low amplitude were rejected so as to optimize the signal-to-noise ratio in our analyses, allowing for a correct detection of instantaneous theta phase and frequency. Sessions were rejected if the power spectrum at 8 Hz (typically the theta peak) was less than twice the power spectrum at 6 Hz or 12 Hz (typically the throughs in LFP around the theta peak) for the same session. In recordings where both entorhinal drives had LFPs that passed the criterion, only the one with the highest ratio of P₈ / max(P₆,P₁₂) was used, where P_f represents the power spectrum at a frequency of f Hz.

Spike sorting and cell classification

Spike sorting was performed offline using graphical cluster-cutting software (Tint; Axona Ltd). Clustering was performed manually in two-dimensional projections of the multidimensional parameter space (consisting of waveform amplitudes), using autocorrelation and cross-correlation functions as additional separation tools and separation criteria. In general, the stability of the tetrodes allowed for all sessions in a day to be merged for clustering purposes.

Estimation of velocity, acceleration, and theta frequency

Theta phase was obtained from the Hilbert transform of the band-pass filtered LFP signal (between 6 and 12 Hz) and unwrapped by adding or subtracting 360° every time a jump in phase with absolute value higher than 180° occurred between two consecutive samples. Note that this procedure filtered out high frequencies, such as harmonics of theta. For this reason, potential variations in the shape of the theta cycle, caused by variations in the relative weight of different harmonics, did not affect our estimation of instantaneous theta frequency. In the bottomless car experiments, where exact repetitions of trajectory allowed for averaging over multiple trials, the frequency at time t was estimated from the average in phase difference between t + 60 ms and t – 60 ms. In a similar way, speed was estimated as the difference in position between t + 100 ms and t – 100 ms, while acceleration was estimated from the difference in speed between t + 100 ms and t – 100 ms, which is equivalent to the position at time t + 200 ms plus the position at time t – 200 ms minus twice the position at time t. Both smoothing windows (60 ms and 100 ms) were the smallest necessary to make the average signal visually clear in terms of signal to noise (Figure 1B).

In free foraging experiments, stronger smoothing along the temporal dimension was required in order to rely on single-trial estimations of frequency, speed and acceleration. Instantaneous theta frequency was computed by applying a Kalman filter and smoother (RTS) (MATLAB toolbox https://www.cs.ubc.ca/∼murphyk/Software/Kalman/kalman.html) to the phase obtained through the Hilbert transform (as in the previous case). The hidden state vector was composed by theta phase and its derivative, instantaneous theta frequency, while the observation vector included only theta phase. The system matrix was set to $F=\left|\begin{array}{ll}1\hfill & 1\hfill \\ 0\hfill & 1\hfill \end{array}\right|$ and the observation matrix to $H=\left|\begin{array}{ll}1\hfill & 0\hfill \end{array}\right|$. The parameters controlling the amount of smoothing were $Q=\left|\begin{array}{ll}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right|$ (system covariance) and $R=5$ (observation covariance). An evaluation of this smoothing scheme can be found in Figure S5.

In 2-dimensional free foraging experiments, the x and y components of the velocity (v_x, v_y) and acceleration (a_x, a_y) vectors were computed from the tracked positions adapting the same Kalman filter. The hidden state vector was composed by position and its derivatives up to second order X_hidd = [x, v_x, a_x, y, v_y, a_y], while the observation vector included only the positions tracked by LEDs, X_obs = [x,y]. The system matrix was set to $F=\left|\begin{array}{ll}A\hfill & Z_{\mathrm{3,3}}\hfill \\ Z_{\mathrm{3,3}}\hfill & A\hfill \end{array}\right|$, where Z_3,3 denotes a 3 × 3 matrix filled with zeros and $A=\left|\begin{array}{lll}1\hfill & 1\hfill & 0.5\hfill \\ 0\hfill & 1\hfill & 1\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right|$. The observation matrix was $H=\left|\begin{array}{l}100000\hfill \\ 000100\hfill \end{array}\right|$. While these matrixes define the kinematics of any system with speed and acceleration in 2-dimensions, the crucial smoothing parameters were $Q$ (system covariance), a matrix filled with zeros and diagonal elements [50, 0.02, 0.01, 50, 0.2, 0.01], and $R=\left|\begin{array}{ll}100\hfill & 0\hfill \\ 0\hfill & 100\hfill \end{array}\right|$ (observation covariance). An evaluation of this smoothing scheme can be found in Figure S5. The same Kalman filter parameters were used in a previous publication (Kropff et al., 2015).

In addition, episodes of resting, grooming or other non-navigational behaviors were filtered out. To do so, instantaneous traveled distance at time t was defined as the distance between the positions of the animal at time t+0.5 s and t-0.5 s. We only considered data points where the instantaneous traveled distance was consistently higher than 5 cm in a window of 0.5 s around timestamp t.

Average of raw LFP oscillations

Due to destructive interference, windows of LFP oscillations cut around an event such as acceleration or deceleration onset cannot be directly averaged. To obtain a reliable estimation of temporal evolution of the LFP averaged across multiple trials while avoiding destructive interference, the following procedure was used. Raw LFP traces were first filtered using a 5 Hz high-pass filter to remove slow oscillation effects associated to acceleration (data not shown). Windows of 1 s were then cut around acceleration or deceleration onsets. Each window contained 4800 samples and could be represented by a single point in a space with dimension N = 4800. The collection of all windows (points in a high dimensional space) corresponding to either acceleration or deceleration events were clustered using the k-means algorithm implemented in the MATLAB (MathWorks, MA) function kmeans(). To have a good coverage of all theta phases, the number of clusters was set to k = 20. Cluster centroids (i.e., averages of windows with similar data) representative of at least 20 data windows were used for visualization of mean theta oscillation behavior in response to acceleration or deceleration (Figure 1C).

Intrinsic firing frequency in the rhythmic spiking of cells

To estimate intrinsic firing frequency in small windows of data, a parametric model of the lag between spikes was used (Climer et al., 2015). This method has been shown to be more robust than others based on spike-time autocorrelograms when the overall number of spikes is very low. For every cell, the 4 ms bin histogram of spike lags (pooling together lags between consecutive and non-consecutive spikes) was obtained. If properly normalized, the spike-lag histogram represents an estimation of probability of a cell to spike at time t given that it spiked at time 0. To analyze the effect of different degrees of speed or acceleration, only spikes passing a certain criterion, such as occurring at a given range of speeds or within a window of time after some event, were used to compute the spike-lag histogram. Next, spike-lag histograms for all cells in a given group were averaged to obtain the population spike-lag histogram of that group (Figure S2D).

The theta frequency associated with a population spike-lag histogram was estimated as parameter F of the equation

$$f\left(t\right)=A-Bt+C{e}^{-Dt}+E\text{cos}\left(2\pi Ft\right)e^{-Gt}$$

which was fitted to each histogram using the MATLAB function fit() over the range t = 16 to 300 ms. Note that the equation is versatile in the sense that it includes the possibility of a linear or an exponential decay of the non-oscillatory part of the histogram, covering a wide range of situations. To allow for visual comparisons across conditions or cell types, the population spike-lag histograms and the fitted curves were normalized by f(0) = A+C+E.

A similar procedure was used to estimate the intrinsic firing period of cells in terms of LFP theta phase (Figure S4). To do this, spike-lag histograms were constructed with differences in spike unwrapped theta phase rather than with differences in spike times, and 3° bins were used. Note that unwrapped theta phase is monotonically increasing, and thus analyses of these data use linear rather than circular statistics.

In some cases, when acceleration events were steep and short (Figures 2A and 2B), the size of the temporal windows from which spikes were included was critical. To get an estimate of the highest transient acceleration levels, windows had to be as short as possible (in the order of tens of milliseconds). However, the method needs substantial numbers of spikes, which would not be available using too short windows, as well as at least one full theta period. We used 500 ms as a compromise between including as many spikes as possible on one side and narrowing the window to capture only spikes that happened when acceleration was high on the other. Given that acceleration episodes could last less than 500 ms (e.g., Figures 1D and 1E use windows of 200 ms), the intrinsic firing frequencies that we report for isolated positive acceleration events are underestimations.

Shuffling

Chance-level statistics was constructed for a given variable W through a shuffling procedure. For each scenario described below, data were shuffled N times (N specified in the main text) and a surrogate value of W was calculated on each of the shuffling instances. The collection of N surrogate W values constituted the chance level distribution of W. A direct comparison between the actual value of W and its chance level distribution was used to obtain the associated p value.

Intrinsic firing frequency, 2 speed-step protocol

Every run had a single acceleration or deceleration window. In every shuffling step, this window was displaced to fall randomly either inside the fast or slow constant running speed periods of the same run, avoiding resting periods. In a single shuffling step the displacement was different for different runs. The shuffled distribution was constructed with equal contributions of slow and fast running windows (Figures 2A and 2B).

Intrinsic firing frequency, open field

To find the baseline distribution of intrinsic firing frequency for various populations of cells and levels of speed or acceleration, the windows of selected data were displaced in time by a random interval not shorter than 20 s and not longer than the total duration T of the session where the cell was recorded minus 20 s. For resulting times greater than T, modulo T was applied. In this way, windows randomly fell in any part of the session avoiding 20 s to each side of their actual temporal location (Figures 3D–3F). In a single shuffling step, different cells were displaced by a different interval, related to each cell’s T. For plots in Figure 3, distributions of shuffles corresponding to positive and negative acceleration windows were pooled together for visualization purposes, but analyses and p values were obtained considering only the corresponding shuffled distribution.

Modulation of intrinsic firing frequency by speed

Segments of constant running speed where classified by their speed group (7, 14, 21 or 28 cm s^-1). Modulation was assessed by correlating intrinsic theta frequency and speed group across segments. Each shuffling step consisted of randomly rearranging the speed-group tags (Figure S3).

Spatial maps in the bottomless car

The spikes in each run were displaced in time by an interval smaller than the duration of the run T, and a modulus T was applied for spikes with timestamps larger than T, thus avoiding resting periods. Although T was roughly the same for all runs, the displacement was pseudo-randomly selected for each run in an independent way. Maps, correlations and other measures were computed with the new timestamps for each run.

Theta frequency versus acceleration in the open field

Episodes of resting, grooming or other non-navigational behaviors were removed by defining the instantaneous traveled distance at time t as the distance between the positions of the animal at time t+0.5 s and t-0.5 s, considering for our analyses data points where the instantaneous traveled distance was consistently higher than 5 cm for half a second around the timestamp t.

Frequency versus acceleration color maps

Color maps in Figure 3A where obtained from a histogram of theta frequency as a function of the 2D acceleration vector, which was represented in polar coordinates through its magnitude a and its direction relative to the direction of velocity θav. Velocity was represented as always pointing to the north, so that θav = 0, when acceleration and velocity point in the same direction (positive acceleration), was represented in the north part of the plot. The width of angular bins was 3.6° and that of acceleration bins was 20 cm s^-2. Since data were distributed in a large number of bins with low coverage in each one, especially for high acceleration, color maps were smoothed using a Gaussian filter with a standard deviation of 30 cm s^-2 and10°.

Linear acceleration

For analyses of positive and negative open field acceleration, such as maps in Figure 3B, it only makes sense to consider episodes when cos(θav) is close to either 1 (positive acceleration; North) or −1 (negative acceleration; South). We thus defined linear acceleration in the open field as a^∗sign(cos(θav)) only for timestamps where |cos(θav)| > 0.9 (black dashed lines in Figure 3A). Plots of frequency versus acceleration (e.g., Figure 3B) included only data where the sign of acceleration was properly defined, and no smoothing was applied in the plot. All analyses, such as those in Figures 3D–3F, also included only timestamps where the sign of acceleration was properly defined.

Cell type classification

Descriptive scores for each cell type and shuffling procedures to obtain 99^th percentile classification thresholds are identical to those used in Kropff et al. (2015). We here summarize the procedures to obtain the scores.

Grid cells

A grid score was determined for each cell from a series of expanding circular samples of the cell's spatial autocorrelogram (2.5 cm bins), each centered on the central peak but with the central peak excluded (Sargolini et al., 2006; Stensola et al., 2012). The radius of the central peak was defined as either the first local minimum in a curve showing correlation as a function of average distance from the center, or as the first incidence where the correlation was under 0.2, whichever occurred first. The radius of the successive circular samples was increased in steps of 1 bin (2.5 cm) from a minimum of 10 cm more than the radius of the central peak, to a maximum of 90 cm. For each sample, we calculated the Pearson correlation of the ring with its rotation in α degrees first for angles of 60° and 120° and then for angles of 30°, 90° and 150°. We then defined the minimum difference between any of the elements in the first group (60° and 120°) and any of the elements in the second (30°, 90° and 150°). The cell’s grid score was defined as the highest minimum difference between group-1 and group-2 rotations in the entire set of successive circular samples.

Head direction cells

The head-direction score or mean vector length of a cell's circular firing rate distribution was computed as the absolute value of its head-direction tuning map’s angular mean |∑ h_k exp(-i θ_k)|, where θ_k is the k^th bin’s angle and h_k the corresponding firing rate normalized by the overall mean firing rate (Boccara et al., 2010).

Border cells

A border score was computed for each cell as the difference between the maximal length of a wall touching on any single firing field of the cell and the average distance of the field from the nearest wall, divided by the sum of those values (Solstad et al., 2008). The range of border scores was thus −1 to 1. Firing fields were defined as collections of neighboring pixels with firing rates higher than 20% of the cell’s peak firing rate and a size of at least 200 cm².

Speed cells

The cell's speed score was computed as the Pearson correlation between instantaneous firing rate and instantaneous running speed, excluding segments of running at a speed < 2 cm s^-1 (Kropff et al., 2015).

Place cells

Spatial information rate (Skaggs et al., 1996) for a cell was computed as ∑ p_k λ_k log₂(λ_k), where p_k is the k^th spatial bin’s occupancy probability and λ_k the corresponding firing rate normalized by the overall mean firing.

Interneurons

A cell fell under the category of putative fast spiking if its mean firing rate was above 10 Hz and its spike width below 0.3 ms (Buetfering et al., 2014; Kropff et al., 2015).

Modeled theta frequency

The theta frequency model in Figure 5B included the two key ingredients of rectification and slow decay. Rectified acceleration was defined as a_R = a for a > 0 and a_R = 0 otherwise, where a is modeled or tracked acceleration. Slow decaying rectified acceleration a_S was defined for the first timestamp t₁ as a_R(t₁). For any other time bin t_i, it was defined as the largest value between a_R(t_i) and exp(- 0.1)^∗a_R(t_i-1), which given the sampling rate of 50 Hz introduced an effective exponential decay with a constant of 0.2 s, only for episodes where acceleration was negative or decayed faster than that. Finally, modeled theta frequency for any timestamp t_i was defined as θ(t_i) = 8 Hz + a_S(t_i) / 100, with an increase of 1 Hz for every 100 cm s^-2 of positive acceleration. Note that we do not claim this model to be the best possible fit to our data but we utilize it for illustrative purposes given its simplicity.

Fast and slow components of theta frequency

The curve describing theta frequency as a function of time was filtered with low-pass, high-pass or wavelet filters, to capture different dynamical regimes in theta frequency temporal variations. Whenever the zero frequency component (i.e., the mean theta frequency) was filtered out (high-pass or wavelet filters), it was added back to the resulting signal to facilitate visual comparisons. This is why the instantaneous components in Figures 6A and 6E vary around 8 Hz rather than around 0 Hz.

Spatial information rate, stability, and decoding

Spatial information of grid maps was assessed in the same way as for place maps (see “cell type classification” section). Stability was computed as the correlation between the spatial maps obtained in the first and second half of the session for each cell. For decoding, all grid cells recorded in rat 14740 in either right or left runs were used, pooling together even if recorded in different days (the reproducible spatial trajectory allowed for this). Population activity vectors for the first and the second halves of each session were constructed for all 2.5 cm bins along the track. Those obtained from the first half of each session were used as templates of expected population firing rate for each bin, while those obtained from the second half were used to decode position at each bin by choosing the template that maximized Pearson correlation with the bin’s population vector. Decoding errors were defined as decoded positions that were further away than 25 cm from the actual bin.

Statistical tests

Statistical tests were in general non-parametric, except where indicated, and whether they were one or two-sided is indicated in each case. In many cases the baseline statistics was assessed through shuffling, as described in the corresponding section of the STAR methods.

Appendix - Correlation between speed and theta frequency

Theta frequency is here assumed to depend on acceleration alone. The aim is to understand the emergence of a spurious correlation with speed, dependent on the form of the relationship between theta frequency and acceleration. The Pearson product-moment coefficient is here used to assess correlation between any two variables x and y with corresponding standard deviations σ_x and σ_y. It can be thought of as

$$\text{PC}\left(\text{x},\text{y}\right)=\frac{\text{CV}\left(\text{x},\text{y}\right)}{{\text{σ}}_{\text{x}}{\text{σ}}_{\text{y}}},$$

where the covariance CV(x,y) is

$$\text{CV}\left(\text{x},\text{y}\right)=\text{E}\left(\text{xy}\right)-\text{E}\left(\text{x}\right)\text{E}\left(\text{y}\right),$$

E() denoting the expected value. Since the standard deviations are always finite and positive, the sign of the correlation is given by that of the covariance.

Correlation between speed and acceleration

The covariance between speed (v) and acceleration (a) over a temporal window of size T can be obtained by replacing expected values by temporal averages,

$$\text{CV}\left(\text{v},\text{a}\right)=\frac{1}{\text{T}}\underset{0}{\overset{\text{T}}{\int }}\text{v a dt}-\bar{\text{v}}\frac{1}{\text{T}}\underset{0}{\overset{\text{T}}{\int }}\text{a dt,}$$

where $\bar{\text{v}}=\frac{1}{\text{T}}\underset{0}{\overset{\text{T}}{\int }}\text{v dt}$ is the mean speed. The integrals can be solved using the fact that the acceleration is the derivative of speed,

$$\text{CV}\left(\text{a},\text{v}\right)=\frac{1}{2\text{T}}\left({\text{v}}^2\left(\text{T}\right)-{\text{v}}^2\left(0\right)\right)-\bar{\text{v}}\frac{1}{\text{T}}\left(\text{v}\left(\text{T}\right)-\text{v}\left(0\right)\right).$$

If initial and final speed are the same, the covariance is strictly zero. Alternatively, since there is a limit for the speed of a rat, both terms (the difference and the squared difference between initial and final speed) are bounded, and vanish for large enough T. Hence, if the window under consideration is large enough, the covariance (and thus the correlation) between speed and acceleration are zero.

Theta frequency as a linear function of acceleration

If theta frequency F is modeled as a linear function of acceleration

$$\text{F}\left(\text{t}\right)=\text{A}+\text{B a}\left(\text{t}\right),$$

then $\text{E}\left(\text{F v}\right)=\text{A E}\left(\text{v}\right)+\text{B E}\left(\text{a v}\right)$ and $\text{E}\left(\text{F}\right)\text{E}\left(\text{v}\right)=\text{A E}\left(\text{v}\right)+\text{B E}\left(\text{a}\right)\text{E}\left(\text{v}\right)$. The covariance between theta frequency and speed would be

$$\text{CV}\left(\text{F},\text{v}\right)=\text{B CV}\left(\text{a},\text{v}\right),$$

which, as explained before, vanishes for large enough T. Hence, if theta frequency behaved as a linear function of acceleration, its correlation with speed would be zero.

Correlation between speed and rectified acceleration

Let a⁺ be the positive-only or rectified acceleration, given by

$${\text{a}}^{+}\left(\text{t}\right)=\{\begin{array}{l}a\left(\text{t}\right)ifa\left(\text{t}\right)\ge 0\hfill \\ 0ifa\left(t\right)<0\hfill \end{array}.$$

With this definition,

$$\text{E}\left({\text{a}}^{+}\text{ v}\right)\approx \frac{1}{\text{T}}\underset{0}{\overset{\text{T}}{\int }}{\text{a}}^{+}\text{ v dt}=\frac{1}{\text{T}}\sum _{\text{k}}\frac{{\text{v}}^2\left({\text{t}}_{\text{k}}^{\text{F}}\right)-{\text{v}}^2\left({\text{t}}_{\text{k}}^{\text{I}}\right)}{2},$$ (1)

where k is an index that runs through all segments of data with positive acceleration. Each segment starts at a speed trough with value v(t^I_k)and ends at the next consecutive speed peak with value v(t^F_k) > v(t^I_k). Note that since the contribution of each segment is strictly positive and since the number of segments scales in the general case with T, the fact that T is large is no longer enough to make E(a⁺v) vanish, so this term will be significantly positive. Similarly,

$$\text{E}\left({\text{a}}^{+}\right)\text{ E}\left(\text{v}\right)\approx \frac{\bar{\text{v}}}{\text{T}}\sum _{\text{k}}\text{v}\left({\text{t}}_{\text{k}}^{\text{F}}\right)-\text{v}\left({\text{t}}_{\text{k}}^{\text{I}}\right)$$ (2)

is also positive and cannot be presumed to vanish with large T.

Merging Equation 1 and Equation 2,

$$\text{CV}\left({\text{a}}^{+},\text{v}\right)\approx \frac{1}{\text{T}}\sum _{\text{k}}\frac{{\text{v}}^2\left({\text{t}}_{\text{k}}^{\text{F}}\right)-{\text{v}}^2\left({\text{t}}_{\text{k}}^{\text{I}}\right)}{2}-\bar{\text{v}}\left(\text{v}\left({\text{t}}_{\text{k}}^{\text{F}}\right)-\text{v}\left({\text{t}}_{\text{k}}^{\text{I}}\right)\right)=\frac{1}{\text{T}}\sum _{\text{k}}\left(\text{v}\left({\text{t}}_{\text{k}}^{\text{F}}\right)-\text{v}\left({\text{t}}_{\text{k}}^{\text{I}}\right)\right)\left(\frac{\text{v}\left({\text{t}}_{\text{k}}^{\text{F}}\right)+\text{v}\left({\text{t}}_{\text{k}}^{\text{I}}\right)}{2}-\bar{\text{v}}\right).$$

The first factor in each term of the sum over k in the right hand side is the (positive) peak depth, while the second factor can be positive or negative depending on whether the half-height of each speed peak is higher or lower than the average speed. Thus, the sign of the covariance between rectified acceleration and speed is in principle different from zero and can be either positive or negative. Note, however, that in typical experiments rats spend most of their time running at low speeds, with very transient excursions into high speed regions. This situation favors low average speed and high peak half-height, resulting in an overall positive covariance.

If theta is modeled as a linear function of the rectified acceleration, the arguments of the previous subsection apply, and the sign of the correlation between theta frequency and speed will also be significantly positive.

In sum, the asymmetrical modulation of theta by positive, but not negative, acceleration is enough to create spurious correlations between speed and theta frequency that do not vanish with the size of the dataset. These non-vanishing correlations are positive rather than negative due to the preference of low speeds in typical rat behavior.

Published: February 9, 2021

Supporting citations

The following references appear in the supplemental information: Aghajan et al. (2015); Geisler et al. (2007); Mehta et al. (2002); Tsodyks et al. (1996).