Factors influencing the COVID-19 daily deaths' peak across European countries

Abstract

Objectives

The purpose of this study was to determine predictors of the height of coronavirus disease 2019 (COVID-19) daily deaths' peak and time to the peak, to explain their variability across European countries.

Study design

For 34 European countries, publicly available data were collected on daily numbers of COVID-19 deaths, population size, healthcare capacity, government restrictions and their timing, tourism and change in mobility during the pandemic.

Methods

Univariate and multivariate generalised linear models using different selection algorithms (forward, backward, stepwise and genetic algorithm) were analysed with height of COVID-19 daily deaths' peak and time to the peak as dependent variables.

Results

The proportion of the population living in urban areas, mobility at the day of first reported death and number of infections when borders were closed were assessed as significant predictors of the height of COVID-19 daily deaths' peak. Testing the model with a variety of selection algorithms provided consistent results. Total hospital bed capacity, population size, the number of foreign travellers and the day of border closure were found to be significant predictors of time to COVID-19 daily deaths' peak.

Conclusions

Our analysis demonstrated that countries with higher proportions of the population living in urban areas, countries with lower reduction in mobility at the beginning of the pandemic and countries having more infected people when closing borders experienced a higher peak of COVID-19 deaths. Greater bed capacity, bigger population size and later border closure could result in delaying time to reach the deaths' peak, whereas a high number of foreign travellers could accelerate it.

Introduction

The infectious coronavirus disease 2019 (COVID-19) outbreak was announced as a pandemic by the World Health Organization (WHO) on March 11, 2020.¹ By the end of March, Europe exceeded Asia and became the region experiencing the highest percentage of mortality from the virus across the world,² until June 10, 2020, when the rapidly growing COVID-19 mortality rate in the Americas exceeded all other continents.³ As per the WHO report from July 5, 2020, 38% of the global mortality due to COVID-19 was from Europe.⁴

Because incidence and mortality rates varied between countries, numerous studies have recently been published investigating factors associated with COVID-19 infection and death rates across countries. A variety of potential predictors have been assessed in the literature, such as country-specific demographic characteristics, economic and social indicators,5, 6, 7, 8 mobility scores and social distancing measures,^{9 , 10} ecological and environmental perspectives,^{8 , 11} as well as health characteristics and comorbidities that increase people's vulnerability.¹² To assess the relationship between covariates and COVID-19 incidence or mortality, the most common approach used by authors was to analyse multivariate regression models of the number of daily or total number of infections or deaths up to a given time point as outcomes.

In this study, we used data on numbers of deaths, not infections, because the former has a much higher degree of reliability than the latter, being better monitored and less dependent on the number of tests performed. Because all European countries seem to already reach the peak of deaths by June 3, 2020, from the first wave of COVID-19, our idea was to use height of daily deaths' peak as a primary outcome and time to the peak as a secondary outcome.

To the best of our knowledge, this perspective has not been investigated so far. When raw and cumulative daily numbers of infections and deaths are subject to deviations from between-country differences in reporting and depend on the date up to which the analysis is performed, the maximum number of daily deaths can be assessed as an interesting new indicator of the magnitude of disease mortality.

This study aims to detect significant drivers of COVID-19 mortality with the use of multivariate generalised linear models (GLMs) and distinct selection algorithms, to explain the variability of height of and time to the deaths' peak among European countries. This will enable us to draw conclusions about how governments and societies can improve future response in similar pandemic or global life-threatening situations.

Methods

Data collection

A total of 34 European countries were included in the analysis. The height of COVID-19 daily deaths' peak was the primary outcome of interest, defined as the maximum daily reported number of people who died owing to COVID-19 per country up to June 3, 2020, divided by the number of inhabitants.

The secondary outcome of interest was time to COVID-19 daily deaths' peak, defined as the number of days from the day when the first death was reported in a country up to the day of reaching the COVID-19 daily deaths' peak.

A set of explanatory variables used to predict outcomes consisted of the following: (1) healthcare capacity—all-bed capacity (the number of hospital beds), intensive care unit (ICU) capacity (the number of ICUs) and number of tests conducted up to the peak; (2) government restrictions and associated factors—‘stay-at-home’ order date, date of closure of educational facilities, date of imposing restrictions on gatherings, business closure date, border closure date, total number of COVID-19–infected people when borders were closed and total number of COVID-19 deaths when borders were closed; (3) indicators of the population size—size of the population of the country (January 2020), percentage of the population living in urban areas and percentage of the population living in metropolitan cities with more than 1 million inhabitants; (4) median age; (5) tourism—number of travellers who arrived at airports in 2018 and number of foreign tourists in 2018 (any touristic accommodation); and (6) mean mobility score at the day of the first reported COVID-19 death—calculated across mobility scores at retail and recreation places, workplaces and transit stations.

All dates were considered as the number of days after the day of the first reported COVID-19 death in each country. Variables indicating healthcare capacity and tourism were considered in relation to the population size of a given country (per inhabitant or 1 million inhabitants).

Data sources

Data on COVID-19 deaths, infections, the number of tests, bed capacity, government restrictions, population size and urban population size were taken from the Institute for Health Metrics and Evaluation.¹³ Missing dates of government restrictions, if officially issued, were found on Wikipedia.¹⁴

Mobility scores were uploaded from Google COVID-19 Community Mobility Reports.¹⁵ Scores were reported as percentage changes from a usual mobility calculated before the pandemic in Europe, between January and February 2020. Scores were subject to oscillations owing to daily reporting and the presence of weekends and holidays; therefore, we used smoothed scores produced using a non-parametric technique that uses local weighted regression and fits a smooth curve through points in a scatter plot, called ‘loess regression’.¹⁶

Data on the number of passengers who arrived at airports, tourism and the population living in metropolitan areas were downloaded from Eurostat¹⁷ and other sources.18, 19, 20, 21

Missing data and imputation

If government restrictions were not officially set, the date was imputed with the date of the peak in each country. Missing data on mobility for Cyprus and Iceland were imputed with average scores of the remaining countries.

Statistical analysis

Descriptive statistics on outcomes and explanatory variables were produced. Because the distribution of height of the deaths' peak per population size was right skewed, a logarithmic transformation was applied.

Factors influencing the height of deaths' peak were analysed using a univariate and multivariate GLM with a normal distribution function and logarithmic link function. The base case analysis was performed using data available for 34 countries and explanatory variables with a P-value <0.1 in univariate GLMs. To avoid multicollinearity between independent variables, Pearson correlations were investigated to detect highly correlated pairs of variables. The correlation was assessed as high if the absolute value exceeded 0.7 and as moderate if the absolute value was in a range of 0.5–0.7.²²

Owing to a relatively low sample size, a risk of bias could appear for models with a too high number of covariates. Therefore, sensitivity analyses were performed using a variety of selection algorithms: stepwise, backward, forward and genetic algorithm, to limit the number of covariates, increase model precision and improve model fit. A criterion of having a P-value lower than 0.1 was applied for each variable to stay in a model (for backward and stepwise) and to enter a model (for forward and stepwise). For the genetic algorithm, the best model was fitted based on the value of Akaike Information Criterion (AIC) corrected for small sample sizes (AICC). Models with only main effects were considered. Additional sensitivity analysis was performed removing countries for which imputation of government restriction dates was needed.

Similar methods were used to analyse time to deaths' peak but without any transformation because it seemed to follow a normal distribution. GLMs with a normal distribution function and identity link function were analysed.

Given a country-level analysis, Moran's I and Geary's C statistics^{23 , 24} were produced to check the spatial autocorrelation in values of outcomes and to determine if it should be considered in models.

For all analyses, a P-value lower than 0.05 was considered statistically significant. For each GLM, fit statistics such as AIC and AICC were produced, with lower values indicating better fit.

Analyses were performed using SAS 9.4 software. R 3.6.2 was used to apply the genetic algorithm with the package glmulti.²⁵

Results

Descriptive analysis

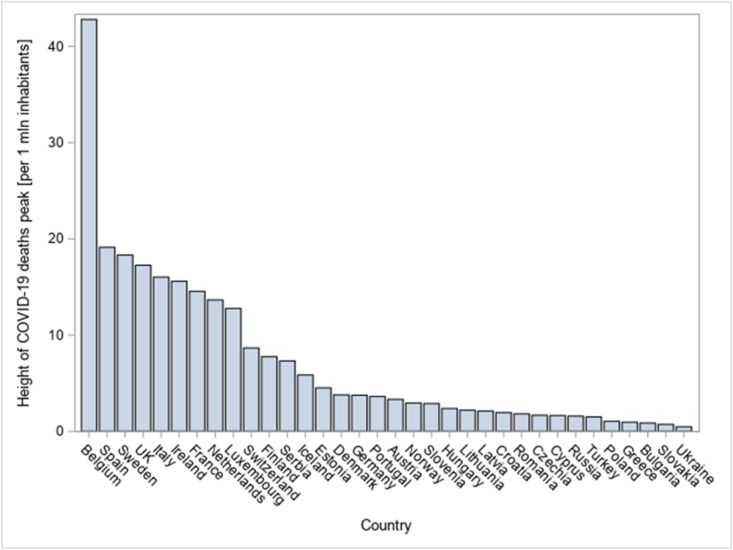
The characteristics of the countries included in the study are presented in Table 1 , and a histogram of the height of COVID-19 deaths' peak is depicted in Fig. 1 . The graph presenting height of the deaths' peak by country is provided in Fig. 2 .

Table 1.

Characteristics of the countries included in the analysis.

Variable	N	Mean	SD	Median	Lower quartile	Upper quartile	Minimum	Maximum
Peak height (no. of deaths per 1 mln inhabitants)	34	7.22	8.65	3.48	1.68	12.78	0.48	42.80
Peak height (raw no. of deaths)	34	180.50	322.67	32.50	8.00	185.00	2.00	1172.00
Peak time (no. of days after the first death was reported)	34	31.32	13.94	31.00	22.00	40.00	2.00	71.00
All-bed capacity (per 1 mln inhabitants)	34	4940.25	1744.89	4634.17	3427.67	6623.84	2512.45	8248.80
ICU bed capacity (per 1 mln inhabitants)	34	141.14	82.61	110.94	86.50	191.75	20.72	349.20
Total no. of tests up to the time of the peak (per 1 mln inhabitants)	34	763.09	743.98	526.54	443.77	824.78	148.92	4166.11
Stay-at-home order day	34	8.74	10.33	8.00	1.00	14.00	−6.00	41.00
Day of closure of educational facilities	34	−0.26	8.31	0.50	−3.00	4.00	−22.00	17.00
Day of imposing restrictions on gatherings	34	−1.76	8.67	−1.00	−6.00	2.00	−21.00	17.00
Business closure day	34	3.32	10.14	2.00	−1.00	7.00	−16.00	41.00
Population size (January 2020)	34	23.82	33.02	9.33	4.94	37.85	0.34	145.93
Proportion living in urban areas	34	0.74	0.12	0.74	0.66	0.83	0.54	0.98
Proportion living in metropolitan cities with more than 1 mln inhabitants	34	0.28	0.19	0.31	0.12	0.44	0.00	0.56
Median age	34	41.85	2.96	42.50	40.50	44.00	32.00	46.70
Arrivals at airports in 2018 (per 1 inhabitant)	34	2.27	2.63	1.52	0.84	2.79	0.24	14.86
No. of foreign tourists in 2018 (per 1 inhabitant)	34	1.25	1.32	0.79	0.47	1.46	0.14	6.73
Mobility score at the day of the first reported death	34	−23.45	18.93	−20.02	−44.09	−5.28	−56.42	0.16
Border closure day	34	6.71	15.53	2.50	−1.00	11.00	−19.00	46.00
No. of COVID-19 infections when borders were closed (per 1 mln inhabitants)	34	490.54	1116.56	83.39	21.53	245.88	0.07	5223.83
No. of COVID-19 deaths when borders were closed (per 1 mln inhabitants)	34	28.56	71.73	0.27	0.00	3.17	0.00	297.90

COVID-19, coronavirus disease 2019; ICU, intensive care unit; SD, standard deviation; mln, million.

Fig. 1.

Histogram of the height of COVID-19 daily deaths' peak per 1 million inhabitants with a fitted log-normal curve. The histogram presents the distribution of height of COVID-19 deaths' peak per 1 million inhabitants across 34 countries. A log-normal curve was fitted to the distribution with a scale parameter sigma of 1.12 and location parameter zeta of 1.38, assuming logarithm of height of the deaths' peak is normally distributed [Normal(zeta, sigma)]. COVID-19, coronavirus disease 2019.

Fig. 2.

Height of COVID-19 daily deaths' peak per 1 million inhabitants across countries. The plot presents the height of COVID-19 deaths' peak per 1 million inhabitants across 34 countries, with Belgium having an outstandingly highest peak per population size (>40 deaths per 1 million inhabitants). COVID-19, coronavirus disease 2019.

The median height of the peak per 1 million inhabitants was equal to 3.48 deaths per day ([lower quartile; upper quartile] = [1.68; 12.78]), with Belgium reaching an outstandingly higher peak than other countries. As can be seen from these statistics and the histogram, the height of the deaths' peak does not follow a normal distribution, but it can be well approximated using a log-normal distribution. The median time to the peak equalled 31 days from the first death reported in each country, with a comparable mean (31.32, standard deviation = 13.94). Average numbers of days when closing schools/universities and when gatherings were banned were both negative (−0.26 and −1.76, respectively).

Moran's I and Geary's C statistics for height of the deaths' peak were discordant; therefore, spatial autocorrelation was not considered in the main analysis of height of the deaths' peak, but considered in sensitivity analysis (Supplementary Materials). Moran's I and Geary's C statistics for time to peak both indicated no significant spatial autocorrelation; therefore, this was not considered in the analysis of time to the peak.

Height of the deaths' peak

Univariate GLMs of height of the peak were analysed (Table 2 ). Eight factors turned out to be significant: the day of closure of educational facilities, day of imposing restrictions on gatherings, business closure date, proportion of the population living in urban areas, mobility score at the day of the first reported death, border closure day, the number of COVID-19 infections when borders were closed and the number of COVID-19 deaths when borders were closed. All of them have positive estimates. Stay-at-home order day and the proportion of the population living in metropolitan cities with >1 million inhabitants were close to reaching the significance level (P < 0.1). Pearson correlations between variables reaching or close to reaching significance in univariate models were verified (Supplementary Materials).

Table 2.

Results of the univariate and multivariate GLM of height of COVID-19 deaths' peak, with normal distribution and logit link function.

Variable	Univariate analysis				Multivariate analysis
					Base case GLM (full model)				Base case GLM + selection algorithms (final model)
	Estimate	Wald 95% confidence limit		P-value	Estimate	Wald 95% confidence limit		P-value	Estimate	Wald 95% confidence limit		P-value
		Lower	Upper			Lower	Upper			Lower	Upper
All-bed capacity (per 1 mln inhabitants)	−0.0002	−0.001	0.0001	0.109	–	–	–	–	–	–	–	–
ICU bed capacity (per 1 mln inhabitants)	−0.002	−0.008	0.003	0.404	–	–	–	–	–	–	–	–
Total no. of tests up to the time of the peak (per 1 mln inhabitants)	0.000	−0.001	0.001	0.961	–	–	–	–	–	–	–	–
Stay-at-home order day	0.027	−0.001	0.053	0.057∗∗	–	–	–	–	–	–	–	–
Day of closure of educational facilities	0.067	0.028	0.107	0.001∗	–	–	–	–	–	–	–	–
Day of imposing restrictions on gatherings	0.045	0.006	0.084	0.023∗	–	–	–	–	–	–	–	–
Business closure day	0.029	0.009	0.049	0.005∗	−0.001	−0.022	0.020	0.944	–	–	–	–
Population size (mln)	0.001	−0.009	0.011	0.877	–	–	–	–	–	–	–	–
Proportion living in urban areas	8.117	3.695	12.539	<0.001∗	7.127	3.642	10.611	<0.001∗	6.848	4.016	9.680	<0.001∗
Proportion living in metropolitan cities with more than 1 mln inhabitants	2.428	−0.464	5.319	0.099∗∗	1.063	−1.331	3.457	0.384	–	–	–	–
Median age	−0.0003	−0.120	0.120	0.996	–	–	–	–	–	–	–	–
Arrivals at airports in 2018 (per 1 inhabitant)	0.016	−0.097	0.129	0.784	–	–	–	–	–	–	–	–
No. of foreign tourists in 2018 (per 1 inhabitant)	−0.076	−0.421	0.270	0.668	–	–	–	–	–	–	–	–
Mobility score at the day of the first reported death	0.048	0.001	0.096	0.046∗	0.041	−0.0004	0.083	0.052∗	0.049	0.022	0.077	<0.001∗
Border closure day	0.025	0.010	0.041	0.002∗	−0.005	−0.030	0.021	0.729	–	–	–	–
No. of COVID-19 infections when borders were closed (per 1 mln inhabitants)	0.0002	0.0000	0.004	0.022∗	0.0003	−0.0001	0.001	0.113	0.0002	0.0001	0.0003	0.016∗
No. of COVID-19 deaths when borders were closed (per 1 mln inhabitants)	0.004	0.001	0.007	0.002∗	–	–	–	–	–	–	–	–
Multivariate model statistics
Scale	–	–	–	–	5.020	3.958	6.367	–	5.092	4.015	6.458	–
AIC	–	–	–	–	222.203	–	–	–	217.169	–	–	–
AICC	–	–	–	–	227.963	–	–	–	219.312	–	–	–

∗P-value <0.05; ∗∗P-value <0.1.

AIC, Akaike Information Criterion; AICC, AIC corrected for small sample sizes; GLM, generalised linear model; ICU, intensive care unit; mln, million; COVID-19, coronavirus disease 2019.

Univariate and multivariate GLMs with normal distribution and logit link function were used to explore factors associated with height of COVID-19 deaths' peak as of June 3, 2020. Each model was run using 34 observations. Variables significant in univariate models were included in the multivariate base case model, avoiding highly correlated pairs. The final multivariate model was selected based on the use of selection algorithms (backward, forward, stepwise and genetic algorithm).

A base case multivariate GLM included six covariates. The proportion of the population living in urban areas was found to be significant (P < 0.001), and the mobility score at the day of the first reported death was very close to reaching significance (P = 0.052). The results are presented in Table 2. Considering the small sample size (N = 34), selection algorithms were applied to the base case model. All algorithms were consistent and selected the model with three significant parameters (‘final’ model), indicating its best fit. The proportion of the population living in urban areas (6.848, P < 0.001), mobility score at the day of the first reported death (0.049, P < 0.001) and number of infections when borders were closed per 1 million inhabitants (0.0002, P = 0.016) were all significantly associated with the height of the deaths' peak (Table 2).

Analysis of data removing countries with imputed dates of business or border closure (N = 29) provided consistent results with regard to the significance of all three covariates from the final models (Supplementary Materials). In the model with spatial autocorrelation, the effects of the proportion of the population living in urban areas and of number of infections when borders were closed remained positive and statistically significant (P = 0.022 and 0.012, respectively), but the effect of the mobility score was no longer significant (P = 0.400) (Supplementary Materials).

Time to the deaths' peak

Univariate GLMs of time to the peak were analysed (Table 3 ). Nine factors turned out to be potentially significant (with P < 0.1): all-bed capacity, ICU bed capacity, day of closure of educational facilities, day of imposing restrictions on gatherings, population size, arrivals at airports per inhabitant, the number of foreign tourists per inhabitant, the mobility score at the day of the first reported death and the day of border closure. Most of these factors have positive estimates, except the numbers of arrivals and tourists. As for the next step, linear correlations between them were verified. The results can be found in Supplementary Materials.

Table 3.

Results of the univariate and multivariate GLM of time to COVID-19 deaths' peak, with normal distribution and identity link function.

Variable	Univariate analysis				Multivariate analysis
					Base case GLM (full model)				Base case GLM + selection algorithms (final model)
	Estimate	Wald 95% confidence limit		P-value	Estimate	Wald 95% confidence limit		P-value	Estimate	Wald 95% confidence limit		P-value
		Lower	Upper			Lower	Upper			Lower	Upper
All-bed capacity (per 1 mln inhabitants)	0.003	0.001	0.006	0.012∗	0.003	0.001	0.005	0.006∗	0.003	0.001	0.005	0.004∗
ICU bed capacity (per 1 mln inhabitants)	0.046	−0.008	0.101	0.095∗∗	−0.007	−0.049	0.034	0.731	–	–	–	–
Total no. of tests up to the time of the peak (per 1 mln inhabitants)	−0.002	−0.008	0.005	0.598	–	–	–	–	–	–	–	–
Stay-at-home order day	0.201	−0.248	0.649	0.381	–	–	–	–	–	–	–	–
Day of closure of educational facilities	0.680	0.164	1.195	0.010∗	–	–	–	–	–	–	–	–
Day of imposing restrictions on gatherings	0.530	0.019	1.040	0.042∗	–	–	–	–	–	–	–	–
Business closure day	0.365	−0.081	0.810	0.108	–	–	–	–	–	–	–	–
Population size (mln)	0.250	0.135	0.364	<0.001∗	0.117	0.002	0.231	0.047∗	0.142	0.037	0.246	0.008∗
Proportion living in urban areas	0.508	−37.667	38.683	0.979	–	–	–	–	–	–	–	–
Proportion living in metropolitan cities with more than 1 mln inhabitants	13.812	−10.931	38.554	0.274	–	–	–	–	–	–	–	–
Median age	−0.278	−1.860	1.304	0.730	–	–	–	–	–	–	–	–
Arrivals at airports in 2018 (per 1 inhabitant)	−1.908	−3.573	−0.243	0.025∗	–	–	–	–	–	–	–	–
No. of foreign tourists in 2018 (per 1 inhabitant)	−5.099	−8.203	−1.995	0.001∗	−2.872	−5.341	−0.403	0.023∗	−2.651	−5.137	−0.165	0.037∗
Mobility score at the day of the first reported death	0.337	0.117	0.557	0.003∗	0.132	−0.092	0.356	0.249	–	–	–	–
Border closure day	0.326	0.045	0.607	0.023∗	0.215	−0.047	0.477	0.108	0.297	0.079	0.514	0.008∗
No. of COVID-19 infections when borders were closed (per 1 mln inhabitants)	0.001	−0.004	0.005	0.739	–	–	–	–
No. of COVID-19 deaths when borders were closed (per 1 mln inhabitants)	0.038	−0.026	0.102	0.244	–	–	–	–	–	–	–	–
Multivariate model statistics
Scale	–	–	–	–	8.713	6.870	11.050	–	8.901	7.018	11.289	–
AIC	–	–	–	–	259.693	–	–	–	257.146	–	–	–
AICC	–	–	–	–	265.453	–	–	–	260.257	–	–	–

∗P-value <0.05; ∗∗P-value <0.1.

AIC, Akaike Information Criterion; AICC, AIC corrected for small sample sizes; GLM, generalised linear model; ICU, intensive care unit; mln, million; COVID-19, coronavirus disease 2019.

Univariate and multivariate GLMs with normal distribution and identity link function were used to explore factors associated with time to COVID-19 deaths' peak (starting from the day when the first death was reported in a given country), as of June 3, 2020. Each model was run using 34 observations. Variables significant in univariate models were included in the multivariate base case model, avoiding highly correlated pairs. The final multivariate model was selected based on the use of selection algorithms (backward, forward, stepwise and genetic algorithm).

A base case multivariate GLM was run using six explanatory variables. All-bed capacity, population size in millions and the number of foreign tourists per inhabitant were found significantly related to time to the COVID-19 deaths' peak. The results are presented in Table 3. Considering the small sample size (N = 34), selection algorithms were applied to the aforementioned multivariate model. The ‘final’ model had four covariates and was selected by the backward and the genetic algorithm (Supplementary Materials). All-bed capacity per 1 million inhabitants (0.003, P = 0.004), population size in millions (0.142, P = 0.008), the number of foreign tourists per inhabitant (−2.651, P = 0.037) and border closure day (0.297, P = 0.008) were all significantly associated with time to the deaths' peak (Table 3).

Analysis of data removing countries with imputed border closure dates (N = 31) provided consistent results with regard to the significance of all-bed capacity and population size, whereas the number of foreign tourists and border closure day were close in reaching significance, with P < 0.1 (Supplementary Materials).

Discussion

This study provides some evidence about factors associated with COVID-19 mortality peak and time to the peak. One of the strongest predictors of the COVID-19 mortality peak identified in our analysis was the proportion of the population living in urban areas. The relationship between urbanisation and COVID-19 infection ratio was earlier outlined by the United Nations Association,²⁶ estimating that 90% of all reported COVID-19 cases (by July 2020) came from urban areas, becoming the epicentre of the pandemic. High population density increases the propensity of virus spread by increasing the contact rates of individuals. However, some authors²⁷ warn readers against putting too much weight on urban density, arguing that large cities just faced the coronavirus earlier, owing to the higher number of incoming people, and that the timing of start of the epidemic was of bigger interest than population density itself. This observation seems to contradict that of our study because neither the proportion of the population living in urban areas nor that living in metropolitan cities was related to time to deaths' peak.

The number of infections when borders were closed was found to be another important factor associated with the height of COVID-19 deaths' peak, whereas a positive association between border closure day and time to reach the peak was observed. It shows that stopping arrivals to the country at the earlier stage of the epidemic can be crucial in reducing the peak height, stopping the increase in the daily number of deaths earlier and, consequently, flattening the death curve. These findings contradict those of the study by Chaudhry et al.²⁸ who showed no association between rapid border closures and COVID-19 mortality using cumulative data as of April 2020. However, the peak height and mortality may not be strongly correlated. For example, some countries experienced a point peak and dropping fast (France, Spain, Italy), whereas other countries experienced a flattened peak with mortality staying high over a long period of time (US, Brazil, Mexico).²⁹

The difference in average mobility before the pandemic and at the day when the first death was reported in a country was found to be associated with height of the deaths' peak. Previous studies confirm that changes in social distancing covariates can flatten the curve by changing the peak death rate.^{9 , 10} The impact of mobility was no longer significant when accounting for spatial autocorrelation, but this might be due to similarity in policies between the neighbouring countries, leading to similar outcomes.

Tourism indicators were found not to be associated with height of the deaths' peak, but were found to be significant drivers of time to reach the peak. It suggests that the magnitude of inbound tourism can have an impact on accelerating the moment of reaching the peak. However, Aldibasi et al.⁵ and Garcia de Alcaniz et al.⁸ found tourism to be a significant predictor of COVID-19 mortality and infection rates. Ostig and Askin³⁰ also found a significant positive relationship between the number of airline passengers and number of COVID-19 infections.

Another conclusion resulting from the study is that timing of government restrictions, especially border closure, can be found to be an important factor in terms of COVID-19 mortality. What can be observed for many countries is that government restrictions took place several days before any death was reported in a country. Therefore, increase or decrease in mortality can be interpreted as a result of undertaking preventive action by the government. However, when some countries began lockdown too late (Italy, France, United Kingdom), others may have started it earlier than necessary (Poland, Slovakia). Previous studies suggested that there are no significant benefits of very restrictive interventions such as mandatory stay-at-home order.^{31 , 32} Furthermore, prevention and treatment of non-communicable diseases have been severely disrupted since the pandemic began.^{33 , 34} Thus, the balance between confinement timing and avoidance of prolonged lockdown is essential to prevent societies from deep recession³⁵ and negative consequences on health outcomes.

There is no general conclusion on the association between COVID-19 fatality and hospital bed capacity in the literature. Our study showed lack of association between bed capacity and height of the deaths' peak, but higher bed capacity was related to longer time to peak. Garcia de Alcaniz et al.⁸ showed no association between hospital bed density and both the number of infections and number of deaths at any moment of the pandemic. On the contrary, Sorci et al⁷ showed that the case fatality rate was negatively associated with the number of hospital beds per inhabitants. High bed capacity may be associated with more intensive treatment delaying time to death for a number of patients, thus delaying time to peak, but does not affect the peak's height.

Limitations

Our study has several limitations. Data of a limited number of countries were used. We decided not to include countries for which comparative evidence could not be found. Our idea was to focus only on Europe, not to merge it with countries from other continents, and avoid data incomparability issues and eventual difference in the strain as the virus mutates rapidly. However, the number of observations can be assessed as high enough to draw reliable conclusions. Stability of results was tested using different selection algorithms, which was consistent with main findings.

The set of included explanatory variables can be viewed as non-exhaustive. We decided to focus on variables important from a social perspective, assuming that urbanisation, mobility, tourism and government restrictions are more of interest to inform upcoming decisions than other approaches observed in the literature, for example, environmental perspective.^{8 , 11}

Another limitation was associated with data imputation. Countries with imputed government restriction dates were therefore excluded in sensitivity analysis, leading to generally consistent findings.

Conclusions

This study demonstrated significant drivers of COVID-19 mortality magnitude in Europe and shed light on reasons behind variability between countries. The higher proportion of the population living in urban areas, lack of rapid reduction in mobility and delayed government restrictions correlated with a higher COVID-19 deaths' peak. These findings can help improve future response in similar situations or in case of new waves.

Author statements

Acknowledgements

The authors wish to thank Saima Khan (ApotheCom) for proofreading and editing support.

Ethical approval

This study does not require ethical approval as it was conducted using country-level data and involved information freely available in the public domain.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.

Competing interests

None.

Contributors

M.T. conceived the study; K.J. collected and analysed the data; K.J., M.T. and S.A. interpreted the results; K.J. wrote the first draft of the manuscript; K.J., M.T. and S.A. revised the manuscript and approved the final version.

Appendix A. Supplementary data

The following is the Supplementary data to this article: