In silico simulations reveal that RYR distribution affects the dynamics of calcium release in cardiac myocytes

Iaparov et al. use in silico modeling to test the effect of changes in the geometric arrangement of RYR channels on calcium release in cardiac myocytes. Their simulations predict a coupling between RYR distribution at the calcium release site and dyad function.

Abstract

The dyads of cardiac myocytes contain ryanodine receptors (RYRs) that generate calcium sparks upon activation. To test how geometric factors of RYR distribution contribute to the formation of calcium sparks, which cannot be addressed experimentally, we performed in silico simulations on a large set of models of calcium release sites (CRSs). Our models covered the observed range of RYR number, density, and spatial arrangement. The calcium release function of CRSs was modeled by RYR openings, with an open probability dependent on concentrations of free Ca²⁺ and Mg²⁺ ions, in a rapidly buffered system, with a constant open RYR calcium current. We found that simulations of spontaneous sparks by repeatedly opening one of the RYRs in a CRS produced three different types of calcium release events (CREs) in any of the models. Transformation of simulated CREs into fluorescence signals yielded calcium sparks with characteristics close to the observed ones. CRE occurrence varied broadly with the spatial distribution of RYRs in the CRS but did not consistently correlate with RYR number, surface density, or calcium current. However, it correlated with RYR coupling strength, defined as the weighted product of RYR vicinity and calcium current, so that CRE characteristics of all models followed the same state-response function. This finding revealed the synergy between structure and function of CRSs in shaping dyad function. Lastly, rearrangements of RYRs simulating hypothetical experiments on splitting and compaction of a dyad revealed an increased propensity to generate spontaneous sparks and an overall increase in calcium release in smaller and more compact dyads, thus underlying the importance and physiological role of RYR arrangement in cardiac myocytes.

Introduction

Calcium spark is a miniature transient increase of fluorescence intensity observable in the cytosol of cardiac myocytes using calcium-sensitive fluorescent dyes (Cheng et al., 1993; López-López et al., 1994). It represents a local event of calcium release that appears at dyads under specific experimental conditions. The dyads are intracellular structural complexes of cardiac myocytes, where terminal cisternae of the SR connect to the sarcolemma (Sun et al., 1995; Franzini-Armstrong et al., 1998). Under physiological conditions, the local calcium release events (CREs) are triggered in synchrony at all dyads in the whole volume of a myocyte in response to the influx of Ca²⁺ ions through sarcolemmal calcium channels activated by incoming action potential (Cannell et al., 1995; López-López et al., 1995). The resulting global calcium release provides myofibrillar sarcomeres with calcium ions needed for contraction (Eisner et al., 2017).

Calcium sparks also occur in resting cardiac myocytes. Under physiological conditions, these spontaneous sparks occur at low frequency; however, under pathological conditions, their frequency may increase and even initiate arrhythmogenic calcium waves (Cheng et al., 1996; Lukyanenko and Gyorke, 1999). Spontaneous calcium sparks also originate at dyads, but independently of the sarcolemmal voltage-activated calcium channels (Cheng et al., 1993). Their activation results from a spontaneous opening of one of the ryanodine receptors (RYRs), calcium release channels clustered at a terminal cisterna. The released Ca²⁺ ions activate nearby RYRs by the calcium-induced calcium release mechanism (Fabiato, 1983) and thus give rise to the local spark. Calcium sparks depend primarily on RYR function, which is regulated by cytosolic and luminal Ca²⁺ ions, cytosolic Mg²⁺, and cytosolic ATP²⁻, as well as by numerous regulatory proteins and processes (Meissner, 2002, 2004). For physical reasons, it should also depend on the group characteristics of RYR clusters. The question of how the distribution of RYRs in the cisternae affects the properties of calcium sparks remains open.

The structure of terminal cisternae studied by EM revealed common features in their construction (Franzini-Armstrong et al., 1999; Hayashi et al., 2009) as well as their substantial structural variability (Novotova et al., 2009; Novotova et al., 2013; Novotová et al., 2020). Super-resolution localization studies revealed a tendency of RYRs to form irregular clusters of variable size and surface density (Baddeley et al., 2009; Hou et al., 2015; Macquaide et al., 2015; Galice et al., 2018; Jayasinghe et al., 2018; Kolstad et al., 2018; Asghari et al., 2020). Changes in the size, shape, and content of terminal cisternae, regarding the number of RYRs and amount of calsequestrin, accompany changes in the structure of dyads (Asghari et al., 2020; Drum et al., 2020; Novotová et al., 2020). It should be noted that the positions of spontaneous calcium sparks, termed calcium release sites (CRSs), were associated with terminal cisternae according to indirect observations, such as colocalization of the spark fluorescence with that of t-tubules and z-discs (Parker et al., 1996; Cleemann et al., 1998; Hiess et al., 2015). Our understanding of the terminal cisterna as the substrate of calcium sparks is complicated by the difficulty to estimate explicitly the composition of the source of calcium flux. It is not clear how RYRs of a terminal cisterna participate in the formation of calcium sparks. Is it the whole cisterna, one of its RYR clusters, or even only a single RYR, which determines calcium sparks?

The calcium release function of CRSs can be studied only indirectly, in particular by monitoring CREs, such as calcium sparks or calcium spikes (Cheng et al., 1993; Song et al., 1998). Despite the recent progress in technologies, these approaches have limited spatiotemporal resolution and signal-to-noise ratio, inherent to the calcium-sensitive fluorescent dyes (Smith et al., 1998; Zahradníková et al., 2007). CREs vary broadly from invisible events, named quarks (Lipp and Niggli, 1996), through miniature “quarky calcium release” (Brochet et al., 2011; Shang et al., 2014), to brief sparks (Cheng et al., 1993) and prolonged sparks (Zima et al., 2008; Brochet et al., 2011). The CRE signal varies even if recorded repeatedly at the same spot (Sobie et al., 2006; Zima et al., 2008; Janíček et al., 2012; Shang et al., 2014). Interpretation of local fluorescent signals is difficult since it is based on data obtained either indirectly or in artificial systems. Therefore, theoretical approaches could be of help to formulate and verify working hypotheses (Soeller and Cannell, 2004; Williams et al., 2007; Soeller et al., 2009; Williams et al., 2011; Stern et al., 2013).

According to recent understanding, calcium sparks result from group activity of numerous RYRs clustered at CRSs. A close association of RYRs was observed in cardiac dyads (Asghari et al., 2014) and purified cardiac RYRs (Cabra et al., 2016); however, only a small fraction of RYRs, whether in situ or in vitro, physically interact (Zahradníková et al., 2010a; Jayasinghe et al., 2018). The first estimates of the junctional SR surface area per RYR were close to 900 nm² (i.e., 30 × 30 nm; Franzini-Armstrong et al., 1999; Soeller et al., 2007). This corresponds to a tightly packed RYR cluster. The more recent estimates report values in the range of 3,000−12,500 nm² (Baddeley et al., 2009; Hayashi et al., 2009; Hou et al., 2015; Galice et al., 2018; Jayasinghe et al., 2018). The average number of RYRs per CRS, often used as a measure of CRS size, was estimated in the range of 8–22 for terminal cisternae attached to the surface sarcolemma (Baddeley et al., 2009; Jayasinghe et al., 2018), and 8–100 for terminal cisternae attached to the tubular sarcolemma (Soeller et al., 2007; Hayashi et al., 2009; Scriven et al., 2010; Hou et al., 2015; Galice et al., 2018). The existence of clusters with RYRs separated by the edge-to-edge gap of >100–150 nm led to the postulation of superclusters (Baddeley et al., 2009; Hou et al., 2015; Macquaide et al., 2015). Thus, the definition of CRS size by the number of its RYRs is somewhat fuzzy. However, the question of how the CRS size, RYR number, and RYR surface density are related to calcium spark amplitude and duration is of fundamental physiological importance, for instance, for understanding the changing calcium release function during postnatal development (Ziman et al., 2010; Louch et al., 2015; Macková et al., 2017) or in various pathologies (Song et al., 2006; Wu et al., 2012).

The understanding of cardiac dyads can be advanced by mathematical modeling, which allows for the exploration of the whole range of experimental data through the parametric space of defined models. In this modeling study, we addressed mainly the issues of calcium spark variability related to geometrical factors of RYR arrangement at CRSs. We developed a set of models to compare CREs produced by CRSs differing in RYR number, arrangement, surface density, and single-channel calcium current. The model parameters spanned the whole range of relevant findings published recently. Activation of RYRs was simulated by a gating model conforming to the experimentally observed sensitivity of the cardiac RYR to activation by Ca²⁺ ions and inhibition by Mg²⁺ ions (Laver et al., 1997; Zahradníková et al., 2003). This allowed us to elucidate how the CRS determinants affect the properties of local CREs.

Materials and methods

Simulations

Programs for construction of the topology of CRSs and simulation of the activity of RYRs at CRSs were written in C++. The algorithms are described in Model formulation. Both programs were parallelized using the OpenMP API (https://www.openmp.org). Parallel generation of random numbers was performed using OpenMP Parallel Statistical Random Number Generator OMPRNG (M. Bognar, University of Iowa, Iowa City, IA; https://homepage.stat.uiowa.edu/~mbognar/omprng/). The Uran supercomputer at Krasovskii Institute of Mathematics and Mechanics of the Ural Branch of the Russian Academy of Sciences was used for part of the model calculations. Cytosolic calcium signals were simulated using CalC (Matveev et al., 2002).

Analyses

Data analysis was performed in OriginPRO version 2020b (OriginLab). The data were fitted by theoretical functions using the Levenberg-Marquardt method.

Model formulation

Models of a CRS were represented by a group of RYRs characterized by geometrical and functional descriptors. The geometrical descriptors included the number of RYRs in the CRS (N_RYR), the area of CRS per one RYR (A_C/R), arrangement patterns of RYR distribution (checkerboard [ChB], side by side [SbS], and isolated RYRs), and coordinates of RYRs. The functional descriptors included the RYR single-channel calcium current (i_Ca), the on- and off-rate constants of RYR gating (k_co and k_oc, respectively), and parameters of calcium diffusion and binding to buffers. The values of N_RYR, A_C/R, and i_Ca, as well as arrangement patterns were varied within the range of published values, and their impact on the generation of CREs was evaluated.

The model of RYR gating

We used a simple two-state RYR gating model to minimize requirements for computational power (Eq. 1), with the open probability dependent on free Ca²⁺ and Mg²⁺ concentration:

$$\mathrm{C}\underset{k_{oc}}{\overset{k_{co}}{\rightleftharpoons }}\mathrm{O}.$$ (1)

The gating model obeyed experimental observations—namely, the RYR open probability at low Ca²⁺ concentration and the effect of Mg²⁺ binding to the RYR inhibition sites (Laver et al., 1997; Zahradníková et al., 2003; Tencerová et al., 2012). The value of the off-rate constant k_oc = 0.45 ms⁻¹ was set in correspondence to the mean RYR open time (2.2 ms), estimated in the presence of ATP and Mg²⁺ on the cytosolic RYR side and at a realistic Ca²⁺ concentration on the luminal RYR side (Zahradníková et al., 2003). Similar values under similar conditions were reported by Györke and Györke (1998) and Laver and Honen (2008). The on-rate constant k_co was made dependent on the cytosolic [Ca²⁺] and [Mg²⁺] as

$$k_{co}\left(\left[{\mathrm{Ca}}^{2+}\right],\left[{\mathrm{Mg}}^{2+}\right]\right)=\frac{k_{oc}{P}_a\left(\left[{\mathrm{Ca}}^{2+}\right],\left[{\mathrm{Mg}}^{2+}\right]\right)}{1-P_a\left(\left[{\mathrm{Ca}}^{2+}\right],\left[{\mathrm{Mg}}^{2+}\right]\right)}$$ (2)

(Iaparov et al., 2019), where P_a is the Ca²⁺- and Mg²⁺-dependent open probability of the allosteric homotetrameric gating model according to Zahradníková et al. (2010b). The [Ca²⁺] and [Mg²⁺] are free ion concentrations calculated for coordinates of the center of an RYR. The steady-state open probability of this model,

$$P_O=\frac{k_{co}}{k_{co}+k_{oc}},$$ (3)

was thus dependent on [Ca²⁺] and [Mg²⁺], as shown in Fig. 1 for 1 mM [Mg²⁺] used in all CRS simulations. Under these conditions, the maximum steady-state open probability $P_O^{max}$ was 0.31.

Figure 1.

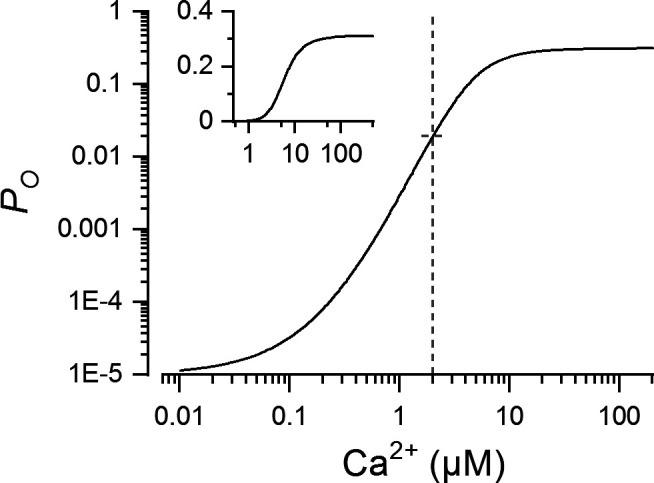
Calcium dependence of RYR open probability (Po) for the two-state gating model. Po was calculated by Eqs. 2 and 3. The dashed line indicates the Ca²⁺ concentration used for demarcating the iso-concentration level in Fig. 2. The inset shows the same data with the ordinate on a linear scale.

Generation of CRSs

The variable clustering of RYRs in terminal cisternae was modeled by generating a large set of CRSs with different RYR arrangement that was varied following experimental data. Four topologically different CRS arrangement patterns (Fig. 2 and Table 1) were made by placing 10, 20, 40, or 80 RYRs on the CRS plane at calculated or experimentally determined positions (see below) to encompass the range of reported CRS sizes and RYR surface densities (Baddeley et al., 2009; Hou et al., 2015; Galice et al., 2018; Jayasinghe et al., 2018).

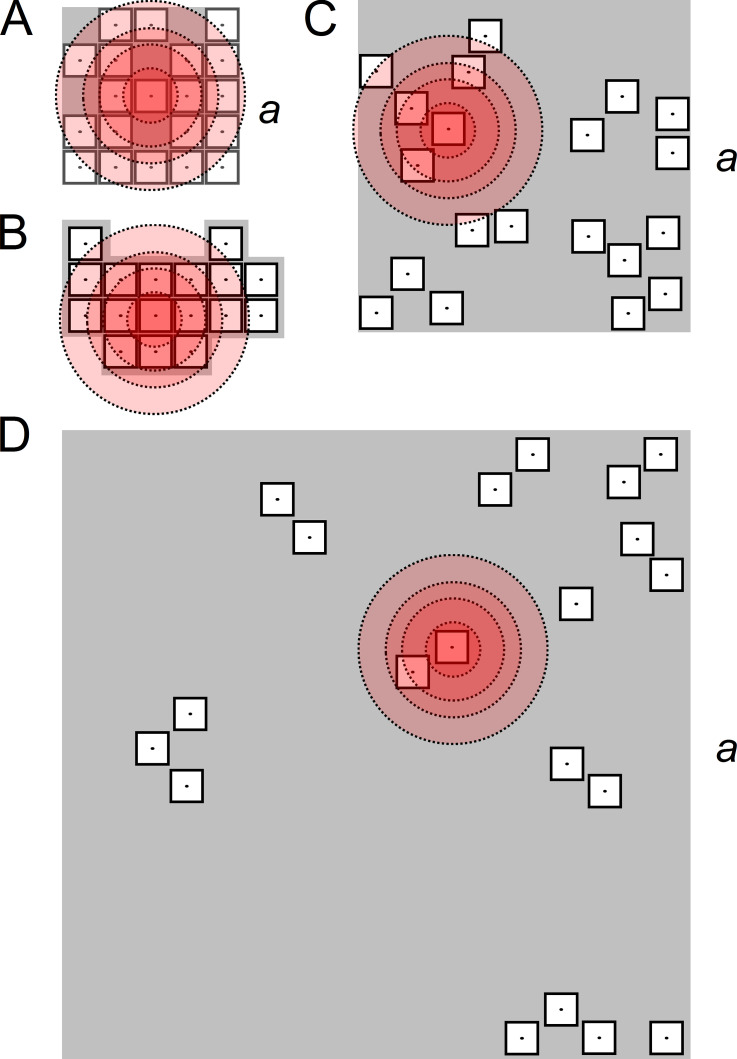
Figure 2.

Example geometric models of CRSs of different density types. (A) A compact square CRS with 20 RYRs arranged side by side on a 5 × 5 lattice; a = 150 nm. (B) A compact contact network CRS with 17 RYRs arranged side by side according to Walker et al., 2015. (C) A narrow CRS with 20 RYRs distributed according to pattern B (Table 1); a = 264 nm. (D) A wide CRS with 20 RYRs distributed according to pattern B (Table 1); a = 501 nm. The shadowed areas represent the planes of the CRSs. The empty squares with dots represent RYRs with a central ion channel, the point source of Ca²⁺ flux. The concentric circles of increasing diameter depict 2 µM [Ca²⁺] levels calculated for i_Ca of 0.04, 0.15, 0.25, and 0.4 pA, at which the steady-state open probability of a RYR would be 2% (see Fig. 1).

Table 1. Pattern composition of narrow and wide CRSs.

Pattern	NRYR	CRS composition
		Chb		SbS		Both		Isl
		F	N	F	N	F	N	F	N
A	10	0.821	9	0.051	0	0.013	0	0.115	1
	20		18		0		0		2
	40		33		2		0		5
	80		66		4		1		9
B	10	0.500	5	0.400	4	0.067	1	0.033	0
	20		10		8		2		0
	40		20		16		3		1
	80		40		32		5		3
C	10	0.165	2	0.691	7	0.041	0	0.103	1
	20		3		14		1		2
	40		6		28		2		4
	80		13		56		3		8

“Both” indicates both ChB and SbS. F, the average fraction of RYRs in the specific configuration determined by Asghari et al. (2014) for 0.1, 1.0, and 4.0 mmol/l Mg²⁺ (patterns A, B, and C, respectively); Isl, isolated RYR configuration; N, the number of RYRs in each specific configuration and pattern, calculated from the given N_RYR and the average fraction F.

To characterize the packing of RYRs in CRSs, we used the A_C/R (nm²), that is, the average area of CRS associated with one RYR, which is more suitable for geometrical considerations than the RYR surface density (nm⁻²). The N_RYR and the A_C/R were used to calculate the side a of the CRS as $a=\sqrt{N_{RyR}.A_{C/R}}.$ Three CRS density type models were used in this study to cover the whole range of reported A_C/R values.

The compact-type CRSs were of two variants. The square variants of compact CRSs (Fig. 2 A) contained the given number of RYRs placed side by side on a rectangular grid of 30 × 30-nm squares. To accommodate the given number of RYRs in the square grid, the empty positions were placed at random. The resulting A_C/R was 1,440, 1,125, 1,103, and 911 nm² per RYR, respectively, for 10, 20, 40, and 80 RYRs in the CRS (areas equivalent to squares with sides of 38, 34, 33, and 30 nm). For each N_RYR, a set of five compact square CRSs was generated (altogether 20 CRSs). The irregular variants of compact CRS (Fig. 2 B) used the experimentally determined coordinates (Walker et al., 2015) of 9–96 RYRs placed on a contact network grid with 31-nm spacing. Altogether, 107 of these CRSs had A_C/R equal to 961 nm² per RYR (the area equivalent to a square with a side of 31 nm).

The narrow-type CRSs (Fig. 2 C) had RYR surface density corresponding to that estimated by Jayasinghe et al., 2018. All narrow CRSs had an A_C/R of 3,481 nm² (the area equivalent to a square with a side of 59 nm). For each N_RYR and each pattern (Table 1), a set of 100 CRSs with different RYR coordinates was generated (altogether 1,200 narrow CRSs).

The wide-type CRSs (Fig. 2 D) had RYR surface density corresponding to that estimated by Galice et al., 2018. All wide CRSs had an A_C/R of 12,544 nm² (the area equivalent to a square with a side of 112 nm). For each N_RYR and each pattern (Table 1), a set of 100 CRSs of different RYR coordinates was generated (altogether 1,200 wide CRSs).

Arrangement of RYRs in compact CRSs followed the side-by-side configuration (Yin et al., 2005; Groff and Smith, 2008; Walker et al., 2015). The topology of the narrow and wide CRSs consisted of RYRs arranged into three patterns with defined proportions of neighbors in the ChB configuration, the SbS configuration, and the isolated position, as observed by EM (Asghari et al., 2014) under different experimental conditions (Table 1). Pattern A was dominated by RYRs in the ChB configuration, typical for low cytosolic Mg²⁺ concentrations. Pattern C was dominated by RYRs in the SbS configuration, typical for high cytosolic Mg²⁺ concentrations. The balanced pattern (B) contained the ChB, SbS, and isolated RYR configurations, as observed for near-physiological conditions. The placement of RYRs in the narrow and wide CRSs according to patterns A, B, or C was solved as an optimization problem (Iaparov et al., 2017; Iaparov et al., 2019). The prescribed distribution was achieved with the use of the global optimization algorithm GSA (genetic simulated annealing; Xu et al., 2011), which is a combination of a genetic algorithm and simulated annealing. Briefly, the algorithm generates a random distribution of the given number of RYRs (N_RYR) and then minimizes the sum of squares of differences between the prescribed and the achieved number of channels in each arrangement. Minimization proceeded until the prescribed configuration was exactly achieved. The GSA is a stochastic algorithm; thus, each execution generated a CRS with different RYR coordinates but with the same distribution of the configurations (Table 1). The RYR coordinates of individual CRSs were used to calculate their set of inter-RYR distances.

Simulation and analysis of CREs

Each CRS model was subjected to simulations of CREs in which the stochastically simulated activity of all RYRs was recorded for 100 ms. The stochastic nature of RYR gating results in temporal fluctuations of open RYRs; therefore, each simulation of the CRS activity was repeated 10,000 times for each CRS model. This means that each RYR of the CRS was initialized by 10,000/N_RYR times (on average).

To unveil the impact of calcium current passed by a single RYR on spark generation by CRS models of diverse types, we used four i_Ca values of 0.04, 0.15, 0.25, and 0.4 pA. These were kept constant during simulations. The calcium current through a single RYR or a single CRS has not yet been determined in situ. Numerous experimental difficulties make the estimates ambiguous because of their dependence on many variables that are difficult to control in experiments. Janíček et al. (2012) concluded that the calcium release flux per single RYR should be near 0.4 pA, a value satisfying estimates by independent experiments. In previous CRS modeling studies, i_Ca of 0.04 pA (Groff and Smith, 2008), 0.15 pA (Walker et al., 2015), or 0.6 pA (Cannell et al., 2013) were used for spark simulations.

The concentration of calcium ions inside the CRS is not homogenous (Valent et al., 2007; Walker et al., 2014). At each locality, it depends on the positions of open RYRs and the single-channel calcium current in a complex manner, with it being affected by the diffusion rates, the geometry of the CRS, buffering by mobile and immobile buffers, and calcium-binding kinetics. In this study, calcium concentrations at each RYR position were calculated using the Naraghi and Neher approximation for calcium diffusion in the cytosolic half-space delimited by the plane of the CRS, based on the supposition of instantaneous formation of a steady-state calcium gradient upon RYR opening and sufficient calcium buffering capacity of the cytosol (Naraghi and Neher, 1997). The spatial [Ca²⁺] profile around an RYR is then an explicit function of mean reaction times of calcium ions with buffers and of the buffering capacity and mobility of each buffer. Buffering of Ca²⁺ by calmodulin, ATP, and Fluo-4 was calculated using parameters of Ca²⁺ diffusion and the concentrations, equilibrium constants, and rate constants of Ca²⁺ binding to ATP, calmodulin, and Fluo-4 taken from Hake et al. (2012). A record of the number of open RYRs in time was generated using the Gillespie algorithm (Gillespie, 1977). Briefly, each CRE was started by an opening of the selected RYR. Calcium influx changed calcium distribution in the CRS and, correspondingly, the opening rate constants of individual RYRs. These stayed constant until the next opening or closure of any RYR in the CRS because of the instantaneous and stationary calcium gradient approximation (see above). The Gillespie algorithm determines the channel that changes its state—opens or closes—and the time of this change. The identity index of the RYR that would change its state was sampled from the distribution of probabilities of state transitions of individual RYRs, which was for each RYR equal to the ratio of its transition rate constant to the sum of rate constants over all RYRs. The time of the change was sampled from the exponential distribution of waiting times calculated for a rate constant equal to the sum of instantaneous values of transition rate constants over all RYRs in the CRS (k_co for closed RYRs and k_oc for open RYRs). The resulting transition led to a new calcium distribution in the CRS and a new set of opening rate constants. The algorithm was repeated until the end of the simulation.

The simulated traces of RYR activity (i.e., the CREs), were characterized by the number of simultaneously open RYRs at the peak of the trace $\left(N_O^{peak}\right),$ by the time to peak (TTP; the time to the first occurrence of $N_O^{peak}),$ and by the relative amplitude of the peak (A_rel), normalized to the number of RYRs in the CRS as:

$$A_{rel}=\left(N_O^{peak}-1\right)/N_{RyR},$$ (4)

where $\left(N_O^{peak}-1\right)$ is the maximal number of simultaneously recruited RYRs. These CRE characteristics were used for constructing histograms and for further analyses as described below.

Calculations of fluorescence signals from CRE traces

The fluorescence signal was calculated from the time course of the total calcium current produced by a CRE taken as a spherical source with a 200-nm diameter and considering spherically symmetrical calcium diffusion, binding of calcium to cytosolic buffers, and fluorescence proportional to the concentration of calcium-bound Fluo-4, as described in Hake et al. (2012) and Walker et al. (2014). Parameters of binding and diffusion of ATP, calmodulin, troponin, and Fluo-4 were taken from Hake et al. (2012), and those of the sarcolemmal and SR membrane buffers were taken from Zahradníková et al. (2007). The calculated spatial profile of Ca²⁺-bound Fluo-4 concentration was convolved with a Gaussian point spread function to approximate the image observed by fluorescent microscopy (Smith et al., 1998).

Spatial determinants of CRSs

According to the calcium-induced calcium release theory, Ca²⁺ ions are the interaction element between RYRs that spreads by diffusion. In published models of CRSs, this fact was handled in different ways. For CRSs with uniform RYR arrangement, Williams et al. (2011) introduced the mean-field approximation of Ca²⁺-mediated RYR–RYR interaction. This approximation does not apply to the general case of a nonuniform arrangement of RYRs (Iaparov et al., 2019). For compactly packed RYRs on a regular lattice, Walker et al. (2014) used the maximum eigenvalue of the RYR adjacency matrix as an overall parameter characterizing RYR arrangement. The adjacency principle, however, does not adequately characterize the geometry of nonadjacent freely distributed RYRs. Other measures of RYR arrangement, namely the average nearest-neighbor distance, the four nearest-neighbor distances, and the mean RYR occupancy, all related to the RYR surface density and mean RYR–RYR distance in CRSs (Cosi et al., 2019), correlated with parameters of simulated calcium sparks relatively weakly. Recently, we have found (Iaparov et al., 2017) that a promising predictor of spark occurrence for general CRSs could be the maximum eigenvalue of the RYR inverse distance matrix, which, however, is difficult to perceive for its somewhat abstract meaning. Therefore, we define here new geometric parameters, namely, the closeness and vicinity that characterize the spatial disposition of RYRs in a general CRS more conceivably and allow for interpretation of simulated CREs on common grounds, as demonstrated in Results.

Let us consider the steady-state solution of the diffusion equation that relates the Ca²⁺ distribution to the positions of open RYRs. Generally, in an unbuffered system, the concentration of Ca²⁺ ions at individual RYR positions is proportional to the sum of reciprocal values of distances D_ij to the open RYRs, [Ca²⁺]_RYRi ∝ ∑_j1/D_ij (Crank, 1975; nota bene: the presence of calcium buffers, considered in this study, decreases the concentration of free Ca²⁺ ions and distorts their steady-state distribution [Naraghi and Neher, 1997]; thus, the above relationship between RYR positions and Ca²⁺ distribution should be understood as an upper bound in formulations of Ca²⁺ mediated RYR–RYR interactions used below). The inverse of the distance can be thought of as the closeness C_ij = 1/D_ij, where indices i and j correspond to elements of the RYR distance matrix. This means that the formation of a CRE by interacting RYRs may be related to the RYR closeness matrix C composed of elements C_ij, where the elements of the i^th row correspond to the closeness of the remaining RYRs (j ≠ i) to the i^th RYR. Let us further consider a linear transformation on a CRS plane yielding all coordinates of its elements multiplied by a factor K. This transforms the distances between RYRs in proportion to K, and the surface area per RYR in proportion to the square of K. Thus, when the surface area of a CRS, given as S_CRS = A_C/R × N_RYR, is changed, the distances between RYRs are changed proportionally to the square root of the change in surface area—that is, C_ij ∝ $1/\sqrt{A_{C/R}}$ when N_RYR is constant, or C_ij ∝ $1/\sqrt{N_{RyR}}$ when A_C/R is constant. Considering these relationships allows us to characterize RYR distribution in the CRS by a new parameter—the normalized closeness $v_{ij}=C_{ij}\sqrt{N_{RyR}}$—which we named the vicinity of i^th RYR to j^th RYR. The effect of Ca²⁺ flux through the i^th RYR on the whole CRS can then be considered a function of the average vicinity v_i of the i^th RYR to the N_RYR − 1 remaining RYRs defined as

$$v_i=\frac{{{\displaystyle \sum }}_{j,j\ne i}{v}_{ij}}{N_{RyR}-1}=\frac{\sqrt{N_{RyR}}{{\displaystyle \sum }}_{j,j\ne i}{C}_{ij}}{N_{RyR}-1}.$$ (5)

The average vicinity, in contrast to the average closeness, does not change when the surface area of CRS is altered by changing N_RYR at a given A_C/R. The whole CRS can be then characterized by the mean vicinity of all its RYRs (i.e., the group RYR vicinity v):

$$v=\frac{{{\displaystyle \sum }}_i{v}_i}{N_{RyR}}.$$ (6)

The group RYR vicinity defined in this way thus represents a CRS state variable characterizing the spatial component of the RYR–RYR interaction potential. As such, it will be used later for the analysis of simulated CREs. In contrast to the surface density, the vicinity characterizes the distribution of RYRs in the CRS.

Since CRS activity upon the opening of the i^th RYR depends also on the calcium current through this RYR, we defined a combined state variable φ_i pertinent to and characterizing the i^th RYR as the weighed product of calcium current and RYR vicinity:

$${\phi }_i=v_i.i_{Ca}{}^{\alpha } \left({\mathrm{in} \mathrm{units} \mathrm{of} \mathrm{A}}^{\alpha }{ \mathrm{m}}^{-1}\right)$$ (7)

where the power α is the weight factor for relative contributions of calcium current and vicinity of the i^th initiating RYR to the CRS response. Developing this idea to account for CRS activation by the opening of any of its RYRs, the group RYR vicinity v (Eq. 6) allows us to define a state variable for the whole CRS as

$$\phi = v\cdot i_{Ca}{}^{\alpha }(A^a{m}^{-1}).$$ (8)

From the point of physical meaning, the CRS state variables φ_i and φ could be considered to be indicators of RYR coupling strength, since they increase with increasing vicinity and with increasing calcium influx.

Values of the exponent α were found by approximating the relations of CRE characteristics to their respective RYR coupling strengths—φ_i or φ, as appropriate—using a general state-response function:

$$F\left(x\right)=F_{max}\frac{x^n}{x^n+ K^n},$$ (9)

where x stays for φ_i or φ, F_max is the maximal response, K is x at half-maximum, and n is the slope factor.

Model limitations

Several simplifications were applied to keep computational costs reasonable. The model of RYR gating provides a realistic calcium dependence of RYR open probability; however, both the allosteric effect of Ca²⁺ and Mg²⁺ binding on RYR activation (Zahradník et al., 2005; Zahradníková et al., 2010b) and the Mg²⁺ binding at the inhibition site (Laver et al., 1997; Zahradníková et al., 2003) are modeled by a decrease of the RYR activation rate. As a result, the kinetics of RYR activation may differ to some extent.

The models of CRSs do not account for the effect of SR lumen depletion on single-channel calcium current. This simplification was necessary to understand the effect of geometric factors alone. Nevertheless, the effect of i_ca amplitude on the formation of CREs was tested extensively.

The use of a simplified model of buffered calcium diffusion in semi-infinite space (Naraghi and Neher, 1997), instead of a full reaction-diffusion model of the dyadic gap (Valent et al., 2007), substantially speeded up calculations but also undervalued the buildup of calcium concentrations at individual RYRs. However, considering that the activation of RYRs after an RYR opening proceeds much slower than the build-up of the calcium gradient (Soeller and Cannell, 1997; Valent et al., 2007), this simplification should not weaken the correlations described in Results.

Online supplemental material

The activity of individual RYRs and the corresponding calcium concentration changes in the CRS plane, corresponding to the records of RYR activity in Fig. 3 A, are shown in the videos. Video 1 shows the temporal evolution of RYR activity and calcium concentration changes during a typical quark. Video 2 shows the temporal evolution of RYR activity and calcium concentration changes during a typical blip. Video 3 shows the temporal evolution of RYR activity and calcium concentration changes during a typical spark.

Figure 3.

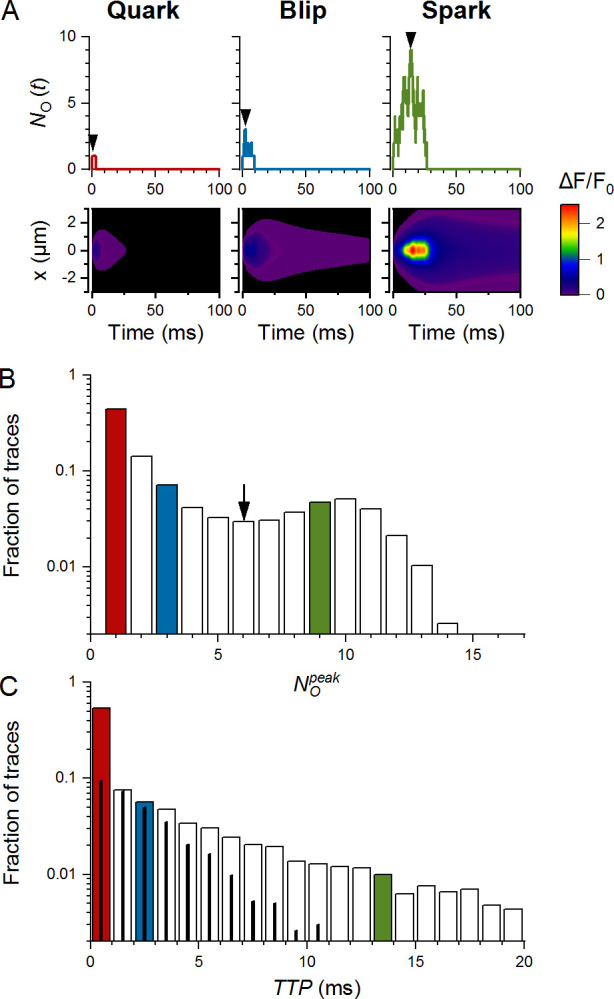
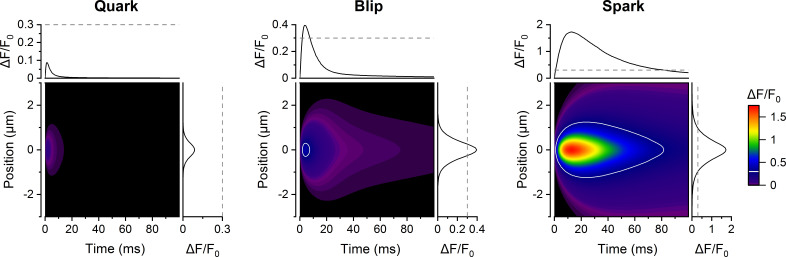
Types and characteristics of CREs. The exemplified data set consisted of 10,000 CREs, generated in a narrow CRS of pattern B, 20 RYRs, and i_Ca of 0.25 pA. The color-coded histogram bins correspond to traces of the same color. (A) Examples of three types of CREs: a quark (left), a blip (center), and a spark (right), shown as simulated time courses of N_O (upper panels) and as their calculated x-t fluorescence signals (lower panels). Arrowheads indicate positions of $N_O^{peak}$ and TTP. The color map indicates the relative amplitude of fluorescence signals, common for all three images. (B) The distribution of $N_O^{peak}$ values in the data set. Quarks, blips, and sparks represented 44%, 32%, and 24% of traces, respectively. The nadir of the histogram was at six simultaneously open RYRs (arrow). (C) The distribution of TTP values in the data set. The thin black columns correspond to the fraction of blips. The red, blue, and green columns in B and C correspond to the three respective events depicted in A. Note the logarithmic scales on the ordinates.

Video 1.

The temporal evolution of RYR activity and calcium concentration changes during a typical quark. Playback speed is 1/1,000 of the real speed. The flow of time is indicated in the right panel.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012685.v1.mp4/source

Video 2.

The temporal evolution of RYR activity and calcium concentration changes during a typical blip. Playback speed is 1/1,000 of the real speed. The flow of time is indicated in the right panel.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012685.v2.mp4/source

Video 3.

The temporal evolution of RYR activity and calcium concentration changes during a typical spark. Playback speed is 1/1,000 of the real speed. The flow of time is indicated in the right panel.

https://movie.rupress.org/media/by_doi/10.1085/jgp.202012685.v3.mp4/source

Results

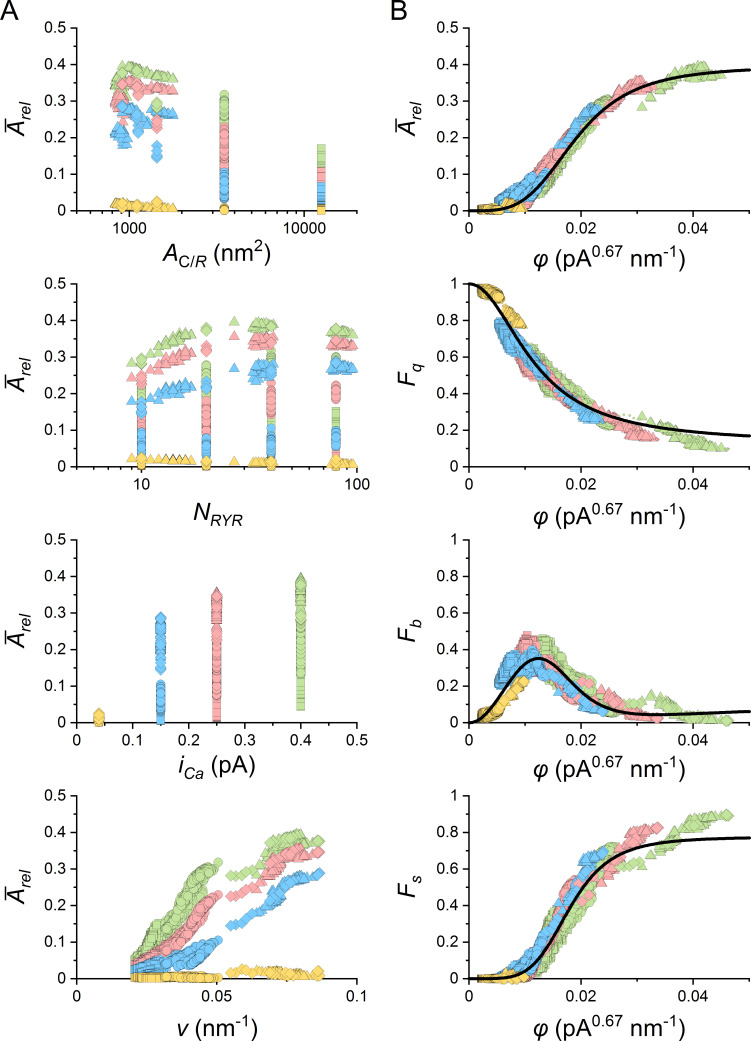
This study surveys CREs generated by 10,108 CRS models. Each model CRS was defined by a set of CRS determinants covering the range of published data, including the number of RYRs, CRS density type, the arrangement of RYRs into specific patterns, and single-channel calcium current values. CRE simulation was initiated by opening of one of the RYRs in the CRS and recording for 100 ms. CRE records were characterized by their $N_O^{peak},$ relative amplitude, TTP, and the molar amount of calcium ions released during the event (n_Ca). CRS activity was characterized by the average relative amplitude Ā_rel and the fraction of different response types and their average time course (see below) calculated from 10,000 simulations.

Basic characteristics of simulated CREs

CRSs responded to the initial RYR opening by three very distinct types of CREs (Fig. 3), classified and named as follows.

The smallest CRE responses consisted of the initial RYR opening alone, which did not trigger other RYR openings. We named them quarks in analogy to the smallest CREs experimentally observed in situ (Lipp and Niggli, 1996; Brochet et al., 2011; Wescott et al., 2016). Durations of simulated quarks followed exponential distribution. The fluorescence image of a quark (Fig. 3 A) showed peak intensity below experimental resolution.

Intermediate CRE responses, emerging as openings of a few RYRs that deactivated rapidly, were named blips. At the peak of blips, the number of simultaneously open RYRs was typically between two and eight. Typical blips peaked in <1.5 ms and ceased completely in <15 ms. The fluorescence image of a blip (Fig. 3 A) showed peak intensity near the limit of experimental resolution (nota bene: the term blip used here is not meant to refer to calcium transients described by Swillens et al. [1998] as blips for inositol 1,4,5-trisphosphate receptor activity).

Responses containing openings of many RYRs with TTP typically above 3 ms that deactivated typically within 50 ms were named as sparks for their obvious similarity to real calcium sparks. The fluorescence image of a spark (Fig. 3 A) showed peak intensity above the limit of experimental resolution at all inspected i_Ca values.

The simulated gating activity of individual RYRs and the corresponding changes of calcium concentration in the CRS plane for quarks, blips, and sparks are demonstrated in Video 1, Video 2, and Video 3.

The amplitude histograms of all CREs (see the example in Fig. 3 B) showed a clear nadir under most CRS settings. The histograms were used to estimate the relative occurrences (fractions) of quarks, blips, and sparks in the simulation data sets obtained for all CRS determinants. The fraction of CREs in the first bin $\left(N_O^{peak}=1\right)$ was assigned to quarks (F_q). The sum of CRE fractions in bins from $N_O^{peak}=2$ to the nadir of the histogram was assigned to blips (F_b), and the sum of CRE fractions for bins above the nadir was assigned to sparks (F_s). The TTP histograms of simulated CRSs (Fig. 3 C) usually showed a monotonic decrease.

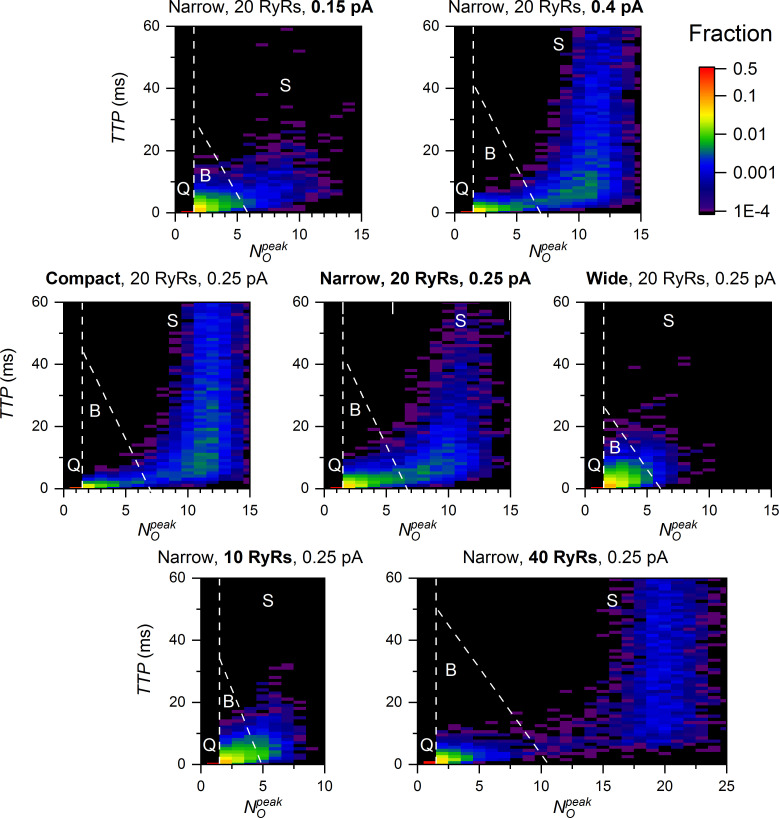
Correlations of peak amplitudes and TTPs showed that quarks, blips, and sparks could be distinguished from each other as regions of distinct fractional occurrence, as exemplified for selected CRS models in Fig. 4. The quarks are unique for their constant amplitude and TTP $(N_O^{peak}=1;$ TTP = 0) by definition. The blips have a TTP almost independent of their amplitude, while the TTP of sparks varies the broader, the higher is their amplitude. Similarly, the TTP of blips was shorter in CRSs of higher i_Ca (top row), more compact density type (middle row), and higher N_RYR (bottom row). In the case of sparks, the $N_O^{peak}$ and the fractional occurrence were higher and the TTP was longer in CRSs of higher i_Ca, more compact density type, and higher N_RYR. This apparent tripartite CRS activity stems solely from the stochastic gating of RYRs. Its relation to the CRS determinants will be analyzed below.

Figure 4.

${\mathit{N}}_{\mathbf{O}}^{\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}\mathbf{,}$TTP, and fraction of CREs. The dashed lines indicate boundaries between CREs of quark (Q), blip (B), and spark (S) type. The fraction of CREs in individual bins is indicated by the color map (top right).

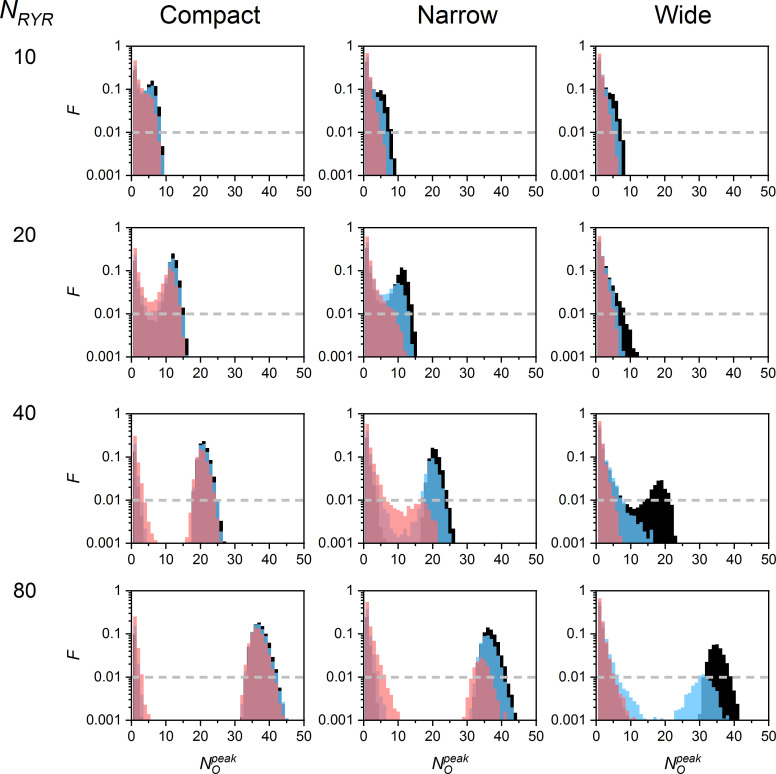
CREs depend on CRS determinants

The distributions of $N_O^{peak}$ values varied substantially with CRS determinants (Fig. 5). The quarks and blips prevailed when the RYR number, density, and i_Ca were low, while the sparks dominated when at least one of these parameters was high. When i_Ca was very low, the sparks activated exclusively in large compact CRSs, but rarely (not shown). In CRSs with N_RYR = 10, the distribution of $N_O^{peak}$ values often did not have a clear nadir; thus, the distinction between blips and sparks was not so prominent.

Figure 5.

${\mathit{N}}_{\mathbf{O}}^{\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}$ values of CREs in CRSs of various density types, N_RYR, and i_Ca. The black, blue, and red bins correspond to CREs generated by i_Ca of 0.4, 0.25, and 0.15 pA, respectively. The dashed lines denote the occurrence level of 1%. The exemplified data sets consisted of 10,000 simulated CREs generated for one typical CRS of each type and size. The narrow and wide CRS types were of pattern B. F, the fraction of traces.

The $N_O^{peak}$ in individual sparks never reached N_RYR, but due to the occurrence of approximately four reopenings per RYR on average, it often highly exceeded the expected values given by N_RYR × $P_O^{peak}.$ $N_O^{peak}$ approached N_RYR only in the smallest compact CRSs. In the largest compact CRSs, $N_O^{peak}$ reached only ∼55% of N_RYR, even at the largest i_Ca values. Generally, lower i_Ca values or lower vicinities resulted in a lower fraction of RYRs open at the peak of the CRE. This was due to the lower [Ca²⁺] at RYRs distant from a source RYR, resulting in their lower probability of opening and longer closures (Fig. 2, and Videos 1, 2, and 3).

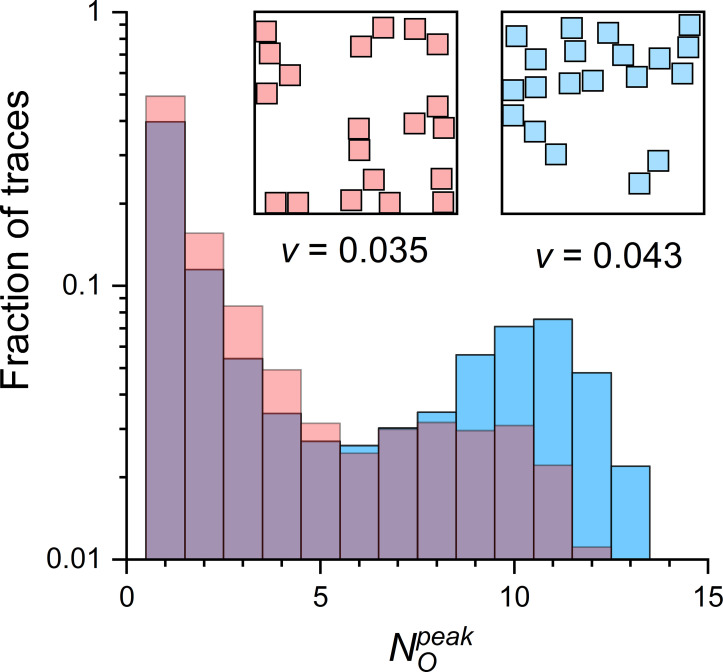
Ca²⁺-mediated interactions between RYRs depend on distances between RYRs. The distances have a different distribution in different CRSs of the same RYR surface density. The distribution of RYRs in CRSs is conveniently characterized by their group vicinity (Eq. 6), which increases with the extent of RYR clustering. CRS models of the three density types had group RYR vicinities different to the extent that their ranges almost did not overlap (compact CRSs: v = 0.055 − 0.87; narrow CRSs: v = 0.031 − 0.051; wide CRSs: v = 0.021 − 0.036; see Table 2 in Iaparov et al. [2020] Preprint for details).

CRSs of identical density and pattern type, but of different RYR distribution, yielded different amplitude distributions of their simulated CREs (Fig. 6). The probability that the two CRE distributions are the same for the two CRSs differing only in their RYR group vicinity v was extremely low. Thus, the different fractional occurrence of quarks, blips, and sparks in the two CRSs was highly statistically significant. This result can be seen as evidence that the distribution of RYRs in real dyads affects calcium release activity. This also means, however, that the RYR group vicinity is a good integral descriptor of RYR clustering.

Figure 6.

${\mathit{N}}_{\mathbf{O}}^{\mathbf{p}\mathbf{e}\mathbf{a}\mathbf{k}}$ distribution of two CRSs differing in RYR vicinity. The histograms were constructed from 10,000 simulated CREs per compared CRS, shown as red and blue columns. Both CRSs were of the narrow type, pattern B, 20 RYRs, and i_Ca = 0.25 pA. (Insets) The two CRSs were selected from the set of 100 CRSs generated for the same determinants; red RYRs had the lowest and blue RYRs had the highest RYR vicinity (v) in the CRS set.

CRS activity relates to CRS coupling strength quantitatively

The above analysis confirmed a close relation of CRS activity to CRS determinants (Figs. 4, 5, and 6); however, the characteristics of CREs did not correlate with CRS determinants, as exemplified by the average relative amplitude of CREs in Fig. 7 A. A similar lack of correlation was present in the relative occurrence of different CRE types. The only exception was a partial correlation of CRS activity with RYR group vicinity v, albeit different at different i_Ca values (Fig. 7 A, bottom). Therefore, we correlated the CRE characteristics with the RYR coupling strength φ that combines the RYR group vicinity and i_Ca (Eq. 8). The weight exponent α in Eq. 8 was found by approximating the relation of estimated CREs characteristics (A_rel, F_q, F_b, F_s) to the coupling strength φ of their respective CRS models, defined by Eq. 8 using state-response functions (Eq. 9). Since A_rel and F_s increased with increasing φ, both could be approximated by Eq. 9 directly. However, as the relationships between F_q or F_b and φ were decreasing or bell-shaped functions, we applied Eq. 9 through complementary relationships based on the fraction of non-quarks F_nq(φ) = 1 − F_q(φ); that is, F_q(φ) = 1 − F_nq(φ) and F_b(φ) = F_nq(φ) − F_s(φ). The whole dataset of the evaluated CRE characteristics, paired with their corresponding φ values (Eq. 8), was fitted collectively using a common value of the weight factor α. This was possible because α is related to the cytosolic calcium buffering, which is homogeneous within the CRS.

Figure 7.

Relationships between characteristics of CREs and determinants of CRSs. (A) The relationship between the average relative CRE amplitude Ā_rel and the corresponding value of CRS area per RYR (A_C/R), number of RYRs per CRS (N_RYR), i_Ca, and RYR group vicinity (ν). (B) The relationship between the characteristics of CREs and the corresponding RYR coupling strength φ values rectified with the optimized weight factor α = 0.67. The lines show the respective best-fit curves calculated by Eq. 9 for parameters given in Table 2. In A and B, yellow, blue, red, and green symbols denote data for i_Ca values of 0.04, 0.15, 0.25, and 0.40 pA, respectively. Squares and circles denote data for all wide and narrow CRSs (1,200 geometric models per CRS density type containing 10–80 RYRs). Diamonds and triangles denote data for the two types of compact CRSs (20 and 107 geometric models, respectively, containing 9–96 RYRs). Ā_rel, average A_rel; F_b, the fraction of blips; F_q, the fraction of quarks; F_s, the fraction of sparks.

The CRE characteristics correlated very well with RYR coupling strength φ for α = 0.67 (Fig. 7 B). Agreement between the data and the theoretical functions was very high (Table 2). Of note is that the values of φ varied 25 times across all wide, narrow, compact, and contact network CRS models.

Table 2. Parameters of functional dependencies of CRE characteristics on RYR coupling strength φ.

Weight factor α = 0.67 ± 0.002
	Fmax	K	n
${\overline{A}}_{rel}\left(\phi \right)$	0.40 ± 0.004	0.019 ± 1E-4	3.69 ± 0.05
Fnq(φ)	0.87 ± 0.003	0.012 ± 5E-5	2.07 ± 0.01
Fs(φ)	0.78 ± 0.002	0.018 ± 5E-5	4.87 ± 0.02

See Fig. 7 B. The parameters F_max, K, and n of fitting functions ${\overline{A}}_{rel}\left(\phi \right),$ F_nq(φ), and F_s(φ) are defined by Eq. 9, and the weight factor α by Eq. 8. R² = 0.98; 10,108 data points.

The existence of a functional relationship between φ and CRE characteristics for all CRS density types and the whole range of N_RYR and i_Ca values proves that φ is a true descriptor of the CRS state. Thus, the coupling strength φ predicts the propensity of a CRS to produce sparks upon a spontaneous opening of one of its RYRs.

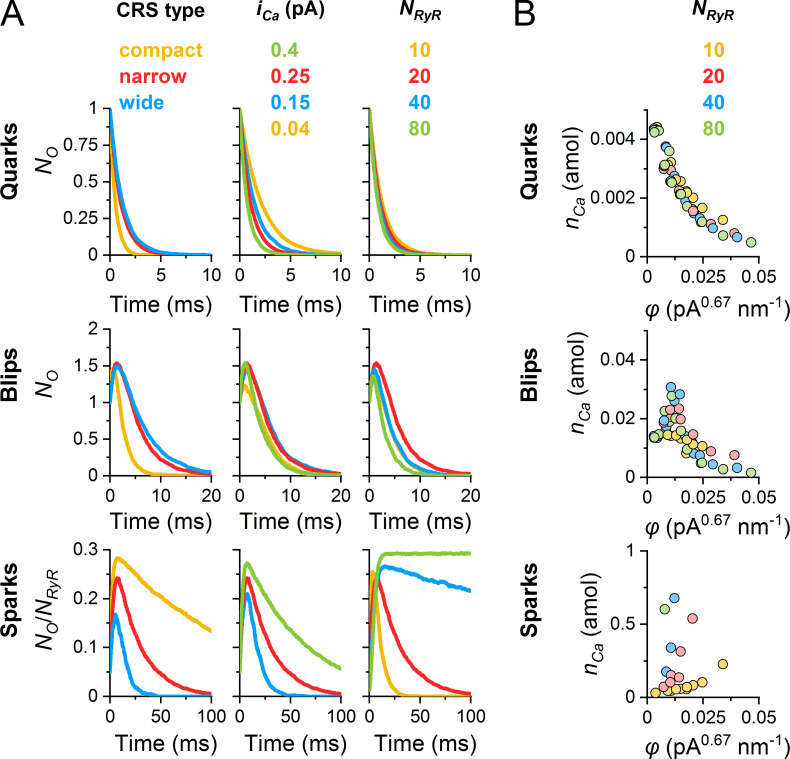
Kinetics of CREs and the amount of calcium released relate to CRS determinants

Hand in hand with the amplitudes and relative occurrences, the kinetics of CREs also varied. For convenience, we analyzed the averaged CREs since individual CREs fluctuated substantially. A single quark terminates abruptly upon closure of the open RYR at a random time; however, the averaged quarks declined exponentially (Fig. 8 A, top). The rate constant of the average quark decline was faster than the off-rate constant of the RYR gating model since RYR openings in CRSs were curtailed by activation of blips and sparks. As a result, a typical decay time of quarks was ∼2.2 ms for small, wide CRS and ∼0.2 ms for large, compact CRSs. This also means that larger and denser RYR clusters lead to faster responses of blips and sparks to the initial RYR opening.

Figure 8.

Kinetics of averaged CREs in CRS models. The data were obtained from 10,000 simulated CREs generated for one typical CRS of each type and size. The narrow and wide CRS types were of pattern B. (A) The averaged time courses of quarks, blips, and sparks. Left: The range of CRS density types with N_RYR = 20 and i_Ca = 0.25 pA. Center: Narrow CRSs with N_RYR = 20 and the indicated range of i_Ca values. Right: Narrow CRSs with i_Ca of 0.25 pA and the indicated range of N_RYR values. The color coding is valid for individual columns only. (B) The amount of calcium ions n_Ca released during average quarks, blips, and sparks plotted against the respective RYR coupling strength φ with weight factor α (n_Ca of sparks not terminating within the simulation time are not shown). N_RyR, number of RYRs in the CRS.

The time course of averaged blips was always biphasic (Fig. 8 A, middle). Their TTP was ∼1–1.5 ms in CRSs of low φ values, but at large φ values, it dropped to 0.1 ms due to the increased rate of spark formation (not shown). Typically, the blips terminated in full within 5–20 ms.

The time course of averaged sparks depended strongly on CRS determinants (Fig. 8 A, bottom). For the narrow CRS and i_Ca of 0.25 pA, the rate of spark activation was remarkably slower when the number of RYRs was larger. For 10 and 20 RYRs in the CRS, the averaged sparks peaked between 3 and 7 ms, while for 40 and 80 RYRs, the averaged sparks peaked between 10 and 30 ms. This indicates that even when the formation of the Ca gradient is instantaneous, as defined by the diffusion model, the spread of RYR activation in the CRS takes its time (see Videos 1, 2, and 3).

Termination of sparks was very complex. During individual sparks, the fraction of open RYRs fluctuated strongly and sometimes highly exceeded the steady-state P_O. In large CRSs of high φ values, the average spark did not decline markedly until the end of the simulation, and the average fraction of open RYRs approached the maximum steady-state P_O of the RYR model. This was the case in 25% of the 40 tested combinations of CRS determinants—CRS sizes, RYR densities, and i_Ca values—that produced sparks. About 27% of conditions, characterized by somewhat lower coupling strengths, resulted in partial spark deactivation; however, the largest fraction of CRS combinations (48%) led to sparks fully terminating within 100 ms. It should be noted that, at the lowest coupling strengths, sparks did not occur.

Myocyte contraction depends on the total amount of calcium ions released at the CRSs. Fig. 8 B shows the dependence of the amount of released calcium during CREs on the coupling strength φ. For quarks and blips, this amount, n_Ca, decreased with increasing φ, with no dependence on the number of RYRs in CRS. In the case of sparks, n_Ca increased with increasing φ, but even more steeply for larger N_RYR. These differences are because, at low coupling strength, the activation of blips shortens the duration of quarks. At large coupling strengths, increased activation of a spark results in shorter durations of blips. It is worth noting that the amount of calcium released in quarks, blips, and sparks differs by orders of magnitude (Fig. 8 B).

The amount of released calcium predicted by the inspected CRS models can be compared with experimental estimates. In the case of a narrow CRS with 20 RYRs and i_Ca of 0.25 pA, used as an example in the above analyses, the amount of released Ca²⁺ was 0.002, 0.02, and 0.3 amol for the average quark, blip, and spark, respectively. An average CRE released 0.1 amol Ca²⁺. These numbers can be compared with the amount of 0.1 amol necessary to increase the free cytosolic calcium from 100 nM to 1 µM in a volume served by one couplon (100 µM total Ca²⁺ in 1 µm³; Bers, 2001; Soeller et al., 2007), and with the 0.06 amol per spark, estimated from Janíček et al. (2012). For comparison, the amount of calcium stored in one cisterna can be estimated as 0.07 amol based on the published data (Hake et al., 2012).

The effectiveness of spark initiation depends on the initiating RYR

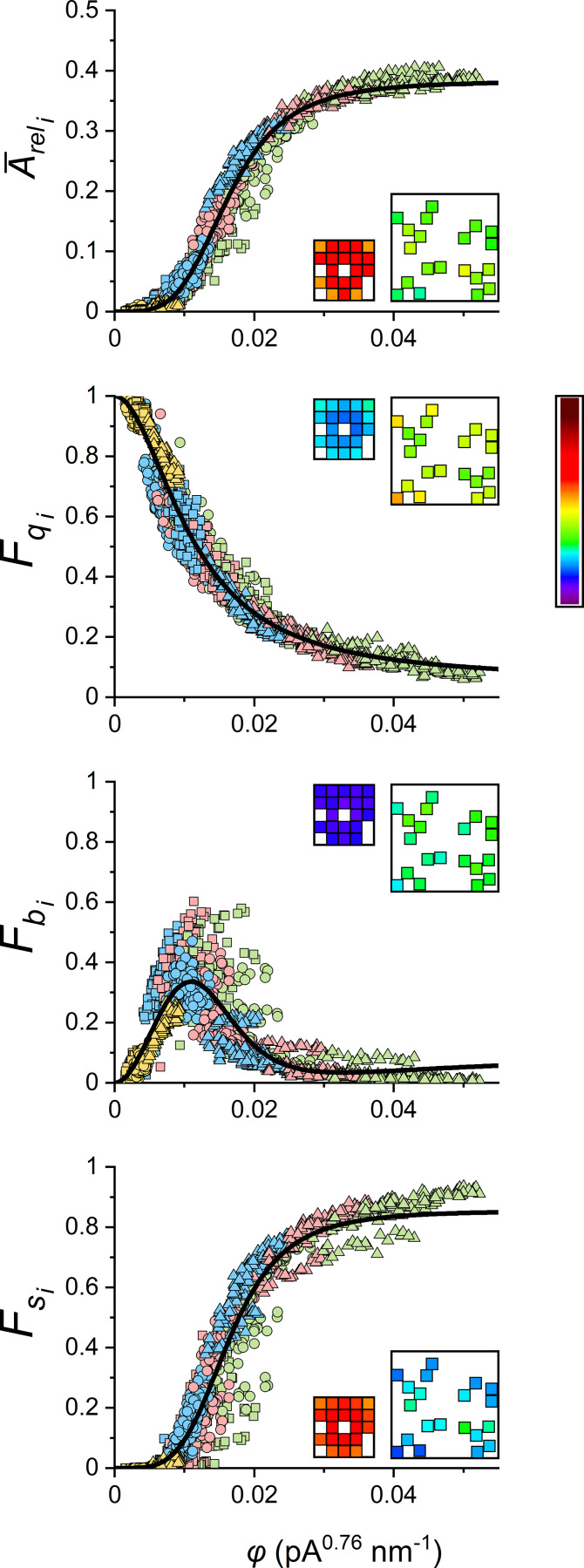
In simulation studies on contact network CRSs, Walker et al., 2014, 2015 showed that the efficiency of spark activation depends on the position of the initiating RYR. A substantial increase in spark fidelity was observed only if the initiating RYR channel was located in the core of the CRS, since RYRs at the periphery had fewer neighbor RYRs than RYRs in the core of the CRS. Although a similar phenomenon could also be expected in less dense CRSs, the extent of RYR recruitment in CRSs of different internal disposition could not be predicted; therefore, we analyzed the recruitment of RYRs by RYR openings at all RYR positions in the CRS for the defined range of CRS determinants (N_RYR, A_C/S, and i_Ca). The initiating RYR, characterized by its coupling strength φ_i, affected distinctly the relative occurrence and the average relative amplitude of CRS responses $\left({\overline{A}}_{rel}\right),$ as summarized in Fig. 9. It is apparent that differences between RYRs with higher and lower levels of local clustering (i.e., with higher and lower vicinity) become more apparent in CRSs with lower group RYR vicinity (insets in individual panels of Fig. 9).

Figure 9.

Relationships between characteristics of CREs and the coupling strength φ_i of the initiating RYR_i. The lines show the respective best global fit of all data points by functions ${\overline{A}}_{re{l}_i},$ $F_{q_i}=1- F_{n{q}_i},$ $F_{b_i}=F_{n{q}_i}-F_{s_i},$ and $F_{s_i}.$ The best-fit parameters are given in Table 3. Indices i indicate pertinence to initiating RYR. Yellow, blue, red, and green symbols denote results for i_Ca values of 0.04, 0.15, 0.25, and 0.4 pA, respectively. The squares, circles, and triangles represent wide, narrow, and compact CRSs, respectively. Insets: The exemplar compact and narrow CRSs with 20 RYRs at i_Ca = 0.25 pA, both showing (average) response values for n = 10,000 simulations, 500 for each of the individual initiating RYRs, color-coded according to the look-up table bar (right) scaled for the range of the respective ordinates.${\overline{A}}_{re{l}_i} ,$ average relative CRE amplitude; $F_{b_i}$ the fraction of blips; $F_{q_i},$ the fraction of quarks; $F_{s_i},$ the fraction of sparks.

A typical compact, narrow, and wide CRS with N_RYR of 20, 40, and 80 RYRs per CRS was analyzed for the whole range of studied i_Ca values (0.04, 0.15, 0.25, and 0.4 pA). Altogether, 560 RYRs in 12 CRSs were examined. The dependences of CRE characteristics on φ_i are shown in Fig. 10. The average relative amplitude $\left({\overline{A}}_{re{l}_i}\right)$ and the fraction of sparks $\left(F_{s_i}\right)$ increased, while the fraction of quarks $\left(F_{q_i}\right)$ decreased with increasing φ_i. The fractional occurrence of blips $\left({F_b}_{{}_i}\right)$ showed a maximum of ∼0.4 in the lower intermediate range of φ_i values. The dependences of CRE characteristics on φ_i were approximated by the respective functions derived from Eqs. 7 and 9. The value of the exponent α was found by relating all observed event characteristics of all simulated CRSs to the variable φ_i in parallel. The best-fit parameters are summarized in Table 3. The RYR coupling strength φ_i allowed us to line up relationships across spark characteristics and CRS density types at different N_RYR and i_Ca.

Figure 10.

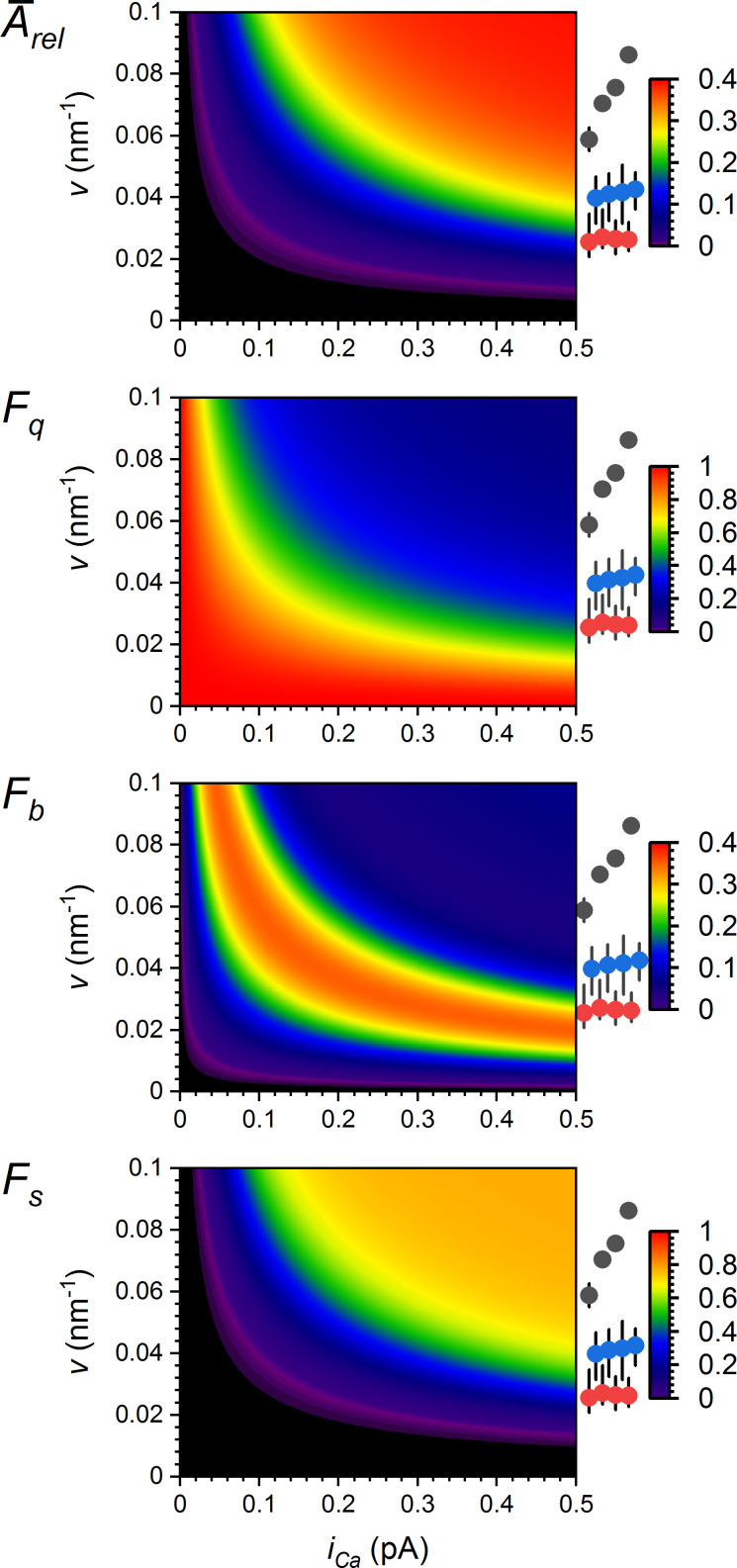
Synergy graphs relating the group RYR vicinity and single-channel calcium current to CRE characteristics. The graph values, color-coded by colormaps (right), were calculated using Eqs. 8 and 9 and Table 2. The symbols on the right side of each plot indicate the group vicinities (v; mean and range) for compact (black), narrow (blue), and wide (red) CRSs, calculated for N_RYR of 10, 20, 40, and 80 (from left to right, respectively). Ā_rel, average A_rel; F_b, the fraction of blips; F_q, the fraction of quarks; F_s, the fraction of sparks.

Table 3. Parameters of CRE dependence on the RYR coupling strength φ_i.

α = 0.76 ± 0.004
	Fmax	K	n
${\overline{A}}_{re{l}_i}$	0.38 ± 0.005	0.016 ± 2E-4	4.08 ± 0.13
$F_{n{q}_i}$	0.95 ± 0.005	0.011 ± 1E-4	1.96 ± 0.02
$F_{s_i}$	0.86 ± 0.003	0.016 ± 1E-4	4.33 ± 0.05

The parameters F_max, K, and n of fitting functions ${Ā}_{re{l}_i}\left(\phi \right),$ $F_{n{q}_i}\left(\phi \right),$ and $F_{s_i}\left(\phi \right)$ are defined by Eq. 9, and the weight factor α by Eq. 7. R² = 0.96 for 6,720 data points.

CRS spark activity results from synergy between RYR vicinity and i_Ca

The previous sections demonstrated a functional relationship between spark activity and the coupling strength characterizing individual RYRs (φ_i) as well as whole CRSs (φ). Since φ values are products of two quantities (Eqs. 7 and 8), we need to know the contribution of each to the formation of CREs. Fig. 10 summarizes the calculated dependences of relative CRE amplitudes and relative occurrences of quarks, blips, and sparks on a wide range of i_Ca and v values. For comparison, the vicinities of CRS models used for the simulations are marked on the right side. For all CRE characteristics, the hyperbolic relationships draw limits in which the CRSs of a specific density type can be effectively active. These relationships also indicate under what geometric conditions CRSs can be effectively controlled by calcium flux, as well as under what conditions CRSs would not activate at any physiologically possible i_Ca. The amplification of the effect of v by i_Ca, and vice versa, is a manifestation of the synergy between i_Ca and v.

Calcium fluorescence signals calculated from CREs

The question is, how are the simulated CREs related to calcium sparks observed in cardiac myocytes by confocal fluorescence microscopy. The fluorescence signal of calcium sparks is proportional to local [Ca²⁺]. Since it is quantitatively related to calcium release flux, it can be calculated from the simulated CREs, e.g., as described by Smith et al. (1998) and Zahradníková et al. (2007). Fluorescence intensities calculated for the averaged $N_O\left(t\right)$ records of the quark, blip, and spark (red traces in Fig. 8 A, left) are shown in Fig. 11 as x-t images in confocal microscopy experiments. The characteristics of the respective fluorescence signals are summarized in Table 4. The fluorescence of an average quark is below the standard resolution limit of confocal microscopy, as expected (Lipp and Niggli, 1996; Niggli and Egger, 2002). According to our estimates, a quark could be visible if the calcium current were large and the RYR openings were simultaneously long, or if the cytosolic buffering capacity for calcium were small, or if the free diffusion space were restricted (e.g., by membranous organelles). The fluorescence of an average blip resembles quarky calcium releases, as observed by several laboratories (Brochet et al., 2011; Shang et al., 2014). The fluorescence of an average spark resembles, by its appearance, typical calcium sparks, as observed by many laboratories. For comparison, Zahradníková et al. (2007) reported spark amplitude of 1.75 ΔF/F₀ units, a TTP of 16 ms, and full duration at half-maximun of 38 ms. Thus, these calculations confirmed the adequacy of the use of simulated CREs for inferences on CRS behavior and mechanisms of local calcium release.

Figure 11.

Calculated fluorescence x-t images of simulated CREs. The color-coded contour plots indicate the fluorescence increase of 50 µM Fluo-4 in the cytosol as if recorded in the line-scan mode at position (micrometer) and time (millisecond) from the point source (narrow CRS, N_RYR = 20, i_Ca = 0.25 pA) in response to release fluxes calculated for the average time courses of quarks, blips, and sparks (corresponding to blue traces in Fig. 8 A, left). The white contour lines (middle and right) indicate the detection limit of 0.3 ΔF/F₀ units; the quark (left) did not reach the detection limit. The corresponding time and spatial fluorescence profiles at the peak are shown at and above the images. The colormap shown on the right side is common to all three panels.

Table 4. Parameters of CRE fluorescence signals.

CRE	Maximum ΔF/F0	TTP (ms)	FDHM (ms)	FWHM (μm)
Quark	0.09	1.5	3.6	0.86
Blip	0.40	4	9.8	1.00
Spark	1.72	13	38.0	1.21

CRE fluorescence signals are shown in Fig. 11. FDHM, full duration at half maximum; FWHM, full width at half maximum.

Local calcium release is shaped by RYR patterns and CRS arrangement

The finding by Asghari et al. (2014) of a direct relationship between RYR arrangement in dyads and the concentration of Mg²⁺ ions opened the question of its role in the physiological regulation of excitation–contraction coupling in cardiac myocytes. We tested whether the arrangement of RYRs into ChB and SbS patterns (see Table 1) would generate physiologically meaningful differences in CRS activity in the given simulation settings. For narrow CRSs and i_Ca of 0.25 pA, the relative occurrences of quarks, blips, and sparks showed only minor differences between tested patterns when N_RYR was the same (Table 5). Although statistical testing indicated that F_q, F_b, or F_s values were significantly different between some CRS patterns at some N_RYR values, these differences were not consistent for CRSs with different N_RYR.

Table 5. Dependence of fractions of event types on RYR patterns.

NRYR	Fraction	Pattern A	Pattern B	Pattern C
10	Fq	52.9 ± 0.3	52.6 ± 0.3	55.9 ± 0.3
	Fb	28.5 ± 0.1	29.5 ± 0.2	29.9 ± 0.1
	Fs	18.5 ± 0.4	17.9 ± 0.5	14.3 ± 0.3
20	Fq	46.7 ± 0.2	45.1 ± 0.2	45.1 ± 0.2
	Fb	30.4 ± 0.2	27.8 ± 0.2	29.0 ± 0.2
	Fs	22.9 ± 0.3	27.0 ± 0.4	25.9 ± 0.4
40	Fq	39.2 ± 0.2	40.4 ± 0.1	39.8 ± 0.1
	Fb	20.2 ± 0.2	21.4 ± 0.2	20.0 ± 0.1
	Fs	40.7 ± 0.3	38.3 ± 0.3	40.2 ± 0.2
80	Fq	36.3 ± 0.1	35.6 ± 0.1	36.2 ± 0.1
	Fb	14.6 ± 0.1	14.4 ± 0.1	14.8 ± 0.0
	Fs	49.0 ± 0.2	50.0 ± 0.1	49.0 ± 0.1

Narrow CRSs; i_Ca = 0.25 pA. All values are given as mean ± SD. F_q + F_b + F_s = 1. F_b, fraction of blips; F_q, fraction of quarks; F_s, fraction of sparks.

Generally, the differences in the fraction of quarks, blips, and sparks between CRSs of different pattern types, but of the same N_RYR, were much smaller than those between CRSs of the same pattern type but with different N_RYR. These results could be expected since the only interaction factor controlling the activation of RYRs implemented in this study was the local calcium concentration. Despite the steep gradient at an open RYR, the concentration of Ca²⁺ was similar at the nearest neighbor RYR whether in SbS or the slightly more distant ChB position. Nevertheless, the coupled gating or another type of RYR–RYR interaction might contribute differently to the activation of CRSs with different pattern types. To reveal this, an extended RYR gating model would need to be inspected.

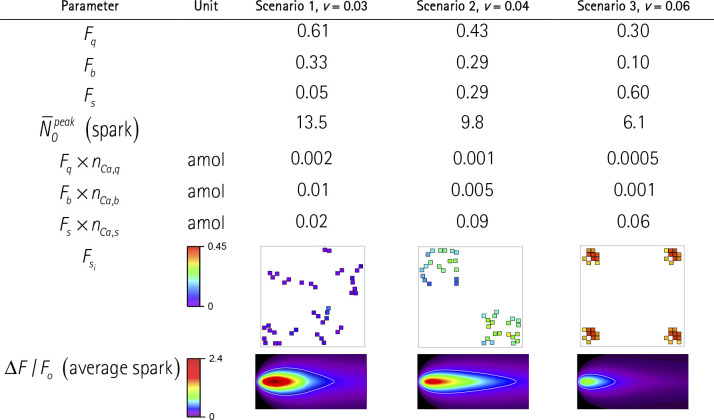
In previous sections, we analyzed the effects of RYR arrangement at the level of a single CRS. In real experiments, the spatial resolution of calcium sparks is less than the physical size of a CRS; thus, the proximate CRSs cannot be resolved. The question is whether assembling RYRs into either one or a few proximate, but independent, CRSs could be distinguished by their activity pattern. We compared the formation of sparks in three scenarios differing in the arrangement of 40 RYRs into one, two, or four independent CRSs (Table 6) so that no CRS is affected by Ca²⁺ diffusion from the activated CRSs (nota bene: in multicluster models of dyads, the approximation of independent RYR clusters would correspond to edge-to-edge separation of RYR clusters larger than 150 nm [Macquaide et al., 2015; Kolstad et al., 2018]). The single large, wide CRS with 40 RYRs represents the first scenario, in which all RYRs are coupled by diffusing calcium. The second scenario comprises two independent nonidentical CRSs, each of the narrow type and with 20 RYRs. The third scenario comprises four independent nonidentical CRSs, each with 10 RYRs in the compact arrangement. In all scenarios, the simulations were started by activation of an RYR in only one of the CRSs. This CRE activation procedure tallies the frequency of initializing RYR opening per scenario since the total number of RYRs is the same in each scenario.

Table 6. Properties of quarks, blips, and sparks in a group of 40 RYRs assembled into one, two, or four CRSs of different RYR vicinities.

Calculated for i_Ca = 0.25pA. F_q, F_b, F_s are fractions of quarks, blips, and sparks per CRS, respectively. ${\overline{N}}_O^{peak}$ (spark) indicates the average number of RYRs open at the peak of spark. n_Ca,q, n_Ca,b, and n_Ca,s are the amount of calcium released per average quark, blip, and spark, respectively. the F_x × n_Ca,x indicate the weighted amounts of calcium released by quarks, blips, and sparks in individual scenarios. F_si indicates the fraction of sparks per individual RYRs color-coded according to the color map. ΔF/F₀ is the fluorescence of line scan images for averaged sparks (6 µm vertical × 100 ms horizontal) color coded according to the color map. The white contour lines indicate the detection limit of 0.3 ΔF/F₀ units. Note that the individual CRSs are not spatially resolved.

Changes in CRS activity calculated for these scenarios showed dramatic differences in the averaged CRE responses (Table 6). The single large CRS with 40 RYRs of low vicinity produced sparks rather rarely, just in five of 100 initiating RYR openings. The two 20 RYR CRSs of the narrow type (i.e., with a higher RYR vicinity) produced 29 sparks, and the four 10 RYR CRSs of the compact type—and thus of the highest RYR vicinity—produced as many as 60 sparks of 100 initiating RYR openings. In these scenarios, the average number of simultaneously open RYRs in sparks, ${\overline{N}}_O^{peak}$ (Table 6), and the amount of calcium released per spark, n_Ca,s (not shown), were predictably reduced following the reduction of N_RYR per one CRS. However, since the decrease in the spark amplitude was counteracted by the increase in the spark frequency, the amount of calcium released by sparks per one initiating RYR opening (F_s × n_Ca,s; Table 6) was substantially larger in the two-CRS case relative to the single-CRS case, but it was intermediate in the four-CRS case. On the contrary, compacting the RYRs into a few small CRSs resulted in a smaller amount of sparkless release (F_q × n_Ca,q, and F_b × n_Ca,b; Table 6).

Analysis of RYR activity in individual CRSs shown in Table 6 revealed that the propensity of RYRs to initiate a spark, $F_{s_i},$ increased with increasing RYR vicinity, in agreement with previous simulations (Fig. 9). The fluorescence of averaged sparks (Table 6) corresponded to the time course of RYR activity in the respective CRSs (Fig. 8). Compared with the one-CRS scenario, the two- and four-CRS scenarios produced sparks with a progressively smaller amplitude; however, the spark produced by the two-CRS scenario was longer, while that produced by the four-CRS scenario was shorter. These changes are in line with previous findings on the relationships between spark amplitude and duration, on one hand, and the vicinity and the number of interacting RYRs, on the other hand (Fig. 8).

Altogether, these simulations suggest that the frequency and amplitude of calcium sparks generated by a set of unresolved CRSs depend strongly on the number, size, and density type of these CRSs. Moreover, the fine structure of CRSs determines the ratio of “invisible” nonspark calcium release (Ca leak) and “visible” spark-related calcium release.

Discussion

Recent experimental and theoretical studies indicated the importance of dyad structure and RYR clustering on spontaneous calcium spark formation (Cannell et al., 2013; Walker et al., 2014, 2015; Kolstad et al., 2018; Cosi et al., 2019) as well as on triggered calcium release (Zahradnik et al., 2013; Cosi et al., 2019; Novotová et al., 2020). In this study, we used a large set of CRS geometries that approximated the structural data by constrained random distribution of RYRs in CRS (Iaparov et al., 2017; Iaparov et al., 2019).

This allowed us to solve the role of geometric factors of cardiac dyads in the formation of elementary CREs. The modeling approach allowed for wide-ranging exploration of dyad-defining determinants implemented into numerous models of CRSs, which would not be feasible in real experiments. The scope was limited to a realistic range of determinants, as estimated thus far. The in silico experiments emulated spontaneous CREs observed in resting cardiac myocytes. The openings of a single RYR in the CRS generated CREs that were recorded and analyzed. Under a majority of CRS conditions, three types of CREs, namely, quarks, blips, and sparks, were generated. Their relative occurrence, amplitude, and kinetics revealed high cooperativity between the number, arrangement, and single-channel calcium current of RYRs in the formation of CRS responses. This finding was explained by introducing the RYR coupling strength φ, defined as a weighted contribution of microscopic CRS determinants—the single-channel calcium current and the vicinity of RYRs in the CRS, where the RYR vicinity is a new determinant that characterizes the arrangement of RYRs in the CRS, invariant to CRS size.

RYR vicinity (Eqs. 4 and 5) characterizes distances between RYRs in the group by a single numerical value. Unlike the RYR surface density or the number of RYRs in the CRS, the vicinity resolves the differences in the distribution of RYRs in dyads. In other words, two CRSs that have the same number of RYRs and the same surface density may have different group vicinity values. Likewise, two RYRs in two CRSs of different surface densities may have the same RYR vicinity value. To generalize, the vicinity is a measure of the RYR interaction potential since it increases with increasing RYR clustering. The previously used concept of adjacency or nearest neighborhood (Walker et al., 2014) attributes the interaction potential only to close neighbors, resulting in discretized levels of RYR–RYR interactions. In contrast to the RYR surface density or mean RYR occupancy used in previous models (Cannell et al., 2013; Cosi et al., 2019), the vicinity characterizes the whole CRS (Eq. 6) as well as individual RYRs (Eq. 5) according to their global or local geometric dispositions.

We defined the coupling strength φ (Eqs. 7 and 8) as an internal determinant of CRS productivity, which combines the vicinity of interacting elements (RYRs) with the strength of the interaction agents ([Ca²⁺] and weighted i_Ca). It turned out that the amplitudes, kinetic characteristics, and probabilities of occurrence of all CRE types correlated well with this CRS determinant. Importantly, the optimal correlation was obtained with a single value of the weight factor α (Figs. 7 B and 8). Therefore, coupling strength φ could be thought of as a measure of effective calcium concentration in the dyadic gap (Eq. 9), although its dimension A^α m⁻¹ corresponds to a linear current density or calcium flux per distance or perimeter. What is important, however, is that the same relationship could be applied to responses of CRS models built on the experimentally determined (Walker et al., 2015) and algorithm-generated RYR distributions (Iaparov et al., 2019) at a wide range of RYR surface densities. Taken together, these multiparametric correlations on the grounds of generalized RYR geometries support the intuitive understanding that the vicinity and i_Ca of RYRs determine the activity of CRS in synergy (Fig. 10).

The RYR coupling strength φ has some similarity to the previously introduced concept of coupling strength c* (DeRemigio and Smith, 2005; Groff and Smith, 2008), which was used as an ad hoc input parameter in calculations to characterize the average calcium concentration increase in the CRS caused by the opening of a single channel. Therefore, this parameter cannot be decomposed into a geometric and a functional component. The coupling strength c* underestimates the interaction of RYRs in noncompact CRS (Iaparov et al., 2019), and thus cannot consolidate the correlations between the properties of CREs and the determinants of general CRSs. In contrast, the RYR coupling strength φ conveniently integrates the geometric and functional aspects of CRS activity. Its effective value is determined ex post by approximating the characteristics of simulated CREs by a function of RYR vicinity, calcium current, and the weighing factor α. The coupling strengths φ and φ_i deliver the synergic character of RYR clustering and calcium current and thus allow for prediction of the relative occurrence of quarks, blips, and sparks, as well as their amplitudes and activation kinetics in the whole range of studied CRS characteristics; however, individual responses of a CRS may vary broadly, as does the chance of RYR opening. Taken from the other side, CRS and RYR coupling strength determine the propensity of CRSs to generate specific types of CREs, their amplitudes, and their time courses. They may predict whether a specific CRS will generate preferentially quarks, blips, or sparks (Fig. 10). The coupling strength makes it possible to explain the deterministic relationship between the stochastic processes of RYR gating, the random RYR distribution, and calcium diffusion, on the one hand, and the generation of CREs, on the other hand. To fully accomplish these goals, we need new models of CRS with an improved definition of the control of RYR gating by luminal calcium at both luminal (Terentyev et al., 2002; Laver, 2007; Tencerová et al., 2012) and cytosolic sites (Sobie et al., 2002; Laver, 2007) that would account for the fact that the coupling strengths φ and φ_i decline with SR depletion. Another open question is the existence and relevance of direct RYR–RYR interactions that occur during coupled gating (Stern et al., 1999; Marx et al., 2001) or other yet unrevealed coupling mechanisms.

All CRS models explored in this study responded to activation by CREs of amplitudes and time courses that were highly variable. The CRE variability was high in CRSs of any RYR arrangement, despite the single-channel current value being constant during CREs, and thus could be fully attributed to the gating and group behavior of RYRs. However, the geometric disposition of RYRs substantially modulated the characteristics of CREs. CREs of all three types were generated by any CRS model, although not at any i_Ca value; however, their relative occurrences were widely different. Moreover, repeated activation of the same CRS by the same initiating RYR also produced all three types of CREs (Figs. 4 and 6). Therefore, we suppose that the various types of local CREs observed in cardiac myocytes under otherwise the same conditions represent a fundamental variability of CRS responses. In other words, the experiments indicating a broad range of calcium spark amplitudes (Wang et al., 2004; Zima et al., 2008; Brochet et al., 2011; Janíček et al., 2012) and durations (Zima et al., 2008; Brochet et al., 2011), or even opening of one or a few RYRs (Wang et al., 2004; Janíček et al., 2012), have support in the theory of CRS operation.

The theoretical study by Stern et al. (1999) predicted that calcium release may terminate even in the absence of a specific termination mechanism due to stochastic attrition. Recent studies of CRS at a constant RYR current predicted a threshold value of calcium current below which any CRS event will terminate (Maltsev et al., 2019; Gillespie, 2020). This study revealed the stochastic termination dominating in blips and prominent in sparks. The picture of calcium spark termination, emerging from our simulations, points to a complex interplay between CRS determinants and kinetics of RYR gating. Importantly, however, sparks produced by the tested CRSs differed too broadly in their duration. This is at odds with the observed characteristics of spark termination. Without luminal regulation, typical calcium sparks in large dyads and at high SR calcium loads would be much higher and would last much longer than physiologically useful. In myocytes, therefore, spark termination has to involve control mechanisms that would set properly the duration of local CREs.

Experimental implications

The results of these simulations may be of help to settle some experimental problems. For instance, they indicate that the single openings of RYRs, classified here as quarks, produce fluorescence signals too small to be detectable as local CREs in myocytes under conditions close to physiological. The activity of a small group of RYRs produces blips that release calcium ions in amounts sufficient to generate calcium signals that are close to the detection limit. The spark-like activity of a larger group of RYRs yields large calcium signals under a broad range of CRS settings. In noncompact CRSs, the rate of RYR recruitment seems to be relatively slow, and thus well-designed fluorescence measurements may characterize the kinetics of calcium sparks even when convoluted with the kinetics of calcium binding by a fluorescent dye. This may help to better resolve the fine structure of the CRE source, since the amplitude and kinetics of calcium sparks strongly depend on the distribution of RYRs within one or several CRSs (Table 6).

According to these simulations, brief sparks are produced by CRSs with either a small number of RYRs or a low group vicinity or a smaller RYR calcium current. Slowly terminating sparks are produced by CRSs with either a large number of RYRs or a high group vicinity or a high i_Ca. Large sparks are produced by CRSs with a large number of RYRs, and their amplitude can be further increased by a large coupling strength (Fig. 8).

It is well documented that, during a calcium spark, a substantial local depletion of luminal Ca²⁺ concentration occurs (Brochet et al., 2005), amounting to 40–90% (Zima et al., 2008; Kong et al., 2013). Considering the example of narrow CRS with 20 RYRs and i_Ca of 0.25 pA, an ∼40% decrease in i_Ca would result in transformation of 72% of sparks to blips or quarks. According to Kong et al. (2013), 40% depletion may be achieved 10 ms after the start of a CRE. In the example CRS, however, 90% of peak activation is achieved in <5 ms, and therefore even such a rapid depletion would affect only slightly the number of recruited RYRs or the fraction of sparks, but would significantly curtail the duration of calcium release flux. Similar considerations propose that dyadic SR cisternae with low Ca content or with lower RYR Ca conductance may have a much lower probability of calcium spark activation and, conversely, a higher contribution of nonspark calcium release in the form of quarks and blips, as previously observed by Zima et al. (2010).

For calcium release experiments, especially those aimed at pathological mechanisms, of consideration can be the changes in RYR distribution. According to these simulations, the change in RYR vicinity affects the CRS propensity to generate sparks (Table 6), which can be easily measured and could be correctly interpreted if the SR calcium content was constant. The RYR vicinity also correlates with the rate of spark activation (Fig. 8 A) since the coupling strength is directly proportional to the vicinity. This is in agreement with previous experimental data and simulations (Kolstad et al., 2018).

The calculated amount of calcium released per quark and per blip is 10–100 times smaller than that released per spark according to these simulations; however, it may contribute significantly to calcium leak from the SR when their occurrence is high. Importantly, the ratio of invisible nonspark calcium release (Ca leak) and visible spark-related calcium release depends strongly on the distribution of a given number of RYRs into one or several optically unresolvable CRSs (Table 6).

The results presented in Fig. 8 may partially explain the effect of the store overload-induced calcium release (Kong et al., 2007), since they predict a strong increase in spark occurrence and duration upon an increase of i_Ca. Similar considerations may be applied to observations and interpretation of calcium waves in cardiac myocytes that accompany the development of arrhythmias in injured or failing myocardia.