Evidence of a liquid–liquid transition in a glass-forming ionic liquid

Significance

The liquid–liquid transition (LLT) in a single-component liquid reflects changes in the liquid structure on the molecular level. In the case of ionic liquids (ILs), a hierarchical liquid structure is present due to charge-alternation constraints and segregation of nonpolar alkyl chains. We present experimental evidence of structural reorganization in a glass-forming IL corresponding to an LLT. The change in liquid structure correlates to changes in the dynamics and dielectric properties of the IL, which may be useful for potential applications.

Abstract

A liquid–liquid transition (LLT) is a transformation from one liquid to another through a first-order transition. The LLT is fundamental to the understanding of the liquid state and has been reported in a few materials such as silicon, phosphorus, triphenyl phosphite, and water. Furthermore, it has been suggested that the unique properties of materials such as water, which is critical for life on the planet, are linked to the existence of the LLT. However, the experimental evidence for the existence of an LLT in many molecular liquids remains controversial, due to the prevalence and high propensity of the materials to crystallize. Here, we show evidence of an LLT in a glass-forming trihexyltetradecylphosphonium borohydride ionic liquid that shows no tendency to crystallize under normal laboratory conditions. We observe a step-like increase in the static dielectric permittivity at the transition. Furthermore, the sizes of nonpolar local domains and ion-coordination numbers deduced from wide-angle X-ray scattering also change abruptly at the LLT. We independently corroborate these changes in local organization using Raman spectroscopy. The experimental access to the evolution of local order and structural dynamics across a liquid–liquid transition opens up unprecedented possibilities to understand the nature of the liquid state.

The isotropic liquid state has been typically regarded as singular and related to the gas state, differing only by a change in density. This physical picture of liquids has now been upended by numerous examples of distinct locally favorable structures separated by first-order phase transitions arising in single-component liquid systems ranging from atomic liquids, like silicon (1) or phosphorous (2), to molecular liquids, such as water (3, 4) or triphenyl phosphite (5–7), to metallic glass-formers (8). The mechanism of the transition separating distinct liquid structures, referred to as a liquid–liquid transition (LLT) (5, 9–13), remains an ongoing mystery in condensed-matter physics. The existence of the LLT implies the coexistence of two competing, yet distinguishable, liquid states where the notion of structural analogy to the homogeneous and isotropic gas or spatially symmetric and periodic crystal bears no consequence (14). Therefore, it is reasonable to expect that the LLT holds the key to deeper fundamental understanding of the nature of the liquid state. However, one of the technical challenges in this area is the fact that LLTs are usually observed in materials below their melting points, where full or partial crystallization is prevalent. Thus, unambiguous assignment of LLTs in many of the materials identified earlier remains controversial. Here, we present studies of a glass-forming ionic liquid (IL), for which no evidence of crystallization or microscale crystals exist, under the standard experimental conditions. We apply an array of experimental techniques and take advantage of unique local structures in ILs to unequivocally demonstrate the evolution of local order and structural dynamics as the LLT is traversed upon cooling.

The theoretical treatment of the liquid state by Tanaka (15–17) is perhaps the simplest explanation involving the coexistence of multiple competing liquid structures at the molecular level. Dubbed the two-order-parameter model, this theory describes the liquid state in terms of two competing types of ordering: density ($\rho$), which describes the differences between liquid and gas phases remarkably well; and the bond-order parameter ($S$). The bond-order parameter is linked to locally favored packing of molecules in the liquid state differing from the symmetries favored by the density-order parameter, $\rho$. Hence, what is referred to as bond order in the liquid state effectively describes the specific anisotropic interactions that arise in the condensed liquid state due to many-body interactions. Theoretically, such anisotropic interactions could outcompete the “normal” liquid structures defined by $\rho$ such that the dynamic glass transition is observed upon cooling and vitrification (16). However, it is also theorized that the competition between $\rho$ and $S$ indicates the coexistence of two structurally distinct liquid states, which are used to describe the critical-point-like phenomena observed at LLTs.

Among the classes of liquids that have been predicted or observed to undergo LLTs, ILs have been thus far summarily ignored. Due to the controversial nature of LLTs, this is not surprising, but when one considers the common trope of hierarchical structure in ILs, it seems even more surprising that the possibility of multiple liquid states separated by a first-order phase transition has not been explored previously. All ILs organize in a charge-alternation structure based on the charges of the individual cations and anions as necessitated by the constraint of charge neutrality, which means that, overall, every positive charge must be balanced by a negative charge. This constraint has been shown to hold down to molecular length scales, despite the fact that the ions that compose ILs have been shown to not form long-lived ion pairs, but, rather, each ion exists within a cloud or shell of oppositely charged ions to ensure local and temporal charge neutrality (18). In addition, due to the large asymmetric structures of the constituent ions in ILs, regions of high charge density surrounding the charged centers of the cations and anions (polar domains) tend to segregate from regions of low charge density typically occupied by alkyl chains (nonpolar domain), thus forming mesoscale aggregated structures that extend beyond the length scale of the constituent ions (19–22). The additional layer of molecular order introduced by mesoscale aggregation leads to a variety of potential liquid morphologies, depending on the relative sizes of the high-charge and low-charge regions on the ions, as well as the number of nearest-neighbor ions allowed in a given IL (18). Typically, the nonpolar region can form islands or a bicontinuous phase, depending on the length of alkyl side chains on the ions. Also, depending on the cation structure, the liquid can exhibit either globular polar networks, as in the case of imidazolium-based ILs, or filamentous (thread-like) polar networks, as in the case of tetraalkylphosphonium-based ILs with long alkyl side chains (18). Due to the hierarchical structure of ILs and the presence of long alkyl chains, ILs possess internal degrees of freedom not found in the examples of atomic and molecular liquids referenced above. These internal degrees of freedom would allow for conformational changes with temperature that could result in the LLT. Until now, one could only speculate that the LLT could be possible in an IL, but these glass-forming systems are ideal models to test the existence and underlying mechanisms of LLTs. Here, we provide experimental evidence of a temperature-driven structural reorganization of an IL characteristic of the LLT.

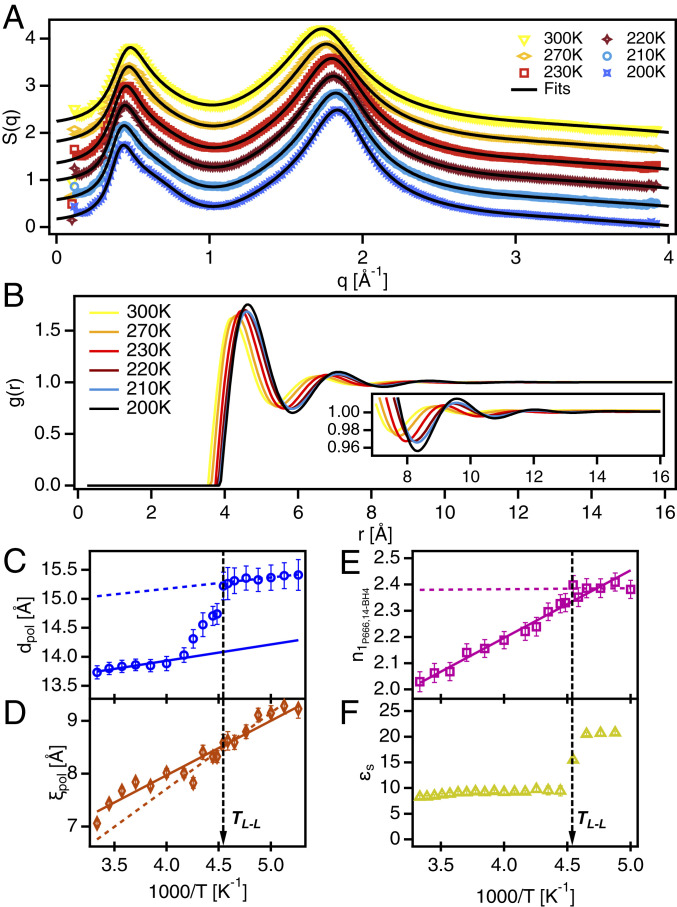
ILs that bear the trihexyltetradecylphosphonium cation ([${\mathrm{P}}_{\mathrm{666,14}}$]⁺) are organized in a hierarchical structure, particularly exhibiting a filamentous morphology characterized by the alternation of positively charged phosphonium centers and the negative charges on the anions comprising the threads of the polar network, which are surrounded by the nonpolar region where the alkyl side chains reside (23). The resulting structure and morphology of a [${\mathrm{P}}_{\mathrm{666,14}}$]⁺-based IL does depend on the specific anion, but in the case of trihexyltetradecylphosphonium borohydride (${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$), the main features of the hierarchical IL structure can be identified by using wide-angle X-ray scattering (WAXS) (24–26). The WAXS intensity data from ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$ (Fig. 1A) shows the charge adjacency peak around 1.8 Å⁻¹. The charge-alternation structure is evident as a shoulder around 0.65 Å⁻¹ on the high-q side of the polarity-alternation structure around 0.45 Å⁻¹. Information revealed from the analysis of the WAXS data based on the Tuebner–Strey model (22) (SI Appendix) indicates that the polarity-alternation structure undergoes a nonmonotonic change associated with the LLT. The periodicity (${\mathrm{d}}_{pol}$; Fig. 1C) and correlation length (${\xi }_{pol}$; Fig. 1D) show a reorganization in structure at the largest length scale in the system. Turning to the radial distribution function [g(r); Fig. 1B], the evidence of structural reorganization becomes clearer. Integration of the primary peak in $g\left(r\right)$ indicates that the ion-coordination number, $n_{1_{P\mathrm{666,14}-BH4}}$, must increase across the LLT (27) (Fig. 1E). Ultimately, the WAXS data reveal an extension of the polarity alternation structure with an increase in ion-coordination number. These results provide a rationalization for the stepwise increase in the static dielectric permittivity, ${\epsilon }_s$ (Fig. 1F). With the increase in the number of ions in the first coordination shell, coupled with the extension and ordering of the polarity-alternation structure, an interfacial polarization mechanism emerges, which strongly contributes to ${\epsilon }_s$.

Fig. 1.

Reorganization of mesoscopic structure in [${\mathrm{P}}_{\mathrm{666,14}}$]⁺[BH₄]⁻. (A) X-ray scattering intensity, S(q), at various temperatures, offset in the y axis for clarity. Solid black lines represent fits to the data using two Teubner–Strey equations below q = 1 and three Lorentz functions above q = 1. (B) Radial distribution function, g(r), calculated from fits to S(q). (B, Inset) Detail of g(r) between 7 and 16 Å⁻¹. (C) Periodicity, d, of the polarity alternation structure, i.e. first sharp diffraction peak. (D) Correlation length, $\xi$, of the polarity alternation structure. (E) Coordination number from the first shell based on integrated area of the first peak in g(r). (F) Static dielectric permittivity measured using BDS. Solid and dotted lines in C–E represent linear fits to the data to serve as guides for the eye. Vertical dashed black lines indicate the LLT temperature.

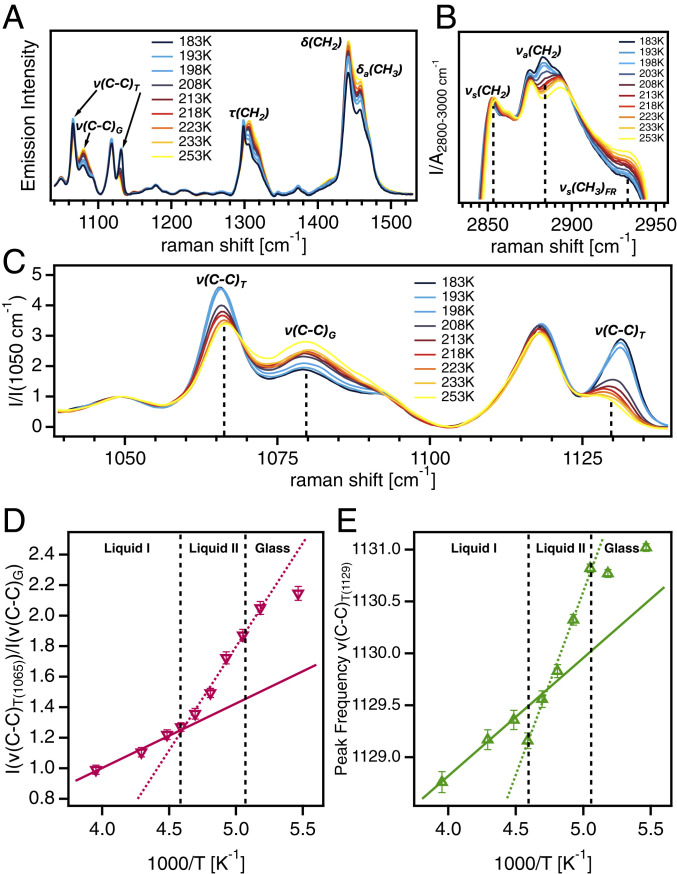
Regarding the extension and ordering of the polarity-alternation structure, which is dependent on the configuration of the alkyl chains on the [${\mathrm{P}}_{\mathrm{666,14}}$]⁺ cation, the Raman spectra (Fig. 2) exhibit features associated with the structural transition stemming from changes in the aliphatic groups attached to the phosphonium cations (28–30). Three distinct regions associated with vibrational modes of the alkyl chains are present in the Raman spectra between 1,050 ${\mathrm{c}\mathrm{m}}^{-1}$ and 1,500 ${\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 2A). The C–C stretching modes denoted $\nu \left(C-C\right)$ appear as three peaks around 1,065 ${\mathrm{c}\mathrm{m}}^{-1}$, 1,079 ${\mathrm{c}\mathrm{m}}^{-1}$, and 1,130 ${\mathrm{c}\mathrm{m}}^{-1}$ (29). These modes provide information about the conformational order of the alkyl chains, where the peaks at 1,065 ${\mathrm{c}\mathrm{m}}^{-1}$ and 1,130 ${\mathrm{c}\mathrm{m}}^{-1}$ indicate trans conformers ($\nu {\left(C-C\right)}_T$), and the peak at 1,079 ${\mathrm{c}\mathrm{m}}^{-1}$ corresponds to the gauche conformation. In Fig. 2C, the region between 1,040 ${\mathrm{c}\mathrm{m}}^{-1}$ and 1,140 ${\mathrm{c}\mathrm{m}}^{-1}$ is zoomed in to show the changes in intensity and peak frequency of the $\nu \left(C-C\right)$ modes with temperature more clearly. The intensity ratio of the $\nu {\left(C-C\right)}_T$ peak at 1,065 ${\mathrm{c}\mathrm{m}}^{-1}$ to the $\nu {\left(C-C\right)}_G$ peak at 1,079 ${\mathrm{c}\mathrm{m}}^{-1}$ yields the relative number of trans to gauche conformers (Fig. 2D). The trend of this ratio with respect to temperature shows a change in slope at the LLT corresponding to an increase in the number of trans conformers in the low temperature liquid II state. Likewise, the intensity and the peak frequency of the $\nu {\left(C-C\right)}_T$ peak around 1,130 ${\mathrm{c}\mathrm{m}}^{-1}$ is sensitive to the number of trans conformers in the liquid. The intensity of this peak increases as the liquid is cooled (Fig. 2C) and the peak shifts to higher frequency (Fig. 2E). The increase in the peak frequency of this mode (Fig. 2E) exhibits a nonmonotonic trend similar to the intensity ratio in Fig. 2D with a change in slope observed at the LLT temperature, $T_{L-L}$, corresponding to an increase in the number of trans conformers and increased ordering of the alkyl chains. Spectral bands around 1,300 ${\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 2A) correspond to ${\mathrm{C}\mathrm{H}}_2$ twisting modes, denoted as $\tau \left(C{H}_2\right)$, are superimposed on other modes corresponding to methylene deformation (29). The relative intensities and positions of these modes correspond to the degree of coupling between alkyl chains and the relative number of trans to gauche conformers. The shift in the dominance from the mode at 1,305 ${\mathrm{c}\mathrm{m}}^{-1}$ to the $\tau \left(C{H}_2\right)$ mode at 1,300 ${\mathrm{c}\mathrm{m}}^{-1}$ as the liquid is cooled reflects an increase in both chain coupling and the relative number of trans conformers. The peaks at 1,440 ${\mathrm{c}\mathrm{m}}^{-1}$ and 1,457 ${\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 2A) correlate to ${\mathrm{C}\mathrm{H}}_2$ bending denoted $\delta \left(C{H}_2\right)$ and antisymmetric ${\mathrm{C}\mathrm{H}}_3$ bending denoted ${\delta }_a\left(C{H}_3\right)$, respectively (29). A decrease in the ratio of the integrated areas of these peaks A [${\delta }_a\left(C{H}_3\right)$]/A [$\delta \left(C{H}_2\right)$] (SI Appendix, Fig. S3C) is linked to reduced intramolecular motion of methylene and methyl groups and increased chain coupling. This quantity decreases monotonically with temperature down to $T_g$, indicating the slowing down of local motions in the alkyl chains accompanying the dynamic glass transition. Due to the localized origins of these spectral bands, they are not sensitive to the structural reorganization associated with the LLT. The spectral region between 2,800 ${\mathrm{c}\mathrm{m}}^{-1}$ and 3,000 ${\mathrm{c}\mathrm{m}}^{-1}$ (Fig. 2B) includes numerous overlapping peaks dominated by C–H stretching modes around 2,852 ${\mathrm{c}\mathrm{m}}^{-1}$ (${\nu }_s\left(C{H}_2\right)$), 2,883 ${\mathrm{c}\mathrm{m}}^{-1}$ (${\nu }_a\left(C{H}_2\right)$), and 2,935 ${\mathrm{c}\mathrm{m}}^{-1}$ (${\nu }_s{\left(C{H}_3\right)}_{FR}$) (29). The temperature evolution of these modes indicates increased chain coupling and conformational order. It is evident from Fig. 2B that while the ${\nu }_a\left(C{H}_2\right)$ and ${\nu }_s{\left(C{H}_3\right)}_{FR}$ envelopes increase in intensity as the liquid is cooled, the ${\nu }_s\left(C{H}_2\right)$ mode diminishes ,which suggests the development of a more ordered arrangement of the alkyl chains.

Fig. 2.

Ordering of alkyl chains across the LLT. (A) Raman spectra of ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$ at various temperatures from 1,040 ${\mathrm{c}\mathrm{m}}^{-1}$ to 1,530 ${\mathrm{c}\mathrm{m}}^{-1}$. (B) Raman spectra of [${\mathrm{P}}_{\mathrm{666,14}}$]⁺[BH₄]⁻ at various temperatures from 2,835 ${\mathrm{c}\mathrm{m}}^{-1}$ to 2,955 ${\mathrm{c}\mathrm{m}}^{-1}$. (C) Normalized Raman spectra between 1,040 ${\mathrm{c}\mathrm{m}}^{-1}$ and 1,140 ${\mathrm{c}\mathrm{m}}^{-1}$. (D) Ratio of the intensity of the $\nu {\left(C-C\right)}_T$ peak at 1,065 ${\mathrm{c}\mathrm{m}}^{-1}$ to the ${\nu \left(C-C\right)}_G$ peak at 1,079 ${\mathrm{c}\mathrm{m}}^{-1}$. (E) Peak frequency of the $\nu {\left(C-C\right)}_T$ mode around 1,130 ${\mathrm{c}\mathrm{m}}^{-1}$. Solid and dotted lines represent linear fits to the data to serve as guides for the eye. Vertical dashed black lines indicate the transition from liquid I to liquid II to the glassy state.

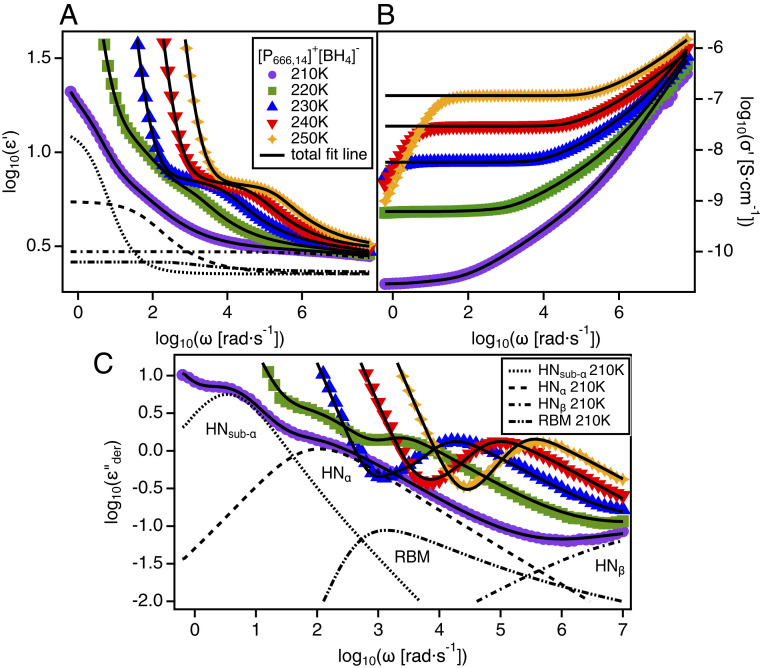
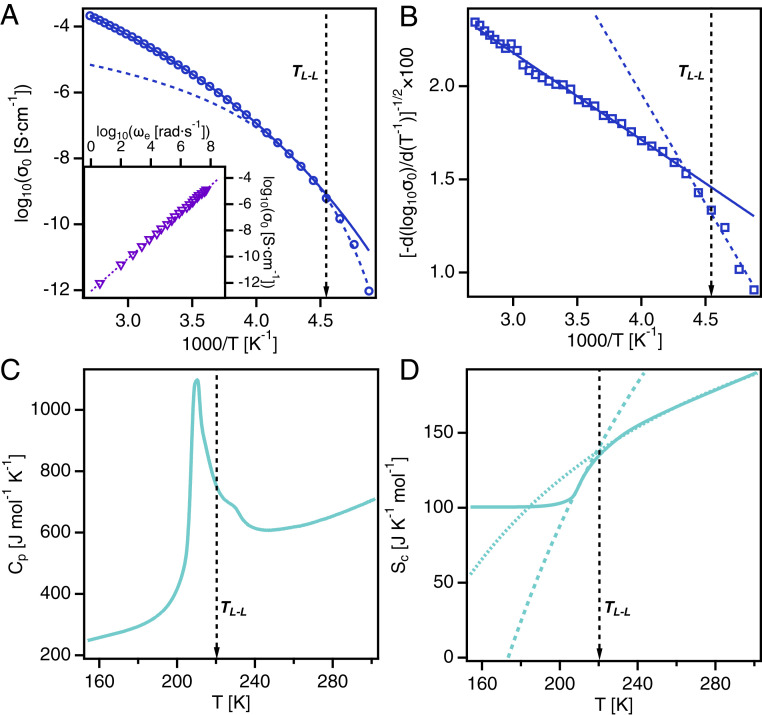
A significant feature of the IL ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$ is that it shows no tendency to crystallize under laboratory conditions. As observed from WAXS, no sharp peaks were observed across the temperature range from the calorimetric glass-transition temperature, $T_g$, up to room temperature, which would indicate the existence of crystalline symmetry within the isotropic liquid phase. Further, stronger evidence for the absence of crystallization was found in the dielectric and calorimetry data. The dielectric spectra (Fig. 3) showed no evidence of crystallization, which would appear as large changes in relaxation rates and, especially, intensities by multiple decades. Instead, the dielectric spectra showed progressive slowing of the relaxation rates characteristic of the dynamic glass transition. The slow sub-$\alpha$ relaxation, most prominently observed in the $\epsilon {”}_{der}$ spectra in Fig. 3C, provides additional evidence for the LLT. This relaxation emerges around 220 K, corresponding to $T_{L-L}$ observed in the WAXS and Raman data. The slow relaxation in ILs has been linked to interfacial polarization arising from mesoscale ordering of the polar and nonpolar domains in the liquid structure (31, 32). This process that appears in the low-temperature liquid II state is directly connected to the increase in ${\epsilon }_s$ shown in Fig. 1F. Furthermore, the DC ionic conductivity ${\sigma }_0$ data (Fig. 4A) obtained from the dielectric spectroscopy measurements show a temperature trend that follows the Vogel–Fulcher–Tammann (VFT) equation (SI Appendix) typical of glass-forming ion conductors (33). Evidence of crystallization would appear as a sharp decrease in ${\sigma }_0$ by an order of magnitude or more, but it is clear from Fig. 4A that no such change occurs. Likewise, the heat capacity ($C_p$) data (Fig. 4C), as measured by differential scanning calorimetry (DSC), reveals that crystallization does not occur as the liquid is heated from the glassy state below $T_g$ to room temperature (34). However, a sharp enthalpic peak is present in the $C_p$ data, approximately 20 K above the $T_g$, which cannot be explained by crystallization. This anomalous spike was reversible upon thermal cycling (SI Appendix, Fig. S5) and signifies a first-order-like transition between two liquid states.

Fig. 3.

Dielectric spectra of ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$. (A) Real part of the complex dielectric function, ${\epsilon }^{\prime }$, versus radial frequency, $\omega$, at various temperatures. (B) Real part of the complex conductivity, ${\sigma }^{\prime }$, versus radial frequency, $\omega$, at various temperatures. (C) Derivative representation of the imaginary part of the complex dielectric function, ${\epsilon }_{der}^{″}=\left(-\pi /2\right)\left[\partial {\epsilon }^{\prime }/\partial \ln \left(\omega \right)\right]$, versus radial frequency, ω, at various temperatures. Solid black lines show fits to the data using a combination of Havriliak–Negami (HN) functions and the Random Barrier Model (RBM) with a power-law function to account for electrode polarization (SI Appendix, Eq. S7). Dashed lines show the individual HN functions and RBM function used to fit the 210 K data. Note that the sub-$\alpha$ relaxation only appears in the spectra at or below 220 K.

Fig. 4.

Dynamic shift and thermodynamic transition in ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$. (A) Direct current (DC) conductivity versus inverse temperature. Two VFT fits are necessary to describe the data. (A, Inset) Barton–Namikawa–Nakajima plot shows that DC conductivity is coupled to primary relaxation across the LLT. (B) Difference quotient indicates that two VFT description is necessary to account for ion dynamics. (C) Heat capacity measured on heating at 10 K/min shows an enthalpic peak at the LLT temperature. (D) Configurational entropy indicates that two AG fits are necessary to describe the data. Solid and dotted lines represent fits to the data to serve as guides for the eye.

This thermodynamic feature occurs at the same temperature as the structural changes observed in the WAXS and Raman data. It makes sense to ask whether the changes in the liquid structure that occur at this thermodynamic transition have an effect on the ion dynamics in the system. Fig. 4 A, Inset shows that the Barton–Namikawa–Nakajima relation holds for this IL across the full temperature range studied, which ultimately implies that ${\sigma }_0$ is coupled to the structural relaxation rate of the liquid as commonly observed for aprotic ILs (35). Therefore, we use ${\sigma }_0$ as a proxy to analyze the ion dynamics of the system. The differential quotient analysis (Fig. 4B) is used to determine the parameters associated with the temperature dependence of ${\sigma }_0$ and the structural relaxation rate by association. In this difference quotient representation, VFT-like behavior typical of glass-forming systems would yield a linear dependence of a single, negative slope with inverse temperature (33). The change in slope in Fig. 4B points to a dynamic shift that occurs at the onset of the thermodynamic transition, above $T_{L-L}$. This discrepancy is likely due to the increase in the number of locally favorable liquid structures as the ion dynamics slow down upon cooling. Further cooling of the sample then results in the first-order transition from liquid I to liquid II. Specifically, the steeper slope at temperatures below the transition corresponds to an increase in fragility of the system. This result would suggest that the dynamics of ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$ necessitates two VFT functions to account for the full temperature range from $T_g$ to room temperature. The Adam–Gibbs (AG) model of the dynamic glass transition was employed to unravel the connection between the dynamic shift and the thermodynamic transition. The configurational entropy $S_c$ (Fig. 4D) can be calculated by integrating the $C_p$ data (36) (SI Appendix). For a typical glass-forming system, the AG model predicts that $S_c$ should follow a smooth, monotonic curve approaching the glass transition that can be described by two parameters: $S_{\infty }$, which accounts for the high temperature limit of $S_c$, and $T_k$, which is the Kauzmann temperature or ideal glass-transition temperature (37). The parameters of the AG model can be related to the VFT parameters that describe the ion dynamics with $T_k=T_0$, where $T_0$ is the Vogel temperature that appears in the VFT equation (38). The shift in the dynamics in this IL suggests that the material can exist in two distinct liquid states, each with unique properties and structures. The values of the VFT and AG fits to the dielectric and calorimetric data are given in SI Appendix, Table S1, along with the calculated glass transition temperatures, $T_g$, and fragilities, $m$. Remarkably, $T_0$ and $T_k$ from the fits are in quantitative agreement, which shows that the dynamic shift is coupled to the thermodynamic transition.

At present, we can only speculate on the mechanism of the LLT in ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$. The WAXS results suggest that the morphology of the charge-alternation structure changes from a three-dimensional network of single-strand filaments to double-strand filaments based on the increase in the ion-coordination number. The temporal evolution of the dielectric spectra (SI Appendix, Fig. S4) was measured at 210 K over the course of 1 h to investigate the phase-ordering kinetics of the LLT. However, no change in the dielectric spectra was observed over the course of the measurements, and the LLT had already occurred in the sample by the time the set temperature was reached. This suggests that the LLT proceeds rapidly in this material, indicating that the transition occurs via spinodal decomposition, which generally has a shorter lag time and faster kinetics than that of a nucleation and growth mechanism (39, 40).

In summary, the IL, trihexyltetradecylphosphonium borohydride, was found to undergo a discontinuous change in the extension of its polarity-alternation structure, corresponding to an abrupt increase in the ion-coordination number, indicating a decisive enhancement in local order at the transition. This structural change was found to coincide with enhanced ordering of the alkyl chains in the nonpolar domain as well. As shown by calorimetric data, a first-order thermodynamic transition occurs at the temperature of the structural reorganization. Furthermore, dielectric spectroscopy showed a step-like change in the static dielectric permittivity and a drastic shift in ion dynamics, as well. Overall, these results unequivocally suggest an LLT. Given the variety of systems available, ILs are indeed a unique class of model glass-forming liquids to probe the underlying mechanisms controlling LLTs and, ultimately, the glass transition. The relative ease with which molecular structures and interactions can be systematically varied in ILs will prove useful in these efforts to address the many open fundamental questions regarding the nature of liquid state.

Materials and Methods

Synthesis of ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$.

The IL used in this study was synthesized from [${\mathrm{P}}_{\mathrm{666,14}}$]⁺ [Cl]⁻ by metathesis methods (41–45). Sodium borohydride (catalog no. 213462; 99%), chloroform (catalog no. CX1059-1), and sodium hydroxide (catalog no. 795429; ≥97%) were acquired from MilliporeSigma. The salt [${\mathrm{P}}_{\mathrm{666,14}}$]⁺ [Cl]⁻ (>93%, CYPHOS^® IL 101; Chemical Abstracts Service No. 258864-54-9) was a product of Cytec Canada Inc. (Cytec is currently owned by Solvay).

To initiate IL synthesis, 10.0 g (19.3 mmol) of [P_666,14]⁺ [Cl]⁻ was introduced to a 250-mL round-bottom flask already containing 100 mL of chloroform, followed by stirring for 30 min. To this reaction mixture, 1.0 equivalent of the sodium salt (${\mathrm{N}\mathrm{a}\mathrm{B}\mathrm{H}}_4$) was added, followed by the addition of 100 mL of Millipore water (18.2 M$\mathrm{\Omega }$cm). The reaction mixture was stirred for 2 h, then allowed to stand for an additional 30 min for chloroform–water phase separation. Centrifugation was performed to encourage phase disentanglement. The dense chloroform layer was washed with Millipore water five times to remove traces of NaCl by-product residing within the organic layer. Following aqueous washes, the chloroform layer was taken and dried over anhydrous ${\mathrm{M}\mathrm{g}\mathrm{S}\mathrm{O}}_4$. The chloroform layer was filtered through sintered glass to remove the drying agent, and the chloroform was removed on a rotary evaporator to isolate the IL as a free-flowing liquid.

The ¹H NMR (500 MHz, ${\mathrm{C}\mathrm{D}\mathrm{C}\mathrm{l}}_3$) spectra of ${\left[{\mathrm{P}}_{\mathrm{666,14}}\right]}^{+}{\left[{\mathrm{B}\mathrm{H}}_4\right]}^{-}$, assigned as follows, validate a successful synthesis:

[P_666,14]⁺[BH₄]^−: δ 2.363 (m, 8H), 1.718 (s, 2H), 1.520 (m, 16 H), 1.325 (m, 14 H), 1.267 (m, 16H), 0.909 (t, 12H), 0.268 (s, 1H), 0.105 (s, 1H), −0.058 (s, 1H), −0.222 (s, 1H).

WAXS.

The WAXS measurements were performed on the Xenocs Xeuss 3.0 small-angle X-ray scattering instrument at the Joint Institute for Advanced Materials. The sample was first dried under vacuum ($<10^{-6}$ bar) at 340 K for 24 h and then loaded into a fused silica capillary tube with 1.5-mm outside diameter and 0.01-mm wall thickness. The capillary tube was sealed with a clear epoxy prior the measurement. The temperature of the sample was controlled with a Linkam HFSX350 stage to within $\pm$0.1 K using liquid nitrogen as a coolant. The scattering intensity was measured under vacuum in the q-range from 0.13 to 3.9 Å⁻¹. The sample was initially measured at room temperature and then cooled to 195 K (below $T_g$) at 10 K/min. The sample was held at each temperature for 60 s before collecting data over a 120-s integration time. Measurements were taken at a series of temperatures upon heating the sample from below $T_g$ back to room temperature.

Raman Spectroscopy.

Raman measurements were performed by using the Horiba LabRAM HR Evolution confocal Raman microscope with a 532-nm excitation laser at 50% power, a 50× long working distance (LWD) objective, over three 15-s accumulations, and 1,800-gratings-per-millimeter filter to achieve 0.5-${\mathrm{c}\mathrm{m}}^{-1}$ resolution. The sample was first dried under vacuum ($<10^{-6}$ bar) at 340 K for 24 h. A drop of the sample was then loaded into a Linkam THMS600 temperature stage with silica windows to control the temperature to within $\pm$0.1 K using liquid nitrogen as the coolant, and the sample thickness was maintained at approximately 150 $\mathrm{\mu }$m using Teflon spacers. The sample was measured in the temperature range from 183 K to 253 K on cooling at 5 K/min and heating at 10 K/min, pausing at each temperature for the duration of the measurement. Variations between the cooling and heating data were minimal.

Broadband Dielectric Spectroscopy.

Broadband dielectric spectroscopy (BDS) measurements were performed in the frequency range of $10^{-1}$ to $10^7$Hz by using a Novocontrol High Resolution Dielectric Alpha Analyzer with a Quatro liquid nitrogen temperature control system with $\pm$0.1 K temperature stability. The BDS measurements were carried out by using gold-plated brass electrodes, 20 mm in diameter, with Teflon spacers approximately 150 $\mu$m in thickness. The sample was dried under vacuum ($<10^{-6}$ bar) at 340 K for 24 h prior to being loaded between the electrodes using a syringe and inserted into the cryostat. Prior to measurement, the samples were annealed at 340 K for more than 2 h to ensure that the spectra were not changing with time. Dielectric spectra were collected in 5-K intervals on cooling from 340 K to 150 K and then on heating back to 340 K in 10-K intervals. This temperature sweep was repeated to ensure thermal reproducibility. For each temperature point, the sample took approximately 10 min for the temperature to stabilize and 5 min to measure the full frequency range. For temporal dielectric measurements, the sample was prepared as described above. The sample was initially heated to 340 K to equilibrate the high-temperature liquid structure. The sample was then rapidly cooled at about 10 K/min to 210 K in between $T_g$ and $T_{LL}$. Once the temperature stabilized, measurements were performed from $10^{-1}$ to $10^7$ Hz every 360 s up to 1 h.

DSC.

DSC measurements were conducted by using a TA Instruments Q2000 DSC instrument. The sample was weighed into an aluminum pan of predetermined weight by using a Mettler Toledo microbalance with an accuracy of 0.1 $\mu$g and hermetically sealed before being loaded into the DCS instrument. An empty aluminum pan of the same type was used as a reference. The sample was initially heated to 340 K to erase its thermal history. The DSC data were measured at a temperature ramp rate of 10 K/min from 340 K down to 150 K and back up to 340 K. This temperature sweep was cycled three times to ensure thermal reproducibility of the data.

Data Availability

All study data are included in the article and/or SI Appendix.