Vaccinating the oldest against COVID-19 saves both the most lives and most years of life

Abstract

Many competing criteria are under consideration for prioritizing COVID-19 vaccination. Two criteria based on age are demographic: lives saved and years of future life saved. Vaccinating the very old against COVID-19 saves the most lives, but, since older age is accompanied by falling life expectancy, it is widely supposed that these two goals are in conflict. We show this to be mistaken. The age patterns of COVID-19 mortality are such that vaccinating the oldest first saves the most lives and, surprisingly, also maximizes years of remaining life expectancy. We demonstrate this relationship empirically in the United States, Germany, and South Korea and with mathematical analysis of life tables. Our age-risk results, under usual conditions, also apply to health risks.

Margaret Keenan received the first vaccination against COVID-19 given in the United Kingdom just a week before her 91st birthday (1). In contexts where vaccine allocation is based on age, prioritizing the very old, who have the highest risk of dying, averts the most deaths. But, from the point of view of saving years of remaining life, it seems that it might be better to target younger people, who are less likely to die quickly of another cause if they can be protected from the coronavirus.

Common intuition suggests a trade-off between saving the maximum number of lives and saving the most future life. Such a trade-off is central to philosophical and ethical discussions (2–4), and epidemiological and public health studies often report both numbers of deaths and numbers of years of life lost (YLL) (5–7) in quests for balanced health intervention priorities.

Here we show that this intuition about demographic trade-offs is wrong in the case of COVID-19. While it is true that remaining life expectancy declines with age, this decline is overwhelmed by the exponentially increasing risk of death. For COVID-19, it turns out that vaccinating first the oldest old saves the most lives and also the most life left. Early guidelines from the Centers for Disease Control and Prevention list those aged “65+” as one priority group among several. But, even in terms of YLL, the oldest old in this group should be first in line.

Naturally, many complex considerations besides age impinge on vaccination strategies, and we defer to epidemiologists, ethicists, and experts in health-related sciences for comprehensive studies that include transmission dynamics and other priorities. Our aim in this report is strictly demographic. We take one—narrow but central—aspect of the picture, and show that formal demography can avert one common misunderstanding.

Concepts

We write $v_d\left(x\right)$ for the expected lives saved per vaccination of a person aged $x$. Each death averted at age $x$ prevents the loss of $e\left(x\right)$ years of potential life. The product $v_e\left(x\right)=v_d\left(x\right)e\left(x\right)$ gives the expected years of life saved per vaccination.

The age pattern of mortality reduction per vaccination $v_d\left(x\right)$ depends on the age pattern of vaccine efficacy and on the age pattern of mortality risk. (The mortality risk reflects the combined effects of infection risk and the infection fatality rate [IFR].) Early trial results suggest that there are not yet detectable differences in vaccine efficacy by age (8). COVID-19 mortality risk rises exponentially with age at nearly the same rate as all-cause mortality (9, 10).

These two stylized facts together allow expected person-years saved per vaccination to be expressed as

$$v_e\left(x\right)=\theta \cdot \rho \cdot h\left(x\right)\cdot e\left(x\right),$$ [1]

with vaccine efficacy being a constant $\theta$ over age, and COVID-19 mortality being a constant fraction $\rho$ of all-cause mortality, $h\left(x\right)$.

Observations

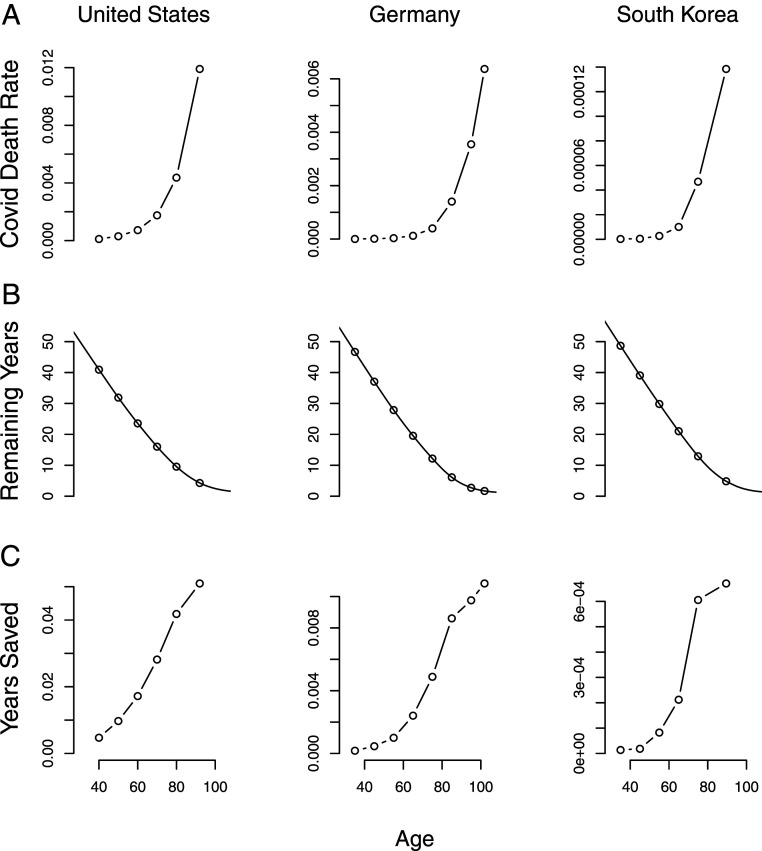
Fig. 1 shows age profiles of COVID-19 mortality rates, remaining life expectancy, and person-years saved per vaccination for the United States, Germany, and South Korea. COVID-19 mortality rates (Fig. 1A) grow at a nearly constant exponential rate in all three countries (9). Within an age-based framework, vaccination of the oldest group will clearly maximize $v_d\left(x\right)$, lives saved.

Fig. 1.

Age patterns of (A) COVID-19 death rates, (B) remaining life expectancy, and (C) person-years saved per effective vaccination in the United States, Germany, and South Korea. In all three countries, within an age-based framework, vaccination of the oldest group will maximize person-years saved per effective vaccination. (Details are provided in Materials and Methods).

Remaining life expectancies (Fig. 1B) decline fairly linearly in the same manner in all three countries, flattening out only at very old ages.

Years saved per vaccination (Fig. 1C) rise with age, with the oldest age saving the most remaining life. Some decline in the rate of increase occurs at older ages in Germany and South Korea, but the maximum is still reached at the oldest ages.

The rate of exponential increase with age of COVID-19 mortality is similar in all three countries, about 11% per year. The differences between age groups are enormous. Assuming equal effectiveness over age, vaccines given to 90-year-olds would save 3 times more lives than would the same doses given to 80-year-olds—and more than 80 times as many lives were the doses given to 50-year-olds.

In terms of maximizing person-years of remaining life, vaccinating a 90-year-old in the United States would be expected to save twice as many person-years as vaccinating a 75-year-old, and 6 times as many as vaccinating a 50-year-old.

Mathematical Generalization

The pattern of increasing years of life saved is not an accidental feature of the particular mortality schedules presented in Fig. 1. It is a general mathematical property holding for a class of mortality models including all of the main models favored by demographers for describing rising age-specific rates from midadulthood onward. In Materials and Methods, we establish inequality (Eq.2) which guarantees that years of life saved increases with age. A prime example satisfying the inequality is the Gompertz model which posits exponentially rising mortality with age and gives good fits to the empirical schedules in Fig. 1. Other models satisfying the inequality are the Weibull models with rates increasing like a power of age, and logistic models with rates that begin to diverge from Gompertz patterns at extreme ages and level out into mortality plateaus.

A corollary applies to health status, assuming the popular “proportional hazards” approach. Vaccinating those at age $x$ who are in poorer health will save more years of life than vaccinating healthy people of the same age.

Discussion

Allocating scarce COVID-19 vaccine doses involves many complex trade-offs. However, a conflict between minimizing the count of deaths and maximizing remaining life is not one of them.

Contrary views are widespread. The World Health Organization, for example, rejected the use of YLL as an allocation criterion in part because “a priority approach relying on YLL could be viewed as disrespectful to older people by failing to address their disproportionately higher risk of death” (11). Our empirical analysis shows it is easier than thought to set such fears aside and to give vaccine priority to the oldest old and those in the most vulnerable states of health.

The assumptions of our formal investigation can be relaxed somewhat. COVID-19 mortality rates rise slightly faster with age than all-cause mortality rates [about 1% faster (9)], so our results would continue to hold if it is found that vaccination effectiveness declines slightly with age. Likewise, the period mortality rates in Fig. 1 presumably rise a little more steeply than the cohort rates driving actual future years lived. In situations where those in long-term care have already been prioritized, a relevant question for further prioritization is the steepness of the mortality age gradient for the remaining population. This is an area of active research (10).

The age-based mathematical analysis can be extended, using common assumptions, to other risk factors such as health status. Under the proportional hazards Gompertz model, giving priority to people most at risk due to combinations of age and health status will save both the most lives and life left.

Our findings give further support to announced priority rankings that vaccinate first those most at risk for dying from COVID-19. Our analysis is not a replacement for more comprehensive modeling accounting for both the direct and indirect effects of vaccines. Rather, in the case of COVID-19, we show that a general property of life tables can be invoked to wipe away the potential conflict between saving lives and maximizing future years of life. Giving COVID-19 vaccines to those facing the highest risk of death from the disease accomplishes both of these goals.

Materials and Methods

Data and Methods for Fig. 1.

COVID-19 death rates by age are calculated per capita, using cumulative data from late fall 2020 based on data from the Institut National d’Etudes Demographiques (INED) (12). The last week of reporting available was November 24 in Germany, November 28 in the United States, and December 2 in South Korea.

Life expectancy profiles are from the Human Mortality Database (HMD) (13), using recent period life tables (2017 for the United States and Germany, and 2018 for South Korea). Life expectancy was interpolated to the midpoint of all COVID-19 mortality reporting age groups. The average age of death from COVID-19 for the open interval was approximated using all-cause HMD life tables as follows: $85+$ (92.0) for the United States, $100+$ (101.9) for Germany, and $80+$ (89.5) for South Korea.

Mathematical Proofs.

We use continuous notation for the hazard $h\left(x\right)$ and cumulative hazard $H\left(x\right)$, with $H\left(0\right)=0$, $maxH\left(x\right)=\infty$, and $h\left(x\right)>0$. As in Eq. 1, years of life saved are assumed to be proportional to the product given by

$$g\left(x\right)=h\left(x\right)\hspace{0.17em}e\left(x\right)=h\left(x\right){\int }_x^{\infty }{e}^{-H\left(y\right)}\hspace{0.17em}dy/e^{-H\left(x\right)},$$

with the integral and its denominator defining $e\left(x\right)$, life expectancy at age $x$.

Proposition: Suppose that the hazard $h\left(x\right)$ is twice differentiable and for all ages $x$,

$${\left(\frac{d\hspace{0.17em}\log h\left(x\right)}{dx}\right)}^2>\frac{d^2\hspace{0.17em}\log h\left(x\right)}{d{x}^2}.$$ [2]

Then $g\left(x\right)=h\left(x\right)e\left(x\right)$ is monotone increasing in age.

Proof: Consider the inverse function for the nondecreasing function $H$ and let $\lambda$ be the composition of the hazard with this inverse function. That is, $h\left(x\right)=\lambda \left(u\right)$ when $H\left(x\right)=u$, and $h\left(y\right)=\lambda \left(u+t\right)$ when $H\left(y\right)=u+t$. Using $dH\left(y\right)=h\left(y\right)dy$ to change the variable of integration from $y$ to $t$ (and absorbing the factor $h\left(x\right)$ that appears outside the integral), we find that the value $\tilde{g}\left(u\right)$ of $g\left(x\right)$ corresponding to $u$ is given by

$$\tilde{g}\left(u\right)={\int }_0^{\infty }\hspace{0.17em}\frac{\lambda \left(u\right)\hspace{0.17em}dt}{\lambda \left(u+t\right)\hspace{0.17em}{e}^t}.$$ [3]

For $\delta >0$,

$$\begin{array}{ll}\hfill \tilde{g}\left(u+\delta \right)& ={\int }_0^{\infty }\hspace{0.17em}\frac{\lambda \left(u+\delta \right)\hspace{0.17em}dt}{\lambda \left(u+\delta +t\right)\hspace{0.17em}{e}^t}\hfill \\ \hfill & ={\int }_0^{\infty }\hspace{0.17em}\left(\frac{\lambda \left(u+\delta \right)\lambda \left(u+t\right)}{\lambda \left(u\right)\hspace{0.17em}\lambda \left(u+t+\delta \right)}\right)\frac{\lambda \left(u\right)\hspace{0.17em}dt}{\lambda \left(u+t\right)\hspace{0.17em}{e}^t}.\hfill \end{array}$$

Write $\mathrm{\Phi }$ for the fraction in brackets inside the integral. Define ages $x_1\dots$ by $H\left(x_1\right)=u$, $H\left(x_2\right)=u+\delta$, $H\left(x_3\right)=u+t$, and $H\left(x_4\right)=u+t+\delta$, and put $f\left(x\right)=\log h\left(x\right)$. From the definition of $\lambda$ in terms of the inverse function of $H$, we can write $\log \mathrm{\Phi }$ as $\left(f\left(x_2\right)-f\left(x_1\right)\right)-\left(f\left(x_4\right)-f\left(x_3\right)\right)$.

For small $\delta$, we have

$$\delta ={\int }_{x_1}^{x_2}\hspace{0.17em}h\left(y\right)\hspace{0.17em}dy\approx \left(x_2-x_1\right)h\left(x_1\right),$$

and similarly for the relationship between $\delta$ and $x_4-x_3$. Thus

$$\begin{array}{ll}\hfill \log \mathrm{\Phi }& \approx \frac{\delta }{h\left(x_1\right)}\hspace{0.17em}{\left.\frac{df}{dx}\right|}_{x_1}-\frac{\delta }{h\left(x_3\right)}\hspace{0.17em}{\left.\frac{df}{dx}\right|}_{x_3}\hfill \\ \hfill & =\delta {\int }_{x_1}^{x_3}\hspace{0.17em}\frac{-d}{dx}\left(e^{-f\left(x\right)}\hspace{0.17em}\frac{df}{dx}\right)\hspace{0.17em}dx.\hfill \end{array}$$

By assumption, the last integrand ${\left(df/dx\right)}^2\hspace{0.17em}{e}^{-f}-\left(d^2\hspace{0.17em}f/d{x}^2\right)e^{-f}$ is greater than zero. That assures us that $\log \mathrm{\Phi }$ is positive for all $u$ and all $t$, making $\tilde{g}\left(u+\delta \right)$ greater than $\tilde{g}\left(u\right)$ and thus making $g\left(x\right)$ a monotone increasing function of $x$. Q.E.D.

As stated in Mathematical Generalization, most demographic models in common use for later adult age-specific mortality satisfy the conditions of the proposition. For exponentially increasing Gompertz hazards given by $h\left(x\right)=\alpha \exp \left(\beta x\right)$ for $\alpha >0$ and $\beta >0$, the right-hand side of Eq. 2 vanishes. For logistic hazards with $h\left(x\right)=\alpha /\left(1+\exp \left(-\beta x\right)\right)$, the right-hand side is negative. For Weibull hazards with $h\left(x\right)=x^{\beta -1}$ with $\beta >1$, it is also negative. Thus the proposition holds for all these models. Artificial hazard functions like $h\left(x\right)=\exp \left(x^{\beta }\right)$ for some values of $\beta$ fail to satisfy the condition for some $x$, but these have little empirical relevance.

Remark: In the presence of a proportional hazard multiplier $s>0$, $h\left(x\right)$ is replaced by a product $s\hspace{0.17em}h\left(x\right)$, and $H\left(x\right)$ is replaced by a product $s\hspace{0.17em}H\left(x\right)$. Using the inverse of the original, baseline cumulative hazard $H$ to implement the change of variables, under the rescaled hazard rates, in the counterpart of Eq. 3, $\lambda \left(u\right)$ in the numerator becomes $s\lambda \left(u\right)$, and $e^t$ in the denominator becomes $e^{st}$, but $\lambda \left(u+t\right)$ in the denominator remains unchanged, since it derives from the change of variables. Under a further change of variables from $t$ to $\tau =st$, we have

$${\tilde{g}}_s\left(u\right)={\int }_0^{\infty }\hspace{0.17em}\frac{\lambda \left(u\right)\hspace{0.17em}d\tau }{\lambda \left(u+\tau /s\right)\hspace{0.17em}{e}^{\tau }}.$$

As long as $h\left(x\right)$ and therefore $\lambda \left(u\right)$ are monotone increasing functions and $s>1$, $\lambda \left(u+\tau /s\right)$ is smaller than $\lambda \left(u+\tau \right)$ for all $\tau >0$, and therefore ${\tilde{g}}_{s>1}\left(u\right)$ is bigger than ${\tilde{g}}_{s=1}\left(u\right)$. At any fixed age, those with a higher risk multiplier have higher values for years of life saved.

For Gompertz hazards $h\left(x\right)$, a stronger property holds. A person with proportional hazards multiplier $s$ faces hazards

$$sh\left(x\right)=s\alpha e^{\beta \hspace{0.17em}x}=h\left(x+\log \left(s\right)/\beta \right).$$

In other words, such a person experiences the same hazards as would a person $\log \left(s\right)/\beta$ years older who has no multiplier, implying that orderings of risk by $h\left(x\right)$ and by $g\left(x\right)$ come out to be the same.

Data Availability

Previously published data were used for this work (Human Mortality Database and INED “Demographics of COVID-19 Deaths").