Generalization Error Analysis for Deep Convolutional Neural Network with Transfer Learning in Breast Cancer Diagnosis

Abstract

Deep convolutional neural network (DCNN), now popularly called artificial intelligence (AI), has shown the potential to improve over previous computer-assisted tools in medical imaging developed in the past decades. A DCNN has millions of free parameters that need to be trained, but the training sample set is limited in size for most medical imaging tasks so that transfer learning is typically used. Automatic data mining may be an efficient way to enlarge the collected data set but the data can be noisy such as incorrect labels or even a wrong type of images. In this work we studied the generalization error of DCNN with transfer learning in medical imaging for the task of classifying malignant and benign masses on mammograms. With a finite available data set, we simulated a training set containing corrupted data or noisy labels. The balance between learning and memorization of the DCNN was manipulated by varying the proportion of corrupted data in the training set. The generalization error of DCNN was analyzed by the area under the receiver operating characteristic curve for the training and test sets and the weight changes after transfer learning. The study demonstrates that the transfer learning strategy of DCNN for such tasks needs to be designed properly, taking into consideration the constraints of the available training set having limited size and quality for the classification task at hand, to minimize memorization and improve generalizability.

1. INTRODUCTION

Achieving high generalization performance on unseen cases even with a training set of limited size is the goal of machine learning. In the past few years, studies have shown that deep learning based machine learning algorithms have the potential to generate models with low generalization error (Goodfellow et al., 2016). In parallel, deep learning methods with transfer learning in medical imaging have shown a similar trend (Sahiner et al., 2019; Litjens et al., 2017; Mazurowski et al., 2018). In this work, we studied the generalization error for the task of breast cancer diagnosis using deep convolutional neural network (DCNN), which has been shown to be an important machine learning tool for breast imaging applications (Chan et al., 2019).

The early application of CNNs to the classification of microcalcifications (Chan et al., 1993; Chan et al., 1995a) and masses (Chan et al., 1994; Sahiner et al., 1996) on mammograms showed the potential of using CNN to learn and identify mammographic patterns. The recent evolution of the CNN models into deep learning for detection and characterization of breast lesions in mammography and digital breast tomosynthesis continues to demonstrate the usefulness of CNNs for breast cancer diagnosis.(Samala et al., 2016a; Huynh et al., 2016; Samala et al., 2016b; Samala et al., 2017; Antropova et al., 2017; Mendel et al., 2018; Samala et al., 2019) Deep CNNs contain millions of parameters to train while medical image data sets are typically much smaller than those available in other computer vision field. Thus it is important to understand the generalization error in medical imaging tasks under the constraint of limited training sets.

The generalizability of classifier performance on unknown cases depends on training sample size.(Chan et al., 1999; Sahiner et al., 2008) From a classifier design perspective, the generalization error can occur due to memorization of the training data, over-fitting, sampling error or a classifier model with too many parameters relative to the finite training sample size. DCNN has an inherent capability to memorize data due to the large learning capacity from its millions of trainable weights. There is no systematic theoretical understanding to quantify the generalizability of DCNN in association with transfer learning or variations in DCNN structure design that includes different types of layers, cost function, optimization algorithm and the order in which the layers are connected (Zhang et al., 2016). In this work we designed a series of simulation experiments in an attempt to gain some understanding of the generalization error of DCNN for the task of breast cancer diagnosis when transfer learning is used.

Generalization error in machine learning can be decomposed into approximation error and estimation error (Niyogi and Girosi, 1996). Approximation error is attributed to either insufficient or abundant representational capacity of a finite sized network. Estimation error is attributed to insufficient training sample size. Generalization error is also affected by noise in the training data, particularly when large medical imaging data are collected with automatic annotations using natural language processing of the electronic health records (Trivedi et al., 2018). Zhang et al (Zhang et al., 2016) studied the generalization error for DCNNs when they were trained using natural scene images with corrupted data and concluded that regularization alone did not explain the low generalization error of DCNNs. In our previous work, we studied the estimation error due to training sample size for breast cancer diagnosis (Samala et al., 2019). At 100% of the training data used in this and our previous study, we found that the variance in estimation error is low so that we assume that it does not influence the generalization error significantly. For all the mammograms used in this study, the mass locations were marked by a mammography quality standards act (MQSA) radiologist with over 30 years of experience in breast imaging using all the available clinical information. Thus the noise in the data set is assumed to be negligible. In the current work, we study the approximation error of DCNN with transfer learning for classification of breast masses on mammograms as malignant or benign while estimation error is assumed constant. We simulate several difficult classification tasks by corrupting the labels or shuffling the pixels of the training set. We vary the transfer learning strategies to select the optimal transfer learning network, and vary the learning capacity of a transfer learning network by freezing different number of layers. By analyzing the generalization errors and weight updates for the different classification tasks, we attempt to gain understanding of the learning capacity and the balance between learning and memorization. Our pilot study (Richter et al., 2018) using a smaller dataset and a single DCNN structure revealed some trends. However, it had limitations due to usage of smaller input image patch size than those of the ImageNet data used for pre-training, (Krizhevsky et al., 2012; Szegedy et al., 2015) which necessitated initializing the weights of all fully connected layers of the DCNN structure such that the relative changes in weights in the fully connected layers by transfer learning could not be compared with those in the other layers. In the current extended study, we remove this limitation by using an input image patch size consistent with the ImageNet data.

2. MATERIALS AND METHODS

2. 1. Data Sets

With Institutional Review Board (IRB) approval, 3,411 breast mammograms were retrospectively collected. Cases of digitized screen-film mammograms (SFM) and full-field digital mammograms (DM) were collected from the patient files at the University of Michigan (UM). Additional SFM cases were collected from the Digital Database for Screening Mammography (DDSM) (Lee et al., 2017). For the cases collected at UM, a Mammography Quality Standard Act (MQSA) qualified radiologist with over 30 years of experience in breast imaging marked the mass with a bounding box using all available clinical information. SFMs digitized at 50 μm x 50 μm were pixel averaged and subsampled to a pixel size of 100 μm x 100 μm by averaging every 2x2 adjacent pixels. All DMs were acquired with GE mammography systems with a pixel size of 100 μm x 100 μm. A 256 x 256-pixel region of interest (ROI) was then extracted for each mass present in all views resulting in 3,578 unique ROIs, which included 1467 malignant and 1774 benign masses in SFM ROIs and 96 malignant and 241 benign masses in DM ROIs. Mammograms were not rescaled to fit the lesion in the ROI size to avoid distorting the image characteristics (e.g., size, spatial resolution, noise, texture) of the lesion relative to the others in the data set and lesions exceeding the ROI size were excluded. All mammograms were background corrected (Chan et al., 1995b; Sahiner et al., 1996) to reduce exposure variations. The detailed implementation of the background correction for the SFM and DM ROIs was discussed previously (Samala et al., 2016a; Samala et al., 2016b). Briefly, a weighted background image was calculated within the 256 × 256-pixel area and subtracted from the original ROI to obtain the background corrected ROI. The 12-bit mammography ROIs with a gray level range of [0,4095] is transformed to [550, 2000] using the background correction method that preserves the details of the masses. The ROIs are not normalized to [0, 1] but used as is to train the DCNN. Our previous study (Samala et al., 2016a; Samala et al., 2016b) has shown that the use of the background-corrected SFM and DM ROIs improved the DCNN training stability and detection performance. The training on mixed data from the two similar imaging modalities also has the advantage of additional transfer learning and thus improving classification performance (Samala et al., 2017; Samala et al., 2019). In the current study, the ROIs were randomly separated into four partitions by patient to be used in a 4-fold cross-validation. The ROIs were augmented by rotating four times and flipping two times, resulting in a 1:8 data augmentation. Tensorflow software library was used to develop the DCNN on an NVIDIA Tesla K40 and 1080 Ti GPUs. Regularization was achieved through jittering in the input layer with a probability of 0.2 and batch normalization.

2. 2. Transfer Learning

Two DCNN structures, AlexNet and GoogLeNet were selected for this study as shown in fig. 1. Both structures are frequently used in medical imaging studies using transfer learning.(Mohamed et al., 2018; Yap et al., 2018; Samala et al., 2016b; Huynh et al., 2016; Han et al., 2017; Chi et al., 2017; Lakhani and Sundaram, 2017) AlexNet proposed by Krizhevsky et al. (Krizhevsky et al., 2012) has five convolutional layers and three fully connected layers. Two fully connected layers were later added to adapt it to two-class classification tasks in our previous study (Samala et al., 2017). GoogLeNet (Szegedy et al., 2015) has two convolutional layers, 9 inception blocks and a fully connected layer. An inception block concatenates parallel implementation of 1×1, 3×3, 5×5 convolutions and 3×3 max pooling layers. Other popular DCNN structures used in medical imaging through transfer learning are variations of AlexNet or GoogLeNet. For example, VGG16 with thirteen convolutional layers and three fully connected layers was used in lung nodule diagnosis (Nishio et al., 2018). The DCNN structure Inception-ResNet, which is an upgrade from Inception-V3, an upgrade of GoogLeNet (also known as Inception-V1) with the addition of ResNet principles (Szegedy et al., 2017), was used for the liver steatosis assessment in ultrasound imaging (Byra et al., 2018). We chose AlexNet and GoogLeNet DCNNs for the current study because they are frequently used in medical imaging and they provide the foundation that many other newer versions are built on. The relatively few layers also facilitate our layer-by-layer analysis of the learning. In addition, the GoogLeNet has 6.7 million weights to be trained while the AlexNet has over 60 million weights and they represent two types of DCNN with very different network capacities.

Fig. 1.

DCNN structures of AlexNet (top) and GoogLeNet (bottom). The input is an image patch of size 256 × 256 pixels and the output is a binary classification of 0 (benign) and 1 (malignant).

Both DCNN structures were initialized with pre-trained weights from the ImageNet data set. During transfer learning, the amount of ‘knowledge’ transfer from the ImageNet-trained DCNN to the target task is determined by varying the depth at which the layers are frozen in the direction from input to output. This is based on the theory that the shallow layers (layers closer to the input) typically extract generic features while decomposing the input image into different components based on high-frequency patterns, and the deeper layers (layers closer to the output) process these components to give appropriate weights based on the expected output of the training classes. Thus the shallow layers are generic features similar to those from Gabor filters (Krizhevsky et al., 2012; Samala et al., 2018) and the deeper layers are usually specific to the task being trained for. This property of the transfer learning is studied in the next section.

2. 3. Transfer Learning Networks

There are two approaches to training the DCNN after the transfer of weights from the ImageNet classification task (source) to medical imaging task (target): (a) training from the transferred weights in the target domain without freezing any layers or (b) freezing one or more early layers and training the deeper layers in the target domain. We denote the first scenario where all the layers are allowed to be trained as C₀ while the rest of the transfer learning networks as C_n (or I_n) where n is the layer (or inception block) up to which all layers (or inception blocks) are frozen. For example, in AlexNet transfer network C₃, all the layers from C₁ to C₃ are frozen and the rest of the layers from C₄ to F₁₀ are allowed to be trained. We analyzed nine transfer learning networks for AlexNet and eleven transfer learning networks for GoogLeNet using four-fold cross-validation. Following the notation above, the transfer network trained with C_n or I_n frozen will be denoted as “AlexNet-C_n” or “GoogLeNet-I_n” in the following discussion. Three types of explicit regularization methods were used during the DCNN training: cropping the input ROI with a probability of 0.2, random vertical flipping with a probability of 0.5 and batch normalization. Learning rates of 0.001 and 0.0001 were used for AlexNet and GoogLeNet, respectively, with Adam stochastic optimizer. Mini-batches of size 64 were used for training. These hyperparameters were chosen based on the literature and our previous experience. The same set of hyperparameters was used for all experiments except that the training was allowed to continue until the training AUC curve reached a stable plateau, the number of epochs thus depended on the DCNN structure and the training conditions.

2.4. Experimental analysis

In the context of understanding generalization error of DCNN for classification of breast cancer, we used experimental analysis to investigate AlexNet and GoogLeNet with different network capacities. We simulated two types of corruptions for the training set in each fold of the cross validation as described in the following. In all experiments, the ROIs in the test fold were not corrupted.

1. Corruption of the class labels: We generated a corrupted training set with (p*100%) of corruption as follows. For a given mass ROI in the training set, a random number r uniformly distributed between 0 and 1 was drawn, if r < p, the label of the mass ROI was flipped. We varied the probability p from 0 to 0.5 in increments of 0.1 to obtain 0% to 50% label corruption in the training sets. At zero probability the DCNN was trained with true labels (0 for benign and 1 for malignant). The reason for flipping a maximum of 50% of the labels was that it was the worst case scenario for the classifier. For corruption greater than 50%, the classifier training would basically be the same as that of (100% minus corruption%) except that the meaning of the label was reversed which the classifier should not care. For example, if the labels were 100% flipped, i.e., all malignant mass ROIs were labeled as 0 and all benign mass ROIs were labeled as 1, the two class labels in the training set were still clearly separated and the classifier should be trained as well as the true labels in terms of classifying the two classes although the output scores would be flipped.

2. Corruption of the input training images: We shuffled the pixel locations of each training ROI in two ways: (i) shuffling with a chosen fixed rule, i.e., one random permutation pattern of the pixel locations was created and applied to all training images, and (ii) shuffling with random rules, i.e., a different random permutation pattern of the pixel locations was created and applied to each training image. Examples of mass ROIs for the pixel shuffling are shown in fig. 2.

Fig. 2.

Examples of mass ROIs of from SFM and DM and the corresponding pixel shuffled ROIs. Left two masses are malignant and right two masses are benign.

From the transfer learning networks described in Section 2.3, we chose two transfer learning networks to analyze the effect of noisy labels and noisy input images; one with the first convolutional layer frozen and the other with all convolutional layers frozen. These two transfer learning structures represent the extreme cases of transfer learning, in which the least and the most of the ‘knowledge’ learned from ImageNet was transferred from the source to the target task, respectively.

2. 5. Evaluation methods

The receiver operating characteristic (ROC) curve was used to assess the DCNN performance. The area under the ROC curve (AUC) was calculated using trapezoidal rule for efficiency. A four-fold cross-validation was performed for all experiments. The available data set was randomly partitioned into 4 approximately equal subsets by case. In each of the four folds, three subsets were combined as the training set and the remaining subset was used for testing. After each subset was used as test set once, the AUCs from the four test subsets were averaged for each experiment and used for comparison. Some experiments were repeated to assess the sensitivity of the DCNN to random stochastic initialization of the weights and random batching of the training data. Different random seeds were used for selecting the mini-batches of training samples that were input to the DCNN during training. During the selection of the optimal transfer network, the experiments were repeated five times.

Transfer learning takes advantage of the weights of the DCNN that have learned to extract features from the source domain images rather than learning from scratch, and as such, reduces the training samples required for the stochastic gradient descent method to search for a global minimum closer to the optimal solution when the DCNN is retrained for a new target task. In that sense, the change of the weights from the source domain to the target domain is an indication of the amount of learning needed for the target task. The root-mean-squared difference (RMSD) between the ImageNet-trained weights and the weights after transfer training with the mammography data is thus a measure of the learning and used as an indicator of the effort needed by the DCNN to learn or memorize new patterns and labels.

3. RESULTS

3. 1. Selection of optimal transfer network

The amount of ‘knowledge’ transfer from ImageNet to the mammography task was examined by using four-fold cross-validation. The robustness of the classifier was evaluated using the mean and variance of the classifier performance on the validation set from five repeated experiments with random stochastic initialization. Fig. 3 shows the transfer learning networks with different degrees of constraints in retraining by freezing the consecutive shallow layers up to C_n, F_n, or I_n. The cross-validation AUC for the classification of the malignant and benign masses by the two DCNN structures across the four folds are plotted and a mean curve was drawn to indicate the trend. A relatively low performance is observed if all the layers are allowed to train (C₀). The worst performance is obtained if all the layers are frozen (F₈ for AlexNet and I_5c for GoogLeNet), which indicates that directly applying the ImageNet-trained DCNN to the breast mass classification task without any retraining is not an effective approach although the performance is still much better than random (AUC of 0.5). The AlexNet has a broad maximum between C₁ and C₃ while the GoogLeNet reaches a maximum at C₁₂. Between the best and the worst transfer networks, the AUC gradually decreases as more and more layers are frozen, limiting its learning capacity to adapt to the new target domain. For the following experiments, we chose the best (AlexNet-C₁ and GoogLeNet-C₁₂) and the worst (AlexNet-C₅ and GoogLeNet-I_5c) transfer learning structures. Note that, for AlexNet, the worst performing transfer learning structure F₈ could have been chosen, but C₅ was chosen instead so that the selection was consistent with GoogLeNet where the worst performing transfer learning structure was a convolutional type layer (inception block).

Fig. 3.

Four-fold cross-validation results of transfer learning networks for AlexNet and GoogLeNet. All experiments were repeated five times to assess the sensitivity of the DCNN to random stochastic initialization of the weights. The test AUCs for the four folds were plotted offset horizontally to facilitate viewing. The mean across the folds is indicated by the blue dotted line. The horizontal axis label represents the layer (or inception block) up to which the layers were frozen during transfer learning: C₀ indicates all the layers were allowed to train, C_n (or F_n, I_n) indicates layers up to C_n (or F_n , I_n) were frozen and the rest of the layers were allowed to train. The input training data was uncorrupted. The best test AUC was observed when the first convolutional layer was frozen achieving average AUCs of 0.81±0.04 and 0.83±0.03 for AlexNet and GoogLeNet, respectively, in the four-fold cross-validation.

3. 2. Learning curves/Learning capacity

The AlexNet and GoogLeNet represent two DCNNs with different network capacities. We varied the learning capacity of these two networks by changing the number of layers up to which the network was frozen. To understand the learning capacity of the DCNN to learn or memorize new labels or patterns, the learning curves in terms of the AUC vs number-of-epochs curves for the training set are plotted in fig. 4 and 5. Each data point shows the mean and the standard deviation estimated from the four training cycles of the 4-fold cross-validation. Two extremes of the transfer learning schemes, C₁ and C₅ for AlexNet and C₁₂ and I_5c for GoogLeNet, are shown with varying degrees of label corruption. The rate at which the DCNNs achieve a training AUC closer to 1.0 is an indication of the balance between the complexity of the task and the learning capacity. For a fixed learning capacity or a transfer learning scheme, as the percentage of label corruption increased, the training converged at about the same epoch but at different speed. Within the same type of transfer learning networks (fig. 4(a) vs 4(b), or fig. 4(c) vs 4(d)), freezing more layers slowed down the training convergence speed. In the case of GoogLeNet-I_5c (fig. 4(d)) that had fewer fully connected layers and nodes than AlexNet-C₅ (fig. 4(b)), the training AUC leveled off far below 1.0 and the asymptotic AUC value decreased as the percentage of corrupted label increased. This indicates GoogLeNet may require some of the convolutional layers in addition to the fully connected layer to learn a difficult task.

Fig. 4.

Learning curves for classifying breast masses with label corruption by AlexNet (top row) and GoogLeNet (bottom row). (a) and (c) are for transfer network with only the first convolutional layer frozen. (b) and (d) are for transfer network with all convolutional layers frozen. Each data point shows the mean and the standard deviation estimated from the four training AUCs from the 4-fold cross-validation. Note the difference in the range of the horizontal axis between the top and bottom rows.

Fig. 5.

Learning curves for classifying breast mass images corrupted by pixel shuffling (fixed and random permutation) by (a) AlexNet and (b) GoogLeNet using two transfer learning networks each. Each data point shows the mean and the standard deviation estimated from the four training AUCs from the 4-fold cross-validation. Note the difference in the range of the horizontal axis between (a) and (b). The AlexNet-C₅ curves eventually reached a training AUC of 1 at over 1000 epochs.

For the task of classifying pixel-shuffled images, the relative trends of the four transfer learning networks were similar to those observed for the label corruption tasks. For both the AlexNet and the GoogLeNet, freezing more layers reduced the training convergence speed; AlexNet slowly approached an AUC of 1 at over 1000 epochs while GoogLeNet-I_5c could not learn very well and leveled off far below an AUC of 1 as shown in fig. 5(b). For AlexNet (fig. 5(a)), learning the fixed shuffling patterns was faster than learning the random shuffling patterns for either frozen scheme. For GoogLeNet (fig. 5(b)), the learning rates were essentially the same for the two shuffling patterns for both frozen schemes.

3. 3. Generalization error change

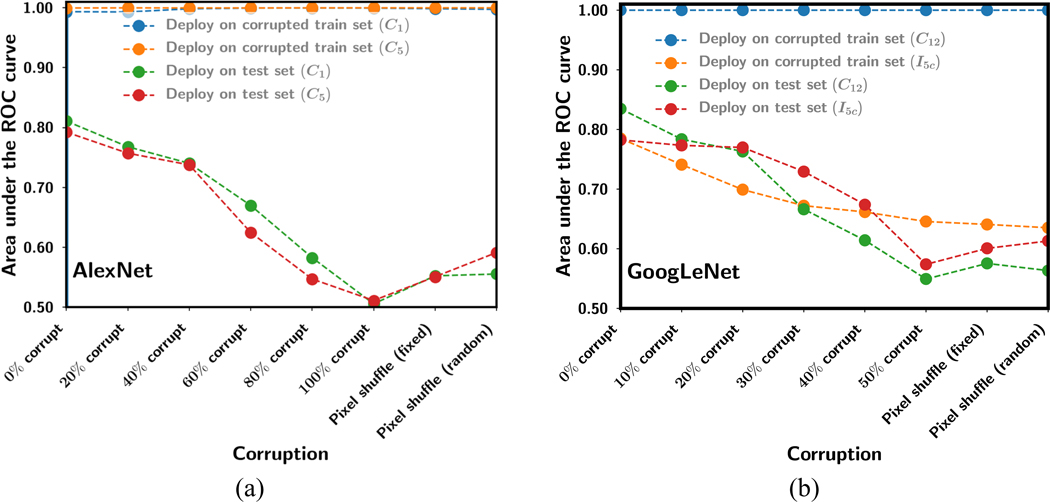
The generalization errors between the training and the test sets for all the experiments for the AlexNet and GoogLeNet fine-tuned with training sets of various degrees of corruption are shown in fig. 6. The mean AUC of the training sets and the corresponding mean AUC of the test sets from 4-fold cross-validation are plotted. The test AUCs were obtained at an epoch where the training AUCs reached a stable plateau, which were different for different tasks and transfer networks (fig. 4 and fig. 5).

Fig. 6.

Generalization error between training and test obtained as the mean AUC of the training sets and the corresponding mean AUC of the test sets from 4-fold cross-validation for the various amount or type of corruption on the training set. The test sets were not corrupted. (a) AlexNet, (b) GoogLeNet for two transfer learning networks each.

In general, increasing the label corruption of the training set reduced the performance on the uncorrupted test set. For AlexNet-C₁ and GoogLeNet-C₁₂ with most layers allowed to be trained during transfer learning, their large learning capacity led them to overfitting to or memorizing the corrupted training patterns or labels even though there was less and less consistent information to learn, while losing most of their “knowledge” in extracting features from uncorrupted images. On the other hand, when all convolutional/inception layers were frozen, the feature extraction capability learned from pre-training with ImageNet was retained but not fine-tuned to the target domain images. The test AUC performance could reach an AUC of over 0.7 if the fully connected layers were properly fine-tuned with uncorrupted target domain data as shown in Fig. 3 and the 0% corruption condition in Fig. 6. However, as the % corruption increased, AlexNet-C₅ that had multiple fully connected layers became increasingly overfitted to the corrupted data and was unable to differentiate the uncorrupted features extracted from the test images. GoogLeNet-I_5c with most of the layers frozen had only one fully connected layer available for retraining. It did not train well with training AUC far below 1.0, indicating that it could not overfit to the confusing training data and therefore appeared to be most resilient to label corruption and pixel shuffling, with the test AUC higher than that of GoogLeNet-C₁₂ for corruptions worse than 20% label corruption.

3. 4. Weight change as a function of learning

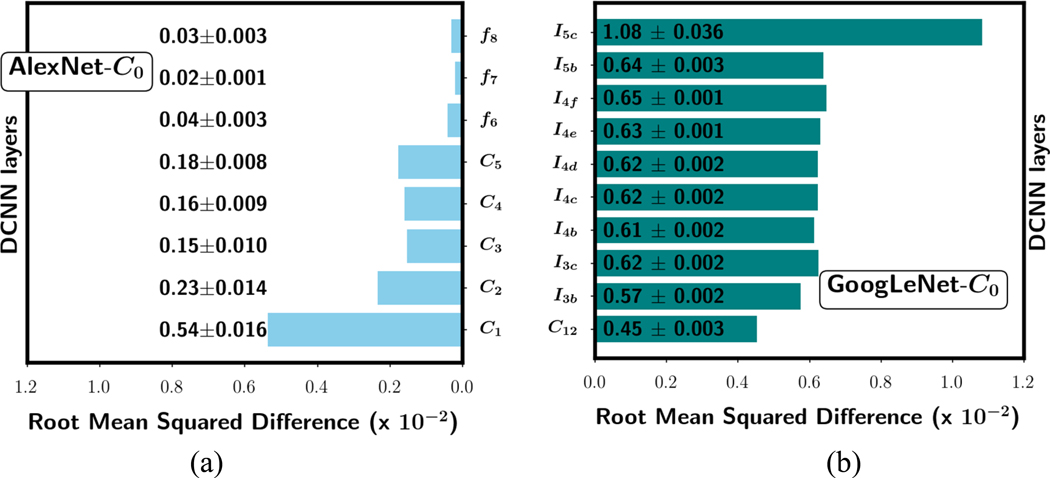
Fig. 7 shows examples of the RMSD of the weights between the ImageNet-trained DCNN and the DCNN without frozen layers (C₀) after fine-tuning with the uncorrupted data in one of the four training folds. In case of an inception block in the GoogLeNet, the RMSD is calculated between corresponding weights over all the convolutional kernels in the block. GoogLeNet-C₀ shows a higher RMSD than AlexNet-C₀. The smaller average change of the weights in the AlexNet may be because it has ten times more weights to accommodate the adaptation to the new task. Both DCNNs achieved a similar mean AUC of 0.81 (fig. 3). However, the weight changes in the two DCNNs show opposite patterns: AlexNet had the highest RMSD at the shallow layer with decreasing trend towards the deeper layer. GoogLeNet had the highest RMSD at the deepest layer and, except for the first layer, all the layers in between had similar RMSD values. Similar trends were observed for the three other folds but only one was plotted in the figure (similarly for fig. 8 and fig. 9) as example.

Fig. 7.

Mean RMSD of the weight changes in each layer averaged over the four training folds for (a) AlexNet-C₀ and (b) GoogLeNet-C₀ networks after transfer learning. The mean and standard deviation values for each layer are shown for the corresponding bar. The training set was uncorrupted and none of the layers was frozen during transfer learning.

Fig. 8.

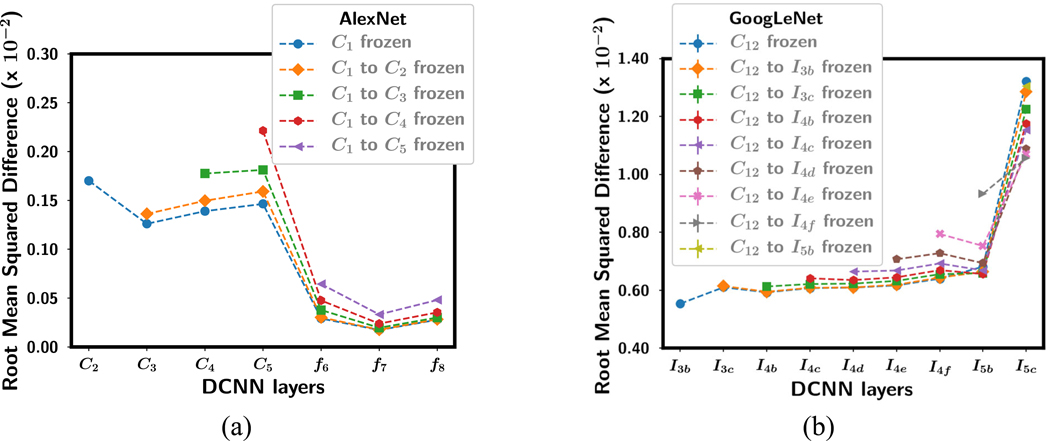
Mean RMSD of the weight changes in each layer averaged over the four training folds for (a) AlexNet and (b) GoogLeNet after transfer learning with uncorrupted data. The standard deviations were in the range of 0.001 to 0.03, smaller than the symbols of the data points, so that they were not plotted. The convolutional layers that were frozen during training were shown in the legend. Note that the horizontal axis shows the DCNN layer where the RMSD shown in the vertical axis was calculated. The RMSD value of the frozen layers was zero and not plotted. Note the difference in the scaling of the vertical axis between (a) and (b).

Fig. 9.

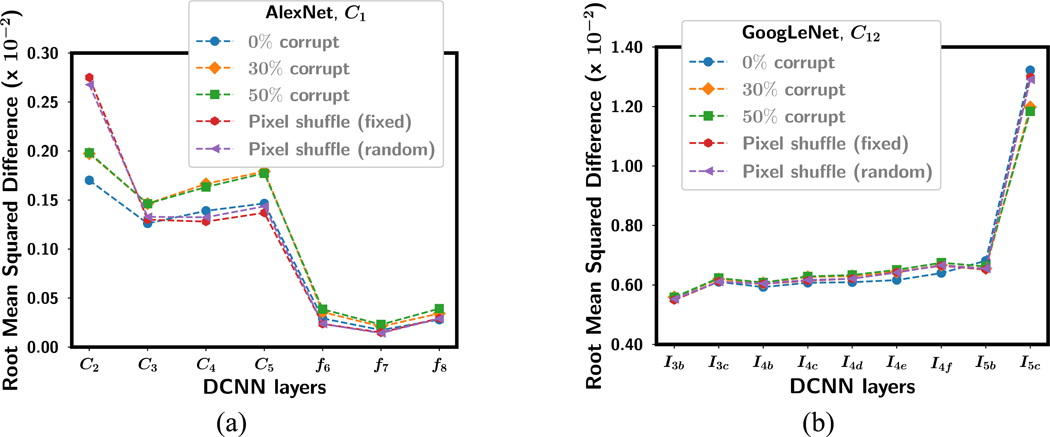
Mean RMSD of the weight changes in each layer averaged over the four training folds for (a) AlexNet-C₁ and (b) GoogLeNet-C₁₂ with the first convolutional layer frozen after transfer learning with corrupted data. The standard deviations were in the range of 0.001 to 0.03, smaller than the symbols of the data points, so that they were not plotted. The horizontal axis shows the DCNN layer where the RMSD shown in the vertical axis was calculated. Note the difference in the scaling of the vertical axis between (a) and (b).

For all the transfer networks with one or more frozen layers, the mean RMSD over the four training folds is shown in fig. 8 after fine-tuning with uncorrupted data. The frozen layers in each transfer network with an RMSD of 0 are not plotted. For the AlexNet, as more and more layers were frozen, the RMSD for the layers that were allowed to be fine-tuned with the target task increased, probably because there were fewer weights that could be adjusted to adapt to the new task so that each weight change was greater. For the GoogLeNet, the RMSD in the shallow layers also increased but the deeper layer decreased, resulting in smaller difference in RMSD between the shallow and the deepest layer.

Fig. 9 shows the RMSD for each layer in AlexNet-C₁ and GoogLeNet-C₁₂ after fine-tuning with label corruption (0%, 30% and 50%) and the pixel shuffle (fixed and random permutation) images. For the label corruption tasks, there is a trend that the RMSD in each layer increased as the classification task became more difficult (e.g., percentage of corruption increased) except for the two deepest layers of the GoogLeNet. For the pixel shuffling tasks, the RMSD was higher than the label corruption tasks in the first trainable layer of the AlexNet and in the deepest layer of the GoogLeNet. This may indicate that adaptation to new features occurs most intensely in these layers for the two DCNNs.

4. DISCUSSION

The large network capacity in DCNNs is a cause for concern in medical imaging due to the limited sample size available for training. In this work, we designed experiments to study the balance between learning and memorization by changing the transfer learning capacity and the classification task with varied degrees of corruption in the training set. Our experimental results for breast cancer diagnosis in mammography show that DCNN can learn generalizable features or memorize patterns depending on the transfer learning strategy and the corruption condition used for training. This result also aligns with the previous study by Zhang et al(Zhang et al., 2016) using ImageNet for training DCNNs from scratch.

In transfer learning, the amount of knowledge transfer and the learning capacity of a pre-trained DCNN being fine-tuned to the target task can be controlled by freezing the DCNN at different depths and allowing the rest of the layers to train. The ‘knowledge’ transfer between the source and the target domain can also vary depending on the complexity of the target task and the difference between the two domains. For the task of identifying mammographic patterns without corruption, the AlexNet and the GoogLeNet follow a similar trend as shown in fig. 3. When the first convolutional layer was frozen, the AlexNet and the GoogLeNet achieved a relatively high AUCs of 0.81±0.04 and 0.83±0.03, respectively. Not freezing any layers gave a lower performance than freezing the first convolution layer, probably because the first layer was already well trained by the large ImageNet data to extract generic features, which may be adversely disturbed by fine-tuning with the relatively small training set of mammography data that have very different image characteristics. On the other hand, there was a gradual drop of classification performance between freezing the first convolutional layers and freezing all the layers, indicating that every deeper layer contributed to learning useful features specific to the target task. The AUC for the last transfer learning network, AlexNet-F₈ and GoogLeNet-I_5c were 0.73±0.04 and 0.77±0.04, respectively. Over the entire range of transfer learning schemes, GoogLeNet performed slightly better than AlexNet.

DCNN has large capacity to learn or memorize by having over millions of parameters, which can become excessive when the amount of data available for training is small. With over 60 million parameters, AlexNet memorized the corrupted labels irrespective of how many convolutional layers were frozen (fig. 4(b)). However, GoogLeNet with only one fully connected layer struggled to train (or memorize) as the label corruption increased when all convolutional layers were frozen (fig. 4(d)), but it preserved some knowledge on feature classification from the ImageNet pre-training and was able to generalize better to the test set (fig. 6(b)). Controlling the number of convolutional layers to be fine-tuned in transfer learning can therefore be considered a way of regularization against overfitting in the mass classification task for DCNN structures with few fully connected layers. In addition, if the quality of the training data collected in the target domain is poor, it may be better to use the DCNN that has been well trained in the source domain as a feature extractor without transfer learning for classification in the target domain.

From the results of the label corruption experiments in fig. 4(a) to 4(c), when the learning capacity was large because many layers were allowed to be trained, stochastic gradient descent was able to train with any amount of label corruption, indicating memorization rather than learning in the process. But when the learning capacity was reduced to one fully connected layer (fig. 4(d)), the training never reached an AUC of 1. For AlexNet with many fully connected nodes and layers, whether the convolutional layers are allowed to train (fig. 4(a)) or not allowed to train (fig. 4(b) has no effect on the DCNNs’ ability to memorize confusing noisy labels regardless of the quality of the extracted image features. The pixel shuffling experiments (fig. 5) further confirmed the memorization capability of the multiple convolutional layers or fully connected layers even for very challenging tasks where the training set contained no consistent image features. The results showed that while these DCNNs can memorize all images reaching a training AUC of 1, their generalizability decreases with increasing data corruption. Our experiments with the mammographic mass classification task therefore provide explicit evidence that differentiates memorization and overfitting from learning, and that the strategies such as batch normalization fails to guard against overfitting.

In cross-domain multi-stage transfer learning where new patterns have to be learned, allowing convolutional layers to be trained is useful. However, at a stage where the training sample size is small, it may be beneficial to freeze some convolutional layers to reduce the number of weights to be trained (Samala et al., 2019) and the risk of memorization. Our work with the mammographic mass classification task demonstrated these trends, but the balance between the learning capacity and the amount of new knowledge to be learned will depend on the similarity of the domains and the availability of the relative amount of training samples with good quality or correct labeling, and will have to be experimentally determined for each situation.

The RMSD between the weights of ImageNet-trained DCNN and the weights of transfer learned DCNN for corresponding nodes and layers is used to understand the “amount” of learning for different transfer learning networks. Fig. 7 to Fig. 9 show that the RMSD was consistently higher for all GoogLeNet transfer networks than AlexNet transfer networks even though both achieved a similar test AUC for the C₀ transfer learning network when they were trained with images without any corruption. AlexNet has over 60 million parameters compared to GoogLeNet with 6.7 million parameters. In case of AlexNet, the highest RMSD is always the first non-frozen convolutional layer. On the contrary, for GoogLeNet the highest RMSD is always the last inception block. This may indicate that most of the learning of the new target patterns is accomplished by the first convolutional layers in AlexNet but most learning in GoogLeNet occurs in the deepest layer. Nevertheless, fig. 3 shows that both DCNN structures follow similar trend in transfer learning in terms of generalization performance. An explanation for the difference in the layer depth where more intense learning occurs within the network may be attributed to the structure of the inception block. The inception block is designed with the idea that using multiple convolutional layers with different kernel sizes in parallel will alleviate the need to carefully design the DCNN. The presence of the 1×1 convolution may be passing the input ROIs with small downscaling to the deeper layers thus resulting in the highest RMSD at the deepest layer before the last fully connected layer.

In summary, our novel contributions in this work include the following: (a) For the mammographic mass classification task, we used an experimental approach to probing the balance between learning and memorization during transfer learning of two very different DCNNs, AlexNet and GoogLeNet. Our study provided explicit evidence that differentiated learning from memorization and overfitting under various training and data quality conditions. (b) The AlexNet and GoogLeNet have vast capabilities to memorize corrupted or mislabeled data. Thus substantial errors in the collected data such as those through scraping of medical records to label imaging data in the clinic could result in large generalization error. Deeper DCNNs with greater learning capacity may have even greater risk of overfitting. (c) The performances of the DCNNs that had their deeper layers fine-tuned with good quality training mammography data were superior to those of the corresponding DCNNs that had all convolutional layers frozen during fine-tuning, i.e., using the ImageNet pre-trained DCNNs as feature extractors, indicating that fine-tuning the deeper convolutional layers is important for the DCNN to learn new image characteristics specific to the target task. (d) The relative performance of the two DCNNs in ImageNet domain was not directly translatable to mammography domain with transfer learning. Although GoogLeNet achieved a 6.7% top-5 error on the ImageNet classification challenge that was significantly lower than the 16.4% by AlexNet, the AUCs for AlexNet and GoogLeNet after transfer learning for the mass classification task were comparable at 0.81±0.04 and 0.83±0.03. (e) Our experimental approach to the study of the mass classification task was shown to work for both AlexNet and GoogLeNet despite the large differences in their structures and the different trends in the RMSD observed in our layer-wise analysis. Since many newer and deeper networks are evolved from these two networks, we expect that similar approach should be applicable to other DCNN structures.

Our experimental study has several limitations. We used four-fold cross validation without an independent test set because of the limited data set available. Nevertheless, we did not tune the network parameters with the validation set and the hyper-parameters were fixed except for the training epoch that was determined by the stable plateau of the learning curve with the training set. The GoogLeNet (0.83±0.03) provided a slightly higher performance than the AlexNet (0.81±0.04) for the no-corruption scenario (fig. 3) in this study but further study will be of interest to evaluate if the difference between the DCNNs for the mammography classification task is statistically significant when a larger training set becomes available in the future. Between approximation error and estimation error that make up the generalization error, we focused on the former in this study using a fixed data set size. However, in our previous work we had analyzed in detail the finite training sample size effect on transfer learning for AlexNet, which provided information about estimation error to some extent (Samala et al., 2019). Combining the analysis of both types of errors would increase the complexity of the current work. We analyzed the generalization errors using only two DCNNs as examples. The selection of AlexNet and GoogLeNet was based on their frequent usage in medical imaging and also considered as the base structures for several newer versions of DCNNs. The DCNNs with relatively few layers were chosen to serve our purpose of layer-by-layer analysis of the learning in these two representative types of DCNNs that have very different number of weights distributed in very different structures. However, the observed learning patterns of these base structures should be applicable to their newer versions of greater depths.

5. CONCLUSION

When training a DCNN for a medical imaging task with transfer learning from a different source task, it is important to understand the generalization error effect on the possible transfer learning networks. We analyzed the generalization error using a breast mass classification task as example. We simulated a range of training data quality by introducing noise in the form of label corruption and pixel shuffling, and studied the balance between learning and memorization for DCNNs of varied learning capacity by freezing different number of convolutional layers during transfer learning. We observed experimental evidence that DCNN has the ability to learn while is also prone to memorization or overfitting depending on the quality of the mammography training data and the transfer learning strategy. Training with noisy data with as few as 10% corrupted labels could increase generalization error. This study thus demonstrates that it is important to design properly the transfer learning strategy for DCNN, taking into consideration the quality of the available training sets and the properties of the classification tasks for transfer learning at hand, so as to minimize overfitting and improve generalizability.