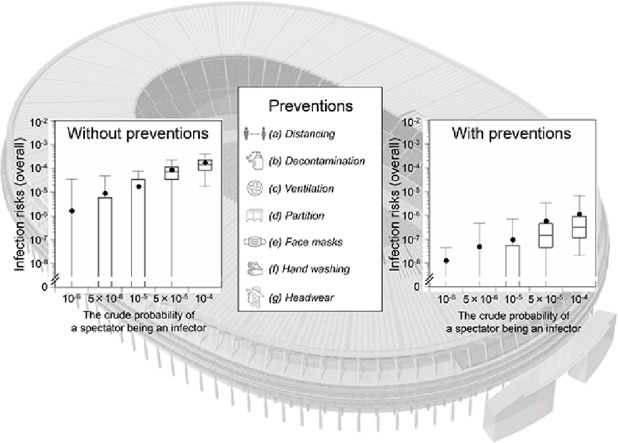
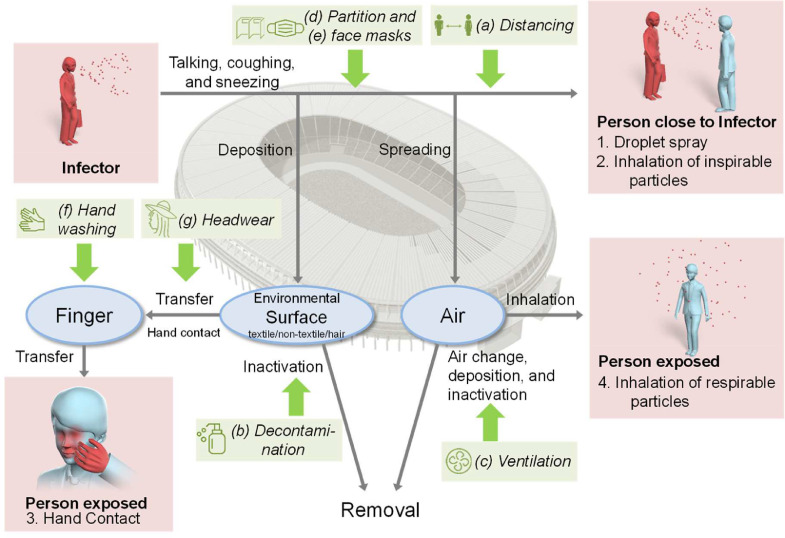
Abstract
The 2020 Olympic/Paralympic Games have been postponed to 2021, due to the COVID-19 pandemic. We developed a model that integrated source–environment–receptor pathways to evaluate how preventive efforts can reduce the infection risk among spectators at the opening ceremony of Tokyo Olympic Games. We simulated viral loads of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emitted from infectors through talking/coughing/sneezing and modeled temporal environmental behaviors, including virus inactivation and transfer. We performed Monte Carlo simulations to estimate the expected number of newly infected individuals with and without preventive measures, yielding the crude probability of a spectator being an infector among the 60,000 people expected to attend the opening ceremony. Two indicators, i.e., the expected number of newly infected individuals and the newly infected individuals per infector entry, were proposed to demonstrate the extent of achievable infection risk reduction levels by implementing possible preventive measures. A no-prevention scenario produced 1.5–1.7 newly infected individuals per infector entry, whereas a combination of cooperative preventive measures by organizers and the spectators achieved a 99% risk reduction, corresponding to 0.009–0.012 newly infected individuals per infector entry. The expected number of newly infected individuals was calculated as 0.005 for the combination of cooperative preventive scenarios with the crude probability of a spectator being an infector of 1 × 10−5. Based on our estimates, a combination of cooperative preventions between organizers and spectators is required to prevent a viral spread at the Tokyo Olympic/Paralympic Games. Further, under the assumption that society accepts < 10 newly infected persons traced to events held during the entire Olympic/Paralympic Games, we propose a crude probability of infectors of < 5 × 10−5 as a benchmark for the suppression of the infection. This is the first study to develop a model that can assess the infection risk among spectators due to exposure pathways at a mass gathering event.
Keywords: COVID-19, Infection risk, Mass gathering event, Solution-focused risk assessment, Tokyo 2020 Olympic/Paralympic Games
Graphical abstract
1. Introduction
The global coronavirus disease 2019 (COVID-19) pandemic caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has inflicted negative impacts on health and tremendous losses of human lives, with over 110 million confirmed cases and 2.4 million deaths (as of February 21, 2021) (World Health Organization, 2021). Since mass gathering events are regarded as key routes of spread and virus outbreaks (James et al., 2020; Walker et al., 2020), mandatory or voluntary bans and postponement have been implemented. Other measures to prevent the spread include physical distancing, mandatory face-mask wearing, and lockdown of cities (Agarwal and Sunitha, 2020; Jüni et al., 2020). Apart from times of war, the one-year-postponement of the Tokyo 2020 Olympic/Paralympic Games is unprecedented in the history of the Olympic Games. Considering the current global COVID-19 situation, the Tokyo Olympic/Paralympic Games may not take place even in July 2021.
Decision making for holding mass gathering events, including the Olympic Games, can be addressed using a risk-based approach (McCloskey et al., 2020) with the preventive measures recognized to minimize the associated infection risks (Tam et al., 2012). Here, we propose an evaluation of the risk of mass gathering events, such as the Olympic Games, beyond “problem-focused thinking” by assessing the preventive and control measures based on the “solution-focused risk assessment” concept (Finkel, 2011). Sound and timely quantitative risk assessment can be based on available scientific data and up-to-date COVID-19-statistics.
Infection risk models include the susceptible–infected–recovered (SIR) model, which evaluates temporal changes in infection risks in a population, and the environmental exposure model, which integrates pertinent source–environment–receptor pathways. While the SIR model is useful for evaluating public policies, such as quarantines, related to the time course of a pandemic (Roda et al., 2020), the environmental exposure model can assess the infection risks from individual pathways, including direct exposure through droplet spray and inhalation of inspirable particles, and indirect transmission over contaminated surfaces and objects (Jones, 2020; Nicas and Sun, 2006). Nicas and Jones (2009) adapted the environmental exposure model to assess the relative contributions of the exposure pathways to influenza infection risk in the context of a healthcare worker attending a patient. Jones (2020) also adapted the model to assess the relative contributions of transmission routes for COVID-19 among healthcare personnel. Zhang and Li (2018) expanded the environmental exposure model to assess influenza infection risks between 1 infector and 37 non-infectors. Although some studies have used environmental exposure models to assess the risk of COVID-19 in healthcare environments (Jones, 2020; Mizukoshi et al., 2021), there are no examples of models that have been extended to cover mass gathering events. Such models are needed to enable assessment of the infection risk assessment and the effects of preventive measures.
Herein, we developed an environmental exposure model to assess the COVID-19 infection risks for spectators at a mass gathering event and evaluated the effectiveness of potential preventive measures for reducing infection risks. Here, we used the opening ceremony of the Tokyo 2020 Olympics as an example of a mass gathering event; however, the model developed can be applied to assess spectators’ risk of infection at mass gathering events in general. We assessed the expected number of newly infected individuals with and without prevention using the crude probability of a spectator being an infector (P 0). We demonstrated the extent of achievable levels of infection risk reduction by implementing potential preventive measures.
2. Methods
2.1. Base scenarios
In this study, we evaluated the infection risk in scenarios both with and without preventive measures applied. The base scenarios (i.e., scenarios without preventive measures) were unrealistic; however, they were used to quantitatively assess the effectiveness of preventive measures by comparing the risk of infection with and without the application of such measures.
We simulated loads of SARS-CoV-2 emitted from asymptomatic infectors by talking/coughing/sneezing, modeled temporal environmental behavior including virus inactivation and transfer, and estimated the expected infection risks among the spectators attending the opening ceremony of the Olympic Games (Fig. 1 ). Infectors generally consist of symptomatic and asymptomatic individuals. However, because symptomatic infectors are either identified by testing or their symptoms prevent them from coming to the venue, only asymptomatic infectors were considered as participants in the opening ceremony. The number of spectators was assumed to be 60,000, based on the existing execution plan of the ceremony (Japan Sport Council, 2020). Data on facilities also came from the Japan National Stadium, which is scheduled to host the opening ceremony of the Tokyo Olympic Games (Japan Sport Council, 2019; 2013; 2014). We assumed that all non-infectors were susceptible to SARS-CoV-2.
Fig. 1.
The exposure pathway model at the opening ceremony of the Tokyo Olympic Games. Arrows (→) indicate the directions of virus transmission between humans and environmental media. Dashed boxes show exposure pathways: (1) droplet spray, (2) inhalation of inspirable particles, (3) hand contact, and (4) inhalation of respirable particles. Text in italics shows seven preventive measures: (a) physical distancing among the spectators at entrances and exits, (b) decontamination of surfaces in concessions, (c) enhanced stadium air ventilation, (d) partitioning of spectators in the stands, (e) mandatory face masks at concourses, restrooms, and concessions, (f) hand washing with soap in restrooms, and (g) wearing hats or other headwear in the stands.
We set the crude probability of a spectator being an infector (P 0) with given scenarios of 1 × 10−6, 5 × 10−6, 1 × 10−5, 5 × 10−5, and 1 × 10−4, with P 0 representing the prevalence of an infector among spectators. The prevalence of infectors can be approximated by the product of the daily incidence rate of infectors (I 0) and the number of days with infectivity (Gordis, 2014). Symptomatic individuals experience 2.3 days of infectivity before symptom onset and 7 days of infectivity after symptom onsets (He et al., 2020b). Thus, the total number of days of infectivity is 9.3, regardless of whether the individual is asymptomatic or symptomatic. The ratio of the number of asymptomatic infected individuals to the number of all infected individuals (Rateasym) is 46% (He et al., 2020a). Therefore, P0 can be expressed by the function in eq. 1.
| (1) |
The P 0 of 1 × 10−6, 5 × 10−6, 1 × 10−5, 5 × 10−5, and 1 × 10−4 corresponds to the I 0 of 1.8 × 10−7, 9.1 × 10−7, 1.8 × 10−6, 9.1 × 10−6, and 1.8 × 10−5 infected individuals per day, respectively.
For example, if P 0 is 10−4 and there are 60,000 spectators, the expected number of infectors is 6, but in reality, the number of infectors and the probability of their entry are calculated according to the binomial theorem. Therefore, we estimated the probability that the number of infectors participating in the ceremony is m (P 1_ m) from P 0, the number of spectators (n = 60,000), and the binomial distribution as in eq. 2 (Table S1).
| (2) |
P 1_ m was calculated as the number of m=l, if P 1_ m was > 10−3, and then other residual probabilities were apportioned into P 1_ l +1. The number of infectors who participated in the ceremony of the Tokyo Olympic Games was considered to follow the probabilities shown in Table S1.
2.2. Environmental exposure model
We developed an environmental exposure model by referring to previous studies (Jones, 2020; Nicas and Jones, 2009; Nicas and Sun, 2006; Zhang and Li, 2018) (Fig. 1). We considered the following four pathways. Persons close to an infector were exposed through talking, coughs, and sneezes. The exposure pathways consisted of direct exposure through (1) droplet spray and (2) inhalation of inspirable particles. We assumed a surface area of 10,000 cm2, where the virus was deposited near the infector (Nicas and Sun, 2006). Deposited surfaces included environmental surfaces and the hair of persons sitting immediately in front of the infector in the stands. Deposited viruses were partly inactivated and also transferred to the fingers of other persons, eventually raising the (3) risk of hand-to-face contact exposure contaminating mucous surfaces. A minor portion (10−6) (Nicas and Sun, 2006) of the emitted viruses were attached to particles dispersed in air and were partly lost through air exchange, deposition, and inactivation processes. Persons were exposed to viruses through (4) inhalation of respirable particles.
The ceremony of the Olympic Games is expected to last for 3 h. An infector was assumed to behave as follows during waiting times, in addition to ceremony viewing. The infector would spend 15 min waiting at the concourses to enter, 15 min in the restroom, 15 min at concessions, 240 min in the stands, and 15 min to exit at the concourses. The infector was assumed to be accompanied by two persons who were not infected. These three persons stayed together in line at the concourses (for entry and exit) and in the stands. During the 15 min stay in the restroom, the infector spent 13 min waiting and 2 min in a toilet (Nakagawa et al., 2008). At concessions, the infector spent 14 min waiting and 1 min ordering. In the stands, each accompanier had a seat on either side of the infector.
Considering the human behavior and environmental pathways above, we classified exposed persons into five categories: (1) accompaniers of the infector, (2) persons sitting immediately in front of the infector in the stands, (3) persons exposed in restrooms, (4) persons exposed in concessions, and (5) others. We estimated the expected infection risks and the corresponding number of infected individuals for each category and calculated the overall infection risks. The initial virus densities in the air and on surface materials (i.e., the densities before the ceremony) were assumed to be null. All the model parameters are listed in Table S2.
2.3. Virus emission
We set the SARS-CoV-2 RNA concentrations in saliva as the arithmetic mean of 2.6 × 107 copies/mL (standard deviation: 4.1 × 107 copies/mL), according to a clinical report that quantified SARS-CoV-2 RNA in saliva using reverse transcription-quantitative PCR (To et al., 2020). We assumed that the SARS-CoV-2 RNA concentrations in saliva follow a log-normal distribution. The viral viability ratio, defined as the ratio of the number of viable virus particles to that of viral RNA copies in saliva, was set as 0.1 plaque-forming unit (PFU)/copy because the ratio of the median tissue culture infectious dose (TCID50) to the viral RNA copies in the saliva of ferrets was 0.15 (Kim et al., 2020) and the ratio of PFU to TCID50 was 0.7 (Covés-Datson et al., 2020). The product of 0.15 and 0.7 was rounded to 0.1.
SARS-CoV-2 can be spread through talking, coughing, and sneezing. Previous studies (Nicas and Jones, 2009; Nicas and Sun, 2006) divided particles with an aerodynamic diameter of 100 or 150 μm into small and large particles as the source of inhalation of inspirable particles and droplet spray, respectively. However, a recent study showed that 12–21 μm particles, prior to dehydration, could cause droplet spray (Stadnytskyi et al., 2020). This indicates that the size classification of 100 or 150 μm used in previous studies (Nicas and Jones, 2009; Nicas and Sun, 2006) could underestimate droplet exposure and overestimate inhalation of inspirable particles. We therefore followed a previous study (Zhang and Li, 2018) and divided saliva particles into small particles (with an aerodynamic diameter of < 10 μm) and large particles (> 10 μm) as sources of inspirable particles and droplet spray, respectively. The saliva volume in small particles was 8.82 × 10−8 mL for 1 min of talking, 1.65 × 10−7 mL for one coughing event, and 1.27 × 10−6 mL for one sneezing event (Zhang and Li, 2018). The saliva volume in large particles was 3.09 × 10−3 mL for 1 min of talking, 6.15 × 10−3 mL for one coughing event, and 4.75 × 10−2 mL for one sneezing event (Zhang and Li, 2018).
We considered whether a virus emission event occurred in a given 1-min-time window. We assumed that infectors talked, coughed, and sneezed independently as events of virus emission. The probability of talking for 1 min was set at 0.2, estimated from an observation of sports viewing where four persons talked 30,725 Japanese characters in 1 h 33 min 29 sec (Sumino et al., 2010) and an assumption that 1 min of talking corresponds to 400 Japanese characters. We assumed that the probability of talking for one minute was the same for non-Japanese people. We assumed that the infectors do not talk in the restrooms or while waiting at concessions but only for 1 min when they placed an order at concessions.
The cough probability per min for asymptomatic infectors was 0.013 (a value for healthy persons (Yousaf et al., 2013)). The sneeze probability per min for asymptomatic infectors was assumed to be 0.0057, which was estimated from the sneeze probability for symptomatic infectors and the ratio of cough probability between asymptomatic and symptomatic infectors (Chen and Liao, 2010; Yousaf et al., 2013; Zhang and Li, 2018).
2.4. Infection risk (base scenarios)
2.4.1. Accompaniers of infectors
Exposure pathways for accompaniers of infectors include (1) droplet spray, (2) inhalation of inspirable particles, (3) hand contact, and (4) inhalation of respirable particles. The number of accompanying persons per infector was 2, as described above.
-
(1)
Droplet spray
The persons were directly exposed to SARS-CoV-2 in large particles via droplet spray. We assumed that the probability that an infector talked/coughed/sneezed near an accompanier at the concourses (P i_a_c) was 50% and that the probability that an accompanier looked at an infector when the infector talked/coughed/sneezed to the accompanier (P a_i_c) was 50%. Similarly, we assumed that these probabilities in the stands (P i_a_s and P a_i_s) were 25% and 50%, respectively. Namely, in the stands, an infector talked/coughed/sneezed toward an accompanier on the right or left at a probability of 25% each, and forward at a probability of 50% (P i_f_s). We considered that droplet spray exposure could occur when an infector talked/coughed/sneezed toward an accompanier and when an accompanier looked at the infector. Large particles were assumed to spread as a three-dimensional cone with a 60° angle (Nicas and Jones, 2009; Nicas and Sun, 2006), and the physical distance between an infector and an accompanier at the concourses and in the stands was set at 0.5 m (Japan Sport Council, 2014). The area of the droplet spray that spread to an accompanier was therefore estimated to be 2.6 × 10−1 m2. Since the area of facial mucous tissue (i.e., lips, eyes, and nostrils) is 1.5 × 10−3 m2 (Nicas and Jones, 2009; Nicas and Sun, 2006), the number of SARS-CoV-2 particles transmitted in a droplet spray that strikes any mucous surface was considered to be 5.7 × 10−3. Doses from droplet spray exposure (D 1_drop (t) [PFU]) were estimated as in eq. 3.
| (3) |
where V 1_ l (t) represented the number of emitted viable SARS-CoV-2 in large particles sprayed toward an accompanier of an infector at time t [PFU].
-
(2)
Inhalation of inspirable particles
The pathway of inhaling inspirable particles was considered according to previous studies (Nicas and Sun, 2006; Nicas and Jones, 2009; Jones, 2020; (Mizukoshi et al., 2021). This pathway involves an exposure in which a person in the vicinity of an infector directly inhales the virus attached to small particles immediately after those particles are emitted by the infector. We assumed that exposure through inhalation of inspirable particles could occur when an infector talked/coughed/sneezed toward an accompanier. We considered that this process could occur even when the accompanier did not look directly at the infector. The virus was assumed to spread as a three-dimensional cone with a 60° angle, similar to the droplet spray exposure and previous studies (Nicas and Jones, 2009; Nicas and Sun, 2006). The accompanier was exposed to 1.5 × 10−2 of emitted viruses in small particles spread forward to the accompanier, based on the air cone volume (4.4 × 10−2 m3 at a distance of 0.5 m), volume per breath (1.3 × 10−3 m3; estimated from a breath rate of 0.02 m3/min and a breath frequency of 15 min−1) and inhaled only 50% of the exhaled particles (Nicas and Jones, 2009; Nicas and Sun, 2006). Doses from exposure through inhalation of inspirable particles (D 1_insp (t) [PFU]) were estimated using eq. 4.
| (4) |
where V 1_ s (t) was the amount of emitted viable virus in small particles spread forward to an accompanier of an infector at time t [PFU].
-
(3)
Hand contact
SARS-CoV-2 contained in small and large particles was considered to settle onto a surface area of 10,000 cm2 near an infector. We considered that surfaces in proximity to an accompanier were contaminated when an infector talked/coughed/sneezed toward the accompanier in the stands. Of the deposited viruses, 50% were apportioned to textile and non-textile materials, respectively. The probability that an accompanier touched a contaminated surface in the stands was assumed to be 0.05 per min for textile surfaces and 0.1 per min for non-textile surfaces. The probability of facial mucosal membrane touch was 1.6 × 10−1 per min based on the observation of 26 persons who collectively touched facial mucosal membranes unconsciously 1024 times in 4 h (Kwok et al., 2015).
Virus transfer efficiencies from textile and non-textile surfaces to fingers were 2.5 × 10−3 and 7.9 × 10−2 per touch event, respectively, which were adapted from a study determining the transfer efficiencies of influenza A virus from paper tissues and stainless steel, respectively (Nicas and Jones, 2009). Based on the deposition areas (total of 10,000 cm2; 50% each for textile surfaces and non-textile surfaces), five fingertip areas (10 cm2) (Nicas and Sun, 2006), and the virus transfer efficiency (2.5 × 10−3 for textile surfaces and 7.9 × 10−2 for non-textile surfaces), virus transfer rate from surfaces in the stands to fingers per touch event was 5.0 × 10−6 (=10/(10,000 × 0.5) × 2.5 × 10−3) for textile surfaces and 1.6 × 10−4 (=10/(10,000 × 0.5) × 7.9 × 10−2) for non-textile surfaces.
The virus inactivation rate was 3.3 × 10−3 min−1 for a textile surface (λ 1 t) and 2.1 × 10−3 min−1 for a non-textile surface (λ 1 nt), from a recent measurement of SARS-CoV-2 inactivation in cardboard and stainless steel (van Doremalen et al., 2020). We assumed that virus inactivation on the fingers was negligible, which is the worst-case scenario.
The viral transfer efficiency from a fingertip to facial mucosal membranes per touch was 0.35 (Nicas and Sun, 2006). Considering that touch involves one fingertip of the five fingers on the same hand (0.2) (Nicas and Sun, 2006), the viral transfer rate from all five fingers to facial mucosal membranes per touch was 7.0 × 10−2.
Viral loads on textile surfaces (S 1_ t (t) [PFU]), non-textile surfaces (S 1_ nt (t) [PFU]), and fingers (F 1 (t) [PFU]), and doses from hand-contact exposure (D 1_h (t) [PFU]), were estimated as shown in eqs. 5–8.
| (5) |
| (6) |
| (7) |
| (8) |
where V 1 (t) represents the number of viable virus that spread toward an accompanier of an infector at time t [PFU], At is the ratio of viral particles deposited onto textile surfaces to the total number of deposited virus particles (0.5), Ant is the ratio of virus particles deposited onto non-textile surfaces to the total number of deposited virus particles (0.5), ∆t is time step (0.01 min), λ 2 t = 5.0 × 10−6 (when the accompanier touched the textile surfaces [touch probability was 0.05 per min]) or 0 (other times), λ 2 nt = 1.6 × 10−4 (when the accompanier touched the non-textile surfaces [touch probability was 0.1 per min]) or 0 (other times), and λ 3 = 7.0 × 10−2 (when the accompanier touched the facial mucosal membranes [touch probability was 1.6 × 10−1 per min]) or 0 (other times).
-
(4)
Inhalation of respirable particles
We considered that 10−6 of the viruses emitted were present in respirable particles and distributed in uniform concentrations in the air (Nicas and Sun, 2006). The doses from exposure through inhalation of respirable particles were the same, irrespective of the five types of persons exposed (i.e., accompaniers of infectors, persons sitting immediately in front of infectors in the stands, persons exposed in restrooms, persons exposed at concessions, and others). We assumed two airborne exposure scenarios in different locations, that is, in the stands and in other locations (concourses, restrooms, and concessions). Since spectators spent 15 min for entry at the concourses, 15 min in the restrooms, 15 min at concessions, 240 min in the stands, and then 15 min to exit at the concourses, as described above, exposure through inhalation of respirable particles in air in the stands could occur at t = 45–285 min. Similarly, we considered exposure through inhalation of respirable particles in the air at the concourses, restrooms, and concessions at t = 0–45 min and 285–300 min.
The effective volume of the stands was 220,000 m3, which was estimated from the floor area (44,000 m2) and an effective height of 5 m. The total effective volume of the concourses, restrooms, and concessions was 145,680 m3, estimated from the sum of the concourses (floor area 29,700 m2 and assumed effective height of 4 m), restrooms (8,400 m2 × 2.2 m), and concessions (2,100 m2 × 4 m). Data on the floor area were retrieved from a floor plan of the stadium (Japan Sport Council, 2013).
The air change per h was set at 12.5 for both the stands and other areas based on the Japanese building standard law. The ventilation rate (λ 4) was therefore estimated as 2.1 × 10−1 min−1.
The virus inactivation rate in the air (λ 5) was 1.1 × 10−2 min−1, based on an experimental measurement of SARS-CoV-2 inactivation in aerosols (van Doremalen et al., 2020). The deposition rate (λ 6) was 5.4 × 10−3 min−1 (Nicas and Jones, 2009).
The inhalation rate of viruses from the air in the stands by a person (λ 7 s) was 9.1 × 10−8 min−1, which was estimated from the breath rate (0.02 m3/min) and the effective volume of the stands. Similarly, the inhalation rate of viruses from the air at the concourses, restrooms, and concessions by a person (λ 7 crc) was estimated to be 1.4 × 10−7 min−1. A total inhalation rate by 60,000 spectators was 5.5 × 10−3 min−1 for the stands (λ 7 s _ all) and 8.2 × 10−3 min−1 for other locations (λ 7 crc _ all).
The total virus removal rate in the stands (λ 8 s) was 2.3 × 10−1 min−1 (=λ 4+ λ 5+ λ 6+ λ 7 s _ all). The total virus removal rate at the concourses, restrooms, and concessions (λ 8 crc) was 2.3 × 10−1 min−1 (t = 0–45 min and 285–300 min) and 2.2 × 10−1 min−1 (t = 45–285 min).
Viral loads in the air in the stands (Airs (t) [PFU]) and at the concourses, restrooms, and concessions (Aircrc (t) [PFU]), doses from exposure through inhalation of respirable particles in the stands (Dresp _ s (t) [PFU]) and at the concourses, restrooms, and concessions (Dresp _ crc (t) [PFU]), and total doses from exposure through inhalation of respirable particles (Dresp (t) [PFU]) were estimated using eqs. 9–13.
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
where Vall_s (t) represents the number of viable viral particles emitted from all the infectors that were subsequently dispersed in the air in the stands (t = 45–285 min) [PFU], and Vall_crc (t) represents the number of viable viral particles emitted from all infectors that subsequently dispersed into the air at the concourses, restrooms, and concessions (t = 0–45 min and 285–300 min) [PFU].
Total doses for the combined pathways for an accompanier of an infector (D 1_ total (t) [PFU]) were estimated using eq. 14.
| (14) |
2.4.2. Persons sitting immediately in front of infectors in the stands
Exposure for persons sitting immediately in front of infectors in the stands consist of the following pathways: (1) inhalation of inspirable particles, (2) hand contact with contaminated hair, and (3) inhalation of respirable particles. The number of persons per infector was 1.
-
(1)
Inhalation of inspirable particles
Exposure through inhalation of inspirable particles was estimated similarly to the estimation for an accompanier of an infector. In this regard, we assumed that the probability that an infector talked/coughed/sneezed forward in the stands (P i_f_s) was 50%. The physical distance between an infector and a person sitting in the seat immediately in front was 0.5 m, i.e., the same distance as between the infector and an accompanier. Doses through inhalation of inspirable particles (D 2_insp (t) [PFU]) were estimated using eq. 15.
| (15) |
where V 2_ s (t) represents the number of emitted viable viruses in small particles spread toward a person sitting immediately in front of the infector at time t [PFU].
-
(2)
Hand contact with contaminated hair
We considered that viruses in small and large particles settled onto the hair of a person sitting immediately in front of an infector when an infector talked/coughed/sneezed forward in the stands. The exposure from hand contact occurred when the person touched his/her hair and then any facial mucous membranes.
The area of hair was assumed to be 300 cm2. The probability of touching the hair touch was 5.9 × 10-2 per min based on the observation of 26 persons that touched their hair 369 times in 4 h (Kwok et al., 2015). The virus transfer efficiency from hair to fingers per touch was set at 2.5 × 10−3, that is, similar to that for a textile surface. The virus transfer rate from hair to fingers per touch was therefore calculated as 8.3 × 10−5 (=10/300 × 2.5 × 10−3). We assumed that virus inactivation in hair was negligible. The probability of a facial mucosal membrane touch and the virus transfer rate from fingers to facial mucosal membranes was the same as that for an accompanier of an infector.
Viral loads on hair (H 2 (t) [PFU]) and fingers (F 2 (t) [PFU]) and the doses from hand-contact exposure (D 2_h (t) [PFU]) were estimated as shown in eqs. 16–18.
| (16) |
| (17) |
| (18) |
where V 2 (t) represents the number of viable viruses that spread toward a person sitting immediately in front of an infector in the stands at time t [PFU], Ah is the ratio of viruses deposited onto the hair to the total number of deposited viruses (300/10,000 = 3.0 × 10−2), λ 9 = 8.3 × 10−5 (when the person sitting immediately in front of the infector touched his/her hair [touch probability is 5.9 × 10−2 per min]) or 0 (other time).
Doses from exposure through inhalation of respirable particles were Dresp (t), as described above. Total doses through all the pathways for a person sitting immediately in front of an infector (D 2_ total (t) [PFU]) were estimated as shown in eq. 19.
| (19) |
2.4.3. Persons exposed in the restrooms
Exposure for persons exposed in the restrooms included the following pathways: (1) hand contact with doorknobs in the restrooms and (2) inhalation of respirable particles. Since the number of spectators and the number of restrooms in the stadium is 60,000 and approximately 2,000 (Japan Sport Council, 2019), respectively, on average one toilet is used by 30 persons, under the assumption that spectators use the restrooms only once. The expected number of people who use a toilet after an infector is estimated to be 15. Therefore, we set the number of persons exposed in the restrooms per infector at 15. We estimated the expected doses for the person using a toilet after an infector and assumed that doses were the same among the other 14 persons.
-
(1)
Hand contact with doorknobs in the restrooms
We considered that a doorknob was contaminated through the deposition of viruses emitted from an infector when he/she coughed/sneezed in a restroom at t = 28–30 min. The doorknob was set at an area of 20 cm2 and classified as a non-textile material. The next toilet user after an infector was assumed to touch the doorknob when he/she exited from the toilet at t = 32 min. The virus transfer rate from the doorknob to fingers per touch was 4.0 × 10−2 (=10/20 × 7.9 × 10−2). The probability of touching facial mucosal membranes and the virus transfer rate from fingers to facial mucosal membranes were the same as for an accompanier of an infector.
Virus loads on the doorknob (S 3_ nt (t) [PFU]) and fingers (F 3 (t) [PFU]), and the doses from hand-contact exposure (D 3_h (t) [PFU]) were estimated as shown in eqs. 20–22.
| (20) |
| (21) |
| (22) |
where V 3 (t) represents the number of viable viral particles spread to a toilet in a restroom at time t [PFU], A 3 is the ratio of virus particles deposited onto the doorknob to the total number of deposited virus particles (20/10,000 = 2.0 × 10−3), λ 10 = 4.0 × 10−2 (when the next toilet user touched the doorknob at t = 32 min) or 0 (other time).
Together with Dresp (t), the total doses through all the pathways for a person exposed in the restrooms (D 3_ total (t) [PFU]) were estimated as shown in eq. 23.
| (23) |
2.4.4. Persons exposed at concessions
Exposure for persons exposed at concessions included the following pathways: (1) hand contact while ordering and (2) inhalation of respirable particles. We assumed that a person would spend 14 min waiting in the concession and 1 min while ordering. We set the expected number of persons exposed in the concessions per infector at 30 because we set the number of persons exposed in the restrooms per infector at 15, as described above, and the duration of toilet use per person (2 min) was 2 times longer than that of ordering time at a concession. We estimated the expected doses for the person who attended the concession immediately after an infector and assumed that the same doses were applicable to the other 29 persons.
-
(1)
Hand contact while ordering
We considered that surface materials in proximity to the infector placing an order were contaminated through the deposition of viral particles. We assumed that an infector talked for 1 min while ordering at t = 44–45. The infector was also assumed to cough/sneeze at this time following a certain probability, as described in “Virus emission.” A total of 20% of the surface area (10,000 cm2) where the virus particles deposited was considered textile and the rest (80%) was non-textile. The person who attended the concession immediately after an infector was assumed to touch the contaminated non-textile surface when he/she completed the order at t = 46 min. The virus transfer rate from contaminated non-textile surfaces at the concessions to fingers per touch event was 9.9 × 10−5 (=10/(0.8 × 10,000) × 7.9 × 10−2). The probability of touching facial mucosal membranes and the virus transfer rate from fingers to facial mucosal membranes were the same as for an accompanier of an infector.
The virus loads on non-textile surfaces at the concessions (S 4_ nt (t) [PFU]) and fingers (F 4 (t) [PFU]) and the doses from hand-contact exposure (D 4_h (t) [PFU]) were estimated as shown in eqs. 24–26.
| (24) |
| (25) |
| (26) |
where V 4 (t) represented the number of viable virus particles spread on site at time t [PFU], A 4 is the deposition ratio of non-textile surfaces in proximity (0.8), λ 11 = 9.9 × 10−5 (when the next concession user completed the order at t = 46 min) or 0 (other time).
The total doses from the two pathways (hand-contact at order and inhalation of respirable particles) for a person who was exposed at concessions (D 4_ total (t) [PFU]) were estimated as eq. 27.
| (27) |
2.4.5. Other persons
The expected number of other persons was calculated from the difference between the number of spectators (60,000) and the sum of the total number of infectors and four categories of persons who were exposed (accompaniers of infectors, persons sitting immediately in front of infectors in the stands, persons exposed in the restrooms, and persons exposed at concessions). The exposure pathway for other persons was inhalation of respirable particles only, with the expected doses (D 5_ total (t) [PFU]), therefore Dresp (t).
2.5. Preventive measures
It is not determined what preventive measures will be taken at the Tokyo 2020 Olympic and Paralympic Games. Through risk assessment, we can evaluate possible preventions to make an informed decision on holding the Games. Among prospective preventions (Boyce and Pittet, 2002; Chu et al., 2020; Johnson et al., 2009; Kampf et al., 2020), seven possible and pragmatic measures were considered: (a) physical distancing of spectators at entrances and exits, (b) decontamination of surfaces in concessions, (c) enhanced stadium air ventilation, (d) partitioning of spectators in the stands, (e) mandatory face masks at the concourses, restrooms, and concessions, (f) hand washing with soap in restrooms, and (g) wearing hats or other headwear in the stands. Four preventions (a–d) are organizer-oriented and three (e–g) are spectator-oriented.
-
(a)
Distancing
In this prevention scenario, we assumed a greater physical distancing of 1.5 m between an infector and an accompanier at the entry and exit than indicated in base scenarios (0.5 m).
-
(b)
Decontamination
We assumed that 99.9% of the viruses in the ordering places were inactivated/removed through decontamination at the time of ordering. A previous study reported that different types of biocidal agents exhibited greater than 99.9% inactivation of coronaviruses (Kampf et al., 2020). We simulated the model for this prevention by changing “λ 11 × S 4_ nt (t)” to “λ 11 × S 4_ nt (t) × 0.001” in eq. 25.
-
(c)
Ventilation
In this prevention scenario, we assumed that the air change per hour in the stands and at the concourses, restrooms, and concessions was increased to 25 compared to base scenarios of 12.5.
-
(d)
Partitioning
Partitioning is a typical physical method used to prevent direct exposure of droplet spray and surface contamination (Fang et al., 2020). We assumed that by installing partitions between individual spectators in the stands, we exclude the exposure pathways of droplet spray and hand contact in the stands from accompaniers.
-
(e)
Face masks
In this prevention scenario, the spectators were assumed to wear face masks only at the concourses, restrooms, and concessions. The use of a certain type of surgical mask can effectively reduce droplet transmission by 99% (Fischer et al., 2020). Five types of surgical masks also showed > 95% reduction in bacterial aerosols emitted into the air (Rengasamy et al., 2009). The effectiveness of face masks has also been reported elsewhere (Chu et al., 2020). However, in practice, considerable portions of emitted virus particles are likely to leak from the gaps between the mask and the face. We therefore assumed that face-mask wearing could reduce the emission of viruses in large particles by 95% but the removal of viruses in small particles was not expected. Furthermore, the use of masks reduced the probability of facial mucosal membrane touch per min from 1.6 × 10−1 to 5.4 × 10−2, because touches of the eyes accounted for 33% of the facial mucosal membrane touches involving the eyes, nose, and mouth (Kwok et al., 2015).
-
(f)
Hand washing
Inactivation of viruses by hand washing with soap was reported elsewhere (Boyce and Pittet, 2002). We assumed that all the spectators washed their hands with soap in the restrooms after using the toilets, thereby inactivating 99% of the virus. In this prevention scenario, we simulated the model by changing “λ 10 × S 3_ nt (t)” to “λ 10 × S 3_ nt (t) × 0.01” in eq. 21.
-
(g)
Headwear
Hair contamination can be a pathway of exposure through hand contact in persons sitting immediately in front of infectors. We assumed that protecting the hair by wearing a hat or other headwear in the stands could exclude hand contact in persons sitting immediately in front of infectors.
2.6. Dose-response model
The expected symptomatic infection risk Psymp (Di) was estimated for five types of persons using a dose-response model for SARS-CoV (Watanabe et al., 2010) as shown in eqs. 28–29. This model was used in a recent risk assessment study of SARS-CoV-2 (Jones, 2020).
| (28) |
| (29) |
where i = 1~5 and k = 410 (Watanabe et al., 2010).
The exponential model used in this study described the dose-response relationship of the pooled data set for SARS-CoV-inoculated mice, with death as an endpoint. The fatality rates of severe diseases such as SARS-CoV-2 depend on the vitality of the infected individuals and the presence/absence of medical treatment. Since mice are generally more sensitive than humans and cannot receive medical treatment, infection of mice with this illness is considered to eventually result in death. We therefore assumed that death as the endpoint for mice can be regarded as an illness for humans. The expected infection risks, including asymptomatic infection P (Di), were estimated by considering Rateasym, as shown in eq. 30. Rateasym has an arithmetic mean of 0.460 and a standard deviation of 0.141, according to a meta-analysis of clinical observations of COVID-19 (He et al., 2020a). We assumed that the probability of Rateasym follows a normal distribution left- and right-censored with 0 and 1, respectively.
| (30) |
The overall infection risk among spectators was estimated from the P(Di) of the five types of persons exposed and the corresponding number of persons.
2.7. Sensitivity analysis
As described in the “Virus emission” section, we assumed that aerosolized saliva particles can be classified as small and large particles, with an aerodynamic diameter of < 10 μm and > 10 μm, respectively. To investigate the effect of the virus load of small or large particles on the infection risk, we performed a sensitivity analysis. We calculated the overall infection risks under the assumption that the viral load in small or large particles were 3, 5, and 10 times greater than those in a reference scenario. In addition, we conducted a sensitivity analysis to change the probability that an accompanier was looking at an infector (P a_i_c and P a_i_s) and the probability that an infector was talking/coughing/sneezing toward an accompanier or forward in the stands (P i_a_s and P i_f_s) (see section 2.4.1 (1)). Specifically, P a_i_c and P a_i_s were changed from 50% to 10%, 25%, or 100%, and P i_a_s and P i_f_s were changed from 25% and 50% to 0% and 100%, 10% and 80%, or 20% and 60%, respectively. To address the uncertainty of the dose-response model, we also performed analyses using the lower (k = 190) and upper (k = 770) limits of the 95% confidence interval (Watanabe et al., 2010). Simulations were run at P 0 = 1 × 10−4 using all seven preventive measures. The results of the analysis showed that the average overall infection risk would increase by 2.54, 3.73, and 7.27 times when the viral loads in large particles were assumed to increase by 3-, 5-, and 10-fold, respectively (Fig. S1). In contrast, the differences in the calculated overall infection risk due to the differences in viral loads in small particles fell within the variation of the output of the Monte Carlo simulations. The average overall infection risks were 0.27, 0.56, and 1.74 times the reference scenario when P a_i_c and P a_i_s were 10%, 25%, and 100%, respectively, whereas the changes in P i_a_s and P i_f_s made no significant difference in the results. Changing the k to the lower and upper limits of the 95% confidence interval resulted in average overall infection risks of 2.36 and 0.45 times the reference value. This indicates that the viral load in large particles, P a_i_c and P a_i_s, and k are key parameters that affect the overall infection risk.
2.8. Simulations
We ran model simulations under the following 33 conditions: (1) base scenarios with 5 conditions (i.e., P 0 = 1 × 10−6, 5 × 10−6, 1 × 10−5, 5 × 10−5, and 1 × 10−4); (2) prevention scenarios (P 0 = 1 × 10−4) with 10 conditions (i.e., seven individual prevention scenarios, four organizer-oriented preventions (a–d), three spectator-oriented preventions (e–g), and all seven preventions (a–g)); (3) the seven preventive measures with 4 conditions with other P 0 (i.e., P 0 = 1 × 10−6, 5 × 10−6, 1 × 10−5, and 5 × 10−5); and (4) the sensitivity analysis with all seven preventions with 14 conditions at P 0 = 1 × 10−4 (i.e., viral loads in small and large particles were set at 3-, 5-, and 10-fold compared to a reference scenario; P a_i_c and P a_i_s changed to 10%, 25%, or 100%; P i_a_s:P i_f_s changed to 0%:100%, 10%:80%, or 20%:60%; k changed to either 190 or 770).
We ran the simulation with a time step of 0.01 min and performed Monte Carlo simulations with 1,000 iterations for each condition. The Monte Carlo simulations estimated the distribution and average (arithmetic means) of infection risk from the expected exposures using a dose-response model. For the base scenario with P 0 = 1 × 10−4, we performed the simulation with 10,000 iterations to confirm that the relative standard deviation for 1,000 iterations was ≤ 2% (Fig. S2). M.M. used Oracle Crystal Ball software (version 11.1.2.4.850; Oracle) for the simulations. F.M., T.Y., and Y.I. independently performed analysis using R software (version 4.0.0) (R Development Core Team, 2020) to confirm the results of M.M.’s analyses.
3. Results
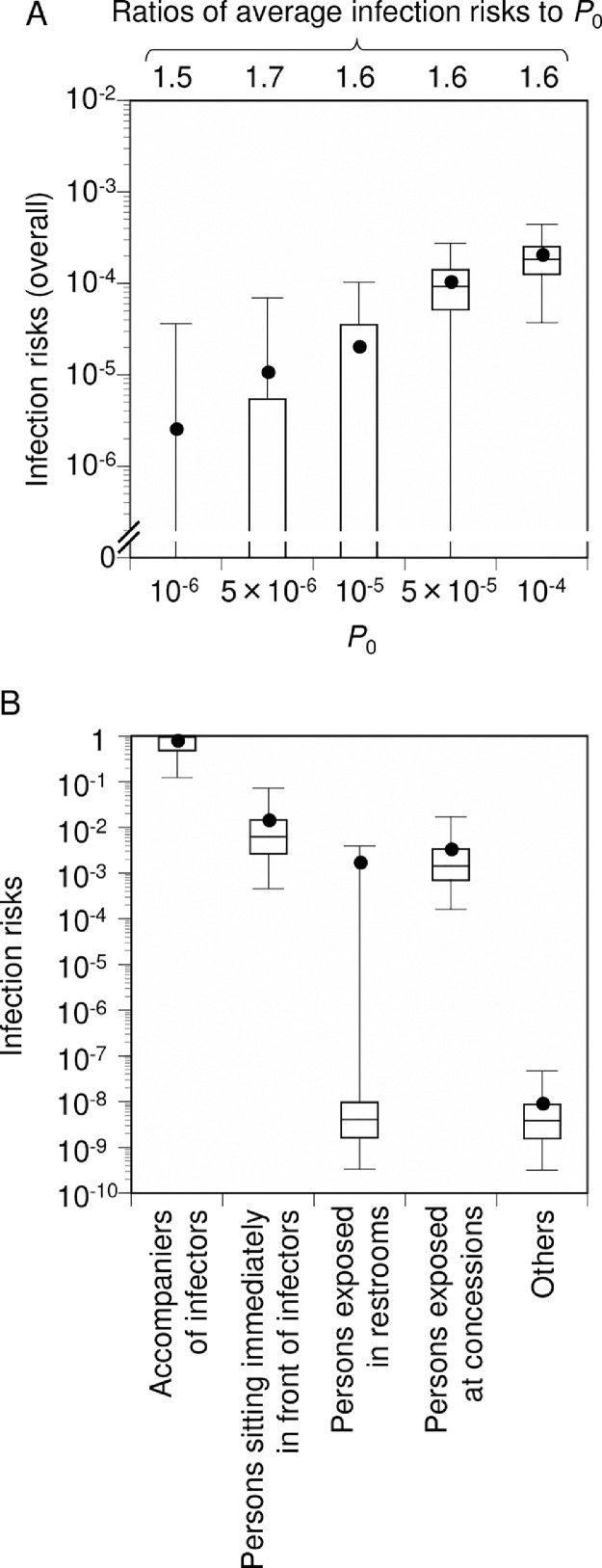
The average overall infection risk (i.e., overall risks among all the spectators except for the infectors) from the no-prevention base scenarios with P 0 of 1 × 10−6 to 1 × 10−4 was 1.5 × 10−6 (75th percentile of 0) to 1.6 × 10−4 (2.2 × 10−4) (Fig. 2 A). The ratios of average infection risks to P 0 ranged from 1.5 to 1.7, so the entry of one infector was expected to result in 1.5–1.7 new infections within a 5-h stay (including entrance, waiting, and exit times) at the opening ceremony. The base scenario with P 0 of 1 × 10−4 had an average risk (75th percentile) of 7.5 × 10−1 (1.0) for accompaniers of infectors, 1.4 × 10−2 (1.5 × 10−2) for persons sitting immediately in front of infectors, 1.6 × 10−3 (9.7 × 10−9) for persons using restrooms, 3.1 × 10−3 (3.3 × 10−3) for persons exposed at concessions, and 8.5 × 10−9 (8.6 × 10−9) for others (Fig. 2B).
Fig. 2.
Base scenario for infection risks among spectators (no-prevention). Comparison of overall infection risks under five simulation conditions with different crude probabilities of a spectator being an infector (P0) (A). Comparison of infection risks among five categories of spectators obtained from simulations with P0 of 10−4 (B). A ratio of average infection risk to P0 corresponds to newly infected individuals per one infector entry into the stadium at the opening ceremony. Box-and-whisker plots represent the following percentiles: 2.5, 25, 50, 75, and 97.5. Closed circles represent average values (arithmetic mean). Monte Carlo simulations were performed with 1,000 iterations for each condition.
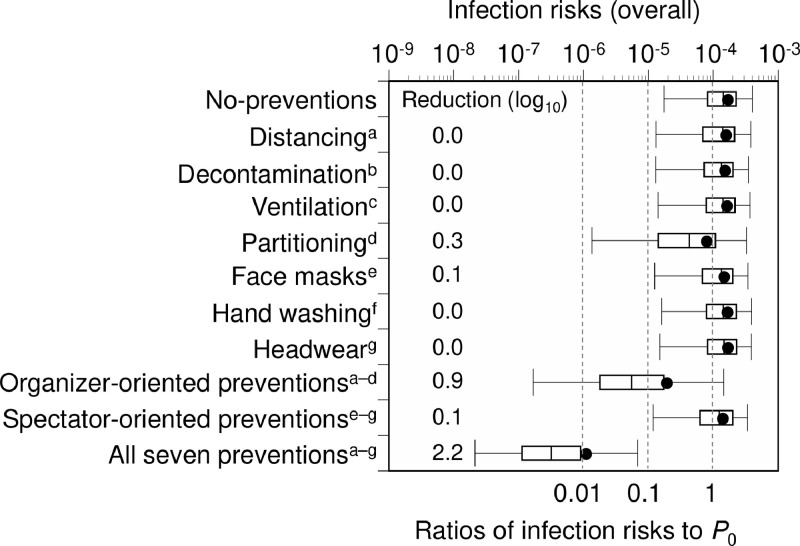
Prevention scenarios with P 0 of 1 × 10−4 estimated that partitioning reduces the risk of infection by an average 0.3 log10, with other single measures providing ≤ 0.1 log10 average estimated risk reductions (Fig. 3 ). The combination of four organizer-oriented preventions yielded a 0.9 log10 estimated risk reduction, with a higher average risk reduction of 2.2 log10 when all seven preventions were applied, indicating a synergy between organizer- and spectator-oriented prevention.
Fig. 3.
Comparison of infection risks among spectators in different prevention scenarios at a crude probability of a spectator being an infector (P0) of 10−4. Comparison of overall infection risks among no-prevention, seven individual preventions, organizer-oriented preventions, spectator-oriented preventions, and all preventions combined. a Physical distancing of spectators at entrances and exits. bDecontamination of surfaces in concessions. c Enhanced stadium air ventilation. dPartitioning of spectators in the stands. e Mandatory face masks at concourses, restrooms, and concessions. fHand washing with soap in restrooms. g Wearing hats or other headwear in the stands. Four preventions (a–d) are organizer-oriented; three (e–g) are spectator-oriented. Risk reduction values were calculated from the average of the no-prevention scenario and respective prevention(s) scenarios. Box-and-whisker plots represent 2.5, 25, 50, 75, and 97.5 percentiles. Closed circles represent average infection risks. Monte Carlo simulations were performed with 1,000 iterations for each condition.
All seven prevention scenarios with P 0 of 1 × 10−6 to 1 × 10−4 gave an average overall infection risk estimate of 1.2 × 10−8 (75th percentile of 0) to 1.1 × 10−6 (9.1 × 10−7) (Fig. 4 ). The ratios of the average infection risks to P 0 ranged from 0.009 to 0.012, corresponding to 2.1–2.3 log10 risk reduction. The expected number of newly infected individuals was calculated as 0.0007 to 0.064 for P 0 of 1 × 10−6 to 1 × 10−4.
Fig. 4.
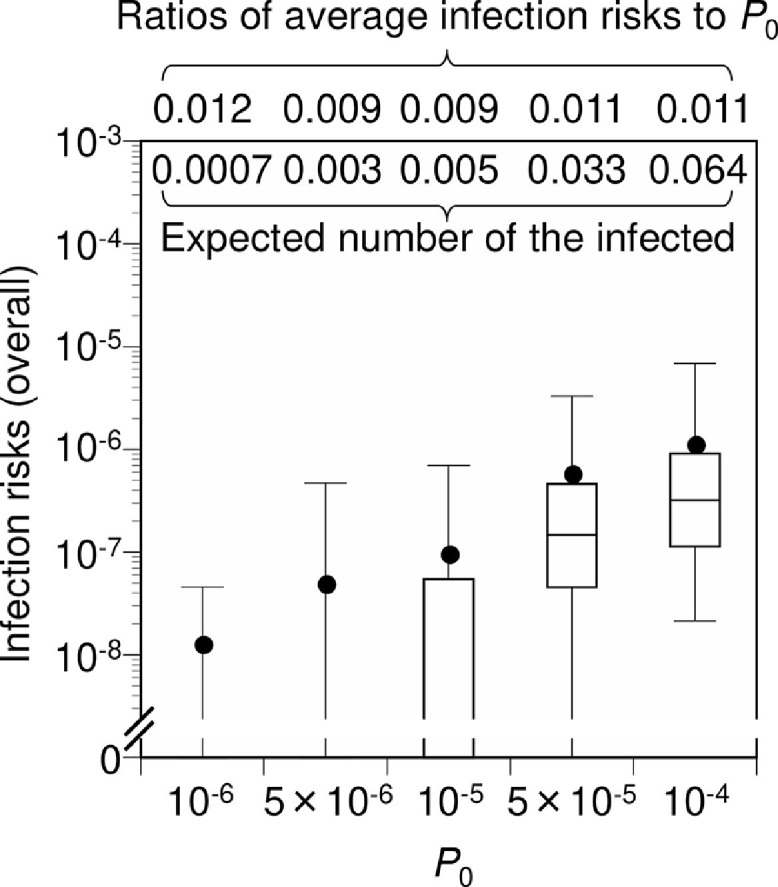
Infection risks among spectators in the scenario of all preventive measures combined. The expected number of newly infected individuals was obtained by multiplying the average overall infection risk by the number of non-infectors. Box-and-whisker plots represent 2.5, 25, 50, 75, and 97.5 percentiles. Closed circles represent average infection risks. Monte Carlo simulations were performed with 1,000 iterations for each condition. P0 is the crude probability of a spectator being an infector.
4. Discussion
In this study, we developed a model to assess the infection risk among spectators due to exposure pathways at a mass gathering event, using the opening ceremony of the Tokyo 2020 Olympics as an example. The advantage of the model developed is that it enables us to quantitatively assess the infection risk of mass gathering events and to calculate the effects of preventive measures on reducing that infection risk. Note that we assumed that all non-infectors were susceptible to SARS-CoV-2. If 50% of the population is not susceptible to the virus, the infection risk is cut in half. Thus, an increase in the proportion of people who have antibodies would reduce not only the incidence and prevalence of infectors, but also the infection risk among spectators at the opening ceremony of the Tokyo 2020 Olympics.
The environmental exposure model revealed variable infection risks for the opening ceremony depending on the virus transmission pathways and individual preventive measures resulted in insufficient risk reductions. Strikingly, a 2 log10 estimated risk reduction was achieved by combining all the evaluated preventive methods, suggesting synergy of spectators and organizers.
Our aim was not to judge the possibility of holding the Games. The infection risk is never null with current COVID-19 outbreaks, and society must decide on what are acceptable risk levels. Our intention was to demonstrate the achievable levels of infection risk reduction by implementing potential preventive measures. Infectious disease outbreaks have occurred in past Olympic Games (Enock and Jacobs, 2008), and the world must make informed decisions based on science when considering holding a mass gathering event like the Tokyo Olympic/Paralympic Games. Knowing the infection risk level provides a better understanding during societal debates and decision making, and we provide two viewpoints.
The first is the ratio of the average infection risk to P 0, which represents the expected number of newly infected individuals per infector entry. The concept is similar to a basic reproduction number (R 0), briefly defined as the expected number of secondary cases produced in a completely susceptible population by a typical infected individual (Diekmann et al., 1990). The epidemic spread can be prevented if R 0 < 1. The ratio of the average viral infection risk to P 0 estimated in this study represents the estimation for the 5-h event; therefore accepting this from a preventive perspective may be difficult if this value is > 0.1. Notably, a combination of all seven preventions can achieve a value of ~ 0.01. The second viewpoint is the expected number of newly infected individuals. The expected number of one newly infected individual among the 60,000 people expected at the opening ceremony in the spectators is unlikely to be acceptable for suppression of the infection during the Games, wherein the total number of spectators is scheduled to be approximately 10 million people. If society accepts < 10 newly infected persons due to the events during the entire period of the Olympic/Paralympic Games, P 0 should be approximately < 5 × 10−5, assuming that the infection risks at other events are similar to those of the opening ceremony. This P 0 benchmark of 5 × 10−5 corresponds to 91 infected individuals per day in a population of 10 million people using eq. 1. As of February 21, 2021, approximately 250 new cases were confirmed per day in the population of 10 million people in Tokyo (Tokyo Metropolis, 2021), which is higher than the benchmark value from our study. The actual infections in Tokyo may also be higher than the official number because of asymptomatic COVID-19 patients (He et al., 2020a) and the restricted diagnostic testing (Sawano et al., 2020).
This study had some sources of uncertainty. First, since the SARS-CoV-2 infectivity titer in human saliva has not been reported, we used the data obtained from experimentally infected ferrets instead. We also used a dose-response model for SARS-CoV that was developed using an animal (mouse) model because no quantitative dose-response model for SARS-CoV-2 is currently available. A sensitivity analysis applying the upper and lower limits of the 95% confidence intervals for the dose response parameter k resulted in a variation in the estimated infection risk of an approximately twofold (Fig. S1). Second, regarding virus emissions, although we used the saliva volume for talking, coughing, and sneezing, a potential difference due to voice loudness was not considered. We assumed that the aerosolized saliva particles could be classified into small or large particles (< 10 μm and > 10 μm, respectively), where small particles were regarded as sources of inhalation of inspirable particles and large particles as sources of droplet spray (Zhang and Li, 2018). We also assumed that viral loads per volume were uniform, irrespective of particle size. As suggested by the sensitivity analysis (Fig. S1), the viral loads in large particles may play an important role in the overall infection risk. The classification of particles with an aerodynamic diameter threshold of 10 μm, rather than 100 or 150 μm, might have prevented the underestimation of the infection risk; however, the use of more detailed parameter conditions related to the occurrence and behavior of the virus depending on particle sizes may be necessary to further reduce the uncertainty. Third, this study assumed that virus inactivation on fingers and hair could be negligible, which could lead to the overestimation of the infection risk. Fourth, this study might have underestimated the effect of face masks on infection risk reduction: a recent study showed that surgical masks can reduce virus emission and uptake in small particles by 70% and 50%, respectively (Ueki et al., 2020). Fifth, the probability that an accompanier would be looking at an infector as the infector talked/coughed/sneezed toward the accompanier (P a_i_c and P a_i_s) was set at 50%; however, accompaniers may avoid exposure to droplets. Similarly, the direction of talking/coughing/sneezing in the stands were assumed to be 50% for forward direction (P i_f_s) and 25% toward each neighbor on the right and left (P i_a_s); however, in practice, infectors could cough or sneeze toward a direction in which a person is not present. The sensitivity analysis showed the probability that P a_i_c and P a_i_s played significant roles in estimating the infection risk (Fig. S1). Improved awareness of infection prevention may further reduce infection risks. Sixth, the model was not verified based on the observation of infection as a nature of this study. This can improve with further studies on model verification. Epidemiological data on infection cases and environmental virus contamination data are expected to validate and advance the model. Seventh, the environmental exposure model was applied to assess the risk of infection during the mass gathering event in this study. The advantage of this model is that the effect of preventions on infection risk reduction can be evaluated by assessing exposure from each pathway. Conversely, the model is limited in representing the behavior of individuals. In future, the combination of the agent-based model (Saito et al., 2013) with the environmental exposure model is expected to express differences in individuals’ behavior. Although this study aimed to perform a sound and timely solution-focused risk assessment, science and society continue to evolve daily under the ongoing COVID-19 global pandemic. It is advisable to set up models using up-to-date scientific findings aimed at furthering the risk assessment in other mass gathering events.
Despite the uncertainty above, our analysis shows that reducing the threat of COVID-19 to the Games depends on maintaining the prevalence of infectious individuals at a certain level and implementing cooperative preventions by both organizers and spectators. Management of infection risks outside the stadiums and among spectators, staff, and athletes is also essential. The estimates in this study will be useful to facilitate social debates among stakeholders, including the International Olympic Committee, Japanese Olympic Committees, the Japanese Government, Tokyo Metropolitan Government, other local governments, the Tokyo Organising Committee, athletes, and citizens worldwide. Importantly, both policy- and public-oriented actions are necessary to maintain the prevalence of infectious individuals at a certain level and design effective preventive measures toward holding the Tokyo 2020 Olympic and Paralympic Games.
Furthermore, to the best of our knowledge, this is the first study to develop a model that can assess the infection risk among spectators due to exposure pathways at a mass gathering event. This model can be applied in the future to assess the infection risk at such events, including sports (baseball, soccer, etc.) and festivals.
CRediT authorship contribution statement
Michio Murakami: Conceptualization, Data curation, Formal analysis, Methodology, Visualization, Project administration, Writing – original draft. Fuminari Miura: Methodology, Validation, Writing – review & editing. Masaaki Kitajima: Data curation, Methodology, Writing – review & editing. Kenkichi Fujii: Data curation, Methodology, Writing – review & editing. Tetsuo Yasutaka: Data curation, Methodology, Validation, Visualization, Writing – review & editing. Yuichi Iwasaki: Methodology, Validation, Writing – review & editing. Kyoko Ono: Data curation, Methodology, Writing – review & editing. Yuzo Shimazu: Data curation, Writing – review & editing. Sumire Sorano: Data curation, Writing – review & editing. Tomoaki Okuda: Writing – review & editing. Akihiko Ozaki: Data curation, Writing – review & editing. Kotoe Katayama: Writing – review & editing. Yoshitaka Nishikawa: Writing – review & editing. Yurie Kobashi: Writing – review & editing. Toyoaki Sawano: Writing – review & editing. Toshiki Abe: Writing – review & editing. Masaya M. Saito: Writing – review & editing. Masaharu Tsubokura: Data curation, Writing – review & editing. Wataru Naito: Data curation, Writing – review & editing. Seiya Imoto: Project administration, Supervision, Writing – review & editing.
Declaration of Competing Interests
A.O. receives a personal fee from MNES Inc., unrelated to the submitted work. Other authors declare no competing interests. This research project comprises other members from two private companies, Kao Corporation and NVIDIA Corporation, Japan. K.F. is affiliated with Kao Corporation, but no other authors receive any financial support from the Kao Corporation or NVIDIA. Y.I. and W.N. received financial support from the Kao Corporation for their 3-year collaborative research project until March 2020 in context outside the submitted work. T.Y., T.O., and W.N. will receive financial support from the Kao Corporation for their collaborative project from April 2021. No external financial support is used for this article. The findings and conclusions of this article are solely the responsibility of the authors and do not represent the official views of any institution.
Acknowledgments
We thank Editage and Business Quest Limited Company for language editing. We thank Mr. Tsukasa Fujita for his support.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.mran.2021.100162.
Appendix. Supplementary materials
References
- Agarwal V., Sunitha B.K. COVID –19: Current pandemic and its societal impact. Int. J. Adv. Sci. Technol. 2020;29:432–439. [Google Scholar]
- Boyce J.M., Pittet D. Guideline for hand hygiene in health-care settings: Recommendations of the Healthcare Infection Control Practices Advisory Committee and the HICPAC/SHEA/APIC/IDSA Hand Hygiene Task Force. Infect. Control Hosp. Epidemiol. 2002;23:S3–S40. doi: 10.1086/503164. [DOI] [PubMed] [Google Scholar]
- Chen S.C., Liao C.M. Probabilistic indoor transmission modeling for influenza (sub)type viruses. J. Infect. 2010;60:26–35. doi: 10.1016/j.jinf.2009.09.015. [DOI] [PubMed] [Google Scholar]
- Chu D.K., Akl E.A., Duda S., Solo K., Yaacoub S., Schünemann H.J., El-harakeh A., Bognanni A., Lotfi T., Loeb M., Hajizadeh A., Bak A., Izcovich A., Cuello-Garcia C.A., Chen C., Harris D.J., Borowiack E., Chamseddine F., Schünemann F., Morgano G.P., Muti Schünemann G.E.U., Chen G., Zhao H., Neumann I., Chan J., Khabsa J., Hneiny L., Harrison L., Smith M., Rizk N., Giorgi Rossi P., AbiHanna P., El-khoury R., Stalteri R., Baldeh T., Piggott T., Zhang Y., Saad Z., Khamis A., Reinap M. Physical distancing, face masks, and eye protection to prevent person-to-person transmission of SARS-CoV-2 and COVID-19: A systematic review and meta-analysis. Lancet. 2020;395:1973–1987. doi: 10.1016/S0140-6736(20)31142-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Covés-Datson E.M., King S.R., Legendre M., Gupta A., Chan S.M., Gitlin E., Kulkarni V.V., Pantaleón García J., Smee D.F., Lipka E., Evans S.E., Tarbet E.B., Ono A., Markovitz D.M. A molecularly engineered antiviral banana lectin inhibits fusion and is efficacious against influenza virus infection in vivo. Proc. Natl. Acad. Sci. USA. 2020;117:2122–2132. doi: 10.1073/pnas.1915152117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Metz J.A.J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- Enock K.E., Jacobs J. The Olympic and Paralympic Games 2012: Literature review of the logistical planning and operational challenges for public health. Public He. 2008;122:1229–1238. doi: 10.1016/j.puhe.2008.04.016. [DOI] [PubMed] [Google Scholar]
- Fang D., Pan S., Li Z., Yuan T., Jiang B., Gan D., Sheng B., Han J., Wang T., Liu Z. Large-scale public venues as medical emergency sites in disasters: Lessons from COVID-19 and the use of Fangcang shelter hospitals in Wuhan, China. BMJ Glob. Health. 2020;5 doi: 10.1136/bmjgh-2020-002815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finkel A.M. Solution-focused risk assessment”: A proposal for the fusion of environmental analysis and action. Hum. Ecol. Risk Assess. 2011;17:754–787. [Google Scholar]
- Fischer E.P., Fischer M.C., Grass D., Henrion I., Warren W.S., Westman E. Low-cost measurement of facemask efficacy for filtering expelled droplets during speech. Sci. Adv. 2020:eabd3083. doi: 10.1126/sciadv.abd3083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordis L. Fifth Edition. Elsevier Philadephia; United States: 2014. Epidemiology. [Google Scholar]
- He W., Yi G.Y., Zhu Y. Estimation of the basic reproduction number, average incubation time, asymptomatic infection rate, and case fatality rate for COVID-19: Meta-analysis and sensitivity analysis. J. Med. Virol. 2020 doi: 10.1002/jmv.26041. Online ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X., Lau E.H.Y., Wu P., Deng X., Wang J., Hao X., Lau Y.C., Wong J.Y., Guan Y., Tan X., Mo X., Chen Y., Liao B., Chen W., Hu F., Zhang Q., Zhong M., Wu Y., Zhao L., Zhang F., Cowling B.J., Li F., Leung G.M. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020;26:672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Jüni P., Rothenbühler M., Bobos P., Thorpe K.E., Da Costa B.R., Fisman D.N., Slutsky A.S., Gesink D. Impact of climate and public health interventions on the COVID-19 pandemic: A prospective cohort study. CMAJ. 2020;192:E566–E573. doi: 10.1503/cmaj.200920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- James A., Eagle L., Phillips C., Hedges D.S., Bodenhamer C., Brown R., Wheeler J.G., Kirking H. High COVID-19 attack rate among attendees at events at a church - Arkansas, March 2020. MMWR Morb. Mortal. Wkly. Rep. 2020;69:632–635. doi: 10.15585/mmwr.mm6920e2. [DOI] [PubMed] [Google Scholar]
- Japan Sport Council . 2020. About Japan National Stadium.https://www.jpnsport.go.jp/kokuritu/Portals/0/kokuritu/project-summary/kokuritsukyougijounitsuite.pdf Accessed on October 15 2020. (in Japanese) [Google Scholar]
- Japan Sport Council . 2019. News release.https://www.jpnsport.go.jp/corp/Portals/0/News-Release/H31/191129.pdf Accessed on October 15, 2020. (in Japanese) [Google Scholar]
- Japan Sport Council . 2013. Tentative basic design condition of Japan National Stadium.https://www.jpnsport.go.jp/newstadium/Portals/0/yushikishakaigi/20131211_yushikisha4_shiryo1.pdf Accessed on October 15, 2020. (in Japanese) [Google Scholar]
- Japan Sport Council . 2014. Tentative basic design explanations of Japan National Stadium.https://www.jpnsport.go.jp/newstadium/Portals/0/yushikishakaigi/20140528_yushikisha5_shiryo1_2.pdf Accessed on October 15, 2020. (in Japanese) [Google Scholar]
- Johnson D.F., Druce J.D., Birch C., Grayson M.L. A quantitative assessment of the efficacy of surgical and N95 masks to filter influenza virus in patients with acute influenza infection. Clin. Infect. Dis. 2009;49:275–277. doi: 10.1086/600041. [DOI] [PubMed] [Google Scholar]
- Jones R.M. Relative contributions of transmission routes for COVID-19 among healthcare personnel providing patient care. J. Occup. Environ. Hyg. 2020;17:408–415. doi: 10.1080/15459624.2020.1784427. [DOI] [PubMed] [Google Scholar]
- Kampf G., Todt D., Pfaender S., Steinmann E. Persistence of coronaviruses on inanimate surfaces and their inactivation with biocidal agents. J. Hosp. Infect. 2020;104:246–251. doi: 10.1016/j.jhin.2020.01.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.I., Kim S.G., Kim S.M., Kim E.H., Park S.J., Yu K.M., Chang J.H., Kim E.J., Lee S., Casel M.A.B., Um J., Song M.S., Jeong H.W., Lai V.D., Kim Y., Chin B.S., Park J.S., Chung K.H., Foo S.S., Poo H., Mo I.P., Lee O.J., Webby R.J., Jung J.U., Choi Y.K. Infection and rapid transmission of SARS-CoV-2 in ferrets. Cell Host Microbe. 2020;27:704–709. doi: 10.1016/j.chom.2020.03.023. e702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwok Y.L., Gralton J., McLaws M.L. Face touching: a frequent habit that has implications for hand hygiene. Am. J. Infect. Control. 2015;43:112–114. doi: 10.1016/j.ajic.2014.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCloskey B., Zumla A., Lim P.L., Endericks T., Arbon P., Cicero A., Borodina M. A risk-based approach is best for decision making on holding mass gathering events. Lancet. 2020;395:1256–1257. doi: 10.1016/S0140-6736(20)30794-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizukoshi A., Nakama C., Okumura J., Azuma K. Assessing the risk of COVID-19 from multiple pathways of exposure to SARS-CoV-2: Modeling in health-care settings and effectiveness of nonpharmaceutical interventions. Environ. Int. 2021;147 doi: 10.1016/j.envint.2020.106338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakagawa Y., Koshikawa Y., Murakawa S., Takatsu Y. Estimation on the number of transfer passengers and analysis on the fixture usage of toilet in railway stations. Transactions. AIJ. 2008;73:765–772. (in Japanese) [Google Scholar]
- Nicas M., Jones R.M. Relative contributions of four exposure pathways to influenza infection risk. Risk Anal. 2009;29:1292–1303. doi: 10.1111/j.1539-6924.2009.01253.x. [DOI] [PubMed] [Google Scholar]
- Nicas M., Sun G. An integrated model of infection risk in a health-care environment. Risk Anal. 2006;26:1085–1096. doi: 10.1111/j.1539-6924.2006.00802.x. [DOI] [PubMed] [Google Scholar]
- R Development Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2020. R: A language and environment for statistical computing.http://www.R-project.org Accessed on August 15 2020. [Google Scholar]
- Rengasamy S., Miller A., Eimer B.C., Shaffer R.E. Filtration performance of FDA-cleared surgical masks. J Int Soc Respir Prot. 2009;26:54–70. [PMC free article] [PubMed] [Google Scholar]
- Roda W.C., Varughese M.B., Han D., Li M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect. Dis. Modelling. 2020;5:271–281. doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito M.M., Imoto S., Yamaguchi R., Tsubokura M., Kami M., Nakada H., Sato H., Miyano S., Higuchi T. Enhancement of collective immunity in Tokyo Metropolitan area by selective vaccination against an emerging influenza pandemic. PLOS ONE. 2013;8:e72866. doi: 10.1371/journal.pone.0072866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawano T., Kotera Y., Ozaki A., Murayama A., Tanimoto T., Sah R., Wang J. Underestimation of COVID-19 cases in Japan: an analysis of RT-PCR testing for COVID-19 among 47 prefectures in Japan. QJM-Int. J. Med. 2020;113:551–555. doi: 10.1093/qjmed/hcaa209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadnytskyi V., Bax C.E., Bax A., Anfinrud P. The airborne lifetime of small speech droplets and their potential importance in SARS-CoV-2 transmission. P. Natl. Acad. Sci. USA. 2020;117:11875. doi: 10.1073/pnas.2006874117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumino M., Yamazaki T., Takeshita S., Shiokawa K. How do sports viewers watch a game?: A trial mainly on conversation analysis. J. Jpn. Soc. Sports Indust. 2010;20:243–252. (in Japanese) [Google Scholar]
- Tam J.S., Barbeschi M., Shapovalova N., Briand S., Memish Z.A., Kieny M.P. Research agenda for mass gatherings: A call to action. Lancet Infect. Dis. 2012;12:231–239. doi: 10.1016/S1473-3099(11)70353-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- To K.K., Tsang O.T., Chik-Yan Yip C., Chan K.H., Wu T.C., Chan J.M.C., Leung W.S., Chik T.S., Choi C.Y., Kandamby D.H., Lung D.C., Tam A.R., Poon R.W., Fung A.Y., Hung I.F., Cheng V.C., Chan J.F., Yuen K.Y. Consistent detection of 2019 novel coronavirus in saliva. Clin. Infect. Dis. 2020;71:841–843. doi: 10.1093/cid/ciaa149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokyo Metropolis, 2021. Updates on COVID-19 in Tokyo. https://stopcovid19.metro.tokyo.lg.jp/en/. Accessed on February 22, 2021.
- Ueki H., Furusawa Y., Iwatsuki-Horimoto K., Imai M., Kabata H., Nishimura H., Kawaoka Y. Effectiveness of face masks in preventing airborne transmission of SARS-CoV-2. mSphere. 2020;5:e00637. doi: 10.1128/mSphere.00637-20. -00620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Doremalen N., Bushmaker T., Morris D.H., Holbrook M.G., Gamble A., Williamson B.N., Tamin A., Harcourt J.L., Thornburg N.J., Gerber S.I., Lloyd-Smith J.O., de Wit E., Munster V.J. Aerosol and Surface Stability of SARS-CoV-2 as Compared with SARS-CoV-1. N. Engl. J. Med. 2020;382:1564–1567. doi: 10.1056/NEJMc2004973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker A., Houwaart T., Wienemann T., Vasconcelos M.K., Strelow D., Senff T., Hülse L., Adams O., Andree M., Hauka S., Feldt T., Jensen B.-E., Keitel V., Kindgen-Milles D., Timm J., Pfeffer K., Dilthey A.T. Genetic structure of SARS-CoV-2 reflects clonal superspreading and multiple independent introduction events, North-Rhine Westphalia, Germany, February and March 2020. Eurosurveillance. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.22.2000746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watanabe T., Bartrand T.A., Weir M.H., Omura T., Haas C.N. Development of a dose-response model for SARS coronavirus. Risk Anal. 2010;30:1129–1138. doi: 10.1111/j.1539-6924.2010.01427.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization . 2021. WHO Coronavirus Disease (COVID-19) Dashboard.https://covid19.who.int/ Accessed on February 22, 2021. [PubMed] [Google Scholar]
- Yousaf N., Monteiro W., Matos S., Birring S.S., Pavord I.D. Cough frequency in health and disease. Eur. Respir. J. 2013;41:241–243. doi: 10.1183/09031936.00089312. [DOI] [PubMed] [Google Scholar]
- Zhang N., Li Y. Transmission of influenza A in a student office based on realistic person-to-person contact and surface touch behaviour. Int. J. Environ. Res. Public Health. 2018;15:1699. doi: 10.3390/ijerph15081699. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.